Quelles méthodes de réglage des séquences connaissez-vous. Séquences de nombres

20.09.2019

Exemples de séquence

Exemples de séquences infiniment croissantes

Considérons une séquence. Le terme général de cette suite est . Écrivons les premiers termes :
.
On peut voir que lorsque le nombre n augmente, les éléments augmentent indéfiniment vers valeurs positives. On peut dire que cette suite tend vers : à .

Considérons maintenant une séquence avec un terme commun . Voici quelques-uns de ses premiers membres :
.
Lorsque le nombre n augmente, les éléments de cette séquence augmentent indéfiniment dans valeur absolue, mais n'ont pas de signe constant. C'est-à-dire que cette séquence tend vers : à .

Exemples de suites convergeant vers un nombre fini

Considérons une séquence. Son membre commun Les premiers termes sont les suivants :
.
On peut voir que lorsque le nombre n augmente, les éléments de cette suite se rapprochent de leur valeur limite a = 0 : à . Ainsi, chaque terme suivant est plus proche de zéro que le précédent. Dans un sens, on peut supposer qu'il existe une valeur approximative pour le nombre a = 0 avec une erreur. Il est clair que lorsque n croît, cette erreur tend vers zéro, c'est-à-dire qu'en choisissant n, l'erreur peut être rendue arbitrairement petite. De plus, pour toute erreur donnée ε > 0 vous pouvez spécifier un nombre N tel que pour tous les éléments dont le nombre est supérieur à N : , l'écart du nombre par rapport à Valeur limite a ne dépassera pas l'erreur ε : .

Ensuite, considérez la séquence. Son membre commun Voici quelques-uns de ses premiers membres :
.
Dans cette séquence, les termes pairs sont nuls. Les membres avec un n impair sont . Par conséquent, à mesure que n grandit, leurs valeurs se rapprochent de la valeur limite a = 0 . Cela découle également du fait que
.
Comme dans l'exemple précédent, nous pouvons spécifier une erreur arbitrairement petite ε > 0 , pour lequel il est possible de trouver un nombre N tel que les éléments de nombre supérieur à N s'écartent de la valeur limite a = 0 par une valeur ne dépassant pas l'erreur spécifiée. Par conséquent, cette suite converge vers la valeur a = 0 : à .

Exemples de séquences divergentes

Considérons une séquence avec le terme commun suivant :

Voici ses premiers membres :

.
On peut voir que les termes avec des nombres pairs :
,
converger vers la valeur a 1 = 0 . Membres avec des nombres impairs :
,
converger vers la valeur a 2 = 2 . La séquence elle-même, à mesure que n croît, ne converge vers aucune valeur.

Séquence avec des termes distribués dans l'intervalle (0;1)

Considérons maintenant une séquence plus intéressante. Prenez un segment sur la droite numérique. Divisons-le en deux. Nous obtenons deux segments. Laisser
.
Chacun des segments est à nouveau divisé en deux. Nous obtenons quatre segments. Laisser
.
Divisez à nouveau chaque segment en deux. Prenons

.
Etc.

On obtient ainsi une suite dont les éléments sont répartis dans un intervalle ouvert (0; 1) . Quel que soit le point que nous prenons de l'intervalle fermé , on peut toujours trouver des membres de la séquence qui sont arbitrairement proches de ce point, ou qui coïncident avec lui.

Ensuite, à partir de la séquence d'origine, on peut distinguer une sous-séquence qui convergera vers un point arbitraire de l'intervalle . Autrement dit, à mesure que le nombre n augmente, les membres de la sous-séquence se rapprochent de plus en plus du point présélectionné.

Par exemple, pour le point a = 0 vous pouvez choisir la sous-séquence suivante :
.
= 0 .

Pour le point a = 1 choisissez la sous-séquence suivante :
.
Les membres de cette sous-suite convergent vers la valeur a = 1 .

Puisqu'il existe des sous-suites qui convergent vers différentes significations, alors la séquence originale elle-même ne converge vers aucun nombre.

Séquence contenant tous les nombres rationnels

Construisons maintenant une séquence qui contient tous les nombres rationnels. De plus, chaque nombre rationnel sera inclus dans une telle séquence un nombre infini de fois.

Le nombre rationnel r peut être représenté comme suit :
,
où est un entier ; - Naturel.
Nous devons attribuer à chaque nombre naturel n une paire de nombres p et q afin que toute paire de p et q soit incluse dans notre séquence.

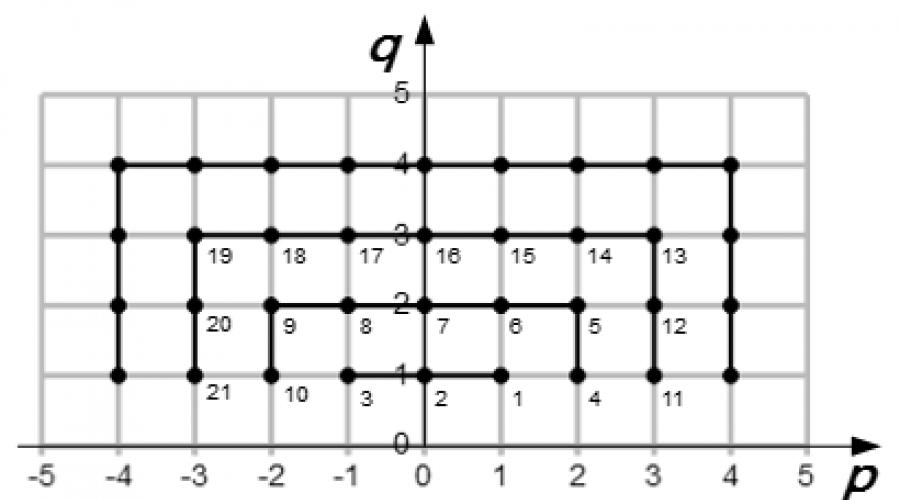
Pour ce faire, dessinez les axes p et q sur le plan. Nous traçons des lignes de grille à travers des valeurs entières p et q . Alors chaque nœud de ce maillage avec correspondra à nombre rationnel. L'ensemble des nombres rationnels sera représenté par un ensemble de nœuds. Nous devons trouver un moyen de numéroter tous les nœuds afin de ne manquer aucun nœud. Ceci est facile à faire si l'on numérote les nœuds selon les carrés dont les centres sont situés au point (0; 0) (voir l'image). Dans ce cas, les parties inférieures des carrés avec q < 1 nous n'avons pas besoin. Par conséquent, ils ne sont pas représentés sur la figure.

Ainsi, pour le côté supérieur du premier carré, nous avons :
.
Ensuite, nous numérotons la partie supérieure du carré suivant :

.
Nous numérotons la partie supérieure du carré suivant :

.
Etc.

De cette façon, nous obtenons une séquence contenant tous les nombres rationnels. On peut voir que tout nombre rationnel apparaît dans cette séquence un nombre infini de fois. En effet, avec le nœud , cette séquence comprendra également des nœuds , où est un nombre naturel. Mais tous ces nœuds correspondent au même nombre rationnel.

Ensuite, à partir de la séquence que nous avons construite, nous pouvons sélectionner une sous-séquence (ayant un nombre infini d'éléments), dont tous les éléments sont égaux à un nombre rationnel prédéterminé. Puisque la séquence que nous avons construite a des sous-séquences convergeant vers des nombres différents, la séquence ne converge vers aucun nombre.

Conclusion

Nous avons donné ici une définition précise de la suite numérique. Nous avons également abordé la question de sa convergence, basée sur des idées intuitives. La définition exacte de la convergence est discutée sur la page Détermination de la limite d'une séquence. Les propriétés et théorèmes associés sont décrits sur la page

2. Déterminez opération arithmétique, à l'aide duquel la moyenne a été obtenue à partir des deux nombres extrêmes, et au lieu du signe *, insérez le nombre manquant : ,3104.62.51043.60.94

3. Les élèves ont résolu la tâche dans laquelle il est demandé de trouver les nombres manquants. Ils ont obtenu des réponses différentes. Trouvez les règles selon lesquelles les gars ont rempli les cellules. Tâche Réponse 1 Réponse

Définition d'une séquence numérique On dit qu'une séquence numérique est donnée si, selon une loi, un certain nombre (un membre de la séquence) est attribué de manière unique à tout nombre naturel (numéro de lieu). À vue générale la correspondance indiquée peut être représentée comme suit : y 1, y 2, y 3, y 4, y 5, …, y n, … … n … Le nombre n est le n-ième membre de la séquence. La séquence entière est généralement notée (y n).

Manière analytique de spécifier des suites numériques Une suite est spécifiée analytiquement si la formule du nième membre est spécifiée. Par exemple, 1) y n= n 2 - affectation analytique de la séquence 1, 4, 9, 16, ... 2) y n= С - séquence constante (stationnaire) 2) y n= 2 n - affectation analytique de la séquence 2 , 4, 8, 16, … Résoudre 585

Méthode récurrente de spécification des suites numériques La méthode récurrente de spécification d'une suite est qu'elles indiquent une règle qui permet de calculer le nième terme si ses membres précédents sont connus 1) une progression arithmétique est donnée par des relations récursives ) progression géométrique– b 1 \u003d b, b n + 1 \u003d b n * q

Ancrage 591, 592 (a, b) 594, – 614 (a)

Borne supérieure Une suite (y n) est dite bornée par le haut si tous ses membres sont au plus un certain nombre. En d'autres termes, une suite (y n) est bornée par le haut s'il existe un nombre M tel que pour tout n l'inégalité y n M soit vérifiée. M est la borne supérieure de la suite Par exemple, -1, -4, -9, -16, …, -n 2, …

Bornée par le bas Une suite (y n) est dite bornée par le bas si tous ses membres sont au moins un certain nombre. En d'autres termes, la suite (y n) est bornée par le haut s'il existe un nombre m tel que pour tout n l'inégalité y n m soit vérifiée. m est la borne inférieure de la suite Par exemple, 1, 4, 9, 16, …, n 2, …

Limitation d'une séquence Une séquence (y n) est dite bornée s'il est possible de spécifier deux nombres A et B entre lesquels se trouvent tous les membres de la séquence. L'inégalité Ay n B A est la borne inférieure, B est la borne supérieure Par exemple, 1 est la borne supérieure, 0 est la borne inférieure

Suite décroissante Une suite est dite décroissante si chaque membre est inférieur au précédent : y 1 > y 2 > y 3 > y 4 > y 5 > ... > y n > ... Par exemple, y 2 > y 3 > y 4 > y 5 > … > y n > … Par exemple, « > y 2 > y 3 > y 4 > y 5 > … > y n > … Par exemple », > y 2 > y 3 > y 4 > y 5 > … > y n > … Par exemple," title="(!LANG:Séquence décroissante Une séquence est dite décroissante si chacun de ses membres est inférieur au précédent : y 1 > y 2 > y 3 > y 4 > y 5 > … > y n > … Par exemple,"> title="Suite décroissante Une suite est dite décroissante si chaque membre est inférieur au précédent : y 1 > y 2 > y 3 > y 4 > y 5 > ... > y n > ... Par exemple,"> !} 23

Travail de vérification Option 1Option 2 1. La suite numérique est donnée par la formule a) Calcule les quatre premiers termes de cette suite b) Le nombre fait-il partie de la suite ? b) Le nombre 12,25 fait-il partie de la séquence ? 2. Formuler le ème terme de la suite 2, 5, 10, 17, 26,…1, 2, 4, 8, 16,…

Une séquence numérique est un cas particulier de fonction numérique, de sorte qu'un certain nombre de propriétés de fonctions sont également prises en compte pour les séquences.

1. Définition . Sous-séquence ( oui n} est dit croissant si chacun de ses termes (sauf le premier) est plus grand que le précédent :

y 1 < y 2 < y 3 < … < oui n < oui n+1 < ….

2. Définition.Séquence ( oui n} est dit décroissant si chacun de ses termes (sauf le premier) est inférieur au précédent :

y 1 > y 2 > y 3 > … > oui n> oui n+1 > … .

3. Les séquences croissantes et décroissantes sont unies par un terme commun - les séquences monotones.

Par exemple: y 1 = 1; oui n= n 2… est une suite croissante. y 1 = 1 ; est une suite descendante. y 1 = 1 ; – cette suite n'est pas non croissante non décroissante.

4. Définition. Une suite est dite périodique s'il existe un entier naturel T tel que, à partir d'un certain n, l'égalité yn = yn+T soit vérifiée. Le nombre T est appelé la longueur de la période.

5. Une séquence est dite bornée par le bas si tous ses membres sont au moins un certain nombre.

6. Une suite est dite bornée par le haut si tous ses membres sont au plus un certain nombre.

7. Une suite est dite bornée si elle est bornée à la fois au-dessus et au-dessous, c'est-à-dire il existe un nombre positif tel que tous les termes de la suite donnée ne dépassent pas ce nombre en valeur absolue. (Mais être limité des deux côtés ne signifie pas nécessairement qu'il est fini.)

8. Une séquence ne peut avoir qu'une seule limite.

9. Toute suite non décroissante bornée au-dessus a une limite (lim).

10. Toute suite non croissante bornée ci-dessous a une limite.

La limite de la séquence est un point (nombre) au voisinage duquel se situent la majorité des membres de la séquence, ils se rapprochent de cette limite, mais ne l'atteignent pas.

Géométrique et progression arithmétique sont des cas particuliers de la suite.

Méthodes de séquençage :

Les séquences peuvent être spécifiées de différentes manières, parmi lesquelles trois sont particulièrement importantes : analytique, descriptive et récurrente.

1. La suite est donnée analytiquement si la formule de son nième membre est donnée :

Exemple. yn \u003d 2n - 1 - une suite de nombres impairs : 1, 3, 5, 7, 9, ...

2. Une manière descriptive de définir une séquence numérique consiste à expliquer à partir de quels éléments la séquence est construite.

Exemple 1. "Tous les membres de la séquence sont égaux à 1." Cela signifie que nous parlons d'une suite stationnaire 1, 1, 1, …, 1, ….

Exemple 2. "La séquence se compose de tous nombres premiers Dans l'ordre croissant". Ainsi, la séquence 2, 3, 5, 7, 11, … est donnée. Avec cette méthode de spécification de la séquence dans cet exemple il est difficile de répondre à quoi, disons, le 1000e élément de la séquence est égal.

3. La façon récurrente de spécifier une suite est d'indiquer une règle qui permet de calculer nième terme séquence si ses membres précédents sont connus. Le nom méthode récurrente vient du mot latin recurrere - retourner. Le plus souvent, dans de tels cas, une formule est indiquée qui permet d'exprimer le nième membre de la séquence en fonction des précédents, et 1 à 2 membres initiaux de la séquence sont spécifiés.

Exemple 1. y1 = 3 ; yn = yn–1 + 4 si n = 2, 3, 4,….

Ici y1 = 3 ; y2 = 3 + 4 = 7 ; y3 = 7 + 4 = 11 ; ….

On voit que la séquence obtenue dans cet exemple peut également être spécifiée analytiquement : yn = 4n – 1.

Exemple 2 y 1 = 1; y 2 = 1; oui n = oui n–2 + oui n-1 si n = 3, 4,….

Ici: y 1 = 1; y 2 = 1; y 3 = 1 + 1 = 2; y 4 = 1 + 2 = 3; y 5 = 2 + 3 = 5; y 6 = 3 + 5 = 8;

La séquence composée dans cet exemple est spécialement étudiée en mathématiques car elle possède un certain nombre de propriétés et d'applications intéressantes. C'est ce qu'on appelle la suite de Fibonacci - du nom du mathématicien italien du XIIIe siècle. Définir la suite de Fibonacci récursivement est très facile, mais analytiquement c'est très difficile. n-ème nombre de Fibonacci est exprimé par son numéro de série la formule suivante.

A première vue, la formule de nème nombre de Fibonacci semble invraisemblable, puisque la formule qui spécifie la suite des nombres naturels contient à elle seule racines carrées, mais vous pouvez vérifier "manuellement" la validité de cette formule pour les premières n.

Histoire de Fibonacci :

Fibonacci (Léonard de Pise), ch. 1175–1250

mathématicien italien. Né à Pise, est devenu le premier grand mathématicien d'Europe à la fin du Moyen Age. C'est le besoin pratique d'établir des contacts d'affaires qui l'a conduit aux mathématiques. Il a publié ses livres sur l'arithmétique, l'algèbre et d'autres disciplines mathématiques. Des mathématiciens musulmans, il a appris le système de nombres inventé en Inde et déjà adopté dans le monde arabe, et a été convaincu de sa supériorité (ces nombres étaient les précurseurs des chiffres arabes modernes).

Léonard de Pise, dit Fibonacci, fut le premier des grands mathématiciens européens de la fin du Moyen Âge. Né à Pise dans une riche famille de marchands, il est entré en mathématiques par un besoin purement pratique d'établir des contacts commerciaux. Dans sa jeunesse, Leonardo a beaucoup voyagé, accompagnant son père lors de voyages d'affaires. Par exemple, nous connaissons son long séjour à Byzance et en Sicile. Au cours de ces voyages, il interagissait beaucoup avec les scientifiques locaux.

La séquence de nombres qui porte aujourd'hui son nom est née du problème des lapins que Fibonacci a décrit dans son Liber abacci, écrit en 1202 :

Un homme a mis une paire de lapins dans un enclos, entouré de tous côtés par un mur. Combien de couples de lapins ce couple peut-il donner naissance par an, si l'on sait que chaque mois, à partir du second, chaque couple de lapins produit un couple ?

Vous pouvez vous assurer que le nombre de couples dans chacun des douze prochains mois du mois sera respectivement de 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...

En d'autres termes, le nombre de paires de lapins crée une série dont chaque terme est la somme des deux précédents. Elle est connue sous le nom de série de Fibonacci et les nombres eux-mêmes sont les nombres de Fibonacci. Il s'avère que cette séquence possède de nombreuses propriétés mathématiquement intéressantes. Voici un exemple : vous pouvez diviser une ligne en deux segments de sorte que le rapport entre le segment le plus grand et le plus petit soit proportionnel au rapport entre la ligne entière et le segment le plus grand. Ce facteur de proportionnalité, approximativement égal à 1,618, est connu sous le nom de nombre d'or. À la Renaissance, on croyait que cette proportion, observée dans les structures architecturales, était la plus agréable à l'œil. Si vous prenez des paires de Fibonacci consécutives et que vous divisez le plus grand nombre de chaque paire par le plus petit, votre résultat se rapprochera progressivement du nombre d'or.

Depuis que Fibonacci a découvert sa séquence, même des phénomènes naturels ont été découverts dans lesquels cette séquence semble jouer un rôle important. L'un d'eux est la phyllotaxie (disposition des feuilles) - la règle selon laquelle, par exemple, les graines sont situées dans une inflorescence de tournesol. Les graines de tournesol sont disposées en deux spirales. Les nombres indiquant le nombre de graines dans chacune des spirales sont membres d'une séquence mathématique étonnante. Les graines sont disposées en deux rangées de spirales, dont l'une va dans le sens des aiguilles d'une montre, l'autre en sens inverse. Et quel est le nombre de graines dans chaque cas ? 34 et 55.

Tache 1:

Écris les cinq premiers termes de la suite.

1. un n \u003d 2 n + 1/2 n

et n \u003d 2 n + 1/2 n

Tâche numéro 2 :

Écrivez la formule du terme commun d'une suite de nombres naturels multiples de 3.

Réponse : 0,3,6,9,12,15,.... 3n, et n = 3n

Tâche numéro 3 :

Écrivez la formule du terme commun d'une suite de nombres naturels qui, lorsqu'ils sont divisés par 4, ont un reste de 1.

Réponse : 5,9,13,17,21....... 4 n +1 et n = 4n+1

N° 19. Fonction.

La fonction (affichage, opérateur, transformation) est un concept mathématique qui reflète la relation entre les éléments des ensembles. On peut dire qu'une fonction est une « loi » selon laquelle chaque élément d'un ensemble (appelé domaine de définition) se voit attribuer un élément d'un autre ensemble (appelé domaine de valeurs).

Une fonction est une dépendance d'une variable D'un autre. En d'autres termes, la relation entre les quantités.

Le concept mathématique d'une fonction exprime une idée intuitive de la façon dont une quantité détermine complètement la valeur d'une autre quantité. Ainsi, la valeur de la variable x détermine de manière unique la valeur de l'expression, et la valeur du mois détermine de manière unique la valeur du mois qui la suit, et toute personne peut être comparée à une autre personne - son père. De même, un algorithme préconçu, étant donné des données d'entrée variables, produit certaines données de sortie.

Souvent, le terme "fonction" fait référence à une fonction numérique ; c'est-à-dire une fonction qui met des nombres en correspondance avec d'autres. Ces fonctions sont commodément représentées sur les figures sous forme de graphiques.

Une autre définition peut être donnée. Une fonction est une fonction spécifique action sur une variable.

Cela signifie que nous prenons la valeur , faisons une action avec elle (par exemple, nous la mettons au carré ou calculons son logarithme) - et nous obtenons la valeur .

Donnons une autre définition d'une fonction - celle que l'on trouve le plus souvent dans les manuels.

Une fonction est une correspondance entre deux ensembles, chaque élément du premier ensemble correspondant à un et un seul élément du second ensemble.

Par exemple, la fonction affecte à chaque nombre réel un nombre deux fois plus grand que .

L'ensemble des éléments d'un certain F. substitué à x est appelé son domaine de définition, et l'ensemble des éléments y d'un certain F. est appelé sa plage de valeurs.

Historique du terme :

Le terme "fonction" (dans un sens un peu plus étroit) a été utilisé pour la première fois par Leibniz (1692). À son tour, Johann Bernoulli, dans une lettre au même Leibniz, a utilisé ce terme dans un sens plus proche du sens moderne. Initialement, le concept de fonction était indiscernable du concept de représentation analytique. Par la suite, la définition de la fonction donnée par Euler (1751) est apparue, puis - par Lacroix (1806) - presque en forme moderne. Pour terminer, définition générale fonctions (en forme moderne, mais pour fonctions numériques) a été donnée par Lobachevsky (1834) et Dirichlet (1837). À fin XIX siècle, le concept de fonction a dépassé le cadre des systèmes numériques. Les fonctions vectorielles ont été les premières à le faire, Frege a rapidement introduit les fonctions logiques (1879), et après l'avènement de la théorie des ensembles, Dedekind (1887) et Peano (1911) ont formulé la définition universelle moderne.

N° 20. Façons de définir une fonction.

Il existe 4 façons de définir une fonction :

1. tabulaire Assez commun, est de dresser une table d'individu

valeurs d'argument et leurs valeurs de fonction correspondantes. Cette méthode de définition d'une fonction est utilisée lorsque le domaine de la fonction est un ensemble fini discret.

C'est pratique lorsque f est un ensemble fini, mais lorsque f est infini, seules les paires sélectionnées (x, y) sont indiquées.

Avec la méthode tabulaire de spécification d'une fonction, il est possible de calculer approximativement les valeurs de la fonction qui ne sont pas contenues dans le tableau, correspondant aux valeurs intermédiaires de l'argument. Pour ce faire, utilisez la méthode d'interpolation.

Avantages: précision, rapidité, facile à trouver dans le tableau des valeurs Valeur souhaitée les fonctions. Les avantages de la manière tabulaire de spécifier une fonction sont qu'elle permet de déterminer certains valeurs spécifiques immédiatement, sans mesures ni calculs supplémentaires.

Défauts: incomplétude, manque de clarté. Dans certains cas, le tableau ne définit pas complètement la fonction, mais seulement pour certaines valeurs de l'argument et ne fournit pas de représentation visuelle de la nature du changement de la fonction en fonction du changement de l'argument.

2. analytique(formules). Le plus souvent, une loi établissant un lien entre

argument et fonction, est spécifié au moyen de formules. Cette façon de définir une fonction est appelée analytique. C'est le plus important pour MA (analyse mathématique), puisque les méthodes de MA (calcul différentiel, intégral) suggèrent ce mode de réglage. La même fonction peut être donnée diverses formules: y=∣sin( X)∣y=√1−cos2( X) Parfois, dans différentes parties de leurs domaines, la fonction définie peut être donnée par différentes formules F(X)={F 1(X),X∈ré 1 fn(X),X∈Dn ∪nk=1Dk=ré(F). Souvent, avec cette méthode de définition d'une fonction, le domaine de définition n'est pas indiqué, alors le domaine de définition est compris comme le domaine naturel de définition, c'est-à-dire l'ensemble de toutes les valeurs x pour lesquelles la fonction prend une valeur réelle.

Cette méthode permet pour chaque valeur numérique de l'argument x de trouver exactement ou avec une certaine précision la valeur numérique correspondante de la fonction y.

Un cas particulier de la manière analytique de définir une fonction est de définir une fonction par une équation de la forme F(x,y)=0 (1) Si cette équation a la propriété que ∀ X∈D correspond uniquement y, tel que F(X,y)=0, alors on dit que l'équation (1) sur D définit implicitement une fonction. Un autre cas particulier de définition d'une fonction est paramétrique, avec chaque couple ( X,y)∈F défini à l'aide d'une paire de fonctions X=ϕ( t),y=ψ( t) où t∈M.

SÉQUENCES NUMÉRIQUES VI

§ 127. Séquences de nombres et comment les régler. Suites finies et infinies.

Considérez les trois ensembles de nombres suivants :

Il est naturel de considérer que chaque numéro de l'une quelconque de ces collections est pourvu d'un numéro en fonction de la place qu'il occupe dans cette collection. Par exemple, dans le deuxième ensemble, le numéro 1 a le numéro 1, le numéro 1/2 a le numéro 2, le numéro 1/3 a le numéro 3, et ainsi de suite.

Au contraire, quel que soit le numéro que nous indiquons, dans chacune de ces collections il y a un numéro muni de ce numéro. Par exemple, le numéro 2 dans la première séquence a le numéro 2, dans la seconde - le nombre - 1/2, dans la troisième - le nombre sin 2. De même, le nombre 10 a : dans la première séquence - le nombre 10, dans le second - le nombre - 1/10, dans le troisième - le nombre sin 10, etc. Ainsi, dans les ensembles ci-dessus, chaque nombre a un nombre bien défini et est entièrement déterminé par ce nombre.

Une collection de nombres, chacun avec son propre numéro P (P = 1, 2, 3, ...) s'appelle une suite de nombres.

Les numéros individuels d'une séquence sont appelés ses membres et sont généralement désignés comme suit : le premier membre un 1 seconde un 2 , .... P ème membre un n etc. La séquence numérique entière est notée

un 1 , un 2 , un 3 , ... , un n, ... ou ( un n }.

Spécifiez une séquence numérique - cela signifie indiquer comment l'un ou l'autre de ses membres est trouvé, si le numéro de la place occupée par celui-ci est connu. Il existe de nombreuses façons de spécifier des séquences numériques. Ci-dessous, nous nous concentrerons sur certains d'entre eux.

1. Habituellement, une séquence numérique est spécifiée à l'aide d'une formule qui vous permet de déterminer ce membre par le numéro d'un membre de la séquence. Par exemple, si l'on sait que pour tout P

un n = n 2 ,

un 1 = 1, un 2 = 4, un 3 = 9

etc. Quand un n= péché π / 2 P nous aurons: un 1 = péché π / 2 = 1, un 2 = péché π = 0, un 3 = péché 3 π / 2 = - 1, un 4 = péché 2 π = 0 etc...

Une formule qui vous permet de trouver n'importe quel membre d'une suite numérique par son numéro s'appelle la formule d'un membre commun d'une suite numérique.

2. Il y a des cas où une séquence est spécifiée en décrivant ses membres. Par exemple, disons que la suite

1,4; 1,41; 1,414; 1,4142; ...

est composé de valeurs approchées de √2 avec un déficit d'une précision de 0,1 ; 0,01 ; 0,001 ; 0,0001 etc. B cas similaires il est parfois impossible d'établir le terme général de formule ; néanmoins, la séquence s'avère complètement déterminée.

3. Parfois, les premiers membres de la séquence sont indiqués, et tous les autres membres sont déterminés par ces membres donnés selon une règle ou une autre. Laissez, par exemple,

un 1 = 1, un 2 = 1,

et chaque terme suivant est défini comme la somme des deux précédents. Autrement dit, pour tout P > 3

un n = un n- 1 + un n- 2

C'est ainsi qu'est déterminée la suite numérique 1, 1, 2, 3, 5, 8, 13, 21, 34, .... dont les membres sont appelés "nombres de Fibonacci" [d'après le mathématicien italien Léonard de Pise ( vers 1170-1250), qui s'appelait aussi Fibonacci, ce qui signifie "fils de Bonaccio"]. Ils possèdent de nombreuses propriétés intéressantes, dont l'examen dépasse cependant le cadre de notre programme.

Une séquence peut contenir un nombre fini ou infini de membres.

Une séquence constituée d'un nombre fini de membres est appelée une séquence finie, et une séquence constituée d'un nombre infini de membres est appelée une séquence infinie.

Par exemple, la séquence de tous les nombres positifs pairs 2, 4, 6, 8, 10, 12, ... est infinie, tandis que la séquence des nombres positifs pairs à un chiffre 2, 4, 6, 8 est finie.

Des exercices

932. Ecrivez les 4 premiers nombres de la suite avec un membre commun :

933. Trouvez la formule du terme général pour chacune des séquences données :

a) 1, 3, 5, 7, 9, ... ; . e) TG 45°, TG 22°30", TG 11°15", ... ;

b) 2, 4, 6, 8, 10, ... ; e) 1, - 1/2, 1/4, - 1/8, 1/16, ...;

c) 3, -3, 3, -3, 3, ...; g) 1, 9, 25, 49, 81.....

d) 1/3, 1/9, 1/27, 1/81, .... ;

934. La suite de toutes les racines positives de l'équation est-elle finie ?

un péché x = x - une; b) tg X = X ; c) le péché x = hache + b ?

Leçon #32 Date ____________

Algèbre

Classe : 9 "B"

Sujet : "Séquence numérique et façons de la définir."

Le but de la leçon : les élèves doivent savoir ce qu'est une suite de nombres ; façons de définir une séquence numérique ; pouvoir distinguer différentes manières affectations de suites numériques.

Matériel didactique : polycopiés, notes de référence.

Aides techniques à la formation : présentation sur le thème "Suites numériques".

Pendant les cours.

1. Moment organisationnel.

2. Fixer les objectifs de la leçon.

Aujourd'hui, dans la leçon, vous apprendrez :

Qu'est-ce qu'une séquence ?

Quels types de séquences existe-t-il ?

Comment la séquence de nombres est-elle spécifiée ?

Apprenez à écrire une séquence à l'aide d'une formule et de ses nombreux éléments.

Apprenez à trouver les membres d'une séquence.

3. Travail sur le matériel étudié.

3.1. Phase préparatoire.

Les gars, testons vos compétences logiques. Je cite quelques mots, et vous devriez continuer :

-Lundi Mardi,…..

- Janvier février mars…;

- Glebova L, Ganovichev E, Dryakhlov V, Ibraeva G, ... .. (liste de classe);

–10,11,12,…99;

D'après les réponses des gars, il est conclu que les tâches ci-dessus sont des séquences, c'est-à-dire une sorte de série ordonnée de nombres ou de concepts, lorsque chaque nombre ou concept est strictement à sa place, et si les membres sont échangés, la séquence sera violé (mardi, jeudi, lundi n'est qu'une liste des jours de la semaine). Ainsi, le sujet de la leçon est une séquence numérique.

3.1. Explication du nouveau matériel. (Matériel de démonstration)

Analysez les réponses des élèves, définissez la séquence de nombres et montrez comment définir des séquences de nombres.

(Travailler avec le manuel pp. 66 - 67)

Définition 1. La fonction y = f(x), xN est appelée fonction d'un argument naturel ou d'une suite numérique et notée : y = f(n) ou y 1 , y 2 , y 3 , ..., y n , ... ou (o n).

Dans ce cas, la variable indépendante est un nombre naturel.

Le plus souvent, les séquences seront notées comme suit : ( un n), (b n), (Avec n) etc.

Définition 2. Membres de la séquence.

Les éléments qui forment une séquence sont appelés membres de la séquence.

Nouveaux concepts : le membre précédent et le membre suivant de la séquence,

un 1 …un P (1er et nième membre de la séquence)

Méthodes de définition d'une séquence numérique.

manière analytique.

N'importe quel nième élément les séquences peuvent être déterminées à l'aide d'une formule. (démo)

Exemples d'analyse

Exemple 1 La suite des nombres pairs : y = 2n.

Exemple 2 La suite du carré des nombres naturels : y = n 2 ;

1, 4, 9, 16, 25, ..., n 2 , ... .

Exemple 3 Séquence stationnaire : y = C ;

C, C, C, ..., C, ... .

Cas particulier : y = 5 ; 5, 5, 5, ..., 5, ... .

Exemple 4. Séquence y = 2 n ;

2, 2 2 , 2 3 , 2 4 , ..., 2 n , ... .

manière verbale.

Les règles de définition de la séquence sont décrites en mots, sans spécifier de formules ou lorsqu'il n'y a pas de motifs entre les éléments de la séquence.

Exemple 1. Approximations de nombresπ.

Exemple 2 Séquence de nombres premiers : 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, .... .

Exemple 3 Suite de nombres divisibles par 5.

Exemple 2 Ensemble aléatoire de nombres : 1, 4, 12, 25, 26, 33, 39, ... .

Exemple 3 La séquence des nombres pairs 2, 4, 6, 8, 10, 12, 14, 16, ... .

manière récursive.

La méthode récurrente consiste à spécifier une règle qui permet de calculer le nième membre de la séquence si ses premiers membres sont spécifiés (au moins un premier membre) et une formule qui permet de calculer son prochain membre à partir des membres précédents. Terme récurrent dérivé du mot latin se reproduire , ce qui signifie revenir . Lors du calcul des membres de la séquence selon cette règle, nous revenons tout le temps en arrière, calculant le membre suivant en fonction du précédent. Une caractéristique de cette méthode est que pour déterminer, par exemple, le 100e membre de la séquence, vous devez d'abord déterminer tous les 99 membres précédents.

Exemple 1 . un 1 \u003d un, un n + 1 \u003d un n +0,7. Soit a 1 =5, alors la séquence ressemblera à : 5 ; 5,7 ; 6.4 ; 7.1 ; 7,8 ; 8,5 ; ... .

Exemple 2 b 1 \u003d b, b n +1 \u003d ½ b n. Soit b 1 =23, alors la séquence ressemblera à : 23 ; 11,5 ; 5,75 ; 2,875 ; ... .

Exemple 3 Suite de Fibonacci. Cette suite se définit facilement récursivement : y 1 =1, y 2 =1,y n -2 +y n -1 si n=3, 4, 5, 6, ... . Cela ressemblera à :

1, 1,2, 3, 5, 8, 13, 21, 34, 55, ... . (P ième terme de cette suite est égal à la somme des deux termes précédents)

Il est difficile de définir analytiquement la suite de Fibonacci, mais c'est possible. La formule par laquelle tout élément de cette séquence est déterminé ressemble à ceci :

Informations Complémentaires:

Le marchand italien Léonard de Pise (1180-1240), mieux connu sous le surnom de Fibonacci, était un important mathématicien médiéval. A l'aide de cette séquence, Fibonacci a déterminé le nombre φ (phi); φ=1,618033989.

Manière graphique

Les membres d'une séquence peuvent être représentés sous forme de points sur le plan de coordonnées. Pour ce faire, le nombre est tracé le long de l'axe horizontal et la valeur du membre correspondant de la séquence est tracée le long de l'axe vertical.

Pour consolider les méthodes d'assignation, je vous demande de donner quelques exemples de séquences qui se précisent soit verbalement, soit analytiquement, soit de manière récurrente.

Types de séquences de nombres

(Sur les séquences listées ci-dessous, des types de séquences sont élaborés).

Travailler avec le manuel p.69-70

1) Croissant - si chaque terme est inférieur au suivant, c'est-à-dire un n un n +1.

2) Décroissant - si chaque terme est supérieur au suivant, c'est-à-dire un n un n +1 .

3) Sans fin.

4) Ultime.

5) Alternance.

6) Constante (stationnaire).

Une suite croissante ou décroissante est dite monotone.

3; 6; 9; 12; 15; 18;…

–1; 2; –3; 4; –5; …
1, 4, 9, 16 ,…
–1; 2; –3; 4; –5; 6; …
3; 3; 3; 3; …; 3; … .

Travailler avec le manuel: faites-le oralement n ° 150, 159 pp. 71, 72

3.2. Consolidation du nouveau matériel. Résolution de problème.

Pour consolider les connaissances, des exemples sont choisis en fonction du niveau de préparation des étudiants.

Exemple 1Écrire une formule possible pour le nième élément de la suite (y n) :

a) 1, 3, 5, 7, 9, 11, ... ;

b) 4, 8, 12, 16, 20, ... ;

La solution.

a) C'est une suite de nombres impairs. Analytiquement, cette séquence peut être donnée par la formule y = 2n+1.

b) Il s'agit d'une séquence numérique dans laquelle l'élément suivant est plus grand que le précédent de 4. Analytiquement, cette séquence peut être spécifiée par la formule y = 4n.

Exemple 2. Écrire les dix premiers éléments de la suite donnée de façon récurrente : y 1 =1, y 2 =2, y n = y n -2 +y n -1 si n = 3, 4, 5, 6, ... .

La solution.

Chaque élément suivant de cette séquence est égal à la somme des deux éléments précédents.

Exemple 3 La séquence (y n) est donnée de façon récurrente : y 1 =1, y 2 =2,y n =5y n -1 - 6y n -2 . Spécifiez cette séquence analytiquement.

La solution.

Trouvez les premiers éléments de la séquence.

y 3 =5y 2 -6y 1 =10-6=4 ;

y 4 \u003d 5y 3 -6y 2 \u003d 20-12 \u003d 8;

y 5 \u003d 5y 4 -6y 3 \u003d 40-24 \u003d 16;

y 6 \u003d 5y 5 -6y 4 \u003d 80-48 \u003d 32;

y 7 \u003d 5y 6 -6y 5 \u003d 160-96 \u003d 64.

On obtient la suite : 1 ; 2 ; quatre ; huit; 16; 32; 64 ; ... qui peut être représenté comme

2 0 ; 2 1 ; 2 2 ; 2 3 ; 2 4 ; 2 5 ; 2 6 ... .

n = 1 ; 2 ; 3 ; quatre ; 5 ; 6 ; sept... .

En analysant la séquence, on obtient la régularité suivante : y = 2 n -1 .

Exemple 4 Soit une suite y n =24n+36-5n 2 .

a) Combien de termes positifs a-t-il ?

b) Trouve le plus grand élément de la suite.

c) Y a-t-il un plus petit élément dans cette suite ?

Cette séquence numérique est une fonction de la forme y = -5x 2 +24x+36, où x

a) Trouvez les valeurs de la fonction pour lesquelles -5x 2 +24x+360. Résolvons l'équation -5x 2 +24x+36=0.

D \u003d b 2 -4ac \u003d 1296, X 1 \u003d 6, X 2 \u003d -1,2.

L'équation de l'axe de symétrie de la parabole y \u003d -5x 2 +24x + 36 peut être trouvée par la formule x \u003d, on obtient : x \u003d 2,4.

L'inégalité -5x 2 +24x+360 vaut pour -1.2 Cet intervalle contient cinq nombres naturels (1, 2, 3, 4, 5). Il y a donc cinq éléments positifs de la séquence dans la séquence donnée.

b) Le plus grand élément de la séquence est déterminé par la méthode de sélection et il est égal à y 2 =64.

dans) plus petit élément non.

3.4 Tâches pour un travail indépendant

Quelles méthodes de réglage des séquences connaissez-vous. Séquences de nombres

Lire aussi

Exemples de séquence

Exemples de séquences infiniment croissantes

Exemples de suites convergeant vers un nombre fini

Exemples de séquences divergentes

Séquence avec des termes distribués dans l'intervalle (0;1)

Séquence contenant tous les nombres rationnels

Conclusion