Progresie aritmetică. Teorie detaliată cu exemple (2019)
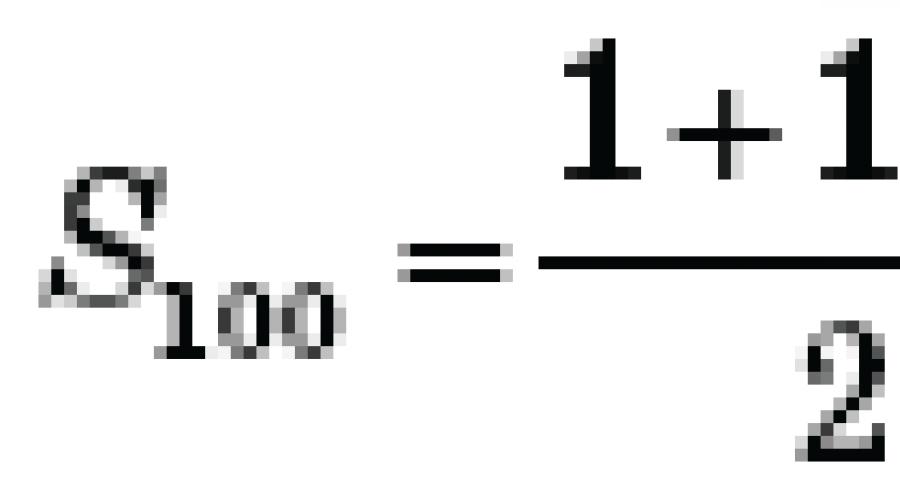
Citeste si
Motto-ul lecției noastre vor fi cuvintele matematicianului rus V.P. Ermakova: „În matematică, ar trebui să ne amintim nu formulele, ci procesele gândirii.”
În timpul orelor
Formularea problemei
Pe tablă este un portret al lui Gauss. Un profesor sau un elev căruia i s-a dat sarcina să pregătească un mesaj în prealabil spune că atunci când Gauss era la școală, profesorul le-a cerut elevilor să adune toate numerele naturale de la 1 la 100. Micul Gauss a rezolvat această problemă într-un minut.
Întrebare . Cum a primit Gauss răspunsul?
Căutați soluții
Elevii își exprimă ipotezele, apoi însumează: realizând că sumele 1 + 100, 2 + 99 etc. sunt egale, Gauss a înmulțit 101 cu 50, adică cu numărul de astfel de sume. Cu alte cuvinte, a observat un model care este inerent progresie aritmetică.
Derivarea formulei sumei n primii termeni ai unei progresii aritmetice
Scrieți subiectul lecției pe tablă și în caiete. Elevii, împreună cu profesorul, notează derivarea formulei:
Lăsa A 1 ; A 2 ; A 3 ; A 4 ; ...; un n – 2 ; un n – 1 ; un n- progresia aritmetica.
Fixare primară
1. Să rezolvăm, folosind formula (1), problema lui Gauss:
![]()
2. Folosind formula (1), rezolvați oral problemele (condițiile lor sunt scrise pe tablă sau cod pozitiv), ( un n) - progresie aritmetică:
A) A 1 = 2, A 10 = 20. S 10 - ?
b) A 1 = –5, A 7 = 1. S 7 - ? [–14]
V) A 1 = –2, A 6 = –17. S 6 - ? [–57]
G) A 1 = –5, A 11 = 5. S 11 - ?
3. Finalizați sarcina.
Dat :( un n) - progresie aritmetică;
A 1 = 3, A 60 = 57.
Găsi: S 60 .
Soluţie. Să folosim formula sumei n primii termeni ai unei progresii aritmetice
Răspuns: 1800.
Întrebare suplimentară. Câte tipuri de probleme diferite pot fi rezolvate prin această formulă?
Răspuns. Patru tipuri de sarcini:
Găsiți suma S n;
Găsiți primul termen al unei progresii aritmetice A 1 ;
Găsi n-al-lea membru al unei progresii aritmetice un n;
Aflați numărul de membri ai unei progresii aritmetice.
4. Completați sarcina: nr. 369(b).
Aflați suma celor șaizeci și unu de termeni ai unei progresii aritmetice ( un n), Dacă A 1 = –10,5, A 60 = 51,5.
Soluţie. ![]()
Răspuns: 1230.
Întrebare suplimentară. Scrieți formula n al-lea membru al unei progresii aritmetice.
Răspuns: un n = A 1 + d(n – 1).
5. Calculați formula pentru primii nouă termeni ai unei progresii aritmetice ( b n),
Dacă b 1 = –17, d =
6.
Este posibil să se calculeze imediat folosind o formulă?
Nu, pentru că al nouălea termen este necunoscut.
Cum să-l găsesc?
Conform formulei n al-lea membru al unei progresii aritmetice.
Soluţie. b 9 = b 1 + 8d = –17 + 8∙6 = 31;
![]()
Răspuns: 63.
Întrebare. Este posibil să găsiți suma fără a calcula al nouălea termen al progresiei?
Formularea problemei
Problemă: obțineți formula sumei n primii termeni ai unei progresii aritmetice, cunoscându-i primul termen și diferența d.
(Ieșirea formulei la tablă de către student.)
Rezolvăm nr. 371(a) folosind noua formulă (2):
Consolidați verbal formulele (2) ( condițiile sarcinii sunt scrise pe tablă).
(un n
1. A 1 = 3, d = 4. S 4 - ?
2. A 1 = 2, d = –5. S 3 - ? [–9]
Întrebați elevii ce întrebări nu înțeleg.
Muncă independentă
Opțiunea 1
Dat: (un n) este o progresie aritmetică.1. A 1 = –3, A 6 = 21. S 6 - ?
2. A 1 = 6, d = –3. S 4 - ?
Opțiunea 2
Dat: (un n) este o progresie aritmetică.
1.A 1 = 2, A 8 = –23. S 8 - ? [–84]
2.A 1 = –7, d = 4. S 5 - ?
Elevii schimbă caietele și verifică reciproc soluțiile.
Rezumați asimilarea materialului pe baza rezultatelor muncii independente.
lecția 4
Numele subiectului algebra
clasa 9
UMK Algebră. Clasa a 9-a La 14:00 Partea 1. Un manual pentru studenții instituțiilor de învățământ / A. G. Mordkovich. - M.: Mnemosyne, 2012 - 160 p. Partea 2. Caiet de sarcini pentru studenții instituțiilor de învățământ [A. G. Mordkovich și alții]; ed. A. G. Mordkovici. - M.: Mnemosyne, 2012 - 270
Nivel de bază de educație
Subiectul lecției " Proprietatea caracteristică a unei progresii aritmetice"
Numărul total de ore dedicate studiului temei 5
Locul lecției în sistemul de lecții pe tema 4
Scopul lecției:
Cunoașterea proprietății caracteristice a membrilor unei progresii aritmetice.
Sarcini lecţie:
1) Educativ - deduceți și demonstrați proprietate caracteristică progresie aritmetică; pentru a forma capacitatea de a aplica proprietatea unei progresii aritmetice în rezolvarea problemelor
2) Dezvoltarea – dezvoltarea capacității de a compara concepte matematice, de a găsi asemănări și diferențe, capacitatea de a observa, de a observa tipare, de a raționa prin analogie; pentru a forma capacitatea de a construi și interpreta un model matematic al unei situații reale.
3) Educativ - pentru a promova dezvoltarea interesului pentru matematică și aplicațiile sale, activitatea, capacitatea de a comunica și de a-și apăra în mod rezonabil opiniile.
Echipament: calculator, proiector multimedia, prezentare
Rezultatele așteptate: În această lecție, trebuie să stabilim o relație între membrii unei progresii aritmetice și să rezolvăm probleme care utilizează proprietățile progresiilor aritmetice.
II. Actualizarea cunoștințelor elevilor
Sondaj frontal:
Ce este o progresie aritmetică?
Cum este definită o progresie aritmetică?
- Denumiți formula P al-lea membru al unei progresii aritmetice.
2. Dictare matematică.(Temele sunt distribuite pe cartonașe)
1 opțiune
№1. Având în vedere o progresie aritmetică
1;4;7;11;…
№2. A 1 =, d= Găsiți un 11 -?
№3. Aflați suma (S) a primilor sute de termeni ai unei progresii aritmetice (a n) dacă A 1 =-9, d=4
Opțiunea 2
Nr. 1. Se dă o progresie aritmetică -
9;6;3;0;;… Găsiți primul său termen și diferența.
№2. A 1 =0,2, d= .Găsi A 11 - ?
Numarul 3. Aflați suma (S) a primilor sute de termeni ai unei progresii aritmetice (a n) dacă A 1 =70, d=-1
III. Învățarea de materiale noi. (diapozitivul 1-3)
1. Luați în considerare o progresie aritmetică ( X P): 2; 5; 8; 11; 14.
Să aflăm dacă există o legătură între oricare trei membri consecutivi ai progresiei? Vă sugerez să faceți singuri această legătură. Pentru a face acest lucru, vom face muncă de cercetare.
 = (5.)
= (5.)
 = (8.)
= (8.)
 = (11.)
= (11.)
Ce concluzie se poate trage despre relația dintre membrii unei progresii aritmetice?
Concluzie: „Fiecare membru al progresiei aritmetice, începând cu al doilea, este egal cu media aritmetică a membrilor anteriori și următori”.
2. Deoarece am presupus acest lucru pe baza unei anumite secvențe, această afirmație ar trebui demonstrată:
Lăsa ( X P) este o progresie aritmetică, atunci
X P – X P – 1 = X P + 1 – X P, acesta este
2X P = X P – 1 + X P + 1 ,
| X P = |
Ar trebui plătit Atentie speciala elevilor că această afirmație este proprietate progresie aritmetică. Și dacă formulăm afirmația inversă și o putem demonstra, cum se va numi? Va fi semn progresie aritmetică: „Dacă în secvența ( X P) fiecare termen, începând cu al doilea, este egal cu media aritmetică a termenilor anteriori și următori, atunci această succesiune este o progresie aritmetică.
Lăsa X P =  , Unde P≥ 2, apoi 2 X P = X P – 1 + X P + 1,
, Unde P≥ 2, apoi 2 X P = X P – 1 + X P + 1,
X P – X P – 1 = X P + 1 – X P, adică diferența dintre membrii următori și anteriori ai secvenței ( X P) ramane constant. Mijloace, ( X P) este o progresie aritmetică.
IV. Formarea deprinderilor și abilităților.
Rezolvați verbal #16.40 folosind proprietatea caracteristică a unei progresii aritmetice:
A)  Apoi
Apoi 
b)  Apoi A 18 + A 20 = 2 A 19 = 2 5 = 10;
Apoi A 18 + A 20 = 2 A 19 = 2 5 = 10;
2. Rezolvați nr. 16.42 (b) cu comentarii pe loc.
Dacă A 14 + A 16 = -20, atunci A 15 = –20: 2 = –10;
Dacă A 29 + A 31 = 40 atunci A 30 = 40: 2 = 20;
Sa gasim A 15 + A 30 = –10 + 20 = 10.
Răspuns: 10.
3. Rezolvați numărul 16.44 de pe tablă și în caiete.
După proprietatea caracteristică, expresiile date trebuie să satisfacă relația
 2la = 5la – 3; 3la = 3; la = 1.
2la = 5la – 3; 3la = 3; la = 1.
Raspunsul 1.
4. Rezolvați #16.46. Soluția este explicată de profesor.
a) Vorbim despre suma termenilor progresiei aritmetice finale 104; 112; 120; … 992. Această progresie are A 1 = 104; A n = 992; d= 8. Mai întâi găsim n(numărul de membri ai progresiei):
A n = A 1 + (n –1)d; 992 = 104 + (n – 1) 8;
992 = 8n + 96; n = 112.
Răspuns: 61376.
5. Rezolvați Nr. 16.48 (b; d) pe tablă și în caiete.
b) A 9 = –30; A 19 = -45. Sa gasim A n .
A n = A 1 + (n – 1)d= –18 + (n – 1)(–1,5) = –1,5n – 16,5.
G) A 5 = 0,2; A 16 = -7,5. Sa gasim A n .
A n = 3 – 0,7(n– 1).
A n s e r: b) –18 – 1,5( n- 1); d) 3 – 0,7( n– 1).
6. Rezolvați Nr. 16.68 . Soluția este explicată de profesor.
Folosind proprietatea caracteristică a unei progresii aritmetice, obținem ecuația  X – 3 =
X – 3 =
= (X– 5) 2 ; X 2 – 11X + 28 = 0; X 1 = 7; X 2 \u003d 4 - o rădăcină străină care nu satisface ecuație irațională 
Raspuns: 7.
V. Rezultatele lecției.
Întrebări de la h a shch și m s i:
- Formulați proprietatea unei progresii aritmetice.
Când studiezi algebra în scoala de invatamant general(Clasa a 9-a) Una dintre subiectele importante este studiul șirurilor numerice, care includ progresii - geometrice și aritmetice. În acest articol, vom lua în considerare o progresie aritmetică și exemple cu soluții.
Ce este o progresie aritmetică?
Pentru a înțelege acest lucru, este necesar să se dea o definiție a progresiei luate în considerare, precum și să se dea formulele de bază care vor fi utilizate în continuare în rezolvarea problemelor.
Aritmetică sau este un astfel de set de numere raționale ordonate, fiecare membru al cărora diferă de cel precedent printr-o valoare constantă. Această valoare se numește diferență. Adică, cunoscând orice membru al unei serii ordonate de numere și diferența, puteți restabili întreaga progresie aritmetică.
Să luăm un exemplu. Următoarea succesiune de numere va fi o progresie aritmetică: 4, 8, 12, 16, ..., deoarece diferența în acest caz este 4 (8 - 4 = 12 - 8 = 16 - 12). Dar setul de numere 3, 5, 8, 12, 17 nu mai poate fi atribuit tipului de progresie considerat, deoarece diferența pentru aceasta nu este valoare constantă (5 - 3 ≠ 8 - 5 ≠ 12 - 8 ≠ 17 - 12).

Formule importante
Vom oferi acum formulele de bază care vor fi necesare pentru a rezolva probleme folosind o progresie aritmetică. Notează prin simbol a n al-lea membru secvențe în care n este un număr întreg. Diferența este notată de litera latină d. Atunci următoarele expresii sunt adevărate:
- Pentru a determina valoarea celui de-al n-lea termen, formula este potrivită: a n \u003d (n-1) * d + a 1.
- Pentru a determina suma primilor n termeni: S n = (a n + a 1)*n/2.
Pentru a înțelege orice exemplu de progresie aritmetică cu o soluție în clasa a 9-a, este suficient să ne amintim aceste două formule, deoarece orice probleme de tipul luat în considerare sunt construite pe utilizarea lor. De asemenea, nu uitați că diferența de progresie este determinată de formula: d = a n - a n-1 .
Exemplul #1: Găsirea unui membru necunoscut

Dăm un exemplu simplu de progresie aritmetică și formulele care trebuie folosite pentru rezolvare.
Să fie dată șirul 10, 8, 6, 4, ..., este necesar să găsim cinci termeni în ea.
Din condițiile problemei rezultă deja că primii 4 termeni sunt cunoscuți. Al cincilea poate fi definit în două moduri:
- Să calculăm mai întâi diferența. Avem: d = 8 - 10 = -2. În mod similar, se poate lua oricare alți doi termeni stând unul lângă celălalt. De exemplu, d = 4 - 6 = -2. Deoarece se știe că d \u003d a n - a n-1, apoi d \u003d a 5 - a 4, de unde obținem: a 5 \u003d a 4 + d. Inlocuim valorile cunoscute: a 5 = 4 + (-2) = 2.
- A doua metodă necesită, de asemenea, cunoașterea diferenței progresiei în cauză, așa că mai întâi trebuie să o determinați, așa cum se arată mai sus (d = -2). Știind că primul termen a 1 = 10, folosim formula pentru numărul n al șirului. Avem: a n \u003d (n - 1) * d + a 1 \u003d (n - 1) * (-2) + 10 \u003d 12 - 2 * n. Înlocuind n = 5 în ultima expresie, obținem: a 5 = 12-2 * 5 = 2.
După cum puteți vedea, ambele soluții duc la același rezultat. Rețineți că în acest exemplu diferența d a progresiei este negativă. Astfel de secvențe se numesc descrescătoare deoarece fiecare termen succesiv este mai mic decât cel anterior.
Exemplul #2: diferența de progresie
Acum să complicăm puțin sarcina, să dăm un exemplu despre cum să găsim diferența unei progresii aritmetice.
Se știe că în unele progresii algebrice primul termen este egal cu 6, iar al 7-lea termen este egal cu 18. Este necesar să găsim diferența și să restabilim această secvență la al 7-lea termen.
Să folosim formula pentru a determina termenul necunoscut: a n = (n - 1) * d + a 1 . Înlocuim datele cunoscute din condiție în ea, adică numerele a 1 și a 7, avem: 18 \u003d 6 + 6 * d. Din această expresie, puteți calcula cu ușurință diferența: d = (18 - 6) / 6 = 2. Astfel, s-a răspuns la prima parte a problemei.
Pentru a restabili o secvență de până la 7 termeni, ar trebui să folosiți definiția progresie algebrică, adică a 2 = a 1 + d, a 3 = a 2 + d și așa mai departe. Ca rezultat, restabilim întreaga secvență: a 1 = 6, a 2 = 6 + 2=8, a 3 = 8 + 2 = 10, a 4 = 10 + 2 = 12, a 5 = 12 + 2 = 14 , a 6 = 14 + 2 = 16 și 7 = 18.
Exemplul #3: realizarea unei progresii

Să complicăm și mai mult starea problemei. Acum trebuie să răspundeți la întrebarea cum să găsiți o progresie aritmetică. Putem da următorul exemplu: se dau două numere, de exemplu, 4 și 5. Este necesar să se facă o progresie algebrică astfel încât încă trei termeni să se potrivească între aceștia.
Înainte de a începe să rezolvați această problemă, este necesar să înțelegeți ce loc vor ocupa numerele date în progresia viitoare. Deoarece vor mai exista trei termeni între ei, apoi un 1 \u003d -4 și un 5 \u003d 5. După ce am stabilit acest lucru, trecem la o sarcină similară celei anterioare. Din nou, pentru al n-lea termen, folosim formula, obținem: a 5 \u003d a 1 + 4 * d. De la: d \u003d (a 5 - a 1) / 4 \u003d (5 - (-4)) / 4 \u003d 2,25. Aici nu am primit o valoare întreagă a diferenței, dar este Numar rational, deci formulele pentru progresia algebrică rămân aceleași.
Acum să adăugăm diferența găsită la un 1 și să restabilim membrii lipsă ai progresiei. Obținem: a 1 = - 4, a 2 = - 4 + 2,25 = - 1,75, a 3 = -1,75 + 2,25 = 0,5, a 4 = 0,5 + 2,25 = 2,75, a 5 \u003d 2,75 + 2,25 \u, 50 care a coincis cu starea problemei.
Exemplul #4: primul membru al progresiei

Continuăm să dăm exemple de progresie aritmetică cu o soluție. În toate problemele anterioare, era cunoscut primul număr al progresiei algebrice. Acum luați în considerare o problemă de alt tip: să fie date două numere, unde a 15 = 50 și a 43 = 37. Este necesar să aflăm de la ce număr începe această succesiune.
Formulele care au fost folosite până acum presupun cunoașterea a 1 și d. Nu se știe nimic despre aceste cifre în starea problemei. Cu toate acestea, să scriem expresiile pentru fiecare termen despre care avem informații: a 15 = a 1 + 14 * d și a 43 = a 1 + 42 * d. Avem două ecuații în care există 2 mărimi necunoscute (a 1 și d). Aceasta înseamnă că problema se reduce la rezolvarea unui sistem de ecuații liniare.
Sistemul specificat este cel mai ușor de rezolvat dacă exprimați un 1 în fiecare ecuație și apoi comparați expresiile rezultate. Prima ecuație: a 1 = a 15 - 14 * d = 50 - 14 * d; a doua ecuație: a 1 \u003d a 43 - 42 * d \u003d 37 - 42 * d. Echivalând aceste expresii, obținem: 50 - 14 * d \u003d 37 - 42 * d, de unde diferența d \u003d (37 - 50) / (42 - 14) \u003d - 0,464 (sunt date doar 3 zecimale).
Cunoscând d, puteți folosi oricare dintre cele 2 expresii de mai sus pentru a 1 . De exemplu, mai întâi: a 1 \u003d 50 - 14 * d \u003d 50 - 14 * (- 0,464) \u003d 56,496.
Dacă există îndoieli cu privire la rezultat, îl puteți verifica, de exemplu, determinați al 43-lea membru al progresiei, care este specificat în condiție. Obținem: a 43 \u003d a 1 + 42 * d \u003d 56,496 + 42 * (- 0,464) \u003d 37,008. O mică eroare se datorează faptului că în calcule a fost utilizată rotunjirea la miimi.
Exemplul #5: Sumă
Acum să ne uităm la câteva exemple cu soluții pentru suma unei progresii aritmetice.
Să se dea o progresie numerică de următoarea formă: 1, 2, 3, 4, ...,. Cum se calculează suma a 100 dintre aceste numere?
Datorită dezvoltării tehnologiei informatice, această problemă poate fi rezolvată, adică se adună secvenţial toate numerele care Mașină de calcul va face imediat ce persoana va apăsa tasta Enter. Problema poate fi însă rezolvată mental dacă acordați atenție că seria de numere prezentată este o progresie algebrică, iar diferența ei este 1. Aplicând formula pentru sumă, obținem: S n = n * (a 1 + a n) / 2 = 100 * (1 + 100) / 2 = 5050.
Este curios de observat că această problemă se numește „gaussian” deoarece în începutul XVIII al secolului, celebrul german, încă la vârsta de doar 10 ani, a putut să o rezolve în minte în câteva secunde. Băiatul nu știa formula pentru suma unei progresii algebrice, dar a observat că, dacă adaugi perechi de numere situate la marginile șirului, obții întotdeauna același rezultat, adică 1 + 100 = 2 + 99. = 3 + 98 = ... și, deoarece aceste sume vor fi exact 50 (100 / 2), atunci pentru a obține răspunsul corect, este suficient să înmulțiți 50 cu 101.

Exemplul #6: suma termenilor de la n la m
Un alt exemplu tipic al sumei unei progresii aritmetice este următorul: având în vedere o serie de numere: 3, 7, 11, 15, ..., trebuie să aflați care va fi suma termenilor săi de la 8 la 14.
Problema este rezolvată în două moduri. Primul dintre ei implică găsirea de termeni necunoscuți de la 8 la 14 și apoi însumarea lor secvențială. Deoarece există puțini termeni, această metodă nu este suficient de laborioasă. Cu toate acestea, se propune rezolvarea acestei probleme prin a doua metodă, care este mai universală.
Ideea este de a obține o formulă pentru suma unei progresii algebrice între termenii m și n, unde n > m sunt numere întregi. Pentru ambele cazuri, scriem două expresii pentru suma:
- S m \u003d m * (a m + a 1) / 2.
- S n \u003d n * (a n + a 1) / 2.
Deoarece n > m, este evident că suma 2 o include pe prima. Ultima concluzie înseamnă că dacă luăm diferența dintre aceste sume și îi adăugăm termenul a m (în cazul luării diferenței, se scade din suma S n), atunci obținem răspunsul necesar la problemă. Avem: S mn \u003d S n - S m + a m \u003d n * (a 1 + a n) / 2 - m * (a 1 + a m) / 2 + a m \u003d a 1 * (n - m) / 2 + a n * n / 2 + a m * (1- m / 2). Este necesar să se înlocuiască formule pentru a n și a m în această expresie. Atunci obținem: S mn = a 1 * (n - m) / 2 + n * (a 1 + (n - 1) * d) / 2 + (a 1 + (m - 1) * d) * (1 - m / 2) = a 1 * (n - m + 1) + d * n * (n - 1) / 2 + d * (3 * m - m 2 - 2) / 2.
Formula rezultată este oarecum greoaie, totuși, suma S mn depinde doar de n, m, a 1 și d. În cazul nostru, a 1 = 3, d = 4, n = 14, m = 8. Înlocuind aceste numere, obținem: S mn = 301.

După cum se poate observa din soluțiile de mai sus, toate problemele se bazează pe cunoașterea expresiei pentru al n-lea termen și a formulei pentru suma mulțimii primilor termeni. Înainte de a începe să rezolvați oricare dintre aceste probleme, este recomandat să citiți cu atenție condiția, să înțelegeți clar ce doriți să găsiți și abia apoi să continuați cu soluția.
Un alt sfat este să depuneți eforturi pentru simplitate, adică dacă puteți răspunde la întrebare fără a utiliza calcule matematice complexe, atunci trebuie să faceți exact asta, deoarece în acest caz probabilitatea de a face o greșeală este mai puțin probabilă. De exemplu, în exemplul unei progresii aritmetice cu soluția nr. 6, se poate opri la formula S mn \u003d n * (a 1 + a n) / 2 - m * (a 1 + a m) / 2 + a m, și despărțit sarcină comunăîn subprobleme separate (în acest caz, găsiți mai întâi termenii a n și a m).
Dacă există îndoieli cu privire la rezultat, se recomandă să-l verificați, așa cum s-a făcut în unele dintre exemplele date. Cum să găsești o progresie aritmetică, am aflat. Odată ce îți dai seama, nu este atât de greu.
Primul nivel
Progresie aritmetică. Teorie detaliată cu exemple (2019)
Secvență numerică
Așa că hai să ne așezăm și să începem să scriem câteva numere. De exemplu:
Puteți scrie orice numere și pot fi câte doriți (în cazul nostru, ele). Indiferent câte numere am scrie, putem spune întotdeauna care dintre ele este primul, care este al doilea și tot așa până la ultimul, adică le putem numerota. Acesta este un exemplu de succesiune de numere:
Secvență numerică
De exemplu, pentru secvența noastră:
Numărul atribuit este specific unui singur număr de secvență. Cu alte cuvinte, nu există trei numere secunde în succesiune. Al doilea număr (ca și al-lea număr) este întotdeauna același.
Numărul cu numărul se numește --lea membru al secvenței.
De obicei, numim întreaga secvență o literă (de exemplu,) și fiecare membru al acestei secvențe - aceeași literă cu un index, egală cu numărul acest membru: .
În cazul nostru: 
Să zicem că avem succesiune numerică, în care diferența dintre numerele învecinate este aceeași și egală.
De exemplu: 
etc.
O astfel de succesiune numerică se numește progresie aritmetică.
Termenul de „progresie” a fost introdus de autorul roman Boethius încă din secolul al VI-lea și a fost înțeles într-un sens mai larg ca o secvență numerică nesfârșită. Numele „aritmetică” a fost transferat din teoria proporțiilor continue, în care s-au implicat grecii antici.
Aceasta este o succesiune numerică, fiecare membru al căruia este egal cu cel precedent, adăugat cu același număr. Acest număr se numește diferența unei progresii aritmetice și se notează.
Încercați să determinați care secvențe de numere sunt o progresie aritmetică și care nu sunt:
A)
b)
c)
d)
Am înţeles? Comparați răspunsurile noastre:
Este progresie aritmetică - b, c.
Nu este progresie aritmetică - a, d.
Să revenim la progresia dată () și să încercăm să găsim valoarea celui de-al-lea membru al acesteia. Există Două mod de a-l găsi.
1. Metoda
Putem adăuga la valoarea anterioară a numărului de progresie până ajungem la al treilea termen al progresiei. Este bine că nu avem multe de rezumat - doar trei valori:
Deci, al-lea membru al progresiei aritmetice descrise este egal cu.
2. Metoda
Ce se întâmplă dacă ar trebui să găsim valoarea celui de-al treilea termen al progresiei? Însumarea ne-ar fi luat mai mult de o oră și nu este un fapt că nu am fi făcut greșeli la adunarea numerelor.
Desigur, matematicienii au venit cu o modalitate prin care nu trebuie să adăugați diferența unei progresii aritmetice la valoarea anterioară. Priviți cu atenție imaginea desenată ... Cu siguranță ați observat deja un anumit model, și anume:
De exemplu, să vedem ce formează valoarea celui de-al-lea membru al acestei progresii aritmetice: 
Cu alte cuvinte:
Încercați să găsiți în mod independent în acest fel valoarea unui membru al acestei progresii aritmetice.
Calculat? Comparați intrările dvs. cu răspunsul:
Atenție că ați obținut exact același număr ca în metoda anterioară, când am adăugat succesiv membrii unei progresii aritmetice la valoarea anterioară.
Să încercăm să „depersonalizăm” această formulă – să o introducem forma generala si ia:
|
Ecuația de progresie aritmetică. |
Progresiile aritmetice sunt fie în creștere, fie în scădere.
Crescând- progresii în care fiecare valoare ulterioară a termenilor este mai mare decât cea anterioară.
De exemplu:
Descendentă- progresii în care fiecare valoare ulterioară a termenilor este mai mică decât cea anterioară.
De exemplu:
Formula derivată este utilizată în calculul termenilor atât în termeni crescanți, cât și în termeni descrescători ai unei progresii aritmetice.
Să verificăm în practică.
Ni se oferă o progresie aritmetică constând din următoarele numere:

De atunci:
Astfel, eram convinși că formula funcționează atât în progresie aritmetică descrescătoare, cât și în creștere.
Încercați să găsiți singuri membrii --lea și --lea din această progresie aritmetică.
Să comparăm rezultatele:
Proprietatea progresiei aritmetice
Să complicăm sarcina - derivăm proprietatea unei progresii aritmetice.
Să presupunem că ni se oferă următoarea condiție:
- progresie aritmetică, găsiți valoarea.
E ușor, zici tu, și începeți să numărați după formula pe care o cunoașteți deja:
Fie a, atunci:
Absolut corect. Se pare că mai întâi găsim, apoi îl adăugăm la primul număr și obținem ceea ce căutăm. Dacă progresia este reprezentată de valori mici, atunci nu este nimic complicat, dar dacă ni se dau numere în stare? De acord, există posibilitatea de a face greșeli în calcule.
Acum gândiți-vă, este posibil să rezolvați această problemă într-un singur pas folosind orice formulă? Desigur, da, și vom încerca să-l scoatem acum.
Să notăm termenul dorit al progresiei aritmetice, deoarece știm formula pentru a-l găsi - aceasta este aceeași formulă pe care am derivat-o la început:
, Apoi:
- membrul anterior al progresiei este:
- următorul termen al progresiei este:
Să însumăm membrii anteriori și următori ai progresiei:
Rezultă că suma membrilor anteriori și următori ai progresiei este de două ori valoarea membrului progresiei situat între ei. Cu alte cuvinte, pentru a găsi valoarea unui membru de progresie cu valori anterioare și succesive cunoscute, este necesar să le adunăm și să le împărțim la.
Așa e, avem același număr. Să reparăm materialul. Calculați singur valoarea progresiei, pentru că nu este deloc dificil.
Bine făcut! Știi aproape totul despre progres! Rămâne să aflăm o singură formulă, pe care, potrivit legendei, unul dintre cei mai mari matematicieni ai tuturor timpurilor, „regele matematicienilor” - Karl Gauss, a dedus-o cu ușurință pentru el însuși...
Când Carl Gauss avea 9 ani, profesorul, ocupat să verifice munca elevilor din alte clase, a cerut următoarea sarcină la lecție: „Calculează suma tuturor numere naturale de la până la (după alte surse până la) inclusiv. Care a fost surpriza profesorului când unul dintre elevii săi (era Karl Gauss) după un minut a dat răspunsul corect la sarcină, în timp ce majoritatea colegilor de clasă ai temerului după calcule lungi au primit rezultatul greșit...
Tânărul Carl Gauss a observat un model pe care îl puteți observa cu ușurință.
Să presupunem că avem o progresie aritmetică constând din membri -ti: Trebuie să găsim suma membrilor dați ai progresiei aritmetice. Desigur, putem să însumăm manual toate valorile, dar ce se întâmplă dacă trebuie să găsim suma termenilor săi în sarcină, așa cum căuta Gauss?
Să descriem progresul care ni s-a dat. Priviți cu atenție numerele evidențiate și încercați să efectuați diverse operații matematice cu ele. 
Încercat? Ce ai observat? Dreapta! Sumele lor sunt egale

Acum răspunde, câte astfel de perechi vor fi în progresia dată nouă? Desigur, exact jumătate din toate numerele, adică.
Pe baza faptului că suma a doi termeni ai unei progresii aritmetice este egală și perechi egale similare, obținem că suma totală este egală cu:
.
Astfel, formula pentru suma primilor termeni ai oricărei progresii aritmetice va fi:
În unele probleme, nu cunoaștem al treilea termen, dar cunoaștem diferența de progresie. Încercați să înlocuiți în formula sumei, formula celui de-al-lea membru.
Ce ai primit?
Bine făcut! Acum să revenim la problema care i-a fost dată lui Carl Gauss: calculați singuri care este suma numerelor care încep de la -th și suma numerelor începând de la -th.
Cât ai primit?
Gauss a dovedit că suma termenilor este egală, iar suma termenilor. Asa te-ai hotarat?
De fapt, formula pentru suma membrilor unei progresii aritmetice a fost dovedită de omul de știință grec antic Diophantus încă din secolul al III-lea și, de-a lungul acestui timp, oamenii plini de spirit au folosit proprietățile unei progresii aritmetice cu putere și principal.
De exemplu, imaginați-vă Egiptul anticși cel mai mare șantier de construcție din acea vreme - construcția unei piramide ... Figura arată o parte a acesteia. 
Unde este progresia aici spui tu? Privește cu atenție și găsește un model în numărul de blocuri de nisip din fiecare rând al peretelui piramidei. 
De ce nu o progresie aritmetică? Numărați câte blocuri sunt necesare pentru a construi un perete dacă cărămizi bloc sunt plasate în bază. Sper că nu vei număra mișcând degetul pe monitor, îți amintești ultima formulă și tot ce am spus despre progresia aritmetică?
În acest caz, progresia arată ca în felul următor: .
Diferența de progresie aritmetică.
Numărul de membri ai unei progresii aritmetice.
Să substituim datele noastre în ultimele formule (numărăm numărul de blocuri în 2 moduri).
Metoda 1.
Metoda 2.
Și acum puteți calcula și pe monitor: comparați valorile obținute cu numărul de blocuri care se află în piramida noastră. A fost de acord? Bravo, ai stăpânit suma celor trei termeni ai unei progresii aritmetice.
Desigur, nu poți construi o piramidă din blocurile de la bază, dar din? Încercați să calculați câte cărămizi de nisip sunt necesare pentru a construi un zid cu această condiție.
Ai reușit?
Răspunsul corect este blocurile:
Instruire
Sarcini:
- Masha se pune în formă pentru vară. În fiecare zi crește numărul de genuflexiuni cu. De câte ori se va ghemui Masha în săptămâni dacă a făcut genuflexiuni la primul antrenament.
- Care este suma tuturor numerelor impare conținute în.
- Când depozitează buștenii, tăietorii de lemne le stivuiesc în așa fel încât fiecare strat superior conține un jurnal mai puțin decât cel precedent. Câți bușteni sunt într-o zidărie, dacă baza zidăriei este bușteni.
Raspunsuri:
- Să definim parametrii progresiei aritmetice. În acest caz
(săptămâni = zile).Răspuns:În două săptămâni, Masha ar trebui să se ghemuiască o dată pe zi.
- Primul număr impar, ultimul număr.
Diferența de progresie aritmetică.
Cu toate acestea, numărul de numere impare din - jumătate, verificați acest fapt folosind formula pentru găsirea celui de-al-lea membru al unei progresii aritmetice:Numerele conțin numere impare.
Înlocuim datele disponibile în formula:Răspuns: Suma tuturor numerelor impare conținute în este egală cu.
- Amintiți-vă problema despre piramide. Pentru cazul nostru, a , deoarece fiecare strat superior este redus cu un buștean, există doar o grămadă de straturi, adică.
Înlocuiți datele din formula:Răspuns: Sunt bușteni în zidărie.
Rezumând
- - o succesiune numerică în care diferența dintre numerele adiacente este aceeași și egală. Este în creștere și în scădere.
- Găsirea formulei Al-lea membru al unei progresii aritmetice se scrie prin formula - , unde este numărul de numere din progresie.
- Proprietatea membrilor unei progresii aritmetice- - unde - numărul de numere din progresie.
- Suma membrilor unei progresii aritmetice poate fi găsit în două moduri:
, unde este numărul de valori.
PROGRESIA ARITMETICĂ. NIVEL MEDIU
Secvență numerică
Să ne așezăm și să începem să scriem câteva numere. De exemplu:
Puteți scrie orice numere și pot fi câte doriți. Dar poți spune întotdeauna care dintre ele este primul, care este al doilea și așa mai departe, adică le putem numerota. Acesta este un exemplu de succesiune de numere.
Secvență numerică este un set de numere, fiecăruia cărora li se poate atribui un număr unic.
Cu alte cuvinte, fiecare număr poate fi asociat cu un anumit număr natural și doar unul. Și nu vom atribui acest număr niciunui alt număr din acest set.
Numărul cu numărul se numește --lea membru al secvenței.
De obicei, numim întreaga secvență o literă (de exemplu,) și fiecare membru al acestei secvențe - aceeași literă cu un indice egal cu numărul acestui membru: .
Este foarte convenabil dacă al-lea membru al secvenței poate fi dat printr-o formulă. De exemplu, formula
stabilește secvența:
Și formula este următoarea succesiune:
De exemplu, o progresie aritmetică este o secvență (primul termen aici este egal și diferența). Sau (, diferență).
al n-lea termen formulă
Numim recurentă o formulă în care, pentru a afla cel de-al treilea termen, trebuie să-l cunoști pe anterior sau pe mai multe anterioare:
Pentru a găsi, de exemplu, cel de-al treilea termen al progresiei folosind o astfel de formulă, trebuie să-i calculăm pe cei nouă anteriori. De exemplu, lasa. Apoi:
Ei bine, acum e clar care este formula?
În fiecare linie, adunăm la, înmulțit cu un anumit număr. Pentru ce? Foarte simplu: acesta este numărul membrului curent minus:
Mult mai confortabil acum, nu? Verificăm:
Decide pentru tine:
Într-o progresie aritmetică, găsiți formula pentru al n-lea termen și găsiți al sutelea termen.
Soluţie:
Primul termen este egal. Și care este diferența? Și iată ce:
(la urma urmei, se numește diferență deoarece este egală cu diferența membrilor succesivi ai progresiei).
Deci formula este:
Atunci al sutelea termen este:
Care este suma tuturor numerelor naturale de la până la?
Potrivit legendei, marele matematician Carl Gauss, fiind un băiețel de 9 ani, a calculat această sumă în câteva minute. El a observat că suma primului și ultimului număr este egală, suma celui de-al doilea și penultimul este aceeași, suma celui de-al treilea și al 3-lea de la sfârșit este aceeași și așa mai departe. Câte astfel de perechi există? Așa este, exact jumătate din numărul tuturor numerelor, adică. Asa de,
Formula generală pentru suma primilor termeni ai oricărei progresii aritmetice va fi:
Exemplu:
Aflați suma tuturor multiplilor de două cifre.
Soluţie:
Primul astfel de număr este acesta. Fiecare următor se obține prin adăugarea unui număr celui precedent. Astfel, numerele care ne interesează formează o progresie aritmetică cu primul termen și diferența.
Formula pentru al treilea termen pentru această progresie este:
Câți termeni sunt în progresie dacă toți trebuie să fie de două cifre?
Foarte usor: .
Ultimul termen al progresiei va fi egal. Apoi suma:
Răspuns: .
Acum decideți singuri:
- În fiecare zi, sportivul aleargă cu 1 m mai mult decât în ziua precedentă. Câți kilometri va alerga în săptămâni dacă a alergat km m în prima zi?
- Un biciclist parcurge mai multe mile în fiecare zi decât precedentul. În prima zi a parcurs km. Câte zile trebuie să conducă pentru a parcurge un kilometru? Câți kilometri va parcurge în ultima zi de călătorie?
- Prețul unui frigider în magazin este redus cu aceeași sumă în fiecare an. Stabiliți cât de mult a scăzut prețul unui frigider în fiecare an dacă, scos la vânzare pentru ruble, șase ani mai târziu a fost vândut pentru ruble.
Raspunsuri:
- Cel mai important lucru aici este să recunoașteți progresia aritmetică și să determinați parametrii acesteia. În acest caz, (săptămâni = zile). Trebuie să determinați suma primilor termeni ai acestei progresii:
.
Răspuns: - Aici este dat:, este necesar să se găsească.
Evident, trebuie să utilizați aceeași formulă de sumă ca în problema anterioară:
.
Înlocuiți valorile:Rădăcina evident nu se potrivește, deci răspunsul.
Să calculăm distanța parcursă în ultima zi folosind formula celui de-al treilea termen:
(km).
Răspuns: - Dat: . Găsi: .
Nu devine mai ușor:
(freca).
Răspuns:
PROGRESIA ARITMETICĂ. SCURT DESPRE PRINCIPALA
Aceasta este o succesiune numerică în care diferența dintre numerele adiacente este aceeași și egală.
Progresia aritmetică este în creștere () și în scădere ().
De exemplu:
Formula pentru găsirea celui de-al n-lea membru al unei progresii aritmetice
se scrie sub formă de formulă, unde este numărul de numere din progresie.
Proprietatea membrilor unei progresii aritmetice
Ușurează găsirea unui membru al progresiei dacă membrii săi vecini sunt cunoscuți - unde este numărul de numere din progresie.
Suma membrilor unei progresii aritmetice
Există două moduri de a găsi suma:
Unde este numărul de valori.
Unde este numărul de valori.