Lösen Sie Ungleichungen mit der Intervallmethode online mit Lösung. Quadratische Ungleichungen lösen – Wissens-Hypermarkt
Ungleichheit ist ein Ausdruck mit ≤ oder ≥. Beispiel: 3x – 5 Das Lösen einer Ungleichung bedeutet, alle Werte der Variablen zu finden, für die die Ungleichung gilt. Jede dieser Zahlen ist eine Lösung der Ungleichung, und die Menge aller dieser Lösungen ist ihre viele Lösungen. Ungleichungen, die die gleiche Lösungsmenge haben, heißen äquivalente Ungleichungen.
Lineare Ungleichungen
Die Prinzipien zum Lösen von Ungleichungen ähneln den Prinzipien zum Lösen von Gleichungen.Prinzipien zur Lösung von Ungleichungen
Für alle reellen Zahlen a, b und c:
Das Prinzip der Addition von Ungleichungen: Wenn a Multiplikationsprinzip für Ungleichungen: Wenn a 0 wahr ist, dann ac. Wenn a bc auch wahr ist.
Ähnliche Aussagen gelten auch für a ≤ b.
Wenn beide Seiten einer Ungleichung mit einer negativen Zahl multipliziert werden, muss das Vorzeichen der Ungleichung umgekehrt werden.
Ungleichungen der ersten Ebene, wie in Beispiel 1 (unten), heißen lineare Ungleichungen.
Beispiel 1 Lösen Sie jede der folgenden Ungleichungen. Zeichnen Sie dann eine Reihe von Lösungen.
a) 3x - 5 b) 13 - 7x ≥ 10x - 4
Lösung
Jede Zahl kleiner als 11/5 ist eine Lösung.
Die Lösungsmenge ist (x|x
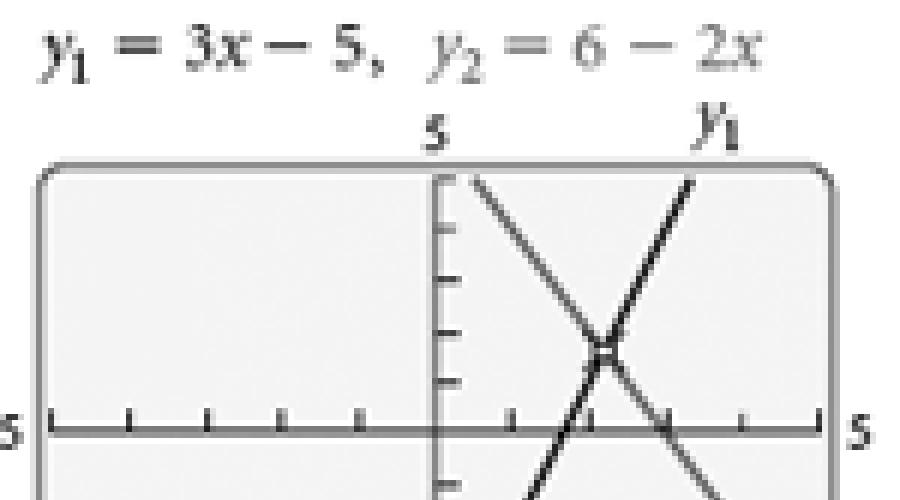
Zur Überprüfung können wir einen Graphen von y 1 = 3x - 5 und y 2 = 6 - 2x zeichnen. Dann ist klar, dass für x 
Die Lösungsmenge ist (x|x ≤ 1) oder (-∞, 1]. Der Graph der Lösungsmenge ist unten dargestellt. ![]()
Doppelte Ungleichungen
Wenn zwei Ungleichungen durch ein Wort verbunden sind Und, oder, dann entsteht es doppelte Ungleichheit. Doppelte Ungleichheit wie
-3
Und 2x + 5 ≤ 7
angerufen verbunden, weil es nutzt Und. Eintrag -3 Doppelte Ungleichungen können mithilfe der Prinzipien der Addition und Multiplikation von Ungleichungen gelöst werden.
Beispiel 2 Lösen Sie -3 Lösung Wir haben
Lösungsmenge (x|x ≤ -1 oder x > 3). Wir können die Lösung auch in Intervallnotation und dem Symbol für schreiben Verbände oder unter Einbeziehung beider Mengen: (-∞ -1] (3, ∞). Der Graph der Lösungsmenge ist unten dargestellt. 
Zur Überprüfung zeichnen wir y 1 = 2x - 5, y 2 = -7 und y 3 = 1 auf. Beachten Sie, dass für (x|x ≤ -1 oder x > 3), y 1 ≤ y 2 oder y 1 > y 3 . 
Ungleichungen mit Absolutwert (Modul)
Ungleichungen enthalten manchmal Moduli. Zur Lösung werden die folgenden Eigenschaften verwendet.
Für einen > 0 und algebraischen Ausdruck x:
|x| |x| > a ist äquivalent zu x oder x > a.
Ähnliche Aussagen für |x| ≤ a und |x| ≥ a.
Zum Beispiel,
|x| |y| ≥ 1 entspricht y ≤ -1 oder y ≥ 1;
und |2x + 3| ≤ 4 entspricht -4 ≤ 2x + 3 ≤ 4.
Beispiel 4 Lösen Sie jede der folgenden Ungleichungen. Stellen Sie die Menge der Lösungen grafisch dar.
a) |3x + 2| b) |5 - 2x| ≥ 1
Lösung
a) |3x + 2|

b) |5 - 2x| ≥ 1
Die Lösungsmenge ist (x|x ≤ 2 oder x ≥ 3) oder (-∞, 2].
Schauen wir uns die gleiche Ungleichung noch einmal an und f (x) > b, Wenn a>0 Und B<0 .
Also das Diagramm in Abbildung 3:

Ein Beispiel für die Lösung einer Ungleichung (1/3) x + 2 > –9. Wie wir feststellen, ist (1/3) x + 2 immer größer als Null, egal welche Zahl wir für x einsetzen.
Antwort: (–∞; +∞) .
Wie werden Ungleichungen der Form gelöst? und f(x)< b , Wo a>1 Und b>0?
Diagramm in Abbildung 4:

Und das folgende Beispiel: 3 3 – x ≥ 8.
Da also 3 > 1 und 8 > 0 ist
3 – x > log 3 8, das heißt
–x > log 3 8 – 3,
X< 3 – log
3 8.
Antwort: (0; 3–log 3 8) .
Wie kann sich die Lösung der Ungleichheit ändern? und f(x)< b
, bei 0
Diagramm in Abbildung 5:

Und das folgende Beispiel: Ungleichung lösen 0,6 2x – 3< 0,36 .
Wenn wir dem Diagramm in Abbildung 5 folgen, erhalten wir
2x – 3 > log 0,6 0,36,
2x – 3 > 2,
2x > 5,
x > 2,5
Antwort: (2,5; +∞) .
Betrachten wir das letzte Schema zur Lösung einer Ungleichung der Form und f(x)< b , bei a>0 Und B<0 , dargestellt in Abbildung 6:

Lösen wir zum Beispiel die Ungleichung:

Wir stellen fest, dass die linke Seite der Ungleichung immer größer als Null ist, egal welche Zahl wir für x einsetzen, und in unserem Fall ist dieser Ausdruck kleiner als -8, d. h. und Null, was bedeutet, dass es keine Lösungen gibt.
Antwort: keine Lösungen.
Wenn Sie wissen, wie Sie die einfachsten exponentiellen Ungleichungen lösen, können Sie fortfahren Lösung exponentieller Ungleichungen.
Beispiel 1.
Finden Sie den größten ganzzahligen Wert von x, der die Ungleichung erfüllt

Da 6 x größer als Null ist (bei keinem x geht der Nenner auf Null), multiplizieren wir beide Seiten der Ungleichung mit 6 x und erhalten:
440 – 2 6 2x > 8, dann
– 2 6 2x > 8 – 440,
– 2 6 2х > – 332,
6 2x< 216,
2x< 3,
X< 1,5. Наибольшее целое число из помежутка (–∞; 1,5) это число 1.
Antwort: 1.
Beispiel 2.
Ungleichheit lösen 2 2 x – 3 2 x + 2 ≤ 0
Bezeichnen wir 2 x mit y, erhalten wir die Ungleichung y 2 – 3y + 2 ≤ 0 und lösen wir diese quadratische Ungleichung.
y 2 – 3y +2 = 0,
y 1 = 1 und y 2 = 2.
Die Äste der Parabel sind nach oben gerichtet, zeichnen wir ein Diagramm:

Dann ist die Lösung der Ungleichung Ungleichung 1< у < 2, вернемся к нашей переменной х и получим неравенство 1< 2 х < 2, решая которое и найдем ответ 0 < x < 1.
Antwort: (0; 1) .
Beispiel 3. Lösen Sie die Ungleichung 5 x +1 – 3 x +2< 2·5 x – 2·3 x –1
Sammeln wir Ausdrücke mit den gleichen Basen in einem Teil der Ungleichung
5 x +1 – 2 5 x< 3 x +2 – 2·3 x –1
Nehmen wir aus den Klammern auf der linken Seite der Ungleichung 5 x und auf der rechten Seite der Ungleichung 3 x und wir erhalten die Ungleichung
5 x (5 – 2)< 3 х (9 – 2/3),
3·5 x< (25/3)·3 х
Teilen Sie beide Seiten der Ungleichung durch den Ausdruck 3 3 x, das Vorzeichen der Ungleichung ändert sich nicht, da 3 3 x eine positive Zahl ist, erhalten wir die Ungleichung:


X< 2 (так как 5/3 > 1).
Antwort: (–∞; 2) .
Wenn Sie Fragen zum Lösen exponentieller Ungleichungen haben oder das Lösen ähnlicher Beispiele üben möchten, melden Sie sich für meine Lektionen an. Nachhilfelehrerin Valentina Galinevskaya.
Wenn Sie Material ganz oder teilweise kopieren, ist ein Link zur Quelle erforderlich.
Ungleichheiten online lösen
Bevor Sie Ungleichungen lösen, müssen Sie gut verstehen, wie Gleichungen gelöst werden.
Es spielt keine Rolle, ob die Ungleichung streng () oder nicht streng (≤, ≥) ist. Der erste Schritt besteht darin, die Gleichung zu lösen, indem das Ungleichheitszeichen durch Gleichheit (=) ersetzt wird.
Lassen Sie uns erklären, was es bedeutet, eine Ungleichung zu lösen.
Nach dem Studium der Gleichungen entsteht im Kopf des Schülers folgendes Bild: Er muss Werte der Variablen finden, damit beide Seiten der Gleichung die gleichen Werte annehmen. Mit anderen Worten: Finden Sie alle Punkte, an denen Gleichheit gilt. Alles ist richtig!
Wenn wir von Ungleichungen sprechen, meinen wir das Finden von Intervallen (Segmenten), in denen die Ungleichung gilt. Wenn die Ungleichung zwei Variablen enthält, sind nicht mehr Intervalle die Lösung, sondern einige Flächen auf der Ebene. Raten Sie selbst, was die Lösung für eine Ungleichheit in drei Variablen sein wird?
Wie löst man Ungleichheiten?
Auf universelle Weise Lösungen für Ungleichungen gelten als Intervallmethode (auch Intervallmethode genannt), die darin besteht, alle Intervalle zu bestimmen, innerhalb deren Grenzen eine bestimmte Ungleichung erfüllt ist.
Ohne auf die Art der Ungleichung einzugehen, kommt es in diesem Fall nicht darauf an, Sie müssen die entsprechende Gleichung lösen und ihre Wurzeln bestimmen, gefolgt von der Bezeichnung dieser Lösungen auf der Zahlenachse.
Wie schreibt man die Lösung einer Ungleichung richtig?
Nachdem Sie die Lösungsintervalle für die Ungleichung bestimmt haben, müssen Sie die Lösung selbst korrekt aufschreiben. Essen wichtige Nuance– Sind die Grenzen der Intervalle in der Lösung enthalten?
Hier ist alles einfach. Wenn die Lösung der Gleichung die ODZ erfüllt und die Ungleichung nicht streng ist, wird der Rand des Intervalls in die Lösung der Ungleichung einbezogen. Ansonsten nein.
Betrachtet man jedes Intervall, kann die Lösung der Ungleichung das Intervall selbst oder ein halbes Intervall (wenn einer seiner Grenzen die Ungleichung erfüllt) oder ein Segment – das Intervall zusammen mit seinen Grenzen – sein.
Denken Sie nicht, dass nur Intervalle, Halbintervalle und Segmente die Ungleichung lösen können. Nein, die Lösung kann auch einzelne Punkte umfassen.
Zum Beispiel hat die Ungleichung |x|≤0 nur eine Lösung – das ist Punkt 0.
Und die Ungleichung |x|
Warum brauchen Sie einen Ungleichheitsrechner?
Der Ungleichungsrechner liefert die richtige Endantwort. In den meisten Fällen wird eine Abbildung einer Zahlenachse oder -ebene bereitgestellt. Es ist sichtbar, ob die Grenzen der Intervalle in die Lösung einbezogen werden oder nicht – die Punkte werden schattiert oder punktiert dargestellt.
Dank Online-Rechner Ungleichungen können Sie überprüfen, ob Sie die Wurzeln der Gleichung richtig gefunden, sie auf der Zahlenachse markiert und die Erfüllung der Ungleichheitsbedingung auf den Intervallen (und Grenzen) überprüft haben?
Wenn Ihre Antwort von der des Rechners abweicht, müssen Sie Ihre Lösung unbedingt noch einmal überprüfen und den Fehler identifizieren.
siehe auch Ein lineares Programmierproblem grafisch lösen, Kanonische Form linearer Programmierprobleme
Das System der Beschränkungen für ein solches Problem besteht aus Ungleichungen in zwei Variablen:
und die Zielfunktion hat die Form F = C 1 X + C 2 j was maximiert werden muss.
Beantworten wir die Frage: Welche Zahlenpaare ( X; j) sind Lösungen für das System der Ungleichungen, das heißt, erfüllen sie jede der Ungleichungen gleichzeitig? Mit anderen Worten: Was bedeutet es, ein System grafisch zu lösen?
Zuerst müssen Sie verstehen, was die Lösung für eine lineare Ungleichung mit zwei Unbekannten ist.
Eine lineare Ungleichung mit zwei Unbekannten zu lösen bedeutet, alle Paare unbekannter Werte zu bestimmen, für die die Ungleichung gilt.
Zum Beispiel Ungleichung 3 X
– 5j≥ 42 erfüllen Paare ( X , j) : (100, 2); (3, –10) usw. Die Aufgabe besteht darin, alle solchen Paare zu finden.
Betrachten wir zwei Ungleichungen: Axt
+ von≤ C, Axt + von≥ C. Gerade Axt + von = C teilt die Ebene in zwei Halbebenen, sodass die Koordinaten der Punkte einer von ihnen die Ungleichung erfüllen Axt + von >C und die andere Ungleichung Axt + +von <C.
Nehmen wir tatsächlich einen Punkt mit Koordinaten X = X 0 ; dann ein Punkt, der auf einer Geraden liegt und eine Abszisse hat X 0, hat eine Ordinate
Lassen Sie es zur Gewissheit kommen A< 0, B>0,
C>0. Alle Punkte mit Abszisse X 0 oben liegend P(zum Beispiel Punkt M), haben y M>j 0 und alle Punkte unterhalb des Punktes P, mit Abszisse X 0 , haben y N<j 0 . Seit X 0 ist ein beliebiger Punkt, dann wird es immer Punkte auf einer Seite der Linie geben, für die Axt+ von > C, eine Halbebene bildend, und auf der anderen Seite - Punkte für die Axt + von< C.

Abbildung 1
Das Ungleichheitszeichen in der Halbebene hängt von den Zahlen ab A, B , C.
Dies führt zu der folgenden Methode zur grafischen Lösung von Systemen lineare Ungleichungen aus zwei Variablen. Um das System zu lösen, benötigen Sie:
- Schreiben Sie für jede Ungleichung die dieser Ungleichung entsprechende Gleichung.
- Konstruieren Sie gerade Linien, die Graphen von durch Gleichungen angegebenen Funktionen sind.
- Bestimmen Sie für jede Gerade die Halbebene, die durch die Ungleichung gegeben ist. Nehmen Sie dazu einen beliebigen Punkt, der nicht auf einer Geraden liegt, und setzen Sie seine Koordinaten in die Ungleichung ein. Wenn die Ungleichung wahr ist, ist die Halbebene, die den gewählten Punkt enthält, die Lösung der ursprünglichen Ungleichung. Wenn die Ungleichung falsch ist, dann ist die Halbebene auf der anderen Seite der Linie die Lösungsmenge dieser Ungleichung.
- Um ein System von Ungleichungen zu lösen, ist es notwendig, die Schnittfläche aller Halbebenen zu finden, die die Lösung für jede Ungleichung des Systems darstellen.
Dieser Bereich kann sich als leer erweisen, dann hat das Ungleichungssystem keine Lösungen und ist inkonsistent. Ansonsten gilt das System als konsistent.
Es kann eine endliche Anzahl oder unendlich viele Lösungen geben. Die Fläche kann ein geschlossenes Polygon oder unbegrenzt sein.
Schauen wir uns drei relevante Beispiele an.
Beispiel 1. Lösen Sie das System grafisch:
X + j – 1 ≤ 0;
–2X - 2j + 5 ≤ 0.
- Betrachten Sie die Gleichungen x+y–1=0 und –2x–2y+5=0, die den Ungleichungen entsprechen;
- Konstruieren wir gerade Linien, die durch diese Gleichungen gegeben sind.

Abbildung 2
Definieren wir die durch die Ungleichungen definierten Halbebenen. Nehmen wir einen beliebigen Punkt, sei (0; 0). Lassen Sie uns überlegen X+ y– 1 0, ersetzen Sie den Punkt (0; 0): 0 + 0 – 1 ≤ 0. Das bedeutet, dass in der Halbebene, in der der Punkt (0; 0) liegt, X + j –
1 ≤ 0, d.h. die unter der Geraden liegende Halbebene ist eine Lösung der ersten Ungleichung. Wenn wir diesen Punkt (0; 0) in den zweiten einsetzen, erhalten wir: –2 ∙ 0 – 2 ∙ 0 + 5 ≤ 0, d.h. in der Halbebene, in der der Punkt (0; 0) liegt, –2 X – 2j+ 5≥ 0, und wir wurden gefragt, wo –2 X
– 2j+ 5 ≤ 0 also in der anderen Halbebene – in der über der Geraden.
Finden wir den Schnittpunkt dieser beiden Halbebenen. Die Geraden sind parallel, die Ebenen schneiden sich also nirgendwo, was bedeutet, dass das System dieser Ungleichungen keine Lösungen hat und inkonsistent ist.
Beispiel 2. Finden Sie grafisch Lösungen für das Ungleichungssystem: 
Abbildung 3
1. Schreiben wir die Gleichungen auf, die den Ungleichungen entsprechen, und konstruieren wir Geraden.
X + 2j– 2 = 0
| X | 2 | 0 |
| j | 0 | 1 |
j – X – 1 = 0
| X | 0 | 2 |
| j | 1 | 3 |
j + 2 = 0;
j = –2.
2. Nachdem wir den Punkt (0; 0) gewählt haben, bestimmen wir die Vorzeichen der Ungleichungen in den Halbebenen:
0 + 2 ∙ 0 – 2 ≤ 0, d.h. X + 2j– 2 ≤ 0 in der Halbebene unterhalb der Geraden;
0 – 0 – 1 ≤ 0, d.h. j –X– 1 ≤ 0 in der Halbebene unterhalb der Geraden;
0 + 2 =2 ≥ 0, d.h. j+ 2 ≥ 0 in der Halbebene über der Geraden.
3. Der Schnittpunkt dieser drei Halbebenen ergibt eine Fläche, die einem Dreieck entspricht. Es ist nicht schwierig, die Eckpunkte der Region als Schnittpunkte der entsprechenden Linien zu finden
Daher, A(–3; –2), IN(0; 1), MIT(6; –2).
Betrachten wir ein weiteres Beispiel, bei dem der resultierende Lösungsbereich des Systems nicht eingeschränkt ist.
Aber rationale Ungleichheiten können heute nicht alles lösen. Genauer gesagt kann nicht nur jeder entscheiden. Das können nur wenige Menschen.
Klitschko
Diese Lektion wird hart sein. So hart, dass nur die Auserwählten das Ende erreichen werden. Daher empfehle ich, vor dem Lesen Frauen, Katzen, schwangere Kinder und ... von Bildschirmen zu entfernen.
Komm schon, es ist eigentlich ganz einfach. Nehmen wir an, Sie beherrschen die Intervallmethode (wenn Sie sie noch nicht beherrschen, empfehle ich, noch einmal nachzulesen) und haben gelernt, wie man Ungleichungen der Form $P\left(x \right) \gt 0$ löst, wobei $ P\left(x \right)$ ist ein Polynom oder Produkt von Polynomen.
Ich glaube, dass es Ihnen nicht schwer fallen wird, zum Beispiel so etwas zu lösen (probieren Sie es übrigens zum Aufwärmen):
\[\begin(align) & \left(2((x)^(2))+3x+4 \right)\left(4x+25 \right) \gt 0; \\ & x\left(2((x)^(2))-3x-20 \right)\left(x-1 \right)\ge 0; \\ & \left(8x-((x)^(4)) \right)((\left(x-5 \right))^(6))\le 0. \\ \end(align)\]
Jetzt komplizieren wir das Problem ein wenig und betrachten nicht nur Polynome, sondern sogenannte rationale Brüche der Form:
wobei $P\left(x \right)$ und $Q\left(x \right)$ dieselben Polynome der Form $((a)_(n))((x)^(n))+( ( a)_(n-1))((x)^(n-1))+...+((a)_(0))$, oder das Produkt solcher Polynome.
Dies wird eine rationale Ungleichheit sein. Der grundlegende Punkt ist das Vorhandensein der Variablen $x$ im Nenner. Dies sind beispielsweise rationale Ungleichungen:
\[\begin(align) & \frac(x-3)(x+7) \lt 0; \\ & \frac(\left(7x+1 \right)\left(11x+2 \right))(13x-4)\ge 0; \\ & \frac(3((x)^(2))+10x+3)(((\left(3-x \right))^(2))\left(4-((x)^( 2)) \right))\ge 0. \\ \end(align)\]
Und das ist keine rationale Ungleichung, sondern die häufigste Ungleichung, die mit der Intervallmethode gelöst werden kann:
\[\frac(((x)^(2))+6x+9)(5)\ge 0\]
Mit Blick auf die Zukunft sage ich gleich: Es gibt mindestens zwei Möglichkeiten, rationale Ungleichungen zu lösen, aber alle laufen auf die eine oder andere Weise auf die uns bereits bekannte Intervallmethode hinaus. Bevor wir diese Methoden analysieren, erinnern wir uns daher an die alten Fakten, sonst ergibt das neue Material keinen Sinn.
Was Sie bereits wissen müssen
Es gibt nie zu viele wichtige Fakten. Wir brauchen wirklich nur vier.
Abgekürzte Multiplikationsformeln
Ja, ja: Sie werden uns im gesamten Mathematiklehrplan der Schule verfolgen. Und auch an der Universität. Es gibt eine ganze Reihe dieser Formeln, aber wir brauchen nur Folgendes:
\[\begin(align) & ((a)^(2))\pm 2ab+((b)^(2))=((\left(a\pm b \right))^(2)); \\ & ((a)^(2))-((b)^(2))=\left(a-b \right)\left(a+b \right); \\ & ((a)^(3))+((b)^(3))=\left(a+b \right)\left(((a)^(2))-ab+((b) ^(2)) \right); \\ & ((a)^(3))-((b)^(3))=\left(a-b \right)\left(((a)^(2))+ab+((b)^( 2))\richtig). \\ \end(align)\]
Achten Sie auf die letzten beiden Formeln – das sind die Summe und Differenz von Würfeln (und nicht der Würfel der Summe oder Differenz!). Sie sind leicht zu merken, wenn Sie bemerken, dass das Vorzeichen in der ersten Klammer mit dem Vorzeichen im Originalausdruck übereinstimmt und in der zweiten Klammer dem Vorzeichen im Originalausdruck entgegengesetzt ist.
Lineare Gleichungen
Das sind die meisten einfache Gleichungen der Form $ax+b=0$, wobei $a$ und $b$ gewöhnliche Zahlen sind und $a\ne 0$. Diese Gleichung lässt sich einfach lösen:
\[\begin(align) & ax+b=0; \\&ax=-b; \\ & x=-\frac(b)(a). \\ \end(align)\]
Ich möchte anmerken, dass wir das Recht haben, durch den Koeffizienten $a$ zu dividieren, da $a\ne 0$ ist. Diese Anforderung ist ziemlich logisch, da wir für $a=0$ Folgendes erhalten:
Erstens gibt es in dieser Gleichung keine Variable $x$. Dies sollte uns im Allgemeinen nicht verwirren (das kommt beispielsweise in der Geometrie häufig vor), aber es handelt sich dennoch nicht mehr um eine lineare Gleichung.
Zweitens hängt die Lösung dieser Gleichung ausschließlich vom Koeffizienten $b$ ab. Wenn $b$ ebenfalls Null ist, dann hat unsere Gleichung die Form $0=0$. Diese Gleichheit gilt immer; das bedeutet, dass $x$ eine beliebige Zahl ist (normalerweise so geschrieben: $x\in \mathbb(R)$). Wenn der Koeffizient $b$ ungleich Null ist, dann ist die Gleichheit $b=0$ nie erfüllt, d.h. Es gibt keine Antworten (schreiben Sie $x\in \varnothing $ und lesen Sie „die Lösungsmenge ist leer“).
Um all diese Schwierigkeiten zu vermeiden, nehmen wir einfach $a\ne 0$ an, was uns in unserem weiteren Denken keineswegs einschränkt.
Quadratische Gleichungen
Ich möchte Sie daran erinnern, dass eine quadratische Gleichung so heißt:
Hier links ist ein Polynom zweiten Grades und wieder $a\ne 0$ (sonst erhalten wir statt einer quadratischen Gleichung eine lineare). Die folgenden Gleichungen werden durch die Diskriminante gelöst:
- Wenn $D \gt 0$, erhalten wir zwei verschiedene Wurzeln;
- Wenn $D=0$, dann ist die Wurzel dieselbe, aber von der zweiten Multiplizität (was für eine Multiplizität ist das und wie wird sie berücksichtigt – dazu später mehr). Oder wir können sagen, dass die Gleichung zwei identische Wurzeln hat;
- Für $D \lt 0$ gibt es überhaupt keine Wurzeln und das Vorzeichen des Polynoms $a((x)^(2))+bx+c$ für jedes $x$ stimmt mit dem Vorzeichen des Koeffizienten $a überein $. Dies ist übrigens eine sehr nützliche Tatsache, über die sie im Algebraunterricht aus irgendeinem Grund vergessen, zu sprechen.
Die Wurzeln selbst werden nach der bekannten Formel berechnet:
\[((x)_(1,2))=\frac(-b\pm \sqrt(D))(2a)\]
Daher übrigens auch die Einschränkungen der Diskriminante. Schließlich Quadratwurzel einer negativen Zahl existiert nicht. Viele Schüler haben ein schreckliches Durcheinander in ihren Köpfen, was Wurzeln betrifft, deshalb habe ich extra eine ganze Lektion aufgeschrieben: Was ist eine Wurzel in der Algebra und wie man sie berechnet – ich empfehle dringend, sie zu lesen :).
Operationen mit rationalen Brüchen
Sie wissen bereits alles, was oben geschrieben wurde, wenn Sie die Intervallmethode studiert haben. Aber was wir jetzt analysieren werden, hat keine Analogien in der Vergangenheit – das ist eine völlig neue Tatsache.
Definition. Ein rationaler Bruch ist ein Ausdruck der Form
\[\frac(P\left(x \right))(Q\left(x \right))\]
wobei $P\left(x \right)$ und $Q\left(x \right)$ Polynome sind.
Offensichtlich ist es einfach, aus einem solchen Bruch eine Ungleichung zu erhalten – Sie müssen nur das Zeichen „größer als“ oder „kleiner als“ rechts hinzufügen. Und etwas weiter werden wir feststellen, dass das Lösen solcher Probleme ein Vergnügen ist, alles ist sehr einfach.
Probleme beginnen, wenn in einem Ausdruck mehrere solcher Brüche vorkommen. Sie müssen auf einen gemeinsamen Nenner gebracht werden – und das ist in diesem Moment erlaubt große Zahl beleidigende Fehler.
Deshalb für erfolgreiche Lösung rationale Gleichungen Zwei Fähigkeiten müssen fest beherrscht werden:
- Faktorisierung des Polynoms $P\left(x \right)$;
- Eigentlich geht es darum, Brüche auf einen gemeinsamen Nenner zu bringen.
Wie faktorisiert man ein Polynom? Ganz einfach. Lassen Sie uns ein Polynom der Form haben
Wir setzen es mit Null gleich. Wir erhalten eine Gleichung $n$ten Grades:
\[((a)_(n))((x)^(n))+((a)_(n-1))((x)^(n-1))+...+(( a)_(1))x+((a)_(0))=0\]
Nehmen wir an, wir haben diese Gleichung gelöst und die Wurzeln $((x)_(1)),\ ...,\ ((x)_(n))$ erhalten (seien Sie nicht beunruhigt: In den meisten Fällen wird dies der Fall sein nicht mehr als zwei dieser Wurzeln). In diesem Fall kann unser ursprüngliches Polynom wie folgt umgeschrieben werden:
\[\begin(align) & P\left(x \right)=((a)_(n))((x)^(n))+((a)_(n-1))((x )^(n-1))+...+((a)_(1))x+((a)_(0))= \\ & =((a)_(n))\left(x -((x)_(1)) \right)\cdot \left(x-((x)_(2)) \right)\cdot ...\cdot \left(x-((x)_( n)) \right) \end(align)\]
Das ist es! Bitte beachten Sie: Der führende Koeffizient $((a)_(n))$ ist nirgendwo verschwunden – er wird als separater Multiplikator vor den Klammern stehen und kann bei Bedarf in jede dieser Klammern eingefügt werden (Übung zeigt). dass es bei $((a)_ (n))\ne \pm 1$ fast immer Brüche zwischen den Wurzeln gibt).
Aufgabe. Vereinfachen Sie den Ausdruck:
\[\frac(((x)^(2))+x-20)(x-4)-\frac(2((x)^(2))-5x+3)(2x-3)-\ frac(4-8x-5((x)^(2)))(x+2)\]
Lösung. Schauen wir uns zunächst die Nenner an: Sie sind alle lineare Binome, und hier gibt es nichts zu faktorisieren. Lassen Sie uns also die Zähler faktorisieren:
\[\begin(align) & ((x)^(2))+x-20=\left(x+5 \right)\left(x-4 \right); \\ & 2((x)^(2))-5x+3=2\left(x-\frac(3)(2) \right)\left(x-1 \right)=\left(2x- 3 \right)\left(x-1 \right); \\ & 4-8x-5((x)^(2))=-5\left(x+2 \right)\left(x-\frac(2)(5) \right)=\left(x +2 \right)\left(2-5x \right). \\\end(align)\]
Bitte beachten Sie: Im zweiten Polynom erschien der führende Koeffizient „2“ in voller Übereinstimmung mit unserem Schema zuerst vor der Klammer und wurde dann in die erste Klammer aufgenommen, da dort der Bruch erschien.
Das Gleiche geschah im dritten Polynom, nur dass dort auch die Reihenfolge der Terme umgekehrt ist. Der Koeffizient „−5“ wurde jedoch letztendlich in die zweite Klammer aufgenommen (denken Sie daran: Sie können den Faktor in nur einer Klammer eingeben!), was uns die Unannehmlichkeiten erspart hat, die mit gebrochenen Wurzeln verbunden sind.
Was das erste Polynom betrifft, ist alles einfach: Seine Wurzeln werden entweder standardmäßig durch die Diskriminante oder mithilfe des Satzes von Vieta gesucht.
Kehren wir zum ursprünglichen Ausdruck zurück und schreiben ihn mit faktorisierten Zählern neu:
\[\begin(matrix) \frac(\left(x+5 \right)\left(x-4 \right))(x-4)-\frac(\left(2x-3 \right)\left( x-1 \right))(2x-3)-\frac(\left(x+2 \right)\left(2-5x \right))(x+2)= \\ =\left(x+5 \right)-\left(x-1 \right)-\left(2-5x \right)= \\ =x+5-x+1-2+5x= \\ =5x+4. \\ \end(matrix)\]
Antwort: 5x+4$.
Wie Sie sehen, nichts Kompliziertes. Ein bisschen Mathematik für die 7. bis 8. Klasse und das war’s. Der Sinn aller Transformationen besteht darin, aus einem komplexen und beängstigenden Ausdruck etwas Einfaches und Leicht zu bearbeitendes zu machen.
Dies wird jedoch nicht immer der Fall sein. Nun werden wir uns einem ernsteren Problem zuwenden.
Aber zuerst wollen wir herausfinden, wie man zwei Brüche auf einen gemeinsamen Nenner bringt. Der Algorithmus ist äußerst einfach:
- Faktorisieren Sie beide Nenner;
- Betrachten Sie den ersten Nenner und addieren Sie dazu die Faktoren, die im zweiten Nenner vorhanden sind, im ersten jedoch nicht. Das resultierende Produkt wird der gemeinsame Nenner sein;
- Finden Sie heraus, welche Faktoren jedem der ursprünglichen Brüche fehlen, damit die Nenner dem gemeinsamen Nenner entsprechen.
Für Sie mag dieser Algorithmus einfach wie Text mit „vielen Buchstaben“ erscheinen. Schauen wir uns daher alles anhand eines konkreten Beispiels an.
Aufgabe. Vereinfachen Sie den Ausdruck:
\[\left(\frac(x)(((x)^(2))+2x+4)+\frac(((x)^(2))+8)(((x)^(3) )-8)-\frac(1)(x-2) \right)\cdot \left(\frac(((x)^(2)))(((x)^(2))-4)- \frac(2)(2-x) \right)\]
Lösung. Es ist besser, solch große Probleme in Teilen zu lösen. Schreiben wir auf, was in der ersten Klammer steht:
\[\frac(x)(((x)^(2))+2x+4)+\frac(((x)^(2))+8)(((x)^(3))-8 )-\frac(1)(x-2)\]
Im Gegensatz zum vorherigen Problem sind die Nenner hier nicht so einfach. Lassen Sie uns jeden von ihnen berücksichtigen.
Das quadratische Trinom $((x)^(2))+2x+4$ kann nicht faktorisiert werden, da die Gleichung $((x)^(2))+2x+4=0$ keine Wurzeln hat (die Diskriminante ist negativ). ). Wir lassen es unverändert.
Der zweite Nenner – das kubische Polynom $((x)^(3))-8$ – ist bei sorgfältiger Betrachtung die Differenz von Würfeln und lässt sich leicht mit den abgekürzten Multiplikationsformeln erweitern:
\[((x)^(3))-8=((x)^(3))-((2)^(3))=\left(x-2 \right)\left(((x) ^(2))+2x+4 \right)\]
Nichts anderes kann faktorisiert werden, da in der ersten Klammer ein lineares Binomial steht und in der zweiten eine uns bereits bekannte Konstruktion, die keine wirklichen Wurzeln hat.
Der dritte Nenner schließlich ist ein lineares Binomial, das nicht erweitert werden kann. Somit wird unsere Gleichung die Form annehmen:
\[\frac(x)(((x)^(2))+2x+4)+\frac(((x)^(2))+8)(\left(x-2 \right)\left (((x)^(2))+2x+4 \right))-\frac(1)(x-2)\]
Es ist ganz offensichtlich, dass der gemeinsame Nenner genau $\left(x-2 \right)\left(((x)^(2))+2x+4 \right)$ sein wird, und alle Brüche darauf zu reduzieren Es ist notwendig, den ersten Bruch mit $\left(x-2 \right)$ und den letzten mit $\left(((x)^(2))+2x+4 \right)$ zu multiplizieren. Dann bleibt nur noch, ähnliche zu geben:
\[\begin(matrix) \frac(x\cdot \left(x-2 \right))(\left(x-2 \right)\left(((x)^(2))+2x+4 \ rechts))+\frac(((x)^(2))+8)(\left(x-2 \right)\left(((x)^(2))+2x+4 \right))- \frac(1\cdot \left(((x)^(2))+2x+4 \right))(\left(x-2 \right)\left(((x)^(2))+2x +4 \right))= \\ =\frac(x\cdot \left(x-2 \right)+\left(((x)^(2))+8 \right)-\left(((x )^(2))+2x+4 \right))(\left(x-2 \right)\left(((x)^(2))+2x+4 \right))= \\ =\frac (((x)^(2))-2x+((x)^(2))+8-((x)^(2))-2x-4)(\left(x-2 \right)\left (((x)^(2))+2x+4 \right))= \\ =\frac(((x)^(2))-4x+4)(\left(x-2 \right)\ left(((x)^(2))+2x+4 \right)). \\ \end(matrix)\]
Achten Sie auf die zweite Zeile: wenn der Nenner bereits gemeinsam ist, d.h. Anstelle von drei separaten Brüchen haben wir einen großen geschrieben; Sie sollten die Klammern nicht sofort entfernen. Es ist besser, eine zusätzliche Zeile zu schreiben und zu beachten, dass beispielsweise vor dem dritten Bruch ein Minus stand – und es nirgendwo hingeht, sondern im Zähler vor der Klammer „hängt“. Das erspart Ihnen viele Fehler.
Nun, in der letzten Zeile ist es nützlich, den Zähler zu faktorisieren. Darüber hinaus handelt es sich um ein exaktes Quadrat, und auch hier kommen uns abgekürzte Multiplikationsformeln zu Hilfe. Wir haben:
\[\frac(((x)^(2))-4x+4)(\left(x-2 \right)\left(((x)^(2))+2x+4 \right))= \frac(((\left(x-2 \right))^(2)))(\left(x-2 \right)\left(((x)^(2))+2x+4 \right) )=\frac(x-2)(((x)^(2))+2x+4)\]
Gehen wir nun genauso mit der zweiten Klammer um. Hier schreibe ich einfach eine Kette von Gleichheiten:
\[\begin(matrix) \frac(((x)^(2)))(((x)^(2))-4)-\frac(2)(2-x)=\frac((( x)^(2)))(\left(x-2 \right)\left(x+2 \right))-\frac(2)(2-x)= \\ =\frac(((x) ^(2)))(\left(x-2 \right)\left(x+2 \right))+\frac(2)(x-2)= \\ =\frac(((x)^( 2)))(\left(x-2 \right)\left(x+2 \right))+\frac(2\cdot \left(x+2 \right))(\left(x-2 \right )\cdot \left(x+2 \right))= \\ =\frac(((x)^(2))+2\cdot \left(x+2 \right))(\left(x-2 \right)\left(x+2 \right))=\frac(((x)^(2))+2x+4)(\left(x-2 \right)\left(x+2 \right) ). \\ \end(matrix)\]
Kehren wir zum ursprünglichen Problem zurück und schauen uns das Produkt an:
\[\frac(x-2)(((x)^(2))+2x+4)\cdot \frac(((x)^(2))+2x+4)(\left(x-2 \right)\left(x+2 \right))=\frac(1)(x+2)\]
Antwort: \[\frac(1)(x+2)\].
Der Sinn dieser Aufgabe ist derselbe wie bei der vorherigen: zu zeigen, wie rationale Ausdrücke vereinfacht werden können, wenn man ihre Transformation mit Bedacht angeht.
Und jetzt, da Sie das alles wissen, kommen wir zum Hauptthema der heutigen Lektion – der Lösung gebrochener rationaler Ungleichungen. Darüber hinaus werden Sie nach einer solchen Vorbereitung die Ungleichheiten selbst wie Nüsse auflösen :)
Der wichtigste Weg, rationale Ungleichheiten zu lösen
Es gibt mindestens zwei Ansätze zur Lösung rationaler Ungleichungen. Nun schauen wir uns eine davon an – diejenige, die im Mathematikunterricht der Schule allgemein akzeptiert wird.
Aber lassen Sie uns zunächst ein wichtiges Detail beachten. Alle Ungleichungen werden in zwei Typen unterteilt:
- Streng: $f\left(x \right) \gt 0$ oder $f\left(x \right) \lt 0$;
- Lax: $f\left(x \right)\ge 0$ oder $f\left(x \right)\le 0$.
Ungleichungen der zweiten Art lassen sich leicht auf die erste reduzieren, ebenso wie die Gleichung:
Diese kleine „Addition“ $f\left(x \right)=0$ führt zu so etwas Unangenehmem wie gefüllten Punkten – wir haben sie in der Intervallmethode kennengelernt. Ansonsten gibt es keine Unterschiede zwischen strengen und nicht strengen Ungleichungen. Schauen wir uns also den universellen Algorithmus an:
- Sammeln Sie alle Nicht-Null-Elemente auf einer Seite des Ungleichheitszeichens. Zum Beispiel links;
- Reduzieren Sie alle Brüche auf einen gemeinsamen Nenner (falls es mehrere solcher Brüche gibt), bringen Sie ähnliche Brüche mit. Faktorisieren Sie dann, wenn möglich, Zähler und Nenner. Auf die eine oder andere Weise erhalten wir eine Ungleichung der Form $\frac(P\left(x \right))(Q\left(x \right))\vee 0$, wobei das „Häkchen“ das Ungleichheitszeichen ist .
- Wir setzen den Zähler mit Null gleich: $P\left(x \right)=0$. Wir lösen diese Gleichung und erhalten die Wurzeln $((x)_(1))$, $((x)_(2))$, $((x)_(3))$, ... Dann benötigen wir dass der Nenner ungleich Null war: $Q\left(x \right)\ne 0$. Natürlich müssen wir im Wesentlichen die Gleichung $Q\left(x \right)=0$ lösen und erhalten die Wurzeln $x_(1)^(*)$, $x_(2)^(*)$ , $x_(3 )^(*)$, ... (in realen Problemen wird es kaum mehr als drei solcher Wurzeln geben).
- Wir markieren alle diese Wurzeln (sowohl mit als auch ohne Sternchen) auf einem einzigen Zahlenstrahl, und die Wurzeln ohne Sterne werden übermalt, und diejenigen mit Sternen werden durchstochen.
- Wir platzieren die „Plus“- und „Minus“-Zeichen und wählen die Intervalle aus, die wir benötigen. Wenn die Ungleichung die Form $f\left(x \right) \gt 0$ hat, dann sind die mit einem „Plus“ gekennzeichneten Intervalle die Antwort. Wenn $f\left(x \right) \lt 0$, dann betrachten wir die Intervalle mit „Minuspunkten“.
Die Praxis zeigt, dass die Punkte 2 und 4 die größten Schwierigkeiten bereiten – kompetente Transformationen und die richtige Anordnung der Zahlen in aufsteigender Reihenfolge. Seien Sie beim letzten Schritt äußerst vorsichtig: Wir platzieren die Schilder immer basierend auf die allerletzte Ungleichung, die geschrieben wurde, bevor mit den Gleichungen fortgefahren wird. Das universelle Regel, geerbt von der Intervallmethode.
Es gibt also ein Schema. Lasst uns üben.
Aufgabe. Lösen Sie die Ungleichung:
\[\frac(x-3)(x+7) \lt 0\]
Lösung. Wir haben eine strikte Ungleichung der Form $f\left(x \right) \lt 0$. Offensichtlich sind die Punkte 1 und 2 aus unserem Diagramm bereits erfüllt: Alle Elemente der Ungleichheit sind auf der linken Seite gesammelt, es besteht keine Notwendigkeit, etwas auf einen gemeinsamen Nenner zu bringen. Kommen wir daher gleich zum dritten Punkt.
Wir setzen den Zähler mit Null gleich:
\[\begin(align) & x-3=0; \\ & x=3. \end(align)\]
Und der Nenner:
\[\begin(align) & x+7=0; \\ & ((x)^(*))=-7. \\ \end(align)\]
Hier stecken viele Menschen fest, denn theoretisch muss man $x+7\ne 0$ aufschreiben, wie es die ODZ verlangt (man kann nicht durch Null dividieren, das ist alles). Aber in Zukunft werden wir die Punkte, die sich aus dem Nenner ergeben, herausstreichen, damit Sie Ihre Berechnungen nicht noch einmal komplizieren müssen – schreiben Sie überall ein Gleichheitszeichen und machen Sie sich keine Sorgen. Dafür wird niemand Punkte abziehen :)
Vierter Punkt. Wir markieren die resultierenden Wurzeln auf dem Zahlenstrahl:
Alle Punkte sind festgehalten, da die Ungleichung streng ist
Bitte beachten Sie: Alle Punkte sind festgelegt, da die ursprüngliche Ungleichung streng ist. Dabei spielt es keine Rolle, ob diese Punkte vom Zähler oder vom Nenner stammen.
Schauen wir uns die Zeichen an. Nehmen wir eine beliebige Zahl $((x)_(0)) \gt 3$. Zum Beispiel $((x)_(0))=100$ (aber mit dem gleichen Erfolg könnte man $((x)_(0))=3,1$ oder $((x)_(0)) = nehmen 1\ 000\ 000$). Wir bekommen:
Rechts von allen Wurzeln haben wir also einen positiven Bereich. Und beim Durchlaufen jeder Wurzel ändert sich das Vorzeichen (das wird nicht immer der Fall sein, aber dazu später mehr). Kommen wir also zum fünften Punkt: Ordnen Sie die Schilder an und wählen Sie das gewünschte aus:
Kehren wir zur letzten Ungleichung zurück, die vor der Lösung der Gleichungen bestand. Tatsächlich stimmt es mit dem Original überein, da wir in dieser Aufgabe keine Transformationen durchgeführt haben.
Da wir eine Ungleichung der Form $f\left(x \right) \lt 0$ lösen müssen, habe ich das Intervall $x\in \left(-7;3 \right)$ schattiert – es ist das einzige markierte mit einem Minuszeichen. Das ist die Antwort.
Antwort: $x\in \left(-7;3 \right)$
Das ist es! Ist es schwierig? Nein, es ist nicht schwierig. Es stimmt, die Aufgabe war einfach. Lassen Sie uns die Mission nun etwas verkomplizieren und eine „ausgefeiltere“ Ungleichung betrachten. Bei der Lösung werde ich nicht mehr so detaillierte Berechnungen anstellen, sondern lediglich die wichtigsten Punkte skizzieren. Im Allgemeinen formatieren wir es so, wie wir es formatieren würden selbständiges Arbeiten oder Prüfung :)
Aufgabe. Lösen Sie die Ungleichung:
\[\frac(\left(7x+1 \right)\left(11x+2 \right))(13x-4)\ge 0\]
Lösung. Dies ist eine nicht strikte Ungleichung der Form $f\left(x \right)\ge 0$. Alle von Null verschiedenen Elemente werden auf der linken Seite gesammelt, es gibt keine unterschiedlichen Nenner. Kommen wir zu den Gleichungen.
Zähler:
\[\begin(align) & \left(7x+1 \right)\left(11x+2 \right)=0 \\ & 7x+1=0\Rightarrow ((x)_(1))=-\ frac(1)(7); \\ & 11x+2=0\Rightarrow ((x)_(2))=-\frac(2)(11). \\ \end(align)\]
Nenner:
\[\begin(align) & 13x-4=0; \\ & 13x=4; \\ & ((x)^(*))=\frac(4)(13). \\ \end(align)\]
Ich weiß nicht, was für ein Perverser dieses Problem verursacht hat, aber die Wurzeln sind nicht besonders gut geworden: Es wäre schwierig, sie auf der Zahlengeraden zu platzieren. Und wenn mit der Wurzel $((x)^(*))=(4)/(13)\;$ alles mehr oder weniger klar ist (dies ist die einzige positive Zahl - sie steht rechts), dann $ ((x)_(1 ))=-(1)/(7)\;$ und $((x)_(2))=-(2)/(11)\;$ erfordern zusätzliche Forschung: welche ist größer?
Das können Sie zum Beispiel so herausfinden:
\[((x)_(1))=-\frac(1)(7)=-\frac(2)(14) \gt -\frac(2)(11)=((x)_(2 ))\]
Ich hoffe, es besteht keine Notwendigkeit zu erklären, warum der numerische Bruch $-(2)/(14)\; \gt -(2)/(11)\;$? Bei Bedarf empfehle ich, sich daran zu erinnern, wie man Operationen mit Brüchen durchführt.
Und wir markieren alle drei Wurzeln auf dem Zahlenstrahl:
Die Punkte des Zählers werden ausgefüllt, die Punkte des Nenners werden punktiert
Wir stellen Schilder auf. Sie können beispielsweise $((x)_(0))=1$ nehmen und das Vorzeichen an dieser Stelle herausfinden:
\[\begin(align) & f\left(x \right)=\frac(\left(7x+1 \right)\left(11x+2 \right))(13x-4); \\ & f\left(1 \right)=\frac(\left(7\cdot 1+1 \right)\left(11\cdot 1+2 \right))(13\cdot 1-4)=\ frac(8\cdot 13)(9) \gt 0. \\\end(align)\]
Die letzte Ungleichung vor den Gleichungen war $f\left(x \right)\ge 0$, daher interessiert uns das Pluszeichen.
Wir haben zwei Mengen: eine ist ein gewöhnliches Segment und die andere ist ein offener Strahl auf der Zahlengeraden.
Antwort: $x\in \left[ -\frac(2)(11);-\frac(1)(7) \right]\bigcup \left(\frac(4)(13);+\infty \right )$
Ein wichtiger Hinweis zu den Zahlen, die wir ersetzen, um das Vorzeichen im ganz rechten Intervall herauszufinden. Es ist absolut nicht notwendig, die Zahl zu ersetzen, die der Wurzel ganz rechts am nächsten liegt. Sie können Milliarden oder sogar „plus-unendlich“ nehmen – in diesem Fall wird das Vorzeichen des Polynoms in der Klammer, Zähler oder Nenner, allein durch das Vorzeichen des führenden Koeffizienten bestimmt.
Schauen wir uns noch einmal die Funktion $f\left(x \right)$ aus der letzten Ungleichung an:
Seine Notation enthält drei Polynome:
\[\begin(align) & ((P)_(1))\left(x \right)=7x+1; \\ & ((P)_(2))\left(x \right)=11x+2; \\ & Q\left(x \right)=13x-4. \end(align)\]
Bei allen handelt es sich um lineare Binome, und alle ihre führenden Koeffizienten (Zahlen 7, 11 und 13) sind positiv. Folglich sind beim Ersetzen sehr großer Zahlen auch die Polynome selbst positiv :).
Diese Regel mag übermäßig kompliziert erscheinen, aber nur auf den ersten Blick, wenn wir sehr einfache Probleme analysieren. Bei schwerwiegenden Ungleichungen können wir durch das Ersetzen von „plus-unendlich“ die Vorzeichen viel schneller herausfinden als mit dem Standardwert $((x)_(0))=100$.
Mit solchen Herausforderungen werden wir sehr bald konfrontiert sein. Aber schauen wir uns zunächst einen alternativen Weg zur Lösung gebrochener rationaler Ungleichungen an.
Alternativer Weg
Diese Technik wurde mir von einem meiner Schüler vorgeschlagen. Ich selbst habe es nie benutzt, aber die Praxis hat gezeigt, dass es für viele Studenten wirklich bequemer ist, Ungleichungen auf diese Weise zu lösen.
Die Ausgangsdaten sind also dieselben. Wir müssen die gebrochene rationale Ungleichung lösen:
\[\frac(P\left(x \right))(Q\left(x \right)) \gt 0\]
Überlegen wir: Warum ist das Polynom $Q\left(x \right)$ „schlechter“ als das Polynom $P\left(x \right)$? Warum müssen wir separate Gruppen von Wurzeln (mit und ohne Sternchen) betrachten, über punktierte Punkte nachdenken usw.? Es ist ganz einfach: Ein Bruch hat einen Definitionsbereich, nach dem der Bruch nur dann Sinn macht, wenn sein Nenner von Null verschieden ist.
Ansonsten gibt es keine Unterschiede zwischen Zähler und Nenner: Wir setzen es auch mit Null gleich, suchen die Wurzeln und markieren sie dann auf dem Zahlenstrahl. Warum also nicht den Bruchstrich (eigentlich das Divisionszeichen) durch die gewöhnliche Multiplikation ersetzen und alle Anforderungen der ODZ in Form einer separaten Ungleichung aufschreiben? Zum Beispiel so:
\[\frac(P\left(x \right))(Q\left(x \right)) \gt 0\Rightarrow \left\( \begin(align) & P\left(x \right)\cdot Q \left(x \right) \gt 0, \\ & Q\left(x \right)\ne 0. \\ \end(align) \right.\]
Bitte beachten Sie: Dieser Ansatz reduziert das Problem auf die Intervallmethode, erschwert die Lösung jedoch überhaupt nicht. Schließlich werden wir das Polynom $Q\left(x \right)$ immer noch mit Null gleichsetzen.
Mal sehen, wie das bei echten Problemen funktioniert.
Aufgabe. Lösen Sie die Ungleichung:
\[\frac(x+8)(x-11) \gt 0\]
Lösung. Kommen wir also zur Intervallmethode:
\[\frac(x+8)(x-11) \gt 0\Rightarrow \left\( \begin(align) & \left(x+8 \right)\left(x-11 \right) \gt 0 , \\ & x-11\ne 0. \\ \end(align) \right.\]
Die erste Ungleichung lässt sich auf elementare Weise lösen. Wir setzen einfach jede Klammer mit Null gleich:
\[\begin(align) & x+8=0\Rightarrow ((x)_(1))=-8; \\ & x-11=0\Rightarrow ((x)_(2))=11. \\ \end(align)\]
Die zweite Ungleichung ist ebenfalls einfach:
Markieren Sie die Punkte $((x)_(1))$ und $((x)_(2))$ auf dem Zahlenstrahl. Alle scheiden aus, da die Ungleichung streng ist:
Der richtige Punkt wurde zweimal ausgestochen. Das ist in Ordnung.Achten Sie auf den Punkt $x=11$. Es stellt sich heraus, dass es „zweifach gestochen“ ist: Einerseits stechen wir es wegen der Schwere der Ungleichheit heraus, andererseits, weil zusätzliche Anforderung ODZ.
In jedem Fall handelt es sich lediglich um eine punktierte Stelle. Deshalb ordnen wir die Vorzeichen für die Ungleichung $\left(x+8 \right)\left(x-11 \right) \gt 0$ – das letzte, das wir gesehen haben, bevor wir mit der Lösung der Gleichungen begonnen haben:
Uns interessieren positive Regionen, da wir eine Ungleichung der Form $f\left(x \right) \gt 0$ lösen – wir werden sie schattieren. Es bleibt nur noch, die Antwort aufzuschreiben.
Antwort. $x\in \left(-\infty ;-8 \right)\bigcup \left(11;+\infty \right)$
Am Beispiel dieser Lösung möchte ich Sie vor einem häufigen Fehler unter Studienanfängern warnen. Nämlich: Öffnen Sie niemals Klammern in Ungleichungen! Versuchen Sie im Gegenteil, alles zu berücksichtigen – das vereinfacht die Lösung und erspart Ihnen viele Probleme.
Versuchen wir nun etwas Komplizierteres.
Aufgabe. Lösen Sie die Ungleichung:
\[\frac(\left(2x-13 \right)\left(12x-9 \right))(15x+33)\le 0\]
Lösung. Dies ist eine nicht strikte Ungleichung der Form $f\left(x \right)\le 0$, daher müssen Sie hier genau auf die schattierten Punkte achten.
Kommen wir zur Intervallmethode:
\[\left\( \begin(align) & \left(2x-13 \right)\left(12x-9 \right)\left(15x+33 \right)\le 0, \\ & 15x+33\ ne 0. \\ \end(align) \right.\]
Kommen wir zur Gleichung:
\[\begin(align) & \left(2x-13 \right)\left(12x-9 \right)\left(15x+33 \right)=0 \\ & 2x-13=0\Rightarrow ((x )_(1))=6,5; \\ & 12x-9=0\Rightarrow ((x)_(2))=0.75; \\ & 15x+33=0\Rightarrow ((x)_(3))=-2.2. \\ \end(align)\]
Wir berücksichtigen die zusätzliche Anforderung:
Wir markieren alle resultierenden Wurzeln auf dem Zahlenstrahl:
Wenn ein Punkt sowohl punktiert als auch ausgefüllt ist, gilt er als punktiertAuch hier „überlappen“ sich zwei Punkte – das ist normal, das wird immer so sein. Es ist nur wichtig zu verstehen, dass es sich bei einem Punkt, der sowohl als durchstochen als auch als übermalt markiert ist, tatsächlich um eine durchstochene Stelle handelt. Diese. „Stechen“ ist eine stärkere Handlung als „Malen“.
Das ist absolut logisch, denn durch das Kneifen markieren wir Punkte, die das Vorzeichen der Funktion beeinflussen, selbst aber nicht an der Antwort beteiligt sind. Und wenn uns die Nummer irgendwann nicht mehr passt (zum Beispiel nicht in die ODZ), streichen wir sie bis zum Ende der Aufgabe aus der Betrachtung.
Hören Sie im Allgemeinen auf zu philosophieren. Wir platzieren Zeichen und übermalen die mit einem Minuszeichen gekennzeichneten Intervalle:
Antwort. $x\in \left(-\infty ;-2.2 \right)\bigcup \left[ 0.75;6.5 \right]$.
Und noch einmal wollte ich Sie auf diese Gleichung aufmerksam machen:
\[\left(2x-13 \right)\left(12x-9 \right)\left(15x+33 \right)=0\]
Nochmals: Öffnen Sie in solchen Gleichungen niemals die Klammern! Du wirst es dir nur noch schwerer machen. Denken Sie daran: Das Produkt ist gleich Null, wenn mindestens einer der Faktoren gleich Null ist. Somit, gegebene Gleichung es „zerfällt“ einfach in mehrere kleinere, die wir im vorherigen Problem gelöst haben.
Unter Berücksichtigung der Vielfalt der Wurzeln
Anhand der vorherigen Probleme ist leicht zu erkennen, dass die nichtstrikten Ungleichungen am schwierigsten sind, da man bei ihnen die schattierten Punkte im Auge behalten muss.
Aber es gibt noch ein noch größeres Übel auf der Welt: Ungleichheiten haben ihre vielfältigen Ursachen. Hier müssen Sie einigen schattierten Punkten nicht mehr folgen – hier darf sich das Ungleichheitszeichen beim Durchlaufen derselben Punkte nicht plötzlich ändern.
So etwas haben wir in dieser Lektion noch nicht betrachtet (obwohl bei der Intervallmethode häufig ein ähnliches Problem aufgetreten ist). Deshalb führen wir eine neue Definition ein:
Definition. Die Wurzel der Gleichung $((\left(x-a \right))^(n))=0$ ist gleich $x=a$ und wird Wurzel der $n$-ten Multiplizität genannt.
Eigentlich sind wir nicht besonders interessiert genauer Wert Vielzahl. Das Einzige, was zählt, ist, ob dieselbe Zahl $n$ gerade oder ungerade ist. Weil:
- Wenn $x=a$ eine Wurzel einer geraden Multiplizität ist, ändert sich das Vorzeichen der Funktion beim Durchlaufen nicht;
- Und umgekehrt, wenn $x=a$ eine Wurzel ungerader Multiplizität ist, ändert sich das Vorzeichen der Funktion.
Alle vorherigen Probleme, die in dieser Lektion behandelt werden, sind ein Sonderfall einer Wurzel einer ungeraden Multiplizität: Überall ist die Multiplizität gleich eins.
Und noch etwas. Bevor wir mit der Lösung von Problemen beginnen, möchte ich Sie auf eine Feinheit aufmerksam machen, die für einen erfahrenen Schüler offensichtlich erscheint, viele Anfänger jedoch in Erstaunen versetzt. Nämlich:
Die Wurzel der Multiplizität $n$ entsteht nur dann, wenn der gesamte Ausdruck mit dieser Potenz erhöht wird: $((\left(x-a \right))^(n))$ und nicht $\left(((x) ^( n))-a \right)$.
Noch einmal: Die Klammer $((\left(x-a \right))^(n))$ gibt uns die Wurzel $x=a$ der Multiplizität $n$, aber die Klammer $\left(((x)^( n)) -a \right)$ oder, wie es oft vorkommt, $(a-((x)^(n)))$ gibt uns eine Wurzel (oder zwei Wurzeln, wenn $n$ gerade ist) der ersten Multiplizität , unabhängig davon, was gleich $n$ ist.
Vergleichen:
\[((\left(x-3 \right))^(5))=0\Rightarrow x=3\left(5k \right)\]
Hier ist alles klar: Die gesamte Klammer wurde auf die fünfte Potenz angehoben, sodass wir am Ausgang die Wurzel der fünften Potenz erhalten haben. Und jetzt:
\[\left(((x)^(2))-4 \right)=0\Rightarrow ((x)^(2))=4\Rightarrow x=\pm 2\]
Wir haben zwei Wurzeln, aber beide haben eine erste Multiplizität. Oder hier ist noch eines:
\[\left(((x)^(10))-1024 \right)=0\Rightarrow ((x)^(10))=1024\Rightarrow x=\pm 2\]
Und lassen Sie sich vom zehnten Grad nicht aus der Ruhe bringen. Die Hauptsache ist, dass 10 eine gerade Zahl ist, also haben wir am Ausgang zwei Wurzeln, und beide haben wiederum das erste Vielfache.
Seien Sie im Allgemeinen vorsichtig: Multiplizität tritt nur auf, wenn Der Grad bezieht sich auf die gesamte Klammer, nicht nur auf die Variable.
Aufgabe. Lösen Sie die Ungleichung:
\[\frac(((x)^(2))((\left(6-x \right))^(3))\left(x+4 \right))(((\left(x+7 \right))^(5)))\ge 0\]
Lösung. Versuchen wir es zu lösen alternativer Weg— durch den Übergang vom Besonderen zum Produkt:
\[\left\( \begin(align) & ((x)^(2))((\left(6-x \right))^(3))\left(x+4 \right)\cdot ( (\left(x+7 \right))^(5))\ge 0, \\ & ((\left(x+7 \right))^(5))\ne 0. \\ \end(align )\Rechts.\]
Behandeln wir die erste Ungleichung mit der Intervallmethode:
\[\begin(align) & ((x)^(2))((\left(6-x \right))^(3))\left(x+4 \right)\cdot ((\left( x+7 \right))^(5))=0; \\ & ((x)^(2))=0\Rightarrow x=0\left(2k \right); \\ & ((\left(6-x \right))^(3))=0\Rightarrow x=6\left(3k \right); \\ & x+4=0\Rightarrow x=-4; \\ & ((\left(x+7 \right))^(5))=0\Rightarrow x=-7\left(5k \right). \\ \end(align)\]
Zusätzlich lösen wir die zweite Ungleichung. Tatsächlich haben wir es bereits gelöst, aber damit die Rezensenten nichts an der Lösung bemängeln, ist es besser, es noch einmal zu lösen:
\[((\left(x+7 \right))^(5))\ne 0\Rightarrow x\ne -7\]
Bitte beachten Sie: In der letzten Ungleichung gibt es keine Multiplizitäten. Tatsächlich: Welchen Unterschied macht es, wie oft man den Punkt $x=-7$ auf dem Zahlenstrahl streicht? Mindestens einmal, mindestens fünf Mal wird das Ergebnis das gleiche sein: eine durchstochene Stelle.
Markieren wir alles, was wir auf dem Zahlenstrahl haben:
Wie gesagt, der Punkt $x=-7$ wird irgendwann durchbrochen. Die Anordnung der Multiplizitäten basiert auf der Lösung der Ungleichung mithilfe der Intervallmethode.
Jetzt müssen nur noch die Schilder angebracht werden:
Da der Punkt $x=0$ eine Wurzel einer geraden Multiplizität ist, ändert sich das Vorzeichen beim Durchgang durch ihn nicht. Die übrigen Punkte haben eine ungerade Vielfachheit, und bei ihnen ist alles einfach.
Antwort. $x\in \left(-\infty ;-7 \right)\bigcup \left[ -4;6 \right]$
Achten Sie noch einmal auf $x=0$. Aufgrund der geraden Vielheit entsteht es interessanter Effekt: alles links davon wird übermalt, alles rechts davon wird ebenfalls übermalt und der Punkt selbst wird komplett übermalt.
Daher muss es beim Aufzeichnen der Antwort nicht isoliert werden. Diese. Es besteht keine Notwendigkeit, so etwas wie $x\in \left[ -4;0 \right]\bigcup \left[ 0;6 \right]$ zu schreiben (obwohl formal eine solche Antwort auch richtig wäre). Stattdessen schreiben wir sofort $x\in \left[ -4;6 \right]$.
Solche Effekte sind nur mit Wurzeln gerader Multiplizität möglich. Und im nächsten Problem werden wir auf die umgekehrte „Manifestation“ dieses Effekts stoßen. Sind Sie bereit?
Aufgabe. Lösen Sie die Ungleichung:
\[\frac(((\left(x-3 \right))^(4))\left(x-4 \right))(((\left(x-1 \right))^(2)) \left(7x-10-((x)^(2)) \right))\ge 0\]
Lösung. Diesmal folgen wir dem Standardschema. Wir setzen den Zähler mit Null gleich:
\[\begin(align) & ((\left(x-3 \right))^(4))\left(x-4 \right)=0; \\ & ((\left(x-3 \right))^(4))=0\Rightarrow ((x)_(1))=3\left(4k \right); \\ & x-4=0\Rightarrow ((x)_(2))=4. \\ \end(align)\]
Und der Nenner:
\[\begin(align) & ((\left(x-1 \right))^(2))\left(7x-10-((x)^(2)) \right)=0; \\ & ((\left(x-1 \right))^(2))=0\Rightarrow x_(1)^(*)=1\left(2k \right); \\ & 7x-10-((x)^(2))=0\Rightarrow x_(2)^(*)=5;\ x_(3)^(*)=2. \\ \end(align)\]
Da wir eine nicht strikte Ungleichung der Form $f\left(x \right)\ge 0$ lösen, werden die Wurzeln aus dem Nenner (die mit Sternchen versehen sind) herausgezogen und diejenigen aus dem Zähler schattiert.
Wir platzieren Schilder und schattieren die mit einem „Plus“ gekennzeichneten Bereiche:
Punkt $x=3$ ist isoliert. Dies ist ein Teil der Antwort
Bevor wir die endgültige Antwort niederschreiben, schauen wir uns das Bild genau an:
- Der Punkt $x=1$ hat eine gerade Multiplizität, ist aber selbst punktiert. Folglich muss es in der Antwort isoliert werden: Sie müssen $x\in \left(-\infty ;1 \right)\bigcup \left(1;2 \right)$ schreiben und nicht $x\in \left(-\ infty ;2 \right)$.
- Der Punkt $x=3$ hat ebenfalls eine gerade Multiplizität und ist schattiert. Die Anordnung der Schilder deutet darauf hin, dass der Punkt selbst zu uns passt, aber ein Schritt nach links oder rechts – und wir befinden uns in einem Bereich, der definitiv nicht zu uns passt. Solche Punkte heißen isoliert und werden in der Form $x\in \left\( 3 \right\)$ geschrieben.
Wir kombinieren alle erhaltenen Teile zu einem gemeinsamen Satz und schreiben die Antwort auf.
Antwort: $x\in \left(-\infty ;1 \right)\bigcup \left(1;2 \right)\bigcup \left\( 3 \right\)\bigcup \left[ 4;5 \right) $
Definition. Ungleichheit lösen bedeutet Finden Sie die Menge aller seiner Lösungen, oder beweisen Sie, dass diese Menge leer ist.
Es scheint: Was könnte hier unverständlich sein? Ja, Tatsache ist, dass Mengen auf unterschiedliche Weise definiert werden können. Schreiben wir noch einmal die Antwort auf die letzte Aufgabe auf:
Wir lesen buchstäblich, was geschrieben steht. Die Variable „x“ gehört zu einer bestimmten Menge, die durch Kombination (das „U“-Zeichen) von vier separaten Mengen erhalten wird:
- Intervall $\left(-\infty ;1 \right)$, was wörtlich „alle Zahlen kleiner als eins, aber nicht die Einheit selbst“ bedeutet;
- Intervall $\left(1;2 \right)$, d.h. „alle Zahlen im Bereich von 1 bis 2, aber nicht die Zahlen 1 und 2 selbst“;
- Die Menge $\left\( 3 \right\)$, bestehend aus einer einzigen Zahl – drei;
- Das Intervall $\left[ 4;5 \right)$ enthält alle Zahlen im Bereich von 4 bis 5 sowie die Vier selbst, aber nicht die Fünf.
Der dritte Punkt ist hier von Interesse. Im Gegensatz zu Intervallen, die unendliche Mengen von Zahlen definieren und nur die Grenzen dieser Mengen angeben, gibt die Menge $\left\( 3 \right\)$ durch Aufzählung genau eine Zahl an.
Um zu verstehen, dass wir bestimmte im Satz enthaltene Zahlen auflisten (und keine Grenzen oder irgendetwas anderes festlegen), werden geschweifte Klammern verwendet. Beispielsweise bedeutet die Notation $\left\( 1;2 \right\)$ genau „eine Menge bestehend aus zwei Zahlen: 1 und 2“, aber kein Segment von 1 bis 2. Verwechseln Sie diese Konzepte auf keinen Fall .
Regel zum Addieren von Vielfachen
Nun, zum Abschluss der heutigen Lektion noch eine kleine Dose von Pavel Berdov :)
Aufmerksame Studierende haben sich wahrscheinlich schon gefragt: Was passiert, wenn Zähler und Nenner die gleichen Wurzeln haben? Die folgende Regel funktioniert also:
Vielfalten identische Wurzeln zusammenklappen. Stets. Auch wenn diese Wurzel sowohl im Zähler als auch im Nenner vorkommt.
Manchmal ist es besser zu entscheiden als zu reden. Deshalb lösen wir das folgende Problem:
Aufgabe. Lösen Sie die Ungleichung:
\[\frac(((x)^(2))+6x+8)(\left(((x)^(2))-16 \right)\left(((x)^(2))+ 9x+14 \right))\ge 0\]
\[\begin(align) & ((x)^(2))+6x+8=0 \\ & ((x)_(1))=-2;\ ((x)_(2))= -4. \\ \end(align)\]
Noch nichts Besonderes. Wir setzen den Nenner mit Null gleich:
\[\begin(align) & \left(((x)^(2))-16 \right)\left(((x)^(2))+9x+14 \right)=0 \\ & ( (x)^(2))-16=0\Rightarrow x_(1)^(*)=4;\ x_(2)^(*)=-4; \\ & ((x)^(2))+9x+14=0\Rightarrow x_(3)^(*)=-7;\ x_(4)^(*)=-2. \\ \end(align)\]
Es wurden zwei identische Wurzeln entdeckt: $((x)_(1))=-2$ und $x_(4)^(*)=-2$. Beide haben die erste Multiplizität. Deshalb ersetzen wir sie durch eine Wurzel $x_(4)^(*)=-2$, aber mit einer Multiplizität von 1+1=2.
Darüber hinaus gibt es auch identische Wurzeln: $((x)_(2))=-4$ und $x_(2)^(*)=-4$. Sie sind auch von der ersten Multiplizität, sodass nur $x_(2)^(*)=-4$ der Multiplizität 1+1=2 übrig bleiben.
Bitte beachten Sie: In beiden Fällen haben wir genau die „punktierte“ Wurzel belassen und die „bemalte“ Wurzel aus der Betrachtung ausgeschlossen. Denn zu Beginn der Lektion waren wir uns einig: Wenn ein Punkt sowohl durchstochen als auch übermalt ist, dann betrachten wir ihn immer noch als durchstochen.
Als Ergebnis haben wir vier Wurzeln, die alle herausgeschnitten wurden:
\[\begin(align) & x_(1)^(*)=4; \\ & x_(2)^(*)=-4\left(2k \right); \\ & x_(3)^(*)=-7; \\ & x_(4)^(*)=-2\left(2k \right). \\ \end(align)\]
Wir markieren sie auf dem Zahlenstrahl unter Berücksichtigung der Multiplizität:
Wir platzieren Schilder und übermalen die für uns interessanten Bereiche:
Alle. Keine isolierten Punkte oder andere Perversionen. Sie können die Antwort aufschreiben.
Antwort. $x\in \left(-\infty ;-7 \right)\bigcup \left(4;+\infty \right)$.
Regel zum Multiplizieren von Vielfachen
Manchmal kommt es zu einer noch unangenehmeren Situation: Eine Gleichung mit mehreren Wurzeln wird selbst potenziert. In diesem Fall ändern sich die Multiplizitäten aller ursprünglichen Wurzeln.
Dies kommt selten vor, daher haben die meisten Studierenden keine Erfahrung mit der Lösung solcher Probleme. Und hier gilt die Regel:
Wenn eine Gleichung auf die n-fache Potenz erhoben wird, erhöhen sich auch die Multiplizitäten aller ihrer Wurzeln um das n-fache.
Mit anderen Worten führt die Potenzierung dazu, dass die Vielfachen mit derselben Potenz multipliziert werden. Schauen wir uns diese Regel anhand eines Beispiels an:
Aufgabe. Lösen Sie die Ungleichung:
\[\frac(x((\left(((x)^(2))-6x+9 \right))^(2))((\left(x-4 \right))^(5)) )(((\left(2-x \right))^(3))((\left(x-1 \right))^(2)))\le 0\]
Lösung. Wir setzen den Zähler mit Null gleich:
Das Produkt ist Null, wenn mindestens einer der Faktoren Null ist. Mit dem ersten Faktor ist alles klar: $x=0$. Doch dann beginnen die Probleme:
\[\begin(align) & ((\left(((x)^(2))-6x+9 \right))^(2))=0; \\ & ((x)^(2))-6x+9=0\left(2k \right); \\ & D=((6)^(3))-4\cdot 9=0 \\ & ((x)_(2))=3\left(2k \right)\left(2k \right) \ \& ((x)_(2))=3\left(4k \right) \\ \end(align)\]
Wie wir sehen, hat die Gleichung $((x)^(2))-6x+9=0$ eine einzelne Wurzel der zweiten Multiplizität: $x=3$. Diese ganze Gleichung wird dann quadriert. Daher beträgt die Multiplizität der Wurzel $2\cdot 2=4$, was wir schließlich aufgeschrieben haben.
\[((\left(x-4 \right))^(5))=0\Rightarrow x=4\left(5k \right)\]
Auch mit dem Nenner gibt es keine Probleme:
\[\begin(align) & ((\left(2-x \right))^(3))((\left(x-1 \right))^(2))=0; \\ & ((\left(2-x \right))^(3))=0\Rightarrow x_(1)^(*)=2\left(3k \right); \\ & ((\left(x-1 \right))^(2))=0\Rightarrow x_(2)^(*)=1\left(2k \right). \\ \end(align)\]
Insgesamt haben wir fünf Punkte bekommen: zwei durchstochen und drei bemalt. Es gibt keine übereinstimmenden Wurzeln im Zähler und Nenner, daher markieren wir sie einfach auf dem Zahlenstrahl:
Wir ordnen die Zeichen unter Berücksichtigung der Vielfältigkeit und übermalen die Intervalle, die uns interessieren:
Wieder ein isolierter Punkt und einer mit einer Reifenpanne
Aufgrund der Wurzeln der geraden Multiplizität haben wir wieder ein paar „nicht standardmäßige“ Elemente erhalten. Dies ist $x\in \left[ 0;1 \right)\bigcup \left(1;2 \right)$ und nicht $x\in \left[ 0;2 \right)$ und außerdem ein isolierter Punkt $ x\in \left\( 3 \right\)$.
Antwort. $x\in \left[ 0;1 \right)\bigcup \left(1;2 \right)\bigcup \left\( 3 \right\)\bigcup \left[ 4;+\infty \right)$
Wie Sie sehen, ist alles nicht so kompliziert. Die Hauptsache ist Aufmerksamkeit. Der letzte Abschnitt dieser Lektion ist den Transformationen gewidmet – denselben Transformationen, die wir gleich zu Beginn besprochen haben.
Vorkonvertierungen
Die Ungleichungen, die wir in diesem Abschnitt untersuchen, können nicht als komplex bezeichnet werden. Im Gegensatz zu den vorherigen Aufgaben müssen Sie hier jedoch Fähigkeiten aus der Theorie der rationalen Brüche anwenden – Faktorisierung und Reduktion auf einen gemeinsamen Nenner.
Wir haben dieses Thema gleich zu Beginn der heutigen Lektion ausführlich besprochen. Wenn Sie nicht sicher sind, ob Sie verstehen, wovon ich spreche, empfehle ich dringend, zurückzugehen und es zu wiederholen. Weil es keinen Sinn macht, Methoden zur Lösung von Ungleichungen vollzustopfen, wenn man bei der Umrechnung von Brüchen „schwebt“.
IN HausaufgabenÜbrigens wird es auch viele ähnliche Aufgaben geben. Sie werden in einem separaten Unterabschnitt platziert. Und dort finden Sie sehr nicht triviale Beispiele. Aber das wird eine Hausaufgabe sein, und jetzt schauen wir uns ein paar solcher Ungleichheiten an.
Aufgabe. Lösen Sie die Ungleichung:
\[\frac(x)(x-1)\le \frac(x-2)(x)\]
Lösung. Alles nach links verschieben:
\[\frac(x)(x-1)-\frac(x-2)(x)\le 0\]
Wir bringen auf einen gemeinsamen Nenner, öffnen die Klammern und bringen ähnliche Begriffe in den Zähler:
\[\begin(align) & \frac(x\cdot x)(\left(x-1 \right)\cdot x)-\frac(\left(x-2 \right)\left(x-1 \ rechts))(x\cdot \left(x-1 \right))\le 0; \\ & \frac(((x)^(2))-\left(((x)^(2))-2x-x+2 \right))(x\left(x-1 \right)) \le 0; \\ & \frac(((x)^(2))-((x)^(2))+3x-2)(x\left(x-1 \right))\le 0; \\ & \frac(3x-2)(x\left(x-1 \right))\le 0. \\\end(align)\]
Jetzt haben wir eine klassische fraktional-rationale Ungleichung vor uns, deren Lösung nicht mehr schwierig ist. Ich schlage vor, es mit einer alternativen Methode zu lösen – durch die Intervallmethode:
\[\begin(align) & \left(3x-2 \right)\cdot x\cdot \left(x-1 \right)=0; \\ & ((x)_(1))=\frac(2)(3);\ ((x)_(2))=0;\ ((x)_(3))=1. \\ \end(align)\]
Vergessen Sie nicht die Einschränkung, die sich aus dem Nenner ergibt:
Wir markieren alle Zahlen und Einschränkungen auf dem Zahlenstrahl:
Alle Wurzeln haben erste Multiplizität. Kein Problem. Wir platzieren einfach Schilder und übermalen die Bereiche, die wir benötigen:
Das ist alles. Sie können die Antwort aufschreiben.
Antwort. $x\in \left(-\infty ;0 \right)\bigcup \left[ (2)/(3)\;;1 \right)$.
Natürlich war das ein sehr einfaches Beispiel. Schauen wir uns das Problem nun genauer an. Übrigens entspricht das Niveau dieser Aufgabe durchaus dem unabhängigen und Tests zu diesem Thema in der 8. Klasse.
Aufgabe. Lösen Sie die Ungleichung:
\[\frac(1)(((x)^(2))+8x-9)\ge \frac(1)(3((x)^(2))-5x+2)\]
Lösung. Alles nach links verschieben:
\[\frac(1)(((x)^(2))+8x-9)-\frac(1)(3((x)^(2))-5x+2)\ge 0\]
Bevor wir beide Brüche auf einen gemeinsamen Nenner bringen, faktorisieren wir diese Nenner. Was ist, wenn die gleichen Klammern herauskommen? Mit dem ersten Nenner ist es einfach:
\[((x)^(2))+8x-9=\left(x-1 \right)\left(x+9 \right)\]
Der zweite ist etwas schwieriger. Fühlen Sie sich frei, einen konstanten Faktor in die Klammer einzufügen, in der der Bruch steht. Denken Sie daran: Das ursprüngliche Polynom hatte ganzzahlige Koeffizienten, daher besteht eine gute Chance, dass die Faktorisierung ganzzahlige Koeffizienten hat (tatsächlich wird dies immer der Fall sein, es sei denn, die Diskriminante ist irrational).
\[\begin(align) & 3((x)^(2))-5x+2=3\left(x-1 \right)\left(x-\frac(2)(3) \right)= \\ & =\left(x-1 \right)\left(3x-2 \right) \end(align)\]
Wie Sie sehen, gibt es eine gemeinsame Klammer: $\left(x-1 \right)$. Wir kehren zur Ungleichung zurück und bringen beide Brüche auf einen gemeinsamen Nenner:
\[\begin(align) & \frac(1)(\left(x-1 \right)\left(x+9 \right))-\frac(1)(\left(x-1 \right)\ left(3x-2 \right))\ge 0; \\ & \frac(1\cdot \left(3x-2 \right)-1\cdot \left(x+9 \right))(\left(x-1 \right)\left(x+9 \right )\left(3x-2 \right))\ge 0; \\ & \frac(3x-2-x-9)(\left(x-1 \right)\left(x+9 \right)\left(3x-2 \right))\ge 0; \\ & \frac(2x-11)(\left(x-1 \right)\left(x+9 \right)\left(3x-2 \right))\ge 0; \\ \end(align)\]
Wir setzen den Nenner mit Null gleich:
\[\begin(align) & \left(x-1 \right)\left(x+9 \right)\left(3x-2 \right)=0; \\ & x_(1)^(*)=1;\ x_(2)^(*)=-9;\ x_(3)^(*)=\frac(2)(3) \\ \end( ausrichten)\]
Keine Vielfachen oder übereinstimmenden Wurzeln. Wir markieren vier Zahlen auf der Linie:
Wir platzieren Schilder:
Wir schreiben die Antwort auf.
Antwort: $x\in \left(-\infty ;-9 \right)\bigcup \left((2)/(3)\;;1 \right)\bigcup \left[ 5.5;+\infty \ right) $.
Alle! So habe ich diese Zeile gelesen :)











