Ordnen Sie die Ungleichungen den Intervallen zu, die ihre Lösungen sind. Lineare Ungleichungen, Beispiele, Lösungen

Was müssen Sie über Ungleichheitssymbole wissen? Ungleichheiten mit Symbol mehr (> ), oder weniger (< ) werden genannt strikt. Mit Symbolen mehr oder gleich (≥ ), kleiner oder gleich (≤ ) werden genannt nicht streng. Symbol nicht gleich (≠ ) sticht heraus, aber man muss auch ständig Beispiele mit diesem Symbol lösen. Und wir werden entscheiden.)

Das Symbol selbst hat keinen großen Einfluss auf den Lösungsprozess. Aber am Ende der Entscheidung, bei der Wahl der endgültigen Antwort, kommt die Bedeutung des Symbols in vollem Umfang zum Vorschein! Das werden wir weiter unten anhand von Beispielen sehen. Da sind einige Witze drin...

Es gibt Ungleichheiten wie Gleichheiten treu und untreu. Hier ist alles einfach, keine Tricks. Sagen wir 5 > 2 ist eine echte Ungleichung. 5 < 2 - falsch.

Dieses Präparat wirkt bei Ungleichheiten jede Form und einfach bis zum Grauen.) Sie müssen nur zwei (nur zwei!) Elementaraktionen korrekt ausführen. Diese Aktionen sind jedem bekannt. Aber charakteristischerweise sind Fehler bei diesen Aktionen der Hauptfehler bei der Lösung von Ungleichheiten, ja... Daher müssen diese Aktionen wiederholt werden. Diese Aktionen werden wie folgt aufgerufen:

Identische Transformationen von Ungleichungen.

Identische Transformationen von Ungleichungen sind identischen Transformationen von Gleichungen sehr ähnlich. Eigentlich ist das das Hauptproblem. Die Unterschiede gehen über Ihren Kopf hinweg und... hier sind Sie.) Deshalb werde ich diese Unterschiede besonders hervorheben. Also die erste identische Transformation von Ungleichungen:

1. Die gleiche Zahl oder derselbe Ausdruck kann auf beiden Seiten der Ungleichung addiert (subtrahiert) werden. Beliebig. Dadurch ändert sich das Ungleichheitszeichen nicht.

In der Praxis wird diese Regel als Übertragung von Termen von der linken Seite der Ungleichung auf die rechte Seite (und umgekehrt) mit Vorzeichenwechsel verwendet. Mit einem Wechsel des Vorzeichens des Termes, nicht der Ungleichung! Die Eins-zu-eins-Regel ist dieselbe wie die Regel für Gleichungen. Hier sind die nächsten Identitätstransformationen in Ungleichungen unterscheidet sich erheblich von denen in Gleichungen. Deshalb markiere ich sie rot:

2. Beide Seiten der Ungleichung können mit demselben Ding multipliziert (dividiert) werdenpositivNummer. Für jedenpositiv Wird sich nicht ändern.

3. Beide Seiten der Ungleichung können mit demselben Ding multipliziert (dividiert) werdenNegativ Nummer. Für jedenNegativNummer. Das Ungleichheitszeichen darauswird sich ins Gegenteil ändern.

Sie erinnern sich (ich hoffe...), dass die Gleichung mit allem multipliziert/dividiert werden kann. Und für jede Zahl und für einen Ausdruck mit einem X. Wenn es nur nicht Null wäre. Das macht ihn, die Gleichung, weder heiß noch kalt.) Es ändert sich nicht. Ungleichungen reagieren jedoch empfindlicher auf Multiplikation/Division.

Ein gutes Beispiel An lange Erinnerung. Schreiben wir eine Ungleichung, die keine Zweifel aufkommen lässt:

5 > 2

Multiplizieren Sie beide Seiten mit +3, wir bekommen:

15 > 6

Irgendwelche Einwände? Es gibt keine Einwände.) Und wenn wir beide Seiten der ursprünglichen Ungleichung mit multiplizieren -3, wir bekommen:

15 > -6

Und das ist eine völlige Lüge.) Eine völlige Lüge! Täuschung des Volkes! Aber sobald man das Ungleichheitszeichen in das Gegenteil ändert, passt alles zusammen:

15 < -6

Ich schwöre nicht nur auf Lügen und Täuschung.) „Ich habe vergessen, das Gleichheitszeichen zu ändern …“- Das heim Fehler bei der Lösung von Ungleichungen. Diese triviale und einfache Regel hat so vielen Menschen geschadet! Was sie vergessen haben...) Also schwöre ich. Vielleicht erinnere ich mich...)

Besonders aufmerksame Menschen werden feststellen, dass Ungleichheit nicht mit einem Ausdruck mit einem X multipliziert werden kann. Respekt vor den Aufmerksamen!) Warum nicht? Die Antwort ist einfach. Wir kennen das Vorzeichen dieses Ausdrucks mit einem X nicht. Es kann positiv oder negativ sein... Daher wissen wir nicht, welches Ungleichheitszeichen wir nach der Multiplikation setzen sollen. Soll ich es ändern oder nicht? Unbekannt. Natürlich kann diese Einschränkung (das Verbot der Multiplikation/Division einer Ungleichung durch einen Ausdruck mit einem x) umgangen werden. Wenn Sie es wirklich brauchen. Aber das ist ein Thema für andere Lektionen.

Das sind alles identische Transformationen von Ungleichungen. Ich möchte Sie noch einmal daran erinnern, dass sie arbeiten beliebig Ungleichheiten Jetzt können Sie zu bestimmten Typen übergehen.

Lineare Ungleichungen. Lösung, Beispiele.

Lineare Ungleichungen sind Ungleichungen, bei denen x in der ersten Potenz liegt und keine Division durch x erfolgt. Typ:

x+3 > 5x-5

Wie werden solche Ungleichheiten gelöst? Sie sind sehr einfach zu lösen! Nämlich: Mit Hilfe von reduzieren wir die verwirrendste lineare Ungleichung direkt zur Antwort. Das ist die Lösung. Ich werde die Hauptpunkte der Entscheidung hervorheben. Um dumme Fehler zu vermeiden.)

Lösen wir diese Ungleichung:

x+3 > 5x-5

Wir lösen es genauso wie eine lineare Gleichung. Mit dem einzigen Unterschied:

Wir achten sorgfältig auf das Ungleichheitszeichen!

Der erste Schritt ist der häufigste. Mit X's - nach links, ohne X's - nach rechts... Dies ist die erste identische Transformation, einfach und problemlos.) Vergessen Sie nur nicht, die Vorzeichen der übertragenen Begriffe zu ändern.

Das Ungleichheitszeichen bleibt:

x-5x > -5-3

Hier sind ähnliche.

Das Ungleichheitszeichen bleibt:

4x > -8

Es bleibt die letzte identische Transformation anzuwenden: beide Seiten durch -4 dividieren.

Teilen durch Negativ Nummer.

Das Ungleichheitszeichen ändert sich ins Gegenteil:

X < 2

Das ist die Antwort.

Auf diese Weise werden alle linearen Ungleichungen gelöst.

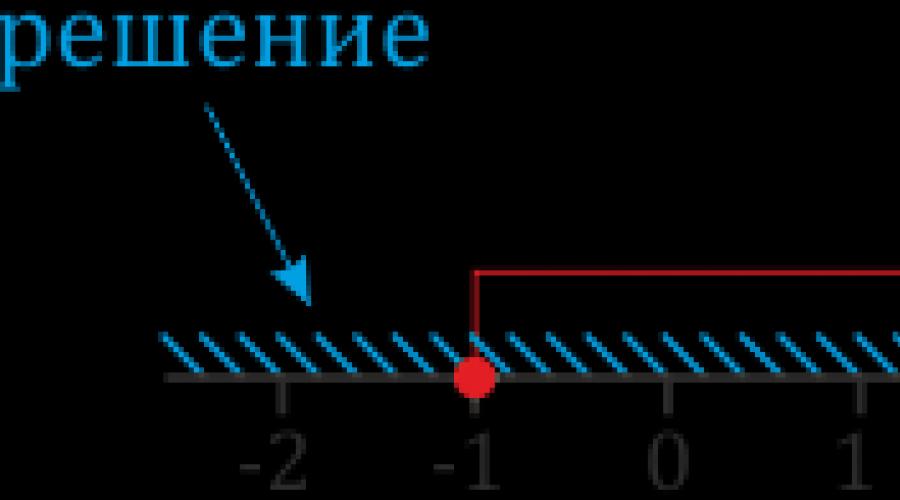
Aufmerksamkeit! Punkt 2 ist weiß gezeichnet, d.h. unbemalt. Innen leer. Das bedeutet, dass sie nicht in der Antwort enthalten ist! Ich habe sie absichtlich so gesund gezeichnet. Einen solchen Punkt (leer, nicht gesund!) nennt man in der Mathematik punktierter Punkt.

Die restlichen Zahlen auf der Achse können markiert werden, sind aber nicht notwendig. Fremde Zahlen, die nichts mit unserer Ungleichung zu tun haben, können verwirrend sein, ja ... Sie müssen nur bedenken, dass die Zahlen in Pfeilrichtung zunehmen, d. h. Zahlen 3, 4, 5 usw. Sind Nach rechts sind Zweien und Zahlen sind 1, 0, -1 usw. - Nach links.

Ungleichung x < 2 - strikt. X ist streng genommen kleiner als zwei. Im Zweifelsfall ist die Überprüfung einfach. Wir setzen die zweifelhafte Zahl in die Ungleichung ein und denken: „Zwei ist kleiner als zwei? Nein, natürlich!“ Genau so. Ungleichheit 2 < 2 falsch. Eine Zwei als Gegenleistung ist nicht angemessen.

Ist einer in Ordnung? Sicherlich. Weniger... Und Null ist gut, und -17 und 0,34... Ja, alle Zahlen, die kleiner als zwei sind, sind gut! Und sogar 1,9999... Zumindest ein bisschen, aber weniger!

Markieren wir also alle diese Zahlen auf der Zahlenachse. Wie? Hier gibt es Optionen. Option eins ist die Schattierung. Wir bewegen die Maus über das Bild (oder berühren das Bild auf dem Tablet) und sehen, dass der Bereich aller x, die die Bedingung x erfüllen, schattiert ist < 2 . Das ist alles.

Schauen wir uns die zweite Option anhand des zweiten Beispiels an:

X ≥ -0,5

Zeichnen Sie eine Achse und markieren Sie die Zahl -0,5. So:

Merken Sie den Unterschied?) Nun ja, es ist schwer, es nicht zu bemerken ... Dieser Punkt ist schwarz! Übermalt. Das bedeutet -0,5 ist in der Antwort enthalten. Hier kann die Überprüfung übrigens jemanden verwirren. Ersetzen wir:

-0,5 ≥ -0,5

Wie so? -0,5 ist nicht mehr als -0,5! Und es gibt noch mehr Icons...

Macht nichts. Bei einer schwachen Ungleichung ist alles geeignet, was zum Symbol passt. UND gleicht gut und mehr Gut. Daher ist -0,5 in der Antwort enthalten.

Also haben wir auf der Achse -0,5 markiert; es müssen noch alle Zahlen markiert werden, die größer als -0,5 sind. Dieses Mal markiere ich den Bereich geeigneter x-Werte Bogen(aus dem Wort Bogen), statt einer Schattierung. Wir bewegen den Cursor über die Zeichnung und sehen diesen Bogen.

Es gibt keinen besonderen Unterschied zwischen der Beschattung und den Armen. Tun Sie, was der Lehrer sagt. Wenn kein Lehrer da ist, zeichnen Sie Bögen. Bei komplexeren Aufgaben ist die Schattierung weniger offensichtlich. Sie können verwirrt sein.

So werden lineare Ungleichungen auf einer Achse gezeichnet. Kommen wir zum nächsten Merkmal der Ungleichungen.

Schreiben Sie die Antwort für Ungleichungen.

Die Gleichungen waren gut.) Wir haben x gefunden und die Antwort aufgeschrieben, zum Beispiel: x=3. Es gibt zwei Formen, Antworten in Ungleichungen zu schreiben. Eine davon ist die endgültige Ungleichheit. Gut für einfache Fälle. Zum Beispiel:

X< 2.

Dies ist eine vollständige Antwort.

Manchmal muss man das Gleiche aufschreiben, aber in unterschiedlicher Form und in numerischen Abständen. Dann beginnt die Aufnahme sehr wissenschaftlich auszusehen):

x ∈ (-∞; 2)

Unter dem Symbol ∈ das Wort ist verborgen "gehört".

Der Eintrag liest sich so: x gehört zum Intervall von minus unendlich bis zwei Nicht beinhaltet. Ganz logisch. X kann eine beliebige Zahl von allen sein mögliche Zahlen von minus unendlich bis zwei. Es kann kein doppeltes X geben, das sagt uns das Wort "Nicht beinhaltet".

Und wo in der Antwort steht das klar? "Nicht beinhaltet"? Diese Tatsache wird in der Antwort vermerkt runden Klammer unmittelbar nach den beiden. Wenn die beiden enthalten wären, wäre die Halterung enthalten Quadrat. Wie dieser: ]. Das folgende Beispiel verwendet eine solche Klammer.

Schreiben wir die Antwort auf: x ≥ -0,5 in Intervallen:

x ∈ [-0,5; +∞)

Liest: x gehört zum Intervall von minus 0,5, einschließlich, bis plus unendlich.

Die Unendlichkeit kann niemals aktiviert werden. Es ist keine Zahl, es ist ein Symbol. Daher steht in solchen Notationen die Unendlichkeit immer neben einer Klammer.

Diese Form der Aufzeichnung eignet sich für komplexe Antworten, die aus mehreren Leerzeichen bestehen. Aber – nur für abschließende Antworten. Bei Zwischenergebnissen, bei denen eine weitere Lösung erwartet wird, ist es besser, die übliche Form in Form einer einfachen Ungleichung zu verwenden. Darauf gehen wir in den entsprechenden Themen ein.

Beliebte Aufgaben mit Ungleichungen.

Die linearen Ungleichungen selbst sind einfach. Daher werden Aufgaben oft schwieriger. Es war also notwendig, nachzudenken. Wenn man es nicht gewohnt ist, ist das nicht sehr angenehm.) Aber es ist nützlich. Ich werde Beispiele für solche Aufgaben zeigen. Es liegt nicht an Ihnen, sie zu lernen, es ist unnötig. Und um bei der Begegnung mit solchen Beispielen keine Angst zu haben. Denken Sie einfach ein wenig nach – und es ist ganz einfach!)

1. Finden Sie zwei beliebige Lösungen für die Ungleichung 3x - 3< 0

Wenn Sie nicht ganz klar sind, was zu tun ist, erinnern Sie sich an die Hauptregel der Mathematik:

Wenn Sie nicht wissen, was Sie brauchen, tun Sie, was Sie können!)

X < 1

Na und? Nichts Besonderes. Was fragen sie uns? Wir werden gebeten, zwei bestimmte Zahlen zu finden, die die Lösung einer Ungleichung darstellen. Diese. Passt zur Antwort. Zwei beliebig Zahlen. Eigentlich ist das verwirrend.) Ein paar 0 und 0,5 sind geeignet. Ein paar -3 und -8. Es gibt unendlich viele dieser Paare! Welche Antwort ist richtig?!

Ich antworte: Alles! Jedes Zahlenpaar, von dem jede kleiner als eins ist, wird die richtige Antwort sein. Schreiben Sie, welches Sie möchten. Lass uns weitermachen.

2. Lösen Sie die Ungleichung:

4x - 3 ≠ 0

Aufgaben in dieser Form sind selten. Aber als Hilfsungleichungen, zum Beispiel beim Finden von ODZ oder beim Finden des Definitionsbereichs einer Funktion, kommen sie ständig vor. Eine solche lineare Ungleichung kann als gewöhnliche lineare Gleichung gelöst werden. Nur überall außer dem „=“-Zeichen ( gleicht) ein Schild anbringen „ ≠ " (nicht gleich). So nähern Sie sich der Antwort mit einem Ungleichheitszeichen:

X ≠ 0,75

In mehr komplexe Beispiele, es ist besser, die Dinge anders zu machen. Aus Gleichheit Ungleichheit machen. So:

4x - 3 = 0

Lösen Sie es ruhig wie gelehrt und erhalten Sie die Antwort:

x = 0,75

Die Hauptsache ist, ganz am Ende, wenn Sie die endgültige Antwort aufschreiben, nicht zu vergessen, dass wir x gefunden haben, was ergibt Gleichwertigkeit. Und wir brauchen - Ungleichheit. Deshalb brauchen wir dieses X nicht wirklich.) Und wir müssen es mit dem richtigen Symbol aufschreiben:

X ≠ 0,75

Dieser Ansatz führt zu weniger Fehlern. Diejenigen, die Gleichungen automatisch lösen. Und für diejenigen, die keine Gleichungen lösen, nützen Ungleichungen tatsächlich nichts...) Ein weiteres Beispiel für eine beliebte Aufgabe:

3. Finden Sie die kleinste ganzzahlige Lösung der Ungleichung:

3(x - 1) < 5x + 9

Zuerst lösen wir einfach die Ungleichung. Wir öffnen die Klammern, verschieben sie, bringen ähnliche mit ... Wir erhalten:

X > - 6

Hat es nicht so geklappt!? Sind Sie den Schildern gefolgt!? Und hinter den Zeichen der Mitglieder und hinter dem Zeichen der Ungleichheit ...

Denken wir noch einmal darüber nach. Wir müssen eine bestimmte Zahl finden, die sowohl der Antwort als auch der Bedingung entspricht „kleinste ganze Zahl“. Wenn es Ihnen nicht sofort klar wird, können Sie einfach eine beliebige Zahl nehmen und es herausfinden. Zwei über minus sechs? Sicherlich! Gibt es eine passende kleinere Zahl? Natürlich. Beispielsweise ist Null größer als -6. Und noch weniger? Wir brauchen das Kleinstmögliche! Minus drei ist mehr als minus sechs! Sie können das Muster bereits erkennen und aufhören, dumm die Zahlen durchzugehen, oder?)

Nehmen wir eine Zahl, die näher bei -6 liegt. Beispiel: -5. Die Antwort ist erfüllt, -5 > - 6. Ist es möglich, eine andere Zahl zu finden, die kleiner als -5, aber größer als -6 ist? Sie können zum Beispiel -5,5... Stop! Uns wurde gesagt ganz Lösung! Würfelt nicht -5,5! Was ist mit minus sechs? Äh-äh! Die Ungleichung ist streng, minus 6 ist keineswegs kleiner als minus 6!

Daher ist die richtige Antwort -5.

Hoffentlich mit einer Auswahl an Werten aus Allgemeine Lösung alles klar. Ein anderes Beispiel:

4. Ungleichung lösen:

7 < 3x+1 < 13

Wow! Dieser Ausdruck heißt dreifache Ungleichheit. Streng genommen handelt es sich dabei um eine Kurzform eines Ungleichheitssystems. Aber solche dreifachen Ungleichungen müssen bei einigen Aufgaben noch gelöst werden... Es kann ohne Systeme gelöst werden. Nach den gleichen identischen Transformationen.

Wir müssen diese Ungleichung vereinfachen und auf reines X übertragen. Aber... Was soll wohin verschoben werden?! An dieser Stelle ist es an der Zeit, sich daran zu erinnern, dass es wichtig ist, sich nach links und rechts zu bewegen Kurzform erste Identitätstransformation.

A vollständige Form hört sich so an: Jede Zahl oder jeder Ausdruck kann auf beiden Seiten der Gleichung addiert/subtrahiert werden (Ungleichung).

Hier gibt es drei Teile. Wir werden also auf alle drei Teile identische Transformationen anwenden!

Lassen Sie uns also den Punkt im mittleren Teil der Ungleichung loswerden. Subtrahieren wir eins vom gesamten Mittelteil. Damit sich die Ungleichung nicht ändert, subtrahieren wir von den verbleibenden beiden Teilen eins. So:

7 -1< 3x+1-1 < 13-1

6 < 3x < 12

Das ist besser, oder?) Es bleibt nur noch, alle drei Teile in drei Teile zu unterteilen:

2 < X < 4

Das ist alles. Das ist die Antwort. X kann eine beliebige Zahl von zwei (ohne) bis vier (ohne) sein. Auch diese Antwort wird in Abständen geschrieben; solche Einträge erfolgen in quadratischen Ungleichungen. Da kommen sie am häufigsten vor.

Am Ende der Lektion werde ich das Wichtigste wiederholen. Der Erfolg bei der Lösung linearer Ungleichungen hängt von der Fähigkeit ab, lineare Gleichungen umzuwandeln und zu vereinfachen. Wenn gleichzeitig Achten Sie auf das Ungleichheitszeichen, es wird keine Probleme geben. Das wünsche ich dir. Keine Probleme.)

Wenn Ihnen diese Seite gefällt...

Übrigens habe ich noch ein paar weitere interessante Seiten für Sie.)

Sie können das Lösen von Beispielen üben und Ihr Niveau herausfinden. Testen mit sofortiger Verifizierung. Lasst uns lernen – mit Interesse!)

Sie können sich mit Funktionen und Ableitungen vertraut machen.

Die Ungleichung ist beispielsweise der Ausdruck \(x>5\).

Arten von Ungleichheiten:

Sind \(a\) und \(b\) Zahlen oder , dann heißt die Ungleichung numerisch. Es geht eigentlich nur darum, zwei Zahlen zu vergleichen. Solche Ungleichheiten werden unterteilt in treu Und untreu.

Zum Beispiel:
\(-5<2\) - верное числовое неравенство, ведь \(-5\) действительно меньше \(2\);

\(17+3\geq 115\) ist eine falsche numerische Ungleichung, da \(17+3=20\) und \(20\) kleiner als \(115\) ist (und nicht größer oder gleich) .

Wenn \(a\) und \(b\) Ausdrücke sind, die eine Variable enthalten, dann gilt Ungleichheit mit Variable. Solche Ungleichungen werden je nach Inhalt in Typen unterteilt:

\(2x+1\geq4(5-x)\)				Variabel nur in der ersten Potenz
\(3x^2-x+5>0\)				Es gibt eine Variable in der zweiten Potenz (Quadrat), aber keine höheren Potenzen (dritte, vierte usw.)
\(\log_(4)((x+1))<3\)
\(2^(x)\leq8^(5x-2)\)

... usw.

Was ist die Lösung einer Ungleichung?

Wenn Sie eine Zahl anstelle einer Variablen in eine Ungleichung einsetzen, wird daraus eine numerische.

Wenn ein gegebener Wert für x die ursprüngliche Ungleichung in eine echte numerische Ungleichung umwandelt, wird sie aufgerufen Lösung für Ungleichheit. Wenn nicht, ist dieser Wert keine Lösung. Und dazu Ungleichheit lösen– Sie müssen alle Lösungen finden (oder zeigen, dass es keine gibt).

Zum Beispiel, Wenn wir die Zahl \(7\) in die lineare Ungleichung \(x+6>10\) einsetzen, erhalten wir die korrekte numerische Ungleichung: \(13>10\). Und wenn wir \(2\\) ersetzen, entsteht eine falsche numerische Ungleichung \(8>10\). Das heißt, \(7\) ist eine Lösung der ursprünglichen Ungleichung, \(2\) jedoch nicht.

Die Ungleichung \(x+6>10\) hat jedoch andere Lösungen. Tatsächlich erhalten wir die korrekten numerischen Ungleichungen, wenn wir \(5\), und \(12\) und \(138\) einsetzen... Und wie können wir alle finden? mögliche Lösungen? Dafür verwenden sie. Für unseren Fall haben wir:

\(x+6>10\) \(|-6\)
\(x>4\)

Das heißt, jede Zahl größer als vier passt zu uns. Jetzt müssen Sie die Antwort aufschreiben. Lösungen für Ungleichungen werden in der Regel numerisch geschrieben und zusätzlich auf der Zahlenachse durch Schraffur markiert. Für unseren Fall haben wir:

Antwort: \(x\in(4;+\infty)\)

Wann ändert sich das Vorzeichen einer Ungleichung?

Es gibt eine große Ungleichheitsfalle, in die Schüler wirklich gerne tappen:

Wenn man eine Ungleichung mit einer negativen Zahl multipliziert (oder dividiert), wird sie umgekehrt („mehr“ durch „weniger“, „mehr oder gleich“ durch „kleiner als oder gleich“ usw.)

Warum passiert das? Um dies zu verstehen, schauen wir uns die Transformationen der numerischen Ungleichung \(3>1\) an. Es ist richtig, drei ist tatsächlich größer als eins. Versuchen wir zunächst, es mit einer beliebigen positiven Zahl zu multiplizieren, zum Beispiel zwei:

\(3>1\) \(|\cdot2\)
\(6>2\)

Wie wir sehen können, bleibt die Ungleichung nach der Multiplikation wahr. Und egal mit welcher positiven Zahl wir multiplizieren, wir erhalten immer die richtige Ungleichung. Versuchen wir nun, mit einer negativen Zahl zu multiplizieren, zum Beispiel minus drei:

\(3>1\) \(|\cdot(-3)\)
\(-9>-3\)

Das Ergebnis ist eine falsche Ungleichung, denn minus neun ist kleiner als minus drei! Das heißt, damit die Ungleichung wahr wird (und daher die Transformation der Multiplikation durch das Negative „legal“ war), müssen Sie das Vergleichszeichen wie folgt umkehren: \(−9<− 3\).
Mit der Division klappt es genauso, das kannst du selbst überprüfen.

Die oben beschriebene Regel gilt für alle Arten von Ungleichungen, nicht nur für numerische.

Beispiel: Lösen Sie die Ungleichung \(2(x+1)-1<7+8x\)
Lösung:

\(2x+2-1<7+8x\)	Bewegen wir \(8x\) nach links und \(2\) und \(-1\) nach rechts, ohne zu vergessen, die Vorzeichen zu ändern
\(2x-8x<7-2+1\)
\(-6x<6\) \(|:(-6)\)	Teilen wir beide Seiten der Ungleichung durch \(-6\) und vergessen wir nicht, von „weniger“ zu „mehr“ zu wechseln.
	Markieren wir ein numerisches Intervall auf der Achse. Ungleichheit, deshalb „herauspicken“ wir den Wert \(-1\) selbst und nehmen ihn nicht als Antwort
	Schreiben wir die Antwort als Intervall

Antwort: \(x\in(-1;\infty)\)

Ungleichheiten und Behinderung

Ungleichungen können, genau wie Gleichungen, Einschränkungen hinsichtlich , also der Werte von x, haben. Dementsprechend sollten diejenigen Werte, die laut DZ nicht akzeptabel sind, aus dem Lösungsspektrum ausgeschlossen werden.

Beispiel: Lösen Sie die Ungleichung \(\sqrt(x+1)<3\)

Lösung: Damit die linke Seite kleiner als \(3\) ist, ist klar, dass der Wurzelausdruck kleiner als \(9\) sein muss (schließlich ist aus \(9\) nur \(3\)). Wir bekommen:

\(x+1<9\) \(|-1\)
\(X<8\)

Alle? Jeder Wert von x, der kleiner als \(8\) ist, passt zu uns? Nein! Denn wenn wir zum Beispiel den Wert \(-5\) nehmen, der der Anforderung zu entsprechen scheint, wird dies keine Lösung für die ursprüngliche Ungleichung sein, da es uns zur Berechnung der Wurzel einer negativen Zahl führen wird.

\(\sqrt(-5+1)<3\)
\(\sqrt(-4)<3\)

Daher müssen wir auch die Einschränkungen beim Wert von X berücksichtigen – es kann nicht sein, dass unter der Wurzel eine negative Zahl steht. Somit haben wir die zweite Anforderung für x:

\(x+1\geq0\)
\(x\geq-1\)

Und damit x die endgültige Lösung ist, muss es beide Anforderungen gleichzeitig erfüllen: Es muss kleiner als \(8\) sein (um eine Lösung zu sein) und größer als \(-1\) (um prinzipiell zulässig zu sein). Wenn wir es auf dem Zahlenstrahl auftragen, erhalten wir die endgültige Antwort:

Antwort: \(\left[-1;8\right)\)

In dem Artikel werden wir darüber nachdenken Ungleichheiten lösen. Wir werden es Ihnen klar und deutlich sagen wie man eine Lösung für Ungleichungen konstruiert, mit klaren Beispielen!

Bevor wir uns mit der Lösung von Ungleichungen anhand von Beispielen befassen, wollen wir die Grundkonzepte verstehen.

Allgemeine Informationen zu Ungleichheiten

Ungleichheit ist ein Ausdruck, in dem Funktionen durch Beziehungszeichen >, verbunden sind. Ungleichungen können sowohl numerischer als auch wörtlicher Natur sein.
Ungleichungen mit zwei Vorzeichen des Verhältnisses werden als doppelt bezeichnet, mit drei als dreifach usw. Zum Beispiel:
a(x) > b(x),
a(x) a(x) b(x),
a(x) b(x).
a(x) Ungleichungen, die das Zeichen > oder oder - enthalten, sind nicht streng.
Lösung der Ungleichung ist ein beliebiger Wert der Variablen, für den diese Ungleichung gilt.
"Ungleichheit lösen" bedeutet, dass wir die Menge aller seiner Lösungen finden müssen. Es gibt verschiedene Methoden zur Lösung von Ungleichungen. Für Ungleichheitslösungen Sie verwenden den Zahlenstrahl, der unendlich ist. Zum Beispiel, Lösung für Ungleichheit x > 3 ist das Intervall von 3 bis +, und die Zahl 3 ist nicht in diesem Intervall enthalten, daher wird der Punkt auf der Geraden durch einen leeren Kreis bezeichnet, weil Die Ungleichheit ist streng.
+
Die Antwort lautet: x (3; +).
Der Wert x=3 ist nicht in der Lösungsmenge enthalten, daher ist die Klammer rund. Das Unendlichkeitszeichen wird immer durch eine Klammer hervorgehoben. Das Zeichen bedeutet „zugehörig“.
Schauen wir uns anhand eines anderen Beispiels mit einem Vorzeichen an, wie man Ungleichungen löst:
x 2
-+
Der Wert x=2 ist in der Lösungsmenge enthalten, daher ist die Klammer quadratisch und der Punkt auf der Geraden wird durch einen ausgefüllten Kreis angezeigt.
Die Antwort wird sein: x.

Der gesamte oben beschriebene Algorithmus ist wie folgt geschrieben:

3 x + 12 ≤ 0 ; 3 x ≤ − 12 ; x ≤ − 4 .

Antwort: x ≤ − 4 oder (− ∞ , − 4 ] .

Beispiel 2

Geben Sie alle verfügbaren Lösungen der Ungleichung − 2, 7 · z > 0 an.

Lösung

Aus der Bedingung sehen wir, dass der Koeffizient a für z gleich – 2,7 ist und b explizit fehlt oder gleich Null ist. Sie können den ersten Schritt des Algorithmus nicht verwenden, sondern sofort mit dem zweiten fortfahren.

Wir teilen beide Seiten der Gleichung durch die Zahl - 2, 7. Da die Zahl negativ ist, muss das Ungleichheitszeichen umgekehrt werden. Das heißt, wir erhalten (− 2, 7 z): (− 2, 7)< 0: (− 2 , 7) , и дальше z < 0 .

Wir werden den gesamten Algorithmus hineinschreiben Kurzform:

− 2, 7 z > 0; z< 0 .

Antwort: z< 0 или (− ∞ , 0) .

Beispiel 3

Lösen Sie die Ungleichung - 5 x - 15 22 ≤ 0.

Lösung

Gemäß der Bedingung sehen wir, dass es notwendig ist, die Ungleichung mit dem Koeffizienten a für die Variable x, die gleich – 5 ist, mit dem Koeffizienten b, der dem Bruch entspricht, zu lösen – 15 22. Es ist notwendig, die Ungleichung zu lösen, indem man dem Algorithmus folgt, das heißt: Verschiebe - 15 22 in einen anderen Teil mit dem entgegengesetzten Vorzeichen, dividiere beide Teile durch - 5, ändere das Vorzeichen der Ungleichung:

5 x ≤ 15 22 ; - 5 x: - 5 ≥ 15 22: - 5 x ≥ - 3 22

Beim letzten Übergang für die rechte Seite wird die Zahlenteilungsregel verwendet verschiedene Zeichen 15 22: - 5 = - 15 22: 5, danach führen wir eine Division durch gemeinsamer Bruch zur natürlichen Zahl - 15 22: 5 = - 15 22 · 1 5 = - 15 · 1 22 · 5 = - 3 22 .

Antwort: x ≥ - 3 22 und [ - 3 22 + ∞) .

Betrachten wir den Fall, dass a = 0 ist. Linearer Ausdruck der Form a x + b< 0 является неравенством 0 · x + b < 0 , где на рассмотрение берется неравенство вида b < 0 , после чего выясняется, оно верное или нет.

Alles basiert darauf, die Lösung der Ungleichung zu finden. Für jeden Wert von x erhalten wir eine numerische Ungleichung der Form b< 0 , потому что при подстановке любого t вместо переменной x , тогда получаем 0 · t + b < 0 , где b < 0 . В случае, если оно верно, то для его решения подходит любое значение. Когда b < 0 неверно, тогда линейное уравнение не имеет решений, потому как не имеется ни одного значения переменной, которое привело бы верному числовому равенству.

Wir betrachten alle Urteile in Form eines Algorithmus zur Lösung linearer Ungleichungen 0 x + b< 0 (≤ , > , ≥) :

Definition 5

Numerische Ungleichung der Form b< 0 (≤ , >, ≥) wahr ist, dann hat die ursprüngliche Ungleichung für jeden Wert eine Lösung, und sie ist falsch, wenn die ursprüngliche Ungleichung keine Lösungen hat.

Beispiel 4

Lösen Sie die Ungleichung 0 x + 7 > 0.

Lösung

Diese lineare Ungleichung 0 x + 7 > 0 kann jeden Wert x annehmen. Dann erhalten wir eine Ungleichung der Form 7 > 0. Die letzte Ungleichung gilt als wahr, was bedeutet, dass jede Zahl ihre Lösung sein kann.

Antwort: Intervall (− ∞ , + ∞) .

Beispiel 5

Finden Sie eine Lösung für die Ungleichung 0 x − 12, 7 ≥ 0.

Lösung

Wenn wir die Variable x durch eine beliebige Zahl ersetzen, erhalten wir, dass die Ungleichung die Form − 12, 7 ≥ 0 annimmt. Es ist falsch. Das heißt, 0 x − 12, 7 ≥ 0 hat keine Lösungen.

Antwort: es gibt keine Lösungen.

Betrachten wir die Lösung linearer Ungleichungen, bei denen beide Koeffizienten gleich Null sind.

Beispiel 6

Bestimmen Sie die unlösbare Ungleichung aus 0 x + 0 > 0 und 0 x + 0 ≥ 0.

Lösung

Wenn wir eine beliebige Zahl anstelle von x einsetzen, erhalten wir zwei Ungleichungen der Form 0 > 0 und 0 ≥ 0. Das erste ist falsch. Das bedeutet, dass 0 x + 0 > 0 keine Lösungen hat und 0 x + 0 ≥ 0 unendlich viele Lösungen hat, also beliebig viele.

Antwort: Die Ungleichung 0 x + 0 > 0 hat keine Lösungen, aber 0 x + 0 ≥ 0 hat Lösungen.

Diese Methode wird im Schulmathematikkurs besprochen. Die Intervallmethode kann aufgelöst werden Verschiedene Arten Ungleichungen, auch linear.

Die Intervallmethode wird für lineare Ungleichungen verwendet, wenn der Wert des Koeffizienten x ungleich 0 ist. Andernfalls müssen Sie mit einer anderen Methode rechnen.

Definition 6

Die Intervallmethode ist:

• Einführung der Funktion y = a · x + b ;
• Suche nach Nullen, um den Definitionsbereich in Intervalle aufzuteilen;
• Definition von Zeichen für ihre Konzepte auf Intervallen.

Lassen Sie uns einen Algorithmus zum Lösen linearer Gleichungen a x + b zusammenstellen< 0 (≤ , >, ≥) für a ≠ 0 mit der Intervallmethode:

• Finden der Nullstellen der Funktion y = a · x + b, um eine Gleichung der Form a · x + b = 0 zu lösen. Wenn a ≠ 0, dann ist die Lösung eine einzelne Wurzel, die die Bezeichnung x 0 annimmt;
• Konstruktion einer Koordinatenlinie mit einem Bild eines Punktes mit der Koordinate x 0, bei einer strengen Ungleichung wird der Punkt durch eine punktierte Eins bezeichnet, bei einer nicht strengen Ungleichung – durch eine schattierte Eins;
• Bestimmen der Vorzeichen der Funktion y = a · x + b auf Intervallen; dazu ist es notwendig, die Werte der Funktion an Punkten im Intervall zu finden;
• Lösen einer Ungleichung mit Vorzeichen > oder ≥ auf der Koordinatenlinie, Hinzufügen einer Schattierung über dem positiven Intervall,< или ≤ над отрицательным промежутком.

Schauen wir uns einige Beispiele für die Lösung linearer Ungleichungen mit der Intervallmethode an.

Beispiel 6

Lösen Sie die Ungleichung − 3 x + 12 > 0.

Lösung

Aus dem Algorithmus folgt, dass Sie zunächst die Wurzel der Gleichung − 3 x + 12 = 0 finden müssen. Wir erhalten, dass − 3 · x = − 12 , x = 4 . Es ist notwendig, eine Koordinatenlinie dort zu zeichnen, wo wir Punkt 4 markieren. Es wird punktiert, da die Ungleichung streng ist. Betrachten Sie die Zeichnung unten.

Es ist notwendig, die Vorzeichen in den Abständen zu bestimmen. Um es auf dem Intervall (− ∞, 4) zu bestimmen, muss die Funktion y = − 3 x + 12 bei x = 3 berechnet werden. Von hier aus erhalten wir − 3 3 + 12 = 3 > 0. Das Vorzeichen des Intervalls ist positiv.

Wir bestimmen das Vorzeichen aus dem Intervall (4, + ∞) und ersetzen dann den Wert x = 5. Wir haben das − 3 5 + 12 = − 3< 0 . Знак на промежутке является отрицательным. Изобразим на числовой прямой, приведенной ниже.

Wir lösen die Ungleichung mit dem >-Zeichen und die Schattierung erfolgt über das positive Intervall. Betrachten Sie die Zeichnung unten.

Aus der Zeichnung geht hervor, dass die gesuchte Lösung die Form (− ∞ , 4) oder x hat< 4 .

Antwort: (− ∞ , 4) oder x< 4 .

Um zu verstehen, wie man grafisch darstellt, ist es notwendig, 4 lineare Ungleichungen als Beispiel zu betrachten: 0, 5 x − 1< 0 , 0 , 5 · x − 1 ≤ 0 , 0 , 5 · x − 1 >0 und 0, 5 x − 1 ≥ 0. Ihre Lösungen werden die Werte von x sein< 2 , x ≤ 2 , x >2 und x ≥ 2. Zeichnen wir dazu ein Diagramm lineare Funktion y = 0,5 x − 1 siehe unten.

Es ist klar, dass

Definition 7

• Lösen der Ungleichung 0, 5 x − 1< 0 считается промежуток, где график функции y = 0 , 5 · x − 1 располагается ниже О х;
• Als Lösung 0, 5 x − 1 ≤ 0 gilt das Intervall, in dem die Funktion y = 0, 5 x − 1 kleiner als O x ist oder zusammenfällt;
• die Lösung 0, 5 · x − 1 > 0 wird als Intervall betrachtet, die Funktion liegt über O x;
• Als Lösung 0, 5 · x − 1 ≥ 0 gilt das Intervall, in dem der Graph über O x oder zusammenfällt.

Bei der grafischen Lösung von Ungleichungen geht es darum, die Intervalle zu finden, die im Diagramm dargestellt werden müssen. In diesem Fall finden wir, dass die linke Seite y = a · x + b hat und die rechte Seite y = 0 hat und mit O x übereinstimmt.

Definition 8

Der Graph der Funktion y = a x + b wird dargestellt:

• beim Lösen der Ungleichung a x + b< 0 определяется промежуток, где график изображен ниже О х;
• Bei der Lösung der Ungleichung a · x + b ≤ 0 wird das Intervall bestimmt, in dem der Graph unterhalb der O x -Achse dargestellt ist oder zusammenfällt;
• Beim Lösen der Ungleichung a · x + b > 0 wird das Intervall bestimmt, in dem der Graph über O x dargestellt ist;
• Beim Lösen der Ungleichung a · x + b ≥ 0 wird das Intervall bestimmt, in dem der Graph über O x liegt oder zusammenfällt.

Beispiel 7

Lösen Sie die Ungleichung - 5 · x - 3 > 0 mithilfe eines Diagramms.

Lösung

Es ist notwendig, einen Graphen der linearen Funktion - 5 · x - 3 > 0 zu erstellen. Diese Linie nimmt ab, da der Koeffizient von x negativ ist. Um die Koordinaten des Schnittpunkts mit O x - 5 · x - 3 > 0 zu bestimmen, erhalten wir den Wert - 3 5. Lassen Sie es uns grafisch darstellen.

Wenn Sie die Ungleichung mit dem >-Zeichen lösen, müssen Sie auf das Intervall über O x achten. Lassen Sie uns den gewünschten Teil des Flugzeugs rot markieren und erhalten

Der erforderliche Spalt beträgt Teil O x Rot. Dies bedeutet, dass der offene Zahlenstrahl - ∞ , - 3 5 eine Lösung der Ungleichung sein wird. Wenn wir aufgrund der Bedingung eine nicht strikte Ungleichung hätten, wäre der Wert des Punktes - 3 5 auch eine Lösung für die Ungleichung. Und es würde mit O x zusammenfallen.

Antwort: - ∞ , - 3 5 oder x< - 3 5 .

Die grafische Lösung wird verwendet, wenn die linke Seite der Funktion y = 0 x + b entspricht, also y = b. Dann ist die Gerade parallel zu O x oder fällt bei b = 0 zusammen. Diese Fälle zeigen, dass die Ungleichung möglicherweise keine Lösungen hat oder dass die Lösung eine beliebige Zahl sein kann.

Beispiel 8

Bestimmen Sie aus den Ungleichungen 0 x + 7< = 0 , 0 · x + 0 ≥ 0 то, которое имеет хотя бы одно решение.

Lösung

Die Darstellung von y = 0 x + 7 ist y = 7, dann wird eine Koordinatenebene mit einer Linie parallel zu O x und oberhalb von O x angegeben. Also 0 x + 7< = 0 решений не имеет, потому как нет промежутков.

Der Graph der Funktion y = 0 x + 0 wird als y = 0 betrachtet, das heißt, die Gerade fällt mit O x zusammen. Das bedeutet, dass die Ungleichung 0 x + 0 ≥ 0 viele Lösungen hat.

Antwort: Die zweite Ungleichung hat eine Lösung für jeden Wert von x.

Ungleichungen, die sich auf linear reduzieren

Die Lösung von Ungleichungen kann auf die Lösung reduziert werden Lineargleichung, die Ungleichungen genannt werden, die sich auf linear reduzieren.

Diese Ungleichungen wurden im Schulunterricht berücksichtigt, da es sich um einen Sonderfall der Lösung von Ungleichungen handelte, der zur Öffnung von Klammern und zur Kürzung ähnlicher Begriffe führte. Betrachten Sie beispielsweise Folgendes: 5 − 2 x > 0, 7 (x − 1) + 3 ≤ 4 x − 2 + x, x - 3 5 - 2 x + 1 > 2 7 x.

Die oben angegebenen Ungleichungen werden immer auf die Form einer linearen Gleichung reduziert. Anschließend werden die Klammern geöffnet und ähnliche Begriffe angegeben und übernommen verschiedene Teile, wobei das Vorzeichen in das Gegenteil geändert wird.

Wenn wir die Ungleichung 5 − 2 x > 0 auf linear reduzieren, stellen wir sie so dar, dass sie die Form − 2 x + 5 > 0 hat, und um die Sekunde zu reduzieren, erhalten wir 7 (x − 1) + 3 ≤ 4 x − 2 + x . Es ist notwendig, die Klammern zu öffnen, ähnliche Begriffe einzubringen, alle Begriffe auf die linke Seite zu verschieben und ähnliche Begriffe einzubringen. Es sieht aus wie das:

7 x − 7 + 3 ≤ 4 x − 2 + x 7 x − 4 ≤ ​​5 x − 2 7 x − 4 − 5 x + 2 ≤ 0 2 x − 2 ≤ 0

Dies führt zur Lösung einer linearen Ungleichung.

Diese Ungleichungen gelten als linear, da sie das gleiche Lösungsprinzip haben und sich danach auf elementare Ungleichungen reduzieren lassen.

Um diese Art von Ungleichung zu lösen, ist es notwendig, sie auf eine lineare zu reduzieren. Es sollte so gemacht werden:

Definition 9

• offene Klammern;
• sammle links Variablen und rechts Zahlen;
• geben Sie ähnliche Begriffe an;
• Teilen Sie beide Seiten durch den Koeffizienten von x.

Beispiel 9

Lösen Sie die Ungleichung 5 · (x + 3) + x ≤ 6 · (x − 3) + 1.

Lösung

Wir öffnen die Klammern, dann erhalten wir eine Ungleichung der Form 5 x + 15 + x ≤ 6 x − 18 + 1. Nachdem wir ähnliche Terme reduziert haben, gilt 6 x + 15 ≤ 6 x − 17. Nachdem wir die Terme von links nach rechts verschoben haben, finden wir, dass 6 x + 15 − 6 x + 17 ≤ 0. Daher gibt es eine Ungleichung der Form 32 ≤ 0 aus der Ungleichung, die man durch die Berechnung von 0 x + 32 ≤ 0 erhält. Es ist ersichtlich, dass die Ungleichung falsch ist, was bedeutet, dass die durch die Bedingung gegebene Ungleichung keine Lösungen hat.

Antwort: keine Lösungen.

Es ist erwähnenswert, dass es viele andere Arten von Ungleichungen gibt, die auf lineare Ungleichungen oder Ungleichungen der oben gezeigten Art reduziert werden können. Zum Beispiel: 5 2 x − 1 ≥ 1 Ist Exponentialgleichung, was sich auf eine lineare Lösung 2 x − 1 ≥ 0 reduziert. Diese Fälle werden bei der Lösung von Ungleichungen dieser Art berücksichtigt.

Wenn Sie einen Fehler im Text bemerken, markieren Sie ihn bitte und drücken Sie Strg+Eingabetaste