So lösen Sie gebrochene rationale Gleichungen. Die einfachsten rationalen Gleichungen

30.09.2019

Lesen Sie auch

Was ist eine Schenkungsurkunde und Schenkungsurkunde für ein Haus?

Wie kann man mit Geldfiguren Geld anlocken?

Aprikosenmarmelade und gefrorene Aprikosen

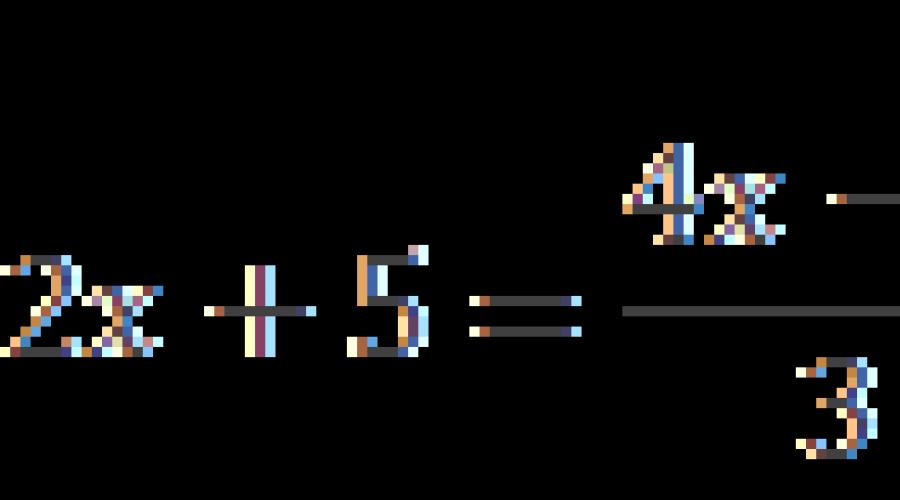
Zur Vereinfachung wird der kleinste gemeinsame Nenner verwendet gegebene Gleichung. Diese Methode wird verwendet, wenn Sie eine gegebene Gleichung nicht mit einem rationalen Ausdruck auf jeder Seite der Gleichung schreiben können (und die Kreuzmultiplikationsmethode verwenden können). Diese Methode wird verwendet, wenn Sie eine rationale Gleichung mit drei oder mehr Brüchen erhalten (bei zwei Brüchen ist es besser, die Kreuzmultiplikation zu verwenden).

Finden Sie den kleinsten gemeinsamen Nenner der Brüche (oder das kleinste gemeinsame Vielfache). NOZ ist die kleinste Zahl, die durch jeden Nenner gleichmäßig teilbar ist.

Manchmal ist NPD eine offensichtliche Zahl. Wenn zum Beispiel die Gleichung x/3 + 1/2 = (3x +1)/6 gegeben wird, dann ist es offensichtlich, dass das kleinste gemeinsame Vielfache der Zahlen 3, 2 und 6 6 ist.
Wenn die NCD nicht offensichtlich ist, notieren Sie die Vielfachen des größten Nenners und finden Sie darunter eines, das ein Vielfaches der anderen Nenner ist. Oft kann der NOD durch einfache Multiplikation zweier Nenner ermittelt werden. Wenn die Gleichung beispielsweise x/8 + 2/6 = (x - 3)/9 ist, dann ist NOS = 8*9 = 72.
Wenn ein oder mehrere Nenner eine Variable enthalten, wird der Vorgang etwas komplizierter (aber nicht unmöglich). In diesem Fall ist der NOC ein Ausdruck (der eine Variable enthält), der durch jeden Nenner dividiert wird. Beispielsweise ist in der Gleichung 5/(x-1) = 1/x + 2/(3x) NOZ = 3x(x-1), da dieser Ausdruck durch jeden Nenner geteilt wird: 3x(x-1)/(x -1 ) = 3x; 3x(x-1)/3x = (x-1); 3x(x-1)/x = 3(x-1).

Multiplizieren Sie sowohl den Zähler als auch den Nenner jedes Bruchs mit einer Zahl, die dem Ergebnis der Division des NOC durch den entsprechenden Nenner jedes Bruchs entspricht.

Da Sie sowohl den Zähler als auch den Nenner mit derselben Zahl multiplizieren, multiplizieren Sie effektiv den Bruch mit 1 (z. B. 2/2 = 1 oder 3/3 = 1).
Verfahren Sie analog, wenn die Variable im Nenner steht. In unserem zweiten Beispiel ist NOZ = 3x(x-1), also multiplizieren Sie 5/(x-1) mit (3x)/(3x), um 5(3x)/(3x)(x-1) zu erhalten; 1/x multipliziert mit 3(x-1)/3(x-1) und Sie erhalten 3(x-1)/3x(x-1); 2/(3x) multipliziert mit (x-1)/(x-1) und Sie erhalten 2(x-1)/3x(x-1).

Finden Sie x. Nachdem Sie die Brüche nun auf einen gemeinsamen Nenner gebracht haben, können Sie den Nenner loswerden. Multiplizieren Sie dazu jede Seite der Gleichung mit dem gemeinsamen Nenner. Lösen Sie dann die resultierende Gleichung, d. h. finden Sie „x“. Isolieren Sie dazu die Variable auf einer Seite der Gleichung.

In unserem Beispiel: 2x/6 + 3/6 = (3x +1)/6. Sie können zwei Brüche mit demselben Nenner addieren. Schreiben Sie die Gleichung also wie folgt: (2x+3)/6=(3x+1)/6. Multiplizieren Sie beide Seiten der Gleichung mit 6 und entfernen Sie die Nenner: 2x+3 = 3x +1. Lösen Sie und erhalten Sie x = 2.
In unserem zweiten Beispiel (mit einer Variablen im Nenner) sieht die Gleichung (nach Reduktion auf einen gemeinsamen Nenner) wie folgt aus: 5(3x)/(3x)(x-1) = 3(x-1)/3x(x -1) + 2 (x-1)/3x(x-1). Indem Sie beide Seiten der Gleichung mit N3 multiplizieren, entfernen Sie den Nenner und erhalten: 5(3x) = 3(x-1) + 2(x-1), oder 15x = 3x - 3 + 2x -2, oder 15x = x - 5 Lösen Sie und erhalten Sie: x = -5/14.

§ 1 Ganzzahlige und gebrochene rationale Gleichungen

In dieser Lektion werden wir uns mit Konzepten wie rationaler Gleichung, rationalem Ausdruck, ganzem Ausdruck und gebrochenem Ausdruck befassen. Betrachten wir die Lösung rationaler Gleichungen.

Eine rationale Gleichung ist eine Gleichung, bei der die linke und rechte Seite rationale Ausdrücke sind.

Rationale Ausdrücke sind:

Bruchteil.

Ein ganzzahliger Ausdruck besteht aus Zahlen, Variablen und ganzzahligen Potenzen unter Verwendung der Operationen Addition, Subtraktion, Multiplikation und Division durch eine Zahl ungleich Null.

Zum Beispiel:

Bruchausdrücke beinhalten die Division durch eine Variable oder einen Ausdruck mit einer Variablen. Zum Beispiel:

Ein Bruchausdruck ist nicht für alle Werte der darin enthaltenen Variablen sinnvoll. Zum Beispiel der Ausdruck

bei x = -9 macht es keinen Sinn, da bei x = -9 der Nenner auf Null geht.

Das bedeutet, dass eine rationale Gleichung ganzzahlig oder gebrochen sein kann.

Eine ganze rationale Gleichung ist eine rationale Gleichung, bei der die linke und rechte Seite ganze Ausdrücke sind.

Zum Beispiel:

Eine gebrochene rationale Gleichung ist eine rationale Gleichung, bei der entweder die linke oder die rechte Seite gebrochene Ausdrücke sind.

Zum Beispiel:

§ 2 Lösung einer gesamten rationalen Gleichung

Betrachten wir die Lösung einer gesamten rationalen Gleichung.

Zum Beispiel:

Multiplizieren wir beide Seiten der Gleichung mit dem kleinsten gemeinsamen Nenner der Nenner der darin enthaltenen Brüche.

Gehen Sie dazu wie folgt vor:

1. Finden Sie den gemeinsamen Nenner für die Nenner 2, 3, 6. Er ist gleich 6;

2. Finden Sie für jeden Bruch einen zusätzlichen Faktor. Teilen Sie dazu den gemeinsamen Nenner 6 durch jeden Nenner

zusätzlicher Faktor für Bruch

3. Multiplizieren Sie die Zähler der Brüche mit ihren entsprechenden zusätzlichen Faktoren. Somit erhalten wir die Gleichung

was der gegebenen Gleichung entspricht

Öffnen wir die Klammern auf der linken Seite, verschieben wir den rechten Teil nach links und ändern das Vorzeichen des Begriffs, wenn er auf das Gegenteil übertragen wird.

Bringen wir ähnliche Terme des Polynoms und erhalten

Wir sehen, dass die Gleichung linear ist.

Nachdem wir es gelöst haben, finden wir, dass x = 0,5.

§ 3 Lösung einer gebrochenen rationalen Gleichung

Betrachten wir die Lösung einer gebrochenen rationalen Gleichung.

Zum Beispiel:

1.Multiplizieren Sie beide Seiten der Gleichung mit dem kleinsten gemeinsamen Nenner der Nenner der darin enthaltenen rationalen Brüche.

Finden wir den gemeinsamen Nenner für die Nenner x + 7 und x - 1.

Es ist gleich ihrem Produkt (x + 7)(x - 1).

2. Finden wir für jeden rationalen Bruch einen zusätzlichen Faktor.

Teilen Sie dazu den gemeinsamen Nenner (x + 7)(x - 1) durch jeden Nenner. Zusätzlicher Faktor für Brüche

gleich x - 1,

zusätzlicher Faktor für Bruch

gleich x+7.

3.Multiplizieren Sie die Zähler der Brüche mit ihren entsprechenden zusätzlichen Faktoren.

Wir erhalten die Gleichung (2x - 1)(x - 1) = (3x + 4)(x + 7), die dieser Gleichung entspricht

4.Multiplizieren Sie das Binomial mit dem Binomial links und rechts und erhalten Sie die folgende Gleichung

5. Wir verschieben die rechte Seite nach links und ändern das Vorzeichen jedes Begriffs, wenn wir ihn ins Gegenteil übertragen:

6. Stellen wir ähnliche Terme des Polynoms vor:

7. Beide Seiten können durch -1 geteilt werden. Wir erhalten eine quadratische Gleichung:

8. Nachdem wir es gelöst haben, werden wir die Wurzeln finden

Da in Gl.

Die linke und rechte Seite sind Bruchausdrücke, und in Bruchausdrücken kann der Nenner für einige Werte der Variablen Null werden. Dann muss überprüft werden, ob der gemeinsame Nenner nicht auf Null geht, wenn x1 und x2 gefunden werden .

Bei x = -27 verschwindet der gemeinsame Nenner (x + 7)(x - 1) nicht; bei x = -1 ist der gemeinsame Nenner auch nicht Null.

Daher sind beide Wurzeln -27 und -1 Wurzeln der Gleichung.

Beim Lösen einer gebrochenen rationalen Gleichung ist es besser, sofort den Bereich akzeptabler Werte anzugeben. Eliminieren Sie die Werte, bei denen der gemeinsame Nenner gegen Null geht.

Betrachten wir ein weiteres Beispiel für die Lösung einer gebrochenen rationalen Gleichung.

Lassen Sie uns zum Beispiel die Gleichung lösen

Wir faktorisieren den Nenner des Bruchs auf der rechten Seite der Gleichung

Wir erhalten die Gleichung

Finden wir den gemeinsamen Nenner für die Nenner (x - 5), x, x(x - 5).

Es wird der Ausdruck x(x - 5) sein.

Lassen Sie uns nun den Bereich akzeptabler Werte der Gleichung ermitteln

Dazu setzen wir den gemeinsamen Nenner mit Null x(x - 5) = 0 gleich.

Wir erhalten eine Gleichung, bei deren Lösung wir feststellen, dass bei x = 0 oder bei x = 5 der gemeinsame Nenner gegen Null geht.

Das bedeutet, dass x = 0 oder x = 5 nicht die Wurzeln unserer Gleichung sein können.

Es können nun weitere Multiplikatoren gefunden werden.

Zusätzlicher Faktor für rationale Brüche

zusätzlicher Faktor für den Bruch

wird (x - 5) sein,

und der zusätzliche Faktor des Bruchs

Wir multiplizieren die Zähler mit den entsprechenden Zusatzfaktoren.

Wir erhalten die Gleichung x(x - 3) + 1(x - 5) = 1(x + 5).

Öffnen wir die Klammern links und rechts, x2 - 3x + x - 5 = x + 5.

Verschieben wir die Begriffe von rechts nach links und ändern dabei das Vorzeichen der übertragenen Begriffe:

X2 - 3x + x - 5 - x - 5 = 0

Und nachdem wir ähnliche Terme herangezogen haben, erhalten wir eine quadratische Gleichung x2 - 3x - 10 = 0. Nachdem wir sie gelöst haben, finden wir die Wurzeln x1 = -2; x2 = 5.

Aber wir haben bereits herausgefunden, dass bei x = 5 der gemeinsame Nenner x(x - 5) gegen Null geht. Daher die Wurzel unserer Gleichung

wird x = -2 sein.

§ 4 Kurze Zusammenfassung der Lektion

Wichtig zu beachten:

Gehen Sie beim Lösen gebrochener rationaler Gleichungen wie folgt vor:

1. Finden Sie den gemeinsamen Nenner der in der Gleichung enthaltenen Brüche. Wenn außerdem die Nenner von Brüchen faktorisiert werden können, faktorisieren Sie sie und finden Sie dann den gemeinsamen Nenner.

2. Multiplizieren Sie beide Seiten der Gleichung mit einem gemeinsamen Nenner: Finden Sie zusätzliche Faktoren, multiplizieren Sie die Zähler mit zusätzlichen Faktoren.

3. Lösen Sie die resultierende ganze Gleichung.

4. Eliminieren Sie aus seinen Wurzeln diejenigen, die den gemeinsamen Nenner verschwinden lassen.

Liste der verwendeten Literatur:

Makarychev Yu.N., N.G. Mindyuk, Neshkov K.I., Suvorova S.B. / Herausgegeben von Telyakovsky S.A. Algebra: Lehrbuch. für die 8. Klasse. Allgemeinbildung Institutionen. - M.: Bildung, 2013.
Mordkovich A.G. Algebra. 8. Klasse: In zwei Teilen. Teil 1: Lehrbuch. für die Allgemeinbildung Institutionen. - M.: Mnemosyne.
Rurukin A.N. Unterrichtsentwicklungen in Algebra: 8. Klasse - M.: VAKO, 2010.
Algebra 8. Klasse: Unterrichtspläne nach dem Lehrbuch von Yu.N. Makarycheva, N.G. Mindyuk, K.I. Neshkova, S.B. Suvorova / Auth.-comp. T.L. Afanasyeva, L.A. Tapilina. -Wolgograd: Lehrer, 2005.

Reden wir weiter darüber Gleichungen lösen. In diesem Artikel gehen wir näher darauf ein rationale Gleichungen und Prinzipien zum Lösen rationaler Gleichungen mit einer Variablen. Lassen Sie uns zunächst herausfinden, welche Art von Gleichungen als rational bezeichnet werden, eine Definition ganzer rationaler und gebrochener rationaler Gleichungen geben und Beispiele nennen. Als nächstes erhalten wir Algorithmen zur Lösung rationaler Gleichungen und betrachten natürlich Lösungen typischer Beispiele mit allen notwendigen Erklärungen.

Seitennavigation.

Basierend auf den angegebenen Definitionen geben wir einige Beispiele für rationale Gleichungen. Zum Beispiel sind x=1, 2·x−12·x 2 ·y·z 3 =0, alles rationale Gleichungen.

Aus den gezeigten Beispielen wird deutlich, dass rationale Gleichungen sowie Gleichungen anderer Art mit einer Variablen oder mit zwei, drei usw. vorliegen können. Variablen. In den folgenden Abschnitten werden wir über das Lösen rationaler Gleichungen mit einer Variablen sprechen. Gleichungen in zwei Variablen lösen und ihre große Zahl verdienen besondere Aufmerksamkeit.

Neben der Division rationaler Gleichungen durch die Anzahl unbekannter Variablen werden sie auch in ganzzahlige und gebrochene Gleichungen unterteilt. Geben wir die entsprechenden Definitionen an.

Definition.

Die rationale Gleichung heißt ganz, wenn sowohl die linke als auch die rechte Seite ganzzahlige rationale Ausdrücke sind.

Definition.

Wenn mindestens einer der Teile einer rationalen Gleichung ein gebrochener Ausdruck ist, dann heißt eine solche Gleichung teilweise rational(oder gebrochen rational).

Es ist klar, dass ganze Gleichungen keine Division durch eine Variable enthalten; im Gegenteil, gebrochene rationale Gleichungen enthalten notwendigerweise eine Division durch eine Variable (oder eine Variable im Nenner). Also 3 x+2=0 und (x+y)·(3·x 2 −1)+x=−y+0,5– das sind ganze rationale Gleichungen, beide Teile sind ganze Ausdrücke. A und x:(5 x 3 +y 2)=3:(x−1):5 sind Beispiele für gebrochene rationale Gleichungen.

Lassen Sie uns zum Abschluss dieses Punktes darauf achten, dass die bisher bekannten linearen Gleichungen und quadratischen Gleichungen vollständige rationale Gleichungen sind.

Ganze Gleichungen lösen

Einer der Hauptansätze zur Lösung ganzer Gleichungen besteht darin, sie auf äquivalente Gleichungen zu reduzieren algebraische Gleichungen. Dies kann jederzeit durch die Durchführung der folgenden äquivalenten Transformationen der Gleichung erfolgen:

Zuerst wird der Ausdruck von der rechten Seite der ursprünglichen Ganzzahlgleichung mit dem umgekehrten Vorzeichen auf die linke Seite übertragen, um auf der rechten Seite Null zu erhalten;
danach steht auf der linken Seite der Gleichung das Ergebnis Standardansicht.

Das Ergebnis ist eine algebraische Gleichung, die der ursprünglichen ganzzahligen Gleichung entspricht. Somit reduziert sich im einfachsten Fall die Lösung ganzer Gleichungen auf die Lösung linearer oder quadratische Gleichungen, und im allgemeinen Fall – zur Lösung einer algebraischen Gleichung vom Grad n. Schauen wir uns zur Verdeutlichung die Lösung des Beispiels an.

Beispiel.

Finden Sie die Wurzeln der gesamten Gleichung 3·(x+1)·(x−3)=x·(2·x−1)−3.

Lösung.

Reduzieren wir die Lösung dieser gesamten Gleichung auf die Lösung einer äquivalenten algebraischen Gleichung. Dazu übertragen wir zunächst den Ausdruck von der rechten auf die linke Seite und erhalten so die Gleichung 3·(x+1)·(x−3)−x·(2·x−1)+3=0. Und zweitens transformieren wir den auf der linken Seite gebildeten Ausdruck in ein Polynom der Standardform, indem wir die notwendigen Schritte vervollständigen: 3·(x+1)·(x−3)−x·(2·x−1)+3= (3 x+3) (x−3)−2 x 2 +x+3= 3 x 2 −9 x+3 x−9−2 x 2 +x+3=x 2 −5 x−6. Somit reduziert sich die Lösung der ursprünglichen ganzzahligen Gleichung auf die Lösung der quadratischen Gleichung x 2 −5·x−6=0.

Wir berechnen seine Diskriminante D=(−5) 2 −4·1·(−6)=25+24=49, es ist positiv, was bedeutet, dass die Gleichung zwei reelle Wurzeln hat, die wir mithilfe der Formel für die Wurzeln einer quadratischen Gleichung finden:

Um ganz sicher zu gehen, lassen Sie es uns tun Überprüfung der gefundenen Wurzeln der Gleichung. Zuerst überprüfen wir die Wurzel 6 und ersetzen sie anstelle der Variablen x in der ursprünglichen Ganzzahlgleichung: 3·(6+1)·(6−3)=6·(2·6−1)−3, was dasselbe ist, 63=63. Dies ist eine gültige numerische Gleichung, daher ist x=6 tatsächlich die Wurzel der Gleichung. Jetzt überprüfen wir die Wurzel −1, die wir haben 3·(−1+1)·(−1−3)=(−1)·(2·(−1)−1)−3, von wo, 0=0 . Wenn x=−1, wird die ursprüngliche Gleichung auch zu einer korrekten numerischen Gleichheit, daher ist x=−1 auch eine Wurzel der Gleichung.

Antwort:

6 , −1 .

Hierbei ist auch zu beachten, dass mit dem Begriff „Grad der Gesamtgleichung“ die Darstellung einer Gesamtgleichung in Form einer algebraischen Gleichung verbunden ist. Geben wir die entsprechende Definition:

Definition.

Die Kraft der gesamten Gleichung wird der Grad einer äquivalenten algebraischen Gleichung genannt.

Nach dieser Definition hat die gesamte Gleichung aus dem vorherigen Beispiel den zweiten Grad.

Dies hätte das Ende der Lösung ganzer rationaler Gleichungen bedeuten können, wenn da nicht eines gewesen wäre … Wie bekannt ist, ist die Lösung algebraischer Gleichungen mit einem höheren Grad als dem zweiten mit erheblichen Schwierigkeiten verbunden, und für Gleichungen mit einem höheren Grad als dem vierten gibt es keine allgemeine Formeln Wurzeln Daher müssen ganze Gleichungen der dritten, vierten und weiterer Gleichungen gelöst werden hohe Abschlüsse Oftmals muss man auf andere Lösungswege zurückgreifen.

In solchen Fällen basiert ein Ansatz zur Lösung ganzer rationaler Gleichungen auf Faktorisierungsmethode. In diesem Fall wird folgender Algorithmus eingehalten:

Zunächst stellen sie sicher, dass auf der rechten Seite der Gleichung eine Null steht; dazu übertragen sie den Ausdruck von der rechten Seite der gesamten Gleichung auf die linke;
Anschließend wird der resultierende Ausdruck auf der linken Seite als Produkt mehrerer Faktoren dargestellt, was es uns ermöglicht, zu einer Reihe einfacherer Gleichungen überzugehen.

Der angegebene Algorithmus zur Lösung einer gesamten Gleichung durch Faktorisierung erfordert eine ausführliche Erläuterung anhand eines Beispiels.

Beispiel.

Lösen Sie die gesamte Gleichung (x 2 −1)·(x 2 −10·x+13)= 2 x (x 2 −10 x+13) .

Lösung.

Zuerst übertragen wir wie üblich den Ausdruck von der rechten Seite auf die linke Seite der Gleichung, vergessen nicht, das Vorzeichen zu ändern, wir erhalten (x 2 −1)·(x 2 −10·x+13)− 2 x (x 2 −10 x+13)=0 . Hier ist es ganz offensichtlich, dass es nicht ratsam ist, die linke Seite der resultierenden Gleichung in ein Polynom der Standardform umzuwandeln, da dies eine algebraische Gleichung vierten Grades der Form ergibt x 4 −12 x 3 +32 x 2 −16 x−13=0, dessen Lösung schwierig ist.

Andererseits ist es offensichtlich, dass wir auf der linken Seite der resultierenden Gleichung x 2 −10 x+13 können und sie somit als Produkt darstellen. Wir haben (x 2 −10 x+13) (x 2 −2 x−1)=0. Die resultierende Gleichung entspricht der ursprünglichen Gesamtgleichung und kann wiederum durch einen Satz zweier quadratischer Gleichungen x 2 −10·x+13=0 und x 2 −2·x−1=0 ersetzt werden. Es ist nicht schwierig, ihre Wurzeln mithilfe bekannter Wurzelformeln durch eine Diskriminante zu finden; die Wurzeln sind gleich. Sie sind die gewünschten Wurzeln der ursprünglichen Gleichung.

Antwort:

Auch nützlich zum Lösen ganzer rationaler Gleichungen Methode zur Einführung einer neuen Variablen. In einigen Fällen können Sie damit zu Gleichungen wechseln, deren Grad niedriger ist als der Grad der ursprünglichen Gesamtgleichung.

Beispiel.

Finden Sie die wahren Wurzeln einer rationalen Gleichung (x 2 +3 x+1) 2 +10=−2 (x 2 +3 x−4).

Lösung.

Diese gesamte rationale Gleichung auf eine algebraische Gleichung zu reduzieren, ist, gelinde gesagt, keine sehr gute Idee, da wir in diesem Fall auf die Notwendigkeit stoßen, eine Gleichung vierten Grades zu lösen, die keine rationalen Wurzeln hat. Daher müssen Sie nach einer anderen Lösung suchen.

Hier ist leicht zu erkennen, dass Sie eine neue Variable y einführen und den Ausdruck x 2 +3·x durch diese ersetzen können. Diese Ersetzung führt uns zur gesamten Gleichung (y+1) 2 +10=−2·(y−4) , die nach dem Verschieben des Ausdrucks −2·(y−4) auf die linke Seite und der anschließenden Transformation des Ausdrucks entsteht dort gebildet, wird auf eine quadratische Gleichung y 2 +4·y+3=0 reduziert. Die Wurzeln dieser Gleichung y=−1 und y=−3 sind leicht zu finden, zum Beispiel können sie basierend auf dem Satz ausgewählt werden, der zum Satz von Vieta invers ist.

Nun kommen wir zum zweiten Teil der Methode zur Einführung einer neuen Variablen, also zur Durchführung einer umgekehrten Ersetzung. Nach Durchführung der umgekehrten Substitution erhalten wir zwei Gleichungen x 2 +3 x=−1 und x 2 +3 x=−3, die als x 2 +3 x+1=0 und x 2 +3 x+3 umgeschrieben werden können =0 . Mit der Formel für die Wurzeln einer quadratischen Gleichung ermitteln wir die Wurzeln der ersten Gleichung. Und die zweite quadratische Gleichung hat keine reellen Wurzeln, da ihre Diskriminante negativ ist (D=3 2 −4·3=9−12=−3 ).

Antwort:

Wenn wir es mit ganzen Gleichungen höheren Grades zu tun haben, müssen wir im Allgemeinen immer bereit sein, nach einer nicht standardmäßigen Methode oder einer künstlichen Technik zu ihrer Lösung zu suchen.

Lösen gebrochener rationaler Gleichungen

Zunächst ist es hilfreich zu verstehen, wie gebrochene rationale Gleichungen der Form gelöst werden, wobei p(x) und q(x) ganzzahlige rationale Ausdrücke sind. Und dann zeigen wir, wie man die Lösung anderer gebrochenrationaler Gleichungen auf die Lösung von Gleichungen des angegebenen Typs reduziert.

Ein Ansatz zur Lösung der Gleichung basiert auf der folgenden Aussage: Der numerische Bruch u/v, wobei v eine Zahl ungleich Null ist (andernfalls stoßen wir auf , was undefiniert ist), ist genau dann gleich Null, wenn sein Zähler ist gleich Null, dann ist genau dann, wenn u=0 . Aufgrund dieser Aussage reduziert sich die Lösung der Gleichung auf die Erfüllung zweier Bedingungen p(x)=0 und q(x)≠0.

Diese Schlussfolgerung entspricht dem Folgenden Algorithmus zur Lösung einer gebrochenen rationalen Gleichung. Um eine gebrochene rationale Gleichung der Form zu lösen, benötigen Sie

löse die gesamte rationale Gleichung p(x)=0 ;
und prüfen Sie, ob die Bedingung q(x)≠0 für jede gefundene Wurzel erfüllt ist, while

wenn wahr, dann ist diese Wurzel die Wurzel der ursprünglichen Gleichung;
ist sie nicht erfüllt, dann ist diese Wurzel irrelevant, das heißt, sie ist nicht die Wurzel der ursprünglichen Gleichung.

Schauen wir uns ein Beispiel für die Verwendung des angekündigten Algorithmus beim Lösen einer gebrochenen rationalen Gleichung an.

Beispiel.

Finden Sie die Wurzeln der Gleichung.

Lösung.

Dies ist eine gebrochene rationale Gleichung und hat die Form, wobei p(x)=3·x−2, q(x)=5·x 2 −2=0.

Gemäß dem Algorithmus zur Lösung gebrochener rationaler Gleichungen dieser Art müssen wir zunächst die Gleichung 3 x−2=0 lösen. Dies ist eine lineare Gleichung, deren Wurzel x=2/3 ist.

Es bleibt noch zu prüfen, ob diese Wurzel die Bedingung 5 x 2 −2≠0 erfüllt. Wir setzen die Zahl 2/3 anstelle von x in den Ausdruck 5 x 2 −2 ein und erhalten . Die Bedingung ist erfüllt, also ist x=2/3 die Wurzel der ursprünglichen Gleichung.

Antwort:

2/3 .

Sie können die Lösung einer gebrochenen rationalen Gleichung von einem etwas anderen Standpunkt aus angehen. Diese Gleichung entspricht der ganzzahligen Gleichung p(x)=0 für die Variable x der ursprünglichen Gleichung. Das heißt, Sie können dabei bleiben Algorithmus zur Lösung einer gebrochenen rationalen Gleichung :

löse die Gleichung p(x)=0 ;
finde die ODZ der Variablen x;
Nehmen Sie Wurzeln, die zum Bereich akzeptabler Werte gehören – sie sind die gewünschten Wurzeln der ursprünglichen gebrochenen rationalen Gleichung.

Lassen Sie uns beispielsweise eine gebrochene rationale Gleichung mit diesem Algorithmus lösen.

Beispiel.

Lösen Sie die Gleichung.

Lösung.

Zuerst lösen wir die quadratische Gleichung x 2 −2·x−11=0. Seine Wurzeln können mit der Wurzelformel für den geraden zweiten Koeffizienten berechnet werden, die wir haben D 1 =(−1) 2 −1·(−11)=12, Und .

Zweitens ermitteln wir die ODZ der Variablen x für die ursprüngliche Gleichung. Es besteht aus allen Zahlen, für die x 2 +3·x≠0 gilt, was dasselbe ist wie x·(x+3)≠0, daher x≠0, x≠−3.

Es bleibt zu prüfen, ob die im ersten Schritt gefundenen Wurzeln in der ODZ enthalten sind. Offensichtlich ja. Daher hat die ursprüngliche gebrochene rationale Gleichung zwei Wurzeln.

Antwort:

Beachten Sie, dass dieser Ansatz profitabler ist als der erste, wenn die ODZ leicht zu finden ist, und insbesondere dann von Vorteil ist, wenn die Wurzeln der Gleichung p(x) = 0 beispielsweise irrational oder rational sind, aber einen ziemlich großen Zähler haben /oder Nenner, zum Beispiel 127/1101 und −31/59. Dies liegt daran, dass in solchen Fällen die Überprüfung der Bedingung q(x)≠0 einen erheblichen Rechenaufwand erfordert und es einfacher ist, Fremdwurzeln mithilfe der ODZ auszuschließen.

In anderen Fällen ist es beim Lösen der Gleichung, insbesondere wenn die Wurzeln der Gleichung p(x) = 0 ganze Zahlen sind, rentabler, den ersten der angegebenen Algorithmen zu verwenden. Das heißt, es ist ratsam, sofort die Wurzeln der gesamten Gleichung p(x)=0 zu finden und dann zu prüfen, ob die Bedingung q(x)≠0 für sie erfüllt ist, anstatt die ODZ zu finden und dann die Gleichung zu lösen p(x)=0 auf dieser ODZ . Dies liegt daran, dass es in solchen Fällen meist einfacher ist, die DZ zu überprüfen als zu finden.

Betrachten wir die Lösung von zwei Beispielen, um die angegebenen Nuancen zu veranschaulichen.

Beispiel.

Finden Sie die Wurzeln der Gleichung.

Lösung.

Lassen Sie uns zunächst die Wurzeln der gesamten Gleichung finden (2 x−1) (x−6) (x 2 −5 x+14) (x+1)=0, zusammengesetzt aus dem Zähler des Bruchs. Die linke Seite dieser Gleichung ist ein Produkt und die rechte Seite ist Null. Daher entspricht diese Gleichung gemäß der Methode zur Lösung von Gleichungen durch Faktorisierung einem Satz von vier Gleichungen 2 x−1=0 , x−6= 0 , x 2 −5 x+ 14=0 , x+1=0 . Drei dieser Gleichungen sind linear und eine quadratisch; wir können sie lösen. Aus der ersten Gleichung ergibt sich x=1/2, aus der zweiten - x=6, aus der dritten - x=7, x=−2, aus der vierten - x=−1.

Mit den gefundenen Wurzeln lässt sich ganz einfach überprüfen, ob der Nenner des Bruchs auf der linken Seite der ursprünglichen Gleichung verschwindet, die Bestimmung der ODZ hingegen ist nicht so einfach, da man dazu eine lösen muss algebraische Gleichung fünften Grades. Daher verzichten wir auf die Suche nach der ODZ und konzentrieren uns stattdessen auf die Überprüfung der Wurzeln. Dazu ersetzen wir sie einzeln anstelle der Variablen x im Ausdruck x 5 −15 x 4 +57 x 3 −13 x 2 +26 x+112, erhalten nach der Substitution, und vergleichen Sie sie mit Null: (1/2) 5 −15·(1/2) 4 + 57·(1/2) 3 −13·(1/2) 2 +26·(1/2)+112= 1/32−15/16+57/8−13/4+13+112= 122+1/32≠0 ;
6 5 −15·6 4 +57·6 3 −13·6 2 +26·6+112= 448≠0 ;
7 5 −15·7 4 +57·7 3 −13·7 2 +26·7+112=0;
(−2) 5 −15·(−2) 4 +57·(−2) 3 −13·(−2) 2 + 26·(−2)+112=−720≠0 ;
(−1) 5 −15·(−1) 4 +57·(−1) 3 −13·(−1) 2 + 26·(−1)+112=0 .

Somit sind 1/2, 6 und −2 die gewünschten Wurzeln der ursprünglichen gebrochenen rationalen Gleichung und 7 und −1 sind Fremdwurzeln.

Antwort:

1/2 , 6 , −2 .

Beispiel.

Finden Sie die Wurzeln einer gebrochenen rationalen Gleichung.

Lösung.

Lassen Sie uns zunächst die Wurzeln der Gleichung finden (5 x 2 −7 x−1) (x−2)=0. Diese Gleichung entspricht einem Satz aus zwei Gleichungen: quadratisch 5·x 2 −7·x−1=0 und linear x−2=0. Mit der Formel für die Wurzeln einer quadratischen Gleichung finden wir zwei Wurzeln und aus der zweiten Gleichung ergibt sich x=2.

Zu überprüfen, ob der Nenner bei den gefundenen Werten von x auf Null geht, ist ziemlich unangenehm. Und die Bestimmung des Bereichs zulässiger Werte der Variablen x in der ursprünglichen Gleichung ist ganz einfach. Deshalb werden wir über ODZ handeln.

In unserem Fall besteht die ODZ der Variablen x der ursprünglichen gebrochenen rationalen Gleichung aus allen Zahlen außer denen, für die die Bedingung x 2 +5·x−14=0 erfüllt ist. Die Wurzeln dieser quadratischen Gleichung sind x=−7 und x=2, woraus wir eine Schlussfolgerung über die ODZ ziehen: Sie besteht aus allen x, so dass .

Es bleibt zu prüfen, ob die gefundenen Wurzeln und x=2 zum Bereich akzeptabler Werte gehören. Die Wurzeln gehören dazu, also sind sie Wurzeln der ursprünglichen Gleichung, und x=2 gehört nicht dazu, also ist es eine fremde Wurzel.

Antwort:

Es wird auch nützlich sein, gesondert auf die Fälle einzugehen, in denen in einer gebrochenen rationalen Gleichung der Form eine Zahl im Zähler steht, das heißt, wenn p(x) durch eine Zahl dargestellt wird. Gleichzeitig

Wenn diese Zahl ungleich Null ist, hat die Gleichung keine Wurzeln, da ein Bruch genau dann gleich Null ist, wenn sein Zähler gleich Null ist;
Wenn diese Zahl Null ist, ist die Wurzel der Gleichung eine beliebige Zahl aus der ODZ.

Beispiel.

Lösung.

Da der Zähler des Bruchs auf der linken Seite der Gleichung eine Zahl ungleich Null enthält, kann der Wert dieses Bruchs für jedes x nicht gleich Null sein. Daher hat diese Gleichung keine Wurzeln.

Antwort:

keine Wurzeln.

Beispiel.

Lösen Sie die Gleichung.

Lösung.

Der Zähler des Bruchs auf der linken Seite dieser gebrochenen rationalen Gleichung enthält Null, sodass der Wert dieses Bruchs für jedes x, für das er sinnvoll ist, Null ist. Mit anderen Worten, die Lösung dieser Gleichung ist jeder Wert von x aus der ODZ dieser Variablen.

Es bleibt noch, diesen Bereich akzeptabler Werte zu bestimmen. Es umfasst alle Werte von x, für die x 4 +5 x 3 ≠0. Die Lösungen der Gleichung x 4 +5 x 3 =0 sind 0 und −5, da diese Gleichung der Gleichung x 3 (x+5)=0 entspricht und diese wiederum der Kombination zweier Gleichungen x entspricht 3 =0 und x +5=0, von wo aus diese Wurzeln sichtbar sind. Daher ist der gewünschte Bereich akzeptabler Werte jedes x außer x=0 und x=−5.

Somit hat eine gebrochene rationale Gleichung unendlich viele Lösungen, bei denen es sich um beliebige Zahlen außer Null und minus fünf handelt.

Antwort:

Schließlich ist es an der Zeit, über die Lösung gebrochener rationaler Gleichungen beliebiger Form zu sprechen. Sie können als r(x)=s(x) geschrieben werden, wobei r(x) und s(x) rationale Ausdrücke sind und mindestens einer von ihnen gebrochen ist. Nehmen wir mit Blick auf die Zukunft an, dass ihre Lösung darin besteht, Gleichungen der uns bereits bekannten Form zu lösen.

Es ist bekannt, dass die Übertragung eines Termes von einem Teil der Gleichung auf einen anderen mit umgekehrtem Vorzeichen zu einer äquivalenten Gleichung führt, daher ist die Gleichung r(x)=s(x) äquivalent zur Gleichung r(x)−s(x). )=0.

Wir wissen auch, dass jedes , identisch mit diesem Ausdruck, möglich ist. Somit können wir den rationalen Ausdruck auf der linken Seite der Gleichung r(x)−s(x)=0 immer in einen identisch gleichen rationalen Bruch der Form umwandeln.

Wir gehen also von der ursprünglichen gebrochenen rationalen Gleichung r(x)=s(x) zur Gleichung über, und ihre Lösung reduziert sich, wie wir oben herausgefunden haben, auf die Lösung der Gleichung p(x)=0.

Hier muss jedoch berücksichtigt werden, dass sich der Bereich zulässiger Werte der Variablen x erweitern kann, wenn r(x)−s(x)=0 durch und dann durch p(x)=0 ersetzt wird .

Folglich kann sich herausstellen, dass die ursprüngliche Gleichung r(x)=s(x) und die Gleichung p(x)=0, zu der wir gelangt sind, ungleich sind, und durch Lösen der Gleichung p(x)=0 können wir Wurzeln erhalten das sind überflüssige Wurzeln der ursprünglichen Gleichung r(x)=s(x) . Sie können fremde Wurzeln identifizieren und nicht in die Antwort einbeziehen, indem Sie entweder eine Prüfung durchführen oder prüfen, ob sie zur ODZ der ursprünglichen Gleichung gehören.

Fassen wir diese Informationen zusammen Algorithmus zur Lösung der gebrochenrationalen Gleichung r(x)=s(x). Um die gebrochene rationale Gleichung r(x)=s(x) zu lösen, benötigen Sie

Erhalten Sie die Null auf der rechten Seite, indem Sie den Ausdruck mit dem umgekehrten Vorzeichen von der rechten Seite verschieben.
Führen Sie Operationen mit Brüchen und Polynomen auf der linken Seite der Gleichung durch und wandeln Sie sie dadurch in einen rationalen Bruch der Form um.
Lösen Sie die Gleichung p(x)=0.
Identifizieren und eliminieren Sie überflüssige Wurzeln, indem Sie sie in die ursprüngliche Gleichung einsetzen oder ihre Zugehörigkeit zur ODZ der ursprünglichen Gleichung überprüfen.

Zur besseren Übersicht zeigen wir die gesamte Kette zur Lösung gebrochener rationaler Gleichungen:
.

Schauen wir uns die Lösungen mehrerer Beispiele mit einer detaillierten Erläuterung des Lösungsprozesses an, um den gegebenen Informationsblock zu verdeutlichen.

Beispiel.

Lösen Sie eine gebrochene rationale Gleichung.

Lösung.

Wir werden gemäß dem soeben erhaltenen Lösungsalgorithmus vorgehen. Und zuerst verschieben wir die Terme von der rechten Seite der Gleichung nach links, wodurch wir zur Gleichung gelangen.

Im zweiten Schritt müssen wir den gebrochenen rationalen Ausdruck auf der linken Seite der resultierenden Gleichung in die Form eines Bruchs umwandeln. Dazu reduzieren wir rationale Brüche auf einen gemeinsamen Nenner und vereinfachen den resultierenden Ausdruck: . So kommen wir zur Gleichung.

An nächste Stufe Wir müssen die Gleichung −2·x−1=0 lösen. Wir finden x=−1/2.

Es bleibt zu prüfen, ob die gefundene Zahl −1/2 keine fremde Wurzel der ursprünglichen Gleichung ist. Dazu können Sie die VA der Variablen x der Originalgleichung überprüfen oder ermitteln. Lassen Sie uns beide Ansätze demonstrieren.

Beginnen wir mit der Überprüfung. Wir setzen die Zahl −1/2 anstelle der Variablen x in die ursprüngliche Gleichung ein und erhalten das Gleiche: −1=−1. Die Substitution ergibt die korrekte numerische Gleichheit, sodass x=−1/2 die Wurzel der ursprünglichen Gleichung ist.

Jetzt zeigen wir, wie der letzte Punkt des Algorithmus durch ODZ ausgeführt wird. Der Bereich akzeptabler Werte der ursprünglichen Gleichung ist die Menge aller Zahlen außer −1 und 0 (bei x=−1 und x=0 verschwinden die Nenner der Brüche). Die im vorherigen Schritt gefundene Wurzel x=−1/2 gehört zur ODZ, daher ist x=−1/2 die Wurzel der ursprünglichen Gleichung.

Antwort:

−1/2 .

Schauen wir uns ein anderes Beispiel an.

Beispiel.

Finden Sie die Wurzeln der Gleichung.

Lösung.

Wir müssen eine gebrochene rationale Gleichung lösen. Gehen wir alle Schritte des Algorithmus durch.

Zuerst verschieben wir den Term von der rechten Seite nach links, wir erhalten .

Zweitens transformieren wir den auf der linken Seite gebildeten Ausdruck: . Als Ergebnis erhalten wir die Gleichung x=0.

Seine Wurzel ist offensichtlich – sie ist Null.

Im vierten Schritt muss noch herausgefunden werden, ob die gefundene Wurzel außerhalb der ursprünglichen gebrochenen rationalen Gleichung liegt. Wenn es in die ursprüngliche Gleichung eingesetzt wird, erhält man den Ausdruck. Offensichtlich macht es keinen Sinn, weil es eine Division durch Null enthält. Daraus schließen wir, dass 0 eine Fremdwurzel ist. Daher hat die ursprüngliche Gleichung keine Wurzeln.

7, was zu Gl. führt. Daraus können wir schließen, dass der Ausdruck im Nenner der linken Seite gleich dem der rechten Seite sein muss, also . Jetzt subtrahieren wir von beiden Seiten des Tripels: . Analog dazu, von wo und weiter.

Die Prüfung zeigt, dass beide gefundenen Wurzeln Wurzeln der ursprünglichen gebrochenen rationalen Gleichung sind.

Antwort:

Referenzen.

Algebra: Lehrbuch für die 8. Klasse. Allgemeinbildung Institutionen / [Yu. N. Makarychev, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova]; bearbeitet von S. A. Telyakovsky. - 16. Aufl. - M.: Bildung, 2008. - 271 S. : krank. - ISBN 978-5-09-019243-9.
Mordkovich A. G. Algebra. 8. Klasse. In 2 Stunden. Teil 1. Lehrbuch für Studierende allgemeinbildender Einrichtungen / A. G. Mordkovich. - 11. Aufl., gelöscht. - M.: Mnemosyne, 2009. - 215 S.: Abb. ISBN 978-5-346-01155-2.
Algebra: 9. Klasse: pädagogisch. für die Allgemeinbildung Institutionen / [Yu. N. Makarychev, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova]; bearbeitet von S. A. Telyakovsky. - 16. Aufl. - M.: Bildung, 2009. - 271 S. : krank. - ISBN 978-5-09-021134-5.

Ein ganzzahliger Ausdruck ist ein mathematischer Ausdruck, der aus Zahlen und Literalvariablen besteht und die Operationen Addition, Subtraktion und Multiplikation verwendet. Zu den Ganzzahlen gehören auch Ausdrücke, die eine Division durch eine beliebige Zahl außer Null beinhalten.

Das Konzept eines gebrochenen rationalen Ausdrucks

Ein Bruchausdruck ist ein mathematischer Ausdruck, der neben den Operationen Addition, Subtraktion und Multiplikation mit Zahlen und Buchstabenvariablen sowie der Division durch eine Zahl ungleich Null auch die Division in Ausdrücke mit Buchstabenvariablen enthält.

Rationale Ausdrücke sind alle ganzen und gebrochenen Ausdrücke. Rationale Gleichungen sind Gleichungen, bei denen die linke und rechte Seite rationale Ausdrücke sind. Wenn in einer rationalen Gleichung die linke und rechte Seite ganzzahlige Ausdrücke sind, dann wird eine solche rationale Gleichung als ganze Zahl bezeichnet.

Wenn in einer rationalen Gleichung die linke oder rechte Seite Bruchausdrücke sind, dann wird eine solche rationale Gleichung Bruch genannt.

Beispiele für gebrochene rationale Ausdrücke

1. x-3/x = -6*x+19

2. (x-4)/(2*x+5) = (x+7)/(x-2)

3. (x-3)/(x-5) + 1/x = (x+5)/(x*(x-5))

Schema zur Lösung einer gebrochenen rationalen Gleichung

1. Finden Sie den gemeinsamen Nenner aller Brüche, die in der Gleichung enthalten sind.

2. Multiplizieren Sie beide Seiten der Gleichung mit einem gemeinsamen Nenner.

3. Lösen Sie die resultierende ganze Gleichung.

4. Überprüfen Sie die Wurzeln und schließen Sie diejenigen aus, die den gemeinsamen Nenner verschwinden lassen.

Da wir gebrochene rationale Gleichungen lösen, gibt es Variablen in den Nennern der Brüche. Das bedeutet, dass sie ein gemeinsamer Nenner sein werden. Und im zweiten Punkt des Algorithmus multiplizieren wir mit einem gemeinsamen Nenner, dann können überflüssige Wurzeln auftauchen. Dann ist der gemeinsame Nenner gleich Null, was bedeutet, dass die Multiplikation damit bedeutungslos ist. Daher ist es am Ende notwendig, die erhaltenen Wurzeln zu überprüfen.

Schauen wir uns ein Beispiel an:

Lösen Sie die gebrochene rationale Gleichung: (x-3)/(x-5) + 1/x = (x+5)/(x*(x-5)).

Wir bleiben dabei allgemeines Schema: Finden wir zunächst den gemeinsamen Nenner aller Brüche. Wir erhalten x*(x-5).

Multiplizieren Sie jeden Bruch mit einem gemeinsamen Nenner und schreiben Sie die resultierende ganze Gleichung.

(x-3)/(x-5) * (x*(x-5))= x*(x+3);
1/x * (x*(x-5)) = (x-5);
(x+5)/(x*(x-5)) * (x*(x-5)) = (x+5);
x*(x+3) + (x-5) = (x+5);

Vereinfachen wir die resultierende Gleichung. Wir bekommen:

x^2+3*x + x-5 - x - 5 =0;
x^2+3*x-10=0;

Wir erhalten eine einfache reduzierte quadratische Gleichung. Wir lösen es mit einer der bekannten Methoden und erhalten die Wurzeln x=-2 und x=5.

Nun überprüfen wir die erhaltenen Lösungen:

Setze die Zahlen -2 und 5 in den gemeinsamen Nenner ein. Bei x=-2 verschwindet der gemeinsame Nenner x*(x-5) nicht, -2*(-2-5)=14. Das bedeutet, dass die Zahl -2 die Wurzel der ursprünglichen gebrochenen rationalen Gleichung ist.

Bei x=5 wird der gemeinsame Nenner x*(x-5) Null. Daher ist diese Zahl nicht die Wurzel der ursprünglichen gebrochenen rationalen Gleichung, da eine Division durch Null erfolgt.

„Fraktionale rationale Gleichungen lösen“

Unterrichtsziele:

Pädagogisch:

Bildung des Konzepts gebrochener rationaler Gleichungen; Betrachten Sie verschiedene Möglichkeiten zur Lösung gebrochener rationaler Gleichungen. Betrachten Sie einen Algorithmus zum Lösen gebrochener rationaler Gleichungen, einschließlich der Bedingung, dass der Bruch gleich Null ist; lehren, gebrochene rationale Gleichungen mithilfe eines Algorithmus zu lösen; Überprüfung des Beherrschungsgrads des Themas durch Durchführung eines Tests.

Entwicklung:

geistige Operationen

Bildung:

pädagogische Aufgaben

Unterrichtsart: Lektion - Erklärung des neuen Materials.

Unterrichtsfortschritt

1. Organisatorischer Moment.

Hallo Leute! An der Tafel stehen Gleichungen, sieh sie dir genau an. Können Sie alle diese Gleichungen lösen? Welche sind das nicht und warum?

Gleichungen, deren linke und rechte Seite gebrochene rationale Ausdrücke sind, werden gebrochene rationale Gleichungen genannt. Was denken Sie, was wir heute im Unterricht lernen werden? Formulieren Sie das Thema der Lektion. Öffnen Sie also Ihre Notizbücher und schreiben Sie das Thema der Lektion „Fraktionale rationale Gleichungen lösen“ auf.

2. Wissen aktualisieren. Frontale Befragung, mündliche Arbeit mit der Klasse.

Und jetzt wiederholen wir das wichtigste theoretische Material, das wir studieren müssen neues Thema. Bitte beantworten Sie folgende Fragen:

1. Was ist eine Gleichung? ( Gleichheit mit einer oder mehreren Variablen.)

2. Wie heißt Gleichung Nr. 1? ( Linear.) Lösung lineare Gleichungen. (Verschieben Sie alles mit der Unbekannten auf die linke Seite der Gleichung, alle Zahlen auf die rechte. Geben Sie ähnliche Begriffe an. Unbekannten Faktor finden).

3. Wie heißt Gleichung Nr. 3? ( Quadrat.) Methoden zur Lösung quadratischer Gleichungen. ( Isolieren eines vollständigen Quadrats mithilfe von Formeln unter Verwendung des Satzes von Vieta und seiner Folgerungen.)

4. Was ist Proportion? ( Gleichheit zweier Verhältnisse.) Die Haupteigenschaft der Proportionen. ( Wenn das Verhältnis stimmt, dann ist das Produkt seiner Extremwerte gleich dem Produkt der Mittelwerte.)

5. Welche Eigenschaften werden beim Lösen von Gleichungen verwendet? ( 1. Wenn Sie einen Term in einer Gleichung von einem Teil zum anderen verschieben und dabei sein Vorzeichen ändern, erhalten Sie eine Gleichung, die der gegebenen Gleichung entspricht. 2. Wenn beide Seiten der Gleichung mit derselben Zahl ungleich Null multipliziert oder dividiert werden, erhalten Sie eine Gleichung, die der angegebenen entspricht.)

6. Wann ist ein Bruch gleich Null? ( Ein Bruch ist gleich Null, wenn der Zähler Null und der Nenner ungleich Null ist..)

3. Erläuterung des neuen Materials.

Lösen Sie Gleichung Nr. 2 in Ihren Notizbüchern und an der Tafel.

Antwort: 10.

Welche gebrochene rationale Gleichung können Sie mithilfe der Grundeigenschaft der Proportionen lösen? (Nr. 5).

(x-2)(x-4) = (x+2)(x+3)

x2-4x-2x+8 = x2+3x+2x+6

x2-6x-x2-5x = 6-8

Lösen Sie Gleichung Nr. 4 in Ihren Notizbüchern und an der Tafel.

Antwort: 1,5.

Welche gebrochene rationale Gleichung können Sie versuchen zu lösen, indem Sie beide Seiten der Gleichung mit dem Nenner multiplizieren? (Nr. 6).

D=1›0, x1=3, x2=4.

Antwort: 3;4.

Versuchen Sie nun, Gleichung Nummer 7 mit einer der folgenden Methoden zu lösen.


(x2-2x-5)x(x-5)=x(x-5)(x+5)
(x2-2x-5)x(x-5)-x(x-5)(x+5)=0
x(x-5)(x2-2x-5-(x+5))=0			x2-2x-5-x-5=0
x(x-5)(x2-3x-10)=0
x=0 x-5=0 x2-3x-10=0
x1=0 x2=5 D=49

Antwort: 0;5;-2.			Antwort: 5;-2.

Erklären Sie, warum das passiert ist? Warum gibt es im einen Fall drei Wurzeln und im anderen zwei? Welche Zahlen sind die Wurzeln dieser gebrochenen rationalen Gleichung?

Bisher sind die Studierenden noch nicht auf das Konzept einer Fremdwurzel gestoßen; es ist für sie tatsächlich sehr schwierig zu verstehen, warum dies passiert ist. Wenn niemand in der Klasse eine klare Erklärung für diese Situation geben kann, stellt der Lehrer Leitfragen.

In den Gleichungen Nr. 2 und 4 stehen Zahlen im Nenner, Nr. 5-7 sind Ausdrücke mit einer Variablen

Der Wert der Variablen, bei dem die Gleichung wahr wird

Machen Sie einen Scheck

Manche Schüler merken beim Testen, dass sie durch Null dividieren müssen. Sie kommen zu dem Schluss, dass die Zahlen 0 und 5 nicht die Wurzeln dieser Gleichung sind. Es stellt sich die Frage: Gibt es eine Möglichkeit, gebrochene rationale Gleichungen zu lösen, die es uns ermöglicht, diesen Fehler zu beseitigen? Ja, diese Methode basiert auf der Bedingung, dass der Bruch gleich Null ist.

x2-3x-10=0, D=49, x1=5, x2=-2.

Wenn x=5, dann ist x(x-5)=0, was bedeutet, dass 5 eine Fremdwurzel ist.

Wenn x=-2, dann x(x-5)≠0.

Antwort: -2.

Versuchen wir, auf diese Weise einen Algorithmus zur Lösung gebrochener rationaler Gleichungen zu formulieren. Kinder formulieren den Algorithmus selbst.

Algorithmus zur Lösung gebrochener rationaler Gleichungen:

1. Verschieben Sie alles auf die linke Seite.

2. Brüche auf einen gemeinsamen Nenner bringen.

3. Erstellen Sie ein System: Ein Bruch ist gleich Null, wenn der Zähler gleich Null und der Nenner ungleich Null ist.

4. Lösen Sie die Gleichung.

5. Überprüfen Sie die Ungleichung, um Fremdwurzeln auszuschließen.

6. Schreiben Sie die Antwort auf.

Diskussion: Wie formalisiert man die Lösung, wenn die Grundeigenschaft der Proportion und Multiplikation beider Seiten der Gleichung mit einem gemeinsamen Nenner verwendet wird? (Fügen Sie der Lösung hinzu: Schließen Sie diejenigen aus ihren Wurzeln aus, die den gemeinsamen Nenner verschwinden lassen.)

4. Erstes Verständnis von neuem Material.

Arbeiten Sie paarweise. Abhängig von der Art der Gleichung entscheiden die Schüler selbst, wie sie die Gleichung lösen. Aufgaben aus dem Lehrbuch „Algebra 8“, 2007: Nr. 000 (b, c, i); Nr. 000(a, d, g). Der Lehrer überwacht die Erledigung der Aufgabe, beantwortet alle auftretenden Fragen und unterstützt leistungsschwache Schüler. Selbsttest: Antworten werden an die Tafel geschrieben.

b) 2 – Fremdwurzel. Antwort: 3.

c) 2 – Fremdwurzel. Antwort: 1.5.

a) Antwort: -12,5.

g) Antwort: 1;1.5.

5. Hausaufgaben machen.

2. Lernen Sie den Algorithmus zum Lösen gebrochener rationaler Gleichungen.

3. Lösen Sie in Notizbüchern Nr. 000 (a, d, e); Nr. 000(g, h).

4. Versuchen Sie, Nr. 000(a) zu lösen (optional).

6. Erledigung einer Kontrollaufgabe zum untersuchten Thema.

Die Arbeit wird auf Zetteln erledigt.

Beispielaufgabe:

A) Welche der Gleichungen sind gebrochenrational?

B) Ein Bruch ist gleich Null, wenn der Zähler ______________________ und der Nenner _______________________ ist.

F) Ist die Zahl -3 die Wurzel der Gleichung Nummer 6?

D) Lösen Sie Gleichung Nr. 7.

Bewertungskriterien für die Aufgabe:

Die Note „5“ wird vergeben, wenn der/die Studierende mehr als 90 % der Aufgabe richtig gelöst hat. „4“ – 75 %–89 % „3“ – 50 %–74 % „2“ wird an einen Schüler vergeben, der weniger als 50 % der Aufgabe erledigt hat. Eine Bewertung von 2 wird im Journal nicht vergeben, 3 ist optional.

7. Reflexion.

Schreiben Sie auf die unabhängigen Arbeitsblätter:

1 – ob die Lektion für Sie interessant und verständlich war; 2 – interessant, aber nicht klar; 3 – nicht interessant, aber verständlich; 4 – nicht interessant, nicht klar.

8. Zusammenfassung der Lektion.

Heute haben wir uns in der Lektion mit gebrochenen rationalen Gleichungen vertraut gemacht und gelernt, wie man diese Gleichungen löst auf verschiedene Weise, testeten ihr Wissen mithilfe einer Schulung selbständiges Arbeiten. Die Ergebnisse Ihrer selbstständigen Arbeit erfahren Sie in der nächsten Lektion und haben zu Hause die Möglichkeit, Ihr Wissen zu festigen.

Welche Methode zur Lösung gebrochener rationaler Gleichungen ist Ihrer Meinung nach einfacher, zugänglicher und rationaler? Was sollten Sie unabhängig von der Methode zur Lösung gebrochener rationaler Gleichungen beachten? Was ist die „Trick“ gebrochener rationaler Gleichungen?

Vielen Dank an alle, die Lektion ist vorbei.