Querbiegefestigkeit. Konzept der Biegeverformung

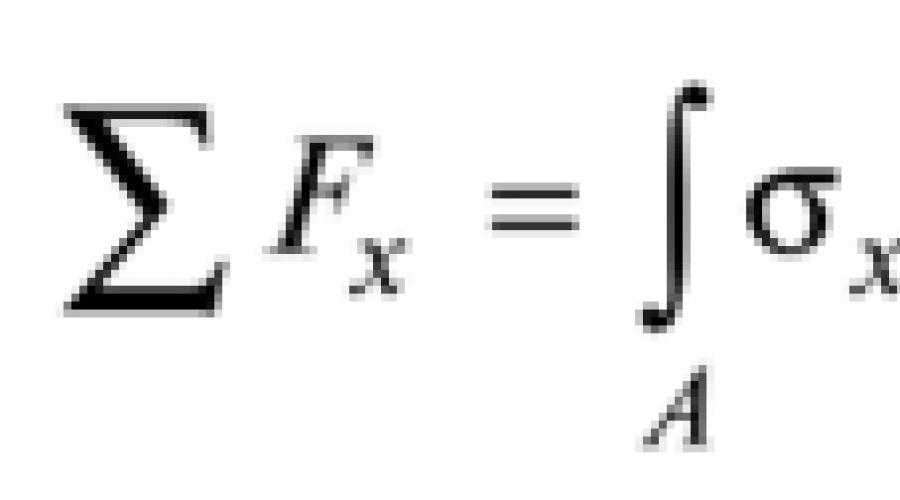
Gerade Kurve ist eine Verformungsart, bei der in den Stabquerschnitten zwei innere Kraftfaktoren entstehen: Biegemoment und Scherkraft.

Saubere Biegung- Dies ist ein Sonderfall der direkten Biegung, bei der in den Stabquerschnitten nur ein Biegemoment auftritt und die Querkraft Null ist.

Ein Beispiel für eine reine Kurve – ein Abschnitt CD auf der Stange AB. Biegemoment ist die Menge Pa ein Paar äußerer Kräfte, die eine Biegung verursachen. Aus dem Gleichgewicht des Stabteils links vom Querschnitt mn Daraus folgt, dass die über diesen Abschnitt verteilten Schnittgrößen statisch dem Moment äquivalent sind M, gleich und entgegengesetzt zum Biegemoment Pa.

Um die Verteilung dieser Schnittgrößen über den Querschnitt zu ermitteln, muss die Verformung des Stabes berücksichtigt werden.

Im einfachsten Fall hat der Stab eine Längssymmetrieebene und unterliegt der Einwirkung äußerer Biegekraftpaare, die in dieser Ebene liegen. Dann erfolgt die Biegung in derselben Ebene.

Stabachse nn 1 ist eine Linie, die durch die Schwerpunkte seiner Querschnitte verläuft.

Der Querschnitt des Stabes sei ein Rechteck. Zeichnen wir zwei vertikale Linien an den Rändern mm Und S. Beim Biegen bleiben diese Linien gerade und drehen sich, sodass sie senkrecht zu den Längsfasern des Stabes bleiben.

Die weitere Biegetheorie basiert auf der Annahme, dass es sich nicht nur um Linien handelt mm Und S, aber der gesamte flache Querschnitt des Stabes bleibt nach dem Biegen flach und normal zu den Längsfasern des Stabes. Daher verändern sich beim Biegen die Querschnitte mm Und S relativ zueinander um Achsen drehen, die senkrecht zur Biegeebene (Zeichenebene) stehen. Dabei erfahren die Längsfasern auf der konvexen Seite eine Spannung und die Fasern auf der konkaven Seite eine Kompression.

Neutrale Oberfläche- Dies ist eine Oberfläche, die beim Biegen keine Verformung erfährt. (Jetzt liegt sie senkrecht zur Zeichnung, der verformten Achse des Stabes nn 1 gehört zu dieser Fläche).

Neutrale Schnittachse- Dies ist der Schnittpunkt einer neutralen Fläche mit einem beliebigen Querschnitt (der nun auch senkrecht zur Zeichnung liegt).

Lassen Sie eine beliebige Faser einen Abstand haben j von einer neutralen Oberfläche. ρ – Krümmungsradius der gekrümmten Achse. Punkt Ö– Krümmungsmittelpunkt. Lasst uns eine Linie ziehen n 1 s 1 parallel mm.SS 1– absolute Faserdehnung.

Relative Erweiterung εx Fasern

Es folgt dem Verformung von Längsfasern proportional zur Entfernung j von der neutralen Oberfläche und umgekehrt proportional zum Krümmungsradius ρ .

Mit der Längsdehnung der Fasern der konvexen Seite des Stabes geht einher seitliche Verengung und die Längsverkürzung der konkaven Seite ist seitliche Ausdehnung, wie im Fall einer einfachen Dehnung und Kompression. Dadurch verändert sich das Aussehen aller Querschnitte, die vertikalen Seiten des Rechtecks ​​werden geneigt. Seitliche Verformung z:

μ - Poissonzahl.

Aufgrund dieser Verzerrung verlaufen alle geraden Querschnittslinien parallel zur Achse z werden so gebogen, dass sie senkrecht zu den Seiten des Abschnitts bleiben. Der Krümmungsradius dieser Kurve R wird mehr sein als ρ im gleichen Sinne wie ε x im absoluten Wert ist größer als ε z und wir bekommen

Diese Verformungen der Längsfasern entsprechen Spannungen

Die Spannung in jeder Faser ist proportional zu ihrem Abstand von der neutralen Achse n 1 n 2. Neutrale Achsenposition und Krümmungsradius ρ – zwei Unbekannte in der Gleichung für σ x – kann aus der Bedingung bestimmt werden, dass über einen beliebigen Querschnitt verteilte Kräfte ein Kräftepaar bilden, das das äußere Moment ausgleicht M.

Das alles gilt auch dann, wenn der Stab keine Längssymmetrieebene hat, in der das Biegemoment wirkt, solange das Biegemoment in der Axialebene wirkt, die eine der beiden enthält Hauptachsen Querschnitt. Diese Flugzeuge heißen Hauptbiegeebenen.

Wenn es eine Symmetrieebene gibt und das Biegemoment in dieser Ebene wirkt, erfolgt die Durchbiegung genau in dieser Ebene. Momente der Schnittgrößen relativ zur Achse z das äußere Moment ausgleichen M. Kraftmomente um die Achse j werden gegenseitig zerstört.

Kräfte, die senkrecht zur Achse des Balkens wirken und sich in einer durch diese Achse verlaufenden Ebene befinden, verursachen eine sogenannte Verformung Querbiegung. Ist die Wirkungsebene der genannten Kräfte – Hauptebene, dann entsteht eine gerade (flache) Querbiegung. Andernfalls wird die Biegung als schräge Querbiegung bezeichnet. Als Balken bezeichnet man einen Balken, der überwiegend einer Biegung unterliegt Strahl 1 .

Im Wesentlichen handelt es sich bei der Querbiegung um eine Kombination aus reiner Biegung und Scherung. Im Zusammenhang mit der Krümmung von Querschnitten aufgrund der ungleichmäßigen Scherverteilung über die Höhe stellt sich die Frage nach der Möglichkeit der Verwendung der Normalspannungsformel σ X, abgeleitet für reine Biegung basierend auf der Hypothese ebener Schnitte.

1 Es wird ein einfeldriger Träger genannt, der an den Enden jeweils einen zylindrischen festen Träger und einen zylindrischen, in Richtung der Trägerachse beweglichen Träger aufweist einfach. Ein Balken, dessen eines Ende festgeklemmt und dessen anderes frei ist, wird als Balken bezeichnet Konsole. Als Balken bezeichnet man einen einfachen Balken, bei dem ein oder zwei Teile über einer Stütze hängen Konsole.

Wenn die Abschnitte außerdem weit von den Stellen entfernt sind, an denen die Last aufgebracht wird (in einem Abstand von mindestens der halben Höhe des Balkenabschnitts), kann wie bei der reinen Biegung davon ausgegangen werden, dass dass die Fasern keinen Druck aufeinander ausüben. Dies bedeutet, dass jede Faser eine einachsige Spannung oder Kompression erfährt.

Unter Einwirkung einer verteilten Last unterscheiden sich die Querkräfte in zwei benachbarten Abschnitten um den Betrag qdx. Daher wird auch die Krümmung der Abschnitte leicht unterschiedlich sein. Außerdem üben die Fasern Druck aufeinander aus. Eine gründliche Untersuchung des Problems zeigt, dass die Länge des Balkens l ziemlich groß im Vergleich zu seiner Höhe H (l/ H> 5), dann haben diese Faktoren auch bei verteilter Belastung keinen wesentlichen Einfluss auf die Normalspannungen in Querschnitt und können daher in praktischen Berechnungen möglicherweise nicht berücksichtigt werden.

ein B C

Reis. 10.5 Abb. 10.6

In Abschnitten unter Einzellast und in deren Nähe ist die Verteilung von σ X weicht vom linearen Gesetz ab. Diese Abweichung ist lokaler Natur und geht nicht mit einem Anstieg einher höchste Belastung(in den extremen Fasern) werden sie in der Praxis meist nicht berücksichtigt.

Also bei Querbiegung (in der Ebene). xy) Normalspannungen werden nach der Formel berechnet

σ X= – [M z(X)/Ich z]j.

Wenn wir zwei benachbarte Abschnitte auf einem lastfreien Abschnitt des Balkens zeichnen, ist die Querkraft in beiden Abschnitten gleich und daher ist die Krümmung der Abschnitte gleich. In diesem Fall jedes Stück Faser ab(Abb. 10.5) wird in eine neue Position verschoben a"b", ohne eine zusätzliche Dehnung zu erfahren und daher den Wert der Normalspannung zu ändern.

Bestimmen wir die Tangentialspannungen im Querschnitt durch ihre paarigen Spannungen, die im Längsschnitt des Balkens wirken.

Wählen Sie ein Längenelement aus dem Holz aus dx(Abb. 10.7 a). Zeichnen wir einen horizontalen Abschnitt in einiger Entfernung bei von der neutralen Achse z, Teilen Sie das Element in zwei Teile (Abb. 10.7) und betrachten Sie das Gleichgewicht des oberen Teils, der eine Basis hat

Breite B. Nach dem Gesetz der Tangentialspannungspaarung sind die im Längsschnitt wirkenden Spannungen gleich den im Querschnitt wirkenden Spannungen. Berücksichtigt man dies, so wird davon ausgegangen, dass die Schubspannungen im Standort vorhanden sind B gleichmäßig verteilt, unter Verwendung der Bedingung ΣХ = 0, erhalten wir:

N * - (N * +dN *)+

wobei: N * die Resultierende der Normalkräfte σ im linken Querschnitt des Elements dx innerhalb der „abgeschnittenen“ Fläche A * ist (Abb. 10.7 d):

wobei: S = - statisches Moment des „abgeschnittenen“ Teils des Querschnitts (schattierter Bereich in Abb. 10.7 c). Deshalb können wir schreiben:

Dann können wir schreiben:

Diese Formel wurde im 19. Jahrhundert vom russischen Wissenschaftler und Ingenieur D.I. Zhuravsky und trägt seinen Namen. Und obwohl es sich bei dieser Formel um eine Näherungsformel handelt, da sie die Spannung über die Breite des Abschnitts mittelt, stimmen die daraus erhaltenen Berechnungsergebnisse gut mit den experimentellen Daten überein.

Um die Schubspannungen an einem beliebigen Querschnittspunkt im Abstand y von der z-Achse zu bestimmen, sollten Sie:

Bestimmen Sie aus dem Diagramm die Größe der im Abschnitt wirkenden Querkraft Q;

Berechnen Sie das Trägheitsmoment I z des gesamten Abschnitts;

Zeichnen Sie durch diesen Punkt eine Ebene parallel zur Ebene xz und bestimmen Sie die Abschnittsbreite B;

Berechnen Sie das statische Moment der abgeschnittenen Fläche S relativ zur Hauptmittelachse z und setzen Sie die gefundenen Werte in die Zhuravsky-Formel ein.

Bestimmen wir als Beispiel Tangentialspannungen in einem rechteckigen Querschnitt (Abb. 10.6, c). Statisches Moment um die Achse z Teile des Abschnitts über Zeile 1-1, in denen die Spannung bestimmt wird, werden in der Form geschrieben:

Sie variiert nach dem Gesetz einer quadratischen Parabel. Abschnittsbreite V für einen rechteckigen Balken ist konstant, dann ist das Gesetz der Änderung der Tangentialspannungen im Abschnitt auch parabolisch (Abb. 10.6, c). Bei y = und y = − sind die Tangentialspannungen Null und liegen auf der neutralen Achse z sie erreichen ihren größten Wert.

Für einen Strahl mit kreisförmigem Querschnitt auf der neutralen Achse gilt:

Saubere Biegung Diese Art der Biegung nennt man, bei der die Aktion stattfindet Nur Biegemoment(Abb. 3.5, A). Zeichnen wir gedanklich die Schnittebene I-I senkrecht zur Längsachse des Balkens im Abstand * vom freien Ende des Balkens, auf den das äußere Moment wirkt m z . Lassen Sie uns ähnliche Aktionen durchführen wie bei der Bestimmung der Spannungen und Dehnungen während der Torsion, nämlich:

• 1) Lassen Sie uns Gleichgewichtsgleichungen für den geistig abgeschnittenen Teil des Teils aufstellen.
• 2) Wir bestimmen die Verformung des Materials des Teils basierend auf den Kompatibilitätsbedingungen der Verformungen der Elementarvolumina eines bestimmten Abschnitts;
• 3) Lösen Sie die Gleichungen des Gleichgewichts und der Kompatibilität von Verformungen.

Aus dem Gleichgewichtszustand des abgeschnittenen Balkenabschnitts (Abb. 3.5, B)

Wir finden, dass das Moment der inneren Kräfte ist Mz gleich dem Moment der äußeren Kräfte t: M = t.

Reis. 3.5.

Das Moment der Schnittgrößen wird durch Normalspannungen o v erzeugt, die entlang der x-Achse gerichtet sind. Bei reiner Biegung gibt es keine äußeren Kräfte, daher ist die Summe der Projektionen der inneren Kräfte auf eine beliebige Koordinatenachse Null. Auf dieser Grundlage schreiben wir die Gleichgewichtsbedingungen in Form von Gleichungen

Wo A- Querschnittsfläche des Balkens (Stab).

Bei reiner Biegung wirken äußere Kräfte Fx, F, Fv sowie Momente äußerer Kräfte t x, t y sind gleich Null. Daher sind die übrigen Gleichgewichtsgleichungen identisch gleich Null.

Aus der Gleichgewichtsbedingung wenn o^O daraus folgt

normale Spannung c x im Querschnitt sowohl positiv als auch negative Werte. (Die Erfahrung zeigt, dass beim Biegen das Material der unteren Seite des Balkens in Abb. 3.5, A gedehnt und das obere gestaucht.) Folglich gibt es im Querschnitt beim Biegen solche Elementarvolumina (der Übergangsschicht von Druck zu Zug), in denen keine Dehnung oder Stauchung stattfindet. Das - neutrale Schicht. Die Schnittlinie der neutralen Schicht mit der Querschnittsebene wird aufgerufen neutrale Linie.

Die Bedingungen für die Kompatibilität von Verformungen von Elementarvolumina beim Biegen werden auf der Grundlage der Hypothese flacher Abschnitte gebildet: Die Querschnitte des Balkens sind vor dem Biegen flach (siehe Abb. 3.5, B) bleibt auch nach dem Biegen flach (Abb. 3.6).

Durch die Einwirkung eines äußeren Moments biegt sich der Balken und die Ebenen Abschnitte I-I und II-II drehen sich relativ zueinander um einen Winkel dy(Abb. 3.6, B). Bei der reinen Biegung ist die Verformung aller Abschnitte entlang der Balkenachse gleich, daher ist der Krümmungsradius pk der neutralen Schicht des Balkens entlang der x-Achse gleich. Als dx= S K-Dip, dann ist die Krümmung der neutralen Schicht gleich 1 / p k = tauchen / dx und ist über die Länge des Balkens konstant.

Die neutrale Schicht wird nicht verformt; ihre Länge vor und nach der Verformung ist gleich dx. Unterhalb dieser Schicht wird das Material gedehnt, darüber wird es gestaucht.

Reis. 3.6.

Der Dehnungswert der gestreckten Schicht, die sich im Abstand y von der neutralen Schicht befindet, ist gleich ydq. Relative Dehnung dieser Schicht:

Somit erhält man im angenommenen Modell eine lineare Verformungsverteilung in Abhängigkeit vom Abstand eines gegebenen Elementarvolumens zur neutralen Schicht, d.h. entlang der Höhe des Balkenabschnitts. Unter der Annahme, dass es keinen gegenseitigen Druck paralleler Materialschichten aufeinander gibt (o y = 0, a, = 0), schreiben wir das Hookesche Gesetz für lineare Dehnung:

Nach (3.13) verteilen sich die Normalspannungen im Balkenquerschnitt nach einem linearen Gesetz. Die Spannung des Elementarvolumens des Materials, das am weitesten von der neutralen Schicht entfernt ist (Abb. 3.6, V), maximal und gleich

? Aufgabe 3.6

Bestimmen Sie die Elastizitätsgrenze einer Stahlklinge mit einer Dicke / = 4 mm und einer Länge / = 80 cm, wenn ihre Biegung in einen Halbkreis keine bleibende Verformung verursacht.

Lösung

Biegespannung o v = Ey/ r k. Nehmen wir y max = T/ 2i r k = / / Zu.

Die Elastizitätsgrenze muss der Bedingung mit уп > c v = entsprechen 1 / 2 kE t /1.

Antwort: o = ] / 2 bis 2 10 11 4 10 _3 / 0,8 = 1570 MPa; Die Streckgrenze dieses Stahls beträgt a t > 1800 MPa und übertrifft damit die a t der stärksten Federstähle. ?

? Problem 3.7

Bestimmen Sie den Mindestradius der Trommel zum Aufwickeln eines Bandes mit einer Dicke von / = 0,1 mm eines Heizelements aus einer Nickellegierung, bei dem das Bandmaterial nicht plastisch verformt wird. Modul E= 1,6 · 10 5 MPa, Elastizitätsgrenze ca. yp = 200 MPa.

Antwort: Mindestradius ð = V 2 ?ir/a yM = У? 1,6-10 11 0,1 10 -3 / (200 10 6) = = 0,04 m?

1. Wenn wir die erste Gleichgewichtsgleichung (3.12) und die Verformungskompatibilitätsgleichung (3.13) zusammen lösen, erhalten wir

Bedeutung E/ r k φ 0 und für alle Elemente gleich dA Integrationsbereiche. Folglich ist diese Gleichheit nur unter der Bedingung erfüllt

Dieses Integral heißt statisches Moment der Querschnittsfläche um die Achsez? Was physikalische Bedeutung dieses Integral?

Nehmen wir eine Platte mit konstanter Dicke /, aber beliebigem Profil (Abb. 3.7). Hängen wir diesen Teller an einer Stelle auf MIT sodass es sich in einer horizontalen Position befindet. Bezeichnen wir mit dem Symbol y m spezifisches Gewicht Material der Platte, dann das Gewicht des Elementarvolumens mit Fläche dA gleicht dq= y JdA. Da sich die Platte im Gleichgewichtszustand befindet, gehen die Kräfteprojektionen auf die Achse von der Gleichheit auf Null über bei wir bekommen

Wo G= y M tA- Gewicht der Schallplatte.

Reis. 3.7.

Die Summe der Kraftmomente aller Kräfte um die Achse z der Durchgang durch einen beliebigen Abschnitt der Platte ist ebenfalls Null:

Bedenkt, dass Yc = G, lasst uns aufschreiben

Wenn also ein Integral der Form J xdA nach Gebiet A gleicht

Null also x c = 0. Das bedeutet, dass Punkt C mit dem Schwerpunkt der Platte zusammenfällt. Daher aus der Gleichheit S z = J ydA = 0 bei Fälligkeit

Beim Biegen folgt, dass der Schwerpunkt des Balkenquerschnitts auf der Neutrallinie liegt.

Daher der Wert Ja Der Querschnitt des Balkens ist Null.

• 1. Die Neutrallinie verläuft beim Biegen durch den Schwerpunkt des Balkenquerschnitts.
• 2. Der Schwerpunkt des Querschnitts ist das Reduktionszentrum der Momente äußerer und innerer Kräfte.

Aufgabe 3.8

Aufgabe 3.9

2. Wenn wir die zweite Gleichgewichtsgleichung (3.12) und die Verformungskompatibilitätsgleichung (3.13) zusammen lösen, erhalten wir

Integral J z= J y 2 dA angerufen Trägheitsmoment der Querachse

Abschnitt des Balkens (Stab) relativ zur z-Achse, durch den Schwerpunkt des Querschnitts verläuft.

Auf diese Weise, M z = E J z / r k. In Anbetracht dessen c x = Ee x = Ey/ r k i E/r k = ein x / ja, wir erhalten die Abhängigkeit der Normalspannungen Oh beim Biegen:

1. Die Biegespannung an einem bestimmten Punkt des Abschnitts hängt nicht vom normalen Elastizitätsmodul ab E, hängt aber vom geometrischen Parameter des Querschnitts ab J z und Entfernungen bei von einem gegebenen Punkt zum Schwerpunkt des Querschnitts.

2. Die maximale Spannung beim Biegen tritt in den Elementarvolumina auf, die am weitesten von der Neutrallinie entfernt sind (siehe Abb. 3.6, V):

Wo W z- Widerstandsmoment des Querschnitts relativ zur Achse Z-

Die Bedingung für die Festigkeit bei reiner Biegung ähnelt der Bedingung für die Festigkeit bei linearer Spannung:

wo [a m | - zulässige Biegespannung.

Es ist offensichtlich, dass die inneren Volumina des Materials, insbesondere in der Nähe der neutralen Achse, praktisch nicht belastet sind (siehe Abb. 3.6, V). Dies widerspricht der Forderung, den Materialverbrauch der Struktur zu minimieren. Im Folgenden zeigen wir einige Möglichkeiten, diesen Widerspruch zu überwinden.

Bei gerader reiner Biegung im Stabquerschnitt gibt es nur eine Leistungsfaktor Biegemoment M x(Abb. 1). Als Q y =dM x /dz=0, Das M x=const und eine reine gerade Biegung kann realisiert werden, wenn die Stange durch Kräftepaare belastet wird, die in den Endabschnitten der Stange wirken. Seit dem Biegemoment M x per Definition gleich der Summe der Momente der Schnittgrößen relativ zur Achse Oh sie steht im Zusammenhang mit Normalspannungen durch die aus dieser Definition hervorgehende Statikgleichung

Formulieren wir die Prämissen der Theorie der reinen geraden Biegung eines prismatischen Stabes. Analysieren wir dazu die Verformungen eines Stabmodells aus niedermoduligem Material, auf dessen Seitenfläche ein Raster aus Längs- und Quermarkierungen angebracht ist (Abb. 2). Da die Querrisiken beim Biegen des Stabes durch in den Endabschnitten wirkende Kräftepaare gerade und senkrecht zu den gekrümmten Längsrisiken bleiben, lässt dies den Schluss zu Ebenenschnitthypothesen, was, wie die Lösung dieses Problems mit den Methoden der Elastizitätstheorie zeigt, keine Hypothese mehr ist, sondern eine exakte Tatsache wird das Gesetz der ebenen Abschnitte. Durch die Messung der Änderung der Abstände zwischen den Längsrisiken kommen wir zu dem Schluss, dass die Hypothese über den Nichtdruck der Längsfasern gültig ist.

Die Orthogonalität der Längs- und Querkratzer vor und nach der Verformung (als Widerspiegelung der Wirkung des Gesetzes der ebenen Schnitte) weist auch auf das Fehlen von Scherungen und Tangentialspannungen in den Quer- und Längsschnitten des Stabes hin.

Abb.1. Zusammenhang zwischen innerer Anstrengung und Spannung

Abb.2. Reines Biegemodell

Somit wird die reine gerade Biegung eines prismatischen Stabes auf einachsige Spannung oder Kompression von Längsfasern durch Spannungen (Index) reduziert G wir werden es im Folgenden weglassen). Dabei befindet sich ein Teil der Fasern in der Zugzone (in Abb. 2 sind dies die unteren Fasern) und der andere Teil in der Druckzone (obere Fasern). Diese Zonen sind durch eine neutrale Schicht getrennt (pp),ändert seine Länge nicht, die Spannung ist Null. Unter Berücksichtigung der oben formulierten Prämissen und der Annahme, dass das Material des Stabes linear elastisch ist, hat das Hookesche Gesetz in diesem Fall die Form: , Lassen Sie uns Formeln für die Krümmung der neutralen Schicht (Krümmungsradius) und Normalspannungen ableiten. Beachten wir zunächst die Konstanz des Querschnitts des prismatischen Stabes und des Biegemoments (M x =const), sorgt für einen konstanten Krümmungsradius der neutralen Schicht über die Länge des Stabes (Abb. 3, A), neutrale Schicht (pp) durch einen Kreisbogen beschrieben.

Betrachten wir einen prismatischen Stab unter Bedingungen direkter reiner Biegung (Abb. 3, a) mit einem um die vertikale Achse symmetrischen Querschnitt OU. Diese Bedingung hat keinen Einfluss auf das Endergebnis (damit eine gerade Biegung möglich ist, muss die Achse übereinstimmen Oh s die Hauptträgheitsachse des Querschnitts, die die Symmetrieachse darstellt). Achse Ochse Legen Sie es auf eine neutrale Ebene und positionieren Sie es dem im Vorhinein unbekannt.

A) Entwurfsschema, B) Belastung und Stress

Betrachten Sie ein aus einem Stab geschnittenes Element mit Länge dz, der der Übersichtlichkeit halber in einem Maßstab mit verzerrten Proportionen in Abb. dargestellt ist. 3, B. Da die Verformungen des Elements, die durch die relative Verschiebung seiner Punkte bestimmt werden, von Interesse sind, kann einer der Endabschnitte des Elements als stationär betrachtet werden. Aufgrund ihrer Kleinheit gehen wir davon aus, dass sich die Querschnittspunkte bei Drehung um diesen Winkel nicht entlang von Bögen, sondern entlang der entsprechenden Tangenten bewegen.

Berechnen wir die relative Verformung der Längsfaser AB, von der neutralen Schicht um beabstandet y:

Aus der Ähnlichkeit von Dreiecken C00 1 Und 0 1 BB 1 folgt dem

Es stellte sich heraus, dass es sich um eine Längsverformung handelte lineare Funktion Abstand von der neutralen Schicht, was eine direkte Folge des Gesetzes der ebenen Schnitte ist

Diese Formel ist nicht geeignet für praktischer Nutzen, da es zwei Unbekannte enthält: die Krümmung der neutralen Schicht und die Position der neutralen Achse Oh, von dem aus die Koordinate gemessen wird u. Um diese Unbekannten zu bestimmen, verwenden wir die Gleichgewichtsgleichungen der Statik. Die erste drückt die Forderung aus, dass die Längskraft gleich Null sein muss

Einsetzen des Ausdrucks (2) in diese Gleichung

und wenn man das berücksichtigt, verstehen wir das

Das Integral auf der linken Seite dieser Gleichung stellt das statische Moment des Stabquerschnitts um die neutrale Achse dar Oh, die nur relativ zur Mittelachse Null sein kann. Daher die neutrale Achse Oh verläuft durch den Schwerpunkt des Querschnitts.

Bei der zweiten statischen Gleichgewichtsgleichung handelt es sich um eine Gleichung, die Normalspannungen mit dem Biegemoment in Beziehung setzt (das sich leicht als äußere Kräfte ausdrücken lässt und daher als gegebener Wert betrachtet wird). Einsetzen des Ausdrucks für in die Copula-Gleichung. Spannungen erhalten wir:

und angesichts dessen Wo J x Hauptzentralträgheitsmoment um die Achse Oh, Für die Krümmung der neutralen Schicht erhalten wir die Formel

Abb.4. Normale Spannungsverteilung

das erstmals 1773 von C. Coulomb erhalten wurde. Zur Koordinierung der Vorzeichen des Biegemoments M x und Normalspannungen wird seit wann ein Minuszeichen auf die rechte Seite der Formel (5) gesetzt M x >0 Normalspannungen bei j>0 erweisen sich als komprimierend. In praktischen Berechnungen ist es jedoch bequemer, ohne die formale Vorzeichenregel einzuhalten, die Spannung nach dem Absolutwert zu bestimmen und das Vorzeichen entsprechend seiner Bedeutung zuzuordnen. Normalspannungen beim reinen Biegen eines prismatischen Stabes sind eine lineare Funktion der Koordinate bei und erreichen höchste Werte in den Fasern, die am weitesten von der neutralen Achse entfernt sind (Abb. 4), d. h.

Hier wird die geometrische Eigenschaft eingeführt , mit einer Dimension von m 3 und genannt Biegewiderstandsmoment. Da für eine gegebene M x Stromspannung max? je weniger, desto mehr Wx, Moment des Widerstands ist geometrisches Merkmal der Biegefestigkeit des Querschnitts. Lassen Sie uns Beispiele für die Berechnung von Widerstandsmomenten für die einfachsten Querschnittsformen geben. Für einen rechteckigen Querschnitt (Abb. 5, A) wir haben J x =bh 3 /12,y max = h/2 Und W x = J x /y max = BH 2/6.Ähnliches gilt für einen Kreis (Abb. 5 ,a J x =d 4 /64, y max =d/2) wir bekommen B x =d 3/32, für einen kreisförmigen Ringabschnitt (Abb. 5, V), welcher

Um die Art der Verformung von Balken (Stäben) beim Biegen visuell darzustellen, wird das folgende Experiment durchgeführt. Auf die Seitenflächen eines Gummibalkens mit rechteckigem Querschnitt wird ein Liniengitter parallel und senkrecht zur Balkenachse aufgebracht (Abb. 30.7, a). Anschließend werden auf den Balken an seinen Enden Momente ausgeübt (Abb. 30.7, b), die in der Symmetrieebene des Balkens wirken und jeden seiner Querschnitte entlang einer der Hauptmittelträgheitsachsen schneiden. Die Ebene, die durch die Achse des Strahls und eine der zentralen Hauptträgheitsachsen jedes seiner Querschnitte verläuft, wird als Hauptebene bezeichnet.

Unter dem Einfluss von Momenten erfährt der Balken eine gerade reine Biegung. Durch die Verformung werden erfahrungsgemäß die Gitterlinien parallel zur Balkenachse gebogen, wobei die Abstände zwischen ihnen gleich bleiben. Wenn in Abb. 30.7, b In Richtung der Momente werden diese Linien im oberen Teil des Balkens verlängert und im unteren Teil verkürzt.

Jede zur Achse des Balkens senkrechte Gitterlinie kann als Spur der Ebene eines Balkenquerschnitts betrachtet werden. Da diese Linien gerade bleiben, kann davon ausgegangen werden, dass die vor der Verformung flachen Querschnitte des Balkens während der Verformung flach bleiben.

Diese auf Erfahrung basierende Annahme ist als Hypothese der ebenen Schnitte oder Bernoulli-Hypothese bekannt (siehe § 6.1).

Die Hypothese der ebenen Schnitte gilt nicht nur für die reine Biegung, sondern auch für die Querbiegung. Für die Querbiegung ist sie näherungsweise und für die reine Biegung streng, was durch theoretische Untersuchungen mit Methoden der Elastizitätstheorie bestätigt wird.

Betrachten wir nun einen geraden Balken mit einem um die vertikale Achse symmetrischen Querschnitt, der am rechten Ende eingebettet und am linken Ende durch ein äußeres Moment belastet ist, das in einer der Hauptebenen des Balkens wirkt (Abb. 31.7). In jedem Querschnitt dieses Balkens treten nur Biegemomente auf, die in derselben Ebene wie das Moment wirken

Somit befindet sich der Balken über seine gesamte Länge in einem Zustand der geraden, reinen Biegung. Einzelne Abschnitte des Trägers können sich auch bei Querbeanspruchung in einem reinen Biegezustand befinden; Beispielsweise erfährt Abschnitt 11 des in Abb. gezeigten Trägers eine reine Biegung. 32,7; in den Abschnitten dieses Abschnitts die Scherkraft

Aus dem betrachteten Balken (siehe Abb. 31.7) wählen wir ein Element der Länge aus. Durch die Verformung bleiben die Abschnitte, wie aus der Bernoulli-Hypothese hervorgeht, flach, neigen sich aber um einen bestimmten Winkel zueinander. Nehmen wir den linken Abschnitt bedingt als stationär an. Durch Drehen des rechten Abschnitts um einen Winkel nimmt er dann die Position ein (Abb. 33.7).

Die geraden Linien schneiden sich an einem bestimmten Punkt A, dem Krümmungsmittelpunkt (oder genauer gesagt der Spur der Krümmungsachse) der Längsfasern des Elements. Die oberen Fasern des betreffenden Elements, wenn in dargestellt Feige. 31,7 in Richtung des Moments werden verlängert und die unteren werden verkürzt. Die Fasern einer Zwischenschicht senkrecht zur Wirkungsebene des Moments behalten ihre Länge. Diese Schicht wird Neutralschicht genannt.

Bezeichnen wir den Krümmungsradius der neutralen Schicht, also den Abstand dieser Schicht zum Krümmungsmittelpunkt A (siehe Abb. 33.7). Betrachten wir eine bestimmte Schicht, die sich im Abstand y von der neutralen Schicht befindet. Die absolute Dehnung der Fasern dieser Schicht ist gleich und die relative Dehnung

Angesichts ähnliche Dreiecke Wir stellen fest, dass daher

In der Biegetheorie wird davon ausgegangen, dass die Längsfasern des Balkens nicht aufeinander drücken. Experimentelle und theoretische Forschung zeigen, dass diese Annahme die Berechnungsergebnisse nicht wesentlich beeinflusst.

Bei reiner Biegung treten in den Balkenquerschnitten keine Schubspannungen auf. Somit unterliegen alle Fasern beim reinen Biegen einachsigen Zug- oder Druckbedingungen.

Nach dem Hookeschen Gesetz gilt für den Fall einachsiger Zug- oder Druckbelastung die Normalspannung o und die entsprechende relative Verformung gebunden an Sucht

oder basierend auf Formel (11.7)

Aus Formel (12.7) folgt, dass die Normalspannungen in den Längsfasern des Balkens direkt proportional zu ihren Abständen y von der neutralen Schicht sind. Folglich sind im Querschnitt des Balkens an jedem Punkt die Normalspannungen proportional zum Abstand y von diesem Punkt zur neutralen Achse, die die Schnittlinie der neutralen Schicht mit dem Querschnitt ist (Abb.

34.7, a). Aus der Symmetrie des Balkens und der Last folgt, dass die neutrale Achse horizontal ist.

An den Punkten der neutralen Achse sind die Normalspannungen Null; Auf der einen Seite der neutralen Achse wirken sie auf Zug und auf der anderen auf Druck.

Das Spannungsdiagramm o ist ein durch eine Gerade begrenztes Diagramm mit den größten absoluten Spannungswerten für die Punkte, die am weitesten von der neutralen Achse entfernt sind (Abb. 34.7b).

Betrachten wir nun die Gleichgewichtsbedingungen des ausgewählten Balkenelements. Stellen wir die Wirkung des linken Teils des Balkens auf den Abschnitt des Elements (siehe Abb. 31.7) in Form eines Biegemoments dar; die verbleibenden Schnittgrößen in diesem Abschnitt sind bei reiner Biegung gleich Null. Stellen wir uns die Wirkung der rechten Seite des Balkens auf den Querschnitt des Elements in Form von Elementarkräften vor, die auf jeden Elementarbereich des Querschnitts (Abb. 35.7) und parallel zur Achse des Elements wirken Strahl.

Erstellen wir sechs Gleichgewichtsbedingungen für ein Element

Hier sind die Summen der Projektionen aller auf das Element bzw. auf die Achsen wirkenden Kräfte – die Summen der Momente aller Kräfte relativ zu den Achsen (Abb. 35.7).

Die Achse fällt mit der neutralen Achse des Abschnitts zusammen und die y-Achse steht senkrecht dazu; beide Achsen liegen in der Querschnittsebene

Eine Elementarkraft erzeugt keine Projektionen auf der y-Achse und verursacht kein Moment um die Achse. Daher sind die Gleichgewichtsgleichungen für alle Werte von o erfüllt.

Die Gleichgewichtsgleichung hat die Form

Setzen wir den Wert von a gemäß Formel (12.7) in Gleichung (13.7) ein:

Da (es wird ein gekrümmtes Balkenelement betrachtet, wofür), dann

Das Integral stellt das statische Moment des Balkenquerschnitts um die neutrale Achse dar. Seine Gleichheit mit Null bedeutet, dass die neutrale Achse (d. h. die Achse) durch den Schwerpunkt des Querschnitts verläuft. Somit liegt der Schwerpunkt aller Querschnitte des Balkens und damit die Achse des Balkens, die die geometrische Lage der Schwerpunkte darstellt, in der neutralen Schicht. Daher ist der Krümmungsradius der neutralen Schicht der Krümmungsradius der gekrümmten Achse des Strahls.

Stellen wir nun eine Gleichgewichtsgleichung in Form der Summe der Momente aller Kräfte auf, die relativ zur neutralen Achse auf das Balkenelement wirken:

Hier wird das Moment der elementaren inneren Kraft relativ zur Achse dargestellt.

Bezeichnen wir die Fläche des Balkenquerschnitts oberhalb der neutralen Achse - unterhalb der neutralen Achse.

Dann stellt es die Resultierende der Elementarkräfte dar, die oberhalb der neutralen Achse und unterhalb der neutralen Achse wirken (Abb. 36.7).

Beide Resultierenden sind im absoluten Wert einander gleich, da ihre algebraische Summe, basierend auf der Bedingung (13.7), gleich Null ist. Diese Resultierenden bilden ein inneres Kräftepaar, das im Querschnitt des Balkens wirkt. Das Moment dieses Kräftepaares, gleich dem Produkt aus der Größe einer von ihnen und dem Abstand zwischen ihnen (Abb. 36.7), ist ein Biegemoment im Querschnitt des Balkens.

Setzen wir den Wert von a gemäß Formel (12.7) in Gleichung (15.7) ein:

Hier wird das axiale Trägheitsmoment dargestellt, d. h. die Achse, die durch den Schwerpunkt des Abschnitts verläuft. Somit,

Ersetzen wir den Wert aus Formel (16.7) in Formel (12.7):

Bei der Ableitung der Formel (17.7) wurde nicht berücksichtigt, dass bei einem von außen gerichteten Drehmoment, wie in Abb. 31.7, nach der anerkannten Vorzeichenregel ist das Biegemoment negativ. Wenn wir dies berücksichtigen, müssen wir vor der rechten Seite der Formel (17.7) ein Minuszeichen setzen. Bei einem positiven Biegemoment im oberen Bereich des Balkens (d. h. bei ) werden die Werte von a dann negativ, was auf das Vorhandensein von Druckspannungen in diesem Bereich hinweist. Normalerweise steht das Minuszeichen jedoch nicht auf der rechten Seite der Formel (17.7) und diese Formel wird nur zur Bestimmung der Absolutwerte der Spannungen a verwendet. Daher sollte man in die Formel (17.7) einsetzen absolute Werte Biegemoment und Ordinate y. Das Vorzeichen der Spannungen lässt sich immer leicht anhand des Vorzeichens des Moments oder der Art der Verformung des Balkens bestimmen.

Stellen wir nun die Gleichgewichtsgleichung in Form der Summe der Momente aller Kräfte auf, die relativ zur y-Achse auf das Balkenelement wirken:

Hier stellt es das Moment der Elementarschnittgröße um die y-Achse dar (siehe Abb. 35.7).

Ersetzen wir den Wert von a gemäß der Formel (12.7) in den Ausdruck (18.7):

Hier stellt das Integral das Zentrifugalträgheitsmoment des Balkenquerschnitts relativ zur y- und Achse dar. Somit,

Aber seit

Bekanntlich (siehe § 7.5) ist das Zentrifugalträgheitsmoment des Abschnitts relativ zu den Hauptträgheitsachsen gleich Null.

Im betrachteten Fall ist die y-Achse die Symmetrieachse des Balkenquerschnitts und daher sind die y-Achsen die Hauptmittelträgheitsachsen dieses Abschnitts. Daher ist hier die Bedingung (19.7) erfüllt.

Für den Fall, dass der Querschnitt des gebogenen Trägers keine Symmetrieachse hat, ist die Bedingung (19.7) erfüllt, wenn die Wirkungsebene des Biegemoments durch eine der zentralen Hauptträgheitsachsen des Querschnitts verläuft oder parallel ist zu dieser Achse.

Wenn die Wirkungsebene des Biegemoments nicht durch eine der zentralen Hauptträgheitsachsen des Balkenquerschnitts verläuft und nicht parallel zu dieser verläuft, ist die Bedingung (19.7) nicht erfüllt und daher nicht gegeben direkte Biegung – der Balken erfährt eine schräge Biegung.

Die Formel (17.7), die die Normalspannung an einem beliebigen Punkt des betrachteten Balkenabschnitts bestimmt, ist anwendbar, sofern die Wirkungsebene des Biegemoments durch eine der Hauptträgheitsachsen dieses Abschnitts verläuft oder parallel zu dieser verläuft . In diesem Fall ist die neutrale Achse des Querschnitts seine Hauptträgheitsachse, senkrecht zur Wirkungsebene des Biegemoments.

Formel (16.7) zeigt, dass bei direkter reiner Biegung die Krümmung der gekrümmten Achse des Balkens direkt proportional zum Produkt aus Elastizitätsmodul E und Trägheitsmoment ist. Wir nennen das Produkt die Steifigkeit des Abschnitts während der Biegung; es wird ausgedrückt in usw.

Bei der reinen Biegung eines Trägers mit konstantem Querschnitt sind die Biegemomente und Querschnittssteifigkeiten über seine Länge konstant. In diesem Fall hat der Krümmungsradius der gekrümmten Achse des Strahls einen konstanten Wert [siehe. Ausdruck (16.7)], das heißt, der Strahl biegt sich entlang eines Kreisbogens.

Aus Formel (17.7) folgt, dass die größten (positiven – Zugspannungen) und kleinsten (negativen – Druckspannungen) Normalspannungen im Querschnitt des Balkens an den Punkten auftreten, die am weitesten von der neutralen Achse entfernt sind und sich auf beiden Seiten davon befinden. Mit einem Querschnitt symmetrisch zur neutralen Achse, absolute Werte die höchsten Zug- und Druckspannungen sind gleich und können durch die Formel ermittelt werden

Bei Abschnitten, die nicht symmetrisch zur neutralen Achse sind, beispielsweise bei einem Dreieck, einem T-Stück usw., sind die Abstände von der neutralen Achse zu den am weitesten entfernten gestreckten und komprimierten Fasern unterschiedlich; Daher gibt es für solche Abschnitte zwei Widerstandsmomente:

Wo sind die Abstände von der neutralen Achse zu den am weitesten entfernten gestreckten und komprimierten Fasern?