Untersuchung von Warteschlangensystemen mithilfe statistischer Modellierung.
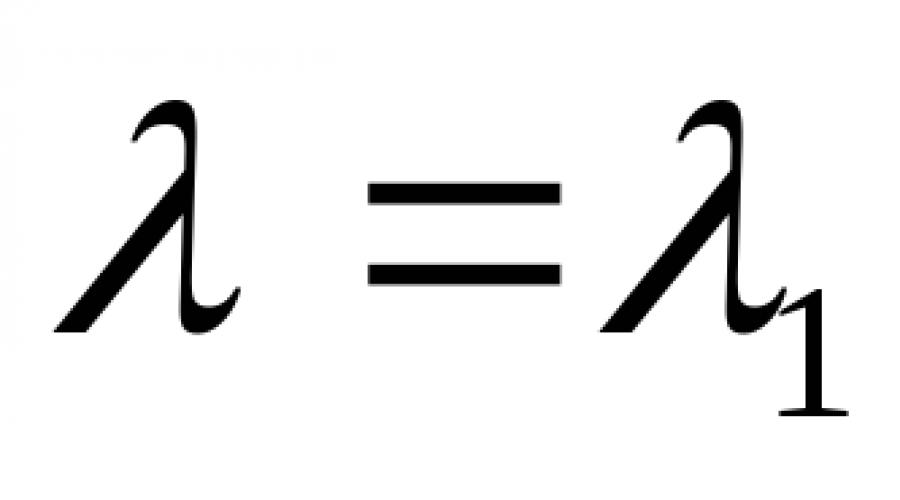
Lesen Sie auch
Die Warteschlangentheorie ist ein Gebiet der angewandten Mathematik, das Methoden aus der Theorie zufälliger Prozesse und der Wahrscheinlichkeitstheorie zum Studium nutzt unterschiedlicher Natur komplexe Systeme. Die Warteschlangentheorie steht nicht in direktem Zusammenhang mit der Optimierung. Sein Zweck besteht darin, auf der Grundlage der Beobachtungsergebnisse des „Eingangs“ zum System seine Fähigkeiten vorherzusagen, den besten Service für eine bestimmte Situation zu organisieren und zu verstehen, wie sich dieser auf die Kosten des Systems als Ganzes auswirkt. Für Systeme im Zusammenhang mit Warteschlangensystemen gibt es eine bestimmte Klasse von Problemen, deren Lösung es uns ermöglicht, für heute relevante Fragen zu beantworten. Mit welcher Intensität sollte die Dienstleistung erbracht bzw. der Prozess bei einer bestimmten Intensität und anderen Parametern des eingehenden Anforderungsflusses durchgeführt werden, um die Warteschlange oder Verzögerung bei der Erstellung eines Dokuments oder einer anderen Art von Informationen zu minimieren? Wie hoch ist die Wahrscheinlichkeit, dass eine Verzögerung oder Warteschlange auftritt, und wie groß ist deren Ausmaß? Wie lange wartet eine Anfrage in der Warteschlange und wie kann ihre Verzögerung minimiert werden? Wie groß ist die Wahrscheinlichkeit, einen Anspruch (Kunden) zu verlieren? Wie hoch sollte die optimale Auslastung der Bereitstellungskanäle sein? Bei welchen Parametern werden die Systeme erreicht? minimale Verluste angekommen? Zu dieser Liste können noch eine Reihe weiterer Aufgaben hinzugefügt werden.
Das Warteschlangensystem (QS) umfasst folgende strukturbildende Objekte: Anforderungsquelle; Eingangsfluss von Anforderungen (Eingang von Bewerbungen); Warteschlange; Servicesystem als eine Reihe von Kanälen für Serviceanfragen; Ausgabestrom (ausgelieferte Bestellungen oder erfüllte Anforderungen). Schauen wir uns ihre Modelle an.
Quelle der Anforderungen. Basierend auf dem Standort der Quelle, die die Anforderungen generiert, werden QSs in offene QSs unterteilt, wenn die Quelle außerhalb des Systems liegt, und geschlossene QSs, wenn sich die Quelle innerhalb des Systems befindet.
Eingabeanforderungen-Stream. Die überwiegende Mehrheit der theoretischen Entwicklungen bei der Untersuchung von Warteschlangensystemen wurde für die Bedingung durchgeführt, dass der Eingabefluss von Anforderungen Poisson ist (der einfachste). Dieser Stream hat eine Reihe wichtiger Eigenschaften. Es ist stationär, gewöhnlich und hat keine Konsequenzen.
Das eingegebene Poisson-Strömungsmodell wird durch eine Funktion der Form dargestellt:
Die nächste wichtige Eigenschaft eines Poisson-Flusses besteht darin, dass das Split-and-Merge-Verfahren wiederum Poisson-Flüsse erzeugt. Dann wird der Eingabestrom aus gebildet N unabhängige Quellen, von denen jede einen Poisson-Fluss mit Intensität erzeugt λ ich (ich=1,2,…, N) , dann wird seine Intensität durch die Formel bestimmt:
|
|
Im Falle der Aufteilung eines Poisson-Flusses in N Unabhängige Flüsse, wir erhalten die Flussintensität λ ich wird gleich sein R ich λ , Wo R ich - Aktie ich – Der Stream im Eingabeanforderungen-Stream.
Warteschlange. Warteschlangen, definiert als eine Reihe von Anfragen, die darauf warten, bedient zu werden, werden durch mehrere Modelle dargestellt: eine Warteschlange mit Ablehnungen, mit einer begrenzten Wartezeit (eine Anfrage wartet eine bestimmte Zeit), einer begrenzten Länge und schließlich einer unbegrenzten Wartezeit . Die Reihenfolge, in der Serviceanfragen eingehen, wird als Warteschlangendisziplin bezeichnet. Anforderungen können angenommen werden, sobald sie eingehen, in zufälliger Reihenfolge, mit Priorität, nach dem Last-First-Prinzip, über bestimmte Kanäle.
Serviceprozess. Der Hauptparameter des Serviceprozesses ist die Zeit, die für die Bearbeitung einer Anfrage durch einen Kanal erforderlich ist. J- T J (J=1,2,…, M) . Größe τ J im Einzelfall wird von einer Reihe von Faktoren bestimmt: der Intensität des Bewerbungseingangs, der Qualifikation des Auftragnehmers, der Arbeitstechnologie, der Umgebung usw. Gesetze der Zufallsvariablenverteilung τ J kann sehr unterschiedlich sein, in praktischen Anwendungen wird jedoch am häufigsten das Exponentialverteilungsgesetz verwendet. Zufällige Variablenverteilungsfunktion τ J hat die Form:
Die wichtigste Eigenschaft der Exponentialverteilung ist die folgende. Wenn mehrere Servicekanäle des gleichen Typs vorhanden sind und die Wahrscheinlichkeit ihrer Auswahl beim Eingang einer Anfrage gleich ist, ist die Verteilung der Servicezeit auf alle möglich M Kanäle sind eine Exponentialfunktion der Form:
Wenn das QS aus inhomogenen Kanälen besteht, dann  , wenn alle Kanäle homogen sind, dann
, wenn alle Kanäle homogen sind, dann  .
.
Ausgabestrom bedienter Anfragen. Der Outputfluss ist der Fluss von Aktivitätsergebnissen, die durch erfüllte Anforderungen in der Idee eines bestimmten Produkts oder einer bestimmten Dienstleistung dargestellt werden. Zu den Hauptparametern des Ausgabeflusses gehören die Intensität der bedienten Anforderungen, die das System verlassen, und die Art der Zeitverteilung zwischen den Zeitpunkten der Produktfreigabe. Im Allgemeinen werden diese Parameter durch das Eingabeflussmodell, die Warteschlangendisziplin und das Servicemodell bestimmt. Für ein QS mit parallelen Kanälen und einphasigem Betrieb gibt es einen Satz, dass bei einem Poisson-Eingangsfluss mit dem Parameter λ und der gleichen Betriebszeitverteilung mit dem Parameter μ für jeden Kanal im stationären Zustand der Ausgangsfluss a hat Poisson-Verteilung mit dem Parameter g. In monophasischen Systemen dient der Ausgangsstrom eines Kanals als Eingangsstrom für einen anderen Kanal. Der Parameter g wird im einfachsten Fall durch die Formel bestimmt:
|
|
|
|
W S - die durchschnittliche Verweildauer einer Anfrage im System. |
|
Die Besonderheit von QS-Modellen ist mit einer recht strengen mathematischen Beschreibung der Funktionsweise von Systemen verbunden, die durch deren Vereinheitlichung nach einer Reihe von Merkmalen erreicht wird. So werden je nach Wartemodell auf die Anforderung zur Leistungsaufnahme folgende QS unterschieden:
System mit Verlusten oder Ausfällen;
Wartesystem;
System mit begrenzter Wartezeit (BO);
System mit begrenzter Warteschlangenlänge (BL).
Basierend auf der Anzahl der Servicekanäle werden Systeme in Einkanal- ( M=1 ) und Mehrkanal ( M>1 ). Die Struktur des QS und die Eigenschaften seiner Objekte sind in Abbildung 1.21 dargestellt.
Eine der Klassifizierungsformen von QS ist die Codeklassifizierung von D. Kendall. Entsprechend dieser Klassifizierung werden die Merkmale des QS in Form von drei, vier oder fünf Zeichen geschrieben. Zum Beispiel, A/ B/ C, Wo A– Art der Verteilung des Eingangsflusses von Anforderungen, B– Art der Dienstzeitverteilung, C– Anzahl der Servicekanäle. Für Poisson- und Exponentialverteilungen wird das Symbol verwendet M, für jede beliebige Verteilung G. Zum Beispiel aufzeichnen M/M/2 bedeutet, dass der Eingabefluss der Anforderungen Poisson ist, die Servicezeit nach einem Exponentialgesetz verteilt ist und es zwei Kanäle im System gibt. Das vierte Zeichen (d) gibt die zulässige Warteschlangenlänge an, das fünfte (e) gibt die Reihenfolge der Anforderungsauswahl an.

Abbildung 1.21 – Struktur und Eigenschaften von QS-Objekten
QS-Modelle können deterministisch oder probabilistisch sein. Im ersten Fall handelt es sich um die Parameter und Variablen des Modells Konstanten, im zweiten - zufällig.
Die Untersuchung von QS besteht darin, Indikatoren zu finden, die die Qualität und Betriebsbedingungen des Dienstleistungssystems charakterisieren, sowie Indikatoren, die die wirtschaftlichen Folgen widerspiegeln getroffene Entscheidungen nach den ersten Indikatoren. Zu den Indikatoren der ersten Gruppe gehören die folgenden.
1. Mit festgelegten oder entworfenen Parametern des Zuflusses:
a) die Wahrscheinlichkeit, dass über einen Zeitraum n Anfragen in das System gelangen T (P N (T)) ;
b) Anwesenheitswahrscheinlichkeit N System Anforderungen (P N ) .
2. Gegebene etablierte oder entworfene Serviceparameter:
a) die Wahrscheinlichkeit, dass alle dienen M Kanäle sind kostenlos (P 0 ) ;
b) die Wahrscheinlichkeit, dass eine bestimmte Anzahl von Kanälen (Manager, Agenten) mit dem Dienst belegt ist (P M ) ;
c) die Wahrscheinlichkeit, dass R Anforderungen liegen in der Warteschlange (P M + R ) .
3. Angesichts der festgelegten oder entworfenen Parameter des Zufluss- und Versorgungssystems:
b) durchschnittliche Anzahl von Kanälen M mit der Wartung beschäftigt: E(M)= M k ;
c) durchschnittliche Anzahl freier Kanäle: E(M 0 )=(M- M k ) ;
d) Kanalauslastungsfaktor (Belegungsfaktor). (K S ) ;
e) Koeffizient der Kanalausfallzeit (Ausfall). (K 0 ) ;
e) relativ (Q) und absolut (A) QS-Kapazität;
g) die durchschnittliche Anzahl der Anforderungen im System (L S ) ;
h) durchschnittliche Anzahl der in der Warteschlange wartenden Anfragen (L Q ) ;
i) durchschnittliche Wartezeit für eine Anfrage in der Warteschlange (W Q ) ;
j) durchschnittliche Verweildauer einer Anforderung im System (W S ) .
Betrachten wir Methoden zur Berechnung von Indikatoren der ersten Gruppe am Beispiel des gängigsten QS-Modells ( M/ M/ M≥2 ) mit Erwartung enthaltend M parallele Versorgungskanäle. Dabei gehen eingehende Anfragen nicht verloren und verlassen das System erst nach einer Wartung. Die Kanäle führen homogene Operationen aus und die Servicezeit jedes Kanals beträgt T nach dem Exponentialgesetz mit Parameter verteilt M, und der eingehende Fluss ist Poisson mit dem Parameter λ ; Die Warteschlangendisziplin ist nicht geregelt und die Anzahl der eingehenden Anfragen ist nicht begrenzt. Das QS-Modell wird als Gleichungssystem für einen stationären Zustand dargestellt.
Bestimmung der Anwesenheitswahrscheinlichkeit N Anforderungen (P N ) im System hängt vom Verhältnis der Anzahl der eingehenden Anfragen ab ( N) pro Zeiteinheit und Anzahl der Servicekanäle ( M).
1. Für die Bedingung wann M=1, P N wird durch die Formel für den mathematischen Erwartungswert einer diskreten Zufallsvariablen bestimmt.
2. Für die Bedingung wann 1≤ N≤ M (Wahrscheinlichkeit, dass alle Anfragen bearbeitet werden oder keine Warteschlange vorhanden ist), P N berechnet nach der Formel:
Wenn ρ/ M<1 , dann die Wahrscheinlichkeit des Fehlens von Anforderungen im System P 0 bestimmt durch die Formel für den stationären Modus:
oder nach der Formel für den mathematischen Erwartungswert einer diskreten Zufallsvariablen:
Die Koeffizienten der Kanalauslastung (Last) und der Kanalausfallzeit werden jeweils durch die Formeln bestimmt:
 Und
Und  .
.
Die durchschnittliche Anzahl der in der Warteschlange stehenden Anfragen ergibt sich aus dem Ausdruck:
 .
.
Die durchschnittliche Wartezeit in der Warteschlange beträgt:
 .
.
Die durchschnittliche Verweildauer einer Anforderung im System wird nach folgender Formel berechnet:
 .
.
Die durchschnittliche Anzahl der Anforderungen im System wird bestimmt durch auf die folgende Weise:
 .
.
Für den allgemeinen Fall L S wird durch die Formel für den mathematischen Erwartungswert einer diskreten Zufallsvariablen bestimmt:
 .
.
Um die Parameter eines probabilistischen Systems und seiner Zufallsprozesse unter dem Gesichtspunkt der Stabilität abzuschätzen, ist vorgesehen, die gefundenen Werte der Eigenschaften von Zufallsfunktionen zu verwenden, bei denen es sich um nichtzufällige Funktionen des Arguments handelt T. Dazu gehören der mathematische Erwartungswert, die Streuung, die Korrelationsfunktion und der Variationskoeffizient, die eine durchschnittliche Implementierung eines Zufallsprozesses (oder einer Zufallsfunktion) über eine Reihe von Beobachtungen charakterisieren. Statistiken werden über die QS-Parameter ermittelt. Zum Beispiel Varianz (D) für die Anzahl der Anforderungen im System wird nach der Formel berechnet:
 .
.
Indikatoren, die die wirtschaftlichen Folgen von Entscheidungen zur Verbesserung des Kundenservices (Verbraucher) charakterisieren, beschränken sich auf die Ermittlung der Wirtschaftlichkeit und der Verluste aufgrund von Serviceverweigerung und Warten auf Service.
Die Wirtschaftlichkeit des Warteschlangensystems beträgt:
Die Höhe der Verluste wird durch die folgenden Ausdrücke bestimmt:
a) System mit Fehlern:
b) System mit Warten:
Um die Nützlichkeit der Verwendung von Methoden der Warteschlangentheorie zur Lösung von Managementproblemen zu demonstrieren, betrachten Sie ein Beispiel für die Schätzung eines niedrigdimensionalen QS.
Beispiel 1.9. Es ist erforderlich, die Wirksamkeit der Zentralisierung mehrerer Abteilungen oder Dienste mit homogenen Funktionen zu bewerten. Bei dem betrachteten Objekt handelt es sich um zwei Taxidienste, die von der Firma Autoservice erworben wurden. Kundenanfragen werden gleichmäßig auf die Dienste verteilt. Der Disponent erhält Taxianfragen mit einer Frequenz von 10 Anrufen pro Stunde. Die durchschnittliche Zeit für die Betreuung eines Kunden beträgt 11,5 Minuten. Taxirufe werden nach dem Poisson-Gesetz zeitlich verteilt, und die Servicedauer für einen Kunden wird nach dem Exponentialgesetz verteilt. Jeder Taxidienst ist mit zwei Wagen ausgestattet.
Es stellt sich die Frage nach der wirtschaftlichen Machbarkeit einer Zentralisierung des Taxiflottenmanagements. Dazu müssen Sie zwei Optionen vergleichen:
1) Option mit unabhängigem Service durch Systeme wie ( M/M/2) bei λ=10 Anrufen/Stunde, τ=11,5 min. Und M= 2;
2) Option mit einem Warteschlangentyp ( M/M/4) mit λ=10*2=20 Anrufen/Stunde, τ=11,5 min. Und M= 4;
Lassen Sie uns zunächst die Service-Auslastungsfaktoren für die erste und zweite Option bestimmen. Bei M= 2 wir haben:
Wie aus der Berechnung hervorgeht, ist die Auslastung des Taxidienstes recht hoch. Offensichtlich ändert sich in der Version mit nichts M= 4, da sowohl Zähler als auch Nenner verdoppelt werden. Auf den ersten Blick führt der Zusammenschluss nicht zu einem wirtschaftlichen Effekt, und da die Untersuchung der Wirksamkeit der Funktionsweise des QS auf die Verbesserung der Qualität der Erfüllung der Verbraucheranforderungen ausgerichtet ist, ist es notwendig, die Parameter zu bewerten, die diesen Bereich charakterisieren Aktivität.
Rechnen wir W Q(durchschnittliche Zeit, die ein Kunde auf ein Taxi wartet).
Für den ersten Fall mit M= 2 haben wir ρ=1,917. Bestimmen wir die Wahrscheinlichkeit, dass das System keine Anforderungen hat ( P 0 ):
Wert nutzen P 0 lasst uns definieren W Q :
 H.
H.
Für den zweiten Fall mit M= 4 haben wir ρ=3,83 und definieren P 0 :
Wenn Wert P 0 =0,0042, das verstehen wir
 H.
H.
Die oben genannten Schätzungen zeigen, dass die Zentralisierung der Dienstleistungen es ermöglicht, die durchschnittliche Zeit, die ein Kunde auf ein per Telefon gerufenes Taxi wartet, um etwa die Hälfte zu reduzieren. Dies ist keine Garantie dafür, dass der Kunde die Bestellung ablehnt, sondern eine deutliche Verkürzung der Wartezeit. In Zukunft muss neben der Schaffung eines einheitlichen Taxidienstes auch über eine Vergrößerung der Taxiflotte nachgedacht werden.
1. Grundkonzepte der Warteschlangentheorie.
2. Darstellung des Problems der Warteschlangentheorie.
3. Ansätze zur Lösung von Problemen in der Warteschlangentheorie.
Knapp Themeninhalt
Die praktische menschliche Tätigkeit ist eng mit verschiedenen Arten von Warteschlangensystemen verbunden. Im Bereich der Wirtschaftswissenschaften gehören dazu Bankdienstleistungen, die Nutzung von Handelseinrichtungen und -dienstleistungen sowie viele andere Arten wirtschaftlicher Aktivitäten.
Jedes Warteschlangensystem kann die folgenden Elemente umfassen:
Eingehender Fluss von Anforderungen oder Serviceanfragen. Dieses Element ist das Hauptelement. Bei der Organisation eines Warteschlangensystems ist es notwendig, den eingehenden Anforderungsfluss und seine Beschreibung zu untersuchen.
Warteschlange. In Fällen, in denen Anforderungen, die in das Warteschlangensystem eingehen, nicht sofort erfüllt werden können, entsteht eine Warteschlange. In einer solchen Situation können die Länge dieser Warteschlange, die Reihenfolge, in der Warteanfragen zur Bearbeitung gesendet werden (wie man „Warteschlangendisziplin“ nennt) und die Wartezeit von Interesse sein.
In einigen Fällen sind Warteschlangensysteme nicht zulässig, d. h. Eine Anfrage, die feststellt, dass das System ausgelastet ist, wird nicht bearbeitet (abgelehnt).
Servicegerät. Dieses Element ist in jedem Warteschlangensystem vorhanden. Nicht nur die zur Bearbeitung einer Anfrage erforderliche Zeit, sondern auch die Länge der Warteschlange und die Wartezeit hängen von den Eigenschaften und Parametern sowie den Methoden zur Organisation des Bediengeräts ab.
Der ausgehende Strom bedienter Anfragen. Dieses Element kann in Fällen sehr wichtig sein, in denen der ausgehende Fluss bedienter Anforderungen für ein anderes Warteschlangensystem eingeht.
In der Regel sind die Anzahl der Anfragen am Eingang eines Warteschlangensystems für einen beliebigen Zeitraum und die Bearbeitungszeit einer Anfrage Zufallsvariablen. Die Funktionsweise eines Warteschlangensystems ist in diesem Fall ein zufälliger Prozess, und Methoden zur Untersuchung solcher Systeme nutzen Simulationsmodellierung. Das Wesen der Probleme und Methoden der Warteschlangentheorie lässt sich jedoch anhand von Beispielen deterministischer Modelle von Warteschlangensystemen und vor allem Modellen der Warteschlangentheorie verstehen.
Die Hauptkomponenten des Warteschlangenmodells sind:
Beschreibung des eingehenden Anforderungsflusses;
eine Beschreibung der Art und Weise, wie die Wartung durchgeführt wird (d. h. eine Beschreibung der Wartungsdisziplin);
Beschreibung der Warteschlangendisziplin (d. h. wie Kunden aus der Warteschlange für den Service ausgewählt werden: „Wer zuerst kommt – mahlt zuerst“, „Zuletzt kommt – mahlt zuerst“, „nach festgelegten Prioritäten“ usw.).
Bei der Erstellung eines Warteschlangenmodells besteht die erste Aufgabe darin, die Hauptkomponenten symbolisch darzustellen und anschließend die Beziehungen zwischen ihnen zu untersuchen.
Die Hauptmerkmale der Warteschlange sind:
Warteschlangenlänge zu unterschiedlichen Zeiten;
die Gesamtdauer des Aufenthalts der Anfrage im Servicesystem (d. h. die Wartezeit in der Warteschlange plus die eigene Servicezeit);
die Zeit, in der das Wartungsgerät im Leerlauf war.
Das Hauptziel der Untersuchung von Warteschlangensystemen besteht darin, ein Gleichgewicht zwischen den zulässigen Belastungen des Ausgabegeräts, der begrenzten Kapazität des Systems und der Irritation der Kunden einerseits und den zulässigen Kosten der Ausgabestellen andererseits herzustellen.
Stellen Sie sich ein Warteschlangensystem vor, das über eine Quelle von Anfragen verfügt, die über ein einziges Bereitstellungsgerät geleitet werden. Es gelten folgende Annahmen:
1. Anfragen kommen in regelmäßigen Abständen. Jedes Intervall hat die Länge a-Einheiten.
2. Anfragen werden in gleichen Zeitintervallen bearbeitet, jedes Intervall hat eine Länge von b Einheiten. In diesem Fall ist das Bediengerät bereit, die nächste Anfrage zu bedienen, sobald die Bearbeitung einer Anfrage abgeschlossen ist.
3. Die Disziplin in der Warteschlange wird nach der Regel „Wer zuerst kommt, mahlt zuerst“ festgelegt. Mit anderen Worten: Wartende Anfragen bilden eine Warteschlange, und wenn der Server frei ist, kommt eine Anfrage mit einer längeren Wartezeit zur Bearbeitung an.
Definieren wir die Warteschlangenlänge als die Gesamtzahl der Anfragen, die bearbeitet werden und in der Warteschlange warten. Stellen wir das formulierte Problem in Form des folgenden Diagramms dar:
Das Verhalten des Systems hängt davon ab, wie die Größen a und b zueinander in Beziehung stehen. Drei Fälle sind möglich: 1) b > a; 2) b = a; 3)b< a. Рассмотрим каждый из этих случаев.
1) Fall b > a. Dies bedeutet, dass die Servicerate 1/b kleiner ist als die Anforderungsankunftsrate 1/a, d. h. Anforderungen werden bedient und verlassen das System langsamer als sie eintreffen. Folglich bildet sich in diesem Fall eine Warteschlange, die sich ständig vergrößert.
2) Fall b = a. Befinden sich keine Anfragen in der Warteschlange, wird sofort mit der Bearbeitung der ersten eingegangenen Anfrage begonnen. Der Dienst endet in dem Moment, in dem die nächste Dienstanfrage eintrifft. Daher wird es keine Anforderungen geben, die darauf warten, bedient zu werden.
Wenn zunächst eine Warteschlange vorhanden ist, bleibt deren Länge konstant.
3) Fall b< a. Это значит, что скорость обслуживания больше, чем скорость поступления требований. Следовательно, какое бы ни было начальное число ожидающих обслуживания требований, длина очереди будет сокращаться до 1 или 0.
Die Anzahl der Anfragen in der Warteschlange sei zu Beginn des Prozesses r 2 (wenn anfangs nur eine Anfrage vorhanden ist (r = 1), wird diese bearbeitet, bevor die nächsten Anfragen zur Bearbeitung eintreffen, und die Warteschlange ist leer ).
Im allgemeinen Fall stehen r Anfragen in der Warteschlange, bevor mit der Bearbeitung begonnen wird. Dann kann die Anzahl der Anfragen (N), die nach dem Start des Serviceprozesses eingehen, solange die Warteschlange verbleibt, durch die Formel bestimmt werden:

wobei die Notation [x] den ganzzahligen Teil der Zahl x bedeutet. Tatsächlich wird es keine Warteschlange geben, wenn N+r Anfragen vollständig das bedienende Gerät durchlaufen. Dies erfordert (N+r)b Zeiteinheiten. Während dieser Zeit werden N Anfragen zur Bearbeitung eingehen, so dass das Servicegerät zum Zeitpunkt des Eintreffens der (N+1)-ten Anfrage frei und bereit ist, sie sofort und ohne Warteschlange zu bedienen. Aber die (N+1)-te Anfrage wird in (N+1)a-Zeiteinheiten zur Bearbeitung eingehen und die folgende Beziehung wird erfüllt:
Beweisen wir, dass in der resultierenden Beziehung N um nicht mehr als 1 größer als die rechte Seite ist. Tatsächlich wird die erste in der Warteschlange stehende Anfrage bereits bearbeitet und die erste neu zur Bearbeitung eingehende Anfrage wird noch nicht in der Warteschlange erscheinen (a > b). Daher gilt folgende Beziehung:
aN (N+r-1)b oder.
Wenn wir also auf der rechten Seite der Beziehung 1 hinzufügen, ist sie identisch mit der rechten Seite der Beziehung. Das heißt, das Hinzufügen von 1 auf der rechten Seite der Beziehung führt zu einer Beziehung – die Bedeutung der Ungleichung ändert sich ins Gegenteil. Das musste bewiesen werden.
Das Offensichtliche ist, dass N eine ganze Zahl ist. Wenn wir also den ganzzahligen Teil von der rechten Seite in Beziehung (10.2) nehmen und 1 dazu addieren, erhalten wir basierend auf den vorherigen Argumenten den Ausdruck (10.1) zur Berechnung von N.
Durch ähnliche Überlegungen und die Verwendung von (10.1) können wir feststellen, dass zur Berechnung der Zeit, die zur Bearbeitung aller ausstehenden Anfragen erforderlich ist, die folgende Formel gültig ist:

Eine wichtige Funktion in der Warteschlangentheorie ist die Service-Wartezeitfunktion. Bezeichnen wir es mit W(t). Definieren wir W(t) als die Zeit, die aufgewendet werden muss, um auf die Bearbeitung einer zum Zeitpunkt t empfangenen Anfrage zu warten (wir gehen davon aus, dass t = 0 dem Beginn des Bearbeitungsprozesses entspricht).

Definieren wir eine Formel für W(t). Es ist leicht zu erkennen, dass bei einer zum Zeitpunkt t T-b (der Wert von T wird mit der Formel (10.3) ermittelten) Serviceanforderung das Servicesystem leer oder gerade freigegeben vorgefunden wird. Eine solche Anforderung muss nicht in der Schlange stehen. Eine Anfrage, die zum Zeitpunkt tT-b eintrifft, findet die Anfragen vor sich in der Warteschlange, und die erste von ihnen wird im selben Moment beim Servicegerät eintreffen. Dieser Wert ergibt sich wie folgt:
(anfänglich (Anzahl der Anfragen, bearbeitet- (Anzahl der empfangenen-)
Warteschlange) - existiert zum Zeitpunkt t) + leniya)
Somit kann die Wartezeit W(t) für die betrachtete Anforderung durch die Formel ausgedrückt werden:
Lassen Sie uns überlegen i-te Anforderung in der Anfangswarteschlange (0
Wenn wir die Ergebnisse bezüglich der Funktion W(t) verallgemeinern, erhalten wir den folgenden Ausdruck dafür:

wobei i die Nummer der i-ten Anfrage in der Anfangswarteschlange ist; Anforderungen kommen zu den Zeiten a, 2a, ...; b = na (n = 1, 2, ...).
Untersuchung von Warteschlangensystemen mithilfe statistischer Modellierungsmethoden
1. Grundprinzipien für die Durchführung von Laborarbeiten
Der Einsatz analytischer und numerischer Methoden zur Untersuchung von QS ist auf Fälle beschränkt, in denen das System Markovian ist und durch die Gleichungen für Reproduktion und Tod beschrieben wird oder auf diese reduziert werden kann. Ansonsten ist die Untersuchung von QS mit der Simulationsmethode möglich, die auf einer wiederholten Computersimulation der im System ablaufenden Prozesse und anschließender statistischer Verarbeitung der erhaltenen Ergebnisse basiert.
Als Hauptgrößen, die die Funktionsweise des untersuchten QS charakterisieren, werden Schätzungen der mathematischen Erwartung der Anzahl der belegten Kanäle, der Warteschlangenlänge, der Wartezeit für Anwendungen in der Warteschlange, der Wahrscheinlichkeiten der Bedienung von Anwendungen usw. verwendet. Somit für die Zeitpunkt t (o £ T £ T N ), wo T N - Simulationszeit kann berechnet werden.
Abschätzung der mathematischen Erwartung der Anzahl belegter Kanäle:
hier ist die Anzahl der belegten Kanäle zum Zeitpunkt t in der j-ten Implementierung; N ist die Anzahl der Implementierungen (Modellläufe);
Schätzung der Wahrscheinlichkeit, dass im System zum Zeitpunkt t:
Hier ist die Anzahl der Implementierungen, in denen zum Zeitpunkt t k Anforderungen im System vorhanden waren.
Abschätzung der Wahrscheinlichkeit, dass ein Anspruch abgelehnt wird:
Dabei ist die Gesamtzahl der Anforderungen, die zum Zeitpunkt t in der j-ten Implementierung aufgetreten sind. - Anzahl der bis zum Zeitpunkt t abgelehnten Anträge;
Schätzung der Streuung der Anzahl belegter Kanäle zum Zeitpunkt t:
Um eine Vorstellung von der Genauigkeit und Zuverlässigkeit dieser Schätzungen zu bekommen, können Konfidenzintervalle Ib für ein gegebenes Konfidenzniveau b ermittelt werden.
Zur mathematischen Erwartung der Anzahl belegter Kanäle
Hier wird tb aus der Student-Verteilung bei (N-1) Freiheitsgraden ermittelt. Für große N (N>30) können Sie anstelle der Student-Verteilung das Normalgesetz verwenden. In diesem Fall
wobei Ф(х) das Integral der Wahrscheinlichkeiten ist:
2. Für Wahrscheinlichkeiten
Für großes N ungefähr
wo - S.K.O. Wahrscheinlichkeitsschätzungen:
Darüber hinaus lassen sich aus Nomogrammen leicht Konfidenzintervallgrenzen für die Wahrscheinlichkeiten ermitteln.
2. Erhalten Sie für eine bestimmte (grundlegende) QS-Option die QS-Modellierungsergebnisse. Wert tCoolWartezeit in der Schlange akzeptierennicht zufälliges tCool>TMaud.TMaud nehmen Sie gemäß den Ergebnissen der Laborarbeit Nr. 1 (die Endzeit des Übergangsprozesses multipliziert mit 2). Anzahl der Implementierungen N=50. Erstellen Sie Diagramme der Änderungen in m L, AN, Pobslund ihre Konfidenzintervalle gegenüber der Zeit. Der Wert der Konfidenzwahrscheinlichkeit wird gleich angenommen?=0,9
Das System lösen Differentialgleichung nach der Runge-Kutta-Methode (die rechten Seiten der Gleichungen werden im Vektor D geschrieben, die Anfangsbedingungen liegen im Vektor x):
Modellieren
SimulationszeitT Maud = 3 (die Endzeit des Übergangsprozesses beträgt nach den Ergebnissen der Laborarbeit 1,3 s).
WartezeitWählen Sie aus Bedingung T erwarten >T Maud , daher Tozhid = 4 s.
Modellparameter:
Eingabefluss (Zeitintervall zwischen Anfragen):
Intensität: 7
Warteschlange:
Warteschlangenlänge: 3
Zeit, die Warteschlange zu verlassen:
Verteilungsgesetz: Deterministisch
Größe: 4
Servicekanäle:
Anzahl der Kanäle: 3
Servicezeit:
Verteilungsgesetz: Exponentiell
Intensität: 2
Ergebnisse des Programms:
Schätzungen mathematischer Erwartungen:
| 1,00 | 6,940 | 0,320 | 0,000 | 3,500 | 0,720 | 0,029 | 2,400 |
| 2,00 | 14,060 | 1,640 | 0,000 | 8,540 | 1,280 | 0,107 | 2,600 |
| 3,00 | 21,040 | 3,480 | 0,000 | 13,500 | 1,440 | 0,169 | 2,620 |
| 4,00 | 28,220 | 5,560 | 0,000 | 18,620 | 1,300 | 0,213 | 2,740 |
| 5,00 | 35,060 | 7,060 | 0,000 | 24,200 | 1,080 | 0,235 | 2,720 |
| 6,00 | 42,460 | 8,860 | 0,000 | 29,240 | 1,660 | 0,244 | 2,700 |
| 7,00 | 49,440 | 10,620 | 0,000 | 35,000 | 1,180 | 0,252 | 2,640 |
| 8,00 | 56,300 | 11,960 | 0,000 | 40,680 | 1,060 | 0,258 | 2,600 |
| 9,00 | 63,040 | 13,480 | 0,000 | 45,720 | 1,220 | 0,264 | 2,620 |
| 10,00 | 69,920 | 14,940 | 0,000 | 50,940 | 1,300 | 0,269 | 2,740 |
| 11,00 | 76,800 | 16,220 | 0,000 | 56,640 | 1,220 | 0,273 | 2,720 |
| 12,00 | 83,780 | 17,500 | 0,000 | 62,380 | 1,300 | 0,274 | 2,600 |
| 13,00 | 90,720 | 19,640 | 0,000 | 67,240 | 1,300 | 0,276 | 2,540 |
| 14,00 | 98,060 | 21,320 | 0,000 | 72,700 | 1,340 | 0,280 | 2,700 |
| 15,00 | 105,420 | 22,960 | 0,000 | 78,400 | 1,360 | 0,283 | 2,700 |
| 16,00 | 112,620 | 24,640 | 0,000 | 84,280 | 1,080 | 0,284 | 2,620 |
| 17,00 | 120,200 | 25,880 | 0,000 | 90,300 | 1,460 | 0,284 | 2,560 |
| 18,00 | 126,640 | 27,500 | 0,000 | 95,300 | 1,260 | 0,287 | 2,580 |
| 19,00 | 133,680 | 28,920 | 0,000 | 100,840 | 1,180 | 0,290 | 2,740 |
| 20,00 | 140,340 | 30,300 | 0,000 | 106,260 | 1,180 | 0,291 | 2,600 |
Schätzungen der Standardabweichungen:
| Zeit | Anzahl der Bewerbungen | Anzahl der Ausfälle | Anzahl der Verluste | Anzahl der Dienste | Warteschlangenlänge | Wartezeit | Besetzte Kanäle |
| 1,00 | 2,745 | 0,785 | 0,000 | 1,941 | 1,000 | 0,046 | 0,916 |
| 2,00 | 3,722 | 2,197 | 0,000 | 3,054 | 1,200 | 0,086 | 0,774 |
| 3,00 | 4,906 | 3,067 | 0,000 | 3,822 | 1,235 | 0,105 | 0,718 |
| 4,00 | 5,231 | 4,176 | 0,000 | 4,151 | 1,204 | 0,100 | 0,558 |
| 5,00 | 5,984 | 5,131 | 0,000 | 4,507 | 1,110 | 0,097 | 0,530 |
| 6,00 | 6,548 | 5,830 | 0,000 | 4,773 | 1,210 | 0,088 | 0,670 |
| 7,00 | 7,518 | 6,495 | 0,000 | 5,355 | 1,125 | 0,085 | 0,624 |
| 8,00 | 7,759 | 6,971 | 0,000 | 5,773 | 1,173 | 0,082 | 0,692 |
| 9,00 | 7,725 | 7,278 | 0,000 | 6,000 | 1,237 | 0,080 | 0,718 |
| 10,00 | 8,143 | 7,882 | 0,000 | 6,077 | 1,100 | 0,080 | 0,558 |
| 11,00 | 9,361 | 8,367 | 0,000 | 6,802 | 1,118 | 0,076 | 0,722 |
| 12,00 | 10,286 | 8,690 | 0,000 | 6,831 | 1,268 | 0,075 | 0,824 |
| 13,00 | 10,438 | 8,885 | 0,000 | 6,553 | 1,204 | 0,070 | 0,780 |
| 14,00 | 10,887 | 9,321 | 0,000 | 6,394 | 1,193 | 0,067 | 0,670 |
| 15,00 | 10,398 | 8,991 | 0,000 | 6,587 | 1,179 | 0,065 | 0,670 |
| 16,00 | 10,805 | 9,333 | 0,000 | 6,600 | 1,110 | 0,063 | 0,745 |
| 17,00 | 11,144 | 9,704 | 0,000 | 7,108 | 1,152 | 0,063 | 0,875 |
| 18,00 | 11,704 | 10,425 | 0,000 | 7,566 | 1,261 | 0,062 | 0,776 |
| 19,00 | 11,853 | 10,665 | 0,000 | 7,606 | 1,089 | 0,061 | 0,521 |
| 20,00 | 11,969 | 10,562 | 0,000 | 8,009 | 1,107 | 0,059 | 0,800 |
Als N = 50, dann werden Konfidenzintervalle unter Berücksichtigung des Kerstellt ? = 0.9, dann t ?berechnet nach dem Normalgesetz:
Mathematische Erwartung der Anzahl belegter Kanäle:
Mn – von L.R. 1
a - Modellierung
Mathematische Erwartung der durchschnittlichen Warteschlangenlänge:
Berechnung des Konfidenzintervalls:
Für die durchschnittliche Warteschlangenlänge:
Lm – von L.R. 1
m - Modellierung
Dienstwahrscheinlichkeit:
Die Servicewahrscheinlichkeit ist gleich der Wahrscheinlichkeit, dass noch nicht n+m Bedarfe im System vorhanden sind, d.h. P Ö = 1 - Pn+m = 1 - P 6
Berechnung des Konfidenzintervalls:
Zur Dienstwahrscheinlichkeit:
Po1 – von L.R. 1
Po - Modellieren
3. Untersuchen Sie für eine bestimmte (Basis-)Version des QS den EinflussTerwartenüber Systemeigenschaften im stationären Betrieb
Ah( T ) - deterministisch, T erwarten =T erwartungen_durchschnittlich
b)H( T ) unterliegt dem Exponentialverteilungsgesetz. Erwarteter Wert T erwarten gleich T erwartungen_durchschnittlich*(0,25; 0,5; 1; 2).
Schlussfolgerungen
In der Laborarbeit Nr. 2 wurden die Ergebnisse der Modellierung der Basisversion des QS gewonnen. Basierend auf den erhaltenen Ergebnissen wurden Diagramme der Anzahl der belegten Kanäle, der durchschnittlichen Warteschlangenlänge und der Dienstwahrscheinlichkeit sowie deren Konfidenzintervalle im Vergleich zur Zeit erstellt. Die auf Basis der Ergebnisse der Laborarbeit Nr. 1 erstellten Kurven fielen in die entsprechenden Konfidenzintervalle.
In diesem Labor arbeit Es wurden die Möglichkeiten untersucht, die Simulationsmethode zur Untersuchung von Warteschlangensystemen einzusetzen. Bei der Analyse der erhaltenen Ergebnisse können wir folgende Schlussfolgerung ziehen: Die Verwendung der Simulationsmethode ist akzeptabel, es ist jedoch vorzuziehen, ein Analysegerät zur Untersuchung des QS zu verwenden, weil Diese Art der QS-Untersuchung ist einfacher und liefert genauere Ergebnisse.
Warteschlangensimulationsmodellierung
Unterrichten
Benötigen Sie Hilfe beim Studium eines Themas?
Unsere Spezialisten beraten oder bieten Nachhilfe zu Themen an, die Sie interessieren.
Reichen Sie Ihre Bewerbung ein Geben Sie gleich das Thema an, um sich über die Möglichkeit einer Beratung zu informieren.
Gegenstand des TMS sind Warteschlangensysteme (QS) und Warteschlangennetzwerke. Unter einem QS versteht man ein dynamisches System, das darauf ausgelegt ist, einen zufälligen Anforderungsfluss mit begrenzten Systemressourcen effizient zu bedienen. Die verallgemeinerte Struktur des QS ist in Abbildung 3.1 dargestellt.
Reis. 3.1. SMO-Schema.
Homogene Anfragen, die am Eingang des QS ankommen, werden je nach erzeugendem Grund in Typen unterteilt, die Intensität des Flusses von Anfragen vom Typ i (i=1...M) wird mit i bezeichnet. Die Gesamtheit der Anfragen aller Art ist der Eingangsstrom des QS.
Bewerbungen werden bearbeitet M Kanäle. Es gibt universelle und spezialisierte Servicekanäle. Für einen universellen Kanal vom Typ j gelten die Verteilungsfunktionen F ji () der Dauer von Bedienanfragen eines beliebigen Typs als bekannt. Für spezialisierte Kanäle sind die Funktionen zur Verteilung der Dauer der Bearbeitungskanäle von Anfragen einiger Typen unsicher, die Zuordnung dieser Anfragen zu einem bestimmten Kanal.
Der Serviceprozess kann auf unterschiedliche Weise dargestellt werden. physische Natur Funktionsprozesse von Wirtschafts-, Produktions-, technischen und anderen Systemen, zum Beispiel Produktlieferungsströme an ein bestimmtes Unternehmen, Teile- und Komponentenströme am Fließband einer Werkstatt, Anfragen zur Verarbeitung von Computerinformationen von entfernten Terminals usw. Charakteristisch für den Betrieb solcher Objekte ist darüber hinaus das zufällige Verhalten von Serviceanfragen (Anforderungen) und deren Abschluss zu zufälligen Zeitpunkten.
Q-Schaltungen können analytisch und mit Simulationsmodellen untersucht werden. Letzteres bietet eine größere Vielseitigkeit.
Betrachten wir das Konzept der Warteschlange.
In jeder elementaren Dienstleistungshandlung können zwei Hauptkomponenten unterschieden werden: die Erwartung einer Dienstleistung durch die Anwendung und die tatsächliche Dienstleistung der Anwendung. Dies kann in Form eines i-ten Bediengeräts P i dargestellt werden, bestehend aus einem Bedarfsspeicher, der gleichzeitig l i =0...L i H Anwendungen enthalten kann, wobei L i H die Kapazität des i-ten ist Akkumulator und einen Anforderungsbearbeitungskanal, k i .
Reis. 3.2. SMO-Gerätediagramm
Jedes Element des Wartungsgeräts P i empfängt Ereignisströme: Ein Anforderungsstrom w i wird an das Laufwerk H i gesendet, und ein Dienststrom u i wird an den Kanal k i gesendet.
Der Fluss der Ereignisse(PS) ist eine Abfolge von Ereignissen, die nacheinander zu zufälligen Zeitpunkten auftreten. Es gibt Ströme homogener und heterogener Ereignisse. Homogen Das PS ist nur durch die Zeitpunkte des Eintreffens dieser Ereignisse (verursachende Momente) gekennzeichnet und wird durch die Folge (t n )=(0t 1 t 2 …t n …) spezifiziert, wobei t n der Zeitpunkt des Eintreffens von ist das n-te Ereignis – eine nicht negative reelle Zahl. OPS kann auch als Folge von Zeitintervallen zwischen dem n-ten und n-1. Ereignis ( n) angegeben werden.
Heterogen PS heißt eine Folge (t n, f n), wobei t n die verursachenden Momente sind; f n – Satz von Ereignisattributen. Beispielsweise können die Zugehörigkeit zu einer bestimmten Anforderungsquelle, das Vorhandensein einer Priorität, die Fähigkeit, von einem bestimmten Kanaltyp bedient zu werden usw. angegeben werden.
Betrachten wir die OPS, für die i ( n ) voneinander unabhängige Zufallsvariablen sind. Dann heißt das PS Strömung mit begrenzte Nachwirkung.
Es heißt PS normal, wenn die Wahrscheinlichkeit, dass mehr als ein Ereignis P 1 (t, t) in einem kleinen Zeitintervall t neben der Zeit t auftritt, vernachlässigbar klein ist.
Wenn für ein beliebiges Intervall t das Ereignis P 0 (t, t) + P 1 (t, t) + P 1 (t, t)=1 ist, ist P 1 (t, t) die Wahrscheinlichkeit von in das Intervall t genau eines Ereignisses fällt. Als Summe der Wahrscheinlichkeiten von Ereignissen, die eine vollständige Gruppe bilden, und solchen, die inkonsistent sind, gilt für einen gewöhnlichen Ereignisfluss P 0 (t, t) + P 1 (t, t) 1, P 1 ( t, t)=(t ), wobei (t) eine Größe ist, deren Kleinheitsordnung höher als t ist, d. h. lim((t))=0 bei t0.
Stationäre PS ist ein Fluss, für den die Wahrscheinlichkeit des Auftretens einer bestimmten Anzahl von Ereignissen in einem Zeitintervall bestimmt ist hängt von der Länge dieses Abschnitts ab und hängt nicht davon ab, wo auf der Zeitachse 0 - t dieser Abschnitt aufgenommen wird. Für OPS ist 0*P 0 (t, t) + 1*P 1 (t, t) = P 1 (t, t) die durchschnittliche Anzahl von Ereignissen im Intervall t. Die durchschnittliche Anzahl der im Bereich t pro Zeiteinheit auftretenden Ereignisse beträgt P 1 (t, t)/t. Betrachten wir den Grenzwert dieses Ausdrucks bei t0
lim P 1 (t, t)/t=(t)*(1/Zeiteinheit).
Wenn diese Grenze existiert, wird sie als Intensität (Dichte) des OPS bezeichnet. Für ein Standard-PS (t)==const.
Bezogen auf den elementaren Servicekanal k i können wir davon ausgehen, dass der Anforderungsfluss w i W, d.h. die Zeitintervalle zwischen den Zeitpunkten des Erscheinens von Anfragen am Eingang k i bilden eine Teilmenge unkontrollierbarer Variablen und der Servicefluss u i U, d.h. Die Zeitintervalle zwischen Beginn und Ende der Bearbeitung einer Anfrage bilden eine Teilmenge der gesteuerten Variablen.
Vom Kanal k i bediente Anfragen und Anfragen, die das verlassene Gerät P i aus verschiedenen Gründen nicht bedient haben, bilden den Ausgabestrom y i Y.
Der Funktionsprozess des Servicegeräts P i kann als Prozess der Änderung der Zustände seiner Elemente im Laufe der Zeit Z i (t) dargestellt werden. Der Übergang in einen neuen Zustand für P i bedeutet eine Änderung der Anzahl der darin enthaltenen Anforderungen (im Kanal k i und im Speicher H i). Das. der Zustandsvektor für P i hat die Form: , wobei der Zustand des Laufwerks ist, (=0 – das Laufwerk ist leer, =1 – es gibt eine Anfrage im Laufwerk..., = – das Laufwerk ist voll belegt; - der Zustand des Kanals k i (=0 - der Kanal ist frei, = 1 Kanal belegt).
Q-Schemata realer Objekte werden durch die Zusammensetzung vieler elementarer Wartungsgeräte P i gebildet. Wenn k ich verschiedene Servicegeräte parallel geschaltet sind, dann findet ein Mehrkanaldienst statt (Mehrkanal-Q-Schema), und wenn Geräte P i und ihre parallelen Zusammensetzungen in Reihe geschaltet sind, dann findet ein Mehrphasendienst statt (Mehrkanal-Q-Schema) Phasen-Q-Schema).
Das. Um ein Q-Schema anzugeben, ist ein Konjugationsoperator R erforderlich, der die Beziehung der Strukturelemente widerspiegelt.
Verbindungen im Q-Schema werden in Form von Pfeilen dargestellt (Flusslinien, die die Bewegungsrichtung von Anforderungen widerspiegeln). Es gibt offene und geschlossene Q-Kreise. IN offen Der Ausgabestrom kann nicht erneut zu einem Element fließen, d. h. es gibt keine Rückmeldung.
Die eigenen (internen) Parameter der Q-Schaltung sind die Anzahl der Phasen L Ф, die Anzahl der Kanäle in jeder Phase, L kj, j=1... L Ф, die Anzahl der Speichergeräte jeder Phase L kj , k=1... L Ф, Kapazität i- der Speicher L i H . Es ist zu beachten, dass in der Warteschlangentheorie je nach Speicherkapazität die folgende Terminologie verwendet wird:
Systeme mit Verlusten (L i H =0, kein Speichergerät);
Systeme mit Erwartung (L i H );
Systeme mit begrenzter Speicherkapazität H i (gemischt).
Bezeichnen wir die gesamte Menge der Eigenparameter des Q-Schemas als Teilmenge H.
Um ein Q-Schema zu definieren, ist es auch notwendig, die Algorithmen für seine Funktionsweise zu beschreiben, die die Regeln für das Verhalten von Anwendungen in verschiedenen mehrdeutigen Situationen bestimmen.
Abhängig vom Ort, an dem solche Situationen auftreten, gibt es Algorithmen (Disziplinen) zum Warten auf Anforderungen im Speicher H i und zur Bearbeitung von Anforderungen über den Kanal k i . Der Heterogenität des Bewerbungsflusses wird durch die Einführung einer Prioritätsklasse Rechnung getragen.
Abhängig von der Dynamik der Prioritäten wird bei Q-Schemata zwischen statisch und dynamisch unterschieden. Statische Prioritäten werden im Voraus vergeben und hängen nicht von den Zuständen des Q-Kreises ab, d. h. Sie werden im Rahmen der Lösung eines bestimmten Modellierungsproblems festgelegt. Während der Simulation entstehen dynamische Prioritäten. Basierend auf den Regeln für die Auswahl von Anwendungen aus dem Speicher H i zur Bedienung durch Kanal k i können wir auswählen relativ Und absolut Prioritäten. Relative Priorität bedeutet, dass ein Anspruch mit höherer Priorität, der im Speicher H ankommt, auf das Ende der Bearbeitung des repräsentierenden Anspruchs durch Kanal k i wartet und erst danach den Kanal belegt. Absolute Priorität bedeutet, dass eine Anfrage mit einer höheren Priorität, die im Speicher ankommt, die Bearbeitung einer Anfrage mit einer niedrigeren Priorität durch den Kanal k i unterbricht und selbst den Kanal belegt (in diesem Fall kann eine von k i verdrängte Anfrage entweder das System verlassen oder kann wieder an eine Stelle in H i geschrieben werden).
Es ist auch notwendig, den Satz von Regeln zu kennen, nach denen Anwendungen N i und k i verlassen: für N i – entweder Überlaufregeln oder Exit-Regeln, die mit dem Ablauf der Wartezeit für eine Anwendung in N i verbunden sind; für k i – Regeln für die Wahl von Routen oder Abfahrtsrichtungen. Darüber hinaus müssen für Anfragen Regeln festgelegt werden, nach denen sie im Kanal k i verbleiben, d.h. Kanalblockierungsregeln. In diesem Fall wird beim Blockieren von k i zwischen Ausgabe und Eingabe unterschieden. Eine solche Blockierung spiegelt das Vorhandensein von Steuerverbindungen im Q-Kreis wider, die den Anforderungsfluss abhängig von den Zuständen des Q-Kreises regeln. Eine Menge möglicher Algorithmen für das Verhalten von Anfragen im Q-Schema kann als ein bestimmter Operator von Algorithmen für das Verhalten von Anfragen dargestellt werden A.
Das. Ein Q-Schema, das den Funktionsprozess eines QS beliebiger Komplexität beschreibt, wird eindeutig als eine Menge von Mengen spezifiziert: Q =
Markov-Zufallsprozesse
Sie sind nach dem herausragenden russischen Mathematiker A.A. Markov benannt, der als erster mit der Untersuchung des probabilistischen Zusammenhangs von Zufallsvariablen begann und eine Theorie entwickelte, die man „Wahrscheinlichkeitsdynamik“ nennen kann. Derzeit werden die Theorie der Markov-Prozesse und ihre Anwendungen in zahlreichen Bereichen eingesetzt, darunter im Operations Research und in der Theorie der optimalen Entscheidungsfindung.
Markov-Prozess- diskret oder kontinuierlich Zufallsprozess X(T), die vollständig durch zwei Größen angegeben werden kann:
· Wahrscheinlichkeit P(X,T), dass die Zufallsvariable X(T) im Moment der Zeit T gleich X, Und
· Wahrscheinlichkeiten P(X 2 , T 2 |X 1 ,T 1) Was wäre, wenn X bei T = T 1 ist gleich X 1, dann um T = T 2 es ist gleich X 2 .
Die zweite dieser Größen heißt Übergangswahrscheinlichkeit vom Staat X 1 um t = t 1 im Staat X 2 um t = t 2 .
Markov-Ketten angerufen diskret nach Zeit und Wert Markov
Prozesse.
Beispiel 1
Nehmen wir an, dass es sich bei einem Wurfspiel um aufeinanderfolgende Münzwürfe handelt; Die Münze wird zu bedingten Zeitpunkten t = 0, 1, ... geworfen und bei jedem Schritt kann der Spieler ±1 mit der gleichen Wahrscheinlichkeit 1/2 gewinnen, sodass sein Gesamtgewinn zum Zeitpunkt t eine Zufallsvariable ξ(t) ist ) mit möglichen Werten j = 0, ±1, ... Vorausgesetzt, dass ξ(t) = k, im nächsten Schritt beträgt der Gewinn bereits ξ(t+1) = k± 1, wobei die angegebenen Werte j = k ± 1 mit der gleichen Wahrscheinlichkeit von 1/2 angenommen werden. Konventionell kann man sagen, dass hier mit entsprechender Wahrscheinlichkeit ein Übergang vom Zustand ξ(t) = erfolgt k um ξ(t+1) = anzugeben k± 1.
19.5.1. Formeln und Definitionen von Markov-Ketten
Wenn wir dieses Beispiel verallgemeinern, können wir uns ein „System“ mit einer abzählbaren Anzahl möglicher „Phasen“-Zustände vorstellen, das im Verlauf der diskreten Zeit t = 0, 1, ... zufällig von Zustand zu Zustand übergeht.
Sei ξ(t) seine Position im Moment t als Ergebnis einer Kette zufälliger Übergänge ξ(0) - ξ(1) - ... - ξ(t) - ... ... (1)
Formal bezeichnen wir alle möglichen Zustände durch ganze Zahlen i = 0, ±1, ... Nehmen wir an, dass für einen bekannten Zustand ξ(t) = k Im nächsten Schritt geht das System mit bedingter Wahrscheinlichkeit in den Zustand ξ(t+1) = j über
p kj = P(ξ(t+1) = j|ξ(t) = k) ... (2)
unabhängig von seinem Verhalten in der Vergangenheit, genauer gesagt, unabhängig von der Kette der Übergänge (1) bis zum Zeitpunkt t:
P(ξ(t+1) = j|ξ(0) = i, ..., ξ(t) = k) = P(ξ(t+1) = j|ξ(t) = k) für alle t, k, j... (3) - Markov-Anwesen.
Dieses probabilistische Schema heißt homogene Markov-Kette mit einer abzählbaren Anzahl von Zuständen- seine Homogenität liegt darin, dass die in (2) definierten Übergangswahrscheinlichkeiten p kj, ∑ j p kj = 1, k = 0, ±1, ..., hängen nicht von der Zeit ab, d. h.
P(ξ(t+1) = j|ξ(t) = k) = P ij - Übergangswahrscheinlichkeitsmatrix in einem Schritt hängt nicht von n ab. Es ist klar, dass P ij eine quadratische Matrix mit nicht negativen Elementen und Einheitssummen über die Zeilen ist. Eine solche Matrix (endlich oder unendlich) wird stochastische Matrix genannt. Als Matrix der Übergangswahrscheinlichkeiten kann jede stochastische Matrix dienen.
Fallstudie 1.
Nehmen wir an, dass ein bestimmtes Unternehmen Geräte in ganz Moskau liefert: in den nördlichen Bezirk (gekennzeichnet mit A), den südlichen Bezirk (B) und den zentralen Bezirk (C). Das Unternehmen verfügt über ein Team von Kurieren, die diese Bereiche bedienen. Es ist klar, dass der Kurier für die nächste Lieferung dorthin geht, wo er ist dieser Moment näher bei ihm. Statistisch wurde Folgendes ermittelt:
1) nach der Lieferung an A erfolgt die nächste Lieferung in 30 Fällen in A, in 30 Fällen – in B und in 40 Fällen – in C;
2) nach der Lieferung an B erfolgt die nächste Lieferung in 40 Fällen in A, in 40 Fällen – in B und in 20 Fällen – in C;
3) Nach der Lieferung an C erfolgt die nächste Lieferung in 50 Fällen in A, in 30 Fällen – in B und in 20 Fällen – in C.
Somit wird das nächste Liefergebiet nur durch die vorherige Lieferung bestimmt.
Die Übsieht folgendermaßen aus:
Beispielsweise ist p 12 = 0,4 die Wahrscheinlichkeit, dass nach der Lieferung in Bereich B die nächste Lieferung in Bereich A erfolgt. Nehmen wir an, dass jede Lieferung mit anschließender Bewegung in den nächsten Bereich 15 Minuten dauert. Dann sind laut statistischen Daten nach 15 Minuten 30 % der Kuriere, die in A waren, in A, 30 % in B und 40 % in C. Denn im nächsten Moment wird jeder der Kuriere definitiv dort sein In einem der Bezirke ist die Summe der Spalten 1. Und da es sich um Wahrscheinlichkeiten handelt, ist jedes Element der Matrix 0<р ij <1. Наиболее важным обстоятельством, которое позволяет интерпретировать данную модель как цепь Маркова, является то, что местонахождение курьера в момент времени t+1 зависит nur vom Standort zum Zeitpunkt t.
Stellen wir nun eine einfache Frage: Wenn der Kurier von C aus startet, wie groß ist die Wahrscheinlichkeit, dass er nach zwei Lieferungen in B ist, d. h. Wie erreicht man B in 2 Schritten? Es gibt also mehrere Wege von C nach B in 2 Schritten:
1) zuerst von C nach C und dann von C nach B;
2) C-->B und B-->B;
3) C-->A und A-->B.
Unter Berücksichtigung der Regel der Multiplikation unabhängiger Ereignisse erhalten wir, dass die gewünschte Wahrscheinlichkeit gleich ist:
P = P(CA)*P(AB) + P(CB)*P(BB) + P(CC)*P(CB)
Zahlenwerte ersetzen:
P = 0,5*0,3 + 0,3*0,4 + 0,2*0,3 = 0,33
Das erhaltene Ergebnis legt nahe, dass, wenn der Kurier seine Arbeit von C aus aufgenommen hat, er in 33 von 100 Fällen nach zwei Lieferungen in B sein wird. Natürlich sind die Berechnungen einfach, aber wenn Sie die Wahrscheinlichkeit nach 5 oder 15 Lieferungen ermitteln müssen, kann das ziemlich viel Zeit in Anspruch nehmen.
Betrachten wir eine einfachere Möglichkeit, solche Wahrscheinlichkeiten zu berechnen. Um die Übergangswahrscheinlichkeiten aus verschiedenen Zuständen in 2 Schritten zu erhalten, quadrieren wir die Matrix P:

Dann ist Element (2, 3) die Wahrscheinlichkeit des Übergangs von C nach B in 2 Schritten, die oben auf andere Weise ermittelt wurde. Beachten Sie, dass die Elemente in der Matrix P2 ebenfalls im Bereich von 0 bis 1 liegen und die Summe der Spalten 1 beträgt.
Das. wenn Sie die Wahrscheinlichkeiten des Übergangs von C nach B in 3 Schritten bestimmen müssen:
1 Weg. p(CA)*P(AB) + p(CB)*P(BB) + p(CC)*P(CB) = 0,37*0,3 + 0,33*0,4 + 0,3*0,3 = 0,333, wobei p(CA) - die Wahrscheinlichkeit des Übergangs von C nach A in 2 Schritten (d. h. dies ist Element (1, 3) der Matrix P 2).
Methode 2. Berechnen Sie die Matrix P3:

Die Matrix der Übergangswahrscheinlichkeiten zur 7. Potenz sieht folgendermaßen aus:

Es ist leicht zu erkennen, dass die Elemente jeder Zeile zu bestimmten Zahlen tendieren. Dies deutet darauf hin, dass nach genug große Menge Bei der Lieferung spielt es keine Rolle, in welchem Bezirk der Kurier seine Arbeit aufgenommen hat. Das. Am Ende der Woche werden ungefähr 38,9 % in A, 33,3 % in B und 27,8 % in C liegen. Eine solche Konvergenz tritt garantiert auf, wenn alle Elemente der Übzum Intervall (0, 1) gehören ).
Warteschlangentheorie
Dies ist der Abschnitt Unternehmensforschung, das eine Vielzahl von berücksichtigt Prozesse in der Wirtschaft, aber auch in der Telefonkommunikation, im Gesundheitswesen und anderen Bereichen als Serviceprozesse, d - ihnen Kutter aushändigen, Kunden in der Wäscherei bedienen - Wäsche waschen usw.).
Trotz aller Vielfalt haben diese Prozesse Gemeinsamkeiten: Anforderungen unregelmäßig (zufällig) zur Zustellung entgegengenommen werden Servicekanal(ein Platz am Pier, ein Fenster im Schankraum) und je nach Belegung, Dienstdauer und anderen Faktoren entsteht Warteschlange von Forderungen.
Die Warteschlangentheorie untersucht die statistischen Muster des Eingangs von Anfragen und entwickelt auf dieser Grundlage Lösungen, d. h. solche Merkmale, bei denen der Zeitaufwand für Warteschlangen einerseits und für Ausfallzeiten von Servicekanälen andererseits am geringsten wäre. Das gesamte System der Produktion und des Konsums von Gütern kann als Massendienstleistungssystem interpretiert werden, in dem Menschen (Kunden) und Güter zusammentreffen. Als Messgrößen werden die Zeitverluste durch Warteschlangen und Ausfallzeiten von Servicekanälen (Einlagerung von Waren in Lagerhallen) herangezogen Effizienz studiert Wirtschaftssystem.
Methoden zur Analyse von Warteschlangensystemen
Die in der Warteschlangentheorie verwendeten Methoden und Modelle können in analytische und Simulationsmethoden unterteilt werden.
analytische Methoden Warteschlangentheorien ermöglichen es, die Eigenschaften eines Systems als einige Funktionen seiner Betriebsparameter zu erhalten. Dadurch wird eine qualitative Analyse des Einflusses einzelner Faktoren auf die Effizienz des QS möglich.
Simulationsmethoden basieren auf der Modellierung von Warteschlangenprozessen am Computer und werden eingesetzt, wenn der Einsatz analytischer Modelle nicht möglich ist.
Derzeit sind Methoden zur Lösung von Warteschlangenproblemen, bei denen es sich um den eingehenden Anforderungsfluss handelt, die theoretisch am besten entwickelten und praktischsten in der Praxis die einfachste (Poisson).
Beim einfachsten Ablauf folgt die Häufigkeit der in das System eingehenden Anfragen dem Poisson-Gesetz, d. h. Wahrscheinlichkeit der rechtzeitigen Ankunft T glatt Zu Anforderungen ergibt sich aus der Formel:
![]()
Der einfachste Fluss hat drei grundlegende Eigenschaften:
1) gewöhnlich,
2) Stationarität und
3) Mangel an Nachwirkung.
Alltäglichkeit Flow bedeutet die praktische Unmöglichkeit des gleichzeitigen Eintreffens von zwei oder mehr Anforderungen. Beispielsweise ist die Wahrscheinlichkeit recht gering, dass aus einer Gruppe von Maschinen, die von einem Team von Mechanikern gewartet werden, mehrere Maschinen gleichzeitig ausfallen.
Stationär ist ein Fluss, für den sich die mathematische Erwartung der Anzahl der pro Zeiteinheit in das System eintretenden Anforderungen (bezeichnet mit A ist der Poisson-Verteilungsparameter) im Laufe der Zeit nicht ändert. Somit ist die Wahrscheinlichkeit, in das System einzudringen ein bestimmter Betrag Anforderungen innerhalb eines bestimmten Zeitraums zu erfüllen Bei hängt von seiner Größe ab und hängt nicht vom Ursprung seiner Zählung auf der Zeitachse ab.
Keine Nachwirkung bedeutet die Anzahl der Anfragen, die das System bisher erhalten hat T, bestimmt nicht, wie viele Anfragen im Zeitraum von in das System eingehen T Vor t + Dt
Wenn zum Beispiel zu einem bestimmten Zeitpunkt ein Fadenbruch an einer Webmaschine auftritt und dieser vom Weber repariert wird, ist dies nicht entscheidend dafür, ob es im nächsten Moment zu einem erneuten Bruch an dieser Webmaschine kommt oder nicht, geschweige denn, dass dies der Fall ist beeinflussen die Wahrscheinlichkeit, dass es bei anderen Webstühlen zu einem Bruch kommt.
Wichtiges Merkmal SMO - Zeit für Wartungsanforderungen im System. Die Bearbeitungszeit für eine Anfrage beträgt in der Regel zufällige Variable und kann daher durch das Verteilungsgesetz beschrieben werden. Am weitesten verbreitet in der Theorie und insbesondere in der praktischen Anwendung ist Exponentielles Verteilungsgesetz der Dienstzeit. Die Verteilungsfunktion für dieses Gesetz hat die Form:

diese. die Wahrscheinlichkeit, dass die Dienstzeit einen bestimmten Wert nicht überschreitet T, wird durch Formel (5.2) bestimmt, wobei µ - Parameter des exponentiellen Gesetzes der Zeitverteilung für die Erfüllung von Anforderungen im System, d. h. Kehrwert der durchschnittlichen Servicezeit
![]()
Warteschlangensysteme werden klassifiziert:
1. Je nachdem Wartebedingungen Dienstbeginn:
· QS mit Verlusten (Ausfällen)
· SMO mit Erwartung
Im SMO mit Misserfolgen Anfragen, die eintreffen, wenn alle Servicekanäle belegt sind, werden abgelehnt und verlassen das System. Ein klassisches Beispiel für ein fehlerhaftes System ist eine Telefonzentrale. Ist der angerufene Teilnehmer besetzt, wird die Verbindungsanfrage mit ihm abgelehnt und verlässt das System.
Im SMO mit Vorfreude Die Anfrage stellt fest, dass alle Bereitstellungskanäle ausgelastet sind, gelangt in eine Warteschlange und wartet, bis [ einer der Bereitstellungskanäle frei wird.
Es werden Abfragen aufgerufen, die eine Warteschlange zulassen, jedoch eine begrenzte Anzahl von Anforderungen enthalten Systeme mit begrenzter Warteschlangenlänge.
QSs, die eine Warteschlange zulassen, jedoch mit einer begrenzten Aufenthaltsdauer jeder Anforderung darin, werden aufgerufen Systeme mit begrenzter Wartezeit.
2. Basierend auf der Anzahl der Servicekanäle werden QS unterteilt in:
Ein-Kanal;
Mehrkanalig.
3. Basierend auf dem Ort der Anforderungsquelle wird das QS unterteilt in:
offen, wenn die Quelle der Anforderung außerhalb des Systems liegt;
geschlossen, wenn die Quelle im System selbst liegt.
19.7. Probleme der Analyse geschlossener und offener Warteschlangensysteme
Geschlossen und offen Systeme, abhängig Abhängig von der Wartezeit kann es sich auch um Warteschlangensysteme mit Wartezeiten handeln. Dies sind die häufigsten SMOs. Sie werden mithilfe analytischer Modelle untersucht.
Warteschlangensystem ist ein System, bei dem Anfragen, die eingehen, wenn alle bedienenden Kanäle belegt sind, in die Warteschlange gestellt und bearbeitet werden, sobald die Kanäle frei werden.
Ein Beispiel für ein Open-Loop-System wäre eine TV-Reparaturwerkstatt. Hier stellen defekte Fernseher die Quelle von Anforderungen für deren Wartung dar; sie befinden sich außerhalb des Systems selbst, sodass die Anzahl der Anforderungen als unbegrenzt angesehen werden kann. Zum geschlossenen QS gehört beispielsweise ein Maschinenbereich, in dem die Maschinen Fehlerquellen und damit Anforderungen an deren Wartung, beispielsweise durch ein Team von Einstellern, darstellen.
Die allgemeine Formulierung des Problems lautet wie folgt. Das System hat P Versorgungskanäle, von denen jeder gleichzeitig nur eine Anforderung bedienen kann.
Das System empfängt den einfachsten (Poisson-)Anforderungsfluss mit Parameter A. Wenn das System zum Zeitpunkt des Eintreffens der nächsten Anforderung bereits mindestens bedient P Anforderungen, d.h. Wenn alle Kanäle belegt sind, wird diese Anforderung in die Warteschlange gestellt und wartet auf den Beginn des Dienstes. Die Bearbeitungszeit jeder Anfrage ist eine Zufallsvariable, die mit dem Parameter einem Exponentialverteilungsgesetz folgt µ .
QS mit Erwartung lassen sich in zwei große Gruppen einteilen: geschlossen und offen. ZU geschlossen Dazu gehören Systeme, bei denen der eingehende Anforderungsfluss aus dem System selbst stammt und begrenzt ist. Beispielsweise muss ein Vorarbeiter, dessen Aufgabe es ist, Maschinen in einer Werkstatt einzurichten, diese regelmäßig warten. Jede Rüstmaschine wird zu einer potenziellen Quelle von Rüstanforderungen. In solchen Systemen ist die Gesamtzahl der zirkulierenden Anforderungen endlich und meist konstant.
Wenn die Versorgungsquelle unendlich viele Nachfragen hat und außerhalb des Systems liegt, wird das System aufgerufen offen. Beispiele für Open-Loop-Systeme sind Geschäfte, Fahrkartenschalter an Bahnhöfen, Häfen usw. Bei diesen Systemen kann der eingehende Nachfragefluss als unbegrenzt angesehen werden. Darüber hinaus sind Open-Loop-QS mit Wartezeiten und einer begrenzten Warteschlangenlänge, mit einer begrenzten Zeit, in der eine Anfrage in der Warteschlange verweilt, usw. weit verbreitet.
Die genannten Merkmale der Funktionsweise von QS mit Erwartung stellen aufgrund ihrer Art bestimmte Bedingungen an den verwendeten mathematischen Apparat. Die Berechnung der Betriebseigenschaften aller dieser QS kann auf der Grundlage der Berechnung der Wahrscheinlichkeiten von QS-Zuständen (sog Erlang-Formeln).
Betrachten wir das Verfahren zur Berechnung der Leistungsmerkmale Open-Loop-Systeme mit Wartezeiten und begrenzter Warteschlangenlänge.
Solche SMOs bestehen aus P Versorgungskanäle, von denen jeder gleichzeitig nur eine Anforderung bedienen kann. Das System empfängt den einfachsten Anforderungsfluss mit Parameter A, und die Bearbeitungszeit der Anforderung ist eine Zufallsvariable, die einem Exponentialverteilungsgesetz mit dem Parameter gehorcht C. Wenn zum Zeitpunkt des Eingangs der nächsten Anfrage alle P Die Kanäle sind besetzt, aber die Warteschlange ist nicht geringer T Anforderungen, dann wird die Anforderung in die Warteschlange gestellt. Wenn es bereits eine Warteschlange gibt T Anforderungen, dann verlässt die erhaltene Anforderung das QS. Mit anderen Worten: Eine Anfrage wird abgelehnt, wenn das System Folgendes enthält p + t Anforderungen. Aus den Gleichungen, die den Zustand solcher Systeme beschreiben, können die folgenden Formeln zur Berechnung ihrer Haupteigenschaften abgeleitet werden.
1. Die Wahrscheinlichkeit, dass alle bedienenden Kanäle frei sind,
 (5.14)
(5.14)
2. Die Wahrscheinlichkeit, dass das System enthält Zu Anforderungen, sofern die Gesamtzahl dieser Anforderungen die Anzahl der bedienenden Kanäle nicht überschreitet; mit anderen Worten, die Wahrscheinlichkeit, dass es beschäftigt ist Zu Kanäle,
| |
3. Die Wahrscheinlichkeit, dass das System enthält Zu Anforderungen, wenn die Anzahl dieser Anforderungen größer ist als die Anzahl der bedienenden Kanäle,
 (5.16)
(5.16)
4. Die Wahrscheinlichkeit, dass alle bedienenden Kanäle belegt sind, beträgt
 (5.17)
(5.17)
5. Wahrscheinlichkeit eines Ausfalls
![]() (5.18)
(5.18)
6. Durchschnittliche Warteschlangenlänge
7. Durchschnittliche Anzahl empfangsfreier Kanäle

Beispiel 2. Das Unternehmen liefert Waren auftragsbezogen und verfügt über vier Fahrzeuge, die rund um die Uhr im Einsatz sind. Der Bestellablauf ist einfach und durchschnittlich geht pro Stunde eine Bewerbung ein. Die Zeit für den Gütertransport unterliegt einem exponentiellen Verteilungsgesetz und im Durchschnitt dauert der Transport einer Ladung eine Stunde. Wenn die Anzahl der Transportaufträge 10 beträgt, nimmt das Unternehmen keine Anträge mehr an, bis die Warteschlange kleiner wird.
Es ist notwendig, die Merkmale des Unternehmens zu ermitteln.
Lösung. Dieses System bezieht sich auf den QS-Typ mit Warteschlange und begrenzter Warteschlangenlänge. Lassen Sie uns die Parameter des Systems ermitteln, indem wir eine Stunde als Zeiteinheit nehmen:
Die Wahrscheinlichkeit, dass alle Autos frei von Gütertransporten sind, ergibt sich aus der Formel (5.14):
Die Wahrscheinlichkeit, dass alle Maschinen besetzt sind, wird durch Formel (5.17) bestimmt und beträgt
Dann ist die Wahrscheinlichkeit der Ablehnung eines Transportauftrags, berechnet nach Formel (5.18), gleich
 und die durchschnittliche Warteschlangenlänge gemäß Formel (5.19) beträgt
und die durchschnittliche Warteschlangenlänge gemäß Formel (5.19) beträgt
![]()
Dann ist die Wahrscheinlichkeit der Ablehnung eines Transportauftrags, berechnet nach Formel (5.18), gleich
und die durchschnittliche Warteschlangenlänge gemäß Formel (5.19) beträgt
So wird der Kunde fast nie eine Ablehnung einer Transportanfrage erhalten, die Fahrzeugladung ist jedoch recht gering. Beispielsweise sind nur in zwei von hundert Fällen alle vier Maschinen belegt.
Betrachten wir nun Algorithmen zur Berechnung der Betriebseigenschaften geschlossenes QS mit Erwartung. Da das System geschlossen ist, sollte der Problemstellung eine Bedingung hinzugefügt werden: Der Fluss eingehender Anforderungen ist begrenzt, d.h. Es können sich keine weiteren Personen gleichzeitig im Servicesystem aufhalten T Anforderungen (T - Anzahl der bedienten Objekte). Solche QS werden auch genannt Systeme mit Wartezeiten und einem begrenzten Nachfragefluss.
Als Kriterium, das die Funktionsqualität des betrachteten Systems charakterisiert, nehmen wir das Verhältnis der durchschnittlichen Warteschlangenlänge zur größten Anzahl gleichzeitig im bedienenden System befindlicher Anforderungen oder das Ausfallzeitverhältnis der bedienten Objekte. Als weiteres Kriterium nehmen wir das Verhältnis der durchschnittlichen Anzahl inaktiver Serving-Kanäle zu ihrer Gesamtzahl oder das Ausfallzeitverhältnis der Serving-Kanäle.
Das erste Kriterium charakterisiert den Zeitverlust durch das Warten auf den Beginn des Dienstes. Das zweite Kriterium zeigt die Vollständigkeit der Auslastung des Dienstleistungssystems und ist für die Aufgaben der Arbeitsorganisation wichtig.
Offensichtlich kann es nur dann zu einer Warteschlange kommen, wenn die Anzahl der Kanäle geringer ist die größte Zahl Anforderungen, die gleichzeitig im bedienenden System vorhanden sind (P< т).
Lassen Sie uns die Reihenfolge der Berechnungen der Eigenschaften eines geschlossenen QS mit Erwartung und die notwendigen Formeln vorstellen.
1. Parameter α=α/µ. -
Systemlastanzeige, d.h. mathematische Erwartung der Anzahl der Anfragen, die während einer Zeit, die der durchschnittlichen Dienstdauer entspricht, in das System eingehen ![]()
2. Wahrscheinlichkeit, dass es beschäftigt ist Zu Versorgungskanäle, sofern die Anzahl der Anforderungen im System die Anzahl der Versorgungskanäle des Systems nicht überschreitet,
 .
. ,
,