Die Summe der entgegengesetzten Winkel eines in einen Kreis eingeschriebenen Vierecks. Beschriftetes Viereck

Ein Viereck ist in einen Kreis eingeschrieben, wenn alle seine Eckpunkte auf dem Kreis liegen. Ein solcher Kreis wird von einem Viereck umschrieben.

So wie nicht jedes Viereck um einen Kreis beschrieben werden kann, kann nicht jedes Viereck in einen Kreis eingeschrieben werden.

Ein in einen Kreis eingeschriebenes konvexes Viereck hat die Eigenschaft, dass sich seine entgegengesetzten Winkel zu 180° addieren. Wenn also ein Viereck ABCD gegeben ist, in dem Winkel A entgegengesetzt zu Winkel C und Winkel B entgegengesetzt zu Winkel D ist, dann ist ∠A + ∠C = 180° und ∠B + ∠D = 180°.

Wenn ein Paar entgegengesetzter Winkel eines Vierecks im Allgemeinen 180° ergibt, dann ergibt die Summe des anderen Paares denselben Betrag. Dies folgt aus der Tatsache, dass in einem konvexen Viereck die Winkelsumme immer 360° beträgt. Diese Tatsache ergibt sich wiederum aus der Tatsache, dass bei konvexen Polygonen die Winkelsumme durch die Formel 180° * (n – 2) bestimmt wird, wobei n die Anzahl der Winkel (oder Seiten) ist.

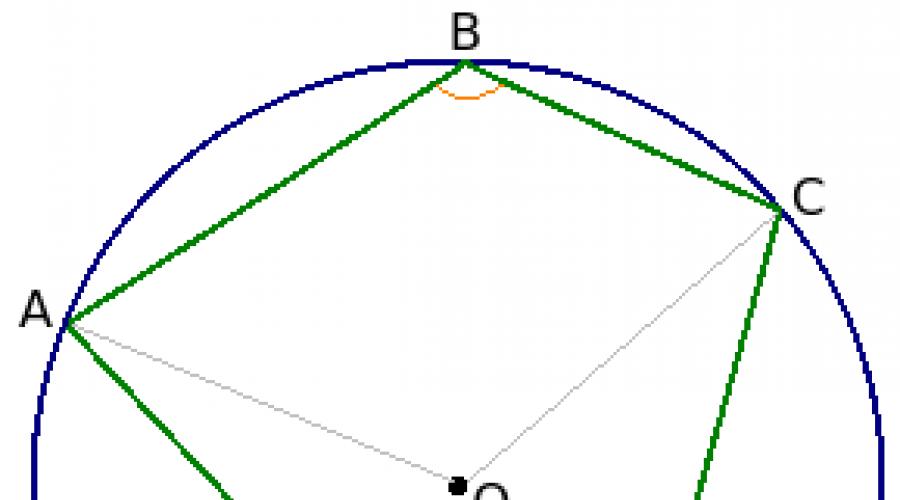
Sie können die Eigenschaft eines beschrifteten Vierecks nachweisen auf die folgende Weise. In den Kreis O sei ein Viereck ABCD einbeschrieben. Wir müssen beweisen, dass ∠B + ∠D = 180°.

Winkel B ist in einen Kreis eingeschrieben. Wie Sie wissen, entspricht ein solcher Winkel der Hälfte des Bogens, auf dem er ruht. In diesem Fall wird Winkel B durch den Bogen-ADC unterstützt, was ∠B = ½◡ADC bedeutet. (Da der Bogen gleich dem Winkel zwischen den ihn bildenden Radien ist, können wir schreiben, dass ∠B = ½∠AOC, dessen innerer Bereich den Punkt D enthält.)

Auf der anderen Seite ruht der Winkel D des Vierecks auf dem Bogen ABC, d. h. ∠D = ½◡ABC.

Da die Seiten der Winkel B und D den Kreis an denselben Punkten (A und C) schneiden, teilen sie den Kreis nur in zwei Bögen – ◡ADC und ◡ABC. Da ein vollständiger Kreis 360° ergibt, ist ◡ADC + ◡ABC = 360°.

Somit wurden die folgenden Gleichheiten erhalten:

∠B = ½◡ADC
∠D = ½◡ABC
◡ADC + ◡ABC = 360°

Lassen Sie uns die Winkelsumme ausdrücken:

∠B + ∠D = ½◡ADC + ½◡ABC

Setzen wir ½ aus Klammern:

∠B + ∠D = ½(◡ADC + ◡ABC)

Ersetzen wir die Summe der Bögen durch ihren Zahlenwert:

∠B + ∠D = ½ * 360° = 180°

Wir haben herausgefunden, dass die Summe der entgegengesetzten Winkel eines eingeschriebenen Vierecks 180° beträgt. Das musste bewiesen werden.

Die Tatsache, dass ein beschriftetes Viereck diese Eigenschaft hat (die Summe der entgegengesetzten Winkel beträgt 180°), bedeutet nicht, dass jedes Viereck, dessen Summe der entgegengesetzten Winkel 180° beträgt, in einen Kreis eingeschrieben werden kann. Obwohl dies in Wirklichkeit der Fall ist. Diese Tatsache wird aufgerufen eingeschriebener viereckiger Test und ist wie folgt formuliert: Wenn die Summe der entgegengesetzten Winkel eines konvexen Vierecks 180° beträgt, dann kann um dieses herum ein Kreis beschrieben (oder in einen Kreis eingeschrieben) werden.

Sie können den Test für ein beschriftetes Viereck durch Widerspruch beweisen. Gegeben sei ein Viereck ABCD, dessen entgegengesetzte Winkel B und D 180° ergeben. In diesem Fall liegt der Winkel D nicht auf dem Kreis. Nehmen Sie dann einen Punkt E auf der Linie, die das Segment CD enthält, so dass er auf dem Kreis liegt. Das Ergebnis ist ein zyklisches Viereck ABCE. Dieses Viereck hat entgegengesetzte Winkel B und E, was bedeutet, dass sie zusammen 180° ergeben. Dies folgt aus der Eigenschaft eines beschrifteten Vierecks.

Es stellt sich heraus, dass ∠B + ∠D = 180° und ∠B + ∠E = 180°. Der Winkel D des Vierecks ABCD in Bezug auf das Dreieck AED ist jedoch außen und daher größer als der Winkel E dieses Dreiecks. Damit sind wir bei einem Widerspruch angelangt. Das heißt, wenn die Summe der entgegengesetzten Winkel eines Vierecks 180° ergibt, dann kann es immer in einen Kreis eingeschrieben werden.

Der Videokurs „Get an A“ beinhaltet alle notwendigen Themen, um das Einheitliche Staatsexamen in Mathematik mit 60-65 Punkten erfolgreich zu bestehen. Komplett alle Probleme 1-13 Profil Einheitliches Staatsexamen Mathematik. Auch zum Bestehen der Grundprüfung in Mathematik geeignet. Wenn Sie das Einheitliche Staatsexamen mit 90-100 Punkten bestehen möchten, müssen Sie Teil 1 in 30 Minuten und ohne Fehler lösen!

Vorbereitungskurs für das Einheitliche Staatsexamen für die Klassen 10-11 sowie für Lehrer. Alles, was Sie zum Lösen von Teil 1 des Einheitlichen Staatsexamens in Mathematik (die ersten 12 Aufgaben) und Aufgabe 13 (Trigonometrie) benötigen. Und das sind mehr als 70 Punkte beim Einheitlichen Staatsexamen, auf die weder ein 100-Punkte-Student noch ein Geisteswissenschaftler verzichten können.

Die ganze nötige Theorie. Schnelle Wege Lösungen, Fallstricke und Geheimnisse des Einheitlichen Staatsexamens. Alle aktuellen Aufgaben von Teil 1 aus der FIPI Task Bank wurden analysiert. Der Kurs entspricht vollständig den Anforderungen des Einheitlichen Staatsexamens 2018.

Der Kurs umfasst 5 große Themen zu je 2,5 Stunden. Jedes Thema wird von Grund auf einfach und klar vermittelt.

Hunderte von Aufgaben zum Einheitlichen Staatsexamen. Textaufgaben und Wahrscheinlichkeitstheorie. Einfache und leicht zu merkende Algorithmen zur Lösung von Problemen. Geometrie. Theorie, Referenzmaterial, Analyse aller Arten von Aufgaben des Einheitlichen Staatsexamens. Stereometrie. Knifflige Tricks Lösungen, nützliche Spickzettel, Entwicklung der räumlichen Vorstellungskraft. Trigonometrie von Grund auf bis zum Problem 13. Verstehen statt pauken. Klare Erklärungen komplexer Konzepte. Algebra. Wurzeln, Potenzen und Logarithmen, Funktion und Ableitung. Grundlage für die Lösung komplexe Aufgaben 2 Teile des Einheitlichen Staatsexamens.

Material aus Wikipedia – der freien Enzyklopädie

• In der euklidischen Geometrie gilt beschriftetes Viereck ist ein Viereck, dessen Eckpunkte alle auf demselben Kreis liegen. Dieser Kreis heißt umschriebener Kreis Viereck, und die Eckpunkte sollen auf demselben Kreis liegen. Der Mittelpunkt dieses Kreises und sein Radius werden jeweils genannt Center Und Radius umschriebener Kreis. Andere Bezeichnungen für dieses Viereck: Ein Viereck liegt auf einem Kreis, die Seiten des letzten Vierecks sind Sehnen des Kreises. Ein konvexes Viereck wird üblicherweise als konvexes Viereck angenommen. Die unten angegebenen Formeln und Eigenschaften gelten im konvexen Fall.
• Sie sagen das, wenn Um ein Viereck kann ein Kreis gezeichnet werden, Das In diesen Kreis ist das Viereck eingeschrieben, umgekehrt.

Allgemeine Kriterien für die Beschriftung eines Vierecks

• Um ein konvexes Viereck $\backslash Pi$ Bogenmaß), das heißt:

$\backslash angle\; A+\backslash angle\; C\; =\; \backslash angle\; B\; +\; \backslash angle\; D\; =\; 180^\backslash circ$

oder in der Figurenschreibweise:

$\backslash alpha\; +\; \backslash gamma\; =\; \backslash beta\; +\; \backslash delta\; =\; \backslash pi\; =\; 180^(\backslash circ).$

• Es ist möglich, einen Kreis um jedes Viereck zu beschreiben, bei dem sich die vier Mittelsenkrechten seiner Seiten in einem Punkt schneiden (oder Mittelsenkrechten seiner Seiten, d. h. Senkrechte zu den Seiten, die durch ihre Mittelpunkte verlaufen).
• Sie können einen Kreis um jedes Viereck beschreiben, das einen solchen hat Außenecke, grenzt an gegebener Innenwinkel, ist genau gleich dem anderen gegenüberliegenden Innenwinkel gegebene Innenecke. Im Wesentlichen handelt es sich bei dieser Bedingung um die Bedingung der Antiparallelität zweier gegenüberliegender Seiten des Vierecks. In Abb. Unten sind die äußeren und angrenzenden inneren Ecken eines grünen Fünfecks dargestellt.

$\backslash displaystyle\; AX\backslash cdot\; XC\; =\; BX\backslash cdot\; XD.$

• Überschneidung X kann innerhalb oder außerhalb des Kreises liegen. Im ersten Fall erhalten wir das zyklische Viereck is A B C D, und im letzteren Fall erhalten wir ein eingeschriebenes Viereck ABDC. Beim Schnitt innerhalb eines Kreises besagt die Gleichheit, dass das Produkt der Längen der Segmente, in denen sich der Punkt befindet X teilt eine Diagonale, ist gleich dem Produkt der Längen der Segmente, in denen der Punkt liegt X teilt eine andere Diagonale. Diese Bedingung ist als „Schnittakkordsatz“ bekannt. In unserem Fall sind die Diagonalen des eingeschriebenen Vierecks die Sehnen des Kreises.
• Ein weiteres Aufnahmekriterium. Konvexes Viereck A B C D Ein Kreis ist genau dann eingeschrieben, wenn

$\backslash tan(\backslash frac(\backslash alpha)(2))\backslash tan(\backslash frac(\backslash gamma)(2))=\backslash tan(\backslash frac(\backslash beta)(2))\backslash tan(\backslash frac(\backslash delta)(\; 2))=1.$

Besondere Kriterien für die Beschriftung eines Vierecks

Ein einfaches eingeschriebenes (ohne sich selbst schneidendes) Viereck ist konvex. Ein Kreis kann genau dann um ein konvexes Viereck beschrieben werden, wenn die Summe seiner entgegengesetzten Winkel gleich 180° ist ( $\backslash Pi$ Bogenmaß). Sie können einen Kreis beschreiben um:

• irgendein Antiparallelogramm
• jedes Rechteck (ein Sonderfall ist ein Quadrat)
• jedes gleichschenklige Trapez
• jedes Viereck, das zwei gegenüberliegende rechte Winkel hat.

Eigenschaften

Formeln mit Diagonalen

$ef=ac+bd$; $\backslash frac(e)(f)\; =\; \backslash frac(a\backslash cdot\; d+b\backslash cdot\; c)(a\backslash cdot\; b+c\backslash cdot\; d).$

In der letzten Formel des Paares angrenzende Seiten Zähler A Und D, B Und C Legen Sie ihre Enden auf eine diagonale Länge e. Eine ähnliche Aussage gilt für den Nenner.

• Formeln für Diagonallängen(Folgen ):

$e\; =\; \backslash sqrt(\backslash frac((ac+bd)(ad+bc))(ab+cd))$ Und $f\; =\; \backslash sqrt(\backslash frac((ac+bd)(ab+cd))(ad+bc))$

Formeln mit Winkeln

Für ein zyklisches Viereck mit einer Folge von Seiten A , B , C , D, mit Halbumfang P und Winkel A zwischen den Parteien A Und D, trigonometrische Winkelfunktionen A werden durch Formeln angegeben

$\backslash cos\; A\; =\; \backslash frac(a^2\; +\; d^2\; -\; b^2\; -\; c^2)(2(ad\; +\; bc)),$ $\backslash sin\; A\; =\; \backslash frac(2\backslash sqrt((p-a)(p-b)(p-c)(p-d)))((ad+bc)),$ $\backslash tan\; \backslash frac(A)(2)\; =\; \backslash sqrt(\backslash frac((p-a)(p-d))((p-b)(p-c))).$

Ecke θ zwischen den Diagonalen steht:S.26

$\backslash tan\; \backslash frac(\backslash theta)(2)\; =\; \backslash sqrt(\backslash frac((p-b)(p-d))((p-a)(p-c))).$

• Wenn gegenüberliegende Seiten A Und C sich in einem Winkel schneiden φ , dann ist es gleich

$\backslash cos(\backslash frac(\backslash varphi)(2))=\backslash sqrt(\backslash frac((p-b)(p-d)(b+d)^2)((ab+cd)(ad+bc))),$

Wo P Es gibt einen Halbumfang. :S.31

Radius eines um ein Viereck umschriebenen Kreises

Parameshvara-Formel

Wenn es sich um ein Viereck mit aufeinanderfolgenden Seiten handelt A , B , C , D und Halbumfang P in einen Kreis eingeschrieben, dann ist sein Radius gleich Parameshwars Formel:P. 84

$R=\; \backslash frac(1)(4)\; \backslash sqrt(\backslash frac((ab+cd)(ad+bc)(ac+bd))((p-a)(p-b)(p-c)(p-d))).$

Es wurde im 15. Jahrhundert (ca. 1380–1460) vom indischen Mathematiker Parameshwar abgeleitet.

• Konvexes Viereck (siehe Abbildung rechts), gebildet aus vier Daten Mikels gerade Linien, ist genau dann in einen Kreis eingeschrieben, wenn der Mikel-Punkt M eines Vierecks liegt auf einer Linie, die zwei der sechs Schnittpunkte der Linien verbindet (diejenigen, die keine Eckpunkte des Vierecks sind). Das ist wenn M liegt auf E.F..

Ein Kriterium dafür, dass ein aus zwei Dreiecken bestehendes Viereck in einen bestimmten Kreis eingeschrieben ist

$f^2\; =\; \backslash frac((ac+bd)(ad+bc))((ab+cd)).$

• Die letzte Bedingung gibt den Ausdruck für die Diagonale an F ein Viereck, das durch die Länge seiner vier Seiten in einen Kreis eingeschrieben ist ( A, B, C, D). Diese Formel folgt unmittelbar beim Multiplizieren und Gleichsetzen des linken und rechten Teils von Formeln, die das Wesentliche ausdrücken Der erste und zweite Satz des Ptolemäus(siehe oben).

Ein Kriterium dafür, dass ein durch eine gerade Linie aus einem Dreieck geschnittenes Viereck in einen bestimmten Kreis eingeschrieben ist

• Eine gerade Linie, die antiparallel zur Seite des Dreiecks verläuft und diese schneidet, schneidet daraus ein Viereck ab, um das sich immer ein Kreis beschreiben lässt.
• Folge. Um ein Antiparallelogramm herum, bei dem zwei gegenüberliegende Seiten antiparallel sind, ist es immer möglich, einen Kreis zu beschreiben.

Fläche eines in einen Kreis eingeschriebenen Vierecks

Variationen der Brahmagupta-Formel

$S=\backslash sqrt((p-a)(p-b)(p-c)(p-d)),$ wobei p der Halbumfang des Vierecks ist. $S=\; \backslash frac(1)(4)\; \backslash sqrt(-\; \backslash begin(vmatrix)$

a & b & c & -d \\ b & a & -d & c \\ c & -d & a & b \\ -d & c & b & a \end(vmatrix))

Andere Flächenformeln

$S\; =\; \backslash tfrac(1)(2)(ab+cd)\backslash sin(B)$ $S\; =\; \backslash tfrac(1)(2)(ac+bd)\backslash sin(\backslash theta),$

Wo θ jeder Winkel zwischen den Diagonalen. Vorausgesetzt, der Winkel A Da es sich nicht um eine gerade Linie handelt, kann die Fläche auch wie folgt ausgedrückt werden: S. 26

$S\; =\; \backslash tfrac(1)(4)(a^2-b^2-c^2+d^2)\backslash tan(A).$ $\backslash displaystyle\; S=2R^2\backslash sin(A)\backslash sin(B)\backslash sin(\backslash theta),$

Wo R ist der Radius des Umkreises. Als direkte Konsequenz haben wir die Ungleichung

$S\backslash le\; 2R^2,$

wobei Gleichheit genau dann möglich ist, wenn dieses Viereck ein Quadrat ist.

Brahmagupta-Vierecke

Brahmagupta-Viereck ist ein in einen Kreis eingeschriebenes Viereck mit ganzzahligen Seitenlängen, ganzzahligen Diagonalen und ganzzahliger Fläche. Alle möglichen Brahmagupta-Vierecke mit Seiten A , B , C , D, mit Diagonalen e , F, mit Fläche S und der Radius des umschriebenen Kreises R kann durch Entfernen der Nenner der folgenden Ausdrücke mit rationalen Parametern erhalten werden T , u, Und v :

$a=$ $b=(1+u^2)(v-t)(1+tv)$ $c=t(1+u^2)(1+v^2)$ $d=(1+v^2)(u-t)(1+tu)$ $e=u(1+t^2)(1+v^2)$ $f=v(1+t^2)(1+u^2)$ $S=UV$ $4R=(1+u^2)(1+v^2)(1+t^2).$

Beispiele

• Besondere in einen Kreis eingeschriebene Vierecke sind: Rechteck, Quadrat, gleichschenkliges oder gleichschenkliges Trapez, Antiparallelogramm.

In einen Kreis eingeschriebene Vierecke mit senkrechten Diagonalen (eingeschriebene orthodiagonale Vierecke)

Eigenschaften von Vierecken, die in einen Kreis mit senkrechten Diagonalen eingeschrieben sind

Umkreisradius und Fläche

Nehmen Sie für ein Viereck, das in einen Kreis mit senkrechten Diagonalen eingeschrieben ist, an, dass der Schnittpunkt der Diagonalen eine Diagonale in Längensegmente unterteilt P 1 und P 2 und teilt die andere Diagonale in Längensegmente Q 1 und Q 2. Dann (Die erste Gleichheit ist Satz 11 von Archimedes) Buch der Lemmas)

$D^2=p\_1^2+p\_2^2+q\_1^2+q\_2^2=a^2+c^2=b^2+d^2,$

Wo D- Durchmesser des Kreises. Dies ist wahr, weil die Diagonalen senkrecht zur Kreissehne verlaufen. Aus diesen Gleichungen folgt der Radius des umschriebenen Kreises R kann geschrieben werden als

$R=\backslash tfrac(1)(2)\backslash sqrt(p\_1^2+p\_2^2+q\_1^2+q\_2^2)$

oder in Bezug auf die Seiten eines Vierecks in der Form

$R=\backslash tfrac(1)(2)\backslash sqrt(a^2+c^2)=\backslash tfrac(1)(2)\backslash sqrt(b^2+d^2).$

Daraus folgt auch

$a^2+b^2+c^2+d^2=8R^2.$

• Für eingeschriebene ordiagonale Vierecke gilt der Satz von Brahmagupta:

Wenn ein zyklisches Viereck senkrechte Diagonalen hat, die sich in einem Punkt schneiden $M$, dann zwei Paare davon antimediatris durch einen Punkt gehen $M$.

Kommentar. In diesem Satz unter Anti-Mediatrix das Segment verstehen $F.E.$ Viereck in der Abbildung rechts (analog zur Mittelsenkrechten (Mediatrix) zur Seite des Dreiecks). Es steht senkrecht auf einer Seite und verläuft gleichzeitig durch die Mitte der gegenüberliegenden Seite des Vierecks.

Schreiben Sie eine Rezension zum Artikel „In einen Kreis eingeschriebene Vierecke“

Anmerkungen

1. Bradley, Christopher J. (2007), Die Algebra der Geometrie: Kartesische, flächenhafte und projektive Koordinaten,Highperception, p. 179, ISBN 1906338000, OCLC
2. . Beschriftete Vierecke.
3. Siddons, A. W. & Hughes, R. T. (1929) Trigonometrie, Cambridge University Press, S. 202, O.C.L.C.
4. Durell, C. V. & Robson, A. (2003), , Courier Dover, ISBN 978-0-486-43229-8 ,
5. Alsina, Claudi & Nelsen, Roger B. (2007), „“, Forum Geometricorum T. 7: 147–9 ,
6. Johnson, Roger A., Erweiterte euklidische Geometrie, Dover Publ., 2007 (ursprünglich 1929).
7. Hoehn, Larry (März 2000), „Zirkumradius eines zyklischen Vierecks“, Mathematische Zeitung T. 84 (499): 69–70
8. .
9. Altshiller-Court, Nathan (2007), Hochschulgeometrie: Eine Einführung in die moderne Geometrie des Dreiecks und des Kreises(2. Aufl.), Courier Dover, S. 131, 137–8, ISBN 978-0-486-45805-2, OCLC
10. Honsberger, Ross (1995), , Episoden der euklidischen Geometrie des 19. und 20. Jahrhunderts, Bd. 37, New Mathematical Library, Cambridge University Press, S. 35–39, ISBN 978-0-88385-639-0
11. Weisstein, Eric W.(Englisch) auf der Wolfram MathWorld-Website.
12. Bradley, Christopher (2011), ,
13. .
14. Coxeter, Harold Scott MacDonald & Greitzer, Samuel L. (1967), , Geometrie überarbeitet, Mathematical Association of America, S. 57, 60, ISBN 978-0-88385-619-2
15. .
16. Andreescu, Titu & Enescu, Bogdan (2004), , Schätze der Mathematikolympiade, Springer, S. 44–46, 50, ISBN 978-0-8176-4305-8
17. .
18. Buchholz, R. H. & MacDougall, J. A. (1999), „“, Bulletin der Australian Mathematical Society T. 59 (2): 263–9 , DOI 10.1017/S0004972700032883
19. .
20. Johnson, Roger A., Erweiterte euklidische Geometrie, Dover Publ. Co., 2007
21. , Mit. 74.
22. .
23. .
24. .
25. Peter, Thomas (September 2003), „Maximierung der Fläche eines Vierecks“, Das College Mathematics Journal T. 34 (4): 315–6
26. Prasolov, Viktor, ,
27. Alsina, Claudi & Nelsen, Roger (2009), , , Mathematical Association of America, p. 64, ISBN 978-0-88385-342-9 ,
28. Sastry, K.R.S. (2002). "" (PDF). Forum Geometricorum 2 : 167–173.
29. Posamentier, Alfred S. & Salkind, Charles T. (1970), , Anspruchsvolle Probleme in der Geometrie(2. Aufl.), Courier Dover, S. 104–5, ISBN 978-0-486-69154-1
30. .
31. .
32. .

siehe auch

Nach Anzahl der Seiten Richtig Dreiecke Vierecke siehe auch

Der Artikel enthält kurze („Harvard“) Verweise auf Veröffentlichungen, die im bibliografischen Teil nicht aufgeführt oder falsch beschrieben sind. Liste defekter Links: , , , , , , , , , – Nun, was, mein Kosak? (Marya Dmitrievna nannte Natascha eine Kosakin) - sagte sie und streichelte Natascha mit ihrer Hand, die sich ihrer Hand ohne Angst und fröhlich näherte. – Ich weiß, dass der Zaubertrank ein Mädchen ist, aber ich liebe sie. Sie holte birnenförmige Yakhon-Ohrringe aus ihrem riesigen Retikül und gab sie Natasha, die zu ihrem Geburtstag strahlte und errötete, wandte sich sofort von ihr ab und wandte sich an Pierre. - Äh, äh! Art! „Komm her“, sagte sie mit gespielt leiser und dünner Stimme. - Komm schon, mein Lieber... Und sie krempelte bedrohlich ihre Ärmel noch höher. Pierre kam näher und sah sie naiv durch seine Brille an. - Komm, komm, mein Lieber! Ich war der Einzige, der deinem Vater die Wahrheit gesagt hat, als er die Gelegenheit dazu hatte, aber Gott befiehlt es dir. Sie hielt inne. Alle schwiegen, warteten darauf, was passieren würde, und hatten das Gefühl, dass es sich nur um ein Vorwort handelte. - Gut, nichts zu sagen! Guter Junge!... Der Vater liegt auf seinem Bett und vergnügt sich damit, den Polizisten auf einen Bären zu setzen. Es ist eine Schande, Vater, es ist eine Schande! Es wäre besser, in den Krieg zu ziehen. Sie wandte sich ab und reichte dem Grafen die Hand, der sich ein Lachen kaum verkneifen konnte. - Nun, komm an den Tisch, ich trinke Tee, ist es Zeit? - sagte Marya Dmitrievna. Der Graf ging mit Marya Dmitrievna voran; dann die Gräfin, die von einem Husarenoberst geführt wurde, die richtige Person, mit dem Nikolai das Regiment einholen sollte. Anna Michailowna – mit Shinshin. Berg schüttelte Vera die Hand. Eine lächelnde Julie Karagina ging mit Nikolai an den Tisch. Hinter ihnen kamen weitere Paare, die sich über den gesamten Saal erstreckten, und hinter ihnen standen nacheinander Kinder, Erzieher und Gouvernanten. Die Kellner begannen sich zu rühren, die Stühle klapperten, im Chor begann Musik zu spielen und die Gäste nahmen ihre Plätze ein. Die Klänge der Hausmusik des Grafen wurden durch die Geräusche von Messern und Gabeln, das Geplapper der Gäste und die leisen Schritte der Kellner ersetzt. An einem Ende des Tisches saß die Gräfin am Kopfende. Rechts ist Marya Dmitrievna, links Anna Michailowna und andere Gäste. Am anderen Ende saßen der Graf, links der Husarenoberst, rechts Shinshin und weitere männliche Gäste. Auf der einen Seite des langen Tisches stehen ältere junge Leute: Vera neben Berg, Pierre neben Boris; auf der anderen Seite - Kinder, Erzieher und Gouvernanten. Hinter dem Kristall, den Flaschen und Vasen mit Obst blickte der Graf auf seine Frau und ihre hohe Mütze mit blauen Bändern und schenkte seinen Nachbarn fleißig Wein ein, ohne dabei sich selbst zu vergessen. Auch die Gräfin warf hinter den Ananas hervor, ihre Pflichten als Hausfrau nicht vergessend, bedeutungsvolle Blicke auf ihren Mann, dessen Glatze und Gesicht sich, wie es ihr schien, durch die Rötung deutlicher von seinen grauen Haaren unterschieden. Bei den Damen gab es ein ständiges Geplapper; In der Herrentoilette wurden die Stimmen immer lauter, besonders die des Husarenobersten, der so viel aß und trank und dabei immer erröteter wurde, dass der Graf ihn den anderen Gästen bereits als Vorbild aufstellte. Mit einem sanften Lächeln sagte Berg zu Vera, dass Liebe kein irdisches, sondern ein himmlisches Gefühl sei. Boris nannte seinen neuen Freund Pierre die Gäste am Tisch und tauschte Blicke mit Natascha, die ihm gegenüber saß. Pierre sprach wenig, schaute neue Gesichter an und aß viel. Ausgehend von zwei Suppen, aus denen er a la Tortue, [Schildkröte] und Kulebyaki bis hin zu Haselhuhn wählte, ließ er kein einziges Gericht und keinen einzigen Wein aus, den ihm der Butler auf geheimnisvolle Weise in einer in eine Serviette gewickelten Flasche hinhielt hinter der Schulter seines Nachbarn hervorrufen und „drey Madeira“, „Ungarisch“ oder „Rheinwein“ sagen. Er stellte das erste der vier Kristallgläser mit dem gräflichen Monogramm vor jedes Gerät und trank genüsslich, wobei er die Gäste mit zunehmend freundlichem Gesichtsausdruck ansah. Natascha, die ihm gegenüber saß, sah Boris an, wie dreizehnjährige Mädchen einen Jungen ansehen, den sie gerade zum ersten Mal geküsst hatten und in den sie verliebt sind. Derselbe Blick von ihr wandte sich manchmal Pierre zu, und unter dem Blick dieses lustigen, lebhaften Mädchens wollte er selbst lachen, ohne zu wissen warum. Nikolai saß weit entfernt von Sonya neben Julie Karagina und sprach wieder mit demselben unwillkürlichen Lächeln zu ihr. Sonya lächelte großartig, wurde aber offenbar von Eifersucht gequält: Sie wurde blass, dann errötete sie und hörte mit aller Kraft zu, was Nikolai und Julie einander sagten. Die Gouvernante blickte sich ruhelos um, als wollte sie sich wehren, falls jemand beschloss, die Kinder zu beleidigen. Der Deutschlehrer versuchte, sich alle möglichen Gerichte, Desserts und Weine einzuprägen, um in einem Brief an seine Familie in Deutschland alles ausführlich zu beschreiben, und war sehr beleidigt darüber, dass der Butler eine in eine Serviette gewickelte Flasche trug ihn herum. Der Deutsche runzelte die Stirn, versuchte zu zeigen, dass er diesen Wein nicht erhalten wollte, war aber beleidigt, weil niemand verstehen wollte, dass er den Wein nicht brauchte, um seinen Durst zu löschen, nicht aus Gier, sondern aus gewissenhafter Neugier. Am männlichen Ende des Tisches wurde das Gespräch immer lebhafter. Der Oberst sagte, dass das Kriegserklärungsmanifest bereits in St. Petersburg veröffentlicht worden sei und dass die Kopie, die er selbst gesehen habe, nun per Kurier dem Oberbefehlshaber zugestellt worden sei. - Und warum fällt es uns schwer, gegen Bonaparte zu kämpfen? - sagte Shinshin. – II a deja rabattu le caquet a l "Autriche. Je crins, que cette fois ce ne soit notre tour. [Er hat bereits die Arroganz Österreichs niedergeschlagen. Ich fürchte, dass wir jetzt nicht an der Reihe sein würden.] Der Oberst war ein untersetzter, großer und sanguinischer Deutscher, offensichtlich ein Diener und Patriot. Er war durch Shinshins Worte beleidigt. „Und dann sind wir ein guter Herrscher“, sagte er und sprach e statt e und ъ statt ь aus. „Dann weiß der Kaiser das. Er sagte in seinem Manifest, dass er den Gefahren, die Russland bedrohen, gleichgültig gegenüberstehen kann und dass die Sicherheit des Reiches, seine Würde und die Heiligkeit seiner Bündnisse wichtig sind“, sagte er und betonte dabei aus irgendeinem Grund besonders das Wort „Gewerkschaften“, als ob dies der Kern der Sache wäre. Und mit seinem charakteristischen unfehlbaren, offiziellen Gedächtnis wiederholte er die einleitenden Worte des Manifests ... „Und der Wunsch, das einzige und unverzichtbare Ziel des Souveräns: den Frieden in Europa auf soliden Grundlagen zu errichten – sie beschlossen, einen Teil davon zu entsenden.“ Armee im Ausland und unternehmen neue Anstrengungen, um dieses Ziel zu erreichen“. „Deshalb sind wir ein guter Herrscher“, schloss er, trank erbaulich ein Glas Wein und blickte ermutigend auf den Grafen zurück. – Connaissez vous le proverbe: [Du kennst das Sprichwort:] „Erema, Erema, du solltest zu Hause sitzen und deine Spindeln schärfen“, sagte Shinshin, zuckte zusammen und lächelte. – Cela nous convient a merveille. [Das ist praktisch für uns.] Warum Suworow – sie haben ihn zerhackt, einen Teller Couture, [auf seinem Kopf] und wo sind unsere Suworows jetzt? Je vous requeste un peu, [ich frage dich] – ständiges Springen vom Russischen ins Russische Französisch, er sagte. „Wir müssen bis zum letzten Blutstropfen kämpfen“, sagte der Oberst und schlug auf den Tisch, „und für unseren Kaiser sterben, und dann wird alles gut.“ Und so viel wie möglich zu streiten (beim Wort „möglich“ hat er seine Stimme besonders in die Länge gezogen), so wenig wie möglich“, endete er und wandte sich wieder an den Grafen. „So beurteilen wir die alten Husaren, das ist alles.“ Wie urteilen Sie, junger Mann und junger Husar? - fügte er hinzu und wandte sich an Nikolai, der, als er hörte, dass es um Krieg ging, seinen Gesprächspartner verließ und den Oberst mit allen Augen ansah und mit allen Ohren zuhörte. „Ich stimme Ihnen voll und ganz zu“, antwortete Nikolai ganz errötet, drehte den Teller und ordnete die Gläser mit einem so entschlossenen und verzweifelten Blick, als wäre er in diesem Moment einer großen Gefahr ausgesetzt, „ich bin überzeugt, dass die Russen sterben müssen.“ „Oder gewinnen“, sagte er. Wie andere empfand er, nachdem das Wort schon gesagt war, dass es für den jetzigen Anlass zu enthusiastisch und pompös und daher umständlich sei. „C"est bien beau ce que vous venez de dire, [Wunderbar! Was du gesagt hast, ist wunderbar]", sagte Julie, die neben ihm saß, seufzend. Sonya zitterte am ganzen Körper und errötete bis zu den Ohren, hinter den Ohren und bis zum Nacken und den Schultern, in Während Nikolai sprach, hörte Pierre den Reden des Obersten zu und nickte zustimmend mit dem Kopf. „Das ist schön“, sagte er. „Ein echter Husar, junger Mann“, rief der Oberst und schlug erneut auf den Tisch. -Worüber machst du da Lärm? – Plötzlich war Marya Dmitrievnas Bassstimme über den Tisch zu hören. -Warum klopfst du auf den Tisch? - Sie wandte sich an den Husaren, - Über wen regen Sie sich auf? Richtig, du denkst, dass die Franzosen vor dir sind? „Ich sage die Wahrheit“, sagte der Husar lächelnd. „Alles über den Krieg“, rief der Graf über den Tisch. - Schließlich kommt mein Sohn, Marya Dmitrievna, mein Sohn kommt. - Und ich habe vier Söhne in der Armee, aber das ist mir egal. Alles ist Gottes Wille: Du wirst auf dem Herd sterben, und im Kampf wird Gott gnädig sein“, ertönte Marya Dmitrievnas dicke Stimme mühelos vom anderen Ende des Tisches. - Ist das so. Und das Gespräch konzentrierte sich wieder – die Damen an ihrem Ende des Tisches, die Männer an seinem. „Aber du wirst nicht fragen“, sagte der kleine Bruder zu Natascha, „aber du wirst nicht fragen!“ „Ich werde fragen“, antwortete Natasha. Ihr Gesicht errötete plötzlich und drückte verzweifelte und fröhliche Entschlossenheit aus. Sie stand auf, forderte Pierre, der ihr gegenüber saß, auf, zuzuhören, und wandte sich an ihre Mutter: - Mama! – ihre kindliche, brustige Stimme ertönte über den Tisch. - Was willst du? – fragte die Gräfin voller Angst, aber als sie am Gesicht ihrer Tochter sah, dass es sich um einen Streich handelte, winkte sie streng mit der Hand und machte eine drohende und ablehnende Geste mit dem Kopf. Das Gespräch verstummte. - Mama! Was für ein Kuchen wird es sein? – Natashas Stimme klang noch entschiedener, ohne zusammenzubrechen. Die Gräfin wollte die Stirn runzeln, konnte es aber nicht. Marya Dmitrievna schüttelte ihren dicken Finger. „Kosak“, sagte sie drohend. Die meisten Gäste blickten die Ältesten an und wussten nicht, wie sie diesen Trick annehmen sollten. - Hier bin ich! - sagte die Gräfin. - Mama! was für einen Kuchen wird es geben? - schrie Natasha jetzt kühn und launisch fröhlich, schon im Vorfeld zuversichtlich, dass ihr Streich gut ankommen würde. Sonya und die dicke Petja versteckten sich vor Lachen. „Deshalb habe ich gefragt“, flüsterte Natasha ihrem kleinen Bruder und Pierre zu, den sie erneut ansah. „Eis, aber sie geben es dir nicht“, sagte Marya Dmitrievna. Natasha sah, dass es nichts gab, wovor sie Angst haben musste, und hatte deshalb keine Angst vor Marya Dmitrievna. - Marya Dmitrievna? was für ein Eis! Ich mag keine Sahne. - Karotte. - Nein, welches? Marya Dmitrievna, welche? – Sie hätte fast geschrien. - Ich möchte wissen! Marya Dmitrievna und die Gräfin lachten, und alle Gäste folgten ihnen. Alle lachten nicht über Marya Dmitrievnas Antwort, sondern über den unfassbaren Mut und die Geschicklichkeit dieses Mädchens, das wusste, wie und es wagte, Marya Dmitrievna so zu behandeln. Natasha geriet erst in Rückstand, als ihr gesagt wurde, dass es Ananas geben würde. Vor dem Eis wurde Champagner serviert. Die Musik begann wieder zu spielen, der Graf küsste die Gräfin, und die Gäste standen auf und gratulierten der Gräfin und stießen mit dem Grafen, den Kindern und untereinander Gläser an. Wieder rannten Kellner herein, Stühle klapperten, und in der gleichen Reihenfolge, aber mit röteren Gesichtern, kehrten die Gäste in den Salon und in das Büro des Grafen zurück. Die Bostoner Tische wurden auseinandergeschoben, die Gesellschaften aufgestellt und die Gäste des Grafen ließen sich in zwei Wohnzimmern, einem Sofazimmer und einer Bibliothek nieder. Der Graf, der seine Karten ausbreitete, konnte der Angewohnheit, einen Mittagsschlaf zu halten, kaum widerstehen und lachte über alles. Der Jüngling versammelte sich, von der Gräfin angeregt, um das Clavichord und die Harfe. Julie spielte auf Wunsch aller als erste ein Stück mit Variationen auf der Harfe und begann zusammen mit anderen Mädchen, Natascha und Nikolai, die für ihre Musikalität bekannt sind, zu bitten, etwas zu singen. Darauf war Natasha, die als großes Mädchen angesprochen wurde, offenbar sehr stolz, gleichzeitig aber auch schüchtern. - Was werden wir singen? - Sie fragte. „Der Schlüssel“, antwortete Nikolai. - Nun, beeilen wir uns. „Boris, komm her“, sagte Natascha. - Wo ist Sonya? Sie sah sich um und rannte hinter ihr her, als sie sah, dass ihre Freundin nicht im Zimmer war. Natasha rannte in Sonyas Zimmer und fand ihre Freundin dort nicht vor. Sie rannte ins Kinderzimmer – und Sonya war nicht da. Natasha erkannte, dass Sonya im Korridor auf der Brust lag. Die Truhe im Flur war der Ort der Sorgen der jüngeren weiblichen Generation des Rostower Hauses. Tatsächlich legte sich Sonya in ihrem luftigen rosa Kleid, das es zerdrückte, mit dem Gesicht nach unten auf das schmutzige, gestreifte Federbett ihres Kindermädchens, auf die Brust, und weinte bitterlich, während sie ihr Gesicht mit den Fingern bedeckte, und schüttelte ihre nackten Schultern. Natashas Gesicht, belebt, mit einem Geburtstag den ganzen Tag, veränderte sich plötzlich: Ihr Blick blieb stehen, dann zitterte ihr breiter Hals, ihre Lippenwinkel hingen herab. - Sonya! Was bist du?... Was, was ist los mit dir? Wow wow!… Und Natasha öffnete ihren großen Mund und wurde völlig dumm und begann wie ein Kind zu brüllen, ohne den Grund zu kennen und nur, weil Sonya weinte. Sonya wollte den Kopf heben, wollte antworten, aber sie konnte nicht und versteckte sich noch mehr. Natasha weinte, setzte sich auf das blaue Federbett und umarmte ihre Freundin. Nachdem Sonya ihre Kräfte gesammelt hatte, stand sie auf, wischte sich die Tränen weg und erzählte die Geschichte. - Nikolenka geht in einer Woche, sein ... Papier ... kam heraus ... er sagte es mir selbst ... Ja, ich würde immer noch nicht weinen ... (sie zeigte den Zettel, den sie in der Hand hielt ihre Hand: Es war ein Gedicht von Nikolai) Ich wollte immer noch nicht weinen, aber du hast es nicht geschafft... niemand kann verstehen... was für eine Seele er hat. Und sie fing wieder an zu weinen, weil seine Seele so gut war. „Du fühlst dich gut... Ich beneide dich nicht... Ich liebe dich und Boris auch“, sagte sie und sammelte ein wenig Kraft, „er ist süß... es gibt keine Hindernisse für dich.“ Und Nikolai ist mein Cousin... Ich brauche... den Metropoliten selbst... und das ist unmöglich. Und dann, wenn Mama... (Sonja dachte an die Gräfin und rief ihre Mutter an), wird sie sagen, dass ich Nikolais Karriere ruiniere, ich habe kein Herz, dass ich undankbar bin, aber wirklich... um Gottes willen... (sie bekreuzigt sich) Ich liebe sie auch so sehr, und euch alle, nur Vera... Wofür? Was habe ich ihr angetan? Ich bin dir so dankbar, dass ich gerne alles opfern würde, aber ich habe nichts... Sonya konnte nicht mehr sprechen und versteckte ihren Kopf wieder in ihren Händen und dem Federbett. Natasha begann sich zu beruhigen, aber ihr Gesicht zeigte, dass sie die Bedeutung der Trauer ihrer Freundin verstand. - Sonya! - sagte sie plötzlich, als hätte sie den wahren Grund für die Trauer ihrer Cousine erraten. – Richtig, Vera hat nach dem Abendessen mit dir gesprochen? Ja? – Ja, Nikolai selbst hat diese Gedichte geschrieben, und ich habe andere abgeschrieben; Sie fand sie auf meinem Tisch und sagte, dass sie sie Mama zeigen würde, und sagte auch, dass ich undankbar sei, dass Mama ihm niemals erlauben würde, mich zu heiraten, und dass er Julie heiraten würde. Du siehst, wie er den ganzen Tag mit ihr zusammen ist... Natasha! Wofür?… Und wieder weinte sie bitterer als zuvor. Natasha hob sie hoch, umarmte sie und begann, unter Tränen zu lächeln, sie zu beruhigen. - Sonya, glaub ihr nicht, Liebling, glaub ihr nicht. Erinnern Sie sich, wie wir alle drei im Sofazimmer mit Nikolenka gesprochen haben? Erinnerst du dich nach dem Abendessen? Schließlich haben wir alles so entschieden, wie es sein würde. Ich kann mich nicht erinnern, wie, aber du erinnerst dich, wie alles gut war und alles möglich war. Hier ist Onkel Shinshins Bruder, mit dem er verheiratet ist Cousin, und wir sind Cousins ​​zweiten Grades. Und Boris sagte, dass dies sehr gut möglich sei. Weißt du, ich habe ihm alles erzählt. Und er ist so klug und so gut“, sagte Natasha ... „Du, Sonya, weine nicht, mein lieber Schatz, Sonya.“ - Und sie küsste sie lachend. - Glaube ist böse, Gott segne sie! Aber alles wird gut, und sie wird es Mama nicht sagen; Nikolenka wird es selbst sagen, und er hat nicht einmal an Julie gedacht. Und sie küsste sie auf den Kopf. Sonya stand auf, und das Kätzchen wurde munter, seine Augen funkelten, und es schien bereit zu sein, mit dem Schwanz zu wedeln, auf seine weichen Pfoten zu springen und wieder mit dem Ball zu spielen, wie es sich für ihn gehörte. - Denkst du? Rechts? Von Gott? – sagte sie und strich schnell ihr Kleid und ihre Haare glatt. - Wirklich, bei Gott! – antwortete Natasha und glättete eine verirrte Haarsträhne unter dem Zopf ihrer Freundin. Und sie lachten beide. - Nun, lasst uns „The Key“ singen gehen. - Lass uns gehen. „Weißt du, dieser dicke Pierre, der mir gegenüber saß, ist so lustig!“ – sagte Natascha plötzlich und blieb stehen. - Ich habe viel Spaß! Und Natasha rannte den Korridor entlang. Sonya schüttelte den Flaum ab und versteckte die Gedichte in ihrem Busen, bis zum Hals mit hervorstehenden Brustknochen, mit leichten, fröhlichen Schritten, mit gerötetem Gesicht, rannte Natascha den Flur entlang zum Sofa hinterher. Auf Wunsch der Gäste sangen die Jugendlichen das „Key“-Quartett, das allen sehr gut gefiel; dann sang Nikolai das Lied, das er gelernt hatte, noch einmal. In einer angenehmen Nacht, im Mondlicht, Stellen Sie sich vor, Sie wären glücklich Dass es noch jemanden auf der Welt gibt, Wer denkt auch an dich! Als sie mit ihrer schönen Hand Entlang der goldenen Harfe gehen, Mit seiner leidenschaftlichen Harmonie Ruft sich selbst an, ruft dich! Noch ein oder zwei Tage, und der Himmel wird kommen ... Aber ah! Dein Freund wird nicht leben! Und er hat noch nicht zu Ende gesungen letzte Worte, als sich die Jugend im Saal zum Tanzen vorbereitete und die Musiker im Chor anfingen, mit den Füßen zu klopfen und zu husten. Pierre saß im Wohnzimmer, wo Shinshin, wie mit einem Besucher aus dem Ausland, mit ihm ein für Pierre langweiliges politisches Gespräch begann, dem sich andere anschlossen. Als die Musik zu spielen begann, betrat Natasha das Wohnzimmer und ging lachend und errötend direkt zu Pierre und sagte: - Mama hat mir gesagt, ich soll dich zum Tanzen bitten. „Ich habe Angst, die Zahlen zu verwechseln“, sagte Pierre, „aber wenn du mein Lehrer sein willst ...“ Und er reichte dem dünnen Mädchen seine dicke Hand und senkte sie tief. Während sich die Paare niederließen und die Musiker Schlange standen, setzte sich Pierre mit seiner kleinen Dame zusammen. Natasha war rundum glücklich; Sie tanzte mit einem Großen, mit jemandem, der aus dem Ausland kam. Sie saß vor allen und redete mit ihm wie ein großes Mädchen. Sie hatte einen Fächer in der Hand, den ihr eine junge Dame zum Halten geschenkt hatte. Und indem sie die weltlichste Pose einnahm (Gott weiß, wo und wann sie das gelernt hatte), sprach sie, indem sie sich Luft zufächelte und durch den Fächer lächelte, zu ihrem Herrn. - Was ist das, was ist das? Schau, schau“, sagte die alte Gräfin, ging durch die Halle und zeigte auf Natascha. Natasha errötete und lachte. - Nun, was ist mit dir, Mama? Nun, welche Art von Jagd suchen Sie? Was ist hier überraschend? Mitten in der dritten Öko-Sitzung begannen sich die Stühle im Wohnzimmer, in dem der Graf und Marya Dmitrievna spielten, zu bewegen, und die meisten Ehrengäste und alten Leute streckten sich nach langem Sitzen und steckten Brieftaschen und Geldbörsen hinein In ihren Taschen gingen sie aus der Halle. Marya Dmitrievna ging mit dem Grafen voraus – beide mit fröhlichen Gesichtern. Mit spielerischer Höflichkeit wie im Ballett reichte der Graf Marya Dmitrievna seine runde Hand. Er richtete sich auf, und sein Gesicht erstrahlte in einem besonders mutigen, verschlagenen Lächeln, und sobald die letzte Figur der Ecosaise getanzt war, klatschte er den Musikern in die Hände und rief dem Chor zu, wobei er sich an die erste Geige wandte: - Semjon! Kennen Sie Danila Kupor? Dies war der Lieblingstanz des Grafen, den er in seiner Jugend getanzt hatte. (Danilo Kupor war tatsächlich eine Figur der Angles.) „Schau dir Papa an“, rief Natasha dem ganzen Saal zu (wobei sie völlig vergaß, dass sie mit einem Großen tanzte), beugte ihren Lockenkopf auf die Knie und brach im ganzen Saal in ihr schallendes Gelächter aus. Tatsächlich blickte jeder im Saal mit einem freudigen Lächeln auf den fröhlichen alten Mann, der neben seiner würdevollen Frau Marya Dmitrievna, die größer war als er, seine Arme umrundete, sie im richtigen Moment schüttelte, seine Schultern streckte und seine verdrehte Mit leicht aufstampfenden Füßen und einem immer strahlenderen Lächeln im runden Gesicht bereitete er das Publikum auf das Kommende vor. Sobald die fröhlichen, trotzigen Geräusche von Danila Kupor, ähnlich einer fröhlichen Plauderei, zu hören waren, waren alle Türen der Halle plötzlich auf der einen Seite mit Männergesichtern und auf der anderen Seite mit lächelnden Frauengesichtern von Dienern gefüllt, die herauskamen Schau dir den fröhlichen Meister an. - Vater gehört uns! Adler! – sagte das Kindermädchen laut von einer Tür. Der Graf tanzte gut und wusste es, aber seine Dame wusste nicht wie und wollte nicht gut tanzen. Ihr riesiger Körper stand aufrecht mit gesenkten Armen mit kräftigen Händen(sie reichte der Gräfin das Taschentuch); Nur eine strenge Sache, aber Schönes Gesicht Sie hat getanzt. Was sich in der gesamten runden Figur des Grafen ausdrückte, drückte sich bei Marya Dmitrievna nur in einem zunehmend lächelnden Gesicht und einer zuckenden Nase aus. Aber wenn der Graf, der immer unzufriedener wurde, das Publikum mit der Überraschung geschickter Drehungen und leichter Sprünge seiner weichen Beine fesselte, lehnte Marya Dmitrievna mit dem geringsten Eifer, ihre Schultern zu bewegen oder ihre Arme abwechselnd zu drehen und zu stampfen, ab weniger ein Eindruck von Verdiensten, die jeder für ihre Fettleibigkeit und allgegenwärtige Strenge schätzte. Der Tanz wurde immer lebhafter. Die Gegenspieler konnten keine Minute auf sich aufmerksam machen und versuchten es auch gar nicht erst. Alles war vom Grafen und Marya Dmitrievna besetzt. Natasha zog an den Ärmeln und Kleidern aller Anwesenden, die bereits die Tänzer im Blick hatten, und forderte sie auf, Papa anzusehen. Während der Tanzpausen holte der Graf tief Luft, winkte und rief den Musikern zu, schnell zu spielen. Schneller, schneller und schneller, schneller und schneller und schneller entfaltete sich der Graf, mal auf Zehenspitzen, mal auf Fersen, stürmte um Marya Dmitrievna herum und drehte schließlich seine Dame zu ihrem Platz, machte den letzten Schritt und hob sein weiches Bein an hinten, beugte seinen verschwitzten Kopf mit lächelndem Gesicht und winkte rundherum rechte Hand unter tosendem Applaus und Gelächter, besonders von Natasha. Beide Tänzer blieben stehen, keuchten schwer und wischten sich mit Batisttaschentüchern ab. „So haben sie in unserer Zeit getanzt, ma chere“, sagte der Graf. - Oh ja, Danila Kupor! - sagte Marya Dmitrievna, ließ den Geist schwer und lange aus und krempelte die Ärmel hoch. Während die Rostows im Saal zu den Klängen müder, verstimmter Musiker die sechste Anglaise tanzten und müde Kellner und Köche das Abendessen zubereiteten, traf Graf Bezukhy der sechste Schlag. Die Ärzte erklärten, dass es keine Hoffnung auf Genesung gebe; dem Patienten wurde eine stille Beichte und die Kommunion abgelegt; Sie bereiteten sich auf die Salbung vor, und im Haus herrschte die Hektik und Erwartungsangst, die in solchen Momenten üblich sind. Vor dem Haus, hinter den Toren, drängten sich Bestatter, versteckten sich vor den herannahenden Kutschen und warteten auf einen reichen Auftrag für die Beerdigung des Grafen. Der Oberbefehlshaber von Moskau, der ständig Adjutanten schickte, um sich nach der Position des Grafen zu erkundigen, kam an diesem Abend selbst, um sich von dem berühmten Adligen Katharinas, Graf Bezukhim, zu verabschieden. Der prächtige Empfangsraum war voll. Alle standen respektvoll auf, als der Oberbefehlshaber, der etwa eine halbe Stunde mit dem Patienten allein war, herauskam, die Verbeugungen leicht erwiderte und versuchte, so schnell wie möglich an den Blicken von Ärzten, Geistlichen und Angehörigen vorbeizukommen auf ihn fixiert. Prinz Wassili, der in diesen Tagen an Gewicht verloren und blass geworden war, verabschiedete sich vom Oberbefehlshaber und wiederholte ihm mehrmals leise etwas. Nachdem er den Oberbefehlshaber verabschiedet hatte, setzte sich Prinz Wassili allein auf einen Stuhl im Flur, kreuzte die Beine, stützte den Ellbogen auf das Knie und schloss die Augen mit der Hand. Nachdem er einige Zeit so gesessen hatte, stand er auf und ging mit ungewöhnlich hastigen Schritten, sich mit erschrockenen Augen umsehend, durch den langen Korridor zur hinteren Hälfte des Hauses, zur ältesten Prinzessin. Die Menschen in dem schwach beleuchteten Raum unterhielten sich ungleichmäßig im Flüsterton, verstummten jedes Mal und schauten mit fragenden und erwartungsvollen Augen zurück zur Tür, die zu den Gemächern des Sterbenden führte, und gaben ein leises Geräusch von sich, als jemand herauskam davon entfernt oder eingegeben haben. „Die menschliche Grenze“, sagte der alte Mann, ein Geistlicher, zu der Dame, die sich neben ihn setzte und ihm naiv zuhörte, „die Grenze ist gesetzt, aber man kann sie nicht überschreiten.“ „Ich frage mich, ob es zu spät ist, eine Salbung durchzuführen?“ - Die Dame fügte den spirituellen Titel hinzu und fragte, als hätte sie zu diesem Thema keine eigene Meinung.

Zurück vorwärts

Aufmerksamkeit! Folienvorschauen dienen nur zu Informationszwecken und stellen möglicherweise nicht alle Funktionen der Präsentation dar. Wenn Sie interessiert sind diese Arbeit Bitte laden Sie die Vollversion herunter.

Ziele.

Lehrreich. Schaffung von Voraussetzungen für die erfolgreiche Beherrschung des Konzepts des beschriebenen Vierecks, seiner Eigenschaften, Merkmale und die Beherrschung der Fähigkeiten, diese in der Praxis anzuwenden.

Entwicklung. Entwicklung mathematischer Fähigkeiten, Schaffung von Voraussetzungen für die Fähigkeit, Vorwärts- und Rückwärtsgedanken zu verallgemeinern und anzuwenden.

Lehrreich. Den Sinn für Schönheit durch die Ästhetik der Zeichnungen kultivieren und das Ungewöhnliche überraschen

Entscheidung, Organisationsbildung, Verantwortung für die Ergebnisse der eigenen Arbeit.

1. Studieren Sie die Definition eines umschriebenen Vierecks.

2. Beweisen Sie die Eigenschaft der Seiten des umschriebenen Vierecks.

3. Führen Sie die Dualität der Eigenschaften der Summen gegenüberliegender Seiten und entgegengesetzter Winkel eingeschriebener und umschriebener Vierecke ein.

4. Vermittlung von Erfahrungen in der praktischen Anwendung der betrachteten Theoreme bei der Lösung von Problemen.

5. Führen Sie eine erste Überwachung des Assimilationsniveaus des neuen Materials durch.

Ausrüstung:

• Computer, Projektor;
• Lehrbuch „Geometrie. 10-11 Klassen“ für die Allgemeinbildung. Institutionen: Basis und Profil. automatische Ebenen EIN V. Pogorelow.

Software: Microsoft Word, Microsoft Power Punkt.

Verwendung eines Computers bei der Vorbereitung eines Lehrers auf eine Unterrichtsstunde.

Mit einem Standard-Windows-Betriebssystemprogramm wurde für den Unterricht Folgendes erstellt:

1. Präsentation.
2. Tische.
3. Blaupausen.
4. Handzettel.

Unterrichtsplan

Zeit organisieren. (2 Minuten.)

Hausaufgaben überprüfen. (5 Minuten.)

Neues Material lernen. (28 Min.)

Selbstständige Arbeit. (7 Min.)

Hausaufgaben.(1 Minute.)

Zusammenfassung der Lektion. (2 Minuten.)

Während des Unterrichts

1. Organisatorischer Moment. Grüße. Geben Sie das Thema und den Zweck der Lektion an. Notieren Sie Datum und Thema der Lektion in Ihrem Notizbuch.

2. Hausaufgaben überprüfen.

3. Neues Material studieren.

Arbeiten Sie am Konzept eines umschriebenen Polygons.

Definition. Das Polygon heißt beschriebenüber einen Kreis, wenn Alle seine Seiten Sorge irgendein Kreis.

Frage. Welche der vorgeschlagenen Polygone werden beschrieben und welche nicht und warum?

<Презентация. Слайд №2>

Beweis der Eigenschaften des umschriebenen Vierecks.

<Презентация. Слайд №3>

Satz. In einem umschriebenen Viereck sind die Summen der gegenüberliegenden Seiten gleich.

Die Studierenden arbeiten mit dem Lehrbuch und schreiben die Formulierung des Satzes in ein Notizbuch.

1. Präsentieren Sie die Formulierung des Theorems in Form eines Bedingungssatzes.

2. Was ist die Bedingung des Satzes?

3. Was ist die Schlussfolgerung des Theorems?

Antwort. Wenn ein Viereck wird um einen Kreis herum beschrieben, Das die Summen der gegenüberliegenden Seiten sind gleich.

Der Nachweis wird geführt, die Studierenden machen sich Notizen in ihren Heften.

<Презентация. Слайд №4>

Lehrer. Notiz Dualität Situationen für Seiten und Winkel von umschriebenen und eingeschriebenen Vierecken.

Festigung des erworbenen Wissens.

Aufgaben.

Die gegenüberliegenden Seiten des beschriebenen Vierecks betragen 8 m und 12 m. Ist es möglich, den Umfang zu finden?

Aufgaben basierend auf fertigen Zeichnungen.<Презентация. Слайд №5>

Antwort. 1. 10 m. 2. 20 m. 3. 21 m

Beweis der Charakteristik eines umschriebenen Vierecks.

Geben Sie den umgekehrten Satz an.

Antwort. Wenn in einem Viereck die Summen der gegenüberliegenden Seiten gleich sind, kann darin ein Kreis eingeschrieben werden. (Zurück zu Folie 2, Abb. 7) <Презентация. Слайд №2>

Lehrer. Klären Sie die Formulierung des Satzes.

Satz. Wenn die Summen der gegenüberliegenden Seiten konvex Wenn ein Viereck gleich ist, kann darin ein Kreis eingeschrieben werden.

Arbeiten mit dem Lehrbuch. Machen Sie sich mit dem Beweis des Tests für ein umschriebenes Viereck anhand des Lehrbuchs vertraut.

Anwendung des erworbenen Wissens.

3. Aufgaben basierend auf fertigen Zeichnungen.

1. Ist es möglich, einen Kreis in ein Viereck mit gegenüberliegenden Seiten von 9 m und 4 m, 10 m und 3 m einzuschreiben?

2. Ist es möglich, einem gleichschenkligen Trapez mit einer Grundfläche von 1 m und 9 m und einer Höhe von 3 m einen Kreis einzuschreiben?

<Презентация. Слайд №6>

Schriftliche Arbeit in Notizbüchern

.

Aufgabe. Finden Sie den Radius eines Kreises, der in eine Raute mit Diagonalen von 6 m und 8 m eingeschrieben ist.

<Презентация. Слайд № 7>

4. Selbstständiges Arbeiten.

1 Option

1. Ist es möglich, einen Kreis einzuschreiben?

1) in ein Rechteck mit den Seiten 7 m und 10 m,

2. Die gegenüberliegenden Seiten eines um einen Kreis umschriebenen Vierecks betragen 7 m und 10 m.

Finden Sie den Umfang des Vierecks.

3. Ein gleichseitiges Trapez mit den Grundflächen 4 m und 16 m wird um einen Kreis beschrieben.

1) Radius des eingeschriebenen Kreises,

Option 2

1. Ist es möglich, einen Kreis einzuschreiben:

1) in einem Parallelogramm mit den Seiten 6 m und 13 m,

2) im Quadrat?

2. Die gegenüberliegenden Seiten eines um einen Kreis umschriebenen Vierecks betragen 9 m und 11 m. Ermitteln Sie den Umfang des Vierecks.

3. Ein gleichseitiges Trapez mit einer Seitenlänge von 5 m wird um einen Kreis mit einem Radius von 2 m umschrieben.

1) die Basis des Trapezes,

2) Radius des umschriebenen Kreises.

5. Hausaufgaben. S.86, Nr. 28, 29, 30.

6. Zusammenfassung der Lektion. Die selbstständige Arbeit wird überprüft und benotet.

<Презентация. Слайд № 8>

"Kreis" Wir haben gesehen, dass ein Kreis um jedes Dreieck herum beschrieben werden kann. Das heißt, für jedes Dreieck gibt es einen Kreis, auf dem alle drei Eckpunkte des Dreiecks „sitzen“. So:

Frage: Lässt sich das Gleiche auch über ein Viereck sagen? Stimmt es, dass es immer einen Kreis geben wird, auf dem alle vier Eckpunkte des Vierecks „sitzen“?

Es stellt sich heraus, dass dies NICHT WAHR ist! Ein Viereck kann NICHT IMMER in einen Kreis eingeschrieben werden. Es gibt eine sehr wichtige Bedingung:

Auf unserem Bild:

.

Schauen Sie, die Winkel und liegen einander gegenüber, das heißt, sie sind entgegengesetzt. Was ist dann mit den Winkeln und? Scheinen sie auch Gegensätze zu sein? Ist es möglich, Winkel und anstelle von Winkeln und zu nehmen?

Natürlich kannst du! Die Hauptsache ist, dass das Viereck zwei entgegengesetzte Winkel hat, deren Summe gleich ist. Die verbleibenden zwei Winkel addieren sich dann ebenfalls von selbst. Glaubst du nicht? Stellen wir sicher. Sehen:

Lassen. Erinnern Sie sich an die Summe aller vier Winkel eines Vierecks? Sicherlich, . Das heißt – immer! . Aber, → .

Da ist Magie!

Denken Sie also genau daran:

Wenn ein Viereck in einen Kreis eingeschrieben ist, dann ist die Summe zweier seiner entgegengesetzten Winkel gleich

umgekehrt:

Wenn ein Viereck zwei entgegengesetzte Winkel hat, deren Summe gleich ist, dann ist das Viereck zyklisch.

Wir werden dies alles hier nicht beweisen (bei Interesse schauen Sie sich die nächsten Theorieebenen an). Aber sehen wir uns an, wozu diese bemerkenswerte Tatsache führt: dass in einem eingeschriebenen Viereck die Summe der entgegengesetzten Winkel gleich ist.

Mir kommt zum Beispiel die Frage in den Sinn: Ist es möglich, einen Kreis um ein Parallelogramm zu beschreiben? Probieren wir zunächst die „Poke-Methode“ aus.

Irgendwie klappt es nicht.

Wenden wir nun das Wissen an:

Nehmen wir an, wir hätten es irgendwie geschafft, einen Kreis auf ein Parallelogramm zu passen. Dann muss es auf jeden Fall sein: , das heißt.

Erinnern wir uns nun an die Eigenschaften eines Parallelogramms:

Jedes Parallelogramm hat gleiche entgegengesetzte Winkel.

Es stellte sich heraus, dass

Was ist mit den Winkeln und? Naja, natürlich das Gleiche.

Beschriftet → →

Parallelogramm→ →

Erstaunlich, oder?

Es stellt sich heraus, dass, wenn ein Parallelogramm in einen Kreis eingeschrieben ist, alle seine Winkel gleich sind, das heißt, es ist ein Rechteck!

Und gleichzeitig - Der Mittelpunkt des Kreises fällt mit dem Schnittpunkt der Diagonalen dieses Rechtecks ​​zusammen. Dies ist sozusagen als Bonus enthalten.

Nun, das heißt, wir haben herausgefunden, dass ein in einen Kreis eingeschriebenes Parallelogramm so ist Rechteck.

Lassen Sie uns nun über das Trapez sprechen. Was passiert, wenn ein Trapez in einen Kreis eingeschrieben ist? Aber es stellt sich heraus, dass es so sein wird gleichschenkliges Trapez . Warum?

Das Trapez sei in einen Kreis eingeschrieben. Andererseits aber aufgrund der Parallelität der Linien und.

Das bedeutet: → → gleichschenkliges Trapez.

Noch einfacher als mit einem Rechteck, oder? Aber Sie müssen sich genau daran erinnern – es wird sich als nützlich erweisen:

Lassen Sie uns die wichtigsten noch einmal auflisten Hauptaussagen Tangente an ein in einen Kreis eingeschriebenes Viereck:

1. Ein Viereck ist genau dann in einen Kreis eingeschrieben, wenn die Summe seiner beiden gegenüberliegenden Winkel gleich ist
2. Ein in einen Kreis eingeschriebenes Parallelogramm – auf jeden Fall Rechteck und der Mittelpunkt des Kreises fällt mit dem Schnittpunkt der Diagonalen zusammen
3. Ein in einen Kreis eingeschriebenes Trapez ist gleichseitig.

Beschriftetes Viereck. Durchschnittsniveau

Es ist bekannt, dass es zu jedem Dreieck einen umschriebenen Kreis gibt (das haben wir im Thema „Der umschriebene Kreis“ bewiesen). Was lässt sich über das Viereck sagen? Es stellt sich heraus, dass NICHT JEDES Viereck kann in einen Kreis eingeschrieben werden, und es gibt einen solchen Satz:

Ein Viereck ist genau dann in einen Kreis eingeschrieben, wenn die Summe seiner entgegengesetzten Winkel gleich ist.

In unserer Zeichnung -

Versuchen wir zu verstehen, warum das so ist? Mit anderen Worten, wir werden diesen Satz nun beweisen. Aber bevor Sie es beweisen, müssen Sie verstehen, wie die Aussage selbst funktioniert. Sind Ihnen die Worte „dann und nur dann“ in der Aussage aufgefallen? Solche Worte bedeuten, dass schädliche Mathematiker zwei Aussagen in eine gepackt haben.

Lassen Sie uns entschlüsseln:

1. „Dann“ bedeutet: Wenn ein Viereck in einen Kreis eingeschrieben ist, dann ist die Summe zweier seiner gegenüberliegenden Winkel gleich.
2. „Nur dann“ bedeutet: Wenn ein Viereck zwei entgegengesetzte Winkel hat, deren Summe gleich ist, dann kann ein solches Viereck in einen Kreis eingeschrieben werden.

Genau wie Alice: „Ich denke, was ich sage“ und „Ich sage, was ich denke.“

Lassen Sie uns nun herausfinden, warum sowohl 1 als auch 2 wahr sind.

Erster 1.

Ein Viereck sei in einen Kreis einbeschrieben. Markieren wir seinen Mittelpunkt und zeichnen wir die Radien und. Was wird passieren? Erinnern Sie sich, dass ein eingeschriebener Winkel halb so groß ist wie der entsprechende Zentralwinkel? Wenn Sie sich erinnern, verwenden wir es jetzt, und wenn nicht, werfen Sie einen Blick auf das Thema "Kreis. Beschrifteter Winkel".

Beschriftet

Beschriftet

Aber schau: .

Wir bekommen das, wenn - dann eingeschrieben ist

Nun, es ist klar, dass es auch passt. (wir müssen auch darüber nachdenken).

Nun „umgekehrt“, also 2.

Es stellt sich heraus, dass in einem Viereck die Summe zweier entgegengesetzter Winkel gleich ist. Sagen wir mal, lass

Wir wissen noch nicht, ob wir einen Kreis um ihn herum beschreiben können. Aber wir wissen mit Sicherheit, dass wir garantiert in der Lage sind, einen Kreis um ein Dreieck zu beschreiben. Also machen wir's.

Wenn ein Punkt nicht auf dem Kreis „sitzt“, landet er zwangsläufig entweder außerhalb oder innerhalb des Kreises.

Betrachten wir beide Fälle.

Lassen Sie den Punkt zunächst außen liegen. Dann schneidet das Segment irgendwann den Kreis. Lasst uns verbinden und. Das Ergebnis ist ein beschriftetes (!) Viereck.

Wir wissen bereits darüber, dass die Summe seiner entgegengesetzten Winkel gleich ist, und zwar gemäß unserer Bedingung.

Es stellt sich heraus, dass es so sein sollte.

Dies kann jedoch unmöglich der Fall sein, da - ein äußerer Gesichtspunkt und ein Mittel ist.

Was ist mit drinnen? Lasst uns ähnliche Dinge tun. Lassen Sie den Punkt im Inneren liegen.

Dann schneidet die Fortsetzung des Segments den Kreis in einem Punkt. Wiederum - ein eingeschriebenes Viereck, und je nach Bedingung muss es erfüllt sein, aber - ein äußerer Winkel für und bedeutet, das heißt, das kann wiederum nicht sein.

Das heißt, ein Punkt kann weder außerhalb noch innerhalb des Kreises liegen – er liegt also auf dem Kreis!

Der ganze Satz ist bewiesen!

Sehen wir uns nun an, welche guten Konsequenzen dieser Satz hat.

Folgerung 1

Ein in einen Kreis eingeschriebenes Parallelogramm kann nur ein Rechteck sein.

Lassen Sie uns verstehen, warum das so ist. Ein Parallelogramm sei in einen Kreis eingeschrieben. Dann sollte es erledigt sein.

Aber aus den Eigenschaften eines Parallelogramms wissen wir das.

Und das Gleiche gilt natürlich auch für die Winkel und.

Es entsteht also ein Rechteck – alle Ecken liegen aneinander.

Darüber hinaus gibt es aber noch eine weitere erfreuliche Tatsache: Der Mittelpunkt des um das Rechteck umschriebenen Kreises fällt mit dem Schnittpunkt der Diagonalen zusammen.

Lassen Sie uns verstehen, warum. Ich hoffe, Sie erinnern sich noch genau daran, dass der durch den Durchmesser begrenzte Winkel eine gerade Linie ist.

Durchmesser,

Durchmesser

was bedeutet, dass es das Zentrum ist. Das ist alles.

Folgerung 2

Ein in einen Kreis eingeschriebenes Trapez ist gleichschenklig.

Das Trapez sei in einen Kreis eingeschrieben. Dann.

Und auch.

Haben wir alles besprochen? Nicht wirklich. Tatsächlich gibt es eine andere, „geheime“ Möglichkeit, ein eingeschriebenes Viereck zu erkennen. Wir werden diese Methode nicht sehr streng (aber klar) formulieren, sondern sie erst auf der letzten Ebene der Theorie beweisen.

Wenn man in einem Viereck ein solches Bild wie hier in der Abbildung beobachten kann (hier sind die auf die Seite der Punkte „blickenden“ Winkel gleich), dann ist ein solches Viereck eingeschrieben.

Dies ist eine sehr wichtige Zeichnung – bei Problemen ist sie oft leichter zu finden gleiche Winkel, als die Summe der Winkel und.

Trotz des völligen Mangels an Genauigkeit in unserer Formulierung ist sie korrekt und wird darüber hinaus von den Prüfern des Einheitlichen Staatsexamens stets akzeptiert. Sie sollten etwa Folgendes schreiben:

„- beschriftet“ – und alles wird gut!

Vergessen Sie dieses wichtige Zeichen nicht – merken Sie sich das Bild, dann fällt es Ihnen vielleicht rechtzeitig bei der Lösung des Problems ins Auge.

Beschriftetes Viereck. Kurzbeschreibung und Grundformeln

Wenn ein Viereck in einen Kreis eingeschrieben ist, dann ist die Summe zweier seiner entgegengesetzten Winkel gleich

umgekehrt:

Wenn ein Viereck zwei entgegengesetzte Winkel hat, deren Summe gleich ist, dann ist das Viereck zyklisch.

Ein Viereck ist genau dann in einen Kreis eingeschrieben, wenn die Summe seiner beiden gegenüberliegenden Winkel gleich ist.

In einen Kreis eingeschriebenes Parallelogramm- sicherlich ein Rechteck, und der Mittelpunkt des Kreises fällt mit dem Schnittpunkt der Diagonalen zusammen.

Ein in einen Kreis eingeschriebenes Trapez ist gleichschenklig.