Rezistența la încovoiere transversală. Conceptul de deformare la încovoiere
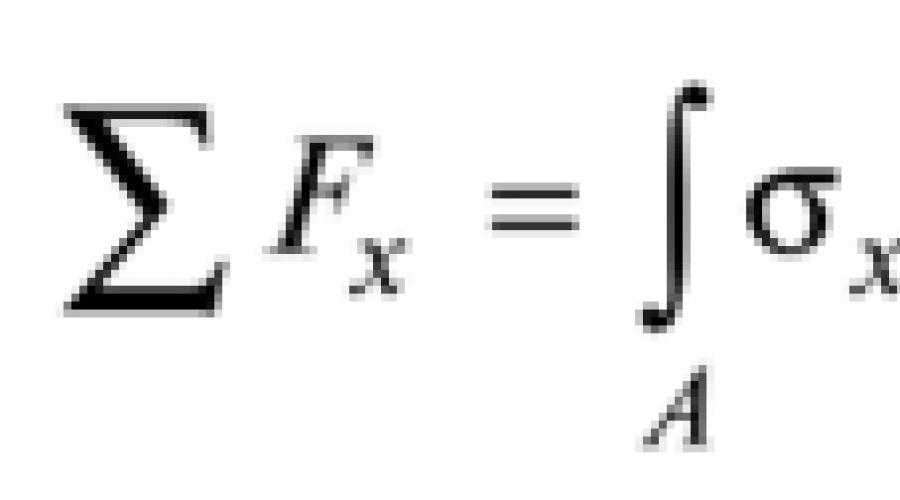
Citeste si
îndoire dreaptă este un tip de deformare în care în secțiunile transversale ale tijei apar doi factori de forță interni: momentul încovoietor și forta bruta.
Curăță curbă- acesta este un caz special de încovoiere directă, în care în secțiunile transversale ale tijei apare doar un moment de încovoiere, iar forța transversală este zero.
Un exemplu de îndoire pură - o secțiune CD pe tija AB. Momentul de îndoire este cantitatea Pa o pereche de forțe externe care provoacă încovoiere. De la echilibrul părții tijei din stânga secțiunii transversale mn rezultă că forţele interne distribuite pe această secţiune sunt echivalente static cu momentul M, egal și opus momentului încovoietor Pa.
Pentru a găsi distribuția acestor forțe interne pe secțiunea transversală, este necesar să se ia în considerare deformarea tijei.
În cel mai simplu caz, tija are un plan longitudinal de simetrie și este supusă acțiunii perechilor de forțe exterioare de îndoire situate în acest plan. Apoi îndoirea va avea loc în același plan.
Axa tijei nn 1 este o linie care trece prin centrele de greutate ale secțiunilor sale transversale.
Fie ca secțiunea transversală a tijei să fie un dreptunghi. Să desenăm două linii verticale pe marginile sale mmȘi pp. La îndoire, aceste linii rămân drepte și se rotesc astfel încât să rămână perpendiculare pe fibrele longitudinale ale tijei.
O altă teorie a îndoirii se bazează pe presupunerea că nu numai linii mmȘi pp, dar întreaga secțiune transversală plană a tijei rămâne, după îndoire, plată și normală cu fibrele longitudinale ale tijei. Prin urmare, în timpul îndoirii, secțiunile transversale mmȘi pp rotiți unul față de celălalt în jurul axelor perpendiculare pe planul de îndoire (planul de desenare). În acest caz, fibrele longitudinale de pe partea convexă suferă tensiune, iar fibrele de pe partea concavă experimentează compresie.
Suprafata neutra- Aceasta este o suprafață care nu suferă deformare la îndoire. (Acum este situat perpendicular pe desen, axa deformată a tijei nn 1 aparține acestei suprafețe).
Axa neutră a secțiunii- aceasta este intersecția unei suprafețe neutre cu orice secțiune transversală (acum situată și perpendicular pe desen).
Lasă o fibră arbitrară să fie la distanță y de pe o suprafață neutră. ρ – raza de curbură a axei curbe. Punct O– centrul de curbură. Să tragem o linie n 1 s 1 paralel mm.ss 1– alungirea absolută a fibrei.
Extensie relativă εx fibre
Rezultă că deformarea fibrelor longitudinale proporțională cu distanța y de la suprafața neutră și invers proporțională cu raza de curbură ρ .
Alungirea longitudinală a fibrelor laturii convexe a tijei este însoțită de îngustarea laterală, iar scurtarea longitudinală a laturii concave este expansiunea laterală, ca și în cazul întinderii și compresiei simple. Din această cauză, aspectul tuturor secțiunilor transversale se modifică, laturile verticale ale dreptunghiului devin înclinate. Deformare laterală z:
μ - Coeficientul lui Poisson.
Datorită acestei distorsiuni, toate liniile drepte în secțiune transversală sunt paralele cu axa z, sunt îndoite astfel încât să rămână normale față de laturile laterale ale secțiunii. Raza de curbură a acestei curbe R va fi mai mult decât ρ în acelaşi sens ca ε x în valoare absolută este mai mare decât ε z și obținem
Aceste deformații ale fibrelor longitudinale corespund solicitărilor
Tensiunea din orice fibră este proporțională cu distanța acesteia față de axa neutră n 1 n 2. Poziția axei neutre și raza de curbură ρ – două necunoscute în ecuația pentru σ x – poate fi determinat din condiția ca forțele distribuite pe orice secțiune transversală formează o pereche de forțe care echilibrează momentul extern M.
Toate cele de mai sus sunt valabile si daca tija nu are un plan longitudinal de simetrie in care actioneaza momentul incovoietor, atata timp cat momentul incovoietor actioneaza in planul axial, care contine unul dintre cele doua axele principale secțiune transversală. Aceste avioane sunt numite planurile principale de îndoire.
Când există un plan de simetrie și momentul încovoietor acționează în acest plan, deviația are loc tocmai în el. Momentele forțelor interne în raport cu axa z echilibrează momentul exterior M. Momente de efort în jurul axei y sunt distruse reciproc.
Forțele care acționează perpendicular pe axa grinzii și situate într-un plan care trece prin această axă provoacă o deformare numită încovoiere transversală. Dacă planul de acţiune al forţelor menţionate – planul principal, apoi are loc o îndoire transversală dreaptă (plată). În caz contrar, îndoirea se numește transversal oblic. O grindă care este supusă predominant îndoirii se numește grindă 1 .
În esență, îndoirea transversală este o combinație de îndoire pură și forfecare. În legătură cu curbura secțiunilor transversale din cauza distribuției neuniforme a forfecelor de-a lungul înălțimii, se pune întrebarea cu privire la posibilitatea utilizării formulei normale a tensiunii σ X, derivat pentru îndoire pură pe baza ipotezei secțiunilor plane.
1 O grindă cu o singură travă, având la capete, respectiv, un suport cilindric fix și unul cilindric mobil în direcția axei grinzii, se numește simplu. Se numește o grindă cu un capăt prins și celălalt liber consolă. Se numește o grindă simplă având una sau două părți atârnând peste un suport consolă.
Dacă, în plus, secțiunile sunt luate departe de locurile în care este aplicată sarcina (la o distanță nu mai mică de jumătate din înălțimea secțiunii grinzii), atunci se poate presupune, ca și în cazul îndoirii pure, ca fibrele să nu exercite presiune unele asupra altora. Aceasta înseamnă că fiecare fibră experimentează tensiune sau compresie uniaxiale.
Sub acțiunea unei sarcini distribuite, forțele transversale din două secțiuni adiacente vor diferi cu o valoare egală cu qdx. Prin urmare, curbura secțiunilor va fi, de asemenea, ușor diferită. În plus, fibrele vor exercita presiune unele asupra altora. Un studiu amănunțit al problemei arată că dacă lungimea fasciculului l destul de mare în comparație cu înălțimea sa h (l/ h> 5), atunci chiar și cu o sarcină distribuită, acești factori nu au un efect semnificativ asupra tensiunilor normale în secțiune transversalăși prin urmare nu pot fi luate în considerare în calculele practice.
a B C
Orez. 10.5 Fig. 10.6
În secțiuni sub sarcini concentrate și în apropierea acestora, distribuția lui σ X se abate de la legea liniară. Această abatere este de natură locală și nu este însoțită de o creștere cel mai mare stres(în fibrele extreme), în practică de obicei nu sunt luate în considerare.
Astfel, cu îndoire transversală (în plan X y) tensiunile normale se calculează folosind formula
σ X= – [M z(X)/Iz]y.
Dacă desenăm două secțiuni adiacente pe o secțiune a grinzii care este liberă de sarcină, atunci forța transversală în ambele secțiuni va fi aceeași și, prin urmare, curbura secțiunilor va fi aceeași. În acest caz, orice bucată de fibră ab(Fig. 10.5) se va muta într-o nouă poziție a"b", fără a suferi o alungire suplimentară și, prin urmare, fără a modifica valoarea tensiunii normale.
Să determinăm tensiunile tangențiale în secțiune transversală prin tensiunile lor pereche care acționează în secțiunea longitudinală a grinzii.
Selectați un element de lungime din lemn dx(Fig. 10.7 a). Să desenăm o secțiune orizontală la distanță la din axa neutră z, împărțind elementul în două părți (Fig. 10.7) și luați în considerare echilibrul părții superioare, care are o bază
lăţime b. În conformitate cu legea împerecherii tensiunilor tangențiale, tensiunile care acționează în secțiunea longitudinală sunt egale cu tensiunile care acționează în secțiunea transversală. Ținând cont de acest lucru, în ipoteza că solicitările de forfecare în șantier b distribuit uniform, folosind condiția ΣХ = 0, obținem:
N * - (N * +dN *)+
unde: N * este rezultanta forțelor normale σ în secțiunea transversală din stânga a elementului dx în zona „decupată” A * (Fig. 10.7 d):
unde: S = - momentul static al părții „decupate” a secțiunii transversale (zona umbrită în Fig. 10.7 c). Prin urmare, putem scrie:
Apoi putem scrie:
Această formulă a fost obținută în secolul al XIX-lea de către savantul și inginerul rus D.I. Zhuravsky și îi poartă numele. Și deși această formulă este aproximativă, deoarece face media tensiunii pe lățimea secțiunii, rezultatele calculelor obținute din aceasta sunt în bună concordanță cu datele experimentale.
Pentru a determina tensiunile de forfecare la un punct arbitrar de secțiune transversală situat la o distanță y de axa z, ar trebui:
Determinați din diagramă mărimea forței transversale Q care acționează în secțiune;
Calculați momentul de inerție I z al întregii secțiuni;
Desenați un plan paralel cu planul prin acest punct xzși determinați lățimea secțiunii b;
Calculați momentul static al zonei tăiate S în raport cu axa centrală principală zși înlocuiți valorile găsite în formula Zhuravsky.
Să determinăm, ca exemplu, tensiunile tangenţiale într-o secţiune transversală dreptunghiulară (Fig. 10.6, c). Moment static în jurul axei z părțile secțiunii de deasupra liniei 1-1, pe care se determină tensiunea, se vor scrie sub forma:
Acesta variază conform legii unei parabole pătrate. Lățimea secțiunii V pentru că o grindă dreptunghiulară este constantă, atunci legea modificării tensiunilor tangenţiale în secţiune va fi şi parabolică (Fig. 10.6, c). La y = și y = − tensiunile tangenţiale sunt nule, iar pe axa neutră z ele ating cea mai mare valoare.
Pentru o grindă cu secțiune transversală circulară pe axa neutră avem.
Curăță curbă Acest tip de îndoire se numește în care are loc acțiunea numai moment de încovoiere(Fig. 3.5, A). Să desenăm mental planul de secțiune I-I perpendicular pe axa longitudinală a grinzii la o distanță * de capătul liber al grinzii la care se aplică momentul exterior m z . Să realizăm acțiuni similare cu cele pe care le-am efectuat la determinarea tensiunilor și deformațiilor în timpul torsiunei și anume:
- 1) să întocmim ecuații de echilibru pentru partea decupată mental a piesei;
- 2) determinăm deformarea materialului piesei pe baza condițiilor de compatibilitate a deformațiilor volumelor elementare ale unei secțiuni date;
- 3) rezolvarea ecuaţiilor de echilibru şi compatibilitate a deformaţiilor.
Din starea de echilibru a secțiunii tăiate a grinzii (Fig. 3.5, b)
constatăm că momentul forţelor interne Mz egal cu momentul forţelor exterioare t: M = t.
Orez. 3.5.
Momentul forțelor interne este creat de solicitările normale o v direcționate de-a lungul axei x. La îndoire pură nu există forțe externe, prin urmare suma proiecțiilor forțelor interne pe orice axă de coordonate este zero. Pe această bază, scriem condițiile de echilibru sub formă de egalități
Unde A- zona secțiunii transversale a grinzii (tijă).
În îndoire pură, forțe externe Fx, F, Fv precum şi momente de forţe exterioare t x, t y sunt egale cu zero. Prin urmare, ecuațiile de echilibru rămase sunt identic egale cu zero.
Din starea de echilibru  când o^O rezultă că
când o^O rezultă că
tensiune normală c xîn secțiune transversală, atât pozitivă cât și valori negative. (Experiența arată că la îndoire, materialul părții inferioare a grinzii din Fig. 3.5, Aîntins, iar cel superior este comprimat.) În consecință, în secțiunea transversală în timpul îndoirii există astfel de volume elementare (ale stratului de tranziție de la compresiune la tensiune) în care nu există alungire sau compresie. Acest - strat neutru. Se numește linia de intersecție a stratului neutru cu planul secțiunii transversale linie neutră.
Condițiile pentru compatibilitatea deformațiilor volumelor elementare în timpul îndoirii se formează pe baza ipotezei secțiunilor plate: secțiunile transversale ale grinzii sunt plate înainte de îndoire (vezi Fig. 3.5, b) va rămâne plat chiar și după îndoire (Fig. 3.6).
Ca urmare a acțiunii unui moment exterior, fasciculul se îndoaie și planurile secțiunile I-Iși II-II se rotesc unul față de celălalt cu un unghi dy(Fig. 3.6, b).În curbarea pură, deformația tuturor secțiunilor de-a lungul axei grinzii este aceeași, prin urmare raza pk de curbură a stratului neutru al grinzii de-a lungul axei x este aceeași. Deoarece dx= p K dip, atunci curbura stratului neutru este egală cu 1 / p k = scufundare / dxși este constantă pe toată lungimea fasciculului.
Stratul neutru nu este deformat; lungimea sa înainte și după deformare este egală cu dx. Sub acest strat materialul este întins, deasupra este comprimat.

Orez. 3.6.
Valoarea de alungire a stratului intins situat la distanta y de cel neutru este egala cu ydq. Alungirea relativă a acestui strat:
Astfel, în modelul adoptat, se obține o distribuție liniară a deformațiilor în funcție de distanța unui volum elementar dat la stratul neutru, adică. de-a lungul înălțimii secțiunii grinzii. Presupunând că nu există o presiune reciprocă a straturilor paralele de material unul asupra celuilalt (o y = 0, a, = 0), scriem legea lui Hooke pentru întinderea liniară:
Conform (3.13), tensiunile normale în secțiunea transversală a grinzii sunt distribuite după o lege liniară. Tensiunea volumului elementar al materialului cel mai îndepărtat de stratul neutru (Fig. 3.6, V), maxim și egal ![]()
? Problema 3.6
Determinați limita elastică a unei lame de oțel cu grosimea / = 4 mm și lungimea / = 80 cm, dacă îndoirea acesteia în semicerc nu provoacă deformare reziduală.
Soluţie
Tensiunea la încovoiere o v = Ei/ r k. Să luăm y max = t/ 2i r k = / / La.
Limita elastică trebuie să corespundă condiției cu уп > c v = 1 / 2 kE t /1.
Raspuns: o = ] / 2 la 2 10 11 4 10 _3 / 0,8 = 1570 MPa; Limita de curgere a acestui oțel este a t > 1800 MPa, care depășește a t a celor mai rezistente oțeluri cu arc. ?
? Problema 3.7
Determinați raza minimă a tamburului pentru înfășurarea unei benzi cu o grosime de / = 0,1 mm a unui element de încălzire dintr-un aliaj de nichel, la care materialul benzii nu este deformat plastic. Modul E= 1,6 10 5 MPa, limită elastică aproximativ yp = 200 MPa.
Răspuns: raza minima р = V 2 ?ir/a yM = У? 1,6-10 11 0,1 10 -3 / (200 10 6) = = 0,04 m?
1. Rezolvând împreună prima ecuație de echilibru (3.12) și ecuația de compatibilitate a deformațiilor (3.13), obținem 
Sens E/ r k φ 0 și același pentru toate elementele dA zone de integrare. În consecință, această egalitate este satisfăcută numai cu condiția

Această integrală se numește momentul static al ariei secțiunii transversale în jurul axeiz? Ce sens fizic această integrală?
Să luăm o placă de grosime constantă /, dar un profil arbitrar (Fig. 3.7). Să atârnăm această farfurie într-un punct CU astfel încât să fie în poziție orizontală. Să notăm cu simbolul y m gravitație specifică materialul plăcii, apoi greutatea volumului elementar cu suprafață dA egală dq= y JdA. Deoarece placa este într-o stare de echilibru, atunci de la egalitatea la zero a proiecțiilor forțelor pe axă la primim

Unde G= y M tA- greutatea înregistrării.

Orez. 3.7.
Suma momentelor forțelor tuturor forțelor în jurul axei z trecerea prin orice secțiune a plăcii este, de asemenea, zero:

Având în vedere că Y c = G, hai sa scriem
Astfel, dacă o integrală de forma J xdA după zonă A egală
zero, atunci x c = 0. Aceasta înseamnă că punctul C coincide cu centrul de greutate al plăcii. Prin urmare, din egalitate S z = J ydA = 0 când scade
la îndoire rezultă că centrul de greutate al secțiunii transversale a fasciculului se află pe linia neutră.
Prin urmare, valoarea y s secțiunea transversală a fasciculului este zero.
- 1. Linia neutră în timpul îndoirii trece prin centrul de greutate al secțiunii transversale a grinzii.
- 2. Centrul de greutate al secțiunii transversale este centrul de reducere al momentelor forțelor externe și interne.
Problema 3.8
Problema 3.9
2. Rezolvând împreună a doua ecuație de echilibru (3.12) și ecuația de compatibilitate a deformațiilor (3.13), obținem

Integral J z= J y 2 dA numit momentul de inerție al transversalei
secțiunea grinzii (tijă) în raport cu axa z, trecând prin centrul de greutate al secțiunii transversale.
Prin urmare, M z = E J z / r k. Având în vedere că c x = Ee x = Ey/ r k i E/ r k = un x / y, obţinem dependenţa tensiunilor normale Oh la îndoire:
1. Efortul de încovoiere într-un punct dat al secțiunii nu depinde de modulul elastic normal E, dar depinde de parametrul geometric al secțiunii transversale J zși distanțe la dintr-un punct dat până la centrul de greutate al secțiunii transversale.
2. Efortul maxim de încovoiere apare în volumele elementare cele mai îndepărtate de linia neutră (vezi Fig. 3.6, V):
Unde W z- momentul de rezistenţă al secţiunii transversale faţă de ax Z-
Condiția de rezistență la îndoire pură este similară cu condiția de rezistență la tensiune liniară:
unde [a m | - efortul de încovoiere admisibil.
Este evident că volumele interne ale materialului, în special în apropierea axei neutre, practic nu sunt încărcate (vezi Fig. 3.6, V). Acest lucru contrazice cerința de a minimiza consumul de material al structurii. Mai jos vom arăta câteva modalități de a depăși această contradicție.
Cu îndoire dreaptă pură în secțiunea transversală a tijei, doar una factor de putere momentul de îndoire M x(Fig. 1). Deoarece Q y =dM x /dz=0, Acea M x=const și îndoirea dreaptă pură pot fi realizate atunci când tija este încărcată cu perechi de forțe aplicate în secțiunile de capăt ale tijei. De la momentul încovoietor M x prin definiţie egală cu suma momentelor forţelor interne raportate la axă Oh este legat de tensiunile normale prin ecuația statică care reiese din această definiție
Să formulăm premisele teoriei curbei drepte pure a unei tije prismatice. Pentru a face acest lucru, să analizăm deformațiile unui model de tijă din material cu modul redus, pe suprafața laterală a căruia este aplicată o grilă de semne longitudinale și transversale (Fig. 2). Deoarece riscurile transversale atunci când tija este îndoită de perechi de forțe aplicate în secțiunile de capăt rămân drepte și perpendiculare pe riscurile longitudinale curbate, acest lucru ne permite să concluzionam că ipotezele secțiunii plane, care, după cum arată rezolvarea acestei probleme folosind metodele teoriei elasticității, încetează să mai fie o ipoteză, devenind un fapt exact. legea secțiunilor plane. Măsurând modificarea distanțelor dintre riscurile longitudinale, ajungem la concluzia că ipoteza despre nepresiunea fibrelor longitudinale este valabilă.
Ortogonalitatea zgârieturilor longitudinale și transversale înainte și după deformare (ca reflectare a acțiunii legii secțiunilor plane) indică, de asemenea, absența forfecării și a tensiunilor tangențiale în secțiunile transversale și longitudinale ale tijei.

Fig.1. Relația dintre efortul intern și tensiune 
Fig.2. Model pur îndoit
Astfel, îndoirea dreaptă pură a unei tije prismatice este redusă la tensiune uniaxială sau compresie a fibrelor longitudinale prin tensiuni (indice G o vom omite în cele ce urmează). În acest caz, o parte din fibre se află în zona de tensiune (în Fig. 2 acestea sunt fibrele inferioare), iar cealaltă parte este în zona de compresie (fibre superioare). Aceste zone sunt separate printr-un strat neutru (pp), nu își schimbă lungimea, tensiunea la care este zero. Luând în considerare premisele formulate mai sus și presupunând că materialul tijei este liniar elastic, adică legea lui Hooke în acest caz are forma: , Să derivăm formule pentru curbura stratului neutru (raza de curbură) și tensiunile normale. Să remarcăm mai întâi că constanța secțiunii transversale a tijei prismatice și momentul încovoietor (M x =const), asigură raza de curbură constantă a stratului neutru de-a lungul lungimii tijei (Fig. 3, A), strat neutru (pp) descrisă de un arc de cerc.
Să considerăm o tijă prismatică în condiții de îndoire pură directă (Fig. 3, a) cu o secțiune transversală simetrică față de axa verticală OU. Această condiție nu va afecta rezultatul final (pentru ca îndoirea dreaptă să fie posibilă, axa trebuie să coincidă Oh s axa principală de inerție a secțiunii transversale, care este axa de simetrie). Axă Bou așezați-l pe un strat neutru, poziționați pe cine necunoscut dinainte.

A) schema de proiectare, b) încordare și stres
Fig.3. Fragment dintr-o curbă curată a fascicululuiLuați în considerare un element tăiat dintr-o tijă cu lungime dz, care este prezentat pe o scară cu proporții distorsionate de dragul clarității în Fig. 3, b. Întrucât deformațiile elementului, determinate de deplasarea relativă a punctelor sale, prezintă interes, una dintre secțiunile de capăt ale elementului poate fi considerată staționară. Datorită micii lor, presupunem că punctele secțiunii transversale, atunci când sunt rotite de acest unghi, se mișcă nu de-a lungul arcelor, ci de-a lungul tangentelor corespunzătoare.
Să calculăm deformația relativă a fibrei longitudinale AB, distanțate de stratul neutru de y:
Din asemănarea triunghiurilor C00 1Și 0 1 BB 1 urmează că
Deformarea longitudinală s-a dovedit a fi funcție liniară distanța față de stratul neutru, care este o consecință directă a legii secțiunilor plane
Această formulă nu este potrivită pentru uz practic, deoarece conține două necunoscute: curbura stratului neutru și poziția axei neutre Oh, de la care se măsoară coordonatele u. Pentru a determina aceste necunoscute, vom folosi ecuațiile de echilibru ale staticii. Prima exprimă cerința ca forța longitudinală să fie egală cu zero
|
Înlocuind expresia (2) în această ecuație
și ținând cont de asta, obținem asta
Integrala din partea stângă a acestei ecuații reprezintă momentul static al secțiunii transversale a tijei în jurul axei neutre Oh, care poate fi zero doar în raport cu axa centrală. Prin urmare axa neutră Oh trece prin centrul de greutate al secțiunii transversale.
A doua ecuație de echilibru static este una care relaționează tensiunile normale cu momentul încovoietor (care poate fi ușor exprimat în termeni de forțe externe și, prin urmare, este considerat o valoare dată). Înlocuind expresia pentru în ecuația de copula. tensiuni, obținem:
![]()
și având în vedere că ![]() Unde J x momentul central principal de inerție față de axă Oh, pentru curbura stratului neutru obținem formula
Unde J x momentul central principal de inerție față de axă Oh, pentru curbura stratului neutru obținem formula

Fig.4. Distribuția normală a tensiunilor
care a fost obținut pentru prima dată de C. Coulomb în 1773. Pentru a coordona semnele momentului încovoietor M xși tensiuni normale, un semn minus este plasat în partea dreaptă a formulei (5), de când M x >0 tensiuni normale la y>0 se dovedesc a fi compresive. Cu toate acestea, în calculele practice, este mai convenabil, fără a adera la regula formală a semnelor, să se determine tensiunea prin valoare absolută și să se atribuie semnul în funcție de sensul său. Tensiunile normale în timpul îndoirii pure a unei tije prismatice sunt o funcție liniară a coordonatei lași ajunge cele mai mari valoriîn fibrele cele mai îndepărtate de axa neutră (Fig. 4), adică.
![]()
Aici este introdusă caracteristica geometrică ![]() , având o dimensiune de m 3 și numită momentul încovoietor de rezistență. Din moment ce pentru un dat M x Voltaj max? cu cât mai puțin, cu atât mai mult Wx, momentul de rezistență este caracteristică geometrică a rezistenței la încovoiere a secțiunii transversale. Să dăm exemple de calculare a momentelor de rezistență pentru cele mai simple forme de secțiuni transversale. Pentru o secțiune transversală dreptunghiulară (Fig. 5, A) avem J x =bh 3 /12,y max = h/2Și W x = J x /y max = bh 2 /6.În mod similar, pentru un cerc (Fig. 5 ,a J x =d 4 /64, y max =d/2) primim W x =d 3/32, pentru o secțiune circulară inelară (Fig. 5, V), care
, având o dimensiune de m 3 și numită momentul încovoietor de rezistență. Din moment ce pentru un dat M x Voltaj max? cu cât mai puțin, cu atât mai mult Wx, momentul de rezistență este caracteristică geometrică a rezistenței la încovoiere a secțiunii transversale. Să dăm exemple de calculare a momentelor de rezistență pentru cele mai simple forme de secțiuni transversale. Pentru o secțiune transversală dreptunghiulară (Fig. 5, A) avem J x =bh 3 /12,y max = h/2Și W x = J x /y max = bh 2 /6.În mod similar, pentru un cerc (Fig. 5 ,a J x =d 4 /64, y max =d/2) primim W x =d 3/32, pentru o secțiune circulară inelară (Fig. 5, V), care
Pentru a reprezenta vizual natura deformării grinzilor (tijelor) în timpul îndoirii, se efectuează următorul experiment. Pe fețele laterale ale unei grinzi de cauciuc cu secțiune transversală dreptunghiulară se aplică o rețea de linii paralele și perpendiculare pe axa grinzii (Fig. 30.7, a). Apoi se aplică momente grinzii la capetele acesteia (Fig. 30.7, b), acționând în planul de simetrie al grinzii, intersectând fiecare dintre secțiunile sale transversale de-a lungul uneia dintre principalele axe centrale de inerție. Planul care trece prin axa grinzii și una dintre principalele axe centrale de inerție ale fiecăreia dintre secțiunile sale transversale va fi numit plan principal.
Sub influența momentelor, fasciculul experimentează o îndoire dreaptă pură. Ca urmare a deformării, după cum arată experiența, liniile grilei paralele cu axa grinzii sunt îndoite, păstrând aceleași distanțe între ele. Când este indicat în fig. 30.7, b în direcția momentelor, aceste linii din partea superioară a grinzii sunt prelungite, iar în partea inferioară sunt scurtate.
Fiecare linie de grilă perpendiculară pe axa fasciculului poate fi considerată ca o urmă a planului unei secțiuni transversale a fasciculului. Deoarece aceste linii rămân drepte, se poate presupune că secțiunile transversale ale grinzii, plate înainte de deformare, rămân plate în timpul deformării.
Această ipoteză, bazată pe experiență, este cunoscută ca ipoteza secțiunilor plane sau ipoteza lui Bernoulli (vezi § 6.1).
Ipoteza secțiunilor plane se aplică nu numai îndoirii pure, ci și îndoirii transversale. Pentru îndoirea transversală este aproximativă, iar pentru îndoirea pură este strictă, ceea ce este confirmat de studiile teoretice efectuate folosind metodele teoriei elasticității.

Să considerăm acum o grindă dreaptă cu o secțiune transversală simetrică față de axa verticală, încorporată la capătul drept și încărcată la capătul stâng cu un moment exterior care acționează într-unul din planurile principale ale grinzii (Fig. 31.7). În fiecare secțiune transversală a acestei grinzi, apar numai momente încovoietoare care acționează în același plan cu momentul

Astfel, fasciculul este într-o stare de îndoire dreaptă, pură pe toată lungimea sa. Secțiunile individuale ale grinzii pot fi într-o stare de încovoiere pură chiar dacă este supusă sarcinilor transversale; de exemplu, secțiunea 11 a grinzii prezentate în fig. prezintă îndoire pură. 32,7; în secţiunile acestei secţiuni forţa tăietoare
Din grinda luată în considerare (vezi Fig. 31.7) selectăm un element de lungime . Ca urmare a deformării, după cum reiese din ipoteza lui Bernoulli, secțiunile vor rămâne plate, dar se vor înclina unele față de altele cu un anumit unghi.Să luăm secțiunea din stânga condiționat ca staționară. Apoi, ca urmare a rotirii secțiunii drepte printr-un unghi, aceasta va lua poziția (Fig. 33.7).
Liniile drepte se vor intersecta într-un anumit punct A, care este centrul de curbură (sau, mai precis, urma axei de curbură) al fibrelor longitudinale ale elementului.Fibrele superioare ale elementului în cauză atunci când sunt prezentate în Smochin. 31,7 în direcția momentului sunt prelungite, iar cele inferioare sunt scurtate. Fibrele unui strat intermediar perpendicular pe planul de acțiune al momentului își păstrează lungimea. Acest strat se numește strat neutru.
Să notăm raza de curbură a stratului neutru, adică distanța de la acest strat până la centrul de curbură A (vezi Fig. 33.7). Să considerăm un anumit strat situat la o distanță y de stratul neutru. Alungirea absolută a fibrelor acestui strat este egală cu și alungirea relativă

Luand in considerare triunghiuri asemănătoare stabilim că Prin urmare,
![]()
În teoria îndoirii, se presupune că fibrele longitudinale ale grinzii nu se apasă unele pe altele. Experimental și cercetare teoretică arată că această ipoteză nu afectează semnificativ rezultatele calculului.
La încovoiere pură, solicitările de forfecare nu apar în secțiunile transversale ale grinzii. Astfel, toate fibrele în îndoire pură sunt în condiții de tensiune sau compresie uniaxiale.
Conform legii lui Hooke, în cazul tensiunii sau compresiei uniaxiale, efortul normal o și corespunzătoare deformare relativă legat de dependență
sau pe baza formulei (11.7)
Din formula (12.7) rezultă că tensiunile normale din fibrele longitudinale ale grinzii sunt direct proporționale cu distanța lor y față de stratul neutru. În consecință, în secțiunea transversală a grinzii în fiecare punct, tensiunile normale sunt proporționale cu distanța y de la acest punct la axa neutră, care este linia de intersecție a stratului neutru cu secțiunea transversală (Fig.
34.7, a). Din simetria grinzii și a sarcinii rezultă că axa neutră este orizontală.


În punctele axei neutre, tensiunile normale sunt zero; pe o parte a axei neutre sunt la tracțiune, iar pe cealaltă sunt compresive.
Diagrama tensiunilor o este un grafic delimitat de o linie dreaptă, cu cele mai mari valori absolute ale tensiunii pentru punctele cele mai îndepărtate de axa neutră (Fig. 34.7b).
Să luăm acum în considerare condițiile de echilibru ale elementului de fascicul selectat. Să reprezentăm acțiunea părții din stânga a grinzii asupra secțiunii elementului (vezi Fig. 31.7) sub forma unui moment încovoietor, forțele interne rămase în această secțiune cu încovoiere pură sunt egale cu zero. Să ne imaginăm acțiunea părții drepte a grinzii asupra secțiunii transversale a elementului sub formă de forțe elementare aplicate fiecărei zone elementare a secțiunii transversale (Fig. 35.7) și paralele cu axa grindă.
Să creăm șase condiții de echilibru pentru un element
Iată sumele proiecțiilor tuturor forțelor care acționează asupra elementului, respectiv, pe axe - sumele momentelor tuturor forțelor raportate la axe (Fig. 35.7).
Axa coincide cu axa neutră a secțiunii și axa y este perpendiculară pe aceasta; ambele aceste axe sunt situate în planul secțiunii transversale
O forță elementară nu produce proiecții pe axa y și nu provoacă un moment în jurul axei. Prin urmare, ecuațiile de echilibru sunt satisfăcute pentru orice valoare a lui o.
Ecuația de echilibru are forma
![]()
Să substituim valoarea lui a în ecuația (13.7) conform formulei (12.7):
![]()
Deoarece (se ia în considerare un element de fascicul curbat, pentru care), atunci
Integrala reprezintă momentul static al secțiunii transversale a grinzii în jurul axei neutre. Egalitatea sa cu zero înseamnă că axa neutră (adică axa) trece prin centrul de greutate al secțiunii transversale. Astfel, centrul de greutate al tuturor secțiunilor transversale ale fasciculului și, prin urmare, axa fasciculului, care este locația geometrică a centrelor de greutate, sunt situate în stratul neutru. Prin urmare, raza de curbură a stratului neutru este raza de curbură a axei curbe a fasciculului.
Să compunem acum ecuația de echilibru sub forma sumei momentelor tuturor forțelor aplicate elementului fasciculului în raport cu axa neutră:
![]()
Aici reprezintă momentul forței interne elementare în raport cu axa.
Să notăm aria secțiunii transversale a fasciculului situat deasupra axei neutre - sub axa neutră.
Apoi va reprezenta rezultanta forțelor elementare aplicate deasupra axei neutre, sub axa neutră (Fig. 36.7).
Ambele rezultate sunt egale între ele în valoare absolută, deoarece suma lor algebrică, bazată pe condiția (13.7), este egală cu zero. Aceste rezultate formează o pereche internă de forțe care acționează în secțiunea transversală a grinzii. Momentul acestei perechi de forțe, egal cu produsul dintre mărimea uneia dintre ele și distanța dintre ele (Fig. 36.7), este un moment încovoietor în secțiunea transversală a grinzii.

Să substituim valoarea lui a în ecuația (15.7) conform formulei (12.7):
Aici reprezintă momentul axial de inerție, adică axa care trece prin centrul de greutate al secțiunii. Prin urmare,
![]()
Să înlocuim valoarea din formula (16.7) în formula (12.7):
![]()
La derivarea formulei (17.7), nu s-a luat în considerare faptul că cu un cuplu extern direcționat, așa cum se arată în Fig. 31.7, conform regulii semnului acceptat, momentul încovoietor este negativ. Dacă luăm în considerare acest lucru, atunci trebuie să punem un semn minus în fața părții drepte a formulei (17.7). Apoi, cu un moment de încovoiere pozitiv în zona superioară a grinzii (adică la ), valorile lui a se vor dovedi a fi negative, ceea ce va indica prezența tensiunilor de compresiune în această zonă. Cu toate acestea, de obicei semnul minus nu este plasat în partea dreaptă a formulei (17.7), iar această formulă este utilizată numai pentru a determina valorile absolute ale tensiunilor a. Prin urmare, ar trebui să se înlocuiască în formula (17.7) valori absolute momentul încovoietor și ordonata y. Semnul tensiunilor este întotdeauna ușor de determinat de semnul momentului sau de natura deformării grinzii.
Să compunem acum ecuația de echilibru sub forma sumei momentelor tuturor forțelor aplicate elementului fascicul relativ la axa y:
![]()
Aici reprezintă momentul forței interne elementare în jurul axei y (vezi Fig. 35.7).
Să substituim valoarea lui a în expresia (18.7) conform formulei (12.7):
Aici integrala reprezintă momentul de inerție centrifugal al secțiunii transversale a fasciculului în raport cu axa y și. Prin urmare,
Dar de atunci
După cum se știe (vezi § 7.5), momentul de inerție centrifugal al secțiunii este egal cu zero față de axele principale de inerție.
În cazul în cauză, axa y este axa de simetrie a secțiunii transversale a grinzii și, prin urmare, axele y și sunt principalele axe centrale de inerție ale acestei secțiuni. Prin urmare, condiția (19.7) este satisfăcută aici.
În cazul în care secțiunea transversală a grinzii îndoite nu are nicio axă de simetrie, condiția (19.7) este îndeplinită dacă planul de acțiune al momentului încovoietor trece prin una dintre principalele axe centrale de inerție ale secțiunii sau este paralel. la această axă.
Dacă planul de acțiune al momentului încovoietor nu trece prin niciuna dintre axele centrale principale de inerție ale secțiunii transversale a grinzii și nu este paralel cu acesta, atunci condiția (19.7) nu este îndeplinită și, prin urmare, nu există îndoire directă - fasciculul experimentează îndoire oblică.
Formula (17.7), care determină solicitarea normală într-un punct arbitrar al secțiunii grinzii luate în considerare, este aplicabilă cu condiția ca planul de acțiune al momentului încovoietor să treacă prin una dintre axele principale de inerție ale acestei secțiuni sau să fie paralel cu acesta. . În acest caz, axa neutră a secțiunii transversale este principala sa axă centrală de inerție, perpendiculară pe planul de acțiune al momentului încovoietor.
Formula (16.7) arată că în timpul încovoierii pure directe, curbura axei curbe a grinzii este direct proporțională cu produsul dintre modulul elastic E și momentul de inerție Vom numi produsul rigiditatea secțiunii în timpul încovoierei; se exprimă în etc.
La îndoirea pură a unei grinzi cu secțiune transversală constantă, momentele de încovoiere și rigiditățile secțiunii sunt constante pe lungimea acesteia. În acest caz, raza de curbură a axei curbe a fasciculului are o valoare constantă [vezi. expresia (16.7)], adică fasciculul se îndoaie de-a lungul unui arc de cerc.
Din formula (17.7) rezultă că cele mai mari (pozitive - tracțiune) și cele mai mici (negative - compresive) tensiuni normale din secțiunea transversală a grinzii apar în punctele cele mai îndepărtate de axa neutră, situate pe ambele părți ale acesteia. Cu o secțiune transversală simetrică față de axa neutră, valori absolute cele mai mari tensiuni de tracțiune și compresiune sunt aceleași și pot fi determinate prin formula
Pentru secțiunile care nu sunt simetrice față de axa neutră, de exemplu, pentru un triunghi, tee etc., distanțele de la axa neutră până la cele mai îndepărtate fibre întinse și comprimate sunt diferite; Prin urmare, pentru astfel de secțiuni există două momente de rezistență:
unde sunt distanţele de la axa neutră până la cele mai îndepărtate fibre întinse şi comprimate.
