Tensiuni maxime de torsiune. Forțe și tensiuni în secțiunile transversale ale grinzii Cum se va modifica tensiunea pe suprafața grinzii rotunde
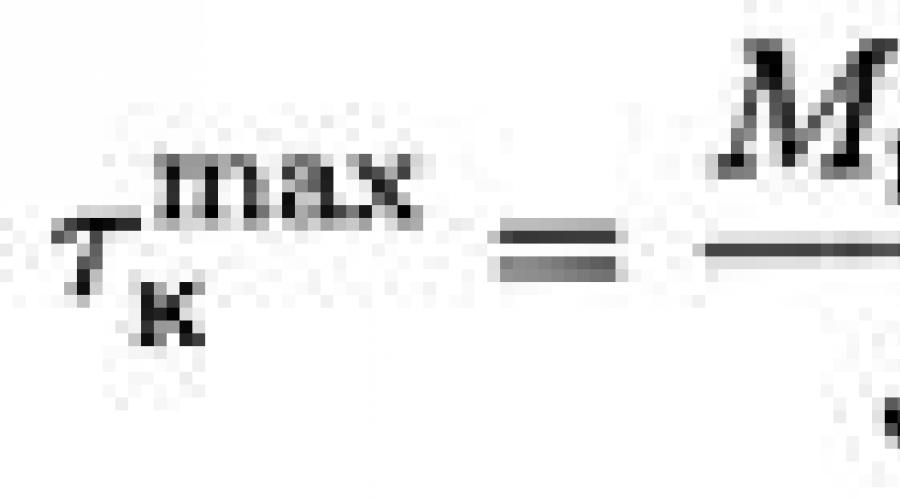
Citeste si
Din formula de determinare a tensiunilor și diagrama de distribuție a tensiunilor tăietoare în timpul torsiune se poate observa că tensiunile maxime apar la suprafață.
Să determinăm tensiunea maximă, ținând cont de faptul că ρ și X = d/ 2, unde d- diametrul barei sectiune rotunda.
Pentru o secțiune circulară, momentul polar de inerție este calculat prin formula (vezi cursul 25).
Stresul maxim apare la suprafață, așa că avem
![]()
De obicei JP /pmax desemna Wp si suna moment de rezistență la răsucire, sau moment polar de rezistență secțiuni
Astfel, pentru a calcula solicitarea maximă pe suprafața unei grinzi rotunde, obținem formula
Pentru secțiunea rotundă
![]()
Pentru o secțiune inelară
Condiție de rezistență la torsiune
Distrugerea fasciculului în timpul torsiune are loc de la suprafață, la calcularea rezistenței, se utilizează condiția de rezistență
![]()
Unde [ τ k ] - efortul de torsiune admisibil.
Tipuri de calcule de rezistență
Există două tipuri de calcule de rezistență.
1. Calcul de proiectare - se determină diametrul grinzii (axului) în secțiunea periculoasă:
![]()

2. Verificați calculul - se verifica indeplinirea conditiei de rezistenta
![]()
3. Determinarea capacității de încărcare (cuplul maxim)
![]()
Calculul rigidității
 La calcularea rigidității, se determină deformația și se compară cu cea admisibilă. Luați în considerare deformarea unei grinzi rotunde sub acțiunea unei perechi externe de forțe cu un moment t(Fig. 27.4).
La calcularea rigidității, se determină deformația și se compară cu cea admisibilă. Luați în considerare deformarea unei grinzi rotunde sub acțiunea unei perechi externe de forțe cu un moment t(Fig. 27.4).
La torsiune, deformația este estimată prin unghiul de răsucire (vezi cursul 26):
Aici φ - unghi de răsucire; γ - unghi de forfecare; l- lungimea barei; R- raza; R=d/2. Unde
Legea lui Hooke are forma τ k = Gγ. Înlocuiți expresia pentru γ , primim
![]()
Muncă GJP numită rigiditatea secțiunii.
Modulul de elasticitate poate fi definit ca G = 0,4E. Pentru oțel G= 0,8 10 5 MPa.
De obicei, unghiul de răsucire este calculat pe metru din lungimea fasciculului (arborelui) φ o.
Condiția de rigiditate la torsiune poate fi scrisă ca
![]()
Unde φ o - unghiul relativ de răsucire, φ o= φ/l; [φ o]≈ 1deg/m = 0,02rad/m - unghi relativ admis de răsucire.
Exemple de rezolvare a problemelor
Exemplul 1 Pe baza calculelor de rezistență și rigiditate, determinați diametrul arborelui necesar pentru transmisia de putere de 63 kW la o viteză de 30 rad/s. Material arbore - oțel, efort de torsiune admisibil 30 MPa; unghiul relativ admis de răsucire [φ o]= 0,02 rad/m; modulul de forfecare G= 0,8 * 10 5 MPa.
Soluţie
1. Determinarea dimensiunilor secțiunii transversale pe baza rezistenței.
Condiție de rezistență la torsiune:
![]()
Determinăm cuplul din formula de putere în timpul rotației:
Din condiția de rezistență, determinăm momentul de rezistență al arborelui în timpul torsii
![]()
Înlocuim valorile în newtoni și mm.
![]()
Determinați diametrul arborelui:
2. Determinarea dimensiunilor secțiunii transversale pe baza rigidității.
Stare de rigiditate la torsiune:
![]()
Din condiția de rigiditate, determinăm momentul de inerție al secțiunii în timpul torsii:
Determinați diametrul arborelui:
3. Selectarea diametrului arborelui necesar pe baza calculelor de rezistență și rigiditate.
Pentru a asigura rezistența și rigiditatea, alegem simultan cea mai mare dintre cele două valori găsite.
Valoarea rezultată trebuie rotunjită folosind un interval de numere preferate. Practic rotunjim valoarea obtinuta astfel incat numarul sa se termine cu 5 sau 0. Luam valoarea d a arborelui = 75 mm.
Pentru a determina diametrul arborelui, este de dorit să se utilizeze intervalul standard de diametre prezentat în apendicele 2.
Exemplul 2În secțiunea transversală a grinzii d= 80 mm efort maxim de forfecare τ max\u003d 40 N / mm 2. Determinați efortul de forfecare într-un punct la 20 mm distanță de centrul secțiunii.
Soluţie
b. Evident,
 |
Exemplul 3În punctele conturului interior al secțiunii transversale a țevii (d 0 = 60 mm; d = 80 mm) apar tensiuni de forfecare egale cu 40 N/mm2. Determinați tensiunile maxime de forfecare care apar în conductă.
Soluţie
Diagrama tensiunilor tangențiale în secțiune transversală este prezentată în fig. 2.37 în. Evident,
![]()
Exemplul 4În secțiunea transversală inelară a fasciculului ( d0= 30 mm; d= 70 mm) apare un cuplu Mz= 3 kN-m. Calculați efortul de forfecare într-un punct la 27 mm distanță de centrul secțiunii.
Soluţie
Tensiunea de forfecare într-un punct arbitrar al secțiunii transversale este calculată prin formula
În acest exemplu Mz= 3 kN-m = 3-10 6 N mm,
![]()
Exemplul 5 Țeavă de oțel(d 0 = l00 mm; d = 120 mm) lungime l= 1,8 m cuplu t aplicat în secțiunile sale de capăt. Determinați valoarea t, la care unghiul de răsucire φ = 0,25°. Cu valoarea găsită t calculați tensiunile maxime de forfecare.
Soluţie
Unghiul de răsucire (în grade/m) pentru o secțiune este calculat prin formula
În acest caz
Înlocuind valorile numerice, obținem
Calculăm tensiunile maxime de forfecare:

 Exemplul 6 Pentru un fascicul dat (Fig. 2.38, A) construiți diagrame de cupluri, tensiuni de forfecare maxime, unghiuri de rotație ale secțiunilor transversale.
Exemplul 6 Pentru un fascicul dat (Fig. 2.38, A) construiți diagrame de cupluri, tensiuni de forfecare maxime, unghiuri de rotație ale secțiunilor transversale.
Soluţie
O grindă dată are secțiuni I, II, III, IV, V(Fig. 2. 38, A). Reamintim că limitele secțiunilor sunt secțiuni în care se aplică momente externe (de răsucire) și locuri de modificare a dimensiunilor secțiunii transversale.
Folosind relația
![]()
construim o diagramă a cuplurilor.
Complot Mzîncepem de la capătul liber al grinzii:
![]()
pentru parcele IIIși IV
pentru site V
Diagrama cuplurilor este prezentată în Fig. 2.38, b. Construim o diagramă a tensiunilor tangențiale maxime de-a lungul lungimii grinzii. Atribuim condiționat τ verificați aceleași semne ca și cuplurile corespunzătoare. Locația activată eu
Locația activată II
Locația activată III
Locația activată IV
Locația activată V

Graficul tensiunilor maxime de forfecare este prezentat în fig. 2.38 în.
Unghiul de rotație al secțiunii transversale a fasciculului la un diametru constant (în cadrul fiecărei secțiuni) al secțiunii și al cuplului este determinat de formula
![]()
Construim o diagramă a unghiurilor de rotație ale secțiunilor transversale. Unghiul de rotație al secțiunii A φ l \u003d 0, deoarece fasciculul este fix în această secțiune.


Schema unghiurilor de rotație ale secțiunilor transversale este prezentată în fig. 2.38 G.
Exemplul 7 pe scripete LA arbore în trepte (Fig. 2.39, A) puterea transferată de la motor N B = 36 kW, scripete DARși DIN respectiv transferate la maşinile de putere N / A= 15 kW și N C= 21 kW. Viteza arborelui P= 300 rpm. Verificați rezistența și rigiditatea arborelui, dacă [ τ K J \u003d 30 N / mm 2, [Θ] \u003d 0,3 grade / m, G \u003d 8,0-10 4 N / mm 2, d1= 45 mm, d2= 50 mm.
 Soluţie
Soluţie
Să calculăm momentele externe (de răsucire) aplicate arborelui:
![]()
Construim o diagramă a cuplurilor. În același timp, deplasându-ne de la capătul stâng al arborelui, luăm în considerare în mod condiționat momentul corespunzător N A, pozitiv Nc- negativ. Diagrama M z este prezentată în fig. 2.39 b. Tensiuni maxime în secțiunile transversale ale secțiunii AB
care este mai mic [t k ] de
Unghiul relativ de răsucire al secțiunii AB
care este mult mai mare decât [Θ] ==0,3 grade/m.
Tensiuni maxime în secțiunile transversale ale secțiunii Soare
care este mai mic [t k ] de
Unghiul relativ de răsucire al secțiunii Soare

care este mult mai mare decât [Θ] = 0,3 grade/m.
În consecință, rezistența arborelui este asigurată, dar rigiditatea nu este.
Exemplul 8 De la motorul cu curea până la arbore 1 puterea transmisă N= 20 kW, Din arbore 1 intră în puț 2 putere N 1= 15 kW și la mașini de lucru - putere N 2= 2 kW și N 3= 3 kW. Din ax 2 puterea este furnizată mașinilor de lucru N 4= 7 kW, N 5= 4 kW, nr. 6= 4 kW (Fig. 2.40, A). Determinați diametrele arborilor d 1 și d 2 din condiția de rezistență și rigiditate, dacă [ τ K J \u003d 25 N / mm 2, [Θ] \u003d 0,25 grade / m, G \u003d 8,0-10 4 N / mm 2. Secțiuni de arbore 1 și 2 să fie considerat constant pe toată lungimea. Viteza arborelui motorului n = 970 rpm, diametre scripete D 1 = 200 mm, D 2 = 400 mm, D 3 = 200 mm, D 4 = 600 mm. Ignorați alunecarea transmisiei prin curea.
Soluţie
Smochin. 2.40 b arborele este prezentat eu. Primește putere N iar puterea este îndepărtată din el Nl, N 2 , N3.
 Determinați viteza unghiulară de rotație a arborelui 1
și momentele de torsiune exterioare m, m 1, t 2, t 3:
Determinați viteza unghiulară de rotație a arborelui 1
și momentele de torsiune exterioare m, m 1, t 2, t 3:

 |
Construim o diagramă de cuplu pentru arborele 1 (Fig. 2.40, în). În același timp, deplasându-ne de la capătul stâng al arborelui, luăm în considerare în mod condiționat momentele corespunzătoare N 3și N 1, pozitiv și N- negativ. Cuplul (maxim) estimat N x 1 max = 354,5 H * m.
Diametrul arborelui 1 din starea de rezistență
Diametrul arborelui 1 din starea de rigiditate ([Θ], rad/mm)

În cele din urmă, acceptăm rotunjirea la valoarea standard d 1 \u003d 58 mm.
Viteza arborelui 2
Pe fig. 2.40 G arborele este prezentat 2; puterea este aplicată arborelui N 1, iar puterea este îndepărtată din el N4, N5, N6.
Calculați momentele de torsiune externe:

Diagrama cuplului arborelui 2 prezentată în fig. 2.40 d. Cuplul (maxim) estimat M i max "= 470 N-m.
Diametrul arborelui 2 din starea de forță
Diametrul arborelui 2 din starea de rigiditate

În sfârșit acceptăm d2= 62 mm.
Exemplul 9 Determinați din condițiile de rezistență și rigiditate puterea N(Fig. 2.41, A), care poate fi transmisă printr-un arbore de oțel cu un diametru d=50 mm, dacă [t la] \u003d 35 N / mm 2, [ΘJ \u003d 0,9 grade / m; G \u003d 8,0 * I0 4 N / mm 2, n= 600 rpm.
 Soluţie
Soluţie
Să calculăm momentele externe aplicate arborelui:
Schema de proiectare arborele este prezentat în fig. 2.41, b.
Pe fig. 2.41, în este prezentată diagrama cuplurilor. Cuplul (maxim) estimat Mz = 9,54N. Stare de forță

![]()
Stare de rigiditate
Condiția limitativă este rigiditatea. Prin urmare, valoarea admisă a puterii transmise [N] = 82,3 kW.
Forța longitudinală N care apare în secțiunea transversală a grinzii este rezultanta forțelor normale interne distribuite pe aria secțiunii transversale și este legată de tensiunile normale care apar în această secțiune prin dependență (4.1):
aici - tensiunea normală într-un punct arbitrar al secțiunii transversale aparținând zonei elementare - aria secțiunii transversale a barei.
Produsul este o forță internă elementară pe suprafață dF.
Valoarea forței longitudinale N în fiecare caz particular poate fi determinată cu ușurință folosind metoda secțiunii, așa cum se arată în paragraful anterior. Pentru a afla mărimile tensiunilor a în fiecare punct al secțiunii transversale a grinzii, este necesar să se cunoască legea distribuției lor pe această secțiune.
Legea distribuției tensiunilor normale în secțiunea transversală a unei grinzi este de obicei descrisă printr-un grafic care arată modificarea acestora în înălțimea sau lățimea secțiunii transversale. Un astfel de grafic se numește diagrama normală a tensiunilor (diagrama a).
Expresia (1.2) poate fi satisfăcută la infinit numere mari tipuri de diagrame de tensiuni a (de exemplu, cu diagramele a prezentate în fig. 4.2). Prin urmare, pentru a clarifica legea distribuției tensiunilor normale în secțiunile transversale ale grinzii, este necesar să se efectueze un experiment.
Să trasăm linii pe suprafața laterală a grinzii înainte de a fi încărcată, perpendicular pe axa grinzii (Fig. 5.2). Fiecare astfel de linie poate fi considerată ca o urmă a planului secțiunii transversale a fasciculului. Când grinda este încărcată cu o forță axială P, aceste linii, după cum arată experiența, rămân drepte și paralele între ele (pozițiile lor după încărcarea grinzii sunt prezentate în Fig. 5.2 prin linii întrerupte). Acest lucru ne permite să presupunem că secțiunile transversale ale grinzii, care sunt plate înainte de încărcare, rămân plate sub acțiunea sarcinii. Un astfel de experiment confirmă conjectura secțiunilor plane (conjectura lui Bernoulli) formulată la sfârșitul § 6.1.
Imaginați-vă mental un fascicul format din nenumărate fibre paralele cu axa sa.


Oricare două secțiuni transversale, atunci când fasciculul este întins, rămân plate și paralele una cu cealaltă, dar se îndepărtează una de cealaltă cu o anumită cantitate; fiecare fibră se alungește cu aceeași cantitate. Și deoarece aceleași alungiri corespund acelorași tensiuni, atunci tensiunile din secțiunile transversale ale tuturor fibrelor (și, în consecință, în toate punctele secțiunii transversale a fasciculului) sunt egale între ele.
Aceasta permite în expresia (1.2) să se ia valoarea lui a din semnul integral. În acest fel,
![]()
Deci, în secțiunile transversale ale grinzii în timpul tensiunii sau compresiei centrale, apar tensiuni normale distribuite uniform, egale cu raportul dintre forța longitudinală și aria secțiunii transversale.
În prezența slăbirii unor secțiuni ale grinzii (de exemplu, găuri pentru nituri), atunci când se determină tensiunile în aceste secțiuni, ar trebui să se ia în considerare aria reală a secțiunii slăbite egală cu suprafata intreaga redus cu aria de atenuare
Pentru o reprezentare vizuală a modificării tensiunilor normale în secțiunile transversale ale tijei (de-a lungul lungimii sale), este reprezentată graficul tensiunilor normale. Axa acestei diagrame este un segment de linie dreaptă egal cu lungimea tijei și paralel cu axa acesteia. Cu o tijă de secțiune transversală constantă, diagrama tensiunilor normale are aceeași formă ca diagrama forțe longitudinale(se deosebește de el doar în scara acceptată). Cu o tijă de secțiune variabilă, aspectul acestor două diagrame este diferit; în special, pentru o bară cu o lege în trepte a modificării secțiunilor transversale, diagrama tensiunilor normale are salturi nu numai în secțiunile în care se aplică sarcini axiale concentrate (unde diagrama forțelor longitudinale are salturi), ci și în locurile în care dimensiunile secțiunilor transversale se modifică. Construcția unei diagrame a distribuției tensiunilor normale de-a lungul lungimii tijei este considerată în exemplul 1.2.
Luați în considerare acum tensiunile din secțiunile înclinate ale grinzii.
Să notăm unghiul dintre secțiunea înclinată și secțiunea transversală (Fig. 6.2, a). Să fim de acord să considerăm unghiul a drept pozitiv atunci când secțiunea transversală trebuie rotită în sens invers acelor de ceasornic cu acest unghi pentru a coincide cu secțiunea înclinată.
După cum se știe deja, alungirea tuturor fibrelor paralele cu axa grinzii, atunci când este întinsă sau comprimată, este aceeași. Acest lucru ne permite să presupunem că tensiunile p în toate punctele secțiunii înclinate (precum și transversale) sunt aceleași.
Considera partea inferioară cherestea tăiată printr-o secțiune (Fig. 6.2, b). Din condițiile de echilibru rezultă că tensiunile sunt paralele cu axa grinzii și direcționate în direcția opusă forței P, iar forța internă care acționează în secțiune este egală cu P. Aici, aria lui secțiunea înclinată este egală cu (unde este aria secțiunii transversale a grinzii).
Prin urmare,
unde - tensiuni normale în secțiunile transversale ale grinzii.
Să descompunăm efortul în două componente ale tensiunii: normală perpendiculară pe planul secțiunii și tangentă ta paralelă cu acest plan (Fig. 6.2, c).

Valorile și ta sunt obținute din expresii
Stresul normal este, în general, considerat a fi pozitiv în tensiune și negativ în compresie. Efortul de forfecare este pozitiv dacă vectorul care îl reprezintă tinde să rotească corpul în jurul oricărui punct C situat pe normala internă a secțiunii, în sensul acelor de ceasornic. Pe fig. 6.2, c prezintă efortul de forfecare pozitiv ta, iar în fig. 6.2, d - negativ.
Din formula (6.2) rezultă că tensiunile normale au valori de la (la la zero (la a). Astfel, cea mai mare (după valoare absolută) tensiunile normale apar în secțiunile transversale ale grinzii. Prin urmare, calculul rezistenței unei grinzi întinse sau comprimate se efectuează în funcție de solicitările normale în secțiunile sale transversale.
CAPITOLUL 9 Forfecare și torsiune
Fasciculul prezentat în fig. 9.13, are patru secțiuni. Dacă luăm în considerare condițiile de echilibru pentru sistemele de forțe aplicate părții tăiate din stânga, atunci putem scrie:
Plot 1 |
a (Fig. 9.13, b). |
|||||||||||||||
Mx 0 : Mcr m x dx 0 ; Mcr |
dx. |
|||||||||||||||
Plot 2 |
ax2 |
a b (Fig. 9.13, c). |
||||||||||||||
Mx 0 : Mcr m x dx M1 0 ; Mcr m x dx M1 . |
||||||||||||||||
Plot 3 |
a b x2 |
a b c (Fig. 9.13, d). |
||||||||||||||
M0; |
x dx M . |
|||||||||||||||
Plot 4 |
a b c x2 a b c d . |
|||||||||||||||
Mx 0 : Mcr m x dx M1 M2 0 ; |
||||||||||||||||
M cr |
m x dx M1 M2 . |
|||||||||||||||
Astfel, cuplul M cr în secțiunea transversală a grinzii este egal cu suma algebrică a momentelor tuturor forțelor externe care acționează pe o parte a secțiunii.
9.2.2. Tensiuni de torsiune și deformații ale unei bare drepte cu secțiune transversală circulară
După cum sa menționat deja, tensiunile de forfecare totale ar putea fi determinate din dependența (9.14) dacă s-ar cunoaște legea distribuției lor pe secțiunea grinzii. Imposibilitatea unei definiții analitice a acestei legi ne obligă să apelăm la studiu pilot deformari ale fasciculului.

V. A. Zhilkin
Luați în considerare o grindă, al cărei capăt din stânga este prins rigid și un moment de torsiune M cr este aplicat la capătul drept. Înainte de a încărca fasciculul cu un moment, pe suprafața sa a fost aplicată o plasă ortogonală cu dimensiunile celulelor a × b (Fig. 9.14, a). După aplicarea momentului de torsiune M kr, capătul drept al grinzii se va roti în raport cu capătul stâng al grinzii printr-un unghi, în timp ce distanțele dintre secțiunile grinzii răsucite nu se vor modifica, iar razele trasate în secțiunea de capăt va rămâne drept, adică se poate presupune că ipoteza secțiunilor plane este îndeplinită (Fig. 9.14, b). Secțiunile care sunt plate înainte de deformarea fasciculului rămân plate după deformare, întorcându-se ca niște hard diskuri, una față de alta la un anumit unghi. Deoarece distanța dintre secțiunile grinzii nu se modifică, longitudinala încordare relativă x 0 este egal cu zero. Liniile longitudinale ale grilei iau o formă elicoidală, dar distanța dintre ele rămâne constantă (prin urmare, y 0 ), celulele grilei dreptunghiulare se transformă în paralelograme, ale căror dimensiuni nu se modifică, adică. volumul elementar selectat al oricărui strat al grinzii este în condiții de forfecare pură.
Să decupăm un element de grindă cu o lungime de dx în două secțiuni transversale (Fig. 9.15). Ca urmare a încărcării fasciculului, secțiunea dreaptă a elementului se va roti față de cea din stânga cu un unghi d. În acest caz, generatoarea cilindrului se va roti printr-un unghi

CAPITOLUL 9 Forfecare și torsiune
schimb. Toate generatoarele cilindrilor interiori de rază se vor roti cu același unghi.
Conform fig. 9,15 arc
ab dx d .
unde d dx se numește unghi relativ de răsucire. Dacă dimensiunile secțiunilor transversale ale unei bare drepte și cuplurile care acționează în ele sunt constante într-o anumită zonă, atunci valoarea este, de asemenea, constantă și egală cu raportul unghi complet răsucirea în această secțiune la lungimea sa L, adică L.
Trecând conform legii lui Hooke la forfecare ( G ) la tensiuni, obținem
Deci, în secțiunile transversale ale grinzii în timpul torsirii, apar tensiuni de forfecare, a căror direcție în fiecare punct este perpendiculară pe raza care leagă acest punct cu centrul secțiunii, iar valoarea este direct proporțională cu

V. A. Zhilkin
distanța punctului față de centru. În centru (la 0 ) eforturile de forfecare sunt egale cu zero; în punctele situate în imediata apropiere a suprafeței exterioare a fasciculului, acestea sunt cele mai mari.
Înlocuind legea distribuției tensiunilor găsite (9.18) în egalitatea (9.14), obținem
Mcr G dF G 2 dF G J , |
||||||||||||||||
unde J d 4 este momentul polar de inerție al traversei circulare |
||||||||||||||||
secțiunea piciorului grinzii. |
||||||||||||||||
Opera de artă G.J. |
numită rigiditatea transversală |
|||||||||||||||
a-a secțiune a grinzii în timpul torsiunei. |
||||||||||||||||
Unitățile de măsură ale rigidității sunt |
||||||||||||||||
sunt N m2, kN m2 etc. |
||||||||||||||||
Din (9.19) găsim unghiul relativ de răsucire al fasciculului |
||||||||||||||||
M cr |
||||||||||||||||
și apoi, excluzând din egalitate (9.18), obținem formula |
||||||||||||||||
pentru tensiunile de torsiune ale grinzii rotunde |
||||||||||||||||
M cr |
||||||||||||||||
Cea mai mare valoare a tensiunii este atinsă în con- |
||||||||||||||||
punctele secțiunii pentru d 2 : |
||||||||||||||||
M cr |
M cr |
M cr |
||||||||||||||
se numește momentul de rezistență la torsiune a unui arbore cu secțiune transversală circulară.
Dimensiunea momentului de rezistență la torsiune - cm3, m3 etc.
care vă permite să determinați unghiul de răsucire al întregului fascicul
GJ cr. |
Dacă grinda are mai multe secțiuni cu expresii analitice diferite pentru M cr sau sensuri diferite rigiditatea secțiunii transversale GJ , atunci
Mcr dx |
|||||
Pentru o bară cu lungimea L de secțiune constantă, încărcată la capete cu perechi concentrate de forțe cu un moment M cr,
Mcr L |
|||||||||||||||||||
| D și d intern. Doar în acest caz J și W cr au nevoie | |||||||||||||||||||
1 c 4 ; W cr |
1 c 4 ; c |
|||||
Diagrama tensiunilor tangențiale în secțiunea unei bare goale este prezentată în fig. 9.17.
Comparația diagramelor de forfecare în grinzile solide și goale indică avantajele arborilor tubulari, deoarece în astfel de arbori materialul este utilizat mai rațional (materialul este îndepărtat în zona solicitărilor scăzute). Ca urmare, distribuția tensiunilor pe secțiunea transversală devine mai uniformă, iar fasciculul în sine devine mai ușor,
decât o grindă de rezistență egală cu aceasta este continuă - Fig. secțiunea 9.17, în ciuda unora
o creștere a roiului în diametrul exterior.
Dar la proiectarea grinzilor de torsiune, trebuie avut în vedere faptul că, în cazul unei secțiuni inelare, fabricarea lor este mai dificilă și, prin urmare, mai costisitoare.
Oblic numit acest tip de încovoiere, în care toate sarcinile externe care provoacă încovoiere acționează într-un singur plan de forță care nu coincide cu niciunul dintre planurile principale.
Luați în considerare o bară prinsă la un capăt și încărcată la capătul liber cu o forță F(Fig. 11.3).
Orez. 11.3. Schemă de proiectare pentru o îndoire oblică
Forta externa F aplicat în unghi față de axă y. Să descompunem forța Fîn componente situate în planurile principale ale fasciculului, apoi:
Momente încovoietoare într-o secțiune arbitrară luate la distanță z de la capătul liber, va fi egal cu:
Astfel, in fiecare sectiune a grinzii actioneaza simultan doua momente incovoietoare care creeaza o indoire in planurile principale. Prin urmare, o îndoire oblică poate fi considerată un caz special de îndoire spațială.
Tensiuni normaleîn secțiunea transversală a grinzii cu îndoire oblică sunt determinate de formula

Pentru a găsi cele mai mari tensiuni normale de tracțiune și compresiune în îndoirea oblică, este necesar să selectați secțiunea periculoasă a grinzii.
Dacă momentele încovoietoare | M x| și | Ale mele| a ajunge nai valori mariîntr-o anumită secțiune, atunci aceasta este secțiunea periculoasă. În acest fel,
Secțiunile periculoase includ și secțiunile în care momentele încovoietoare | M x| și | Ale mele| atinge în același timp valori suficient de mari. Prin urmare, cu îndoirea oblică, pot exista mai multe secțiuni periculoase.
În general, când ![]() - secțiune asimetrică, adică axa neutră nu este perpendiculară pe planul forței. Pentru secțiunile simetrice, îndoirea oblică nu este posibilă.
- secțiune asimetrică, adică axa neutră nu este perpendiculară pe planul forței. Pentru secțiunile simetrice, îndoirea oblică nu este posibilă.
11.3. Poziția axei neutre și a punctelor periculoase
în secţiune transversală. Condiție de rezistență pentru îndoirea oblică.
Determinarea dimensiunilor secțiunii transversale.
Mișcări în îndoire oblică
Poziția axei neutre în îndoire oblică este determinată de formula
![]()
unde este unghiul de înclinare al axei neutre față de axă X;
Unghiul de înclinare a planului forței față de axă la(Fig. 11.3).
În secțiunea periculoasă a grinzii (în încastrare, Fig. 11.3), tensiunile la punctele de colț sunt determinate de formulele:
În îndoirea oblică, ca și în îndoirea spațială, axa neutră împarte secțiunea transversală a fasciculului în două zone - zona de tensiune și zona de compresie. Pentru o secțiune dreptunghiulară, aceste zone sunt prezentate în fig. 11.4.

Orez. 11.4. Schema unei secțiuni a unui fascicul ciupit la o curbă oblică
Pentru a determina tensiunile extreme de tracțiune și compresiune, este necesar să se tragă tangente la secțiune în zonele de tracțiune și compresiune, paralele cu axa neutră (Fig. 11.4).
Punctele de contact cele mai îndepărtate de axa neutră DARși DIN sunt puncte periculoase în zonele de compresie și respectiv de tensiune.
Pentru materialele plastice, atunci când rezistența de proiectare a materialului grinzii în tensiune și compresie sunt egale între ele, adică [ σ p] = = [s c] = [σ ], în secțiunea periculoasă se determină și starea de rezistență poate fi reprezentată ca
Pentru secțiuni simetrice (dreptunghi, secțiune I), condiția de rezistență are următoarea formă:
![]()
Din condiția de rezistență rezultă trei tipuri de calcule:
Control;
Proiectare - determinarea dimensiunilor geometrice ale secțiunii;
Determinarea capacității portante a grinzii (sarcină admisă).
Dacă relația dintre laturile secțiunii transversale este cunoscută, de exemplu, pentru un dreptunghi h = 2b, apoi din starea rezistenței fasciculului ciupit, este posibil să se determine parametrii bși h în felul următor:
![]()
sau ![]()
definitiv .
Parametrii oricărei secțiuni sunt determinați într-un mod similar. Deplasarea completă a secțiunii grinzii în timpul îndoirii oblice, ținând cont de principiul independenței acțiunii forțelor, este definită ca suma geometrică a deplasărilor în planurile principale.
Determinați deplasarea capătului liber al grinzii. Să folosim metoda Vereshchagin. Găsim deplasarea verticală înmulțind diagramele (Fig. 11.5) după formula
![]()
În mod similar, definim deplasarea orizontală:
Apoi deplasarea totală este determinată de formula

Orez. 11.5. Schema de determinare a deplasării complete
la o curbă oblică
Direcția mișcării complete este determinată de unghi β (Fig. 11.6):
![]()
Formula rezultată este identică cu formula pentru determinarea poziției axei neutre a secțiunii fasciculului. Acest lucru ne permite să concluzionam că , adică direcția de deviere este perpendiculară pe axa neutră. În consecință, planul de deviere nu coincide cu planul de încărcare.

Orez. 11.6. Schema de determinare a planului de deformare
la o curbă oblică
Unghiul de abatere al planului de deviere față de axa principală y va fi mai mare, cu cât deplasarea este mai mare. Prin urmare, pentru o grindă cu o secțiune elastică, pentru care raportul J x/Jyîndoirea mare, oblică, este periculoasă, deoarece provoacă deviații și solicitări mari în planul de rigiditate minimă. Pentru un bar cu J x= Jy, deformarea totală se află în planul forței și îndoirea oblică este imposibilă.
11.4. Tensiunea și compresia excentrică a fasciculului. Normal
tensiuni în secțiunile transversale ale grinzii
Tensiune excentrică (comprimare) este un tip de deformare în care forța de tracțiune (de compresie) este paralelă cu axa longitudinală a grinzii, dar punctul de aplicare a acesteia nu coincide cu centrul de greutate al secțiunii transversale.
Acest tip de problemă este adesea folosit în construcții la calcularea stâlpilor de construcție. Luați în considerare compresia excentrică a unei grinzi. Notăm coordonatele punctului de aplicare a forței F prin x Fși la F, iar axele principale ale secțiunii transversale - prin x și y. Axă z direcţionaţi în aşa fel încât coordonatele x Fși la F au fost pozitive (Fig. 11.7, a)
Dacă transferi puterea F paralel cu sine dintr-un punct DIN la centrul de greutate al secțiunii, atunci compresia excentrică poate fi reprezentată ca suma a trei deformații simple: compresiune și încovoiere în două plane (Fig. 11.7, b). Făcând acest lucru, avem:
Tensiuni într-un punct arbitrar al secțiunii sub compresie excentrică, situată în primul cadran, cu coordonate x și y pot fi găsite pe baza principiului independenței acțiunii forțelor:

![]() razele de inerție pătrate ale secțiunii, atunci
razele de inerție pătrate ale secțiunii, atunci
![]()
Unde Xși y sunt coordonatele punctului de secțiune la care se determină solicitarea.
La determinarea tensiunilor, este necesar să se țină cont de semnele coordonatelor atât ale punctului de aplicare a forței externe, cât și ale punctului în care se determină solicitarea.
 Orez. 11.7. Schema unei grinzi cu compresie excentrică
Orez. 11.7. Schema unei grinzi cu compresie excentrică
În cazul tensiunii excentrice a fasciculului în formula rezultată, semnul „minus” trebuie înlocuit cu semnul „plus”.
Dacă doar un moment încovoietor acționează în secțiunea transversală a grinzii în timpul unei curbe drepte sau oblice, atunci există o curbă dreaptă pură sau, respectiv, o curbură oblică pură. Dacă în secțiune transversală acționează și o forță transversală, atunci există o îndoire transversală dreaptă sau oblică transversală. Dacă momentul încovoietor este singurul factor de forță intern, atunci se numește o astfel de îndoire curat(fig.6.2). În prezența unei forțe transversale, se numește îndoire transversal. Strict vorbind, să specii simple rezistența se aplică numai curba pură; îndoirea transversală este denumită în mod condiționat tipuri simple de rezistență, deoarece în majoritatea cazurilor (pentru grinzi suficient de lungi) acțiunea unei forțe transversale poate fi neglijată în calculele de rezistență. Vedeți starea rezistenței la îndoire plată. Când se calculează o grindă pentru îndoire, una dintre cele mai importante este sarcina de a determina rezistența acesteia. Încovoierea plană se numește transversală dacă în secțiunile transversale ale grinzii apar doi factori de forță interni: M - momentul încovoietor și Q - forța transversală și pură dacă apare doar M. În îndoirea transversală, planul forței trece prin axa de simetrie a grinda, care este una dintre principalele axe de inerție ale secțiunii.
Când o grindă este îndoită, unele dintre straturile sale sunt întinse, în timp ce altele sunt comprimate. Între ele se află un strat neutru, care doar se curbează fără a-și schimba lungimea. Linia de intersecție a stratului neutru cu planul secțiunii transversale coincide cu a doua axă principală de inerție și se numește linie neutră (axa neutră).
Din acțiunea momentului încovoietor în secțiunile transversale ale grinzii, apar tensiuni normale, determinate de formula
![]()
unde M este momentul încovoietor în secțiunea considerată;
I este momentul de inerție al secțiunii transversale a fasciculului față de axa neutră;
y este distanța de la axa neutră până la punctul în care sunt determinate tensiunile.
După cum se poate observa din formula (8.1), tensiunile normale în secțiunea grinzii de-a lungul înălțimii sale sunt liniare, atingând o valoare maximă în punctele cele mai îndepărtate de stratul neutru.
![]()
unde W este momentul de rezistență al secțiunii transversale a fasciculului față de axa neutră.
27. Tensiuni tangenţiale în secţiunea transversală a grinzii. formula lui Zhuravsky.
Formula Zhuravsky vă permite să determinați tensiunile tăietoare în încovoiere care apar în punctele secțiunii transversale a grinzii, situate la o distanță de axa neutră x. 
DERIVAREA FORMULEI ZHURAVSKY
Decupăm dintr-o grindă cu secțiune transversală dreptunghiulară (Fig. 7.10, a) un element cu o lungime și o secțiune longitudinală suplimentară tăiate în două părți (Fig. 7.10, b).
Luați în considerare echilibrul părții superioare: din cauza diferenței de momente încovoietoare, apar tensiuni de compresiune diferite. Pentru ca această parte a grinzii să fie în echilibru (), în secțiunea sa longitudinală trebuie să apară o forță tangențială. Ecuația de echilibru pentru o parte a unui fascicul:
unde integrarea se realizează numai pe partea tăiată a ariei secțiunii transversale a grinzii (în Fig. 7.10, umbrită în), ![]() este momentul de inerție static al părții tăiate (umbrite) a ariei secțiunii transversale în raport cu axa neutră x.
este momentul de inerție static al părții tăiate (umbrite) a ariei secțiunii transversale în raport cu axa neutră x.

Să presupunem că tensiunile tăietoare () care apar în secțiunea longitudinală a grinzii sunt distribuite uniform pe lățimea acesteia () la locul secțiunii:
Obținem expresia pentru eforturile de forfecare:

![]() , și , apoi formula pentru tensiunile tăietoare (), care apar în punctele secțiunii transversale a grinzii, situate la o distanță y de axa neutră x:
, și , apoi formula pentru tensiunile tăietoare (), care apar în punctele secțiunii transversale a grinzii, situate la o distanță y de axa neutră x:
formula lui Zhuravsky
Formula lui Zhuravsky a fost obținută în 1855 de D.I. Prin urmare, Zhuravsky îi poartă numele.