Aflarea valorii derivatei unei functii in punctul x0. Aflați valoarea derivatei funcției în punctul x0

Problema B9 oferă un grafic al unei funcții sau derivate din care trebuie să determinați una dintre următoarele mărimi:

1. Valoarea derivatei la un punct x 0,
2. Puncte maxime sau minime (puncte extreme),
3. Intervale de funcții crescătoare și descrescătoare (intervale de monotonitate).

Funcțiile și derivatele prezentate în această problemă sunt întotdeauna continue, făcând soluția mult mai ușoară. În ciuda faptului că sarcina aparține secțiunii analiză matematică, este destul de în competențele chiar și ale celor mai slabi studenți, deoarece aici nu sunt necesare cunoștințe teoretice profunde.

Pentru a găsi valoarea derivatei, punctelor extreme și a intervalelor de monotonitate, există algoritmi simpli și universali - toți vor fi discutați mai jos.

Citiți cu atenție condițiile problemei B9 pentru a nu face greșeli stupide: uneori dați peste texte destul de lungi, dar conditii importante, care influențează cursul deciziei, sunt puține.

Calculul valorii derivate. Metoda în două puncte

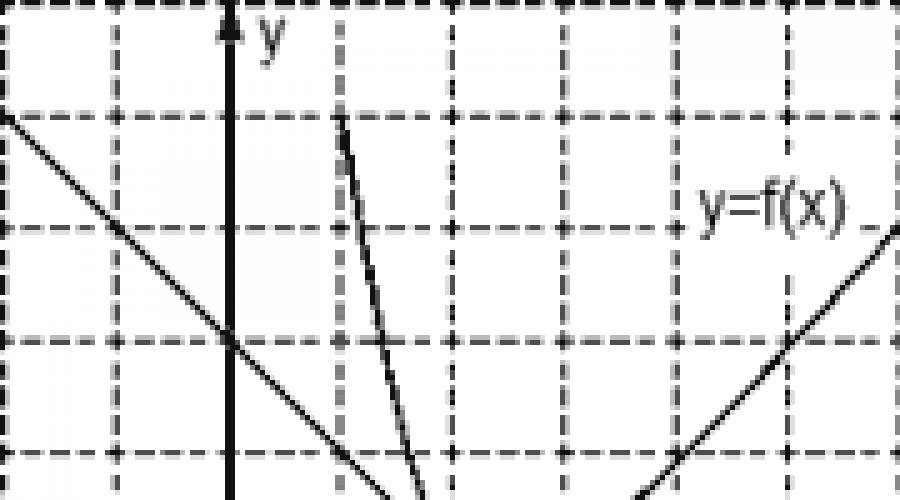
Dacă problemei i se dă un grafic al unei funcții f(x), tangentă la acest grafic la un punct x 0 și este necesar să se găsească valoarea derivatei în acest punct, se aplică următorul algoritm:

1. Găsiți două puncte „adecvate” pe graficul tangentei: coordonatele lor trebuie să fie întregi. Să notăm aceste puncte ca A (x 1 ; y 1) și B (x 2 ; y 2). Notați corect coordonatele - acesta este un punct cheie în soluție și orice greșeală aici va duce la un răspuns incorect.
2. Cunoscând coordonatele, este ușor de calculat incrementul argumentului Δx = x 2 − x 1 și incrementul funcției Δy = y 2 − y 1 .
3. În final, găsim valoarea derivatei D = Δy/Δx. Cu alte cuvinte, trebuie să împărțiți incrementul funcției cu incrementul argumentului - și acesta va fi răspunsul.

Să remarcăm încă o dată: punctele A și B trebuie căutate exact pe tangentă, și nu pe graficul funcției f(x), așa cum se întâmplă adesea. Linia tangentă va conține în mod necesar cel puțin două astfel de puncte - altfel problema nu va fi formulată corect.

Luați în considerare punctele A (−3; 2) și B (−1; 6) și găsiți incrementele:
Δx = x 2 − x 1 = −1 − (−3) = 2; Δy = y 2 − y 1 = 6 − 2 = 4.

Să aflăm valoarea derivatei: D = Δy/Δx = 4/2 = 2.

Sarcină. Figura prezintă un grafic al funcției y = f(x) și o tangentă la aceasta în punctul cu abscisa x 0. Aflați valoarea derivatei funcției f(x) în punctul x 0 .

Luați în considerare punctele A (0; 3) și B (3; 0), găsiți incrementele:
Δx = x 2 − x 1 = 3 − 0 = 3; Δy = y 2 − y 1 = 0 − 3 = −3.

Acum găsim valoarea derivatei: D = Δy/Δx = −3/3 = −1.

Sarcină. Figura prezintă un grafic al funcției y = f(x) și o tangentă la aceasta în punctul cu abscisa x 0. Aflați valoarea derivatei funcției f(x) în punctul x 0 .

Luați în considerare punctele A (0; 2) și B (5; 2) și găsiți incrementele:
Δx = x 2 − x 1 = 5 − 0 = 5; Δy = y 2 − y 1 = 2 − 2 = 0.

Rămâne de găsit valoarea derivatei: D = Δy/Δx = 0/5 = 0.

Din ultimul exemplu, putem formula o regulă: dacă tangenta este paralelă cu axa OX, derivata funcției în punctul de tangență este zero. În acest caz, nici măcar nu trebuie să numărați nimic - doar uitați-vă la grafic.

Calculul punctelor maxime și minime

Uneori, în loc de un grafic al unei funcții, problema B9 oferă un grafic al derivatei și necesită găsirea punctului maxim sau minim al funcției. În această situație, metoda în două puncte este inutilă, dar există un alt algoritm și mai simplu. Mai întâi, să definim terminologia:

1. Punctul x 0 se numește punctul maxim al funcției f(x) dacă într-o vecinătate a acestui punct este valabilă următoarea inegalitate: f(x 0) ≥ f(x).
2. Punctul x 0 se numește punctul minim al funcției f(x) dacă într-o vecinătate a acestui punct este valabilă următoarea inegalitate: f(x 0) ≤ f(x).

Pentru a găsi punctele maxime și minime din graficul derivat, trebuie doar să urmați acești pași:

1. Redesenați graficul derivat, eliminând toate informațiile inutile. După cum arată practica, datele inutile doar interferează cu decizia. Prin urmare, marchem zerourile derivatei pe axa de coordonate - și asta este tot.
2. Aflați semnele derivatei pe intervalele dintre zerouri. Dacă pentru un anumit punct x 0 se știe că f'(x 0) ≠ 0, atunci sunt posibile doar două opțiuni: f'(x 0) ≥ 0 sau f'(x 0) ≤ 0. Semnul derivatei este ușor de determinat din desenul original: dacă graficul derivat se află deasupra axei OX, atunci f'(x) ≥ 0. Și invers, dacă graficul derivat se află sub axa OX, atunci f'(x) ≤ 0.
3. Verificăm din nou zerourile și semnele derivatei. Acolo unde semnul se schimbă de la minus la plus este punctul minim. În schimb, dacă semnul derivatei se schimbă de la plus la minus, acesta este punctul maxim. Numărarea se face întotdeauna de la stânga la dreapta.

Această schemă funcționează numai pentru funcții continue - nu există altele în problema B9.

Sarcină. Figura prezintă un grafic al derivatei funcției f(x) definită pe intervalul [−5; 5]. Aflați punctul minim al funcției f(x) pe acest segment.

Să scăpăm de informațiile inutile și să lăsăm doar granițele [−5; 5] și zerourile derivatei x = −3 și x = 2,5. De asemenea, notăm semnele:

Evident, în punctul x = −3 semnul derivatei se schimbă din minus în plus. Acesta este punctul minim.

Sarcină. Figura prezintă un grafic al derivatei funcției f(x) definită pe intervalul [−3; 7]. Aflați punctul maxim al funcției f(x) pe acest segment.

Să redesenăm graficul, lăsând doar limitele [−3; 7] și zerourile derivatei x = −1,7 și x = 5. Să notăm semnele derivatei pe graficul rezultat. Avem:

Evident, în punctul x = 5 semnul derivatei se schimbă de la plus la minus - acesta este punctul maxim.

Sarcină. Figura prezintă un grafic al derivatei funcției f(x), definită pe intervalul [−6; 4]. Aflați numărul de puncte maxime ale funcției f(x) aparținând segmentului [−4; 3].

Din condițiile problemei rezultă că este suficient să se considere doar partea din grafic limitată de segmentul [−4; 3]. Prin urmare, construim un nou grafic pe care marchem doar granițele [−4; 3] și zerourile derivatei din interiorul acesteia. Și anume, punctele x = −3,5 și x = 2. Se obține:

Pe acest grafic există un singur punct maxim x = 2. În acest punct semnul derivatei se schimbă de la plus la minus.

O mică notă despre punctele cu coordonate care nu sunt întregi. De exemplu, în ultima problemă a fost considerat punctul x = −3,5, dar cu același succes putem lua x = −3,4. Dacă problema este compilată corect, astfel de modificări nu ar trebui să afecteze răspunsul, deoarece punctele „fără un loc fix de reședință” nu participă direct la rezolvarea problemei. Desigur, acest truc nu va funcționa cu puncte întregi.

Găsirea intervalelor de funcții crescătoare și descrescătoare

Într-o astfel de problemă, precum punctele maxime și minime, se propune utilizarea graficului derivat pentru a găsi zone în care funcția în sine crește sau scade. Mai întâi, să definim ce sunt creșterea și descreșterea:

1. Se spune că o funcție f(x) este în creștere pe un segment dacă pentru oricare două puncte x 1 și x 2 din acest segment este adevărată următoarea afirmație: x 1 ≤ x 2 ⇒ f(x 1) ≤ f(x 2) . Cu alte cuvinte, cu cât valoarea argumentului este mai mare, cu atât valoarea funcției este mai mare.
2. O funcție f(x) se numește descrescătoare pe un segment dacă pentru oricare două puncte x 1 și x 2 din acest segment este adevărată următoarea afirmație: x 1 ≤ x 2 ⇒ f(x 1) ≥ f(x 2). Acestea. valoare mai mare argumentul corespunde valorii mai mici a funcției.

Să formulăm condiții suficiente pentru creștere și scădere:

1. Pentru a functie continua f(x) crește pe segment , este suficient ca derivata sa în interiorul segmentului să fie pozitivă, adică. f’(x) ≥ 0.
2. Pentru ca o funcție continuă f(x) să scadă pe segment, este suficient ca derivata ei în interiorul segmentului să fie negativă, i.e. f’(x) ≤ 0.

Să acceptăm aceste afirmații fără dovezi. Astfel, obținem o schemă pentru găsirea intervalelor de creștere și descreștere, care este în multe privințe similară cu algoritmul de calcul al punctelor extreme:

1. Eliminați toate informațiile inutile. În graficul original al derivatei, ne interesează în primul rând zerourile funcției, așa că le vom lăsa doar pe acestea.
2. Marcați semnele derivatei la intervalele dintre zerouri. Unde f’(x) ≥ 0, funcția crește, iar unde f’(x) ≤ 0, ea scade. Dacă problema stabilește restricții asupra variabilei x, le marchem suplimentar pe un nou grafic.
3. Acum că știm comportamentul funcției și constrângerile, rămâne de calculat cantitatea necesară în problemă.

Sarcină. Figura prezintă un grafic al derivatei funcției f(x) definită pe intervalul [−3; 7,5]. Aflați intervalele de scădere ale funcției f(x). În răspunsul dvs., indicați suma numerelor întregi incluse în aceste intervale.

Ca de obicei, să redesenăm graficul și să marchem limitele [−3; 7.5], precum și zerourile derivatei x = −1.5 și x = 5.3. Apoi notăm semnele derivatei. Avem:

Deoarece derivata este negativă pe intervalul (− 1,5), acesta este intervalul funcției descrescătoare. Rămâne să însumăm toate numerele întregi care se află în acest interval:
−1 + 0 + 1 + 2 + 3 + 4 + 5 = 14.

Sarcină. Figura prezintă un grafic al derivatei funcției f(x), definită pe intervalul [−10; 4]. Aflați intervalele de creștere ale funcției f(x). În răspunsul dvs., indicați lungimea celui mai mare dintre ele.

Să scăpăm de informațiile inutile. Să lăsăm doar limitele [−10; 4] și zerourile derivatei, dintre care au fost patru de data aceasta: x = −8, x = −6, x = −3 și x = 2. Să marchem semnele derivatei și să obținem următoarea imagine:

Suntem interesați de intervalele funcției crescătoare, i.e. astfel unde f’(x) ≥ 0. Există două astfel de intervale pe grafic: (−8; −6) și (−3; 2). Să le calculăm lungimile:
l 1 = − 6 − (−8) = 2;
l 2 = 2 − (−3) = 5.

Deoarece trebuie să găsim lungimea celui mai mare dintre intervale, notăm valoarea l 2 = 5 ca răspuns.

Exemplul 1

Referinţă: Următoarele moduri de notare a unei funcții sunt echivalente: În unele sarcini este convenabil să desemnați funcția ca „joc”, iar în altele ca „ef din x”.

Mai întâi găsim derivata:

Exemplul 2

Calculați derivata unei funcții într-un punct

, , studiu complet al funcției si etc.

Exemplul 3

Calculați derivata funcției în punct. Mai întâi să găsim derivata:

Ei bine, asta e cu totul altă chestiune. Să calculăm valoarea derivatei în punctul:

Dacă nu înțelegeți cum a fost găsit derivatul, reveniți la primele două lecții ale subiectului. Dacă aveți dificultăți (neînțelegeri) cu arctangente și semnificațiile sale, Neapărat studiu material metodologic Grafice și proprietăți functii elementare – chiar ultimul paragraf. Pentru că există încă suficiente arctangente pentru vârsta studenților.

Exemplul 4

Calculați derivata funcției în punct.

Ecuația tangentei la graficul unei funcții

Pentru a consolida paragraful anterior, luați în considerare problema găsirii tangentei la graficul funcțieiîn acest moment. Am întâlnit această sarcină la școală și apare și în cursul matematicii superioare.

Să ne uităm la cel mai simplu exemplu de „demonstrație”.

Scrieți o ecuație pentru tangenta la graficul funcției în punctul de abscisă. Voi oferi imediat o soluție grafică gata făcută problemei (în practică, în majoritatea cazurilor, acest lucru nu este necesar):

O definiție strictă a unei tangente este dată folosind definirea derivatei unei funcții, dar deocamdată vom stăpâni partea tehnică a problemei. Cu siguranță aproape toată lumea înțelege intuitiv ce este o tangentă. Dacă o explicați „pe degete”, atunci tangenta la graficul unei funcții este Drept, care se referă la graficul funcției în singurul punct. În acest caz, toate punctele din apropiere ale dreptei sunt situate cât mai aproape posibil de graficul funcției.

Așa cum se aplică în cazul nostru: la tangentă (notația standard) atinge graficul funcției într-un singur punct.

Și sarcina noastră este să găsim ecuația dreptei.

Derivată a unei funcții într-un punct

Cum se află derivata unei funcții într-un punct? Din formulare rezultă două puncte evidente ale acestei sarcini:

1) Este necesar să se găsească derivata.

2) Este necesar să se calculeze valoarea derivatei la un punct dat.

Exemplul 1

Calculați derivata unei funcții într-un punct

Ajutor: Următoarele moduri de notare a unei funcții sunt echivalente:


În unele sarcini este convenabil să desemnați funcția ca „joc”, iar în altele ca „ef din x”.

Mai întâi găsim derivata:

Sper că mulți s-au obișnuit deja să găsească astfel de derivate pe cale orală.

În a doua etapă, calculăm valoarea derivatei în punctul:

Un mic exemplu de încălzire pentru a o rezolva singur:

Exemplul 2

Calculați derivata unei funcții într-un punct

Soluție completă și răspuns la sfârșitul lecției.

Necesitatea de a găsi derivata într-un punct apare în următoarele sarcini: construirea unei tangente la graficul unei funcții (paragraful următor), studiul unei funcții pentru un extremum , studiul unei funcții pentru flexia unui grafic , studiu complet al funcției si etc.

Dar sarcina în cauză are loc în testeși de la sine. Și, de regulă, în astfel de cazuri funcția dată este destul de complexă. În acest sens, să ne uităm la încă două exemple.

Exemplul 3

Calculați derivata unei funcții la punctul .
Mai întâi să găsim derivata:

Derivatul, în principiu, a fost găsit și puteți înlocui valoarea necesară. Dar chiar nu vreau să fac nimic. Expresia este foarte lungă, iar sensul lui „x” este fracționar. Prin urmare, încercăm să simplificăm cât mai mult posibil derivata noastră. În acest caz, să încercăm să aducem ultimii trei termeni la un numitor comun: la punctul .

Acesta este un exemplu de rezolvat singur.

Cum se află valoarea derivatei funcției F(x) în punctul Xo? Cum rezolvi asta?

Dacă formula este dată, atunci găsiți derivata și înlocuiți X-zero în loc de X. calculati
Dacă vorbim despre examenul de stat unificat B-8, grafic, atunci trebuie să găsiți tangenta unghiului (acut sau obtuz) pe care o formează tangenta la axa X (folosind construcția mentală a unui triunghi dreptunghic și determinând tangenta unghiului)

Timur Adilhodzhaev

În primul rând, trebuie să vă decideți asupra semnului. Dacă punctul x0 este situat în partea inferioară a planului de coordonate, atunci semnul din răspuns va fi minus, iar dacă este mai mare, atunci +.
În al doilea rând, trebuie să știi ce este tange într-un dreptunghi. Și acesta este raportul dintre partea opusă (picior) și latura adiacentă (și piciorul). De obicei, pe tablou există câteva semne negre. Din aceste semne pe care le faci triunghi dreptunghic si gasesti tanges.

Cum să găsiți valoarea derivatei funcției f x în punctul x0?

În cazul general, pentru a găsi valoarea derivatei unei funcții în raport cu o variabilă la un moment dat, trebuie să diferențiați funcția dată în raport cu această variabilă. În cazul dumneavoastră, prin variabila X. În expresia rezultată, în loc de X, puneți valoarea lui X în punctul pentru care trebuie să găsiți valoarea derivatei, adică. în cazul dvs., înlocuiți zero X și calculați expresia rezultată.

Ei bine, dorința ta de a înțelege această problemă, după părerea mea, merită fără îndoială un +, pe care îl dau cu conștiința curată.

Această formulare a problemei găsirii derivatei este adesea setată pentru a întări materialul în sensul geometric al derivatului. Se propune un grafic al unei anumite funcții, complet arbitrar și nu dat de ecuaţieși trebuie să găsiți valoarea derivatei (nu derivata în sine, țineți cont!) la punctul specificat X0. Pentru a face acest lucru, se construiește o tangentă la o funcție dată și se găsesc punctele de intersecție a acesteia cu axele de coordonate. Atunci ecuația acestei tangente se întocmește sub forma y=кx+b.

În această ecuație, coeficientul k și va fi valoarea derivatei. Tot ce rămâne este să găsim valoarea coeficientului b. Pentru a face acest lucru, găsim valoarea lui y la x = o, fie ea egală cu 3 - aceasta este valoarea coeficientului b. Înlocuim valorile lui X0 și Y0 în ecuația originală și găsim k - valoarea noastră a derivatei în acest moment.