Le théorème inverse est inférieur. Théorèmes de Ceva et Ménélas

UN V. Shevkine

FMS № 2007

Théorèmes de Ceva et Ménélas sur l'examen d'État unifié

Un article détaillé "Autour des théorèmes de Ceva et de Ménélas" est publié sur notre site dans la rubrique ARTICLES. Il s'adresse aux professeurs de mathématiques et aux lycéens motivés pour avoir une bonne connaissance des mathématiques. Vous pouvez y revenir si vous souhaitez comprendre le problème plus en détail. Dans cette note, nous allons information brève de l'article mentionné et analysez les solutions aux problèmes de la collection pour la préparation à l'examen d'État unifié-2016.

Théorème de Ceva

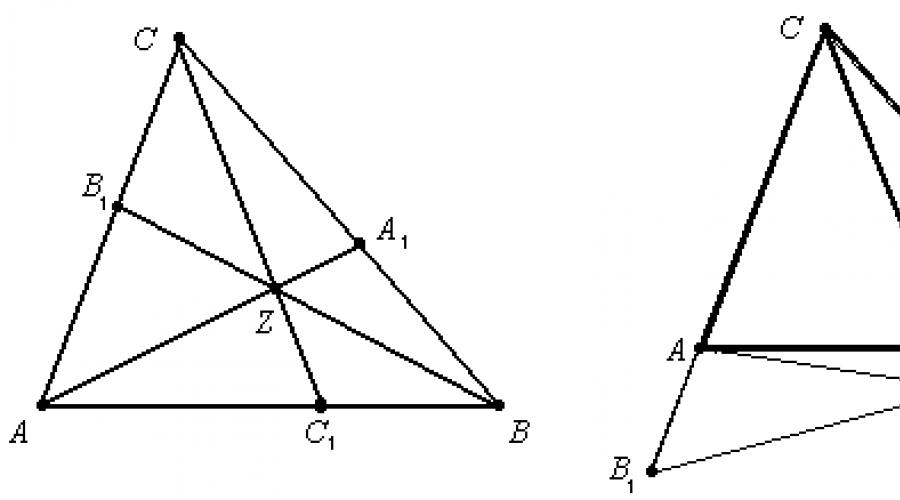
Donnons un triangle abc et sur ses côtés UN B, avant JC et CA les points sont marqués C 1 , UN 1 et B 1 respectivement (Fig. 1).

a) Si les segments AA 1 , BB 1 et CC 1 se croisent en un point, puis

b) Si l'égalité (1) est vraie, alors les segments AA 1 , BB 1 et CC 1 se croisent en un point.

La figure 1 montre le cas où les segments AA 1 , BB 1 et CC 1 se croisent en un point à l'intérieur du triangle. C'est ce qu'on appelle le cas ponctuel intérieur. Le théorème de Ceva est également valable dans le cas d'un point externe, lorsque l'un des points MAIS 1 , B 1 ou DE 1 appartient au côté du triangle, et les deux autres appartiennent aux prolongements des côtés du triangle. Dans ce cas, le point d'intersection des segments AA 1 , BB 1 et CC 1 se trouve à l'extérieur du triangle (Fig. 2).

Comment se souvenir de l'équation de Cheva ?

Faisons attention au mode de mémorisation de l'égalité (1). Les sommets du triangle dans chaque relation et les relations elles-mêmes sont écrits dans le sens de contourner les sommets du triangle abc, en partant du point UN. du point UN aller à l'essentiel B, nous rencontrons un point DE 1, écrivez la fraction
. Plus loin du point À aller à l'essentiel DE, nous rencontrons un point MAIS 1, écrivez la fraction
. Enfin, du point DE aller à l'essentiel MAIS, nous rencontrons un point À 1, écrivez la fraction
. Dans le cas d'un point externe, l'ordre d'écriture des fractions est conservé, bien que les deux "points de partage" du segment soient extérieurs à leurs segments. Dans de tels cas, on dit que le point divise le segment extérieurement.

Notez que tout segment de ligne reliant le sommet d'un triangle à n'importe quel point de la ligne contenant le côté opposé du triangle est appelé ceviana.

Considérons plusieurs manières de prouver l'assertion a) du théorème de Ceva pour le cas d'un point intérieur. Pour prouver le théorème de Ceva, il faut prouver l'énoncé a) par l'une des méthodes proposées ci-dessous, et également prouver l'énoncé b). La preuve de l'assertion b) est donnée après la première méthode de preuve de l'assertion a). Les preuves du théorème de Ceva pour le cas d'un point externe sont effectuées de manière similaire.

Preuve de l'assertion a) du théorème de Ceva en utilisant le théorème sur les segments proportionnels

Laissez trois cevians UNUN 1 , BB 1 et CC 1 se croise en un point Zà l'intérieur du triangle abc.

L'idée de la preuve est de remplacer les rapports des segments d'égalité (1) par les rapports des segments situés sur la même droite.

À travers le point À tracer une ligne parallèle à ceviana SS une . Droit AA 1 coupe la droite construite au point M, et la droite passant par le point C et parallèle AA 1 , - au point J. à travers des points MAIS et DE tracer des lignes droites parallèles aux cevians BB une . Ils franchiront la ligne MV aux points N et R respectivement (fig. 3).

P sur le théorème sur segments proportionnels Nous avons:

,
et
.

Alors les égalités

.

En parallélogrammes ZCTM et ZCRB segments MT, СZ et BRégaux aux côtés opposés d'un parallélogramme. Par conséquent,
et l'égalité est vraie

.

Pour prouver l'assertion b), on utilise l'assertion suivante. Riz. 3

Lemme 1. Si les pointes DE 1 et DE 2 diviser la coupe UN B image interne (ou externe) dans le même sens, en partant du même point, alors ces points coïncident.

Démontrons le lemme pour le cas où les points DE 1 et DE 2 diviser la coupe UN B en interne dans le même sens :
.

Preuve. De l'égalité
suivi des égalités
et
. La dernière d'entre elles n'est remplie qu'à la condition que DE 1 B et DE 2 B sont égaux, c'est-à-dire pourvu que les points DE 1 et DE 2 match.

Preuve du lemme pour le cas où les points DE 1 et DE 2 diviser la coupe UN B extérieurement réalisée de la même manière.

Preuve de l'assertion b) du théorème de Ceva

Soit maintenant l'égalité (1) vraie. Prouvons que les segments AA 1 , BB 1 et CC 1 se croisent en un point.

Laissez les cevians AA 1 et BB 1 se croise en un point Z, tracez un segment passant par ce point CC 2 (DE 2 mensonges sur le segment UN B). Alors, sur la base de l'assertion a), on obtient l'égalité correcte

. (2)

Et En comparant les égalités (1) et (2), nous concluons que
, soit des points DE 1 et DE 2 diviser la coupe UN B dans le même rapport, en partant du même point. Le lemme 1 implique que les points DE 1 et DE 2 match. Cela signifie que les segments AA 1 , BB 1 et CC 1 se croisent en un point, ce qui devait être prouvé.

On peut prouver que la procédure d'écriture de l'égalité (1) ne dépend pas du point et de la direction dans lesquels les sommets du triangle sont contournés.

Exercice 1. Trouver la longueur du segment MAISN dans la figure 4, qui montre les longueurs des autres segments.

Réponse. 8.

Tâche 2. cevians UN M, NE, CK se coupent en un point à l'intérieur du triangle abc. Trouver une attitude
, si
,
. Riz. quatre

Réponse.
.

P nous présentons la preuve du théorème de Ceva de l'article. L'idée de la preuve est de remplacer les rapports des segments d'égalité (1) par les rapports des segments situés sur des droites parallèles.

Laissez tout droit UNUN 1 , BB 1 , CC 1 se croise en un point Oà l'intérieur du triangle abc(Fig. 5). Par le haut DE Triangle abc tracer une ligne parallèle UN B, et ses points d'intersection avec les droites UNUN 1 , BB 1 désignent respectivement UN 2 , B 2 .

De la similitude de deux paires de triangles CC 2 B 1 et ABB 1 , BÊLEMENT 1 et Californie 2 UN 1, fig. 5

nous avons les égalités

,
. (3)

De la similitude des triangles avant JC 1 O et B 2 CO, UNDE 1 O et UN 2 CO nous avons les égalités
, d'où il résulte que

. (4)

P en multipliant les égalités (3) et (4), on obtient l'égalité (1).

L'assertion a) du théorème de Ceva est démontrée.

Considérons les preuves de l'assertion a) du théorème de Ceva à l'aide des aires pour un point intérieur. Il est indiqué dans le livre d'A.G. Myakishev et est basé sur les déclarations que nous formulerons sous forme de devoirs 3 et 4 .

Tâche 3. Le rapport des aires de deux triangles ayant un sommet commun et des bases situées sur la même ligne est égal au rapport des longueurs de ces bases. Démontrez cette affirmation.

Tâche 4. Prouver que si
, alors
et
. Riz. 6

Laissez les segments AA 1 , BB 1 et CC 1 se croise en un point Z(fig. 6), puis

,
. (5)

Et à partir des égalités (5) et le deuxième énoncé de la tâche 4 s'ensuit que
ou
. De même, on obtient que
et
. En multipliant les trois dernières égalités, on obtient :

,

c'est-à-dire que l'égalité (1) est vraie, ce qui devait être prouvé.

L'assertion a) du théorème de Ceva est démontrée.

Tâche 15. Laissez les cevians se croiser en un point à l'intérieur du triangle et divisez-le en 6 triangles dont les aires sont égales à S 1 , S 2 , S 3 , S 4 , S 5 , S 6 (fig. 7). Prouve-le . Riz. sept

Tâche 6. Trouver la région S Triangle CNZ(les aires des autres triangles sont représentées sur la figure 8).

Réponse. 15.

Tâche 7. Trouver la région S Triangle CNO si l'aire du triangle MAISNON est de 10 et
,
(Fig. 9).

Réponse. 30.

Tâche 8. Trouver la région S Triangle CNO si l'aire du triangle MAISavant JC est égal à 88 et ,
(Fig. 9).

R la solution. Puisque , on note
,
. Car , alors on note
,
. Il découle du théorème de Ceva que
, et alors
. Si un
, alors
(Fig. 10). Nous avons trois inconnues ( X, y et S), donc pour trouver S Faisons trois équations.

Car
, alors
= 88. Depuis
, alors
, où
. Car
, alors
.

Alors,
, où
. Riz. Dix

Tâche 9. Dans un triangle abc points K et L appartiennent respectivement aux parties UN B et BC.
,
. P AL et CK. Aire d'un triangle CBP est égal à 1. Trouvez l'aire du triangle abc.

Réponse. 1,75.

J Théorème de Ménélas

Donnons un triangle abc et sur ses côtés CA et CC les points sont marqués B 1 et UN 1 respectivement, et sur le prolongement du côté UN B point marqué C 1 (fig. 11).

a) Si les points MAIS 1 , B 1 et DE 1 mensonge sur la même ligne, puis

. (6)

b) Si l'égalité (7) est vraie, alors les points MAIS 1 , B 1 et DE 1 mensonge sur la même ligne. Riz. Onze

Comment se souvenir de l'égalité de Ménélas ?

La technique de mémorisation de l'égalité (6) est la même que pour l'égalité (1). Les sommets du triangle dans chaque relation et les relations elles-mêmes sont écrits dans le sens de contourner les sommets du triangle abc- de sommet à sommet, en passant par des points de division (internes ou externes).

Tâche 10. Prouver qu'en écrivant l'égalité (6) à partir de n'importe quel sommet du triangle dans n'importe quelle direction, le même résultat est obtenu.

Pour prouver le théorème de Ménélas, il faut prouver l'énoncé a) par l'une des méthodes proposées ci-dessous, et également prouver l'énoncé b). La preuve de l'assertion b) est donnée après la première méthode de preuve de l'assertion a).

Preuve de l'assertion a) en utilisant le théorème sur les segments proportionnels

jefaçon. a) L'idée de la preuve est de remplacer les rapports des longueurs des segments en égalité (6) par les rapports des longueurs des segments se trouvant sur une droite.

Laissez les points MAIS 1 , B 1 et DE 1 mensonge sur la même ligne. À travers le point C traçons une ligne droite je, parallèle à la ligne MAIS 1 B 1 , il coupe la ligne UN Bà ce point M(Fig. 12).

R
est. 12

D'après le théorème des segments proportionnels, on a :
et
.

Alors les égalités
.

Preuve de l'assertion b) du théorème de Ménélas

Soit maintenant l'égalité (6) vraie, nous allons prouver que les points MAIS 1 , B 1 et DE 1 mensonge sur la même ligne. Laissez tout droit UN B et MAIS 1 B 1 se croise en un point DE 2 (fig. 13).

Depuis les pointes MAIS 1 B 1 et DE 2 se trouvent sur la même ligne, puis par l'énoncé a) du théorème de Ménélas

. (7)

D'une comparaison des égalités (6) et (7) nous avons
, d'où il suit que les égalités

,
,
.

La dernière égalité n'est vraie que sous la condition
, c'est-à-dire si les points DE 1 et DE 2 match.

L'assertion b) du théorème de Ménélas est prouvée. Riz. 13

Preuve de l'assertion a) en utilisant la similarité des triangles

L'idée de la preuve est de remplacer les rapports des longueurs des segments d'égalité (6) par les rapports des longueurs des segments situés sur des lignes parallèles.

Laissez les points MAIS 1 , B 1 et DE 1 mensonge sur la même ligne. À partir de points UN, B et C tracer des perpendiculaires AA 0 , BB 0 et SS 0 à cette droite (Fig. 14).

R
est. Quatorze

De la similitude de trois paires de triangles AA 0 B 1 et CC 0 B 1 , CC 0 UN 1 et BB 0 UN 1 , C 1 B 0 B et C 1 UN 0 UN(dans deux coins) nous avons les bonnes égalités

,
,
,

en les multipliant, on obtient :

.

L'assertion a) du théorème de Ménélas est démontrée.

Preuve de l'assertion a) à l'aide des aires

L'idée de la preuve est de remplacer le rapport des longueurs des segments d'égalité (7) par les rapports des aires des triangles.

Laissez les points MAIS 1 , B 1 et DE 1 mensonge sur la même ligne. Relier les points C et C une . Dénoter les aires des triangles S 1 , S 2 , S 3 , S 4 , S 5 (fig. 15).

Alors les égalités

,
,
. (8)

En multipliant les égalités (8), on obtient :

L'assertion a) du théorème de Ménélas est démontrée.

R
est. quinze

Tout comme le théorème de Ceva reste valable si le point d'intersection de Cevian est à l'extérieur du triangle, le théorème de Ménélas reste valable si la sécante ne coupe que les extensions des côtés du triangle. Dans ce cas, on peut parler de l'intersection des côtés du triangle en des points externes.

Preuve de l'assertion a) pour le cas des points externes

P l'embouchure de la sécante coupe les côtés du triangle abc aux points externes, c'est-à-dire coupe les prolongements des côtés UN B,avant JC et CA aux points C 1 , UN 1 et B 1, respectivement, et ces points se trouvent sur la même ligne droite (Fig. 16).

D'après le théorème des segments proportionnels, on a :

et .

Alors les égalités

L'assertion a) du théorème de Ménélas est démontrée. Riz. 16

Notez que la preuve ci-dessus coïncide avec la preuve du théorème de Ménélas pour le cas où la sécante coupe deux côtés du triangle aux points internes et un au point externe.

La preuve de l'assertion b) du théorème de Ménélas pour le cas des points externes est similaire à la preuve donnée ci-dessus.

O enfer11. Dans un triangle abc points MAIS 1 , À 1 mensonge respectivement sur les côtés Soleil et UNDE. P- point d'intersection des segments AA 1 et BB 1 .
,
. Trouver une attitude
.

La solution. Dénoter
,
,
,
(Fig. 17). Par le théorème de Ménélas pour un triangle avant JCÀ 1 et sécante Pennsylvanie 1 écrire la bonne égalité :

,

d'où il suit que

. Riz. 17

Réponse. .

O enfer12 (Université d'Etat de Moscou, cours préparatoires par correspondance). Dans un triangle abc, dont l'aire est 6, sur le côté UN B point pris À, divisant ce côté par rapport à
, et sur le côté CA- point L, partage CA en couple
. Point P intersections de lignes CS et ÀL retiré de la ligne UN Bà une distance de 1,5. Trouver la longueur du côté UN B.

La solution.À partir de points R et DE laissons tomber les perpendiculaires RP et CM directement UN B. Dénoter
,
,
,
(Fig. 18). Par le théorème de Ménélas pour un triangle AKC et sécante PLécris la bonne équation :
, d'où nous obtenons que
,
. Riz. dix-huit

De la similitude des triangles ÀMC et ÀPR(sur deux coins) nous obtenons que
, d'où il suit que
.

Maintenant, connaissant la longueur de la hauteur dessinée sur le côté UN B Triangle abdos, et l'aire de ce triangle, on calcule la longueur du côté :
.

Réponse. 4.

O enfer13. Trois cercles avec des centres MAIS,À,DE, dont les rayons sont liés comme
, se touchent extérieurement aux points X, Oui, Z comme le montre la figure 19. Segments HACHE et PAR se croisent en un point O. Dans quel rapport, en partant du point B, segment de ligne cz divise le segment PAR?

La solution. Dénoter
,
,
(Fig. 19). Car
, puis par l'assertion b) du théorème de Ceva, les segments MAISX, PAR et DEZ se croisent en un point O. Ensuite la tranche cz divise le segment PAR en couple
. Trouvons cette relation. Riz. 19

Par le théorème de Ménélas pour un triangle BCY et sécante BŒUF Nous avons:
, d'où il suit que
.

Réponse. .

Tâche 14 (USE-2016).

points À 1 et DE CA et UN B Triangle abc, en outre UN B 1:B 1 DE =
= CA 1:DE 1 B. Direct BB 1 et SS 1 se croisent en un point O.

un ) Démontrer que la ligne JSC couper le côté en deux Soleil.

UN B 1 CO 1 à l'aire d'un triangle abc s'il est connu que UN B 1:B 1 DE = 1:4.

La solution. a) Laissez la ligne AO traverse le côté avant JC à ce point UN 1 (fig. 20). Par le théorème de Ceva, on a :

. (9)

Car UN B 1:B 1 DE = CA 1:DE 1 B, alors il résulte de l'égalité (9) que
, C'est Californie 1 = MAIS 1 B, ce qui devait être prouvé. Riz. vingt

b) Soit l'aire du triangle UN B 1 O est égal à S. Car UN B 1:B 1 DE CC 1 O est égal à 4 S, et l'aire du triangle AOC est égal à 5 S. Puis l'aire du triangle AOB est aussi égal à 5 S, puisque les triangles AOB et AOC avoir un terrain d'entente AO, et leurs sommets B et Cà égale distance de la ligne AO. Et l'aire du triangle AOC 1 est égal S, car CA 1:DE 1 B = 1:4. Puis l'aire du triangle ABB 1 est égal à 6 S. Car UN B 1:B 1 DE= 1:4, puis l'aire du triangle CC 1 O est égal à 24 S, et l'aire du triangle abc est égal à 30 S. Trouvons maintenant le rapport de l'aire du quadrilatère UN B 1 CO 1 (2S) à l'aire du triangle abc (30S), il est égal à 1:15.

Réponse. 1:15.

Tâche 15 (USE-2016).

points À 1 et DE 1 mensonge sur les côtés respectivement CA et UN B Triangle abc, en outre UN B 1:B 1 DE =
= CA 1:DE 1 B. Direct BB 1 et SS 1 se croisent en un point O.

a) Montrer que la droite JSC couper le côté en deux Soleil.

b) Trouver le rapport de l'aire du quadrilatère UN B 1 CO 1 à l'aire d'un triangle abc s'il est connu que UN B 1:B 1 DE = 1:3.

Réponse. 1:10.

O tache 16 (USE-2016). Sur le segment BD point pris DE. Bissecteur BL abc avec socle Soleil BLD avec socle BD.

a) Démontrer que le triangle CDL isocèle.

b) On sait que cos
abc DL, c'est-à-dire triangle BD point pris DE. Bissecteur BL triangle isocèle abc avec socle Soleil est un côté latéral d'un triangle isocèle BLD avec socle BD.

a) Démontrer que le triangle CDL isocèle.

b) On sait que cos abc= . De quelle manière est le direct DL divise le côté UN B?

Réponse. 4:21.

Littérature

1. Smirnova I.M., Smirnov V.A. Merveilleux points et lignes triangulaires. M. : Mathématiques, 2006, n°17.

2. Myakishev A.G. Éléments de géométrie triangulaire. (Série "Bibliothèque "Éducation mathématique""). M. : MTsNMO, 2002. - 32 p.

3. Géométrie. Chapitres supplémentaires pour le manuel de 8e année : Manuel pour les élèves des écoles et des classes avec étude approfondie / L.S. Atanasyan, V.F. Butuzov, S.B. Kadomtsev et autres - M. : Vita-Press, 2005. - 208 p.

4. Erdniev P., Mantsaev N. Cheva et théorèmes de Ménélas. M. : Kvant, 1990, n° 3, p. 56–59.

5. Sharygin I.F. Théorèmes de Ceva et Ménélas. Moscou : Kvant, 1976, n° 11, pp. 22–30.

6. Vavilov V.V. Médianes et lignes médianes d'un triangle. M. : Mathématiques, 2006, n°1.

7. Efremov Dm. Nouvelle géométrie triangulaire. Odessa, 1902. - 334 p.

8. Mathématiques. 50 variantes de tâches de test typiques / I.V. Yashchenko, M.A. Volkevitch, I.R. Vysotsky et autres; éd. I.V. Iachtchenko. - M.: Maison d'édition "Examen", 2016. - 247 p.

Dans le cours de géométrie il y a des théorèmes qui ne sont pas étudiés en détail à l'école, mais qui peuvent être utiles pour résoudre les plus tâches difficiles OGE et EGE. Ceux-ci incluent, par exemple, le théorème de Ménélas. Traditionnellement, il est étudié dans des classes avec une étude approfondie des mathématiques en 8e année, et dans le programme régulier (selon le manuel d'Atanasyan), le théorème de Ménélas est inclus dans le manuel des classes 10-11.
Pendant ce temps, le résultat de l'étude des ressources Internet qui mentionnent le théorème de Ménélas montre qu'il est généralement formulé de manière incomplète et donc inexacte, et tous les cas de son utilisation, ainsi que la preuve du théorème inverse, ne sont pas donnés. Le but de cet article est de comprendre ce qu'est le théorème de Ménélas, comment et pourquoi il est utilisé, et aussi de partager la méthodologie pour enseigner ce théorème sur cours particuliers tuteur avec les élèves.
Envisager tâche typique(Tâche n ° 26, OGE), qui se produit lors d'examens dans une variété d'options qui ne diffèrent que par le nombre dans la condition.

La solution au problème lui-même est simple - vous pouvez la lire ci-dessous. Dans cet article, cependant, nous nous intéressons principalement à un point légèrement différent, qui est souvent omis, compris comme allant de soi, comme une évidence. Mais l'évidence est ce qui peut être prouvé. Et cela peut être prouvé de différentes manières - généralement ils le prouvent exclusivement à l'aide de la similitude - mais c'est également possible à l'aide du théorème de Ménélas.
Il découle de la condition que, puisque les angles à la base inférieure du trapèze totalisent 90 °, alors si nous prolongeons les côtés, nous obtenons triangle rectangle. De plus, à partir du point d'intersection résultant des extensions des côtés latéraux, un segment est dessiné qui passe par les points médians des bases. Et pourquoi ce segment passe-t-il par ces trois points ? Habituellement, pas un mot n'est dit à ce sujet dans les solutions du problème trouvées sur Internet. Il n'y a même pas de référence au théorème du trapèze à quatre points, encore moins une preuve de cette affirmation. Pendant ce temps, il peut être prouvé en utilisant le théorème de Ménélas, qui est une condition d'appartenance Trois pointsà une seule ligne droite.

Énoncés du théorème de Ménélas
Il est temps de formuler le théorème. Il convient de noter que dans divers manuels et manuels, il en existe des formulations assez différentes, bien que l'essence reste inchangée. Dans le manuel d'Atanasyan et d'autres pour les élèves de la 10e à la 11e année, la formulation suivante du théorème de Ménélas est donnée, appelons-la "vecteur":

Dans le manuel "Geometry grade 10-11" Alexandrov et al., ainsi que dans guide d'étude les mêmes auteurs « Géométrie. 8e année ”une formulation légèrement différente du théorème de Ménélas est donnée, et pour les années 10-11 et pour la 8e année, c'est la même chose:
Trois remarques s'imposent ici.
Remarque 1. Dans les examens, aucun problème ne doit être résolu uniquement à l'aide de vecteurs, pour lesquels exactement "moins un" est utilisé. Par conséquent, pour utilisation pratique la formulation la plus commode est, en fait, une conséquence du théorème d'intervalle (c'est la deuxième formulation en gras). Nous nous limiterons à lui pour une étude plus approfondie du théorème de Ménélas, puisque notre but est d'apprendre à l'appliquer pour résoudre des problèmes.
Remarque 2. Malgré le fait que tous les manuels stipulent clairement le cas où les trois points A 1 , B 1 et C 1 peuvent se trouver sur les prolongements des côtés du triangle (ou sur les lignes contenant les côtés du triangle), sur plusieurs Sites de tutorat sur Internet uniquement le cas est formulé lorsque deux points se trouvent sur deux côtés, et le troisième se trouve sur l'extension du troisième côté. Cela peut difficilement être justifié par le fait que seuls les problèmes du premier type sont rencontrés dans les examens et les problèmes ne peuvent pas être rencontrés lorsque tous ces points se trouvent sur les extensions de trois côtés.
Note 3. Théorème inverse, c'est à dire. la condition pour que trois points se trouvent sur la même ligne droite n'est généralement pas prise en compte du tout, et certains tuteurs conseillent même (???) de ne traiter que le théorème direct et de ne pas considérer le théorème inverse. Pendant ce temps, la preuve de l'énoncé inverse est assez instructive et permet de prouver des énoncés similaires à ceux donnés dans la solution du problème 1. L'expérience de prouver le théorème inverse donnera sans aucun doute un avantage tangible à l'étudiant dans la résolution de problèmes.

Dessins et patrons

Afin d'enseigner à l'étudiant à voir le théorème de Ménélas dans les problèmes et à l'utiliser dans la résolution, il est important de prêter attention aux dessins et aux modèles dans le dossier du théorème pour un cas particulier. Et puisque le théorème lui-même est sous sa forme "pure", c'est-à-dire sans être entouré d'autres segments, les côtés de diverses figures dans les problèmes ne se produisent généralement pas, il est alors plus opportun de montrer le théorème sur des problèmes spécifiques. Et si vous montrez des images comme explication, rendez-les multivariées. Dans le même temps, mettez en surbrillance avec une couleur (par exemple, rouge) la ligne droite, qui est formée de trois points, et bleu - les segments du triangle impliqués dans l'enregistrement du théorème de Ménélas. Dans le même temps, les éléments qui ne participent pas restent noirs :

À première vue, il peut sembler que la formulation du théorème est assez compliquée et pas toujours claire ; car il s'agit de trois fractions. En effet, si l'étudiant n'a pas assez d'expérience, il peut facilement faire une erreur d'écriture et, par conséquent, résoudre le problème de manière incorrecte. Et ici, parfois, les problèmes commencent. Le fait est que les manuels ne se concentrent généralement pas sur la façon de "faire le détour" lors de l'écriture d'un théorème. Rien n'est dit sur les régularités d'écriture du théorème lui-même. Par conséquent, certains tuteurs dessinent même des flèches différentes, dans quel ordre écrire la formule. Et ils demandent aux étudiants de suivre strictement ces directives. C'est en partie correct, mais il est beaucoup plus important de comprendre l'essence du théorème que de l'écrire purement mécaniquement en utilisant la "règle de contournement" et les flèches.
En fait, il est important de ne comprendre que la logique du "by-pass", et elle est si précise qu'il est impossible de se tromper en écrivant la formule. Dans les deux cas a) et b) nous écrivons la formule du triangle AMC.
Pour commencer, nous déterminons nous-mêmes trois points - les sommets du triangle. Nous avons ces points A, M, C. Ensuite, nous déterminons les points situés sur la ligne d'intersection (ligne rouge), ce sont B, P, K. Nous commençons le "mouvement" du haut du triangle, par exemple, de point C. De ce point, nous "allons" au point formé par l'intersection, par exemple, du côté AC et de la ligne d'intersection - nous avons ce point K. Nous écrivons au numérateur de la première fraction - SK. Plus loin du point K, nous "allons" au point restant sur la ligne AC - au point A. Au dénominateur de la première fraction, nous écrivons - KA. Comme le point A appartient aussi à la droite AM, on fait de même avec les segments de la droite AM. Et là encore, nous partons du sommet, puis "allons" à un point sur la ligne d'intersection, après quoi nous allons au sommet M. Après nous être "trouvés" sur la ligne BC, nous faisons de même avec les segments sur cette ligne. Bien sûr, on "passe" de M à B, après quoi on revient à C. Ce "bypass" peut se faire aussi bien dans le sens des aiguilles d'une montre que dans le sens inverse des aiguilles d'une montre. Il est seulement important de comprendre la règle de contournement - d'un sommet à un point sur une ligne droite, et d'un point sur une ligne droite à un autre sommet. Quelque chose comme cela est généralement expliqué par la règle d'écriture du produit des fractions. Le résultat est:
Faisons attention au fait que l'ensemble du "contournement" est reflété dans l'enregistrement et est indiqué par des flèches pour plus de commodité.
Cependant, l'enregistrement résultant peut être récupéré sans effectuer de « parcours ». Une fois les points écrits - les sommets du triangle (A, M, C) et les points - situés sur la ligne d'intersection (B, P, K), ils écrivent également des triplets de lettres désignant les points situés sur chacun des trois lignes. Dans nos cas, ce sont I) B , M , C ; II) A , P , M et III) A , C , K . Après cela, la partie gauche correcte de la formule peut être écrite sans même regarder le dessin et dans n'importe quel ordre. Il nous suffit d'écrire de vraies fractions à partir de chaque triplet de lettres, qui obéissent à la règle - conditionnellement, les lettres "du milieu" sont les points de la ligne d'intersection (rouge). Classiquement, les lettres "extrêmes" sont les points des sommets du triangle (bleu). Lorsque vous écrivez une formule de cette manière, il vous suffit de vous assurer que toute lettre "bleue" (le sommet du triangle) touche une fois le numérateur et le dénominateur. Par exemple.
Cette méthode est particulièrement utile pour les cas comme b) et aussi pour l'auto-test.

Théorème de Ménélas. Preuve de
Il y a plusieurs différentes manières preuve du théorème de Ménélas. Parfois, ils prouvent en utilisant la similitude des triangles, pour lesquels un segment parallèle à AC est tracé à partir du point M (comme sur ce dessin). D'autres tracent une ligne supplémentaire qui n'est pas parallèle à la ligne d'intersection, puis avec des lignes parallèles à la ligne d'intersection, ils semblent "projeter" tous les segments nécessaires sur cette ligne et, en utilisant une généralisation du théorème de Thales (c'est-à-dire le théorème sur les segments proportionnels), dérivez une formule. Cependant, le moyen le plus simple de le prouver est peut-être obtenu en traçant une ligne droite partant du point M parallèle à celui qui se croise. Démontrons ainsi le théorème de Ménélas.
Soit : Triangle ABC. La ligne PK coupe les côtés du triangle et le prolongement du côté MC au point B.
Montrer que l'égalité est vraie :
Preuve. Traçons une poutre MM 1 parallèle à BK. Écrivons les relations auxquelles participent les segments inclus dans la formule du théorème de Ménélas. Dans un cas, considérons les lignes se coupant au point A, et dans l'autre cas, se coupant au point C. Multiplions les parties gauche et droite de ces équations :

Le théorème a été démontré.
Le théorème se démontre de manière similaire pour le cas b).

Du point C on trace un segment CC 1 parallèle à la droite BK. Écrivons les relations auxquelles participent les segments inclus dans la formule du théorème de Ménélas. Dans un cas, on considère des lignes se coupant au point A, et dans l'autre cas, se coupant au point M. Puisque le théorème de Thales ne dit rien sur l'emplacement des segments sur deux lignes qui se croisent, les segments peuvent également être situés sur des côtés opposés du point M. Donc

Le théorème a été démontré.

Nous prouvons maintenant le théorème inverse.
Donné:
Démontrer que les points B, P, K sont sur la même droite.
Preuve. Soit la ligne BP coupe AC en un point K 2 qui ne coïncide pas avec le point K. Puisque BP est une ligne contenant le point K 2 , le théorème de Ménélas qui vient d'être démontré est valable pour lui. Donc, pour cela, nous écrivons
Or, nous venons de montrer que
Il s'ensuit que les points K et K 2 coïncident, puisqu'ils partagent le côté AC dans le même rapport.
Pour le cas b), le théorème se démontre de manière similaire.

Résolution de problèmes à l'aide du théorème de Ménélas

Tout d'abord, revenons au problème 1 et résolvons-le. Relisons-le encore. Faisons un dessin :

Soit un trapèze ABCD. ST - la ligne médiane du trapèze, c'est-à-dire une de ces distances. Les angles A et D totalisent 90°. Nous prolongeons les côtés AB et CD et à leur intersection nous obtenons le point K. Relions le point K au point N - le milieu de BC. Montrons maintenant que le point P, qui est le milieu de la base de AD, appartient aussi à la droite KN. Considérons successivement les triangles ABD et ACD. La droite KP coupe deux côtés de chaque triangle. Supposons que la droite KN coupe la base AD en un point X. D'après le théorème de Ménélas :
Puisque le triangle AKD est rectangle, le point P, qui est le milieu de l'hypoténuse AD, est équidistant de A, D et K. De même, le point N est équidistant des points B, C et K. D'où une base est 36 et l'autre est 2.
La solution. Considérons le triangle BCD. Il est traversé par le rayon AX, où X est le point d'intersection de ce rayon avec le prolongement du côté BC. D'après le théorème de Ménélas :
En substituant (1) à (2) on obtient :

La solution. Soit S 1 , S 2 , S 3 et S 4 les aires des triangles AOB, AOM, BOK et du quadrilatère MOKC respectivement.

Puisque BM est la médiane, alors S ABM = S BMC .
Donc S 1 + S 2 = S 3 + S 4 .
Puisque nous devons trouver le rapport des aires S 1 et S 4, nous divisons les deux côtés de l'équation par S 4 :
Substituons ces valeurs dans la formule (1): A partir du triangle BMC avec la sécante AK, d'après le théorème de Ménélas, on a : A partir du triangle AKC avec la sécante BM, d'après le théorème de Ménélas, on a : Tous les rapports nécessaires sont exprimés en termes de k, et maintenant nous pouvons les substituer dans l'expression (2) :
La solution à ce problème en utilisant le théorème de Ménélas est considérée sur la page.

Note du professeur de mathématiques. L'application du théorème de Ménélas à ce problème est le cas même où cette méthode peut considérablement gagner du temps sur l'examen. Cette tâche est proposée dans la version de démonstration de l'examen d'entrée au lycée de l'École supérieure d'économie pour la 9e année (2019).

© Tuteur de mathématiques à Moscou, Alexander Anatolyevich, 8-968-423-9589.

Décider vous-même

1) La tâche est plus facile. Un point M est marqué sur la médiane BD du triangle ABC tel que BM : MD = m : n. La ligne AM coupe le côté BC au point K.
Trouvez le rapport BK:KC.
2) La tâche est plus difficile. La bissectrice de l'angle A du parallélogramme ABCD coupe le côté BC au point P, et la diagonale BD au point T. On sait que AB : AD = k (0 3) Tâche numéro 26 OGE. Dans le triangle ABC, la bissectrice BE et la médiane AD sont perpendiculaires et ont même longueur égale à 36. Trouver les côtés du triangle ABC.
Indice de tuteur en mathématiques. Sur Internet, il existe une solution à un tel problème à l'aide d'une construction supplémentaire, puis soit de similitude, soit de recherche de zones, et seulement après cela, les côtés du triangle. Ceux. ces deux méthodes nécessitent une construction supplémentaire. Cependant, la solution d'un tel problème à l'aide de la propriété bissectrice et du théorème de Ménélas ne nécessite aucune construction supplémentaire. C'est beaucoup plus simple et plus rationnel.

Classer: 9

Objectifs de la leçon:

1. généraliser, élargir et systématiser les connaissances et les compétences des étudiants; enseigner comment utiliser les connaissances pour résoudre des problèmes complexes;
2. promouvoir le développement de compétences pour l'application indépendante des connaissances dans la résolution de problèmes;
3. développer la pensée logique et le discours mathématique des élèves, la capacité d'analyser, de comparer et de généraliser;
4. éduquer les étudiants à la confiance en soi, à la diligence; Capacité de travailler en équipe.

Objectifs de la leçon:

• Éducatif: répéter les théorèmes de Ménélas et de Ceva ; les appliquer à la résolution de problèmes.
• Développement: apprendre à émettre une hypothèse et à défendre habilement son opinion par des preuves ; tester sa capacité à généraliser et à systématiser ses connaissances.
• Éducatif: accroître l'intérêt pour le sujet et se préparer à résoudre des problèmes plus complexes.

Type de leçon : leçon de généralisation et de systématisation des connaissances.

Équipement: cartes pour le travail de groupe dans la leçon sur un sujet donné, cartes individuelles pour travail indépendant, ordinateur, projecteur multimédia, écran.

Pendant les cours

je mets en scène. Moment organisationnel (1 min.)

L'enseignant explique le sujet et le but de la leçon.

IIe stade. Actualisation des connaissances et compétences de base (10 min.)

Prof: Dans la leçon, nous rappelons les théorèmes de Ménélas et Ceva afin de passer avec succès à la résolution de problèmes. Jetons un coup d'œil à l'écran avec vous. A quel théorème correspond cette image ? (théorème de Ménélas). Essayez d'énoncer clairement le théorème.

Image 1

Soit le point A 1 sur le côté BC du triangle ABC, le point C 1 sur le côté AB, le point B 1 sur le prolongement du côté AC au-delà du point C. Les points A 1 , B 1 et C 1 sont sur la même droite si et seulement si égalité

Prof: Regardons ensemble la photo suivante. Formulez un théorème pour cette figure.

Figure 2

La droite AD coupe deux côtés et le prolongement du troisième côté du triangle BMC.

D'après le théorème de Ménélas

La droite MB coupe deux côtés et le prolongement du troisième côté du triangle ADC.

D'après le théorème de Ménélas

Prof: A quel théorème correspond l'image ? (théorème de Ceva). Formuler un théorème.

figure 3

Soit dans le triangle ABC le point A 1 se trouve sur le côté BC, le point B 1 se trouve sur le côté AC, le point C 1 se trouve sur le côté AB. Les segments AA 1 , BB 1 et CC 1 se coupent en un point si et seulement si l'égalité

Stade III. Résolution de problème. (22 min.)

La classe est divisée en 3 équipes, chacune reçoit une carte avec deux diverses tâches. Le temps est donné pour résoudre, puis l'écran affiche<Рисунки 4-9>. Selon les dessins prêts à l'emploi pour les tâches, les représentants des équipes expliquent à tour de rôle leur solution. Chaque explication est suivie d'une discussion, de réponses aux questions et de vérification de l'exactitude de la solution à l'écran. Tous les membres de l'équipe participent à la discussion. Plus l'équipe est active, plus elle est évaluée haut lors de la synthèse.

Carte 1.

1. Dans le triangle ABC du côté BC le point N est pris tel que NC = 3BN ; sur le prolongement du côté AC, le point M est pris comme point A de sorte que MA = AC. La droite MN coupe le côté AB au point F. Trouver le rapport

2. Démontrer que les médianes d'un triangle se coupent en un point.

solution 1

Figure 4

Par la condition du problème, MA = AC, NC = 3BN. Soit MA = AC =b, BN = k, NC = 3k. La droite MN coupe deux côtés du triangle ABC et le prolongement du troisième.

D'après le théorème de Ménélas

Réponse:

Preuve 2

Figure 5

Soient AM 1 , BM 2 , CM 3 les médianes du triangle ABC. Pour prouver que ces segments se coupent en un point, il suffit de montrer que

Ensuite, par le théorème (inverse) de Ceva, les segments AM 1 , BM 2 et CM 3 se coupent en un point.

Nous avons:

Ainsi, il est prouvé que les médianes d'un triangle se coupent en un point.

Carte 2.

1. Le point N est pris du côté PQ du triangle PQR, et le point L est pris du côté PR, et NQ = LR. Le point d'intersection des segments QL et NR divise QL dans le rapport m:n, en partant du point Q. Trouver

2. Démontrer que les bissectrices d'un triangle se coupent en un point.

solution 1

Figure 6

Par hypothèse NQ = LR, Soit NA = LR =a, QF = km, LF = kn. La droite NR coupe deux côtés du triangle PQL et le prolongement du troisième.

D'après le théorème de Ménélas

Réponse:

Preuve 2

Figure 7

Montrons que

Alors, par le théorème (inverse) de Ceva, AL 1 , BL 2 , CL 3 se coupent en un point. D'après la propriété des bissectrices d'un triangle

En multipliant les égalités obtenues terme à terme, on obtient

Pour les bissectrices d'un triangle, l'égalité de Ceva est satisfaite, par conséquent, elles se coupent en un point.

Carte 3.

1. Dans le triangle ABC AD est la médiane, le point O est le milieu de la médiane. La droite BO coupe le côté AC au point K. Dans quel rapport le point K divise-t-il AC, à partir du point A ?

2. Prouver que si un cercle est inscrit dans un triangle, alors les segments reliant les sommets du triangle aux points de contact des côtés opposés se coupent en un point.

solution 1

Figure 8

Soit BD = DC = a, AO = OD = m. La droite VC coupe deux côtés et le prolongement du troisième côté du triangle ADC.

D'après le théorème de Ménélas

Réponse:

Preuve 2

Figure 9

Soient A 1 , B 1 et C 1 les points tangents du cercle inscrit au triangle ABC. Pour prouver que les segments AA 1 , BB 1 et CC 1 se coupent en un point, il suffit de montrer que l'égalité de Ceva est vraie :

En utilisant la propriété des tangentes tracées à un cercle à partir d'un point, nous introduisons la notation : C 1 B = BA 1 = x, AC 1 = CB 1 = y, BA 1 = AC 1 = z.

L'égalité de Ceva est valable, ce qui signifie que les bissectrices du triangle se coupent en un point.

stade IV. Résolution de problèmes (travail autonome) (8 min.)

Enseignant : Le travail des équipes est terminé et nous allons maintenant commencer un travail indépendant sur les cartes individuelles pour 2 options.

Matériel pour la leçon pour le travail indépendant des étudiants

Option 1. Dans un triangle ABC, dont l'aire est 6, du côté AB, un point K est pris, divisant ce côté dans le rapport AK:BK = 2:3, et du côté AC - point L, divisant AC en le rapport AL:LC = 5:3. Le point Q d'intersection des lignes СК et BL est éloigné de la ligne AB à une distance . Trouver la longueur du côté AB. (Réponse : 4.)

Option 2. Le point K est pris du côté AC du triangle ABC. AK = 1, KS = 3. Le point L est pris du côté AB. AL:LÂ = 2:3, Q est le point d'intersection des droites BK et CL. Trouvez la longueur de la hauteur du triangle ABC, abaissé à partir du sommet B. (Réponse : 1.5.)

Le travail est soumis à l'enseignant pour révision.

Stade V. Résumé de la leçon (2 min.)

Les erreurs sont analysées, les réponses originales et les commentaires sont notés. Les résultats du travail de chaque équipe sont résumés et des notes sont attribuées.

Stade VI. Devoirs (1 min.)

Les devoirs sont constitués des tâches n°11, 12 p.289-290, n°10 p.301.

Dernier mot du professeur (1 min).

Aujourd'hui, vous avez entendu le discours mathématique de l'autre de côté et évalué vos capacités. À l'avenir, nous utiliserons ces discussions pour mieux comprendre le sujet. Les arguments de la leçon étaient amis avec les faits, et la théorie avec la pratique. Merci à tous.

Littérature:

1. Tkachuk V.V. Mathématiques pour un candidat. – M. : MTsNMO, 2005.

— Quel est le point commun entre le théorème de Ménélas et les médicaments ?
Tout le monde les connaît, mais personne n'en parle.
Conversation typique avec un étudiant

C'est un théorème cool qui vous aidera au moment où il semble que rien ne vous aidera. Dans la leçon, nous formulerons le théorème lui-même, envisagerons plusieurs options pour son utilisation, et en dessert, vous trouverez un sévère devoirs. Aller!

Pour commencer, le libellé. Je ne donnerai peut-être pas la version la plus «belle» du théorème, mais la plus compréhensible et la plus pratique.

Théorème de Ménélas. Considérons un triangle arbitraire $ABC$ et une ligne $l$ qui coupe deux côtés de notre triangle en interne et un côté sur la continuation. Notons les points d'intersection de $M$, $N$ et $K$ :

Triangle $ABC$ et sécante $l$

Alors la relation suivante est vraie :

\[\frac(AM)(MB)\cdot \frac(BN)(NC)\cdot \frac(CK)(KA)=1\]

Je tiens à préciser : ne fourrez pas l'emplacement des lettres dans cette formule maléfique ! Maintenant, je vais vous dire un algorithme par lequel vous pouvez toujours restaurer les trois fractions littéralement à la volée. Même pendant l'examen sous stress. Même si vous êtes assis à la géométrie à 3 heures du matin et que vous ne comprenez rien du tout. :)

Le schéma est simple :

1. Nous dessinons un triangle et une sécante. Par exemple, comme le montre le théorème. Nous désignons les sommets et les points avec quelques lettres. Il peut s'agir d'un triangle arbitraire $ABC$ et d'une ligne droite avec des points $M$, $N$, $K$ ou autre - ce n'est pas le sujet.
2. Nous posons un stylo (crayon, marqueur, plume d'oie) à n'importe quel sommet du triangle et commençons à contourner les côtés de ce triangle avec l'approche obligatoire des points d'intersection avec la ligne. Par exemple, si nous allons d'abord du point $A$ au point $B$, alors nous obtenons des segments : $AM$ et $MB$, puis $BN$ et $NC$, puis (attention !) $CK$ et $KA$ . Étant donné que le point $K$ se trouve dans le prolongement du côté $AC$, lors du passage de $C$ à $A$, vous devrez temporairement quitter le triangle.
3. Et maintenant, nous divisons simplement les segments adjacents les uns aux autres exactement dans l'ordre dans lequel nous les avons obtenus lors du contournement : $AM/MB$, $BN/NC$, $CK/KA$ - nous obtenons trois fractions, le produit de qui nous donnera l'unité.

Sur le dessin, cela ressemblera à ceci:

circuits simples, vous permettant de restaurer la formule de T. Ménélas

Et juste quelques commentaires. Plus précisément, ce ne sont même pas des commentaires, mais des réponses à des questions typiques :

• Que se passe-t-il si la droite $l$ passe par le sommet du triangle ? Réponse : rien. Le théorème de Ménélas ne fonctionne pas dans ce cas.
• Que se passe-t-il si vous choisissez un autre sommet pour commencer ou si vous partez dans l'autre sens ? Réponse : ce sera la même chose. Cela change juste l'ordre des fractions.

Je pense que nous avons le bon libellé. Voyons comment tout ce jeu est utilisé pour résoudre des problèmes géométriques complexes.

Pourquoi tout cela est-il nécessaire ?

Avertissement. Une utilisation excessive du théorème de Ménélas pour résoudre des problèmes planimétriques peut causer des dommages irréparables à votre psychisme, car ce théorème accélère considérablement les calculs et vous rappelle d'autres faits importants du cours de géométrie scolaire.

Preuve

Je ne vais pas le prouver. :)

D'accord, laissez-moi le prouver.

Il reste maintenant à comparer les deux valeurs obtenues pour le segment $CT$ :

\[\frac(AM\cdot BN\cdot CK)(BM\cdot CN\cdot AK)=1;\]

\[\frac(AM)(BM)\cdot \frac(BN)(CN)\cdot \frac(CK)(AK)=1;\]

OK, tout est fini maintenant. Il ne reste plus qu'à "peigner" cette formule, en plaçant correctement les lettres à l'intérieur des segments - et la formule est prête. :)

Théorème de Ménélas ou le théorème complet à quatre côtés est connu depuis l'époque La Grèce ancienne. Il a été nommé d'après son auteur, un ancien mathématicien et astronome grec. Ménélas d'Alexandrie(environ 100 après JC). Ce théorème est très beau et simple, mais, malheureusement, il ne reçoit pas l'attention qu'il mérite dans le cours de l'école moderne. Et, en attendant, dans de nombreux cas, cela aide à résoudre très facilement et avec élégance des problèmes géométriques assez complexes.

Théorème 1 (théorème de Ménélas). Soit ∆ABC intersecté par une droite non parallèle au côté AB et coupant respectivement deux de ses côtés AC et BC aux points F et E, mais par la droite AB au point D (Fig. 1),

alors A F FC * CE EB * BD DA = 1

Noter. Pour vous souvenir facilement de cette formule, vous pouvez utiliser la règle suivante : déplacez-vous le long du contour du triangle du sommet au point d'intersection avec la ligne et du point d'intersection au sommet suivant.

Preuve. A partir des sommets A, B, C du triangle, nous traçons trois lignes parallèles, respectivement, jusqu'à ce qu'elles se croisent avec la ligne sécante. Nous aurons trois paires triangles semblables(signe de similitude dans deux coins). Les égalités suivantes découlent de la similitude des triangles

Et maintenant, nous multiplions les données obtenues par les égalités :

Le théorème a été démontré.

Pour ressentir la beauté de ce théorème, essayons de résoudre le problème géométrique proposé ci-dessous avec deux différentes façons: à l'aide d'une construction d'assistance et avec l'aide théorèmes de Ménélas.

Tache 1.

Dans ∆ABC, la bissectrice AD ​​divise le côté BC dans un rapport de 2 : 1. Dans quel rapport la médiane CE divise-t-elle cette bissectrice ?

La solution.

Avec l'aide d'une construction auxiliaire:

Soit S le point d'intersection de la bissectrice AD ​​et de la médiane CE. On complète ∆ASB au parallélogramme ASBK. (Fig. 2)

Il est évident que SE = EK, puisque le point d'intersection du parallélogramme coupe en deux les diagonales. Considérons maintenant les triangles ∆CBK et ∆CDS. Il est facile de voir qu'ils sont semblables (signe de similitude dans deux angles : et comme angles intérieurs unilatéraux de droites parallèles AD et KB et sécante CB). La similitude d'un triangle implique ce qui suit :

En utilisant la condition, on obtient :

CB CD = CD + DB CD = CD + 2CD CB = 3CD CD = 3

Notez maintenant que KB = AS, comme côtés opposés d'un parallélogramme. Alors

AS SD = KB SD = CB CD = 3

Utilisation du théorème de Ménélas.

Considérons ∆ABD et appliquons-lui le théorème de Ménélas (la droite passant par les points C, S, E est une droite sécante) :

BE EA * AS SD * DC CB = 1

Par la condition du théorème, nous avons BE/EA = 1, puisque CE est la médiane, et DC/CB = 1/3, comme nous l'avons déjà calculé plus tôt.

1*AS SD*1 3=1

De là, nous obtenons AS/SD = 3 À première vue, les deux solutions sont assez compactes et approximativement équivalentes. Cependant, l'idée d'une construction supplémentaire pour les écoliers s'avère souvent très compliquée et pas du tout évidente, alors que, connaissant le théorème de Ménélas, il lui suffit de l'appliquer correctement.

Considérons un autre problème dans lequel le théorème de Ménélas fonctionne très bien.

Tâche 2.

Sur les côtés AB et BC ∆ABC, les points M et N sont donnés, respectivement, tels que les égalités suivantes soient vérifiées :

AM MB = CN NA = 1 2

Dans quel rapport le point d'intersection S des segments BN et CM divise-t-il chacun de ces segments (Fig. 3) ?

La solution.

Considérez ∆ABN. On applique le théorème de Ménélas pour ce triangle (la droite passant par les points M, S, C est la sécante)

AM MB * BC SN * CN CA = 1

D'après l'état du problème, nous avons : AM MB = 1 2

NC CA = NC CN + NA = NC CN + 2NC = NC 3 NC = 1 3

En branchant ces résultats, nous obtenons :

1 2 * BS SN * 1 3 = 1

D'où BS / SN = 6. Et, par conséquent, le point S de l'intersection des segments BN et CM divise le segment BN dans le rapport 6 : 1.

Considérez ∆ACM. On applique le théorème de Ménélas pour ce triangle (la droite passant par les points N, S, B est la sécante) :

AN NC * CS SM * MB BA = 1

De la condition du problème nous avons : AN NC = 2

MB BA = MB BM + MA = 2MA 2MA + MA = 2MB 3MA = 2 3

En branchant ces résultats, nous obtenons :

2*CS-SM*2 3=1

Donc CS/SM = 3/4

Et, par conséquent, le point S de l'intersection des segments BN et CM divise le segment CM dans le rapport 3: 4.

Le théorème inverse du théorème de Ménélas est également valable. Cela s'avère souvent encore plus utile. Cela fonctionne particulièrement bien dans les problèmes de preuve. Souvent, avec son aide, même les problèmes de l'Olympiade sont résolus magnifiquement, facilement et rapidement.

Théorème 2(Le théorème inverse de Ménélas). Soit le triangle ABC donné et les points D, E, F appartiennent respectivement aux droites BC, AC, AB (notez qu'ils peuvent se trouver à la fois sur les côtés du triangle ABC et sur leurs extensions) (Fig. 4).

Alors si AF FC * CE EB * BD DA = 1

alors les points D, E, F sont sur la même droite.

Preuve. Démontrons le théorème par contradiction. Supposons que la relation de la condition du théorème soit satisfaite, mais que le point F ne se situe pas sur la droite DE (Fig. 5).

Notons le point d'intersection des lignes DE et AB par la lettre O. Maintenant, nous appliquons le théorème de Ménélas et nous obtenons : AE EC * CD DB * BO OA = 1

Mais, d'autre part, l'égalité BF FA = BO OA

ne peut être exécuté.

Par conséquent, la relation de la condition du théorème ne peut pas être satisfaite. Nous avons une contradiction.

Le théorème a été démontré.

site, avec copie complète ou partielle du matériel, un lien vers la source est requis.