Le théorème de Pythagore dit :

Dans un triangle rectangle, la somme des carrés des jambes est égale au carré de l'hypoténuse :

une 2 + b 2 = c 2,

• un et b- jambes formant un angle droit.
• Avec est l'hypoténuse du triangle.

Formules du théorème de Pythagore

• a = \sqrt(c^(2) - b^(2))
• b = \sqrt (c^(2) - a^(2))
• c = \sqrt (a^(2) + b^(2))

Preuve du théorème de Pythagore

L'aire d'un triangle rectangle est calculée par la formule :

S = \frac(1)(2)ab

Pour calculer l'aire d'un triangle arbitraire, la formule d'aire est la suivante :

• p- demi-périmètre. p=\frac(1)(2)(a+b+c) ,
• r est le rayon du cercle inscrit. Pour un rectangle r=\frac(1)(2)(a+b-c).

Ensuite, nous assimilons les côtés droits des deux formules pour l'aire d'un triangle:

\frac(1)(2) ab = \frac(1)(2)(a+b+c) \frac(1)(2)(a+b-c)

2 ab = (a+b+c) (a+b-c)

2 ab = \left((a+b)^(2) -c^(2) \right)

2ab = a^(2)+2ab+b^(2)-c^(2)

0=a^(2)+b^(2)-c^(2)

c^(2) = a^(2)+b^(2)

Théorème de Pythagore inverse :

Si le carré d'un côté d'un triangle est égal à la somme des carrés des deux autres côtés, alors le triangle est un triangle rectangle. Autrement dit, pour tout triplet de nombres positifs un B et c, tel que

une 2 + b 2 = c 2,

il y a un triangle rectangle avec des jambes un et b et hypoténuse c.

théorème de Pythagore- l'un des théorèmes fondamentaux de la géométrie euclidienne, établissant la relation entre les côtés d'un triangle rectangle. Cela a été prouvé par le scientifique mathématicien et philosophe Pythagore.

Le sens du théorème en ce qu' il peut être utilisé pour prouver d'autres théorèmes et résoudre des problèmes.

Matériels supplémentaires:

Il est remarquable que la propriété indiquée dans le théorème de Pythagore soit une propriété caractéristique d'un triangle rectangle. Cela découle d'un théorème inverse du théorème de Pythagore.

Théorème : Si le carré d'un côté d'un triangle est égal à la somme des carrés des deux autres côtés, alors le triangle est un triangle rectangle.

La formule du Héron

Nous dérivons une formule exprimant le plan d'un triangle en fonction des longueurs de ses côtés. Cette formule est associée au nom de Héron d'Alexandrie, un ancien mathématicien et mécanicien grec qui a probablement vécu au 1er siècle après JC. Heron accorda beaucoup d'attention aux applications pratiques de la géométrie.

Théorème. L'aire S d'un triangle dont les côtés sont a, b, c est calculée par la formule S=, où p est le demi-périmètre du triangle.

Preuve.

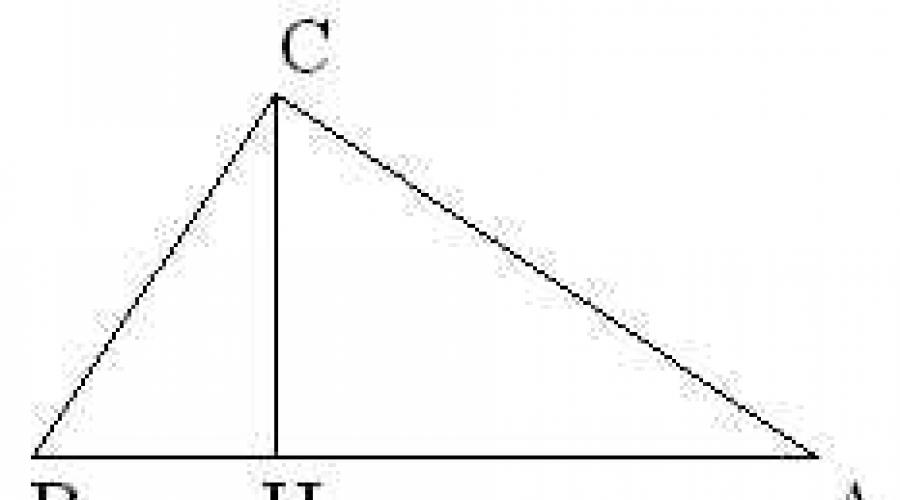
Soit : ?ABC, AB=c, BC=a, AC=b. Les angles A et B sont aigus. CH - hauteur.

Prouver:

Preuve:

Considérons un triangle ABC dans lequel AB=c , BC=a, AC=b. Tout triangle a au moins deux angles aigus. Soient A et B des angles aigus du triangle ABC. Alors la base H de hauteur CH du triangle se trouve sur le côté AB. Introduisons la notation : CH = h, AH=y, HB=x. selon le théorème de Pythagore a 2 - x 2 \u003d h 2 \u003d b 2 -y 2, d'où

Y 2 - x 2 \u003d b 2 - a 2, ou (y - x) (y + x) \u003d b 2 - a 2, et puisque y + x \u003d c, alors y- x \u003d (b2 - a2).

En additionnant les deux dernières égalités, on obtient :

2y = +c, d'où

y \u003d, et donc h 2 \u003d b 2 -y 2 \u003d (b - y) (b + y) \u003d

Objectifs de la leçon:

enseignement général:

• vérifier les connaissances théoriques des étudiants (propriétés d'un triangle rectangle, théorème de Pythagore), la capacité de les utiliser pour résoudre des problèmes;
• après avoir créé une situation-problème, amener les élèves à la « découverte » du théorème de Pythagore inverse.

développement:

• développement de compétences pour appliquer les connaissances théoriques dans la pratique;
• développement de la capacité à formuler des conclusions lors d'observations;
• développement de la mémoire, de l'attention, de l'observation :
• développement de la motivation d'apprentissage par la satisfaction émotionnelle des découvertes, par l'introduction d'éléments de l'histoire du développement des concepts mathématiques.

éducatif:

• cultiver un intérêt constant pour le sujet à travers l'étude de la vie de Pythagore;
• favoriser l'entraide et l'évaluation objective des connaissances des camarades grâce à l'évaluation par les pairs.

Forme de leçon : classe-leçon.

Plan de cours:

• Organisation du temps.
• Vérification des devoirs. Mise à jour des connaissances.
• Résolution de problèmes pratiques à l'aide du théorème de Pythagore.
• Nouveau sujet.
• Consolidation primaire des connaissances.
• Devoirs.
• Résultats des cours.
• Travail indépendant (selon fiches individuelles avec devinettes des aphorismes de Pythagore).

Pendant les cours.

Organisation du temps.

Vérification des devoirs. Mise à jour des connaissances.

Prof: Quelle tâche faisiez-vous à la maison ?

Étudiants:Étant donné deux côtés d'un triangle rectangle, trouvez le troisième côté, disposez les réponses sous la forme d'un tableau. Répétez les propriétés d'un losange et d'un rectangle. Répétez ce qu'on appelle la condition et quelle est la conclusion du théorème. Préparer des rapports sur la vie et l'œuvre de Pythagore. Apportez une corde avec 12 nœuds attachés.

Prof: Vérifier les réponses aux devoirs selon le tableau

(les données sont en noir, les réponses sont en rouge).

Prof: Les déclarations sont écrites au tableau. Si vous êtes d'accord avec eux sur les feuilles de papier en face du numéro de question correspondant, mettez « + », si vous n'êtes pas d'accord, mettez « - ».

Les déclarations sont écrites au tableau.

1. L'hypoténuse est plus grande que la jambe.
2. La somme des angles aigus d'un triangle rectangle est 180 0 .
3. Aire d'un triangle rectangle avec des jambes un et dans calculé par la formule S=ab/2.
4. Le théorème de Pythagore est vrai pour tous les triangles isocèles.
5. Dans un triangle rectangle, la jambe opposée à l'angle 30 0 est égale à la moitié de l'hypoténuse.
6. La somme des carrés des jambes est égale au carré de l'hypoténuse.
7. Le carré de la jambe est égal à la différence des carrés de l'hypoténuse et de la deuxième jambe.
8. Le côté d'un triangle est égal à la somme des deux autres côtés.

Les travaux sont contrôlés par peer review. Les déclarations controversées sont discutées.

Clé des questions théoriques.

Les élèves s'évaluent selon le système suivant :

8 bonnes réponses « 5 » ;
6-7 bonnes réponses "4" ;
4-5 bonnes réponses "3" ;
moins de 4 bonnes réponses « 2 ».

Prof: De quoi avons-nous parlé dans la dernière leçon ?

Étudiant:À propos de Pythagore et de son théorème.

Prof: Formuler le théorème de Pythagore. (Plusieurs élèves lisent le libellé, à ce moment 2-3 élèves le prouvent au tableau noir, 6 élèves aux premiers pupitres sur les feuilles).

Les formules mathématiques sont écrites sur le tableau magnétique des cartes. Choisissez ceux qui reflètent la signification du théorème de Pythagore, où un et dans - cathéters, Avec - hypoténuse.

Alors que les étudiants qui prouvent le théorème au tableau et sur le terrain ne sont pas prêts, la parole est donnée à ceux qui ont préparé des rapports sur la vie et l'œuvre de Pythagore.

Les écoliers travaillant sur le terrain remettent des tracts et écoutent les témoignages de ceux qui ont travaillé au tableau noir.

Prof: Je vous propose des tâches pratiques utilisant le théorème étudié. Nous visiterons d'abord la forêt, après la tempête, puis la campagne.

Tache 1. Après la tempête, l'épicéa s'est cassé. La hauteur de la partie restante est de 4,2 m. La distance entre la base et le sommet tombé est de 5,6 m. Trouvez la hauteur de l'épinette avant la tempête.

Tâche 2. La hauteur de la maison est de 4,4 m La largeur de la pelouse autour de la maison est de 1,4 m Quelle est la longueur de l'échelle pour qu'elle ne marche pas sur la pelouse et atteigne le toit de la maison?

Prof:(la musique joue) Fermez les yeux, pendant quelques minutes nous plongerons dans l'histoire. Nous sommes avec vous dans l'Egypte ancienne. Ici, dans les chantiers navals, les Égyptiens construisent leurs célèbres navires. Mais les arpenteurs-géomètres, eux, mesurent des parcelles de terrain dont les limites ont été emportées après la crue du Nil. Les bâtisseurs construisent des pyramides grandioses qui nous étonnent encore par leur magnificence. Dans toutes ces activités, les Égyptiens devaient utiliser des angles droits. Ils savaient les construire à l'aide d'une corde à 12 nœuds noués à égale distance les uns des autres. Essayez et vous, en vous disputant comme les anciens Égyptiens, construisez des triangles rectangles à l'aide de vos cordes. (Résolvant ce problème, les gars travaillent en groupes de 4 personnes. Au bout d'un moment, quelqu'un montre la construction d'un triangle sur la tablette au tableau noir).

Les côtés du triangle résultant sont 3, 4 et 5. Si vous faites un nœud de plus entre ces nœuds, ses côtés deviendront 6, 8 et 10. Si deux chacun - 9, 12 et 15. Tous ces triangles sont rectangulaires car .

5 2 \u003d 3 2 + 4 2, 10 2 \u003d 6 2 + 8 2, 15 2 \u003d 9 2 + 12 2, etc.

Quelle propriété doit avoir un triangle pour être un triangle rectangle ? (Les élèves essaient de formuler eux-mêmes le théorème de Pythagore inverse, finalement, quelqu'un réussit).

En quoi ce théorème est-il différent du théorème de Pythagore ?

Étudiant: La condition et la conclusion sont inversées.

Prof:À la maison, vous répétiez comment s'appellent ces théorèmes. Alors qu'est-ce qu'on fait maintenant ?

Étudiant: Avec le théorème de Pythagore inverse.

Prof: Notez le sujet de la leçon dans votre cahier. Ouvrez vos manuels à la page 127, relisez cette affirmation, notez-la dans votre cahier et analysez la preuve.

(Après plusieurs minutes de travail indépendant avec le manuel, si vous le souhaitez, une personne au tableau donne une preuve du théorème).

1. Comment s'appelle un triangle de côtés 3, 4 et 5 ? Pourquoi?
2. Quels triangles sont appelés triangles de Pythagore ?
3. Avec quels triangles as-tu travaillé dans tes devoirs ? Et dans les problèmes avec un pin et une échelle ?

Ce théorème aide à résoudre des problèmes dans lesquels il est nécessaire de savoir si les triangles sont des triangles rectangles.

Tâches:

1) Savoir si un triangle est rectangle si ses côtés sont égaux :

a) 12,37 et 35 ; b) 21, 29 et 24.

2) Calculer les hauteurs d'un triangle de côtés 6, 8 et 10 cm.

Page 127 : Théorème de Pythagore inverse. N° 498 (a, b, c) N° 497.

Travail indépendant (réalisé sur des cartes individuelles).

Prof: Chez vous, vous avez répété les propriétés d'un losange et d'un rectangle. Énumérez-les (il y a une conversation avec la classe). Dans la dernière leçon, nous avons parlé du fait que Pythagore était une personne polyvalente. Il était engagé dans la médecine, la musique et l'astronomie, et était également un athlète et a participé aux Jeux Olympiques. Pythagore était aussi philosophe. Beaucoup de ses aphorismes sont encore pertinents pour nous aujourd'hui. Maintenant, vous ferez votre propre travail. Pour chaque tâche, plusieurs réponses sont données, à côté desquelles sont écrits des fragments d'aphorismes pythagoriciens. Votre tâche consiste à résoudre toutes les tâches, à faire une déclaration à partir des fragments reçus et à l'écrire.

Objectifs de la leçon:

Pédagogique : formuler et prouver le théorème de Pythagore et la réciproque du théorème de Pythagore. Montrez leur signification historique et pratique.

Développer: développer l'attention, la mémoire, la pensée logique des élèves, la capacité de raisonner, de comparer, de tirer des conclusions.

Éducatif: cultiver l'intérêt et l'amour pour le sujet, la précision, la capacité d'écouter les camarades et les enseignants.

Équipement: Portrait de Pythagore, affiches avec tâches de consolidation, manuel "Géométrie" de la 7e à la 9e année (I.F. Sharygin).

Plan de cours:

I. Moment organisationnel - 1 min.

II. Vérification des devoirs - 7 min.

III. Discours d'introduction de l'enseignant, rappel historique - 4-5 min.

IV. Formulation et démonstration du théorème de Pythagore - 7 min.

V. Formulation et démonstration du théorème inverse du théorème de Pythagore - 5 min.

Fixation du nouveau matériel :

a) oral - 5-6 minutes.
b) écrit - 7-10 min.

VII. Devoirs - 1 min.

VIII. Résumé de la leçon - 3 min.

Pendant les cours

I. Moment organisationnel.

II. Vérification des devoirs.

p.7.1, n° 3 (au tableau selon le dessin fini).

Condition: La hauteur d'un triangle rectangle divise l'hypoténuse en segments de longueur 1 et 2. Trouvez les jambes de ce triangle.

BC = un ; CA=b; BA=c; BD = a 1 ; DA = b 1 ; CD = hC

Question supplémentaire : écrivez les rapports dans un triangle rectangle.

point 7.1, n° 5. Coupez le triangle rectangle en trois triangles semblables les uns aux autres.

Expliquer.

ASN ~ ABC ~ SVN

(attirez l'attention des élèves sur l'enregistrement correct des sommets correspondants de triangles similaires)

La vérité restera éternelle, dès qu'une personne faible la connaîtra !

Et maintenant, le théorème de Pythagore est vrai, comme à son époque lointaine.

Ce n'est pas un hasard si j'ai commencé ma leçon par les mots du romancier allemand Chamisso. Notre leçon d'aujourd'hui porte sur le théorème de Pythagore. Écrivons le sujet de la leçon.

Devant vous se trouve un portrait du grand Pythagore. Né en 576 av. Après avoir vécu 80 ans, il mourut en 496 av. Connu comme un philosophe et enseignant de la Grèce antique. Il était le fils du marchand Mnesarchus, qui l'emmenait souvent dans ses voyages, grâce auxquels le garçon développa la curiosité et le désir d'apprendre de nouvelles choses. Pythagore est un surnom qui lui est donné pour son éloquence ("Pythagore" signifie "discours persuasif"). Lui-même n'a rien écrit. Toutes ses pensées ont été enregistrées par ses élèves. À la suite de la première conférence qu'il a donnée, Pythagore a acquis 2 000 étudiants qui, avec leurs femmes et leurs enfants, ont formé une immense école et créé un État appelé «Grande Grèce», basé sur les lois et les règles de Pythagore, vénéré comme commandements divins. Il fut le premier à appeler son raisonnement sur le sens de la vie philosophie (philosophie). Il était sujet à la mystification et au comportement démonstratif. Une fois, Pythagore s'est caché sous terre et a appris tout ce qui se passait de sa mère. Puis, flétri comme un squelette, il déclara en assemblée publique qu'il avait été dans l'Hadès, et montra une étonnante conscience des événements terrestres. Pour cela, les habitants touchés l'ont reconnu comme Dieu. Pythagore ne pleurait jamais et était généralement inaccessible aux passions et à l'excitation. Il croyait qu'il venait d'une graine meilleure que l'humain. Toute la vie de Pythagore est une légende qui est descendue jusqu'à notre époque et nous a parlé de l'homme le plus talentueux du monde antique.

La formulation du théorème de Pythagore vous est connue du cours d'algèbre. Souvenons-nous d'elle.

Dans un triangle rectangle, le carré de l'hypoténuse est égal à la somme des carrés des jambes.

Cependant, ce théorème était connu bien des années avant Pythagore. Pendant 1500 ans avant Pythagore, les anciens Égyptiens savaient qu'un triangle avec les côtés 3, 4 et 5 est rectangulaire et utilisaient cette propriété pour construire des angles droits lors de la planification des terres et de la construction de bâtiments. Dans le plus ancien ouvrage mathématique et astronomique chinois qui nous soit parvenu, « Zhiu-bi », écrit 600 ans avant Pythagore, entre autres phrases liées à un triangle rectangle, le théorème de Pythagore est également contenu. Même plus tôt, ce théorème était connu des Hindous. Ainsi, Pythagore n'a pas découvert cette propriété d'un triangle rectangle ; il a probablement été le premier à la généraliser et à la prouver, à la transférer du domaine de la pratique au domaine de la science.

Depuis l'Antiquité, les mathématiciens ont trouvé de plus en plus de preuves du théorème de Pythagore. Il en existe plus de cent cinquante connues. Rappelons la démonstration algébrique du théorème de Pythagore, que nous connaissons depuis le cours d'algèbre. ("Mathématiques. Algèbre. Fonctions. Analyse de données" G.V. Dorofeev, M., "Bubblehead", 2000).

Invitez les élèves à se souvenir de la preuve du dessin et à l'écrire au tableau.

(a + b) 2 \u003d 4 1/2 une * b + c 2 b une

une 2 + 2a * b + b 2 \u003d 2a * b + c 2

une 2 + b 2 = c 2 une une b

Les anciens Hindous, à qui appartient ce raisonnement, ne l'écrivaient généralement pas, mais accompagnaient le dessin d'un seul mot : « Regarde ».

Considérons dans une présentation moderne une des preuves appartenant à Pythagore. Au début de la leçon, nous avons rappelé le théorème sur les rapports dans un triangle rectangle :

h 2 \u003d une 1 * b 1 une 2 \u003d une 1 * c b 2 \u003d b 1 * c

On additionne terme à terme les deux dernières égalités :

b 2 + une 2 \u003d b 1 * c + une 1 * c \u003d (b 1 + une 1) * c 1 \u003d c * c \u003d c 2; une 2 + b 2 = c 2

Malgré l'apparente simplicité de cette preuve, elle est loin d'être la plus simple. Après tout, pour cela, il fallait dessiner une hauteur dans un triangle rectangle et considérer des triangles similaires. Veuillez noter cette preuve dans votre cahier.

Quel est l'inverse de ce théorème ? (... si la condition et la conclusion sont inversées.)

Essayons maintenant de formuler le théorème, inverse du théorème de Pythagore.

Si dans un triangle de côtés a, b et c l'égalité avec 2 \u003d a 2 + b 2 est vraie, alors ce triangle est rectangle et l'angle droit est opposé au côté c.

(Preuve du théorème inverse sur une affiche)

ABC, BC = a,

AC = b, BA = c.

une 2 + b 2 = c 2

Prouver:

ABC - rectangulaire,

Preuve:

Considérons un triangle rectangle A 1 B 1 C 1,

où C 1 \u003d 90 °, A 1 C 1 \u003d a, A 1 C 1 \u003d b.

Ensuite, selon le théorème de Pythagore, B 1 A 1 2 \u003d a 2 + b 2 \u003d c 2.

C'est-à-dire que B 1 A 1 \u003d c A 1 B 1 C 1 \u003d ABC sur trois côtés d'ABC - rectangulaire

C = 90°, ce qui restait à prouver.

1. Selon l'affiche avec des dessins prêts à l'emploi.

Fig.1 : trouver AD si BD = 8, BDA = 30°.

Fig. 2 : trouver CD si BE = 5, BAE = 45°.

Fig. 3 : trouver BD si BC = 17, AD = 16.

2. Un triangle est-il rectangle si ses côtés sont exprimés par des nombres :

Comment appelle-t-on les triplets de nombres dans les deux derniers cas ? (Pythagoricien).

N° 9. Le côté d'un triangle équilatéral est égal à a. Trouver la hauteur de ce triangle, le rayon du cercle circonscrit, le rayon du cercle inscrit.

№ 14. Prouver que dans un triangle rectangle le rayon du cercle circonscrit est égal à la médiane tracée à l'hypoténuse et égale à la moitié de l'hypoténuse.

Item 7.1, pp. 175-177, analyse Théorème 7.4 (théorème de Pythagore généralisé), n° 1 (oral), n° 2, n° 4.

Qu'avez-vous appris de nouveau lors de la leçon d'aujourd'hui ? …………

Pythagore était avant tout un philosophe. Maintenant, je veux vous lire quelques-unes de ses paroles, qui sont pertinentes à notre époque pour vous et moi.

• Ne soulevez pas de poussière sur le chemin de la vie.
• Ne faites que ce qui, à l'avenir, ne vous contrariera pas et ne vous forcera pas à vous repentir.
• Ne faites jamais ce que vous ne savez pas, mais apprenez tout ce que vous devez savoir, et alors vous mènerez une vie tranquille.
• Ne fermez pas les yeux lorsque vous voulez dormir sans comprendre toutes vos actions de la veille.
• Apprenez à vivre simplement et sans luxe.