Étude des systèmes de file d'attente par modélisation statistique.
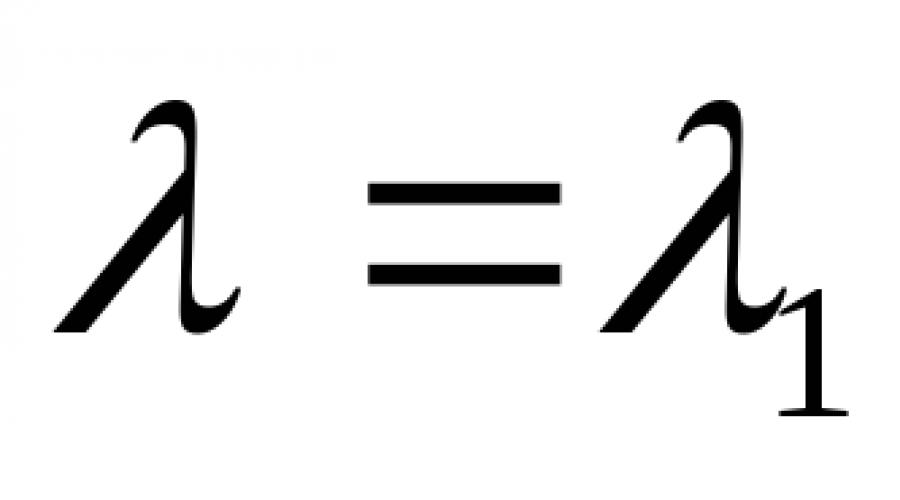
Lire aussi
La théorie des files d'attente est un domaine des mathématiques appliquées qui utilise les méthodes de la théorie des processus aléatoires et de la théorie des probabilités pour étudier nature différente systèmes complexes. La théorie des files d'attente n'est pas directement liée à l'optimisation. Son objectif est de, sur la base des résultats d'observations de « l'entrée » du système, prédire ses capacités et organiser le meilleur service pour une situation particulière et comprendre comment ce dernier affectera le coût du système dans son ensemble. Pour les systèmes liés aux systèmes de file d'attente, il existe une certaine classe de problèmes dont la solution permet de répondre à des questions d'actualité. À quel rythme un service doit-il être exécuté ou un processus doit-il être exécuté à un rythme donné et à d'autres paramètres du flux entrant d'exigences afin de minimiser la file d'attente ou le retard dans la préparation d'un document ou d'un autre type d'information ? Quelle est la probabilité d'un retard ou d'une file d'attente et son ampleur ? Combien de temps la demande est-elle dans la file d'attente et comment minimiser son retard ? Quelle est la probabilité de perdre un sinistre (client) ? Quelle devrait être la charge optimale des canaux de service ? À quels paramètres du système sont atteints pertes minimales arrivé? Un certain nombre d'autres tâches peuvent être ajoutées à cette liste.
Le système de file d'attente (QS) comprend les objets structurants suivants : source des exigences ; flux d'entrée des exigences (réception des candidatures); tour; système de maintenance, en tant qu'ensemble de canaux pour les applications de maintenance ; flux de sortie (applications desservies ou exigences satisfaites). Découvrons leurs modèles.
Source des exigences. Selon l'emplacement de la source qui forme les exigences, les QS sont divisés en ouvert, lorsque la source est à l'extérieur du système, et fermé, lorsque la source est à l'intérieur du système.
Flux d'entrée des exigences. La grande majorité des développements théoriques dans l'étude des systèmes de file d'attente sont faits pour la condition où le flux d'entrée des exigences est de Poisson (le plus simple). Ce flux a un certain nombre de propriétés importantes. Elle est stationnaire, ordinaire et sans conséquence.
Le modèle de flux de Poisson en entrée est représenté par une fonction de la forme :
La propriété suivante du flux de Poisson qu'il est important d'étudier est que la procédure de division et de combinaison produit à nouveau des flux de Poisson. Alors, si le flux d'entrée est formé à partir de N sources indépendantes, dont chacune génère un flux de Poisson d'intensité λ je (je=1,2,…, N) , alors son intensité sera déterminée par la formule :
|
|
Dans le cas de la division du flux de Poisson en N flux indépendants, on obtient que l'intensité du flux λ je sera égal à r je λ , où r je - partager je – ème flux dans le flux d'entrée des exigences.
Tour. Les files d'attente, définies comme un ensemble de demandes en attente de traitement, sont représentées par plusieurs modèles : une file d'attente avec des échecs, une file d'attente avec un temps d'attente limité (un client attend un certain temps), une longueur limitée et, enfin, une file d'attente temps d'attente illimité. L'ordre dans lequel les demandes de service sont reçues est appelé discipline de file d'attente. Les demandes peuvent être acceptées au fur et à mesure qu'elles arrivent, au hasard, avec priorité, selon le principe du "dernier premier", via certains canaux.
Processus d'entretien. Le paramètre principal du processus de service est considéré comme le temps de service de l'exigence par le canal j- t j (j=1,2,…, m) . Évaluer τ j dans chaque cas est déterminé par un certain nombre de facteurs: l'intensité de la réception des candidatures, les qualifications de l'entrepreneur, la technologie de travail, l'environnement, etc. Lois de distribution d'une variable aléatoire τ j peuvent être très différentes, mais la plus largement utilisée dans les applications pratiques est la loi de distribution exponentielle. Fonction de distribution d'une variable aléatoire τ j ressemble à:
La propriété la plus importante de la distribution exponentielle est la suivante. En présence de plusieurs voies de service du même type et d'une probabilité égale de leur sélection à la réception d'une requête, la répartition du temps de service par tous m canaux est une fonction exponentielle de la forme :
Si le QS se compose de canaux hétérogènes, alors  , si tous les canaux sont homogènes, alors
, si tous les canaux sont homogènes, alors  .
.
Le flux de sortie des requêtes traitées. Un flux de sortie est un flux de résultats d'activités représenté par les exigences remplies dans l'idée d'un produit ou d'un service particulier. Les principaux paramètres du flux de sortie comprennent l'intensité de la sortie du système des besoins desservis et la nature de la répartition du temps entre les moments de production. Dans le cas général, ces paramètres sont déterminés par le modèle de flux d'entrée, la discipline de file d'attente et le modèle de service. Pour un QS avec des canaux parallèles et un service monophasé, il existe un théorème selon lequel pour un flux d'entrée de Poisson avec le paramètre λ et la même distribution de temps de service pour chaque canal avec le paramètre μ à l'état stationnaire, le flux de sortie a une distribution de Poisson avec paramètre g. Dans les systèmes monophasiques, le flux de sortie d'un canal sert de flux d'entrée vers un autre canal. Le paramètre g dans le cas le plus simple est déterminé par la formule :
|
|
|
|
O S - temps de séjour moyen d'une exigence dans le système. |
|
Une caractéristique des modèles QS est associée à une description mathématique assez rigoureuse du fonctionnement des systèmes, qui est obtenue en raison de leur unification de plusieurs manières. Ainsi, selon le modèle d'attente, les QS suivants se distinguent par l'exigence de commencer l'entretien :
système avec pertes ou pannes ;
système d'attente ;
système à temps d'attente limité (VO);
un système avec une longueur de file d'attente limitée (DO).
Selon le nombre de canaux de service, les systèmes sont divisés en monocanal ( m=1 ) et multicanal ( m>1 ). La structure du QS et les caractéristiques de ses objets sont présentées dans la Figure 1.21.
L'une des formes de classification QS est la classification par code de D. Kendall. Conformément à cette classification, la caractéristique QS est écrite sous la forme de trois, quatre ou cinq symboles. Par exemple, un/ b/ c, où un– type de distribution du flux d'entrée des exigences, b– type de distribution du temps de service, c– nombre de canaux de service. Pour les distributions de Poisson et exponentielles, prenez le symbole M, pour toute distribution arbitraire g. Par exemple, l'entrée M/M/2 signifie que le flux d'entrée des exigences est de Poisson, que le temps de service est distribué selon la loi exponentielle et qu'il existe deux canaux dans le système. Le quatrième caractère (d) indique la longueur autorisée de la file d'attente, le cinquième (e) indique l'ordre dans lequel les requêtes sont sélectionnées.

Figure 1.21 - Structure et caractéristiques des objets QS
Les modèles QS peuvent être déterministes ou probabilistes. Dans le premier cas, les paramètres et les variables du modèle sont constantes, dans le second - aléatoire.
L'étude du QS consiste à trouver des indicateurs qui caractérisent la qualité et les conditions de travail du système de service et des indicateurs qui reflètent les conséquences économiques décisions prises selon les premiers indicateurs. Les indicateurs du premier groupe comprennent les suivants.
1. Avec des paramètres établis ou de conception du flux entrant :
a) la probabilité de réception de n besoins dans le système pour la période t (P n (J)) ;
b) la probabilité d'avoir n exigences du système (P n ) .
2. Avec des paramètres de service établis ou de conception :
a) la probabilité que tous les services m les chaînes sont gratuites (P 0 ) ;
b) la probabilité qu'un certain nombre de canaux (gestionnaires, agents) soient occupés par le service (P m ) ;
c) la probabilité que r les exigences sont dans la file d'attente (P m + r ) .
3. Avec les paramètres établis ou de conception du flux entrant et du système de service :
b) nombre moyen de canaux m employé par le service : E(m)= m k ;
c) nombre moyen de canaux inactifs : E(m 0 )=(m- m k ) ;
d) utilisation du canal (occupation) (K S ) ;
e) taux d'indisponibilité (défaillance) du canal (K 0 ) ;
f) relatif (Q) et absolu (UN) débit QS ;
g) le nombre moyen d'exigences dans le système (L S ) ;
h) le nombre moyen de requêtes en attente dans la file d'attente (L q ) ;
i) le temps d'attente moyen d'une demande dans la file d'attente (O q ) ;
j) temps de séjour moyen d'une exigence dans le système (O S ) .
Considérez les méthodes de calcul des indicateurs du premier groupe sur l'exemple du modèle QS le plus courant ( M/ M/ m≥2 ) avec une espérance contenant m canaux de service parallèles. Ici, les demandes entrantes ne sont pas perdues et ne quittent le système qu'après le service. Les canaux effectuent des opérations uniformes et le temps de service pour chaque canal t distribué selon la loi exponentielle avec le paramètre m, et le flux entrant est Poisson avec le paramètre λ ; la discipline de la file d'attente n'est pas réglementée et il n'y a pas de limite au nombre de demandes entrantes. Le modèle QS est représenté comme un système d'équations pour un état stationnaire.
Déterminer la probabilité d'avoir n conditions (P n ) dans le système dépend du ratio du nombre de demandes entrantes ( n) par unité de temps et le nombre de canaux de service ( m).
1. Pour la condition où m=1, P n est déterminé par la formule de l'espérance mathématique d'une variable aléatoire discrète.
2. Pour la condition où 1≤ n≤ m (probabilité que toutes les requêtes soient en service ou qu'il n'y ait pas de file d'attente), P n calculé par la formule :
Si ρ/ m<1 , alors la probabilité d'absence d'exigences dans le système P 0 est déterminé par la formule du mode stationnaire :
soit par la formule d'espérance mathématique d'une variable aléatoire discrète :
Les coefficients d'utilisation (charge) des canaux et le temps d'indisponibilité des canaux sont respectivement déterminés par les formules :
 et
et  .
.
Le nombre moyen de requêtes en attente dans la file d'attente est obtenu à partir de l'expression :
 .
.
Le temps d'attente moyen dans la file d'attente sera de :
 .
.
Le temps de séjour moyen d'une exigence dans le système est calculé par la formule :
 .
.
Le nombre moyen d'exigences dans le système est déterminé par de la manière suivante:
 .
.
Pour le cas général L S est déterminé par la formule d'espérance mathématique d'une variable aléatoire discrète :
 .
.
Pour estimer les paramètres d'un système probabiliste et ses processus aléatoires du point de vue de la stabilité, l'utilisation des valeurs trouvées des caractéristiques des fonctions aléatoires, qui sont des fonctions non aléatoires de l'argument, est fournie. t. Ils comprennent valeur attendue, dispersion, fonction de corrélation, coefficient de variation caractérisant une réalisation moyenne d'un processus aléatoire (ou d'une fonction aléatoire) sur un ensemble d'observations. Les statistiques sont trouvées à travers les paramètres QS. Par exemple, la dispersion (ré) pour le nombre d'exigences dans le système est calculé par la formule :
 .
.
Les indicateurs qui caractérisent les conséquences économiques de la prise de décisions pour améliorer le service client (consommateur) sont réduits à la détermination de l'efficacité économique et des pertes dues au refus de service et à l'attente du service.
L'efficacité économique du système de file d'attente sera :
Le montant des pertes est déterminé par les expressions suivantes :
a) système avec pannes :
b) système avec attente :
Afin de démontrer l'utilité d'utiliser les méthodes de la théorie des files d'attente pour résoudre des problèmes de gestion, considérons un exemple d'estimation d'un QS de petite dimension.
Exemple 1.9. Il s'agit d'évaluer l'efficacité de la centralisation de plusieurs départements ou services aux fonctions homogènes. En tant qu'objet, deux services de taxi sont considérés, qui ont été acquis par la société Avtoservice. Les candidatures des clients entre les services sont réparties équitablement. La demande d'un taxi au répartiteur s'accompagne d'une fréquence de 10 appels par heure. Le temps de service moyen par client est de 11,5 minutes. Les appels de taxi sont distribués dans le temps selon la loi de Poisson, et la durée de service pour un client est distribuée selon la loi exponentielle. Chaque service de taxi est équipé de deux voitures.
La question se pose de la faisabilité économique d'une centralisation de la gestion de la flotte de taxis. Pour ce faire, vous devez comparer deux options :
1) option avec service indépendant par systèmes de type ( M/M/2) à λ=10 appels/heure, τ=11,5 min. et m= 2;
2) variante avec une file d'attente de type ( M/M/4) à λ=10*2=20 appels/heure, τ=11,5 min. et m= 4;
Pour commencer, déterminons les facteurs de charge du service pour les première et deuxième options. À m= 2 nous avons :
Comme le montre le calcul, le facteur de charge du service de taxi est assez élevé. Évidemment, cela ne change pas dans la variante avec m= 4, puisque le numérateur et le dénominateur sont doublés. A première vue, l'association ne conduit pas à un effet économique, et puisque l'étude de l'efficacité du fonctionnement du QS est centrée sur l'amélioration de la qualité de la satisfaction des exigences des consommateurs, il est nécessaire d'évaluer les paramètres qui caractérisent ce domaine de activité.
Calculer O q(temps d'attente moyen pour une voiture taxi).
Pour le premier cas avec m= 2 nous avons ρ=1,917. Déterminons la probabilité qu'il n'y ait pas d'exigences dans le système ( P 0 ):
Utiliser la valeur P 0 définir O q :
 h.
h.
Pour le deuxième cas avec m= 4 nous avons ρ=3.83 et définissons P 0 :
Avec une valeur P 0 =0.0042, on obtient que
 h.
h.
Les estimations ci-dessus montrent que la centralisation des services permet de réduire d'environ la moitié le temps d'attente moyen d'un appel de taxi par un client. Ce n'est pas une garantie que le client refusera la commande, mais une réduction significative du temps d'attente. À l'avenir, en plus de créer un service de taxi unifié, il est nécessaire d'examiner la question de l'augmentation de la flotte de taxis.
1. Concepts de base de la théorie des files d'attente.
2. Énoncé du problème de la théorie des files d'attente.
3. Approches pour résoudre des problèmes dans la théorie des files d'attente.
Bref contenu du sujet
L'activité pratique d'une personne est étroitement liée à divers types de systèmes de files d'attente. Dans le domaine de l'économie, il s'agit des services bancaires, de l'utilisation des installations commerciales et des services dans le secteur des services et de nombreux autres types d'activités économiques.
Tout système de file d'attente peut inclure les éléments suivants :
Un flux entrant de demandes ou de demandes de service. Cet élément est le principal. L'étude du flux entrant des besoins et sa description est nécessaire lors de l'organisation de tout système de file d'attente.
Tour. Dans les cas où les demandes entrant dans le système de file d'attente ne peuvent pas être satisfaites immédiatement, une file d'attente apparaît. Dans une telle situation, la longueur de cette file d'attente, l'ordre dans lequel les demandes en attente sont envoyées pour le service (comme on dit, la discipline de la file d'attente), le temps d'attente peuvent être intéressants.
Dans certains cas, les systèmes de file d'attente ne sont pas autorisés, c'est-à-dire la demande qui a rendu le système occupé n'est pas traitée (rejetée).
Appareil de service. Cet élément est présent dans tout système de file d'attente. Non seulement le temps nécessaire pour répondre à une demande, mais également la longueur de la file d'attente et le temps d'attente dépendent des caractéristiques et des paramètres, des méthodes d'organisation du dispositif de service.
Flux sortant de demandes traitées. Cet élément peut être très important dans les cas où le flux sortant de demandes traitées est entrant pour un autre système de file d'attente.
En règle générale, le nombre d'exigences à l'entrée du système de file d'attente pour toute période de temps et le temps de service d'une exigence sont des variables aléatoires. Le fonctionnement du système de file d'attente dans ce cas est un processus aléatoire, et les méthodes d'étude de tels systèmes utilisent la simulation. Cependant, on peut comprendre l'essence des problèmes et des méthodes de la théorie des files d'attente en utilisant des exemples de modèles déterministes de systèmes de files d'attente et, surtout, des modèles de théorie des files d'attente.
Les principaux composants du modèle de file d'attente sont :
description du flux entrant de besoins ;
une description de la manière dont le service est exécuté (c'est-à-dire une description de la discipline du service);
description de la discipline de la file d'attente (c'est-à-dire comment les clients sont sélectionnés dans la file d'attente pour le service : "premier arrivé - premier servi", "dernier arrivé - premier servi", "par priorités spécifiées", etc.).
Lors de la construction d'un modèle de file d'attente, la tâche principale est la représentation symbolique des composants principaux, après quoi les relations entre eux sont étudiées.
Les principales caractéristiques de la file d'attente sont :
longueur de la file d'attente à différents moments ;
la durée totale de l'exigence dans le système de service (c'est-à-dire le temps passé à attendre dans la file d'attente, plus le temps de service propre);
temps pendant lequel l'appareil de service était libre.
L'objectif principal de l'étude des systèmes de file d'attente est d'établir un équilibre entre les charges admissibles du dispositif de desserte, la capacité limitée du système et la gêne du client, d'une part, et le coût admissible des points de desserte, d'autre part. L'autre.
Considérez un système de file d'attente qui a une seule source de revendications passant par un seul serveur. Laissons les hypothèses suivantes se produire :
1. Les demandes arrivent à intervalles réguliers. Chaque intervalle a une longueur de a unités.
2. Les demandes sont traitées pour les mêmes intervalles de temps, chaque intervalle a une longueur de b unités. Dans ce cas, dès que le service d'un besoin est terminé, le dispositif de service est prêt à servir le besoin suivant.
3. La discipline de la file d'attente est établie selon la règle « Premier arrivé - premier servi ». En d'autres termes, les demandes en attente forment une file d'attente, et lorsque le serveur se libère, la demande avec le temps d'attente le plus long arrive pour le service.
Définissons la longueur de la file d'attente comme le nombre total de requêtes en cours de traitement et en attente dans la file d'attente. Représentons le problème formulé sous la forme du schéma suivant :
Le comportement du système dépend de la façon dont les quantités a et b sont liées. Trois cas sont possibles : 1) b > a ; 2) b = un ; 3) b< a. Рассмотрим каждый из этих случаев.
1) Cas b > a. Cela signifie que le taux de service 1/b est inférieur au taux de réception des requêtes 1/a, c'est-à-dire les demandes sont servies et quittent le système plus lentement qu'elles n'arrivent. Par conséquent, dans ce cas, une file d'attente se formera et elle augmentera constamment.
2) Cas b = a. S'il n'y a pas de demandes dans la file d'attente, la première demande reçue commencera immédiatement à être servie. Son service se terminera au même moment où la prochaine exigence de service arrivera. Par conséquent, il n'y aura pas de demandes en attente de traitement.
S'il y a initialement une file d'attente, sa longueur restera constante.
3) Cas b< a. Это значит, что скорость обслуживания больше, чем скорость поступления требований. Следовательно, какое бы ни было начальное число ожидающих обслуживания требований, длина очереди будет сокращаться до 1 или 0.
Soit au début du processus le nombre de requêtes dans la file d'attente r 2 (s'il n'y a initialement qu'une seule requête (r = 1), alors elle sera servie avant que les prochaines requêtes n'arrivent pour le service, et la file d'attente sera vide) .
Dans le cas général, disons que nous avons r clients dans la file d'attente avant le début du service. Ensuite, le nombre de requêtes (N) reçues après le démarrage du processus de service jusqu'à ce que la file d'attente soit préservée peut être déterminé par la formule :

où la notation [x] désigne la partie entière du nombre x. En effet, la file d'attente sera absente si N+r requêtes transitent intégralement par le serveur. Cela nécessitera (N+r)b unités de temps. Pendant ce temps, N clients seront servis, de sorte qu'au moment où le (N + 1)e client arrive, le serveur sera libre et prêt à le servir immédiatement sans aucune file d'attente. Mais la (N + 1)ème exigence arrivera pour le service après (N + 1)a unités de temps, alors que la relation sera satisfaite :
Montrons que N dans la relation obtenue est supérieur au côté droit de pas plus de 1. En effet, le premier client debout dans la file d'attente aura déjà été servi, et le premier client arrivant pour le service n'apparaîtra pas encore dans la file d'attente (un > b). Donc la relation suivante est vraie :
aN (N+r-1)b ou.
Ainsi, si nous ajoutons 1 au côté droit du rapport, alors il sera identiquement égal au côté droit du rapport. C'est-à-dire que l'ajout de 1 au côté droit du rapport le conduit au rapport - le sens de l'inégalité est inversé. C'est ce qu'il fallait prouver.
Il est évident que N est un entier. Par conséquent, si nous prenons la partie entière du côté droit dans la relation (10.2) et lui ajoutons 1, alors, sur la base du raisonnement précédent, nous obtenons l'expression (10.1) pour calculer N.
Par un raisonnement similaire et en utilisant (10.1), nous pouvons trouver que pour calculer le temps nécessaire pour traiter toutes les demandes en attente, la formule est valide :

Dans la théorie des files d'attente, une fonction importante est la fonction de temps d'attente du service. Notons-le par W(t). Définissons W(t) comme le temps qu'il faut passer à attendre le service d'un sinistre arrivé à l'instant t (on suppose que t = 0 correspond au début du processus de service).

Définissons une formule pour W(t). Il est facile de voir qu'un client arrivant pour un service à l'instant t T-b (la valeur de T est déterminée à l'aide de la formule (10.3)) trouvera le système de file d'attente vide ou juste libéré. Une telle demande n'a pas à faire la queue. Une réclamation arrivant au temps tT-b trouvera devant elle les réclamations dans la file d'attente, et la première d'entre elles arrivera sur le serveur au même instant. Cette valeur est obtenue comme suit :
(initial (nombre d'exigences, servi- (nombre d'entrants-
file d'attente) - th au moment t) + leniya)
Ainsi, le temps d'attente W(t) pour le besoin considéré peut être exprimé par la formule :
Envisager ième exigence dans la file d'attente initiale (0
En généralisant les résultats obtenus par rapport à la fonction W(t), on en obtient l'expression suivante :

où i est le numéro de la ième exigence dans la file d'attente initiale ; les requêtes arrivent aux instants a, 2a, ... ; b = na (n = 1, 2, ...).
Étude des systèmes de file d'attente par modélisation statistique
1. Dispositions de base pour l'exécution des travaux de laboratoire
L'utilisation de méthodes analytiques et numériques pour l'étude de QS est limitée aux cas où le système est markovien et est décrit par les équations de naissance et de mort ou peut y être réduit. Sinon, l'étude de QS est possible à l'aide de la méthode de simulation basée sur la simulation informatique multiple des processus se produisant dans le système, suivie d'un traitement statistique des résultats obtenus.
Les estimations de l'espérance mathématique du nombre de canaux occupés, de la longueur de la file d'attente, du temps d'attente des demandes dans la file d'attente, des probabilités de demandes de service, etc. sont utilisées comme principales grandeurs caractérisant le fonctionnement du QS étudié. , pour l'instant t (o £ t £ J n ), où T n - temps de simulation, calculable.
Estimation de l'espérance mathématique du nombre de canaux occupés :
ici - le nombre de canaux occupés à l'instant t dans la jème mise en œuvre ; N est le nombre d'implémentations (exécutions du modèle) ;
Estimation de la probabilité que dans le système à l'instant t :
voici le nombre d'implémentations dans lesquelles à l'instant t il y avait k exigences dans le système ;
Estimation de la probabilité que la demande soit rejetée :
où est le nombre total d'exigences qui sont apparues au moment t dans la jème implémentation ; - le nombre d'exigences rejetées à l'instant t ;
Estimation de la dispersion du nombre de voies occupées à l'instant t :
Pour avoir une idée de la précision et de la fiabilité de ces estimations, des intervalles de confiance Ib peuvent être trouvés pour un niveau de confiance donné b.
Pour l'espérance mathématique du nombre de canaux occupés
Ici tb est trouvé à partir de la distribution de Student à (N-1) degrés de liberté. Pour un grand N (N>30), au lieu de la distribution de Student, vous pouvez utiliser la loi normale. Dans ce cas
où Ф(х) est l'intégrale des probabilités :
2. Pour les probabilités
Pour un grand N, environ
où - S.K.O. estimations de probabilité :
De plus, les limites des intervalles de confiance pour les probabilités peuvent facilement être trouvées à partir des nomogrammes.
2. Pour une version donnée (de base) du QS, obtenir les résultats de la modélisation du QS. La valeur de tohtemps d'attente en ligne pour prendrenon aléatoire toh>TMaude.JMaud prendre en fonction des résultats du compte rendu des travaux de laboratoire n ° 1 (heure de la fin du processus de transition multipliée par 2). Nombre de réalisations N=50. Construire des graphiques de changement m L, unn, Pserviceet leurs intervalles de confiance en fonction du temps. La valeur de la probabilité de confiance est prise égale à?=0,9
Résoudre le système équations différentielles par la méthode de Runge-Kutta (les parties droites des équations sont écrites dans le vecteur D, les conditions initiales sont dans le vecteur x) :
La modélisation
Temps de simulationJ Maud = 3 (selon les résultats des travaux de laboratoire, le temps de fin du processus transitoire est de 1,3 s).
Temps d'attentechoisir parmi la condition T Attendez >T Maud , d'où Tojid = 4 s.
Paramètres du modèle :
Flux d'entrée (intervalle de temps entre les requêtes) :
Intensité : 7
Tour:
Longueur de la file d'attente : 3
Il est temps de quitter la file d'attente :
Loi de distribution : Déterministe
Valeur : 4
Canaux de services :
Nombre de canaux : 3
Temps de service:
Loi de distribution : Exponentielle
Intensité : 2
Les résultats du programme :
Estimations des attentes mathématiques :
| 1,00 | 6,940 | 0,320 | 0,000 | 3,500 | 0,720 | 0,029 | 2,400 |
| 2,00 | 14,060 | 1,640 | 0,000 | 8,540 | 1,280 | 0,107 | 2,600 |
| 3,00 | 21,040 | 3,480 | 0,000 | 13,500 | 1,440 | 0,169 | 2,620 |
| 4,00 | 28,220 | 5,560 | 0,000 | 18,620 | 1,300 | 0,213 | 2,740 |
| 5,00 | 35,060 | 7,060 | 0,000 | 24,200 | 1,080 | 0,235 | 2,720 |
| 6,00 | 42,460 | 8,860 | 0,000 | 29,240 | 1,660 | 0,244 | 2,700 |
| 7,00 | 49,440 | 10,620 | 0,000 | 35,000 | 1,180 | 0,252 | 2,640 |
| 8,00 | 56,300 | 11,960 | 0,000 | 40,680 | 1,060 | 0,258 | 2,600 |
| 9,00 | 63,040 | 13,480 | 0,000 | 45,720 | 1,220 | 0,264 | 2,620 |
| 10,00 | 69,920 | 14,940 | 0,000 | 50,940 | 1,300 | 0,269 | 2,740 |
| 11,00 | 76,800 | 16,220 | 0,000 | 56,640 | 1,220 | 0,273 | 2,720 |
| 12,00 | 83,780 | 17,500 | 0,000 | 62,380 | 1,300 | 0,274 | 2,600 |
| 13,00 | 90,720 | 19,640 | 0,000 | 67,240 | 1,300 | 0,276 | 2,540 |
| 14,00 | 98,060 | 21,320 | 0,000 | 72,700 | 1,340 | 0,280 | 2,700 |
| 15,00 | 105,420 | 22,960 | 0,000 | 78,400 | 1,360 | 0,283 | 2,700 |
| 16,00 | 112,620 | 24,640 | 0,000 | 84,280 | 1,080 | 0,284 | 2,620 |
| 17,00 | 120,200 | 25,880 | 0,000 | 90,300 | 1,460 | 0,284 | 2,560 |
| 18,00 | 126,640 | 27,500 | 0,000 | 95,300 | 1,260 | 0,287 | 2,580 |
| 19,00 | 133,680 | 28,920 | 0,000 | 100,840 | 1,180 | 0,290 | 2,740 |
| 20,00 | 140,340 | 30,300 | 0,000 | 106,260 | 1,180 | 0,291 | 2,600 |
Estimations RMS :
| Temps | Nombre de candidatures | Nombre d'échecs | Nombre de pertes | Nombre de prestations | Longueur de file d'attente | Temps d'attente | Chaînes occupées |
| 1,00 | 2,745 | 0,785 | 0,000 | 1,941 | 1,000 | 0,046 | 0,916 |
| 2,00 | 3,722 | 2,197 | 0,000 | 3,054 | 1,200 | 0,086 | 0,774 |
| 3,00 | 4,906 | 3,067 | 0,000 | 3,822 | 1,235 | 0,105 | 0,718 |
| 4,00 | 5,231 | 4,176 | 0,000 | 4,151 | 1,204 | 0,100 | 0,558 |
| 5,00 | 5,984 | 5,131 | 0,000 | 4,507 | 1,110 | 0,097 | 0,530 |
| 6,00 | 6,548 | 5,830 | 0,000 | 4,773 | 1,210 | 0,088 | 0,670 |
| 7,00 | 7,518 | 6,495 | 0,000 | 5,355 | 1,125 | 0,085 | 0,624 |
| 8,00 | 7,759 | 6,971 | 0,000 | 5,773 | 1,173 | 0,082 | 0,692 |
| 9,00 | 7,725 | 7,278 | 0,000 | 6,000 | 1,237 | 0,080 | 0,718 |
| 10,00 | 8,143 | 7,882 | 0,000 | 6,077 | 1,100 | 0,080 | 0,558 |
| 11,00 | 9,361 | 8,367 | 0,000 | 6,802 | 1,118 | 0,076 | 0,722 |
| 12,00 | 10,286 | 8,690 | 0,000 | 6,831 | 1,268 | 0,075 | 0,824 |
| 13,00 | 10,438 | 8,885 | 0,000 | 6,553 | 1,204 | 0,070 | 0,780 |
| 14,00 | 10,887 | 9,321 | 0,000 | 6,394 | 1,193 | 0,067 | 0,670 |
| 15,00 | 10,398 | 8,991 | 0,000 | 6,587 | 1,179 | 0,065 | 0,670 |
| 16,00 | 10,805 | 9,333 | 0,000 | 6,600 | 1,110 | 0,063 | 0,745 |
| 17,00 | 11,144 | 9,704 | 0,000 | 7,108 | 1,152 | 0,063 | 0,875 |
| 18,00 | 11,704 | 10,425 | 0,000 | 7,566 | 1,261 | 0,062 | 0,776 |
| 19,00 | 11,853 | 10,665 | 0,000 | 7,606 | 1,089 | 0,061 | 0,521 |
| 20,00 | 11,969 | 10,562 | 0,000 | 8,009 | 1,107 | 0,059 | 0,800 |
Car N = 50, puis de construire des intervalles de confiance, sachant que la valeur de la probabilité de confiance ? = 0.9, alors t ?calculé selon la loi normale :
Espérance mathématique du nombre de canaux occupés :
Mn - de L.R. une
a - modelage
Espérance mathématique de la longueur moyenne de la file d'attente :
Calcul de l'intervalle de confiance :
Pour la longueur moyenne de la file d'attente :
Lm - de L.R. une
m - simulation
Probabilité de service :
La probabilité de service est égale à la probabilité qu'il n'y ait pas encore n+m clients dans le système, c'est-à-dire P o = 1 - Pn+m = 1 - P 6
Calcul de l'intervalle de confiance :
Pour la probabilité de service :
Po1 - de L.R. une
Po - modelage
3. Pour une variante QS (de base) donnée, étudiez l'influencetAttendezsur les caractéristiques du système en mode stationnaire
a) H( t ) - déterministe, t Attendez =T attentes_moyenne
b) H( t ) est soumis à la loi de distribution exponentielle. Valeur attendue t Attendez égal à T attentes_moyenne*(0,25 ; 0,5 ; 1 ; 2).
conclusions
Dans le travail de laboratoire n ° 2, les résultats de la modélisation de la version de base du QS ont été obtenus. Selon les résultats obtenus, des graphiques des dépendances du nombre de canaux occupés, de la longueur moyenne de la file d'attente et de la probabilité de service et de leurs intervalles de confiance dans le temps ont été tracés. Les courbes construites à partir des résultats du travail de laboratoire n° 1 sont tombées dans les intervalles de confiance correspondants.
Dans ce travail de laboratoire les possibilités d'utilisation de la méthode de simulation pour l'étude des systèmes de file d'attente ont été étudiées. En analysant les résultats obtenus, nous pouvons tirer la conclusion suivante : l'utilisation de la méthode de simulation est acceptable, mais il est préférable d'utiliser un appareil analytique pour étudier QS, car cette façon d'étudier QS est plus simple et donne des résultats plus précis.
file d'attente de simulation de simulation
Tutorat
Besoin d'aide pour apprendre un sujet ?
Nos experts vous conseilleront ou vous fourniront des services de tutorat sur des sujets qui vous intéressent.
Soumettre une candidature indiquant le sujet dès maintenant pour connaître la possibilité d'obtenir une consultation.
Le sujet du TMS est les systèmes de file d'attente (QS) et les réseaux de file d'attente. Un QS est compris comme un système dynamique conçu pour desservir efficacement un flux aléatoire d'applications avec des ressources système limitées. La structure généralisée du QS est illustrée à la figure 3.1.
Riz. 3.1. Régime SMO.
Les candidatures homogènes entrant dans l'entrée QS sont divisées en types selon le motif générateur, l'intensité du flux de candidatures de type i (i=1…M) est notée i . L'ensemble des applications de tous types constitue le flux QS entrant.
Les applications sont en cours de traitement m canaux. Distinguer les canaux de service universels et spécialisés. Pour un canal universel de type j, les fonctions de répartition F ji () de la durée des sinistres de service de type quelconque sont considérées comme connues. Pour les chaînes spécialisées, les fonctions de répartition pour la durée de service des chaînes de certains types de créances sont indéfinies, l'affectation de ces créances à une chaîne donnée.
En tant que processus de service, divers dans leur nature physique processus de fonctionnement des systèmes économiques, industriels, techniques et autres, par exemple, flux de livraisons de produits à une certaine entreprise, flux de pièces et de composants sur la chaîne de montage d'un atelier, demandes de traitement d'informations informatiques à partir de terminaux distants, etc. Dans le même temps, le fonctionnement de tels objets est caractérisé par un comportement aléatoire des demandes (exigences) de maintenance et d'achèvement de la maintenance à des moments aléatoires.
Q - les schémas peuvent être étudiés analytiquement et par des modèles de simulation. Ce dernier offre une plus grande polyvalence.
Considérez le concept de file d'attente.
Dans tout acte de service élémentaire, on peut distinguer deux composantes principales : l'attente de service par une application et le service effectif d'une application. Cela peut être affiché sous la forme d'un ième dispositif de service P i , constitué d'un accumulateur de requêtes, dans lequel l i =0…L i H requêtes peuvent être localisées simultanément, où L i H est la capacité du ième accumulateur, et un canal de service de demande, k i .
Riz. 3.2. Schéma de l'appareil SMO
Des flux d'événements arrivent sur chaque élément du dispositif de service P i : le flux de requêtes w i entre dans l'accumulateur H i , et le flux de service u i entre dans le canal k i .
Le flux des événements(PS) est une séquence d'événements qui se produisent les uns après les autres à un moment aléatoire. Il existe des flux d'événements homogènes et non homogènes. Homogène PS est caractérisé uniquement par les instants d'arrivée de ces événements (instants générateurs) et est donné par la suite (t n )=(0t 1 t 2 …t n …), où t n est l'instant d'arrivée du nième événement - un nombre réel non négatif. OPS peut également être spécifié comme une séquence d'intervalles de temps entre le n-ième et le n-1-ième événement ( n ).
Hétérogène PS est appelé la séquence (t n , f n ) , où t n - moments provoquants; f n - ensemble de signes d'événement. Par exemple, l'appartenance à l'une ou l'autre source de requêtes, la présence d'une priorité, la possibilité de desserte par l'un ou l'autre type de canal, etc. peuvent être précisées.
Considérons l'OPS, pour lequel i ( n ) sont des variables aléatoires indépendantes les unes des autres. Alors PS est appelé un flux avec séquelle limitée.
PS s'appelle ordinaire, si la probabilité que plus d'un événement P 1 (t, t) tombe sur un petit intervalle de temps t adjacent au temps t est négligeable.
Si pour tout intervalle t l'événement P 0 (t, t) + P 1 (t, t) + Р 1 (t, t)=1, P 1 (t, t) est la probabilité de frapper l'intervalle t d'exactement un événement. Comme la somme des probabilités d'événements qui forment un groupe complet et sont incompatibles, alors pour un flux ordinaire d'événements P 0 (t, t) + P 1 (t, t) 1, Р 1 (t, t)=(t ), où (t) est une valeur dont l'ordre de petitesse est supérieur à t, c'est-à-dire lim((t))=0 pour t0.
Sous-station fixe est appelé un flux pour lequel la probabilité d'occurrence de l'un ou l'autre nombre d'événements dans un intervalle de temps dépend de la longueur de cette section et ne dépend pas de l'endroit où sur l'axe des temps 0 - t cette section est prise. Pour OPS, 0*P 0 (t, t) + 1*P 1 (t, t)= P 1 (t, t) est le nombre moyen d'événements dans l'intervalle t. Le nombre moyen d'événements se produisant dans la section t par unité de temps est P 1 (t, t)/t. Considérons la limite de cette expression à t0
lim P 1 (t, t)/t=(t)*(1/unité).
Si cette limite existe, alors on l'appelle l'intensité (densité) de l'OPS. Pour PS standard (t)==const.
En ce qui concerne le canal de service élémentaire k i, on peut supposer que le flux de requêtes w i W, c'est-à-dire les intervalles de temps entre les instants d'apparition des requêtes à l'entrée k i forment un sous-ensemble de variables incontrôlables, et le flux de service u i U, c'est-à-dire les intervalles de temps entre le début et la fin de la demande de service forment un sous-ensemble de variables commandées.
Les revendications servies par le canal k i et les revendications qui ont quitté le dispositif P i pour diverses raisons n'ont pas été servies, forment le flux de sortie y i Y.
Le processus de fonctionnement du dispositif de service P i peut être représenté comme un processus de changement des états de ses éléments dans le temps Z i (t). Le passage à un nouvel état pour P i signifie un changement du nombre de requêtes qui s'y trouvent (dans le canal k i et l'accumulateur H i). Ce. le vecteur d'état pour P i a la forme : occupé).
Les schémas Q d'objets réels sont formés par la composition de nombreux dispositifs de service élémentaires P i . Si k i différents dispositifs de service sont connectés en parallèle, alors un service multicanal (circuit Q multicanal) a lieu, et si les dispositifs P i et leurs compositions parallèles sont connectés en série, alors un service multiphase a lieu (multi -phase Q-circuit).
Ce. pour spécifier un schéma Q, l'opérateur de conjugaison R est requis, qui reflète la relation des éléments de la structure.
Les liens dans le schéma Q sont représentés par des flèches (lignes de flux reflétant la direction du mouvement des applications). Il existe des circuits Q ouverts et fermés. À ouvert le flux de sortie ne peut plus arriver à aucun élément, c'est-à-dire il n'y a pas de retour d'information.
Les paramètres propres (internes) du schéma Q seront le nombre de phases L Ф, le nombre de canaux dans chaque phase, L kj , j=1 ... L Ф, le nombre de variateurs de chaque phase L kj , k =1 ... L Ф, capacité i- ème lecteur L i H . Il convient de noter que dans la théorie de la file d'attente, en fonction de la capacité de stockage, la terminologie suivante est utilisée :
systèmes avec pertes (L i H =0, il n'y a pas de stockage) ;
systèmes d'attente (L i H );
systèmes à capacité de stockage limitée H i (mixtes).
Désignons l'ensemble des paramètres propres du schéma Q comme un sous-ensemble H.
Pour spécifier le schéma Q, il est également nécessaire de décrire les algorithmes de son fonctionnement, qui déterminent les règles de comportement des applications dans diverses situations ambiguës.
Selon le lieu d'apparition de telles situations, il existe des algorithmes (disciplines) d'attente d'applications dans le stockage H i et de desserte d'applications avec le canal k i . L'hétérogénéité du flux de requêtes est prise en compte en introduisant une classe de priorités.
Selon la dynamique des priorités, les schémas Q sont distingués entre statique et dynamique. Les priorités statiques sont attribuées à l'avance et ne dépendent pas des états du schéma Q, c'est-à-dire ils sont fixés dans la solution d'un problème de modélisation particulier. Des priorités dynamiques apparaissent pendant la simulation. Sur la base des règles de sélection des requêtes du stockage H i pour le service par le canal k i, nous pouvons sélectionner relatif et absolu priorités. Priorité relative signifie qu'une demande avec une priorité plus élevée, qui est arrivée dans le stockage H, attend que le service de la demande de soumission par le canal ki se termine, et seulement après cela, elle occupe le canal. Priorité absolue signifie qu'un client de priorité supérieure entré dans l'accumulateur interrompt le service d'un client de priorité inférieure par le canal k i et occupe lui-même le canal (dans ce cas, le client évincé de k i peut soit quitter le système soit être réécrit à un endroit de H i).
Il faut également connaître l'ensemble des règles par lesquelles les clients quittent H i et k i : pour H i , soit des règles de débordement, soit des règles de sortie associées à l'expiration du temps d'attente du client dans H i ; pour k i - règles de choix des itinéraires ou des directions d'évasion. De plus, il est nécessaire de fixer les règles pour les requêtes, selon lesquelles elles restent dans le canal k i , c'est-à-dire règles de blocage des canaux. En même temps, les verrous k i se distinguent par la sortie et par l'entrée. De tels verrous reflètent la présence de liens de contrôle dans le Q-scheme qui régulent le flux de requêtes en fonction des états du Q-scheme. L'ensemble des algorithmes possibles pour le comportement des réclamations dans le schéma Q peut être représenté comme un certain opérateur d'algorithmes pour le comportement des réclamations MAIS.
Ce. Le schéma Q décrivant le processus de fonctionnement QS de toute complexité est spécifié de manière unique comme un ensemble d'ensembles : Q =
Processus stochastiques de Markov
Ils portent le nom de l'excellent mathématicien russe A.A. Markov, qui a commencé l'étude de la connexion probabiliste des variables aléatoires et a créé une théorie que l'on peut appeler "dynamique des probabilités". À l'heure actuelle, la théorie des processus de Markov et ses applications sont largement utilisées dans divers domaines, notamment la recherche opérationnelle et la théorie de la prise de décision optimale.
Processus de Markov- discret ou continu processus aléatoire X(t), qui peut être complètement spécifié à l'aide de deux grandeurs :
· probabilités P(X,t) que la variable aléatoire X(t) au moment t est égal à X, et
probabilités P(X 2 , t 2 |X 1 ,t 1) et si Xà t = t 1 est égal X 1 , alors t = t 2 est égal à X 2 .
La seconde de ces grandeurs est appelée probabilité de transition hors de l'état X 1 à t = t 1 par état X 2 à t = t 2 .
Chaînes de Markov appelé discret par temps et valeur Markov
processus.
Exemple 1
Supposons que nous parlions de lancers successifs d'une pièce lorsque nous jouons au « lancer » ; la pièce est lancée à des instants conditionnels t = 0, 1, ... et à chaque pas le joueur peut gagner ±1 avec la même probabilité 1/2, donc à l'instant t son gain total est une variable aléatoire ξ(t) avec valeurs possibles j = 0, ±1, ... Sous réserve que ξ(t) = k,à l'étape suivante, le gain sera déjà égal à ξ(t+1) = k± 1, en prenant les valeurs indiquées j = k ± 1 avec la même probabilité 1/2. Classiquement, on peut dire qu'ici, avec la probabilité correspondante, on passe de l'état ξ(t) = kà l'état ξ(t+1) = k± 1.
19.5.1. Formules et définitions des chaînes de Markov
En généralisant cet exemple, on peut imaginer un "système" avec un nombre dénombrable d'états "de phase" possibles, qui passe aléatoirement d'état en état sur un temps discret t = 0, 1, ....
Soit ξ(t) sa position à l'instant t résultant d'une chaîne de transitions aléatoires ξ(0) - ξ(1) - ... - ξ(t) - ... ... (1)
Notons formellement tous les états possibles par des entiers i = 0, ±1, ... Supposons que pour un état connu ξ(t) = kà l'étape suivante, le système passe à l'état ξ(t+1) = j avec probabilité conditionnelle
p kj = P(ξ(t+1) = j|ξ(t) = k) ... (2)
quel que soit son comportement dans le passé, plus précisément quel que soit l'enchaînement des transitions (1) jusqu'à l'instant t :
P(ξ(t+1) = j|ξ(0) = i, ..., ξ(t) = k) = P(ξ(t+1) = j|ξ(t) = k) pour tout t, k, j ... (3) - propriété de Markov.
Un tel schéma probabiliste est appelé chaîne de Markov homogène avec un nombre dénombrable d'états- son homogénéité réside dans le fait que défini en (2) probabilités de transition p kj, ∑ j p kj = 1, k = 0, ±1, ..., ne dépendent pas du temps, c'est-à-dire,
P(ξ(t+1) = j|ξ(t) = k) = P ij - matrice de probabilité de transition en une étape ne dépend pas de n. Il est clair que P ij est une matrice carrée avec des entrées non négatives et des sommes unitaires sur les lignes. Une telle matrice (finie ou infinie) est appelée matrice stochastique. Toute matrice stochastique peut servir de matrice de probabilités de transition.
Supposons qu'une certaine entreprise livre du matériel à Moscou: dans le district nord (notons A), sud (B) et central (C). L'entreprise dispose d'un groupe de coursiers qui dessert ces zones. Il est clair que pour la prochaine livraison, le coursier se rend dans la zone qui est ce moment plus près de lui. Ce qui suit a été statistiquement déterminé :
1) après la livraison à A, la livraison suivante dans 30 cas est effectuée en A, dans 30 cas - en B et dans 40 cas - en C ;
2) après la livraison à B, la prochaine livraison est dans 40 cas à A, dans 40 cas à B et dans 20 cas à C ;
3) après la livraison à C, la prochaine livraison est dans 50 cas à A, dans 30 cas à B et dans 20 cas à C.
Ainsi, la zone de la prochaine livraison n'est déterminée que par la livraison précédente.
La matrice de probabilité de transition ressemblera à ceci :
Par exemple, p 12 = 0,4 est la probabilité qu'après une livraison dans la zone B, la prochaine livraison se fasse dans la zone A. Disons que chaque livraison puis le passage à la zone suivante prend 15 minutes. Ensuite, conformément aux statistiques, après 15 minutes, 30 % des coursiers qui étaient en A seront en A, 30 % seront en B et 40 % en C. Puisqu'au moment suivant chacun des coursiers sera nécessairement être dans l'un des quartiers, alors la somme sur les colonnes est 1. Et puisque nous avons affaire à des probabilités, chaque élément de la matrice est 0<р ij <1. Наиболее важным обстоятельством, которое позволяет интерпретировать данную модель как цепь Маркова, является то, что местонахождение курьера в момент времени t+1 зависит seulement de l'emplacement au temps t.
Posons maintenant une question simple : si le coursier part de C, quelle est la probabilité qu'après avoir effectué deux livraisons, il soit en B, c'est-à-dire Comment pouvez-vous atteindre B en 2 étapes ? Ainsi, il existe plusieurs chemins de C à B en 2 étapes :
1) d'abord de C à C puis de C à B ;
2) C-->B et B-->B ;
3) C-->A et A-->B.
En tenant compte de la règle de multiplication des événements indépendants, on obtient que la probabilité recherchée est égale à :
P = P(CA)*P(AB) + P(CB)*P(BB) + P(CC)*P(CB)
Substitution de valeurs numériques :
P = 0,5*0,3 + 0,3*0,4 + 0,2*0,3 = 0,33
Le résultat obtenu indique que si le coursier a commencé à travailler à partir de C, alors dans 33 cas sur 100, il sera en B après deux livraisons. Il est clair que les calculs sont simples, mais si vous avez besoin de déterminer la probabilité après 5 ou 15 livraisons, cela peut prendre un temps assez long.
Considérons une manière plus simple de calculer ces probabilités. Afin d'obtenir les probabilités de transition de différents états en 2 étapes, nous élevons au carré la matrice P :

Alors l'élément (2, 3) est la probabilité de passer de C à B en 2 étapes, qui a été obtenue ci-dessus d'une manière différente. Notez que les éléments de la matrice P2 vont également de 0 à 1, et la somme sur les colonnes est 1.
Ce. si vous avez besoin de déterminer les probabilités de transition de C à B en 3 étapes :
1 voie. p(CA)*P(AB) + p(CB)*P(BB) + p(CC)*P(CB) = 0,37*0,3 + 0,33*0,4 + 0,3*0,3 = 0,333 où p(CA) - le probabilité de transition de C à A en 2 étapes (c'est-à-dire qu'il s'agit d'un élément (1, 3) de la matrice P 2).
2 voies. Calculer la matrice P 3 :

La matrice des probabilités de transition à la puissance 7 ressemblera à ceci :

Il est facile de voir que les éléments de chaque ligne tendent vers certains nombres. Cela signifie qu'après suffisamment un grand nombre livraison, peu importe dans quel district le coursier a commencé à travailler. Ce. à la fin de la semaine, environ 38,9 % seront en A, 33,3 % seront en B et 27,8 % seront en C. Une telle convergence est garantie si tous les éléments de la matrice de probabilité de transition appartiennent à l'intervalle (0 , 1).
Théorie des files d'attente
C'est la rubrique recherche opérationnelle qui considère divers processus dans l'économie, ainsi que dans les communications téléphoniques, la santé et d'autres domaines, en tant que processus de service, c'est-à-dire satisfaire certaines demandes, commandes (par exemple, l'entretien des navires dans le port - leur déchargement et leur chargement, l'entretien des tourneurs dans la réserve d'outils du atelier - leur fournir des cutters, servir les clients dans la blanchisserie - laver les vêtements, etc.).
Malgré leur diversité, ces processus ont caractéristiques communes: conditions service irrégulier (accidentellement) canal de service(place au poste d'amarrage, une fenêtre dans la salle de transfert) et, en fonction de son emploi, de la durée du service et d'autres facteurs, forme file d'attente des exigences.
La théorie des files d'attente étudie les modèles statistiques de réception des exigences et, sur cette base, développe solutions, c'est-à-dire de telles caractéristiques sous lesquelles le temps passé à attendre dans la file d'attente, d'une part, et sur les canaux de service inactifs, d'autre part, serait le plus faible. L'ensemble du système de production et de consommation de biens peut être interprété comme un système de files d'attente où les personnes (clients) et les biens se rencontrent. La somme du temps perdu à attendre dans les files d'attente et des temps d'arrêt des canaux de service (stockage des marchandises dans les entrepôts) est considérée comme une mesure Efficacitéétudié système économique.
Méthodes d'analyse des systèmes de file d'attente
Les méthodes et modèles utilisés dans la théorie des files d'attente peuvent être conditionnellement divisés en analyse et simulation.
Méthodes analytiques les théories des files d'attente permettent d'obtenir les caractéristiques du système comme certaines fonctions des paramètres de son fonctionnement. Cela permet de mener une analyse qualitative de l'influence des facteurs individuels sur l'efficacité du QS.
Méthodes de simulation sont basés sur la modélisation des processus de mise en file d'attente sur un ordinateur et sont utilisés s'il est impossible d'utiliser des modèles analytiques.
À l'heure actuelle, les méthodes les plus théoriquement développées et pratiques dans les applications pratiques sont les méthodes de résolution des problèmes de file d'attente dans lesquelles le flux entrant d'exigences est le plus simple (Poisson).
Pour le flux le plus simple, la fréquence des requêtes entrant dans le système obéit à la loi de Poisson, c'est-à-dire probabilité d'arrivée dans le temps t lisse à exigences est donnée par la formule :
![]()
Le flux le plus simple a trois propriétés principales :
1) ordinaire,
2) stationnarité et
3) absence de séquelle.
Banalité flux signifie l'impossibilité pratique de recevoir simultanément deux demandes ou plus. Par exemple, la probabilité que plusieurs machines d'un groupe de machines entretenues par une équipe de réparateurs tombent en panne en même temps est assez faible.
Stationnaire un flux est appelé, pour lequel l'espérance mathématique du nombre d'exigences entrant dans le système par unité de temps (notons A, est le paramètre de la distribution de Poisson) ne change pas dans le temps. Ainsi, la probabilité d'entrer dans le système Un certain montant besoins dans un délai donné À dépend de sa valeur et ne dépend pas de l'origine de sa référence sur l'axe des temps.
Pas de séquelle signifie que le nombre de requêtes reçues par le système avant t, ne détermine pas le nombre de demandes qui entreront dans le système sur une période de temps à partir de t avant de t + Dt
Par exemple, si une casse de fil se produit sur un métier à un instant donné et qu'elle est éliminée par le tisseur, alors cela ne détermine pas si une nouvelle casse se produira sur ce métier à l'instant d'après ou non, d'autant plus cela n'affecte pas la probabilité d'une rupture sur d'autres machines.
Caractéristique importante SMO- temps de service des demandes dans le système. Le temps de service d'une exigence est, en règle générale, une variable aléatoire et, par conséquent, peut être décrit par une loi de distribution. Le plus utilisé en théorie et surtout dans les applications pratiques est loi exponentielle de la distribution du temps de service. La fonction de distribution de cette loi est :

ceux. la probabilité que le temps de service ne dépasse pas une certaine valeur t, est défini par la formule (5.2), où µ - paramètre de la loi exponentielle de distribution du temps de service des besoins dans le système, c'est-à-dire l'inverse du temps de service moyen
![]()
Les systèmes de file d'attente sont classés :
1. Selon conditions d'attente démarrage du service :
QS avec pertes (échecs)
CMO avec attente
Dans SMO avec des échecs les demandes arrivant au moment où tous les canaux de service sont occupés sont rejetées et quittent le système. Un exemple classique d'un système avec des pannes est le central téléphonique. Si l'appelé est occupé, la demande de connexion est refusée et quitte le système.
Dans SMO avec attente une requête, ayant trouvé tous les canaux de desserte occupés, se met en file d'attente et attend jusqu'à ce que l'un des canaux de desserte se libère.
Un QS qui autorise une file d'attente, mais avec un nombre limité de requêtes, est appelé systèmes avec une longueur de file d'attente limitée.
Un QS qui autorise une file d'attente, mais avec un temps de séjour limité pour chaque client, est appelé systèmes de latence.
2. Selon le nombre de canaux de service, les QS sont divisés en :
Canal unique ;
À canaux multiples.
3. Selon la localisation de la source des exigences, les QS sont divisés en :
ouvert, lorsque la source de l'exigence est extérieure au système ;
fermé, lorsque la source se trouve dans le système lui-même.
19.7. Problèmes d'analyse des systèmes de file d'attente fermés et ouverts
Fermé et ouvert systèmes, selonà partir du temps d'attente peuvent également être des systèmes de file d'attente avec attente. Ce sont les SMO les plus courants. Ils sont étudiés à l'aide de modèles analytiques.
système de file d'attente Un système est appelé un système dans lequel les demandes reçues à un moment où tous les canaux de desserte sont occupés sont mises en file d'attente et traitées lorsque les canaux se libèrent.
Un exemple de système en boucle ouverte est un atelier de réparation de téléviseurs. Ici, les téléviseurs défectueux sont la source des exigences de maintenance, ils sont en dehors du système lui-même, de sorte que le nombre d'exigences peut être considéré comme illimité. QS fermé comprend, par exemple, un atelier d'usinage, dans lequel les machines sont une source de dysfonctionnements, et, par conséquent, une source d'exigences pour leur maintenance, par exemple, par une équipe d'ajusteurs.
L'énoncé général du problème est le suivant. Le système a P canaux de desserte, chacun d'entre eux ne pouvant répondre qu'à un seul besoin à la fois.
Le système reçoit le flux de requêtes le plus simple (Poisson) avec le paramètre A. P exigences, c'est-à-dire tous les canaux sont occupés, cette demande est mise en file d'attente et attend le début du service. Le temps de service de chaque exigence est une variable aléatoire qui obéit à la loi de distribution exponentielle avec le paramètre µ .
Le QS expectant peut être divisé en deux grands groupes : fermé et ouvert. À fermé inclure des systèmes dans lesquels le flux entrant d'exigences survient dans le système lui-même et est limité. Par exemple, un contremaître dont la tâche est d'installer des machines dans l'atelier doit les entretenir périodiquement. Chaque machine configurée devient une source potentielle d'exigences de configuration. Dans de tels systèmes, le nombre total de créances en circulation est fini et le plus souvent constant.
Si la source d'approvisionnement a un nombre infini de besoins et est située en dehors du système, alors le système est appelé ouvert. Des exemples de systèmes ouverts sont les magasins, les guichets des gares, des ports, etc. Pour ces systèmes, le flux entrant de besoins peut être considéré comme illimité. De plus, les QS en boucle ouverte avec attente et une longueur de file d'attente limitée, avec un temps limité passé dans la file d'attente, etc., sont assez courants.
Les caractéristiques notées du fonctionnement de QS avec attente, en raison de leurs types, imposent certaines conditions à l'appareil mathématique utilisé. Le calcul des caractéristiques de fonctionnement de tous ces QS peut être effectué sur la base du calcul des probabilités des états QS (le soi-disant formules Erlang).
Considérez la procédure de calcul des caractéristiques du travail systèmes en boucle ouverte avec attente et longueur de file d'attente limitée.
Ces SMO sont constitués de P canaux de desserte, chacun d'entre eux ne pouvant répondre qu'à un seul besoin à la fois. Le système reçoit le flux de requêtes le plus simple avec le paramètre A., et le temps de service de la requête est une variable aléatoire qui obéit à une loi de distribution exponentielle avec le paramètre c. Si au moment de la réception de la demande suivante tous P les canaux sont occupés et la file d'attente n'en est pas moins t exigences, la demande est mise en file d'attente. S'il est déjà dans la file d'attente t exigences, alors l'exigence reçue quitte le QS. En d'autres termes, la demande est refusée si le système a n + t conditions. A partir des équations décrivant l'état de tels systèmes, les formules suivantes peuvent être obtenues pour calculer leurs principales caractéristiques.
1. La probabilité que tous les canaux de desserte soient libres,
 (5.14)
(5.14)
2. La probabilité que le système soit à exigences, à condition que le nombre total de ces exigences ne dépasse pas le nombre de canaux de desserte ; autrement dit, la probabilité d'être occupé à canaux,
| |
3. La probabilité que le système soit à exigences, lorsque le nombre de ces exigences est supérieur au nombre de canaux de desserte,
 (5.16)
(5.16)
4. La probabilité que tous les canaux de desserte soient occupés,
 (5.17)
(5.17)
5. Probabilité d'échec
![]() (5.18)
(5.18)
6. Longueur moyenne de la file d'attente
7. Nombre moyen de chaînes gratuites

Exemple 2 L'entreprise est engagée dans la livraison de marchandises sur commande et dispose de quatre machines qui fonctionnent 24 heures sur 24. Le flux des commandes est le plus simple, et en moyenne une candidature est reçue par heure. Le temps de transport des marchandises est soumis à une loi de distribution exponentielle, et en moyenne, le transport d'une cargaison prend une heure. Lorsque le nombre de commandes de transport est de 10, l'entreprise cesse d'accepter les candidatures jusqu'à ce que la file d'attente diminue.
Il est nécessaire de déterminer les caractéristiques de l'entreprise.
La solution. Ce système fait référence au type de QS avec attente et longueur de file d'attente limitée. Trouvons les paramètres du système, en prenant une heure comme unité de temps :
La probabilité que toutes les voitures soient exemptes du transport de marchandises est trouvée par la formule (5.14) :
La probabilité que toutes les machines soient occupées est déterminée par la formule (5.17) et est
Alors la probabilité de refus d'accepter un ordre de transport, calculée par la formule (5.18) sera égale à
 , et la longueur moyenne de la file d'attente conformément à la formule (5.19) sera
, et la longueur moyenne de la file d'attente conformément à la formule (5.19) sera
![]()
Alors la probabilité de refus d'accepter un ordre de transport, calculée par la formule (5.18), sera égale à
et la longueur moyenne de la file d'attente conformément à la formule (5.19) sera
Ainsi, le client ne recevra presque jamais de refus d'accepter une demande de transport, cependant, le chargement des véhicules sera assez faible. Par exemple, dans seulement deux cas sur cent, les quatre voitures seront occupées.
Passons à la considération des algorithmes de calcul des caractéristiques du fonctionnement QS fermé avec attente. Le système étant fermé, une condition doit être ajoutée à l'énoncé du problème : le flux de demandes entrantes est limité, c'est-à-dire plus personne ne peut être dans le système de service en même temps t conditions (t- nombre d'objets servis). Ces SMO sont également appelés des systèmes avec attente et un flux limité de demandes.
Comme critère caractérisant la qualité de fonctionnement du système considéré, nous prendrons le rapport de la longueur moyenne de la file d'attente au plus grand nombre d'exigences qui se trouvent simultanément dans le système serveur, ou le taux d'indisponibilité des objets servis. Comme autre critère, nous prenons le rapport du nombre moyen de canaux de service inactifs à leur nombre total, ou le rapport d'inactivité des canaux de service.
Le premier des critères caractérise la perte de temps due à l'attente de la mise en service. Le deuxième critère montre l'exhaustivité de la charge du système de service et est important dans les tâches d'organisation du travail.
Évidemment, une file d'attente ne peut survenir que lorsque le nombre de canaux est inférieur à le plus grand nombre exigences qui sont simultanément dans le système de service (P< т).
Nous présentons la séquence de calculs des caractéristiques de QS fermé avec espérance et les formules nécessaires.
1. Paramètre α=α/µ. -
indicateur de charge du système, c'est-à-dire l'espérance mathématique du nombre de requêtes entrant dans le système en un temps égal au temps de service moyen ![]()
2. Probabilité d'être occupé à canaux de desserte, à condition que le nombre d'exigences dans le système ne dépasse pas le nombre de canaux de desserte du système,
 .
. ,
,