Le logarithme décimal est 0. Logarithme
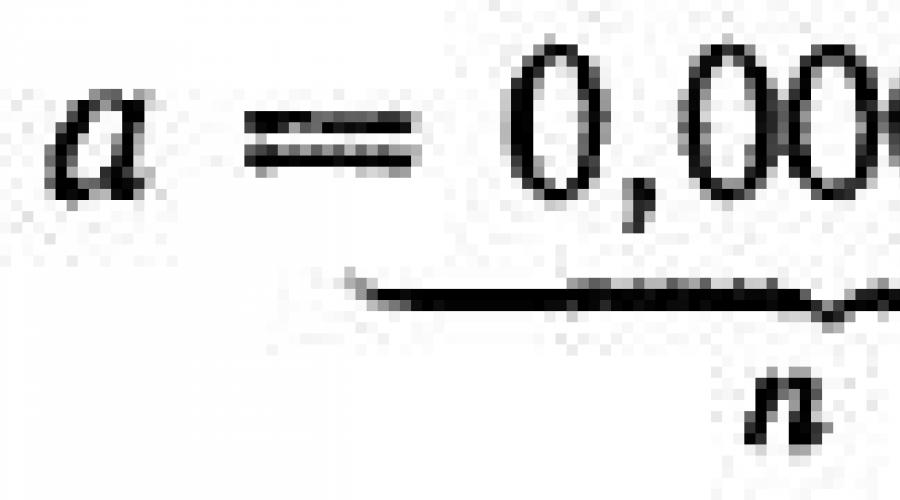
Lire aussi
Donc, nous avons des puissances de deux. Si vous prenez le nombre de la ligne du bas, vous pouvez facilement trouver la puissance à laquelle vous devez élever un deux pour obtenir ce nombre. Par exemple, pour obtenir 16, vous devez élever deux à la puissance quatre. Et pour obtenir 64, vous devez élever deux à la sixième puissance. Cela se voit sur le tableau.
Et maintenant - en fait, la définition du logarithme :
Le logarithme à la base a de l'argument x est la puissance à laquelle le nombre a doit être élevé pour obtenir le nombre x .
Notation: log a x \u003d b, où a est la base, x est l'argument, b est en fait ce à quoi le logarithme est égal.
Par exemple, 2 3 = 8 ⇒ log 2 8 = 3 (le logarithme en base 2 de 8 est trois car 2 3 = 8). Autant enregistrer 2 64 = 6 car 2 6 = 64 .
L'opération consistant à trouver le logarithme d'un nombre dans une base donnée s'appelle le logarithme. Ajoutons donc une nouvelle ligne à notre tableau :
| 2 1 | 2 2 | 2 3 | 2 4 | 2 5 | 2 6 |
| 2 | 4 | 8 | 16 | 32 | 64 |
| bûche 2 2 = 1 | bûche 2 4 = 2 | bûche 2 8 = 3 | bûche 2 16 = 4 | bûche 2 32 = 5 | bûche 2 64 = 6 |
Malheureusement, tous les logarithmes ne sont pas considérés aussi facilement. Par exemple, essayez de trouver log 2 5 . Le nombre 5 n'est pas dans le tableau, mais la logique veut que le logarithme se situe quelque part sur le segment. Parce que 2 2< 5 < 2 3 , а чем больше степень двойки, тем больше получится число.
De tels nombres sont appelés irrationnels : les nombres après la virgule décimale peuvent être écrits indéfiniment, et ils ne se répètent jamais. Si le logarithme s'avère irrationnel, il vaut mieux le laisser ainsi : log 2 5 , log 3 8 , log 5 100 .
Il est important de comprendre que le logarithme est une expression à deux variables (base et argument). Au début, beaucoup de gens confondent où se trouve la base et où se trouve l'argument. Pour éviter les malentendus gênants, il suffit de regarder l'image :
Devant nous n'est rien de plus que la définition du logarithme. Rappelles toi: le logarithme est la puissance, auquel vous devez élever la base pour obtenir l'argument. C'est la base qui est élevée à une puissance - sur l'image, elle est surlignée en rouge. Il s'avère que la base est toujours en bas ! Je dis cette merveilleuse règle à mes élèves dès la première leçon - et il n'y a pas de confusion.
Nous avons compris la définition - il reste à apprendre à compter les logarithmes, c'est-à-dire débarrassez-vous du signe "log". Pour commencer, notons que deux faits importants découlent de la définition :
- L'argument et la raison doivent toujours être Au dessus de zéro. Cela découle de la définition du degré par un exposant rationnel, à laquelle se réduit la définition du logarithme.
- La base doit être différente de l'unité, car une unité pour n'importe quelle puissance est toujours une unité. De ce fait, la question « à quelle puissance faut-il élever un pour en avoir deux » n'a pas de sens. Un tel diplôme n'existe pas !
De telles restrictions sont appelées Plage valide(ODZ). Il s'avère que l'ODZ du logarithme ressemble à ceci : log a x = b ⇒ x > 0 , a > 0 , a ≠ 1 .
Notez qu'il n'y a pas de restrictions sur le nombre b (la valeur du logarithme) n'est pas imposée. Par exemple, le logarithme peut très bien être négatif: log 2 0,5 \u003d -1, car 0,5 = 2 −1 .
Cependant, pour l'instant, nous n'envisageons que expressions numériques, où il n'est pas nécessaire de connaître l'ODZ du logarithme. Toutes les restrictions ont déjà été prises en compte par les compilateurs des problèmes. Mais lorsque les équations logarithmiques et les inégalités entreront en jeu, les exigences du DHS deviendront obligatoires. En effet, dans la base et l'argument, il peut y avoir des constructions très fortes, qui ne correspondent pas nécessairement aux restrictions ci-dessus.
Considérez maintenant régime général calculs de logarithme. Il se compose de trois étapes :
- Exprimer la base a et l'argument x comme une puissance avec un minimum base possible, grandes unités. En cours de route, il vaut mieux se débarrasser des fractions décimales ;
- Résolvez l'équation pour la variable b : x = a b ;
- Le nombre résultant b sera la réponse.
C'est tout! Si le logarithme s'avère irrationnel, cela se verra déjà à la première étape. L'exigence que la base soit supérieure à un est très pertinente : cela réduit le risque d'erreur et simplifie grandement les calculs. Semblable à décimales: si vous les traduisez immédiatement en ordinaires, il y aura beaucoup moins d'erreurs.
Voyons comment ce schéma fonctionne avec des exemples spécifiques :
Une tâche. Calculer le logarithme : log 5 25
- Représentons la base et l'argument sous la forme d'une puissance de cinq : 5 = 5 1 ; 25 = 52 ;
- Réponse reçue : 2.
Faisons et résolvons l'équation :
log 5 25 = b ⇒ (5 1) b = 5 2 ⇒ 5 b = 5 2 ⇒ b = 2 ;
Une tâche. Calculez le logarithme :
Une tâche. Calculer le logarithme : log 4 64
- Représentons la base et l'argument comme une puissance de deux : 4 = 2 2 ; 64 = 26 ;
- Faisons et résolvons l'équation :
log 4 64 = b ⇒ (2 2) b = 2 6 ⇒ 2 2b = 2 6 ⇒ 2b = 6 ⇒ b = 3 ; - Réponse reçue : 3.
Une tâche. Calculer le logarithme : log 16 1
- Représentons la base et l'argument comme une puissance de deux : 16 = 2 4 ; 1 = 20 ;
- Faisons et résolvons l'équation :
log 16 1 = b ⇒ (2 4) b = 2 0 ⇒ 2 4b = 2 0 ⇒ 4b = 0 ⇒ b = 0 ; - Réponse reçue : 0.
Une tâche. Calculer le logarithme : log 7 14
- Représentons la base et l'argument comme une puissance de sept : 7 = 7 1 ; 14 n'est pas représenté comme une puissance de sept, car 7 1< 14 < 7 2 ;
- Il résulte du paragraphe précédent que le logarithme n'est pas considéré ;
- La réponse est inchangée : log 7 14.
Une petite note sur le dernier exemple. Comment s'assurer qu'un nombre n'est pas une puissance exacte d'un autre nombre ? Très simple - il suffit de l'étendre en facteurs premiers. S'il y a au moins deux facteurs distincts dans l'expansion, le nombre n'est pas une puissance exacte.
Une tâche. Découvrez si les puissances exactes du nombre sont : 8 ; 48 ; 81 ; 35; Quatorze .
8 \u003d 2 2 2 \u003d 2 3 - le degré exact, car il n'y a qu'un seul multiplicateur ;
48 = 6 8 = 3 2 2 2 2 = 3 2 4 n'est pas une puissance exacte car il y a deux facteurs : 3 et 2 ;
81 \u003d 9 9 \u003d 3 3 3 3 \u003d 3 4 - degré exact;
35 = 7 5 - encore une fois pas un degré exact ;
14 \u003d 7 2 - encore une fois pas un degré exact;
Nous notons également que nous nombres premiers sont toujours des puissances exactes d'elles-mêmes.
Logarithme décimal
Certains logarithmes sont si courants qu'ils ont un nom et une désignation spéciaux.
Logarithme décimal de l'argument x est le logarithme en base 10, c'est-à-dire la puissance à laquelle vous devez élever le nombre 10 pour obtenir le nombre x. Désignation : lg x .
Par exemple, log 10 = 1 ; log 100 = 2 ; lg 1000 = 3 - etc.
À partir de maintenant, lorsqu'une phrase comme "Find lg 0.01" apparaît dans le manuel, sachez qu'il ne s'agit pas d'une faute de frappe. C'est le logarithme décimal. Cependant, si vous n'êtes pas habitué à une telle désignation, vous pouvez toujours la réécrire :
log x = log 10 x
Tout ce qui est vrai pour les logarithmes ordinaires est également vrai pour les décimaux.
un algorithme naturel
Il existe un autre logarithme qui a sa propre notation. En un sens, il est encore plus important que le nombre décimal. C'est le logarithme naturel.
Le logarithme népérien de x est le logarithme de base e, c'est-à-dire la puissance à laquelle il faut élever le nombre e pour obtenir le nombre x. Désignation : ln x .
Beaucoup se demanderont : qu'est-ce d'autre que le nombre e ? C'est un nombre irrationnel valeur exacte impossible à trouver et à enregistrer. Voici juste les premiers chiffres :
e = 2,718281828459...
Nous n'approfondirons pas ce qu'est ce nombre et pourquoi il est nécessaire. N'oubliez pas que e est la base du logarithme naturel :
ln x = log e x
Ainsi ln e = 1 ; log e 2 = 2 ; En e 16 = 16 - etc. Par contre, ln 2 est un nombre irrationnel. En général, le logarithme naturel de tout nombre rationnel irrationnel. Sauf, bien sûr, l'unité : ln 1 = 0.
Pour les logarithmes naturels, toutes les règles valables pour les logarithmes ordinaires sont valables.
Prenez souvent le chiffre dix. Les logarithmes des nombres en base dix sont appelés décimal. Lorsque vous effectuez des calculs avec le logarithme décimal, il est courant d'opérer avec le signe lg, mais non Journal; tandis que le nombre dix, qui détermine la base, n'est pas indiqué. Oui, nous remplaçons journal 10 105à simplifié lg105; un log102 sur le lg2.
Pour logarithmes décimaux les mêmes caractéristiques que les logarithmes ont avec une base supérieure à un sont typiques. À savoir, les logarithmes décimaux sont caractérisés exclusivement pour les nombres positifs. Les logarithmes décimaux des nombres supérieurs à un sont positifs et les nombres inférieurs à un sont négatifs. de deux nombres non négatifs, le plus grand équivaut au plus grand logarithme décimal, et ainsi de suite. De plus, les logarithmes décimaux ont caractéristiques distinctives et des signes particuliers, qui expliquent pourquoi il est confortable de préférer le nombre dix comme base des logarithmes.
Avant d'analyser ces propriétés, examinons les formulations suivantes.
Partie entière du logarithme décimal d'un nombre un appelé caractéristique, et la fraction mantisse ce logarithme.
Caractéristique du logarithme décimal d'un nombre un indiquée par , et la mantisse par (lg un}.
Prenons, disons, lg 2 ≈ 0,3010. Par conséquent, = 0, (log 2) ≈ 0,3010.
Il en est de même pour lg 543.1 ≈2.7349. En conséquence, = 2, (lg 543,1)≈ 0,7349.
Le calcul des logarithmes décimaux des nombres positifs à partir de tableaux est assez largement utilisé.
Signes caractéristiques des logarithmes décimaux.
Le premier signe du logarithme décimal. un entier non négatif représenté par 1 suivi de zéros est un entier positif égal au nombre de zéros dans le nombre choisi .
Prenons lg 100 = 2, lg 1 00000 = 5.
D'une manière générale, si
Ce un= 10n , d'où l'on tire
lg une = lg 10 n = n lg 10 =P.
Deuxième signe. Le logarithme décimal d'un nombre décimal positif, représenté par un un avec des zéros non significatifs, est - P, où P- le nombre de zéros dans la représentation de ce nombre, compte tenu du zéro des entiers.
Envisager , lg 0,001 = -3, lg 0,000001 = -6.
D'une manière générale, si
,
Ce un= 10-n et il s'avère
lg = lg 10n =-n lg 10 =-n
Troisième signe. La caractéristique du logarithme décimal d'un nombre non négatif supérieur à un est égale au nombre de chiffres de la partie entière de ce nombre, à l'exclusion de un.
Analysons cette caractéristique 1) La caractéristique du logarithme lg 75,631 est égale à 1.
En effet, 10< 75,631 < 100. Из этого можно сделать вывод
LG 10< lg 75,631 < lg 100,
1 < lg 75,631 < 2.
Cela implique,
lg 75,631 = 1 + b,
Décaler une virgule dans une fraction décimale vers la droite ou vers la gauche équivaut à l'opération consistant à multiplier cette fraction par une puissance de dix avec un exposant entier P(positif ou négatif). Et donc, lorsque la virgule décimale d'une fraction décimale positive est décalée vers la gauche ou vers la droite, la mantisse du logarithme décimal de cette fraction ne change pas.
Ainsi, (log 0,0053) = (log 0,53) = (log 0,0000053).
ARTICLE XIII.
LES LOGARITHMES ET LEURS APPLICATIONS.
§ 2. Logarithmes décimaux.
Le dixième logarithme du nombre 1 est 0. Logarithmes décimaux des puissances positives de 10, c'est-à-dire e. les nombres 10, 100, 1000,.... sont, les nombres positifs 1, 2, 3,...., donc en général le logarithme du nombre noté un avec des zéros, est égal au nombre des zéros. Logarithmes décimaux des puissances négatives de 10, soit les fractions 0.1, 0.01, 0.001, .... sont des nombres négatifs -1, -2, -3 ....., de sorte qu'en général le logarithme d'une fraction décimale avec un numérateur un est égal au nombre négatif de zéros du dénominateur.
Les logarithmes de tous les autres nombres commensurables sont incommensurables. Ces logarithmes sont calculés approximativement, généralement avec une précision d'un cent millième, et sont donc exprimés en fractions décimales à cinq chiffres; par exemple lg 3 = 0,47712.
Lors de la présentation de la théorie des logarithmes décimaux, tous les nombres sont supposés être compilés selon le système décimal de leurs unités et fractions, et tous les logarithmes sont exprimés par une fraction décimale contenant 0 entier, avec une augmentation ou une diminution entière. La partie fractionnaire du logarithme est appelée sa mantisse, et toute l'augmentation ou la diminution est sa caractéristique. Les logarithmes des nombres supérieurs à un sont toujours positifs et ont donc une caractéristique positive ; les logarithmes des nombres inférieurs à un sont toujours négatifs, mais ils sont représentés de telle manière que leur mantisse se révèle positive et qu'une caractéristique est négative: par exemple, lg 500 \u003d 0,69897 + 2 ou plus court que 2,69897, et lg 0,05 \u003d 0, 69897-2, qui par souci de brièveté est noté 2,69897, mettant la caractéristique à la place des nombres entiers, mais avec un signe - au-dessus. Ainsi, le logarithme d'un nombre supérieur à un représente la somme arithmétique d'un entier positif et d'une fraction positive, et le logarithme d'un nombre inférieur à un représente la somme algébrique d'un entier négatif avec une fraction positive.
Tout logarithme négatif peut être réduit à la forme artificielle indiquée. Par exemple, nous avons lg 3 / 5 \u003d lg 3 - lg 5 \u003d 0,47712-0,69897 \u003d -0,22185. Pour convertir ce vrai logarithme en une forme artificielle, on lui ajoute 1 et après addition algébrique on indique la soustraction de un pour la correction.
Nous obtenons lg 3 / 5 \u003d lg 0,6 \u003d (1-0,22185) -1 \u003d 0,77815-1. Dans ce cas, il s'avère que la mantisse 0,77815 est celle qui correspond au numérateur 6 de ce nombre, représenté dans le système décimal sous la forme d'une fraction 0,6.
Dans la représentation indiquée des logarithmes décimaux, leurs mantisses et caractéristiques ont des propriétés importantes en rapport avec la désignation décimale des nombres qui leur correspondent. Pour clarifier ces propriétés, notons ce qui suit. Prenons pour forme principale d'un nombre un nombre quelconque compris entre 1 et 10, et, l'exprimant en système décimal, nous le représenterons sous la forme a B c d e F ...., où un il y en a un chiffres significatifs 1, 2, 3, 4, 5, 6, 7, 8, 9 et décimales, b, c, ré, e, f ....... l'essence de tous les nombres, entre lesquels il peut y avoir des zéros. Du fait que le nombre pris est compris entre 1 n 10, son logarithme est compris entre 0 et 1 et donc ce logarithme est constitué d'une mantisse sans caractéristique ou de caractéristique 0. On note ce logarithme sous la forme 0 ,α β γ δ ε ...., où α, β ,γ ,δ, ε l'essence de certains chiffres. Nous multiplions maintenant ce nombre d'une part par les nombres 10, 100, 1000, .... et d'autre part par les nombres 0,1, 0,01, 0,001, ... et appliquons les théorèmes sur les logarithmes du produit et le quotient. On obtient alors une suite de nombres supérieurs à un et une suite de nombres inférieurs à un avec leurs logarithmes :
lg un ,bcde f ....= 0 ,α β γ δ ε ....
lg a B c d e F ....= 1 ,α β γ δ ε ... lg 0,abcde f ....= 1 ,α β γ δ ε ....
lg a B c d e F ....= 2 ,α β γ δ ε ... lg 0.0abcde f ....= 2 ,α β γ δ ε ....
lg a B c d e F ....= 3 ,α β γ δ ε ... lg 0.00abcde f ....= 3 ,α β γ δ ε ....
Lors de l'examen de ces égalités, les propriétés et caractéristiques suivantes de la mantisse sont révélées :
Propriété Mantisse. La mantisse dépend de l'emplacement et du type des chiffres béants du nombre, mais ne dépend pas du tout de la place de la virgule dans la désignation de ce nombre. Mantisses de logarithmes de nombres ayant un rapport décimal, c'est-à-dire ceux dont le rapport multiple est égal à toute puissance positive ou négative de dix sont les mêmes.
Propriété caractéristique. La caractéristique dépend de la catégorie des unités les plus élevées ou des fractions décimales d'un nombre, mais ne dépend pas du tout du type de chiffres dans la désignation de ce nombre.
Si nous appelons des numéros un ,bcde f ...., a B c d e F ...., a B c d e F .... nombres de chiffres positifs - premier, deuxième, troisième, etc., le chiffre du nombre 0,abcde f .... nous considérerons zéro, et les chiffres des nombres 0.0abcde f ...., 0.00abcde f ...., 0.000abcde f .... exprimer en nombres négatifs moins un, moins deux, moins trois, etc., alors il sera possible de dire en général que la caractéristique du logarithme de tout nombre décimal est un de moins que le nombre indiquant le chiffre
101. Sachant que lg 2 \u003d 0,30103, trouvez les logarithmes des nombres 20,2000, 0,2 et 0,00002.
101. Sachant que lg 3 \u003d 0,47712, trouvez les logarithmes des nombres 300, 3000, 0,03 et 0,0003.
102. Sachant que lg 5 \u003d 0,69897, trouvez les logarithmes des nombres 2,5, 500, 0,25 et 0,005.
102. Sachant que lg 7 \u003d 0,84510, trouvez les logarithmes des nombres 0,7, 4,9, 0,049 et 0,0007.
103. Connaissant lg 3=0,47712 et lg 7=0,84510, trouver les logarithmes des nombres 210, 0,021, 3/7, 7/9 et 3/49.
103. Connaissant lg 2=0,30103 et lg 7=0,84510, trouvez les logarithmes des nombres 140, 0,14, 2/7, 7/8 et 2/49.
104. Connaissant lg 3 \u003d 0,47712 et lg 5 \u003d O,69897, trouvez les logarithmes des nombres 1,5, 3/5, 0,12, 5/9 et 0,36.
104. Connaissant lg 5=0,69897 et lg 7=0,84510, trouvez les logarithmes des nombres 3,5, 5/7, 0,28, 5/49 et 1,96.
Les logarithmes décimaux des nombres exprimés par quatre chiffres au maximum sont recherchés directement dans les tableaux, et la mantisse du logarithme souhaité est trouvée dans les tableaux, et la caractéristique est définie en fonction du chiffre du nombre donné.
Si le nombre contient plus de quatre chiffres, la recherche du logarithme s'accompagne d'un calcul supplémentaire. La règle est : pour trouver le logarithme d'un nombre contenant plus de quatre chiffres, il faut chercher dans les tableaux le nombre indiqué par les quatre premiers chiffres et écrire la mantisse correspondant à ces quatre chiffres ; puis multipliez la différence tabulaire des mantisses par le nombre composé des chiffres rejetés, dans le produit, supprimez autant de chiffres à droite qu'ils ont été supprimés dans le nombre donné, et ajoutez le résultat aux derniers chiffres de la mantisse trouvée ; la caractéristique est de mettre, conformément à la décharge d'un nombre donné.
Lorsqu'un nombre est recherché par un logarithme donné et que ce logarithme est contenu dans les tables, alors les nombres du nombre recherché sont trouvés directement à partir des tables, et le chiffre du nombre est déterminé en fonction de la caractéristique du logarithme donné .
Si le logarithme donné n'est pas contenu dans les tables, alors la recherche d'un nombre s'accompagne d'un calcul supplémentaire. La règle est : pour trouver un nombre correspondant à un logarithme donné, dont la mantisse n'est pas contenue dans les tableaux, il faut trouver la plus petite mantisse la plus proche et écrire les chiffres correspondants du nombre; multipliez ensuite la différence entre la mantisse donnée et celle trouvée par 10 et divisez le produit par la différence tabulaire; attribuer le chiffre reçu du quotient à droite des chiffres écrits du nombre, c'est pourquoi l'ensemble de chiffres souhaité sera obtenu; la décharge du nombre doit être déterminée conformément aux caractéristiques du logarithme donné.
105. Trouvez les logarithmes des nombres 8, 141, 954, 420, 640, 1235, 3907, 3010, 18,43, 2,05, 900,1, 0,73, 0,0028, 0,1008, 0,00005.
105. Trouvez les logarithmes des nombres 15,154, 837, 510, 5002,1309-, 8900, 8,315, 790,7, 0,09, 0,6745, 0,000745, 0,04257, 0,00071.
106. Trouvez les logarithmes des nombres 2174,6, 1445,7, 2169,5, 8437,2, 46,472, 6,2853, 0,7893B, 0,054294, 631,074, 2,79556, 0,747428, 0,00237158.
106. Trouvez les logarithmes des nombres 2578,4, 1323,6, 8170,5, 6245,3, 437,65, 87,268, 0,059372, 0,84938, 62,5475, 131,037, 0,593946, 0,00234261.
107. Trouvez les nombres correspondant aux logarithmes de 3,16227, 3,59207, 2,93318, 0,41078, 1,60065, 2,756,86, 3,23528, 1,79692. 4,87800 5,14613.
107. Trouvez les nombres correspondant aux logarithmes de 3,07372, 3,69205, 1,64904, 2,16107, 0,70364, 1,31952, 4,30814, 3,00087, 2,69949, 6,57978.
108. Trouvez le nombre correspondant aux logarithmes de 3,57686, 3,16340, 2,40359, 1,09817, 4,49823, 2,83882, 1,50060, 3,30056, 1,17112, 4,25100.
108. Trouvez les nombres correspondant aux logarithmes de 3,33720, 3,09875, 0,70093, 4,04640, 2,94004, 1,41509, 2,32649, 4,14631, 3,01290, 5,39003.
Les logarithmes positifs des nombres supérieurs à un sont les sommes arithmétiques de leurs caractéristiques et mantisses. Par conséquent, les actions avec eux sont effectuées selon les règles arithmétiques ordinaires.
Les logarithmes négatifs des nombres inférieurs à un sont les sommes algébriques d'une caractéristique négative et d'une mantisse positive. Par conséquent, les opérations avec eux sont effectuées selon des règles algébriques, qui sont complétées par des instructions spéciales liées à la réduction des logarithmes négatifs à leur forme normale. La forme normale du logarithme négatif est celle dans laquelle la caractéristique est un entier négatif et la mantisse est une fraction propre positive.
Pour convertir le véritable logarithme réciproque en sa forme normale artificielle, il faut augmenter valeur absolue son terme entier par un et faire du résultat une caractéristique négative ; puis ajoutez tous les chiffres du terme fractionnaire à 9, et le dernier d'entre eux à 10 et faites du résultat une mantisse positive. Par exemple, -2,57928 = 3,42072.
Convertir la forme artificielle normale d'un logarithme en sa vraie forme Sens négatif, vous devez réduire la caractéristique négative de un et faire du résultat un terme entier de la somme négative ; puis ajoutez tous les chiffres de la mantisse à 9, et le dernier d'entre eux à 10 et faites du résultat un terme fractionnaire de la même somme négative. Par exemple : 4,57406= -3,42594.
109. Convertir en logarithmes artificiels -2,69537, -4, 21283, -0,54225, -1,68307, -3,53820, -5,89990.
109. Convertissez en forme artificielle les logarithmes -3,21729, -1,73273, -5,42936, -0,51395, -2,43780, -4,22990.
110. Trouvez les vraies valeurs des logarithmes 1,33278, 3,52793, 2,95426, 4,32725, 1,39420, 5,67990.
110. Trouvez les valeurs réelles des logarithmes 2,45438, 1,73977, 3,91243, 5,12912, 2,83770, 4,28990.
Les règles pour les opérations algébriques avec des logarithmes négatifs sont exprimées comme suit :
Pour appliquer le logarithme négatif sous sa forme artificielle, vous devez appliquer la mantisse et soustraire la valeur absolue de la caractéristique. Si un entier positif se distingue de l'addition des mantisses, il est alors nécessaire de l'attribuer à la caractéristique du résultat, en y apportant une correction appropriée. Par exemple,
3,89573 + 2 ,78452 = 1 1 ,68025 = 2,68025
1 ,54978 + 2 ,94963=3 1 ,49941=2 ,49941.
Pour soustraire le logarithme négatif sous sa forme artificielle, vous devez soustraire la mantisse et ajouter la valeur absolue de la caractéristique. Si la mantisse à soustraire est grande, alors il est nécessaire de faire une correction de la caractéristique de la réduite afin de séparer une unité positive de la mantisse réduite. Par exemple,
2,53798-3 ,84582=1 1 ,53798-3 ,84582 = 4,69216,
2 ,22689-1 ,64853=3 1 ,22689-1 ,64853=2 ,57836.
Pour multiplier un logarithme négatif par un entier positif, vous devez multiplier sa caractéristique et sa mantisse séparément. Si, lors de la multiplication de la mantisse, un nombre entier positif est attribué, il est alors nécessaire de l'attribuer à la caractéristique du résultat, en y apportant une correction appropriée. Par exemple,
2 ,53729 5=10 2 ,68645=8 ,68645.
Lorsque vous multipliez un logarithme négatif par un montant négatif, remplacez le multiplicateur par sa vraie valeur.
Pour diviser un logarithme négatif par un entier positif, vous devez séparer sa caractéristique et sa mantisse séparément. Si la caractéristique du dividende n'est pas divisible par le diviseur, alors il faut y apporter une correction pour attribuer plusieurs unités positives à la mantisse, et faire de la caractéristique un multiple du diviseur. Par exemple,
3 ,79432: 5=5 2 ,79432: 5=1 ,55886.
Lorsque vous divisez un logarithme négatif par un nombre négatif, vous devez remplacer le dividende par sa vraie valeur.
Effectuez les calculs suivants à l'aide de tables logarithmiques et vérifiez les résultats dans les cas les plus simples en utilisant les méthodes d'action habituelles :
174. Déterminez le volume d'un cône dont la génératrice est de 0,9134 pieds et le rayon de la base est de 0,04278 pieds.
175. Calculer le 15e terme d'une progression multiple dont le premier terme est 2 3/5 et le dénominateur est 1,75.
175. Calculez le premier terme d'une progression multiple, dont le 11e terme est 649,5 et le dénominateur est 1,58.
176. Déterminer le nombre de facteurs un , un 3 , un 5 R . Trouve ça un , où le produit de 10 facteurs est égal à 100.
176. Déterminez le nombre de facteurs. un 2 , un 6 , un 10 ,.... pour que leur produit soit égal au nombre donné R . Trouve ça un , où le produit de 5 facteurs est égal à 10.
177. Le dénominateur de la progression multiple est 1,075, la somme de ses 10 membres est 2017,8. Trouvez le premier terme.
177. Le dénominateur d'une progression multiple est 1,029, la somme de ses 20 membres est 8743,7. Trouvez le vingtième terme.
178 . Exprimer le nombre de termes d'une progression multiple étant donné le premier terme un , dernier et et dénominateur q , puis en choisissant arbitrairement des valeurs numériques un et tu , Récupérer q pour que P
178. Exprimer le nombre de membres d'une progression multiple selon le premier membre un , dernière et et dénominateur q et et q , Récupérer un pour que P était un entier.
179. Déterminer le nombre de facteurs pour que leur produit soit égal à R . Que devrait-il être R pour un =0,5 et b =0,9 le nombre de facteurs était de 10.
179. Déterminer le nombre de facteurs ![]() de sorte que leur produit est égal à R
. Que devrait-il être R
pour un
=0.2 et b
=2 le nombre de facteurs était de 10.
de sorte que leur produit est égal à R
. Que devrait-il être R
pour un
=0.2 et b
=2 le nombre de facteurs était de 10.
180. Exprimer le nombre de termes d'une progression multiple étant donné le premier terme un , plus tard et et le produit de tous les membres R , puis en choisissant arbitrairement des valeurs numériques un et R , Récupérer et suivi du dénominateur q pour que et était un entier.
160. Exprimer le nombre de membres d'une progression multiple selon le premier membre un , le dernier et et le produit de tous les termes R , puis en choisissant arbitrairement des valeurs numériques et et R , Récupérer un suivi du dénominateur q pour que P était un entier.
Résolvez les équations suivantes, si possible - sans l'aide de tables, et sinon, avec des tables :


