Transformationen wörtlicher irrationaler Ausdrücke. Irrationale Gleichungen
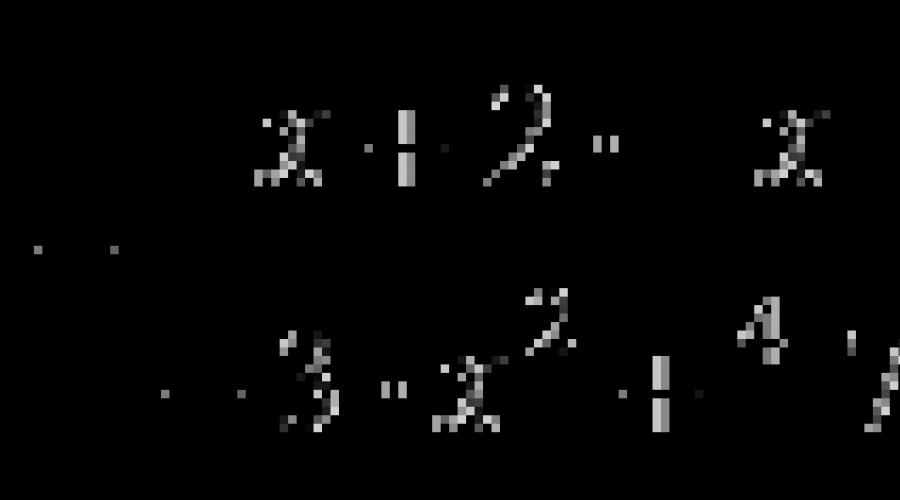
Lesen Sie auch
Bei der Konvertierung arithmetischer Wurzeln werden deren Eigenschaften verwendet (siehe Abschnitt 35).
Schauen wir uns einige Beispiele für die Verwendung der Eigenschaften arithmetischer Wurzeln für die einfachsten Transformationen von Radikalen an. In diesem Fall gehen wir davon aus, dass alle Variablen nur nicht negative Werte annehmen.
Beispiel 1. Extrahieren Sie die Wurzel der Produktlösung. Unter Anwendung der 1°-Eigenschaft erhalten wir:
Beispiel 2. Entfernen Sie den Multiplikator unter dem Wurzelzeichen
Lösung.
Diese Transformation wird als Entfernen des Faktors unter dem Wurzelzeichen bezeichnet. Der Zweck der Transformation besteht darin, den radikalen Ausdruck zu vereinfachen.
Beispiel 3: Vereinfachen
Lösung. Nach Eigenschaft 3° haben wir. Normalerweise versuchen sie, den Wurzelausdruck zu vereinfachen, indem sie die Faktoren aus dem Vorzeichen der Wurzel nehmen. Wir haben
Beispiel 4: Vereinfachen
Lösung. Transformieren wir den Ausdruck, indem wir einen Faktor unter dem Vorzeichen der Wurzel einführen: Nach Eigenschaft 4° gilt
Beispiel 5: Vereinfachen
Lösung. Aufgrund der Eigenschaft von 5° haben wir das Recht, den Exponenten der Wurzel und den Exponenten des Wurzelausdrucks in dasselbe zu dividieren natürliche Zahl. Wenn wir im betrachteten Beispiel die angegebenen Indikatoren durch 3 teilen, erhalten wir
Beispiel 6. Ausdrücke vereinfachen: a)
Lösung: a) Aufgrund der Eigenschaft 1° finden wir, dass es zum Multiplizieren von Wurzeln gleichen Grades ausreicht, die Wurzelausdrücke zu multiplizieren und aus dem erhaltenen Ergebnis die Wurzel gleichen Grades zu extrahieren. Bedeutet,
b) Zunächst müssen wir die Radikale auf einen Indikator reduzieren. Gemäß der Eigenschaft von 5° können wir den Exponenten der Wurzel und den Exponenten des Wurzelausdrucks mit derselben natürlichen Zahl multiplizieren. Deshalb haben wir als nächstes Und nun erhalten wir im resultierenden Ergebnis, indem wir die Indikatoren der Wurzel und den Grad des Wurzelausdrucks durch 3 dividieren
Die Eigenschaften der Wurzeln liegen den nächsten beiden Transformationen zugrunde, die als „Bringen“ unter das Wurzelzeichen und „Herausnehmen“ unter dem Wurzelzeichen bezeichnet werden und denen wir uns nun zuwenden.
Eingabe eines Multiplikators unter dem Vorzeichen der Wurzel
Das Einführen eines Faktors unter dem Vorzeichen impliziert das Ersetzen des Ausdrucks , wobei B und C einige Zahlen oder Ausdrücke sind und n eine natürliche Zahl größer als eins ist, identisch gleicher Ausdruck, mit der Form oder .
Nach der Einführung eines Faktors von 2 unter dem Wurzelzeichen nimmt ein irrationaler Ausdruck beispielsweise die Form an.
Theoretische Basis Diese Transformation, die Regeln für ihre Umsetzung sowie Lösungen für verschiedene typische Beispiele werden im Artikel über die Einführung eines Multiplikators unter dem Zeichen der Wurzel gegeben.
Entfernen des Multiplikators unter dem Wurzelzeichen
Eine Transformation, in gewissem Sinne das Gegenteil der Einführung eines Faktors unter dem Wurzelzeichen, besteht darin, den Faktor unter dem Wurzelzeichen zu entfernen. Es besteht darin, die Wurzel als Produkt für ungerades n oder als Produkt für gerades n darzustellen, wobei B und C einige Zahlen oder Ausdrücke sind.
Kehren wir als Beispiel zum vorherigen Absatz zurück: Der irrationale Ausdruck nimmt nach dem Entfernen des Faktors unter dem Wurzelzeichen die Form an. Ein weiteres Beispiel: Das Entfernen des Faktors unter dem Wurzelzeichen im Ausdruck ergibt das Produkt, das als umgeschrieben werden kann.
Worauf diese Transformation beruht und nach welchen Regeln sie durchgeführt wird, werden wir in einem separaten Artikel die Entfernung des Multiplikators aus dem Zeichen der Wurzel untersuchen. Dort geben wir auch Lösungen für Beispiele und listen Möglichkeiten auf, einen radikalen Ausdruck auf eine für die Multiplikation geeignete Form zu reduzieren.
Brüche mit Wurzeln umwandeln
Irrationale Ausdrücke können Brüche enthalten, deren Wurzeln im Zähler und Nenner liegen. Mit solchen Brüchen können Sie alle grundlegenden Aufgaben ausführen Identitätstransformationen von Brüchen.
Erstens hindert Sie nichts daran, mit Ausdrücken im Zähler und Nenner zu arbeiten. Betrachten Sie als Beispiel den Bruch. Der irrationale Ausdruck im Zähler ist offensichtlich identisch mit , und indem man sich den Eigenschaften von Wurzeln zuwendet, kann der Ausdruck im Nenner durch die Wurzel ersetzt werden. Dadurch wird der ursprüngliche Bruch in die Form umgewandelt.
Zweitens können Sie das Vorzeichen vor einem Bruch ändern, indem Sie das Vorzeichen des Zählers oder Nenners ändern. Beispielsweise finden folgende Transformationen eines irrationalen Ausdrucks statt:  .
.
Drittens ist es manchmal möglich und ratsam, einen Bruchteil zu kürzen. Zum Beispiel, wie man sich das Vergnügen versagt, einen Bruch zu kürzen  zum irrationalen Ausdruck, als Ergebnis erhalten wir
zum irrationalen Ausdruck, als Ergebnis erhalten wir  .
.
Es ist klar, dass in vielen Fällen vor der Reduktion eines Bruchs die Ausdrücke in Zähler und Nenner faktorisiert werden müssen, was in einfachen Fällen durch abgekürzte Multiplikationsformeln erreicht werden kann. Und manchmal hilft es, einen Bruch durch Ersetzen einer Variablen zu kürzen, wodurch Sie vom ursprünglichen Bruch mit Irrationalität zu einem rationalen Bruch übergehen können, mit dem Sie bequemer und vertrauter arbeiten können.
Nehmen wir zum Beispiel den Ausdruck . Lassen Sie uns neue Variablen einführen und in diesen Variablen hat der ursprüngliche Ausdruck die Form. Im Zähler ausgeführt
Irrationale Ausdrücke und ihre Transformationen
Beim letzten Mal haben wir uns daran erinnert (oder gelernt, je nachdem, wer es ist). , lernte, wie man solche Wurzeln extrahiert, ergründete Stück für Stück die grundlegenden Eigenschaften von Wurzeln und entschied sich dagegen komplexe Beispiele mit Wurzeln.
Diese Lektion wird eine Fortsetzung der vorherigen sein und sich den Transformationen einer Vielzahl von Ausdrücken widmen, die alle möglichen Wurzeln enthalten. Solche Ausdrücke heißen irrational. Hier werden Ausdrücke mit Buchstaben, zusätzliche Bedingungen, die Beseitigung der Irrationalität in Brüchen und einige fortgeschrittene Techniken für die Arbeit mit Wurzeln vorgestellt. Die Techniken, die in dieser Lektion besprochen werden, werden eine gute Grundlage für die Lösung von USE-Problemen (und nicht nur) nahezu jeder Komplexitätsstufe sein. Also lasst uns anfangen.
Zunächst werde ich hier die Grundformeln und Eigenschaften von Wurzeln duplizieren. Um nicht von Thema zu Thema zu springen. Hier sind sie:
![]()
![]() bei
bei
![]()
Sie müssen diese Formeln kennen und anwenden können. Und zwar in beide Richtungen – sowohl von links nach rechts als auch von rechts nach links. Auf ihnen basiert die Lösung der meisten Aufgaben mit beliebig komplexen Wurzeln. Beginnen wir zunächst mit dem Einfachsten – mit der direkten Anwendung von Formeln oder deren Kombinationen.
Einfache Anwendung von Formeln
In diesem Teil werden einfache und harmlose Beispiele betrachtet – ohne Buchstaben, Zusatzbedingungen und andere Tricks. Aber auch in ihnen gibt es in der Regel Optionen. Und je ausgefeilter das Beispiel, desto mehr solcher Möglichkeiten gibt es. Und der unerfahrene Student steht vor dem Hauptproblem: Wo soll man anfangen? Die Antwort hier ist einfach: Wenn Sie nicht wissen, was Sie brauchen, tun Sie, was Sie können. Solange Ihr Handeln im Einklang mit den Regeln der Mathematik steht und diesen nicht widerspricht.) Zum Beispiel diese Aufgabe:
Berechnung:
Selbst in einem so einfachen Beispiel gibt es mehrere mögliche Wege zur Antwort.
Die erste besteht darin, einfach die Wurzeln mit der ersten Eigenschaft zu multiplizieren und die Wurzel aus dem Ergebnis zu ziehen:
Die zweite Möglichkeit ist diese: Wir fassen es nicht an, wir arbeiten damit. Wir nehmen den Multiplikator unter dem Wurzelzeichen heraus und dann - entsprechend der ersten Eigenschaft. So:
Sie können so viel entscheiden, wie Sie möchten. Bei jeder Option lautet die Antwort eins bis acht. Beispielsweise ist es für mich einfacher, 4 und 128 zu multiplizieren und 512 zu erhalten, und die Kubikwurzel kann aus dieser Zahl leicht gezogen werden. Wenn sich jemand nicht daran erinnert, dass 512 eine Kubikzahl 8 ist, dann spielt das keine Rolle: Sie können 512 als 2 9 schreiben (die ersten 10 Zweierpotenzen, ich hoffe, Sie erinnern sich?) und die Formel für die Wurzel der Potenz verwenden :
Ein anderes Beispiel.
Berechnung: .
Wenn man nach der ersten Eigenschaft arbeitet (alles unter eine Wurzel stellen), erhält man eine stattliche Menge, aus der man dann die Wurzel extrahieren kann – ebenfalls keinen Zucker. Und es ist keine Tatsache, dass es genau extrahiert wird. Daher ist es hier sinnvoll, die Faktoren unter der Wurzel in der Zahl zu entfernen. Und machen Sie das Beste daraus:
Und jetzt ist alles gut:
Jetzt müssen nur noch die Acht und die Zwei unter eine Wurzel geschrieben werden (gemäß der ersten Eigenschaft) und schon ist die Arbeit erledigt. :) :)
Jetzt addieren wir einige Brüche.
Berechnung:
Das Beispiel ist recht primitiv, bietet aber auch Optionen. Mit dem Multiplikator können Sie den Zähler transformieren und mit dem Nenner reduzieren:

Oder Sie können sofort die Formel zum Teilen von Wurzeln verwenden:

Wie wir sehen, ist hier und da alles richtig.) Wenn man nicht auf halbem Weg stolpert und einen Fehler macht. Aber was kann ich hier falsch machen...
Schauen wir uns nun das jüngste Beispiel aus an Hausaufgaben letzte Stunde:
Vereinfachen:
![]()
Eine völlig unvorstellbare Ansammlung von Wurzeln, und sogar verschachtelte. Was soll ich machen? Die Hauptsache ist, keine Angst zu haben! Hier fallen uns zunächst unter den Wurzeln die Zahlen 2, 4 und 32 auf – Zweierpotenzen. Das erste, was man tun muss, ist, alle Zahlen auf Zweier zu reduzieren: Je mehr, desto mehr identische Zahlen(im Beispiel gilt: je weniger verschiedene, desto einfacher.) Beginnen wir separat mit dem ersten Faktor:
![]()
Die Zahl lässt sich vereinfachen, indem man die Zwei unter der Wurzel durch die Vier im Wurzelexponenten reduziert:
Nun zum Ursprung der Arbeit:
![]() .
.
In der Zahl nehmen wir die beiden als Wurzelzeichen heraus:
Und wir beschäftigen uns mit dem Ausdruck anhand der Wurzel der Wurzelformel:
Der erste Faktor wird also wie folgt geschrieben:
Die verschachtelten Wurzeln sind verschwunden, die Zahlen sind kleiner geworden, was schon jetzt erfreulich ist. Es sind nur die Wurzeln unterschiedlich, aber dabei belassen wir es vorerst. Bei Bedarf werden wir diese in die gleichen umwandeln. Nehmen wir den zweiten Faktor.)
Den zweiten Faktor transformieren wir auf ähnliche Weise, indem wir die Formel der Wurzel des Produkts und der Wurzel der Wurzel verwenden. Bei Bedarf reduzieren wir die Indikatoren nach der fünften Formel:
Wir fügen alles in das Originalbeispiel ein und erhalten:
Habe das Produkt einer ganzen Reihe von absolut verschiedene Wurzeln. Es wäre schön, sie alle auf einen Indikator zu bringen, und dann werden wir sehen. Nun, es ist durchaus möglich. Der größte der Wurzelexponenten ist 12, und alle anderen – 2, 3, 4, 6 – sind Teiler der Zahl 12. Daher reduzieren wir alle Wurzeln gemäß der fünften Eigenschaft auf einen Exponenten – 12:
![]()
Wir zählen und erhalten:
Wir haben keine schöne Nummer bekommen, aber das ist okay. Wir wurden gefragt vereinfachen Ausdruck, nicht zählen. Vereinfacht? Sicherlich! Und die Art der Antwort (ganzzahlig oder nicht) spielt hier keine Rolle mehr.
Einige Additions-/Subtraktionsformeln und abgekürzte Multiplikationsformeln
Leider, allgemeine Formeln Für Addieren und Subtrahieren von Wurzeln nein in Mathematik. In Aufgaben sind diese Aktionen jedoch häufig anzutreffen. Hier ist es notwendig zu verstehen, dass alle Wurzeln genau die gleichen mathematischen Symbole wie Buchstaben in der Algebra sind.) Und für Wurzeln gelten die gleichen Techniken und Regeln wie für Buchstaben – Klammern öffnen, ähnliche Klammern einfügen, abgekürzte Multiplikationsformeln usw. P.
Das ist zum Beispiel jedem klar. Genau so das gleiche Die Wurzeln können ganz einfach addiert/subtrahiert werden:
![]()
![]()
Wenn die Wurzeln unterschiedlich sind, suchen wir nach einer Möglichkeit, sie gleich zu machen – indem wir einen Multiplikator addieren/subtrahieren oder die fünfte Eigenschaft verwenden. Wenn es in keiner Weise vereinfacht wird, sind die Transformationen vielleicht raffinierter.
Schauen wir uns das erste Beispiel an.
Finden Sie die Bedeutung des Ausdrucks: .
Alle drei Wurzeln, obwohl kubisch, stammen aus anders Zahlen. Sie werden nicht rein extrahiert und voneinander addiert/subtrahiert. Daher funktioniert die Verwendung allgemeiner Formeln hier nicht. Was soll ich machen? Lassen Sie uns die Faktoren in jeder Wurzel herausnehmen. Auf jeden Fall wird es nicht schlimmer.) Darüber hinaus gibt es tatsächlich keine anderen Möglichkeiten:
Das ist, .
Das ist die Lösung. Hier sind wir mit Hilfe von verschiedenen Wurzeln zu denselben übergegangen Entfernen des Multiplikators unter der Wurzel. Und dann haben sie einfach ähnliche mitgebracht.) Wir entscheiden weiter.
Finden Sie den Wert eines Ausdrucks:
An der Wurzel aus siebzehn kann man definitiv nichts ändern. Wir arbeiten nach der ersten Eigenschaft – wir bilden eine Wurzel aus dem Produkt zweier Wurzeln:
Schauen wir uns das nun genauer an. Was haben wir unter dem Großen Kubikwurzel? Der Unterschied ist qua... Na klar! Differenz der Quadrate:
Jetzt müssen Sie nur noch die Wurzel extrahieren: .
Berechnung:
Hier müssen Sie mathematischen Einfallsreichtum beweisen.) Wir denken ungefähr auf die folgende Weise: „Im Beispiel also das Produkt aus Wurzeln. Unter einer Wurzel befindet sich die Differenz und unter der anderen die Summe. Sehr ähnlich der Quadratdifferenzformel. Aber... Die Wurzeln sind anders! Der erste ist quadratisch und der zweite vom vierten Grad... Es wäre schön, sie gleich zu machen. Gemäß der fünften Eigenschaft können Sie aus einer Quadratwurzel leicht eine vierte Wurzel bilden. Dazu genügt es, den radikalen Ausdruck zu quadrieren.“
Wenn Sie darüber nachgedacht haben, sind Sie auf halbem Weg zum Erfolg. Absolut richtig! Lassen Sie uns den ersten Faktor in eine vierte Wurzel umwandeln. So:
![]()
Jetzt müssen Sie nichts mehr tun, aber Sie müssen sich die Formel für das Quadrat der Differenz merken. Nur bei Anwendung auf den Wurzeln. Na und? Warum sind Wurzeln schlechter als andere Zahlen oder Ausdrücke?! Wir bauen:
„Hmm, nun ja, sie haben es errichtet, na und? Meerrettich ist nicht süßer als Rettich. Stoppen! Und wenn Sie die vier unter der Wurzel herausnehmen? Dann entsteht derselbe Ausdruck wie unter der zweiten Wurzel, nur mit einem Minus, und genau das wollen wir erreichen!“
Rechts! Nehmen wir vier:
![]() .
.
Und nun – eine Frage der Technik:
So werden komplexe Beispiele entwirrt. Jetzt ist es an der Zeit, mit Brüchen zu üben.
Berechnung:
Es ist klar, dass der Zähler umgerechnet werden muss. Wie? Natürlich mit der Formel des Quadrats der Summe. Haben wir noch andere Möglichkeiten? :) Wir quadrieren es, entfernen die Faktoren, reduzieren die Indikatoren (wo nötig):
Wow! Wir haben genau den Nenner unseres Bruchs erhalten.) Das bedeutet, dass der ganze Bruch offensichtlich gleich eins ist:

Ein anderes Beispiel. Erst jetzt zu einer anderen Formel für die abgekürzte Multiplikation.)
Berechnung:
Es ist klar, dass in der Praxis das Quadrat der Differenz verwendet werden muss. Wir schreiben den Nenner separat aus und – los geht’s!
Wir holen die Faktoren unter den Wurzeln hervor:
![]()
Somit,
Jetzt wird alles Schlechte hervorragend reduziert und es stellt sich heraus:

Nun, lasst es uns auf die nächste Ebene bringen. :) :)
Briefe und zusätzliche Bedingungen
Wörtliche Ausdrücke mit Wurzeln sind eine schwierigere Sache als numerische Ausdrücke und eine unerschöpfliche Quelle ärgerlicher und sehr schwerwiegender Fehler. Schließen wir diese Quelle.) Fehler entstehen dadurch, dass es bei solchen Aufgaben oft um negative Zahlen und Ausdrücke geht. Sie werden uns entweder direkt in der Aufgabe übergeben oder darin versteckt Briefe und zusätzliche Bedingungen. Und während wir mit den Wurzeln arbeiten, müssen wir uns ständig daran erinnern, dass in den Wurzeln steckt sogar Grad Sowohl unter der Wurzel selbst als auch als Ergebnis der Wurzelextraktion sollte es vorhanden sein nicht negativer Ausdruck. Die Schlüsselformel in den Aufgaben dieses Absatzes wird die vierte Formel sein:
Es gibt keine Fragen mit Wurzeln ungeraden Grades – es wird immer alles extrahiert, sowohl positiv als auch negativ. Und das Minus wird, wenn überhaupt, vorgezogen. Kommen wir gleich zu den Wurzeln sogar Grad.) Zum Beispiel eine so kurze Aufgabe.
Vereinfachen: , Wenn .
Es scheint, dass alles einfach ist. Es wird einfach ein X sein.) Aber warum dann? Zusätzlicher Zustand ? In solchen Fällen ist es sinnvoll, mit Zahlen zu schätzen. Rein für mich.) Wenn, dann ist x offensichtlich eine negative Zahl. Minus drei zum Beispiel. Oder minus vierzig. Lassen . Können Sie minus drei auf die vierte Potenz erhöhen? Sicherlich! Das Ergebnis ist 81. Ist es möglich, die vierte Wurzel aus 81 zu ziehen? Warum nicht? Dürfen! Du bekommst drei. Lassen Sie uns nun unsere gesamte Kette analysieren:
Was sehen wir? Die Eingabe war eine negative Zahl und die Ausgabe war bereits positiv. Es war minus drei, jetzt ist es plus drei.) Kehren wir zu den Buchstaben zurück. Modulo wird es ohne Zweifel genau X sein, aber nur X selbst ist minus (bedingt!), und das Ergebnis der Extraktion (wegen der arithmetischen Wurzel!) muss plus sein. Wie bekomme ich ein Plus? Sehr einfach! Dazu genügt es, einer offensichtlich negativen Zahl ein Minus voranzustellen.) Und richtige Lösung sieht so aus:
Übrigens, wenn wir die Formel verwenden würden, würden wir, wenn wir uns an die Definition eines Moduls erinnern, sofort die richtige Antwort erhalten. Weil das
|x| = -x bei x<0.
Nehmen Sie den Faktor aus dem Wurzelzeichen: , Wo .
Der erste Blick fällt auf den radikalen Ausdruck. Hier ist alles in Ordnung. In jedem Fall wird es nicht negativ sein. Beginnen wir mit dem Extrahieren. Mithilfe der Formel für die Wurzel eines Produkts extrahieren wir die Wurzel jedes Faktors:
Ich glaube nicht, dass es nötig ist zu erklären, woher die Module stammen.) Lassen Sie uns nun jedes einzelne Modul analysieren.
Multiplikator | A | Wir lassen es unverändert: Wir haben keine Bedingung für den BriefA. Wir wissen nicht, ob es positiv oder negativ ist. Nächstes Modul |b 2 | kann getrost weggelassen werden: auf jeden Fall der Ausdruckb 2 nicht negativ. Aber ungefähr |c 3 | - Hier liegt bereits ein Problem vor.) Wenn, Dann c 3 <0. Стало быть, модуль надо раскрыть mit einem Minus: | c 3 | = - c 3 . Insgesamt wäre die richtige Lösung:
Und jetzt - das umgekehrte Problem. Nicht ganz einfach, ich warne Sie gleich!
Geben Sie einen Multiplikator unter dem Vorzeichen der Wurzel ein: .
Wenn Sie die Lösung sofort so aufschreiben
dann Sie ist in eine Falle getappt. Das Fehlentscheidung! Was ist los?
Schauen wir uns den Ausdruck unter der Wurzel genauer an. Unter der Wurzel des vierten Grades sollte es, wie wir wissen, sein nicht negativ Ausdruck. Ansonsten hat die Wurzel keine Bedeutung.) Daher Und dies wiederum bedeutet das und ist daher selbst auch nichtpositiv: .
Und der Fehler besteht darin, dass wir an der Wurzel einführen nicht positiv Nummer: der vierte Grad macht daraus nicht negativ und man erhält das falsche Ergebnis – links steht bewusst ein Minus, rechts schon ein Plus. Und an der Wurzel anwenden sogar Grad haben wir nur das Recht nicht negativ Zahlen oder Ausdrücke. Und lassen Sie das Minus, falls vorhanden, vor der Wurzel.) Wie können wir einen nicht negativen Faktor in der Zahl identifizieren?, wissend, dass es selbst völlig negativ ist? Ja, genau das Gleiche! Setzen Sie ein Minus.) Und damit sich nichts ändert, kompensieren Sie es mit einem weiteren Minus. So:
![]()
Und jetzt schon nicht negativ Wir tragen in aller Ruhe die Zahl (-b) unter der Wurzel nach allen Regeln ein:
Dieses Beispiel zeigt deutlich, dass sich im Gegensatz zu anderen Zweigen der Mathematik in den Wurzeln nicht immer automatisch die richtige Antwort aus den Formeln ergibt. Man muss nachdenken und persönlich die richtige Entscheidung treffen.) Vor allem bei den Anmeldungen sollte man vorsichtiger sein Irrationale Gleichungen und Ungleichungen.
Schauen wir uns die nächste wichtige Technik bei der Arbeit mit Wurzeln an – Irrationalität loswerden.
Beseitigung der Irrationalität in Brüchen
Wenn der Ausdruck Wurzeln enthält, dann möchte ich Sie daran erinnern, dass ein solcher Ausdruck aufgerufen wird Ausdruck mit Irrationalität. In manchen Fällen kann es sinnvoll sein, genau diese Irrationalität (d. h. Wurzeln) zu beseitigen. Wie kann man die Wurzel beseitigen? Unsere Wurzel verschwindet, wenn... sie zur Macht erhoben wird. Mit einem Indikator, der entweder dem Wurzelindikator oder einem Vielfachen davon entspricht. Aber wenn wir die Wurzel potenzieren (d. h. die Wurzel so oft mit sich selbst multiplizieren), dann ändert sich der Ausdruck. Nicht gut.) Allerdings gibt es in der Mathematik Themen, bei denen die Multiplikation recht schmerzlos ist. Zum Beispiel in Brüchen. Gemäß der Grundeigenschaft eines Bruchs ändert sich der Wert des Bruchs nicht, wenn Zähler und Nenner mit derselben Zahl multipliziert (dividiert) werden.
Nehmen wir an, wir erhalten diesen Bruch:
Ist es möglich, die Wurzel im Nenner loszuwerden? Dürfen! Dazu muss die Wurzel gewürfelt werden. Was fehlt uns im Nenner eines vollen Würfels? Uns fehlt ein Multiplikator, d.h.. Also multiplizieren wir Zähler und Nenner des Bruchs mit

Die Wurzel im Nenner ist verschwunden. Aber... er erschien im Zähler. Nichts kann getan werden, das ist Schicksal.) Das ist uns nicht mehr wichtig: Wir wurden gebeten, den Nenner von den Wurzeln zu befreien. Freigegeben? Zweifellos.)
Wer sich bereits mit Trigonometrie auskennt, dürfte übrigens darauf geachtet haben, dass beispielsweise in manchen Lehrbüchern und Tabellen unterschiedliche Bezeichnungen verwendet werden: irgendwo und irgendwo. Die Frage ist: Was ist richtig? Antwort: Alles ist richtig!) Wenn Sie das erraten– Dies ist einfach das Ergebnis der Befreiung von der Irrationalität im Nenner des Bruchs. :)
Warum sollten wir uns in Brüchen von der Irrationalität befreien? Welchen Unterschied macht es – liegt die Wurzel im Zähler oder im Nenner? Der Taschenrechner wird sowieso alles berechnen.) Nun, für diejenigen, die sich nicht von einem Taschenrechner trennen, gibt es eigentlich praktisch keinen Unterschied... Aber selbst wenn man auf einen Taschenrechner setzt, kann man darauf achten teilen An ganz Nummer ist immer bequemer und schneller als auf irrational. Und über die Aufteilung in eine Kolumne schweige ich.)
Das folgende Beispiel wird meine Worte nur bestätigen.
Wie können wir hier die Quadratwurzel des Nenners eliminieren? Wenn Zähler und Nenner mit dem Ausdruck multipliziert werden, ist der Nenner das Quadrat der Summe. Die Summe der Quadrate der ersten und zweiten Zahl ergibt nur Zahlen ohne Wurzeln, was sehr erfreulich ist. Allerdings... es wird auftauchen Doppelprodukt die erste Zahl bis zur zweiten, wobei die Wurzel aus drei noch übrig bleibt. Es kanalisiert nicht. Was soll ich machen? Erinnern Sie sich an eine weitere wunderbare Formel für die abgekürzte Multiplikation! Wo es keine Doppelprodukte, sondern nur Quadrate gibt:
Ein Ausdruck, der, wenn er mit einer bestimmten Summe (oder Differenz) multipliziert wird, Folgendes ergibt: Differenz der Quadrate, auch genannt konjugierter Ausdruck. In unserem Beispiel wird der konjugierte Ausdruck den Unterschied ausmachen. Also multiplizieren wir Zähler und Nenner mit dieser Differenz:
Was kann ich sagen? Als Ergebnis unserer Manipulationen verschwand nicht nur die Wurzel des Nenners, sondern auch der Bruch ganz! :) Selbst mit einem Taschenrechner ist es einfacher, die Wurzel aus drei von einer Drei zu subtrahieren, als einen Bruch mit der Wurzel im Nenner zu berechnen. Ein anderes Beispiel.
Befreien Sie sich von der Irrationalität im Nenner eines Bruchs:
Wie komme ich da raus? Formeln für die abgekürzte Multiplikation mit Quadraten funktionieren nicht auf Anhieb – es wird nicht möglich sein, die Wurzeln vollständig zu eliminieren, da unsere Wurzel diesmal nicht quadratisch ist, sondern kubisch. Es ist notwendig, dass die Wurzel irgendwie zu einem Würfel geformt wird. Daher muss eine der Formeln mit Würfeln verwendet werden. Welcher? Lass uns darüber nachdenken. Der Nenner ist die Summe. Wie können wir den Würfel der Wurzel erreichen? Mal partielle quadrierte Differenz! Also wenden wir die Formel an Summe der Würfel. Dieses hier:
Als A Wir haben drei und als Qualität B– Kubikwurzel aus fünf:
Und wieder verschwand der Bruch.) Solche Situationen, in denen nach der Befreiung von der Irrationalität im Nenner eines Bruchs der Bruch selbst zusammen mit den Wurzeln vollständig verschwindet, kommen sehr häufig vor. Wie gefällt Ihnen dieses Beispiel!
Berechnung:
![]()
Versuchen Sie einfach, diese drei Brüche zu addieren! Keine Fehler! :) Ein gemeinsamer Nenner lohnt sich. Was wäre, wenn wir versuchen würden, uns von der Irrationalität im Nenner jedes Bruchs zu befreien? Nun, versuchen wir es:
Wow, wie interessant! Alle Brüche sind weg! Vollständig. Und nun kann das Beispiel auf zwei Arten gelöst werden:
Schlicht und elegant. Und ohne lange und langwierige Berechnungen. :) :)
Deshalb muss man in der Lage sein, die Operation der Befreiung von der Irrationalität in Bruchteilen durchzuführen. Bei solch anspruchsvollen Beispielen ist es das Einzige, was spart, ja.) Natürlich hat niemand die Aufmerksamkeit aufgehoben. Es gibt Aufgaben, bei denen Sie aufgefordert werden, Irrationalität loszuwerden Zähler. Diese Aufgaben unterscheiden sich nicht von den betrachteten, lediglich der Zähler wird von den Wurzeln gelöscht.)
Komplexere Beispiele
Es bleiben noch einige spezielle Techniken für die Arbeit mit Wurzeln zu berücksichtigen und das Entwirren nicht der einfachsten Beispiele zu üben. Und dann reichen die erhaltenen Informationen aus, um Aufgaben mit Wurzeln beliebiger Komplexität zu lösen. Also - machen Sie weiter.) Lassen Sie uns zunächst herausfinden, was mit verschachtelten Wurzeln zu tun ist, wenn die Wurzel-aus-Wurzel-Formel nicht funktioniert. Hier ist zum Beispiel ein Beispiel.
Berechnung:
Die Wurzel liegt unter der Wurzel... Außerdem liegt unter den Wurzeln die Summe oder Differenz. Daher ist hier die Formel für die Wurzel der Wurzel (mit Multiplikation der Exponenten). Es funktioniert nicht. Es muss also etwas dagegen getan werden radikale Ausdrücke: Wir haben einfach keine anderen Möglichkeiten. In solchen Beispielen wird meistens der große Stamm verschlüsselt Perfektes Viereck eine gewisse Menge. Oder Unterschiede. Und die Wurzel des Quadrats ist bereits perfekt gezogen! Und jetzt besteht unsere Aufgabe darin, es zu entschlüsseln.) Eine solche Entschlüsselung gelingt wunderbar Gleichungssystem. Jetzt werden Sie alles selbst sehen.)
Unter der ersten Wurzel haben wir also diesen Ausdruck:
Was wäre, wenn Sie nicht richtig geraten hätten? Lass uns das Prüfen! Wir quadrieren es mit der Formel für das Quadrat der Summe:
Das stimmt.) Aber... Woher habe ich diesen Ausdruck? Aus dem Himmel?
Nein.) Wir werden es ehrlich gesagt etwas niedriger ansetzen. Indem ich einfach diesen Ausdruck verwende, zeige ich genau, wie Aufgabenschreiber solche Quadrate verschlüsseln. :) Was ist 54? Das Summe der Quadrate der ersten und zweiten Zahl. Und aufgepasst, schon ohne Wurzeln! Und die Wurzel bleibt drin Doppelprodukt, was in unserem Fall gleich ist. Daher beginnt die Entschlüsselung solcher Beispiele mit der Suche nach dem Doppelprodukt. Wenn Sie sich mit der üblichen Auswahl entwirren. Und übrigens über Zeichen. Hier ist alles einfach. Wenn vor dem Doppelten ein Plus steht, dann das Quadrat der Summe. Wenn es ein Minus ist, dann die Unterschiede.) Wir haben ein Plus – das heißt das Quadrat der Summe.) Und jetzt – die versprochene analytische Methode der Dekodierung. Durch das System.)
Unter unserer Wurzel hängt also deutlich der Ausdruck (a+b) 2, und unsere Aufgabe ist es zu finden A Und B. In unserem Fall ergibt die Summe der Quadrate 54. Also schreiben wir:
![]()
Verdoppeln Sie nun das Produkt. Wir haben es. Also schreiben wir es auf:
Wir haben dieses System:
![]()
Wir lösen mit der üblichen Substitutionsmethode. Wir drücken zum Beispiel aus der zweiten Gleichung aus und setzen sie in die erste ein:

Lösen wir die erste Gleichung:
Bekommen biquadratisch Gleichung relativA . Wir berechnen die Diskriminante:
Bedeutet,
Wir haben bis zu vier mögliche Werte erhaltenA. Wir fürchten uns nicht. Jetzt werden wir alle unnötigen Dinge aussortieren.) Wenn wir nun für jeden der vier gefundenen Werte die entsprechenden Werte berechnen, erhalten wir vier Lösungen für unser System. Hier sind sie:
Und hier stellt sich die Frage: Welche Lösung ist für uns die richtige? Lass uns darüber nachdenken. Negative Lösungen können sofort verworfen werden: Beim Quadrieren werden die Minuspunkte „ausgebrannt“ und der gesamte radikale Ausdruck als Ganzes ändert sich nicht.) Die ersten beiden Optionen bleiben bestehen. Sie können sie völlig willkürlich wählen: Eine Neuanordnung der Terme ändert immer noch nichts an der Summe.) Sei beispielsweise , a .
Insgesamt haben wir das Quadrat der folgenden Summe unter der Wurzel erhalten:
Alles ist klar.)
Nicht umsonst beschreibe ich den Entscheidungsprozess so ausführlich. Um deutlich zu machen, wie die Entschlüsselung erfolgt.) Es gibt jedoch ein Problem. Die analytische Methode der Dekodierung ist zwar zuverlässig, aber sehr langwierig und umständlich: Sie müssen eine biquadratische Gleichung lösen, vier Lösungen für das System finden und dann noch darüber nachdenken, welche Sie wählen sollen ... Beunruhigend? Ich stimme zu, es ist mühsam. Diese Methode funktioniert in den meisten dieser Beispiele einwandfrei. Allerdings kann man sich sehr oft viel Arbeit ersparen und beide Zahlen kreativ finden. Durch Auswahl.) Ja, ja! Am Beispiel des zweiten Termes (zweite Wurzel) zeige ich nun eine einfachere und schnellere Möglichkeit, das vollständige Quadrat unter der Wurzel zu isolieren.
Jetzt haben wir also diese Wurzel: ![]() .
.
Denken wir mal so: „Unter der Wurzel befindet sich höchstwahrscheinlich ein verschlüsseltes vollständiges Quadrat. Sobald vor dem Doppelten ein Minus steht, bedeutet dies das Quadrat der Differenz. Die Summe der Quadrate der ersten und zweiten Zahl ergibt die Zahl 54. Aber was sind das für Quadrate? 1 und 53? 49 und 5 ? Es gibt zu viele Möglichkeiten ... Nein, es ist besser, mit der doppelten Menge an Produkt zu beginnen, um das Haar zu entwirren. Unserkann geschrieben werden als . Sobald das Produkt verdoppelt, dann verwerfen wir die beiden sofort. Dann Kandidaten für die Rolle a und b bleiben 7 und . Was ist, wenn es 14 ist und/2 ? Nicht ausgeschlossen. Aber wir beginnen immer mit etwas Einfachem!“ Also sei ein . Überprüfen wir sie auf die Summe der Quadrate:
Passiert! Das bedeutet, dass unser radikaler Ausdruck tatsächlich das Quadrat der Differenz ist:
Hier finden Sie eine einfache Möglichkeit, Fehler im System zu vermeiden. Es funktioniert nicht immer, aber in vielen dieser Beispiele reicht es völlig aus. Unter den Wurzeln befinden sich also vollständige Quadrate. Jetzt müssen nur noch die Wurzeln richtig gezogen und das Beispiel berechnet werden:
Schauen wir uns nun eine noch ungewöhnlichere Aufgabe zu Wurzeln an.)
Beweisen Sie, dass die Zahl A– ganze Zahl, wenn .
Nichts wird direkt extrahiert, die Wurzeln sind eingebettet, und das sogar in unterschiedlichem Ausmaß... Ein Albtraum! Die Aufgabe macht jedoch Sinn.) Daher gibt es einen Schlüssel zur Lösung.) Und der Schlüssel hier ist dieser. Bedenken Sie unsere Gleichberechtigung
Wie Gleichung relativ A. Ja Ja! Es wäre schön, die Wurzeln loszuwerden. Unsere Wurzeln sind kubisch, also lasst uns beide Seiten der Gleichung quadrieren. Nach der Formel Würfel der Summe:

Würfel und Kubikwurzeln heben sich gegenseitig auf, und unter jeder großen Wurzel nehmen wir eine Klammer vom Quadrat und fassen das Produkt aus der Differenz und der Summe in eine Quadratdifferenz zusammen:
Separat berechnen wir die Differenz der Quadrate unter den Wurzeln:
Identische Transformationen von Ausdrücken sind eine der Inhaltslinien des Schulmathematikkurses. Identische Transformationen werden häufig zur Lösung von Gleichungen, Ungleichungen, Gleichungssystemen und Ungleichungen verwendet. Darüber hinaus tragen identische Ausdrucksumwandlungen zur Entwicklung von Intelligenz, Flexibilität und Rationalität des Denkens bei.
Die vorgeschlagenen Materialien richten sich an Schüler der 8. Klasse und beinhalten die theoretischen Grundlagen identischer Transformationen von Rational und irrationale Ausdrücke, Arten von Aufgaben zur Transformation solcher Ausdrücke und des Testtextes.
1. Theoretische Grundlagen von Identitätstransformationen
Ausdrücke in der Algebra sind Datensätze, die aus Zahlen und Buchstaben bestehen, die durch Aktionszeichen verbunden sind.
https://pandia.ru/text/80/197/images/image002_92.gif" width="77" height="21 src=">.gif" width="20" height="21 src="> – algebraische Ausdrücke.
Abhängig von den Operationen werden rationale und irrationale Ausdrücke unterschieden.
Algebraische Ausdrücke werden als rational bezeichnet, wenn sie sich auf die darin enthaltenen Buchstaben beziehen A, B, Mit, ... außer Addition, Multiplikation, Subtraktion, Division und Potenzierung werden keine weiteren Operationen durchgeführt.
Algebraische Ausdrücke, die Operationen zum Ziehen der Wurzel einer Variablen oder zum Erhöhen einer rationalen Potenz einer Variablen enthalten, die keine ganze Zahl ist, werden in Bezug auf diese Variable als irrational bezeichnet.
Eine Identitätstransformation eines gegebenen Ausdrucks ist das Ersetzen eines Ausdrucks durch einen anderen, der ihm in einer bestimmten Menge identisch ist.
Die folgenden theoretischen Fakten liegen identischen Transformationen rationaler und irrationaler Ausdrücke zugrunde.
1. Eigenschaften von Graden mit ganzzahligem Exponenten:
![]() , N AN; A 1=A;
, N AN; A 1=A;
, N AN, A¹0; A 0=1, A¹0;
![]() , A¹0;
, A¹0;
, A¹0;
, A¹0;
, A¹0, B¹0;
![]() , A¹0, B¹0.
, A¹0, B¹0.
2. Abgekürzte Multiplikationsformeln:
Wo A, B, Mit– beliebige reelle Zahlen;
Wo A¹0, X 1 und X 2 – Wurzeln der Gleichung ![]() .
.
3. Die Haupteigenschaft von Brüchen und Aktionen auf Brüche:
![]() , Wo B¹0, Mit¹0;
, Wo B¹0, Mit¹0;
; ![]() ;
;
4. Definition einer arithmetischen Wurzel und ihrer Eigenschaften:
![]() ; , B#0; https://pandia.ru/text/80/197/images/image026_24.gif" width="84" height="32">; ;
; , B#0; https://pandia.ru/text/80/197/images/image026_24.gif" width="84" height="32">; ; ![]() ,
,
Wo A, B– nicht negative Zahlen, N AN, N³2, M AN, M³2.
1. Arten von Ausdruckskonvertierungsübungen
Existieren Verschiedene ArtenÜbungen zu identischen Transformationen von Ausdrücken. Erster Typ: Die durchzuführende Konvertierung wird explizit angegeben.
Zum Beispiel.
1. Stellen Sie es als Polynom dar.
Bei der Durchführung dieser Transformation haben wir die Regeln der Multiplikation und Subtraktion von Polynomen, die Formel für die abgekürzte Multiplikation und die Reduktion ähnlicher Terme verwendet.
2. Berücksichtigen Sie Folgendes: ![]() .
.
Bei der Durchführung der Transformation haben wir die Regel verwendet, den gemeinsamen Faktor aus Klammern zu setzen, und zwei abgekürzte Multiplikationsformeln.
3. Reduziere den Bruch:
![]() .
.

Bei der Durchführung der Transformation haben wir die Entfernung des gemeinsamen Faktors aus Klammern, kommutative und kontraktile Gesetze, 2 abgekürzte Multiplikationsformeln und Operationen mit Potenzen verwendet.
4. Entfernen Sie den Faktor unter dem Wurzelzeichen if A³0, B³0, Mit³0: https://pandia.ru/text/80/197/images/image036_17.gif" width="432" height="27">
Wir haben die Regeln für Aktionen auf Wurzeln und die Definition des Moduls einer Zahl verwendet.
5. Eliminieren Sie die Irrationalität im Nenner eines Bruchs. ![]() .
.
Zweiter TypÜbungen sind Übungen, bei denen die Haupttransformation, die durchgeführt werden muss, klar angegeben ist. In solchen Übungen wird die Anforderung meist in einer der folgenden Formen formuliert: Ausdruck vereinfachen, rechnen. Bei der Durchführung solcher Übungen muss zunächst ermittelt werden, welche Transformationen und in welcher Reihenfolge durchgeführt werden müssen, damit der Ausdruck eine kompaktere Form als die gegebene annimmt oder ein numerisches Ergebnis erhalten wird.
Zum Beispiel
6. Vereinfachen Sie den Ausdruck:
Lösung:
![]() .
.
Verwendete Aktionsregeln algebraische Brüche und abgekürzte Multiplikationsformeln.
7. Vereinfachen Sie den Ausdruck:
 .
.
Wenn A³0, B³0, A¹ B.
Wir verwendeten abgekürzte Multiplikationsformeln, Regeln zum Addieren von Brüchen und Multiplizieren irrationaler Ausdrücke, die Identität https://pandia.ru/text/80/197/images/image049_15.gif" width="203" height="29">.
Wir haben die Operation der Auswahl eines vollständigen Quadrats verwendet, die Identität https://pandia.ru/text/80/197/images/image053_11.gif" width="132 height=21" height="21">, if .
Nachweisen:
Da , dann und oder oder oder , d.h. .
Wir haben die Bedingung und Formel für die Würfelsumme verwendet.
Es ist zu beachten, dass in Aufgaben der ersten beiden Arten auch Variablenverknüpfungsbedingungen angegeben werden können.
Zum Beispiel.
10. Finden Sie heraus, ob .
Trainer Nr. 1
Thema: Macht und irrationale Ausdrücke umwandeln
Wahlpflichtprogramm Mathematik für Schüler der 10. Klasse
ProgrammAnwendung. Anwendung grundlegender trigonometrischer Formeln auf Transformation Ausdrücke. Thema 4. Trigonometrische Funktionen und ihre Zeitpläne. Zusammenfassen... . 16.01-20.01 18 Konvertierung sedieren Und irrational Ausdrücke. 23.01-27.01 19 ...
Kalender und thematische Planung des Lehrmaterials Algebra und Beginn der Analysis, 11. Klasse
Kalender und thematische PlanungUnd ein rationaler Indikator. Konvertierung sedieren Und irrational Ausdrücke. 2 2 2 September Eigenschaften von Logarithmen. Konvertierung logarithmisch Ausdrücke. 1 1 1 ... gelten vollumfänglich ab diese Studierende, die hohe Ziele anstreben...
Unterrichtsthema Unterrichtsart (4)
Lektion... Transformation numerisch und alphabetisch Ausdrücke, enthaltend Grad ... Grad Wissen: Konzept Grad mit einem irrationalen Indikator; Grundeigenschaften Grad. In der Lage sein: Sinn finden Grad Mit irrational... 3 bis Thema « Grad positive Zahl...
Thema: Kulturelle und historische Grundlagen für die Entwicklung psychologischen Wissens in der Arbeit Thema: Arbeit als sozialpsychologische Realität
DokumentierenUsw.) Thema Arbeit ist eng mit sozioökonomischen Aspekten verbunden Transformationen. Zum Beispiel ... Umstrukturierung des Bewusstseins, der Instinkte, irrational Trends, d.h. interne Konflikte... Verfügbarkeit prüfen und Grad Schwere eine Person hat bestimmte...
Konvertieren von Ausdrücken mit Quadratwurzeln (1)
LektionHerausgegeben von S.A. Teljakowsky. Thema Lektion: Konvertierung Ausdrücke, enthaltend Quadrat...) Transformation Wurzeln eines Produkts, einer Fraktion und Grad, Multiplikation... (Bildung der Fähigkeit des Identischen Transformationen irrational Ausdrücke). Nr. 421. (an der Tafel...