Protokollieren Sie nach Basis. Der Logarithmus von b zur Basis a wird als Exponent in bezeichnet
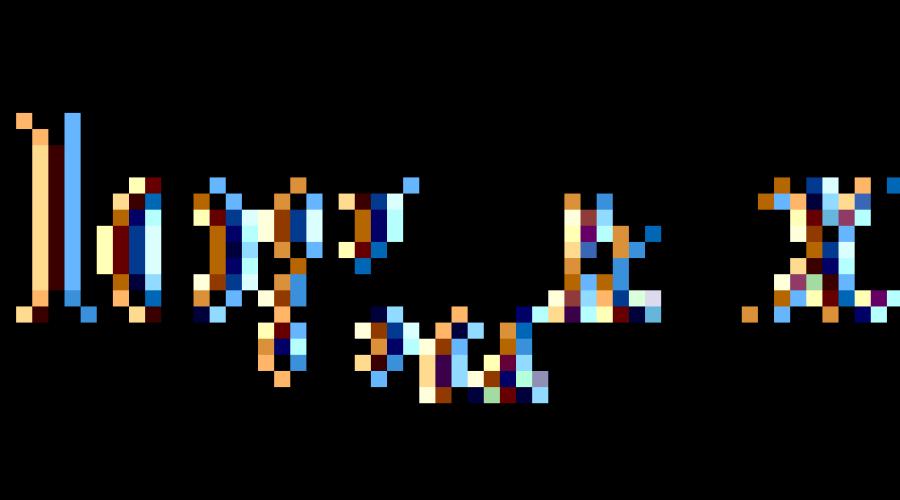
Lesen Sie auch
(aus dem Griechischen λόγος – „Wort“, „Beziehung“ und ἀριθμός – „Zahl“) Zahlen B bezogen auf A(log α B) heißt eine solche Zahl C, Und B= ein c, das heißt, zeichnet log α auf B=C Und b=aC sind gleichwertig. Der Logarithmus macht Sinn, wenn a > 0, a ≠ 1, b > 0.
Mit anderen Worten Logarithmus Zahlen B bezogen auf A als Exponent formuliert, auf den eine Zahl erhöht werden muss A um die Nummer zu bekommen B(Logarithmus existiert nur für positive Zahlen).
Aus dieser Formulierung folgt, dass die Berechnung x= log α B, entspricht der Lösung der Gleichung a x =b.
Zum Beispiel:
log 2 8 = 3, weil 8 = 2 3 .
Wir betonen, dass die angegebene Formulierung des Logarithmus eine sofortige Bestimmung ermöglicht Logarithmuswert, wenn die Zahl unter dem Logarithmuszeichen als bestimmte Potenz der Basis fungiert. Tatsächlich ermöglicht die Formulierung des Logarithmus, das Wenn zu rechtfertigen b=a c, dann der Logarithmus der Zahl B bezogen auf A gleicht Mit. Es ist auch klar, dass das Thema Logarithmen eng mit dem Thema zusammenhängt Potenzen einer Zahl.
Die Berechnung des Logarithmus heißt Logarithmus. Logarithmus ist die mathematische Operation zur Logarithmusbildung. Bei der Logarithmierung werden Produkte von Faktoren in Summen von Termen umgewandelt.
Potenzierung ist die umgekehrte mathematische Operation des Logarithmus. Bei der Potenzierung wird eine bestimmte Base auf den Grad der Expression angehoben, über den die Potenzierung durchgeführt wird. In diesem Fall werden die Summen der Terme in ein Produkt von Faktoren umgewandelt.
Sehr oft werden reelle Logarithmen mit den Basen 2 (binär), Eulerzahl e ≈ 2,718 (natürlicher Logarithmus) und 10 (dezimal) verwendet.
In dieser Phase ist es ratsam, darüber nachzudenken Logarithmusproben Protokoll 7 2 , ln √ 5, lg0.0001.
Und die Einträge lg(-3), log -3 3.2, log -1 -4.3 machen keinen Sinn, da im ersten von ihnen eine negative Zahl unter dem Vorzeichen des Logarithmus steht, im zweiten eine negative Zahl in der Basis, und in der dritten steht eine negative Zahl unter dem Logarithmuszeichen und der Einheit an der Basis.
Bedingungen zur Bestimmung des Logarithmus.
Es lohnt sich, die Bedingungen a > 0, a ≠ 1, b > 0, unter denen wir erhalten, gesondert zu betrachten Definition von Logarithmus. Schauen wir uns an, warum diese Einschränkungen vorgenommen wurden. Dabei hilft uns eine Gleichheit der Form x = log α B, die grundlegende logarithmische Identität genannt, die sich direkt aus der oben angegebenen Definition des Logarithmus ergibt.
Nehmen wir die Bedingung a≠1. Da eins hoch zu jeder Potenz gleich eins ist, gilt die Gleichheit x=log α B kann nur existieren, wenn b=1, aber log 1 1 ist eine beliebige reelle Zahl. Um diese Mehrdeutigkeit zu beseitigen, nehmen wir a≠1.
Beweisen wir die Notwendigkeit der Bedingung a>0. Bei a=0 Nach der Formulierung kann der Logarithmus nur dann existieren, wenn b=0. Und dementsprechend dann log 0 0 kann jede reelle Zahl ungleich Null sein, da Null zu jeder Potenz ungleich Null Null ist. Diese Mehrdeutigkeit kann durch die Bedingung beseitigt werden a≠0. Und wann A<0 wir müssten die Analyse rationaler und irrationaler Werte des Logarithmus ablehnen, da ein Grad mit rationalem und irrationalem Exponenten nur für nichtnegative Basen definiert ist. Aus diesem Grund wird die Bedingung festgelegt a>0.
Und die letzte Bedingung b>0 folgt aus Ungleichheit a>0, da x=log α B, und der Wert des Abschlusses mit positiver Basis A immer positiv.
Merkmale von Logarithmen.
Logarithmen gekennzeichnet durch unverwechselbare Merkmale, was zu ihrer weit verbreiteten Verwendung führte, um sorgfältige Berechnungen erheblich zu erleichtern. Wenn man sich „in die Welt der Logarithmen“ begibt, wird die Multiplikation in eine viel einfachere Addition, die Division in eine Subtraktion und die Potenzierung bzw. Wurzelziehung in eine Multiplikation bzw. Division mit dem Exponenten umgewandelt.
Formulierung von Logarithmen und Tabelle ihrer Werte (z trigonometrische Funktionen) wurde erstmals 1614 vom schottischen Mathematiker John Napier veröffentlicht. Logarithmische Tabellen, die von anderen Wissenschaftlern erweitert und detailliert wurden, wurden häufig in wissenschaftlichen und technischen Berechnungen verwendet und blieben bis zum Einsatz elektronischer Taschenrechner und Computer relevant.
„Abgekürzte Multiplikationsformeln“ – Bei der Multiplikation zweier Polynome wird jeder Term des ersten Polynoms mit jedem Term des zweiten Polynoms multipliziert und die Produkte addiert. Abgekürzte Multiplikationsformeln. Beim Addieren und Subtrahieren von Polynomen werden die Regeln zum Öffnen von Klammern verwendet. Monome sind Produkte aus Zahlen, Variablen und ihren Naturkräften.
„Ein Gleichungssystem lösen“ – Grafische Methode (Algorithmus). Eine Gleichung ist eine Gleichung, die eine oder mehrere Variablen enthält. Gleichung und ihre Eigenschaften. Methode der Determinanten (Algorithmus). Gleichungssystem und seine Lösung. Lösen des Systems mithilfe einer Vergleichsmethode. Lineare Gleichung mit zwei Variablen. Lösen des Systems mit der Additionsmethode.
„Ungleichungssysteme lösen“ – Intervalle. Mathematische Diktate. Es werden Beispiele für Lösungssysteme betrachtet Lineare Ungleichungen. Ungleichheitssysteme lösen. Um ein System linearer Ungleichungen zu lösen, reicht es aus, jede der darin enthaltenen Ungleichungen zu lösen und den Schnittpunkt der Mengen ihrer Lösungen zu finden. Schreiben Sie Ungleichungen auf, deren Lösungsmengen Intervalle sind.
„Beispielhafte Ungleichheiten“ – Zeichen der Ungleichheit. Lösen Sie die Ungleichung. Die einfachste Lösung exponentielle Ungleichungen. Exponentielle Ungleichungen lösen. Was sollten Sie bei der Lösung exponentieller Ungleichungen beachten? Einfache exponentielle Ungleichungen lösen. Eine Ungleichung, die einen unbekannten Exponenten enthält, wird als exponentielle Ungleichung bezeichnet.
„Zahlenverhältnisse“ – Was ist Proportion? Wie heißen die Zahlen m und n im Verhältnis a:m = n:b? Den Quotienten zweier Zahlen nennt man Verhältnis zweier Zahlen. Marketing Lan. Im richtigen Verhältnis ist das Produkt der Extremterme gleich dem Produkt der Mittelterme und umgekehrt. Was ist Haltung? Proportionen. Das Verhältnis kann als Prozentsatz ausgedrückt werden.
„Diskriminante einer quadratischen Gleichung“ – Satz von Vieta. Quadratische Gleichungen. Diskriminant. Welche Gleichungen nennt man unvollständige quadratische Gleichungen? Wie viele Wurzeln hat eine Gleichung, wenn ihre Diskriminante Null ist? Lösung unvollständig quadratische Gleichungen. Wie viele Wurzeln hat eine Gleichung, wenn ihre Diskriminante eine negative Zahl ist?
Insgesamt gibt es 14 Vorträge zum Thema
Logarithmen können wie alle Zahlen auf jede Art addiert, subtrahiert und transformiert werden. Da es sich bei Logarithmen aber nicht gerade um gewöhnliche Zahlen handelt, gibt es hier Regeln, die man nennt Haupteigenschaften.
Diese Regeln müssen Sie unbedingt kennen – ohne sie lässt sich kein einziges ernstes logarithmisches Problem lösen. Darüber hinaus gibt es nur sehr wenige davon – Sie können alles an einem Tag lernen. Also lasst uns anfangen.
Logarithmen addieren und subtrahieren
Betrachten Sie zwei Logarithmen mit derselben Basis: log A X und protokollieren A j. Dann können sie addiert und subtrahiert werden und:
- Protokoll A X+log A j= Protokoll A (X · j);
- Protokoll A X− log A j= Protokoll A (X : j).
Die Summe der Logarithmen ist also gleich dem Logarithmus des Produkts und die Differenz ist gleich dem Logarithmus des Quotienten. Bitte beachten Sie: Der entscheidende Punkt hier ist identische Gründe. Wenn die Gründe unterschiedlich sind, funktionieren diese Regeln nicht!
Diese Formeln helfen Ihnen, einen logarithmischen Ausdruck zu berechnen, auch wenn seine einzelnen Teile nicht berücksichtigt werden (siehe Lektion „Was ist ein Logarithmus“). Schauen Sie sich die Beispiele an und sehen Sie:
Log 6 4 + Log 6 9.
Da Logarithmen die gleichen Basen haben, verwenden wir die Summenformel:
log 6 4 + log 6 9 = log 6 (4 9) = log 6 36 = 2.
Aufgabe. Finden Sie den Wert des Ausdrucks: log 2 48 − log 2 3.
Die Grundlagen sind die gleichen, wir verwenden die Differenzformel:
log 2 48 − log 2 3 = log 2 (48: 3) = log 2 16 = 4.
Aufgabe. Finden Sie den Wert des Ausdrucks: log 3 135 − log 3 5.
Auch hier sind die Grundlagen dieselben, also haben wir:
log 3 135 − log 3 5 = log 3 (135: 5) = log 3 27 = 3.
Wie Sie sehen, bestehen die ursprünglichen Ausdrücke aus „schlechten“ Logarithmen, die nicht separat berechnet werden. Aber nach den Transformationen erhält man ganz normale Zahlen. Viele bauen auf dieser Tatsache auf Testpapiere. Ja, im Einheitlichen Staatsexamen werden prüfungsähnliche Ausdrücke in aller Ernsthaftigkeit (manchmal praktisch ohne Änderungen) angeboten.
Extrahieren des Exponenten aus dem Logarithmus
Jetzt machen wir die Aufgabe etwas komplizierter. Was ist, wenn die Basis oder das Argument eines Logarithmus eine Potenz ist? Dann kann der Exponent dieses Grades nach folgenden Regeln aus dem Vorzeichen des Logarithmus entnommen werden:
Es ist leicht zu erkennen, dass die letzte Regel den ersten beiden folgt. Aber es ist trotzdem besser, sich daran zu erinnern – in manchen Fällen wird es den Rechenaufwand erheblich reduzieren.
Alle diese Regeln machen natürlich Sinn, wenn die ODZ des Logarithmus beachtet wird: A > 0, A ≠ 1, X> 0. Und noch etwas: Lernen Sie, alle Formeln nicht nur von links nach rechts anzuwenden, sondern auch umgekehrt, d. h. Sie können die Zahlen vor dem Logarithmuszeichen in den Logarithmus selbst eingeben. Dies wird am häufigsten benötigt.
Aufgabe. Finden Sie den Wert des Ausdrucks: log 7 49 6 .
Lassen Sie uns den Grad im Argument loswerden, indem wir die erste Formel verwenden:
log 7 49 6 = 6 log 7 49 = 6 2 = 12
Aufgabe. Finden Sie die Bedeutung des Ausdrucks:
[Bildunterschrift]
Beachten Sie, dass der Nenner einen Logarithmus enthält, dessen Basis und Argument exakte Potenzen sind: 16 = 2 4 ; 49 = 7 2. Wir haben:
 [Bildunterschrift]
[Bildunterschrift] Ich denke, das letzte Beispiel bedarf einer Klarstellung. Wo sind die Logarithmen geblieben? Bis zum aller letzter Moment Wir arbeiten nur mit dem Nenner. Wir stellten die Basis und das Argument des dort stehenden Logarithmus in Form von Potenzen dar und entfernten die Exponenten – wir erhielten einen „dreistöckigen“ Bruch.
Schauen wir uns nun den Hauptbruch an. Zähler und Nenner enthalten die gleiche Zahl: log 2 7. Da log 2 7 ≠ 0 ist, können wir den Bruch reduzieren – 2/4 bleiben im Nenner. Nach den Regeln der Arithmetik lässt sich die Vier auf den Zähler übertragen, was auch geschehen ist. Das Ergebnis war die Antwort: 2.
Übergang zu einer neuen Stiftung
Als ich über die Regeln zum Addieren und Subtrahieren von Logarithmen sprach, habe ich ausdrücklich betont, dass diese nur mit den gleichen Basen funktionieren. Was ist, wenn die Gründe unterschiedlich sind? Was ist, wenn es sich nicht um exakte Potenzen derselben Zahl handelt?
Hier helfen Formeln für den Übergang zu einer neuen Stiftung. Formulieren wir sie in Form eines Theorems:
Gegeben sei der Logarithmus log A X. Dann für eine beliebige Zahl C so dass C> 0 und C≠ 1, die Gleichheit gilt:
[Bildunterschrift]
Insbesondere wenn wir sagen C = X, wir bekommen:
[Bildunterschrift]
Aus der zweiten Formel folgt, dass Basis und Argument des Logarithmus vertauscht werden können, allerdings wird in diesem Fall der gesamte Ausdruck „umgedreht“, also der Logarithmus erscheint im Nenner.
Diese Formeln sind in der konventionellen Medizin selten zu finden numerische Ausdrücke. Wie praktisch sie sind, lässt sich nur durch eine Entscheidung beurteilen logarithmische Gleichungen und Ungleichheiten.
Es gibt jedoch Probleme, die nur durch den Umzug in eine neue Stiftung gelöst werden können. Schauen wir uns einige davon an:
Aufgabe. Finden Sie den Wert des Ausdrucks: log 5 16 log 2 25.
Beachten Sie, dass die Argumente beider Logarithmen exakte Potenzen enthalten. Nehmen wir die Indikatoren heraus: log 5 16 = log 5 2 4 = 4log 5 2; log 2 25 = log 2 5 2 = 2log 2 5;
Lassen Sie uns nun den zweiten Logarithmus „umkehren“:
[Bildunterschrift]Da sich das Produkt beim Umordnen der Faktoren nicht ändert, haben wir in aller Ruhe vier und zwei multipliziert und uns dann mit Logarithmen befasst.
Aufgabe. Finden Sie den Wert des Ausdrucks: log 9 100 lg 3.
Basis und Argument des ersten Logarithmus sind exakte Potenzen. Schreiben wir das auf und entfernen wir die Indikatoren:
[Bildunterschrift]Jetzt lasst uns loswerden dezimaler Logarithmus, Umzug in eine neue Basis:
[Bildunterschrift]Grundlegende logarithmische Identität
Im Lösungsprozess ist es oft notwendig, eine Zahl als Logarithmus zu einer gegebenen Basis darzustellen. In diesem Fall helfen uns folgende Formeln:
Im ersten Fall die Nummer N wird zu einem Indikator für den Stellenwert der Argumentation. Nummer N kann absolut alles sein, da es sich nur um einen Logarithmuswert handelt.
Die zweite Formel ist eigentlich eine paraphrasierte Definition. So nennt man es: die grundlegende logarithmische Identität.
Was passiert eigentlich, wenn die Zahl B auf eine solche Potenz erhöhen, dass die Zahl B zu dieser Potenz gibt die Zahl A? Das ist richtig: Sie erhalten dieselbe Nummer A. Lesen Sie diesen Absatz noch einmal sorgfältig durch – viele bleiben dabei hängen.
Wie Formeln für den Übergang zu einer neuen Basis ist die grundlegende logarithmische Identität manchmal die einzig mögliche Lösung.
Aufgabe. Finden Sie die Bedeutung des Ausdrucks:
[Bildunterschrift]
Beachten Sie, dass log 25 64 = log 5 8 – einfach das Quadrat aus der Basis und dem Argument des Logarithmus genommen hat. Unter Berücksichtigung der Regeln zur Potenzmultiplikation mit gleicher Basis erhalten wir:
[Bildunterschrift]Falls es jemand nicht weiß, das war eine echte Aufgabe aus dem Einheitlichen Staatsexamen :)
Logarithmische Einheit und logarithmischer Nullpunkt
Abschließend möchte ich zwei Identitäten nennen, die kaum als Eigenschaften bezeichnet werden können – vielmehr sind sie Konsequenzen der Definition des Logarithmus. Sie tauchen ständig in Problemen auf und bereiten überraschenderweise auch „fortgeschrittenen“ Studierenden Probleme.
- Protokoll A A= 1 ist eine logarithmische Einheit. Denken Sie ein für alle Mal daran: Logarithmus zu jeder Basis A von dieser Basis aus ist gleich eins.
- Protokoll A 1 = 0 ist logarithmischer Nullpunkt. Base A kann alles sein, aber wenn das Argument eins enthält, ist der Logarithmus gleich Null! Weil A 0 = 1 ist eine direkte Konsequenz der Definition.
Das sind alle Eigenschaften. Üben Sie unbedingt die Umsetzung! Laden Sie den Spickzettel zu Beginn der Lektion herunter, drucken Sie ihn aus und lösen Sie die Aufgaben.