Dezimallogarithmus 0 1. Logarithmus
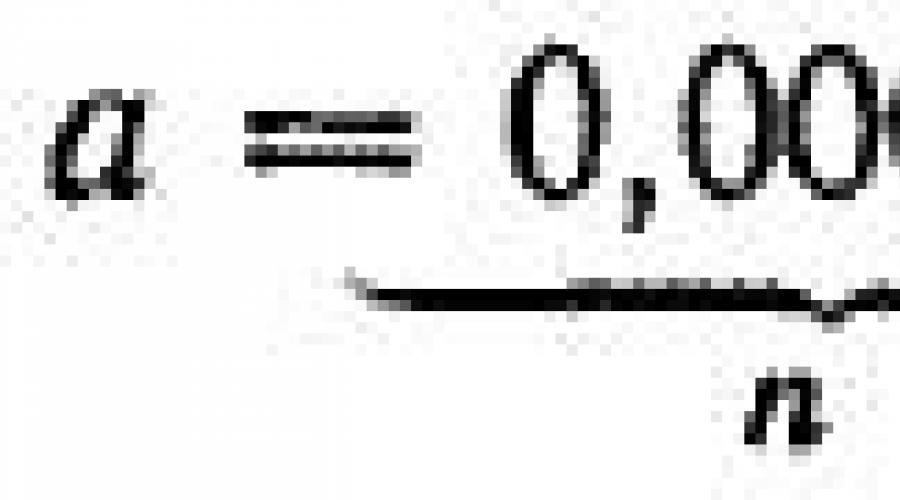
Lesen Sie auch
Sie nehmen oft die Zahl zehn an. Man nennt Logarithmen von Zahlen zur Basis Zehn Dezimal. Bei Berechnungen mit dem dezimalen Logarithmus wird üblicherweise mit dem Vorzeichen operiert lg, und nicht Protokoll; in diesem Fall wird die Zahl Zehn, die die Basis definiert, nicht angegeben. Ja, lass uns ersetzen Protokoll 10 105 zu vereinfachen lg105; A Protokoll 10 2 An lg2.
Für dezimale Logarithmen Typisch sind die gleichen Merkmale wie bei Logarithmen mit einer Basis größer als eins. Dezimale Logarithmen zeichnen sich nämlich ausschließlich durch positive Zahlen aus. Die dezimalen Logarithmen von Zahlen größer als eins sind positiv, die von Zahlen kleiner als eins sind negativ; von zwei nichtnegativen Zahlen entspricht die größere dem größeren dezimalen Logarithmus usw. Darüber hinaus haben dezimale Logarithmen Folgendes Unterscheidungsmerkmale und besondere Merkmale, die erklären, warum es bequem ist, die Zahl Zehn als Basis für Logarithmen zu bevorzugen.
Bevor wir diese Eigenschaften untersuchen, machen wir uns mit den folgenden Formulierungen vertraut.
Ganzzahliger Teil des Dezimallogarithmus einer Zahl A wird genannt charakteristisch, und der Bruch ist Mantisse dieser Logarithmus.
Eigenschaften des dezimalen Logarithmus einer Zahl A wird als angegeben, und die Mantisse als (lg A}.
Nehmen wir beispielsweise log 2 ≈ 0,3010. Dementsprechend = 0, (log 2) ≈ 0,3010.
Ebenso für log 543,1 ≈2,7349. Dementsprechend = 2, (log 543,1)≈ 0,7349.
Die Berechnung dezimaler Logarithmen positiver Zahlen aus Tabellen ist weit verbreitet.
Charakteristische Merkmale dezimaler Logarithmen.
Das erste Vorzeichen des Dezimallogarithmus. Eine nicht negative ganze Zahl, die durch eine Eins gefolgt von Nullen dargestellt wird, ist eine positive ganze Zahl, die der Anzahl der Nullen im Datensatz der ausgewählten Zahl entspricht .
Nehmen wir log 100 = 2, log 1 00000 = 5.
Im Allgemeinen, wenn
Das A= 10N , woraus wir bekommen
lg a = lg 10 n = n lg 10 =P.
Zweites Zeichen. Dezimaler Logarithmus Eine positive Dezimalzahl, dargestellt als Eins mit führenden Nullen, ist - P, Wo P- die Anzahl der Nullen in der Darstellung dieser Zahl unter Berücksichtigung ganzer Nullen.
Lassen Sie uns überlegen , log 0,001 = - 3, log 0,000001 = -6.
Im Allgemeinen, wenn
,
Das A= 10-N und es stellt sich heraus
lga= lg 10N =-n log 10 =-n
Drittes Zeichen. Die Charakteristik des dezimalen Logarithmus einer nicht negativen Zahl größer als eins ist gleich der Anzahl der Ziffern im ganzzahligen Teil dieser Zahl mit Ausnahme von eins.
Lassen Sie uns dieses Merkmal analysieren: 1) Die Charakteristik des Logarithmus lg 75,631 ist gleich 1.
Tatsächlich 10< 75,631 < 100. Из этого можно сделать вывод
LG 10< lg 75,631 < lg 100,
1 < lg 75,631 < 2.
Dies impliziert,
log 75,631 = 1 +b,
Das Verschieben eines Dezimalpunkts in einem Dezimalbruch nach rechts oder links entspricht der Operation, diesen Bruch mit einer Zehnerpotenz mit einem ganzzahligen Exponenten zu multiplizieren P(positiv oder negativ). Wenn daher der Dezimalpunkt in einem positiven Dezimalbruch nach links oder rechts verschoben wird, ändert sich die Mantisse des Dezimallogarithmus dieses Bruchs nicht.
Also (log 0,0053) = (log 0,53) = (log 0,0000053).
Im Folgenden wird der dezimale Logarithmus einfach als Logarithmus bezeichnet.
Der Logarithmus von Eins ist Null.
Logarithmen von Zahlen 10 , 100 , 1000 usw. gleich 1 ,2 ,3 usw., d.h. Es gibt so viele positive Einsen, wie Nullen nach der Eins stehen.
Logarithmen von Zahlen 0,1 ; 0,01 ; 0,001 usw. gleich -1 , -2 , -3 usw., d.h. haben so viele negative Einsen wie Nullen vor der Eins (einschließlich ganzer Nullen).
Die Logarithmen anderer Zahlen haben einen sogenannten Bruchteil Mantisse. Der ganzzahlige Teil eines Logarithmus wird aufgerufen charakteristisch.
Zahlen größer als Einheiten haben positive Logarithmen. Positive Zahlen kleiner als 1 haben negative Logarithmen.
Zum Beispiel 2, log0,5=-0,30103, log0,005=-2,30103.
Negative Logarithmen zur einfacheren Ermittlung eines Logarithmus durch eine Zahl und einer Zahl durch einen Logarithmus werden im obigen Abschnitt nicht dargestellt. natürlich„Form, und in“ künstlich". Ein negativer Logarithmus in künstlicher Form hat positive Mantisse Und negative Charakterisierung.
Zum Beispiel, log0,005=3,69897. Dieser Eintrag bedeutet das log0,005=-3+0,69897=-2,30103.
Um einen negativen Logarithmus von einer natürlichen in eine künstliche Form umzuwandeln, benötigen Sie:
1
. Um eins erhöhen Absolutwert seine Eigenschaften;
2
. Platzieren Sie die resultierende Zahl mit einem Minuszeichen oben;
3
. Alle Ziffern der Mantisse, mit Ausnahme der letzten Ziffer ungleich Null, werden von neun subtrahiert; Subtrahieren Sie die letzte Ziffer ungleich Null von zehn. Die resultierenden Differenzen werden an denselben Stellen der Mantisse geschrieben, an denen sich die subtrahierten Ziffern befanden. Die nachgestellten Nullen bleiben unberührt.
Beispiel 1
. log0,05=-1,30103 zu künstlicher Form führen:
1
. Absoluter Wert des Merkmals 1
erhöhen um 1
; wir bekommen 2
;
2
. Wir schreiben die Eigenschaften der künstlichen Form in das Formular 2
und trennen Sie es durch ein Komma;
3
. Subtrahieren Sie die erste Ziffer der Mantisse 3
aus 9
; wir bekommen 6
; aufschreiben 6
an erster Stelle nach dem Komma. Auf die gleiche Weise erscheinen Zahlen an den folgenden Stellen 9(=9-0)
, 8(=9-1)
, 9(=9-0)
Und 7(=10-3)
.
Als Ergebnis erhalten wir:
-1,30103=2,69897 .
Beispiel 2
. -0,18350
in künstlicher Form darstellen:
1
. Wir steigern 0
An 1
, wir bekommen 1
;
2
. Wir haben 1
;
3
. Zahlen subtrahieren 1
,8
,3
aus 9
; Figur 5
aus 10
; die Null am Ende bleibt unberührt.
Als Ergebnis erhalten wir:
-0,18350=1,81650 .
Um einen negativen Logarithmus von einer künstlichen in eine natürliche Form umzuwandeln, benötigen Sie:
1
. Verringern Sie den absoluten Wert seines Merkmals um eins;
2
. Versehen Sie die resultierende Zahl mit einem Minuszeichen auf der linken Seite.
3
. Gehen Sie mit den Mantissenziffern wie beim Übergang von einer natürlichen zu einer künstlichen Form vor.
Beispiel 3
. 4,689 00
in natürlicher Form vorhanden:
1
. 4-1=3
;
2
. Wir haben -3
;
3
. Subtrahieren Sie Zahlen von der Mantisse 6
,8
Und 9
; Figur 9
aus 10
; zwei Nullen bleiben unberührt.
Als Ergebnis erhalten wir:
4,689 00=-3,311 00 .
1 Negative Zahlen haben überhaupt keinen echten Logarithmus.
2 Alle weiteren Gleichheiten liegen annähernd innerhalb einer halben Einheit des letzten geschriebenen Zeichens.
ABSCHNITT XIII.
Logarithmen und ihre Anwendungen.
§ 2. Dezimale Logarithmen.
Der dezimale Logarithmus der Zahl 1 ist 0. Dezimale Logarithmen positiver Potenzen von 10, d.h. Zahlen 10, 100, 1000,.... im Wesentlichen positive Zahlen 1, 2, 3,..., also im Allgemeinen der Logarithmus einer Zahl, die durch Eins mit Nullen bezeichnet wird, gleich der Zahl Nullen. Dezimale Logarithmen negativer Zehnerpotenzen, d.h. Die Brüche 0,1, 0,01, 0,001, ... sind negative Zahlen -1, -2, -3 ..., daher ist im Allgemeinen der Logarithmus eines Dezimalbruchs mit einem Zähler von eins gleich der negativen Zahl von Nullen des Nenners.
Die Logarithmen aller anderen kommensurablen Zahlen sind inkommensurabel. Solche Logarithmen werden näherungsweise berechnet, normalerweise mit einer Genauigkeit von einem Hunderttausendstel, und werden daher in fünf Ziffern ausgedrückt Dezimalzahlen; zum Beispiel log 3 = 0,47712.
Bei der Darstellung der Theorie der dezimalen Logarithmen wird davon ausgegangen, dass alle Zahlen nach dem Dezimalsystem ihrer Einheiten und Brüche zusammengesetzt sind und alle Logarithmen durch einen Dezimalbruch ausgedrückt werden, der 0 ganze Zahlen enthält, mit einer ganzzahligen Erhöhung oder Verringerung. Der gebrochene Teil eines Logarithmus wird seine Mantisse genannt, und die gesamte Zunahme oder Abnahme wird seine Mantisse genannt charakteristisch. Logarithmen von Zahlen größer eins sind immer positiv und haben daher eine positive Charakteristik; Logarithmen von Zahlen kleiner als eins sind immer negativ, werden aber so dargestellt, dass ihre Mantisse positiv ist und ein Merkmal negativ ist: zum Beispiel log 500 = 0,69897 + 2 oder kürzer 2,69897 und log 0,05 = 0, 69897-2, der der Kürze halber als 2,69897 bezeichnet wird, wobei das Merkmal anstelle von ganzen Zahlen eingesetzt wird, jedoch mit einem Vorzeichen darüber. Somit stellt der Logarithmus einer Zahl größer als eins die arithmetische Summe einer positiven ganzen Zahl und eines positiven Bruchs dar, und der Logarithmus einer Zahl kleiner als eins stellt die algebraische Summe einer negativen ganzen Zahl mit einem positiven Bruch dar.
Jeder negative Logarithmus kann auf die angegebene künstliche Form reduziert werden. Zum Beispiel haben wir log 3 / 5 = log 3 – log 5 = 0,47712-0,69897 = -0,22185. Um diesen echten Logarithmus in eine künstliche Form umzuwandeln, addieren wir 1 dazu und geben nach der algebraischen Addition die Subtraktion von eins zur Korrektur an.
Wir erhalten log 3 / 5 = log 0,6 = (1-0,22185)-1 = 0,77815-1. Es stellt sich heraus, dass die Mantisse 0,77815 dieselbe ist, die dem Zähler 6 dieser Zahl entspricht, dargestellt im Dezimalsystem in Form des Bruchs 0,6.
In der angegebenen Darstellung von Dezimallogarithmen haben ihre Mantisse und Eigenschaften wichtige Eigenschaften im Zusammenhang mit der Bezeichnung der ihnen entsprechenden Zahlen im Dezimalsystem. Um diese Eigenschaften zu erklären, beachten wir Folgendes. Nehmen wir als Haupttyp der Zahl eine beliebige Zahl zwischen 1 und 10 und stellen sie, indem wir sie im Dezimalsystem ausdrücken, in der Form dar a,b,c,d,e,f ...., Wo A da ist einer von bedeutende Zahlen 1, 2, 3, 4, 5, 6, 7, 8, 9 und Dezimalstellen, b,c,d,e,f ....... sind beliebige Zahlen, zwischen denen Nullen stehen dürfen. Aufgrund der Tatsache, dass die genommene Zahl zwischen 1 und 10 liegt, liegt ihr Logarithmus zwischen 0 und 1 und daher besteht dieser Logarithmus aus einer Mantisse ohne Charakteristik oder mit der Charakteristik 0. Bezeichnen wir diesen Logarithmus in der Form 0 ,α β γ δ ε ...., Wo α, β ,γ ,δ, ε die Essenz einiger Zahlen. Multiplizieren wir nun diese Zahl einerseits mit den Zahlen 10, 100, 1000,... und andererseits mit den Zahlen 0,1, 0,01, 0,001,... und wenden die Sätze auf die Logarithmen des Produkts an und der Quotient. Dann erhalten wir eine Reihe von Zahlen größer als eins und eine Reihe von Zahlen kleiner als eins mit ihren Logarithmen:
lg A ,bcde f ....= 0 ,α β γ δ ε ....
lg ab,cde f ....= 1 ,α β γ δ ε ....lg 0,abcde f ....= 1 ,α β γ δ ε ....
lg abc,de f ....= 2 ,α β γ δ ε ....lg 0.0abcde f ....= 2 ,α β γ δ ε ....
lg abcd,e f ....= 3 ,α β γ δ ε ....lg 0.00abcde f ....= 3 ,α β γ δ ε ....
Bei der Betrachtung dieser Gleichheiten zeigen sich folgende Eigenschaften der Mantisse und Charakteristika:
Mantissa-Eigenschaft. Die Mantisse hängt von der Lage und Art der Lückenstellen der Zahl ab, jedoch überhaupt nicht von der Stelle des Kommas in der Bezeichnung dieser Zahl. Mantissen von Logarithmen von Zahlen mit einem Dezimalverhältnis, d.h. diejenigen, deren Vielfachverhältnis gleich einer positiven oder negativen Zehnerpotenz ist, sind gleich.
Charakteristische Eigenschaft. Das Merkmal hängt vom Rang der höchsten Einheiten oder Dezimalbrüche einer Zahl ab, jedoch überhaupt nicht von der Art der Ziffern in der Bezeichnung dieser Zahl.
Wenn wir die Zahlen benennen A ,bcde f ...., ab,cde f ...., abc,de f .... Zahlen mit positiven Ziffern – erste, zweite, dritte usw., Ziffer einer Zahl 0,abcde f .... wir betrachten Null und die Ziffern von Zahlen 0.0abcde f ...., 0.00abcde f ...., 0.000abcde f .... wenn wir negative Zahlen minus eins, minus zwei, minus drei usw. ausdrücken, dann können wir allgemein sagen, dass die Charakteristik des Logarithmus jeder Dezimalzahl um eins kleiner ist als die Zahl, die die Ziffer angibt
101. Da log 2 = 0,30103 ist, ermitteln Sie die Logarithmen der Zahlen 20,2000, 0,2 und 0,00002.
101. Da log 3=0,47712 ist, ermitteln Sie die Logarithmen der Zahlen 300, 3000, 0,03 und 0,0003.
102. Wenn Sie wissen, dass log 5 = 0,69897 ist, ermitteln Sie die Logarithmen der Zahlen 2,5, 500, 0,25 und 0,005.
102. Da log 7 = 0,84510 ist, ermitteln Sie die Logarithmen der Zahlen 0,7, 4,9, 0,049 und 0,0007.
103. Wenn Sie log 3=0,47712 und log 7=0,84510 kennen, ermitteln Sie die Logarithmen der Zahlen 210, 0,021, 3/7, 7/9 und 3/49.
103. Wenn Sie log 2=0,30103 und log 7=0,84510 kennen, ermitteln Sie die Logarithmen der Zahlen 140, 0,14, 2/7, 7/8 und 2/49.
104. Wenn Sie log 3 = 0,47712 und log 5 = O,69897 kennen, ermitteln Sie die Logarithmen der Zahlen 1,5, 3 / 5, 0,12, 5 / 9 und 0,36.
104. Wenn Sie log 5 = 0,69897 und log 7 = 0,84510 kennen, ermitteln Sie die Logarithmen der Zahlen 3,5, 5 / 7, 0,28, 5 / 49 und 1,96.
Dezimallogarithmen von Zahlen, die nicht mehr als vierstellig sind, werden direkt aus den Tabellen ermittelt, aus den Tabellen wird die Mantisse des gewünschten Logarithmus ermittelt und das Merkmal entsprechend dem Rang der gegebenen Zahl festgelegt.
Wenn die Zahl mehr als vier Ziffern enthält, geht mit der Ermittlung des Logarithmus eine zusätzliche Berechnung einher. Die Regel lautet: Um den Logarithmus einer Zahl mit mehr als vier Ziffern zu ermitteln, müssen Sie in den Tabellen die durch die ersten vier Ziffern angegebene Zahl finden und die diesen vier Ziffern entsprechende Mantisse schreiben; dann multipliziere die tabellarische Differenz der Mantisse mit der Zahl, die sich aus den verworfenen Ziffern zusammensetzt, verwirf im Produkt so viele Ziffern von rechts, wie in der gegebenen Zahl verworfen wurden, und addiere das Ergebnis zu den letzten Ziffern der gefundenen Mantisse; Ordnen Sie das Merkmal entsprechend dem Rang der angegebenen Zahl zu.
Wenn eine Zahl anhand eines bestimmten Logarithmus gesucht wird und dieser Logarithmus in Tabellen enthalten ist, werden die Ziffern der gesuchten Zahl direkt aus den Tabellen gefunden und der Rang der Zahl anhand der Eigenschaften des angegebenen Logarithmus bestimmt.
Sollte dieser Logarithmus nicht in den Tabellen enthalten sein, ist mit der Suche nach der Zahl eine zusätzliche Berechnung verbunden. Die Regel lautet: um die Zahl zu finden, die einem bestimmten Logarithmus entspricht, dessen Mantisse nicht in den Tabellen enthalten ist, müssen Sie die nächstkleinere Mantisse finden und die Ziffern der ihr entsprechenden Zahl aufschreiben; dann multiplizieren Sie die Differenz zwischen der gegebenen und der gefundenen Mantisse mit 10 und dividieren Sie das Produkt durch die tabellarische Differenz; addieren Sie die resultierende Ziffer des Quotienten rechts zu den geschriebenen Ziffern der Zahl, wodurch Sie den gewünschten Ziffernsatz erhalten; Der Rang der Zahl muss entsprechend den Eigenschaften des gegebenen Logarithmus bestimmt werden.
105. Finden Sie die Logarithmen der Zahlen 8, 141, 954, 420, 640, 1235, 3907, 3010, 18,43, 2,05, 900,1, 0,73, 0,0028, 0,1008, 0,00005.
105. Finden Sie den Logarithmus der Zahlen 15,154, 837, 510, 5002,1309-, 8900, 8,315, 790,7, 0,09, 0,6745, 0,000745, 0,04257, 0,00071.
106. Finden Sie die Logarithmen der Zahlen 2174,6, 1445,7, 2169,5, 8437,2, 46,472, 6,2853, 0,7893B, 0,054294, 631,074, 2,79556, 0,747428, 0,00237158.
106. Finden Sie die Logarithmen der Zahlen 2578,4, 1323,6, 8170,5, 6245,3, 437,65, 87,268, 0,059372, 0,84938, 62,5475, 131,037, 0,593946, 0,00234261.
107. Finden Sie die Zahlen, die den Logarithmen 3,16227, 3,59207, 2,93318, 0,41078, 1,60065, 2,756,86, 3,23528, 1,79692 entsprechen. 4,87800 5,14613.
107. Finden Sie die Zahlen, die den Logarithmen 3,07372, 3,69205, 1,64904, 2,16107, 0,70364, 1,31952, 4,30814, 3,00087, 2,69949, 6,57978 entsprechen.
108. Finden Sie die Zahl, die den Logarithmen 3,57686, 3,16340, 2,40359, 1,09817, 4,49823, 2,83882, 1,50060, 3,30056, 1,17112, 4,25100 entspricht.
108. Finden Sie die Zahlen, die den Logarithmen 3,33720, 3,09875, 0,70093, 4,04640, 2,94004, 1,41509, 2,32649, 4,14631, 3,01290, 5,39003 entsprechen.
Positive Logarithmen von Zahlen größer als eins sind die arithmetischen Summen ihrer Merkmale und Mantissen. Daher werden Operationen mit ihnen nach den üblichen arithmetischen Regeln durchgeführt.
Negative Logarithmen von Zahlen kleiner als eins sind die algebraischen Summen einer negativen Charakteristik und einer positiven Mantisse. Daher werden Operationen mit ihnen nach algebraischen Regeln durchgeführt, die durch spezielle Anweisungen zur Reduktion negativer Logarithmen auf ihre Normalform ergänzt werden. Die Normalform eines negativen Logarithmus ist eine Form, bei der das Merkmal eine negative ganze Zahl und die Mantisse ein positiver echter Bruch ist.
Um einen echten reflektiven Logarithmus in seine normale künstliche Form umzuwandeln, müssen Sie den Absolutwert seines ganzzahligen Termes um eins erhöhen und das Ergebnis zu einem negativen Merkmal machen; Addieren Sie dann alle Ziffern des Bruchterms zu 9 und die letzte zu 10 und machen Sie das Ergebnis zu einer positiven Mantisse. Beispiel: -2,57928 = 3,42072.
Die künstliche Normalform eines Logarithmus in seine wahre Form umwandeln negative Bedeutung, müssen Sie die negative Eigenschaft um eins reduzieren und das Ergebnis zu einem ganzzahligen Term der negativen Summe machen; Addieren Sie dann alle Ziffern der Mantisse zu 9 und die letzte Ziffer zu 10 und machen Sie das Ergebnis zu einem Bruchteil derselben negativen Summe. Beispiel: 4,57406= -3,42594.
109. Konvertieren Sie Logarithmen in die künstliche Form -2,69537, -4, 21283, -0,54225, -1,68307, -3,53820, -5,89990.
109. Konvertieren Sie Logarithmen in die künstliche Form -3,21729, -1,73273, -5,42936, -0,51395, -2,43780, -4,22990.
110. Finden Sie die wahren Werte der Logarithmen 1,33278, 3,52793, 2,95426, 4,32725, 1,39420, 5,67990.
110. Finden Sie die wahren Werte der Logarithmen 2,45438, 1,73977, 3,91243, 5,12912, 2,83770, 4,28990.
Die Regeln für algebraische Operationen mit negativen Logarithmen lauten wie folgt:
Um einen negativen Logarithmus in seiner künstlichen Form anzuwenden, müssen Sie die Mantisse anwenden und den Absolutwert der Charakteristik subtrahieren. Wenn durch die Addition von Mantissen eine positive ganze Zahl entsteht, müssen Sie diese der Charakteristik des Ergebnisses zuordnen und eine entsprechende Korrektur vornehmen. Zum Beispiel,
3,89573 + 2 ,78452 = 1 1 ,68025 = 2,68025
1 ,54978 + 2 ,94963=3 1 ,49941=2 ,49941.
Um einen negativen Logarithmus in seiner künstlichen Form zu subtrahieren, müssen Sie die Mantisse subtrahieren und den Absolutwert der Charakteristik addieren. Wenn die subtrahierte Mantisse groß ist, müssen Sie die Charakteristik des Minuenden anpassen, um eine positive Einheit vom Minuenden zu trennen. Zum Beispiel,
2,53798-3 ,84582=1 1 ,53798-3 ,84582 = 4,69216,
2 ,22689-1 ,64853=3 1 ,22689-1 ,64853=2 ,57836.
Um einen negativen Logarithmus mit einer positiven ganzen Zahl zu multiplizieren, müssen Sie dessen Charakteristik und Mantisse separat multiplizieren. Wenn bei der Multiplikation mit der Mantisse eine ganze positive Zahl ermittelt wird, müssen Sie diese der Charakteristik des Ergebnisses zuordnen und eine entsprechende Änderung daran vornehmen. Zum Beispiel,
2 ,53729 5=10 2 ,68645=8 ,68645.
Wenn Sie einen negativen Logarithmus mit einer negativen Größe multiplizieren, müssen Sie den Multiplikanden durch seinen wahren Wert ersetzen.
Um einen negativen Logarithmus durch eine positive ganze Zahl zu dividieren, müssen Sie dessen Charakteristik und Mantisse getrennt trennen. Wenn die Kennlinie des Dividenden nicht exakt durch den Divisor teilbar ist, müssen Sie eine Änderung daran vornehmen, um mehrere positive Einheiten in die Mantisse aufzunehmen und die Kennlinie zu einem Vielfachen des Divisors zu machen. Zum Beispiel,
3 ,79432: 5=5 2 ,79432: 5=1 ,55886.
Wenn Sie einen negativen Logarithmus durch eine negative Größe dividieren, müssen Sie den Dividenden durch seinen wahren Wert ersetzen.
Führen Sie die folgenden Berechnungen mit logarithmischen Tabellen durch und überprüfen Sie die Ergebnisse im einfachsten Fall mit gewöhnlichen Methoden:
174. Bestimmen Sie das Volumen eines Kegels, dessen Erzeugende 0,9134 Fuß und dessen Basisradius 0,04278 Fuß beträgt.
175. Berechnen Sie den 15. Term einer Mehrfachfolge, deren erster Term 2 3 / 5 und deren Nenner 1,75 ist.
175. Berechnen Sie den ersten Term einer Mehrfachfolge, deren 11. Term gleich 649,5 ist und deren Nenner 1,58 ist.
176. Bestimmen Sie die Anzahl der Faktoren A , A 3 , A 5 R . Finden Sie so etwas A , bei dem das Produkt von 10 Faktoren gleich 100 ist.
176. Bestimmen Sie die Anzahl der Faktoren. A 2 , A 6 , A 10 ,.... so dass ihr Produkt der angegebenen Zahl entspricht R . Finden Sie so etwas A , bei dem das Produkt von 5 Faktoren gleich 10 ist.
177. Der Nenner der Mehrfachprogression ist 1,075, die Summe ihrer 10 Terme ist 2017,8. Finden Sie den ersten Begriff.
177. Der Nenner der Mehrfachfolge ist 1,029, die Summe ihrer 20 Terme beträgt 8743,7. Finden Sie den zwanzigsten Begriff.
178 . Drücken Sie die Anzahl der Terme einer Mehrfachprogression anhand des ersten Termes aus A , letzter und Nenner Q und dann zufällig numerische Werte auswählen A Und u , abholen Q so dass P
178. Geben Sie die Anzahl der Terme einer Mehrfachprogression anhand des ersten Termes an A , zuletzt Und und Nenner Q Und Und Q , abholen A so dass P war eine ganze Zahl.
179. Bestimmen Sie die Anzahl der Faktoren, sodass ihr Produkt gleich ist R . Wie es sein muss R um zu A =0,5 und B =0,9 betrug die Anzahl der Faktoren 10.
179. Bestimmen Sie die Anzahl der Faktoren ![]() damit ihr Produkt gleich ist R
. Wie es sein muss R
um zu A
=0,2 und B
=2 die Anzahl der Faktoren betrug 10.
damit ihr Produkt gleich ist R
. Wie es sein muss R
um zu A
=0,2 und B
=2 die Anzahl der Faktoren betrug 10.
180. Drücken Sie die Anzahl der Terme einer Mehrfachprogression anhand des ersten Termes aus A , Ich werde folgen Und und das Produkt aller Mitglieder R und dann zufällig numerische Werte auswählen A Und R , abholen Und und dann der Nenner Q so dass Und war eine ganze Zahl.
160. Geben Sie die Anzahl der Terme einer Mehrfachprogression anhand des ersten Termes an A , das letzte und und das Produkt aller Terme R und dann zufällig numerische Werte auswählen Und Und R , abholen A und dann der Nenner Q so dass P war eine ganze Zahl.
Lösen Sie die folgenden Gleichungen, wo möglich – ohne die Hilfe von Tabellen, und wo nicht, mit Tabellen:


