Achsbiegung. Berechnungsschemata für Balken
Lesen Sie auch
Beim Biegen handelt es sich um eine Form der Verformung, bei der die Längsachse des Trägers gebogen wird. Gerade Balken, die sich biegen, werden Balken genannt. Direkte Biegung ist eine Biegung, bei der die auf den Balken wirkenden äußeren Kräfte in einer Ebene (Kraftebene) liegen, die durch die Längsachse des Balkens und die zentrale Hauptträgheitsachse verläuft Querschnitt.
Die Biegung wird als rein bezeichnet, wenn in jedem Balkenquerschnitt nur ein Biegemoment auftritt.
Biegung, bei der gleichzeitig ein Biegemoment und ein Biegemoment im Querschnitt des Trägers wirken. Scherkraft, heißt transversal. Die Schnittlinie der Kraftebene und der Querschnittsebene wird Kraftlinie genannt.
Innere Kraftfaktoren beim Biegen des Balkens.
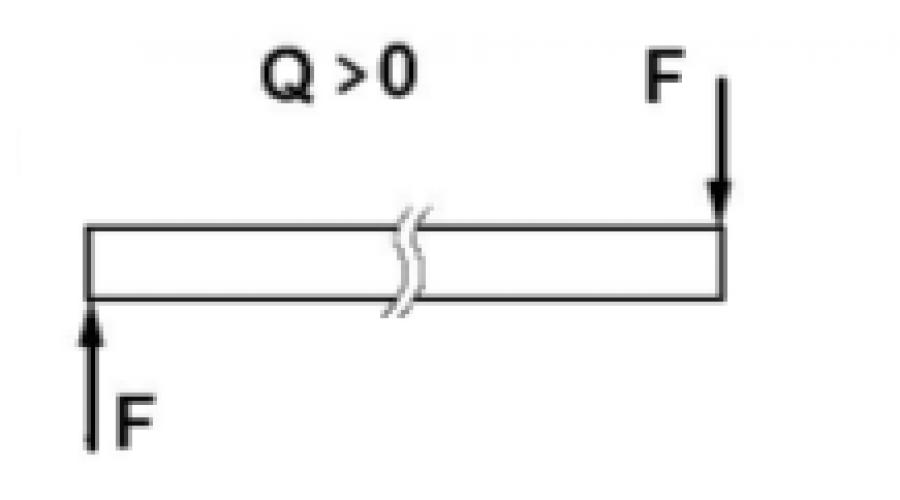
Bei der ebenen Querbiegung entstehen in den Balkenabschnitten zwei Schnittgrößen: die Querkraft Q und das Biegemoment M. Zu deren Ermittlung wird die Schnittmethode verwendet (siehe Vorlesung 1). Die Querkraft Q im Balkenquerschnitt ist gleich der algebraischen Summe der Projektionen aller auf einer Seite des betrachteten Abschnitts wirkenden äußeren Kräfte auf die Schnittebene.
Vorzeichenregel für Querkräfte Q:
Das Biegemoment M in einem Balkenabschnitt ist gleich der algebraischen Summe der Momente aller äußeren Kräfte, die auf eine Seite des betrachteten Abschnitts wirken, bezogen auf den Schwerpunkt dieses Abschnitts.
Vorzeichenregel für Biegemomente M:
Zhuravskys differenzielle Abhängigkeiten.
Es wurden unterschiedliche Zusammenhänge zwischen der Intensität q der Flächenlast, den Ausdrücken für die Querkraft Q und dem Biegemoment M festgestellt:
Basierend auf diesen Abhängigkeiten lassen sich folgende allgemeine Muster von Diagrammen der Querkräfte Q und Biegemomente M identifizieren:
Merkmale interner Diagramme Leistungsfaktoren beim Biegen.
1. In dem Abschnitt des Balkens, in dem keine verteilte Last vorliegt, wird das Q-Diagramm dargestellt gerade Linie , parallel zur Basis des Diagramms und Diagramm M - eine geneigte gerade Linie (Abb. a).
2. In dem Abschnitt, in dem eine konzentrierte Kraft ausgeübt wird, sollte Q im Diagramm angezeigt werden Sprung , gleich dem Wert dieser Kraft, und im Diagramm M - Bruchpunkt (Abb. a).
3. In dem Abschnitt, in dem ein konzentriertes Moment angewendet wird, ändert sich der Wert von Q nicht und das Diagramm M ändert sich nicht Sprung , gleich dem Wert dieses Moments (Abb. 26, b).
4. In einem Strahlabschnitt mit einer Flächenlast der Intensität q ändert sich das Diagramm Q nach einem linearen Gesetz und das Diagramm M nach einem parabolischen Gesetz, und die Konvexität der Parabel ist in Richtung der verteilten Last gerichtet (Abb. c, d).
5. Wenn innerhalb eines charakteristischen Abschnitts das Diagramm Q die Basis des Diagramms schneidet, dann hat das Biegemoment in dem Abschnitt mit Q = 0 einen Extremwert M max oder M min (Abb. d).
Normale Biegespannungen.
Bestimmt durch die Formel:
Das Widerstandsmoment eines Abschnitts gegen Biegung ist die Größe:
Gefährlicher Querschnitt Beim Biegen wird der Querschnitt des Balkens bezeichnet, in dem die maximale Normalspannung auftritt.
Schubspannungen beim geraden Biegen.
Bestimmt durch Zhuravskys Formel für Schubspannungen bei gerader Balkenbiegung:
wobei S ots das statische Moment der Querfläche der abgeschnittenen Schicht aus Längsfasern relativ zur Neutrallinie ist.
Berechnungen der Biegefestigkeit.
1. Bei Verifizierungsberechnung Die maximale Bemessungsspannung wird ermittelt und mit der zulässigen Spannung verglichen:
2. Bei Entwurfsberechnung Die Auswahl des Balkenquerschnitts erfolgt aus der Bedingung:
3. Bei der Ermittlung der zulässigen Belastung wird das zulässige Biegemoment aus der Bedingung ermittelt:
Beugebewegungen.
Unter dem Einfluss der Biegebelastung biegt sich die Balkenachse. In diesem Fall wird eine Spannung der Fasern im konvexen Teil und eine Kompression im konkaven Teil des Balkens beobachtet. Darüber hinaus kommt es zu einer vertikalen Bewegung der Schwerpunkte der Querschnitte und deren Drehung relativ zur neutralen Achse. Zur Charakterisierung der Biegeverformung werden folgende Konzepte verwendet:
Strahlablenkung Y- Bewegung des Schwerpunkts des Balkenquerschnitts in Richtung senkrecht zu seiner Achse.
Die Durchbiegung gilt als positiv, wenn sich der Schwerpunkt nach oben verschiebt. Das Ausmaß der Durchbiegung variiert über die Länge des Balkens, d. h. y = y(z)
Abschnittsdrehwinkel- Winkel θ, um den sich jeder Abschnitt relativ zu seiner ursprünglichen Position dreht. Der Drehwinkel gilt als positiv, wenn der Abschnitt gegen den Uhrzeigersinn gedreht wird. Die Größe des Rotationswinkels variiert entlang der Länge des Strahls und ist eine Funktion von θ = θ (z).
Die gebräuchlichste Methode zur Bestimmung von Verschiebungen ist die Methode Mora Und Wereschtschagins Herrschaft.
Mohrs Methode.
Das Verfahren zur Bestimmung von Verschiebungen nach der Mohr-Methode:
1. An der Stelle, an der die Verschiebung ermittelt werden soll, wird ein „Hilfssystem“ aufgebaut und mit einer Einheitslast belastet. Wenn eine lineare Verschiebung bestimmt wird, wird eine Einheitskraft in ihre Richtung ausgeübt; wenn Winkelverschiebungen bestimmt werden, wird ein Einheitsmoment angewendet.
2. Für jeden Abschnitt des Systems werden Ausdrücke für Biegemomente M f aus der aufgebrachten Last und M 1 aus der Einheitslast notiert.
3. Über alle Abschnitte des Systems werden Mohrsche Integrale berechnet und summiert, was die gewünschte Verschiebung ergibt:
4. Wenn die berechnete Verschiebung ein positives Vorzeichen hat, bedeutet dies, dass ihre Richtung mit der Richtung der Einheitskraft übereinstimmt. Ein negatives Vorzeichen zeigt an, dass die tatsächliche Verschiebung der Richtung der Einheitskraft entgegengesetzt ist.
Wereschtschagins Herrschaft.
Für den Fall, dass das Diagramm der Biegemomente einer bestimmten Last einen willkürlichen Umriss und von einer Einheitslast einen geradlinigen Umriss hat, ist es zweckmäßig, die grafisch-analytische Methode oder die Wereschtschagin-Regel zu verwenden.
wobei A f die Fläche des Diagramms des Biegemoments M f aus einer gegebenen Last ist; y-Koordinate – Ordinate des Diagramms von einer Einheitslast unter dem Schwerpunkt des Diagramms M f; EI x ist die Querschnittssteifigkeit des Balkenabschnitts. Berechnungen nach dieser Formel erfolgen abschnittsweise, wobei das Geradendiagramm jeweils bruchfrei sein sollte. Der Wert (A f *y c) gilt als positiv, wenn sich beide Diagramme auf derselben Seite des Balkens befinden, als negativ, wenn sie sich auf unterschiedlichen Seiten befinden. Ein positives Ergebnis der Multiplikationsdiagramme bedeutet, dass die Bewegungsrichtung mit der Richtung einer Einheitskraft (oder eines Moments) übereinstimmt. Ein komplexes Diagramm M f sollte in einfache Figuren unterteilt werden (es wird die sogenannte „Plotschichtung“ verwendet), für die sich jeweils die Ordinate des Schwerpunkts leicht bestimmen lässt. In diesem Fall wird die Fläche jeder Figur mit der Ordinate unter ihrem Schwerpunkt multipliziert.
Beim Bauen Diagramme der BiegemomenteM bei Bauherren akzeptiert: Ordinaten, die in einem bestimmten Maßstab ausgedrückt werden positiv Werte der Biegemomente, beiseite legen gestreckt Fasern, d.h. - runter, A negativ - oben von der Strahlachse. Daher sagen sie, dass Bauherren Diagramme auf gedehnten Fasern erstellen. Bei den Mechanikern Positive Werte sowohl der Querkraft als auch des Biegemoments werden verschoben hoch. Mechaniker zeichnen Diagramme auf komprimiert Fasern.
Hauptbetonungen beim Biegen. Äquivalente Spannungen.
Im allgemeinen Fall einer direkten Biegung in den Querschnitten eines Trägers gilt: normal Und Tangenten
Stromspannung. Diese Spannungen variieren sowohl entlang der Länge als auch der Höhe des Balkens.
Im Falle einer Biegung ist dies der Fall ebener Spannungszustand.
Betrachten wir ein Diagramm, in dem der Balken mit der Kraft P belastet wird
Größter Normalwert Spannungen entstehen in extrem, Punkte, die am weitesten von der neutralen Linie entfernt sind, und In ihnen treten keine Scherspannungen auf. Also z extrem Fasern Hauptspannungen ungleich Null sind Normalspannungen im Querschnitt.
Auf der Ebene der neutralen Linie im Querschnitt des Balkens gibt es höchste Scherbeanspruchung, A Normalspannungen sind Null. bedeutet in den Fasern neutral Schicht die Hauptspannungen werden durch die Werte der Tangentialspannungen bestimmt.
In diesem Entwurfsschema Die oberen Fasern des Balkens werden gedehnt und die unteren werden gestaucht. Zur Bestimmung der Hauptspannungen verwenden wir den bekannten Ausdruck: 
Voll Spannungsanalyse Stellen wir es uns auf dem Bild vor.
Biegespannungsanalyse
Maximale Hauptspannung σ 1 befindet sich Oberer, höher extreme Fasern und ist auf den unteren äußersten Fasern gleich Null. Hauptspannung σ 3 Es hat am höchsten in Absolutwert Wert auf die unteren Fasern.
Verlauf der Hauptspannungen hängt von der Lasttyp Und Methode zur Befestigung des Balkens.
Beim Lösen von Problemen reicht es separatüberprüfen normal Und getrennt Tangentialspannungen. Allerdings manchmal am stressigsten erweisen sich als dazwischenliegend Fasern, in denen sowohl Normal- als auch Scherspannungen auftreten. Dies geschieht in Abschnitten, in denen Gleichzeitig erreichen sowohl das Biegemoment als auch die Querkraft große Werte - Dies kann bei der Einbettung eines Kragträgers, bei der Auflage eines Balkens mit Kragarm, in Abschnitten unter konzentrierter Krafteinwirkung oder in Abschnitten mit stark wechselnder Breite der Fall sein. Zum Beispiel in einem I-Abschnitt am gefährlichsten die Verbindung von Wand und Regal- es gibt Sowohl Normal- als auch Scherspannungen sind erheblich.
Das Material befindet sich in einem ebenen Spannungszustand und ist erforderlich Überprüfen Sie, ob entsprechende Spannungen vorhanden sind.
Festigkeitsbedingungen für Träger aus Kunststoffmaterialien Von dritte(Theorie maximaler Tangentialspannungen) 
Und vierte(Theorie der Energie von Formänderungen) 
Theorien der Stärke.
In gewalzten Trägern werden die Vergleichsspannungen in der Regel nicht überschritten normaler Stress Bei extremen Fasern sind keine besonderen Tests erforderlich. Etwas anderes - Verbundmetallträger, welche Die Wand ist dünner als bei Walzprofilen auf gleicher Höhe. Häufiger werden geschweißte Verbundträger aus Stahlblechen verwendet. Berechnung der Festigkeit solcher Balken: a) Auswahl des Abschnitts – Höhe, Dicke, Breite und Dicke der Balkensehnen; b) Überprüfung der Festigkeit durch Normal- und Tangentialspannungen; c) Überprüfung der Festigkeit anhand von Vergleichsspannungen.
Bestimmung der Schubspannungen in einem I-Profil. Betrachten wir den Abschnitt Ich glänze S x =96,9 cm 3 ; Yх=2030 cm 4 ; Q=200 kN
Zur Bestimmung der Schubspannung wird diese verwendet Formel
,wobei Q die Scherkraft im Abschnitt ist, S x 0 das statische Moment des Teils des Querschnitts ist, der sich auf einer Seite der Schicht befindet, in der die Tangentialspannungen bestimmt werden, I x das Trägheitsmoment des Ganzen Querschnitt, b ist die Breite des Abschnitts an der Stelle, an der die Scherspannung bestimmt wird
Rechnen wir maximal Schubspannung:
Berechnen wir das statische Moment für obersten Regal: 
Nun lasst uns rechnen Schubspannung: 
Wir bauen Schubspannungsdiagramm:
Betrachten wir den Querschnitt eines Standardprofils in der Form Ich glänze und definieren Scherbeanspruchung, parallel zur Scherkraft wirkend:
Rechnen wir statische Momente einfache Zahlen: 
Dieser Wert kann berechnet werden und ansonsten, unter Ausnutzung der Tatsache, dass für die I-Träger- und Trogabschnitte das statische Moment der Hälfte des Abschnitts angegeben ist. Dazu ist es notwendig, vom bekannten Wert des statischen Moments den Wert des statischen Moments zur Geraden abzuziehen A 1 B 1: 
Die Tangentialspannungen an der Verbindungsstelle zwischen Flansch und Wand ändern sich krampfhaft, als scharf Wandstärke variiert von t st Vor B.
Diagramme der Tangentialspannungen in den Wänden von Trog-, Hohl-Rechteck- und anderen Profilen haben die gleiche Form wie im Fall eines I-Profils. Die Formel umfasst das statische Moment des schattierten Teils des Abschnitts relativ zur X-Achse und der Nenner enthält die Breite des Abschnitts (netto) in der Schicht, in der die Scherspannung bestimmt wird.
Bestimmen wir die Tangentialspannungen für einen Kreisabschnitt.
Da die Schubspannungen auf die Profilkontur gerichtet sein müssen tangential zur Kontur, dann punktuell A Und IN an den Enden einer beliebigen Sehne parallel zum Durchmesser AB, Schubspannungen werden gerichtet senkrecht zu den Radien OA Und OV. Somit, Richtungen Tangentialspannungen an Punkten A, VC irgendwann zusammenlaufen N auf der Y-Achse.
Statisches Moment des abgeschnittenen Teils:
Das heißt, die Schubspannungen ändern sich entsprechend parabolisch Gesetz und wird auf der Ebene der neutralen Linie maximal sein, wenn y 0 =0
Formel zur Bestimmung der Schubspannung (Formel) 
Betrachten Sie einen rechteckigen Abschnitt
Auf Distanz y 0 Von der Mittelachse zeichnen wir Abschnitt 1-1 und bestimmen Sie die Tangentialspannungen. Statischer Moment Bereich abgeschnittenes Teil:
Es sollte bedacht werden, dass es von grundlegender Bedeutung ist gleichgültig, nimm das statische Moment der Fläche schattierter oder verbleibender Teil Querschnitt. Beides statische Momente gleich und entgegengesetzt im Vorzeichen, also ihre Summe, was darstellt statisches Flächenmoment des gesamten Abschnitts relativ zur neutralen Linie, nämlich der zentralen x-Achse, gleich sein null.
Trägheitsmoment eines rechteckigen Abschnitts:
Dann Scherbeanspruchung nach der Formel
Die Variable y 0 ist in der Formel enthalten zweite Grad, d.h. Tangentialspannungen in einem rechteckigen Abschnitt variieren je nach Gesetz einer quadratischen Parabel.
Schubspannung erreicht maximal auf der Ebene der neutralen Linie, d.h. Wann y 0 =0:
,
Wo A ist die Fläche des gesamten Abschnitts.
Festigkeitsbedingung für Tangentialspannungen hat die Form:
, Wo S x 0– statisches Moment des Teils des Querschnitts, der sich auf einer Seite der Schicht befindet, in dem die Schubspannungen bestimmt werden, Ix– Trägheitsmoment des gesamten Querschnitts, B– Abschnittsbreite an der Stelle, an der die Schubspannung bestimmt wird, Q-Seitenkraft, τ
- Scherbeanspruchung, [τ]
— zulässige Tangentialspannung.
Dieser Festigkeitszustand ermöglicht es uns zu produzieren drei Art der Berechnung (drei Arten von Problemen bei der Berechnung der Festigkeit):
1. Nachweisrechnung bzw. Festigkeitsprüfung anhand von Tangentialspannungen:
2. Auswahl der Abschnittsbreite (für einen rechteckigen Abschnitt): 
3. Bestimmung der zulässigen Querkraft (für einen rechteckigen Querschnitt):
Zur Bestimmung Tangenten Betrachten Sie bei Spannungen einen mit Kräften belasteten Balken.
Die Aufgabe, Spannungen zu ermitteln, ist immer statisch unbestimmt und erfordert Engagement geometrisch Und körperlich Gleichungen. Es ist jedoch möglich, dies zu akzeptieren Hypothesen über die Natur der Stressverteilung dass die Aufgabe wird statisch definierbar.
Durch zwei unendlich nahe beieinander liegende Querschnitte 1-1 und 2-2 selektieren wir dz-Element, Lassen Sie uns es im großen Maßstab darstellen und dann einen Längsschnitt 3-3 zeichnen.
In den Abschnitten 1–1 und 2–2, Normalspannungen σ 1, σ 2, die durch die bekannten Formeln bestimmt werden:
Wo M - Biegemoment im Querschnitt, dM - Inkrement Biegemoment bei der Länge dz
Seitenkraft in den Abschnitten 1–1 und 2–2 ist entlang der Hauptmittelachse Y gerichtet und stellt offensichtlich dar die Summe der vertikalen Komponenten der über den Abschnitt verteilten inneren Tangentialspannungen. In der Regel wird auf die Festigkeit der Materialien geachtet Annahme ihrer gleichmäßigen Verteilung über die Breite des Abschnitts.
Zur Bestimmung der Größe der Scherspannungen an einem beliebigen Punkt im Querschnitt, der sich in einiger Entfernung befindet y 0 Zeichnen Sie von der neutralen X-Achse aus eine Ebene parallel zur neutralen Ebene (3-3) durch diesen Punkt und entfernen Sie das abgeschnittene Element. Wir werden die Spannung bestimmen, die über den ABCD-Bereich wirkt. 
Projizieren wir alle Kräfte auf die Z-Achse
Die Resultierende der inneren Längskräfte entlang der rechten Seite ist gleich:
Wo A 0 – Fläche der Fassadenkante, S x 0 – statisches Moment des abgeschnittenen Teils relativ zur X-Achse. Ebenso auf der linken Seite:
Beide Ergebnisse gerichtet auf gegenseitig,
da das Element in ist komprimiert Strahlbereich. Ihr Unterschied wird durch die Tangentialkräfte am unteren Rand von 3-3 ausgeglichen.
Tun wir mal so Schubspannung τüber die Breite des Balkenquerschnitts verteilt b gleichmäßig. Diese Annahme ist umso wahrscheinlicher, je kleiner die Breite im Vergleich zur Höhe des Abschnitts ist. Dann Resultierende der Tangentialkräfte dT gleich dem Spannungswert multipliziert mit der Gesichtsfläche: 
Lasst uns jetzt komponieren Gleichgewichtsgleichung Σz=0: 
oder woher
Lass uns erinnern unterschiedliche Abhängigkeiten, wonach 
Dann erhalten wir die Formel:
Diese Formel heißt Formeln. Diese Formel wurde 1855 erhalten. Hier S x 0 – statisches Moment eines Teils des Querschnitts, auf einer Seite der Schicht liegen, in der die Schubspannungen bestimmt werden, I x – Trägheitsmoment der gesamte Querschnitt, b – Abschnittsbreite an der Stelle, an der die Schubspannung bestimmt wird, Q – Scherkraft im Querschnitt.
— Biegefestigkeitszustand, Wo
- maximales Moment (Modulo) aus dem Diagramm der Biegemomente; 
- axiales Widerstandsmoment des Abschnitts, geometrisch charakteristisch; - zulässige Spannung (σ zul)
- maximale Normalspannung.
Erfolgt die Berechnung gem Grenzzustandsmethode, dann gehen wir statt der zulässigen Spannung in die Berechnung ein Bemessungswiderstand des Materials R.
Arten von Biegefestigkeitsberechnungen
1. Überprüfen Berechnung oder Prüfung der Festigkeit unter Verwendung von Normalspannungen
2. Design Berechnung bzw Auswahl des Abschnitts 
3. Definition zulässig laden (Definition Tragfähigkeit und/oder betriebsbereit Träger Fähigkeiten) 
Bei der Ableitung der Formel zur Berechnung der Normalspannungen berücksichtigen wir den Biegefall, bei dem die Schnittgrößen in den Balkenabschnitten nur auf reduziert werden Biegemoment, A Die Scherkraft ist Null. Dieser Biegefall wird aufgerufen reines Biegen. Betrachten Sie den mittleren Abschnitt des Trägers, der einer reinen Biegung unterliegt.
Bei Belastung biegt sich der Balken so, dass er Die unteren Fasern verlängern sich und die oberen Fasern verkürzen sich.
Da ein Teil der Fasern des Balkens gedehnt und ein Teil komprimiert wird, kommt es zum Übergang von Spannung zu Kompression reibungslos, ohne Sprünge, V Durchschnitt Ein Teil des Balkens befindet sich eine Schicht, deren Fasern sich nur biegen, aber weder Zug noch Druck erfahren. Diese Schicht heißt neutral Schicht. Die Linie, entlang der die neutrale Schicht den Querschnitt des Balkens schneidet, wird aufgerufen neutrale Linie oder neutrale Achse Abschnitte. Auf der Achse des Balkens sind neutrale Linien aufgereiht. Neutrale Linie ist die Zeile, in der Normalspannungen sind Null.
Die auf der Seitenfläche des Strahls senkrecht zur Achse gezeichneten Linien bleiben erhalten Wohnung beim Biegen. Diese experimentellen Daten ermöglichen es, die Schlussfolgerungen der Formeln zu begründen Hypothese ebener Schnitte (Vermutung). Nach dieser Hypothese sind die Abschnitte des Balkens vor dem Biegen flach und senkrecht zu seiner Achse, bleiben flach und verlaufen beim Biegen senkrecht zur gekrümmten Achse des Balkens.
Annahmen zur Ableitung von Normalspannungsformeln: 1) Die Hypothese ebener Schnitte ist erfüllt. 2) Längsfasern drücken nicht aufeinander (Nicht-Druck-Hypothese) und daher befindet sich jede der Fasern in einem Zustand einachsiger Spannung oder Kompression. 3) Verformungen von Fasern hängen nicht von ihrer Position entlang der Querschnittsbreite ab. Folglich bleiben die Normalspannungen, die sich entlang der Höhe des Abschnitts ändern, entlang der Breite gleich. 4) Der Balken hat mindestens eine Symmetrieebene und alle äußeren Kräfte liegen in dieser Ebene. 5) Das Material des Balkens gehorcht dem Hookeschen Gesetz und der Elastizitätsmodul bei Zug und Druck ist gleich. 6) Die Beziehungen zwischen den Abmessungen des Balkens sind so, dass er unter bestimmten Bedingungen funktioniert flache Biegung kein Verziehen oder Einrollen.
Betrachten wir einen Balken mit beliebigem Querschnitt, aber einer Symmetrieachse. 
Biegemoment repräsentiert resultierendes Moment der inneren Normalkräfte, entsteht auf unendlich kleinen Flächen und kann ausgedrückt werden in Integral bilden: 
(1), wobei y der Arm der Elementarkraft relativ zur x-Achse ist
Formel (1) drückt aus statisch Seite des Problems der Biegung eines geraden Balkens, jedoch entlang dieser mit einem bekannten Biegemoment Es ist unmöglich, Normalspannungen zu bestimmen, bis das Gesetz ihrer Verteilung festgelegt ist.
Wählen wir die Balken im Mittelteil aus und überlegen wir Abschnitt der Länge dz, unterliegen einer Biegung. Lassen Sie es uns im vergrößerten Maßstab darstellen.
Abschnitte, die den Bereich dz begrenzen, parallel zueinander, bis sie verformt werden, und nach Aufbringen der Last drehen sich um einen Winkel um ihre neutralen Linien . Die Länge des Fasersegments der neutralen Schicht ändert sich nicht. und wird gleich sein: 
, wo ist es Krümmungsradius die gekrümmte Achse des Balkens. Aber jede andere Faser liegt niedriger oder höher neutrale Schicht, wird seine Länge ändern. Rechnen wir relative Dehnung von Fasern, die sich im Abstand y von der neutralen Schicht befinden. Die relative Dehnung ist das Verhältnis der absoluten Verformung zur ursprünglichen Länge, dann:
Reduzieren wir um und bringen ähnliche Begriffe mit, dann erhalten wir: (2) Diese Formel drückt aus geometrisch Seite des reinen Biegeproblems: Die Verformungen der Fasern sind direkt proportional zu ihren Abständen zur neutralen Schicht.
Kommen wir nun zu betont, d.h. wir werden darüber nachdenken körperlich Seite der Aufgabe. gemäß Annahme ohne Druck Wir verwenden Fasern unter axialem Zug-Druck: dann unter Berücksichtigung der Formel (2)
wir haben 
(3),
diese. normaler Stress beim Biegen entlang der Profilhöhe linear verteilt. An den äußersten Fasern erreichen die Normalspannungen ihren Maximalwert und im Schwerpunkt des Abschnitts sind sie gleich Null. Lasst uns ersetzen (3)
in die Gleichung ein (1)
und nimm den Bruch aus dem Integralzeichen als konstanter Wert, dann haben wir 
. Aber der Ausdruck ist axiales Trägheitsmoment des Abschnitts relativ zur x-Achse - Ich x.
Seine Dimension cm 4, m 4
Dann 
,Wo 
(4) ,wo ist die Krümmung der gekrümmten Achse des Balkens und die Steifigkeit des Balkenabschnitts beim Biegen.
Ersetzen wir den resultierenden Ausdruck Krümmung (4) in den Ausdruck bringen (3)
und wir bekommen Formel zur Berechnung der Normalspannungen an jedem Punkt im Querschnitt: 
(5)
Das. maximal Spannungen entstehen an den Punkten, die am weitesten von der neutralen Linie entfernt sind. Attitüde (6)
angerufen axiales Moment des Abschnittswiderstands. Seine Dimension cm 3, m 3. Das Widerstandsmoment charakterisiert den Einfluss der Form und Abmessungen des Querschnitts auf die Größe der Spannungen.
Dann maximale Spannungen: 
(7)
Biegefestigkeitsbedingung: (8)
Wenn eine Querbiegung auftritt nicht nur Normal-, sondern auch Schubspannungen, Weil verfügbar Scherkraft. Scherbeanspruchung erschweren das Bild der Verformung, sie führen zu Krümmung Querschnitte des Balkens, was zu die Hypothese der ebenen Schnitte wird verletzt. Untersuchungen zeigen jedoch, dass durch Scherspannungen Verformungen entstehen leicht wirken sich auf die nach der Formel berechneten Normalspannungen aus (5) . Somit kommt es bei der Ermittlung von Normalspannungen zu Querbiegung Die Theorie der reinen Biegung ist durchaus anwendbar.
Neutrale Linie. Frage zur Position der neutralen Linie.
Beim Biegen entsteht keine Längskraft, wir können also schreiben 
Ersetzen wir hier die Formel für Normalspannungen (3)
und wir bekommen 
Da der Längselastizitätsmodul des Balkenmaterials ungleich Null ist und die gekrümmte Achse des Balkens einen endlichen Krümmungsradius aufweist, bleibt die Annahme, dass dieses Integral gleich Null ist statisches Flächenmoment Querschnitt des Strahls relativ zur neutralen Linienachse x 
, und da ist sie gleich Null, dann verläuft die Neutrallinie durch den Schwerpunkt des Abschnitts.
Die Bedingung (Fehlen eines Moments der Schnittgrößen relativ zur Feldlinie) ergibt 
oder unter Berücksichtigung (3)
. Aus den gleichen Gründen (siehe oben) 
. Im Integranden - Das Zentrifugalträgheitsmoment des Abschnitts relativ zur x- und y-Achse ist Null, was bedeutet, dass diese Achsen sind Haupt und Zentral und schminken gerade Ecke. Somit, Die Kraft- und Neutrallinien in einer geraden Biegung stehen senkrecht zueinander.
Nach der Installation neutrale Linienposition, einfach zu bauen Normalspannungsdiagramm entlang der Abschnittshöhe. Ihr linear Charakter wird bestimmt Gleichung ersten Grades.
Die Art des Diagramms σ für symmetrische Abschnitte relativ zur Neutrallinie, M<0
Durch die Berechnung eines Balkens zum Biegen „manuell“ auf altmodische Weise können Sie einen der wichtigsten, schönsten und eindeutig mathematisch verifizierten Algorithmen in der Festigkeitslehre von Materialien erlernen. Mithilfe zahlreicher Programme wie „Eingabe der Ausgangsdaten...“
... – get the answer“ ermöglicht es dem modernen Ingenieur heute, viel schneller zu arbeiten als seine Vorgänger vor hundert, fünfzig und sogar zwanzig Jahren. Bei diesem modernen Ansatz ist der Ingenieur jedoch gezwungen, den Autoren des Programms vollkommen zu vertrauen, und mit der Zeit verliert er das Gefühl für die „physikalische Bedeutung“ der Berechnungen. Aber die Autoren des Programms sind Menschen, und Menschen neigen dazu, Fehler zu machen. Wäre dies nicht der Fall, gäbe es nicht für fast jede Software zahlreiche Patches, Releases, „Patches“. Daher denke ich, dass jeder Ingenieur in der Lage sein sollte, die Berechnungsergebnisse manchmal „manuell“ zu überprüfen.
Eine Hilfe (Spickzettel, Memo) zur Berechnung von Trägern für die Biegung finden Sie unten in der Abbildung.
Versuchen wir es anhand eines einfachen Alltagsbeispiels. Nehmen wir an, ich habe beschlossen, in meiner Wohnung eine Reckstange zu bauen. Der Standort wurde bestimmt – ein Korridor mit einer Breite von einem Meter und zwanzig Zentimetern. An gegenüberliegenden Wänden in der erforderlichen Höhe einander gegenüber befestige ich sicher die Halterungen, an denen der Querträger befestigt wird – eine Stange aus St3-Stahl mit einem Außendurchmesser von zweiunddreißig Millimetern. Hält dieser Balken mein Gewicht und die zusätzlichen dynamischen Belastungen, die während der Übungen entstehen?
Wir zeichnen ein Diagramm zur Berechnung eines Balkens zum Biegen. Offensichtlich ist die gefährlichste Methode zum Aufbringen einer externen Last, wenn ich anfange, mich hochzuziehen und eine Hand in der Mitte der Stange einzuhaken.
Ausgangsdaten:
F1 = 900 n – auf den Balken wirkende Kraft (mein Gewicht) ohne Berücksichtigung der Dynamik
d = 32 mm – Außendurchmesser des Stabes, aus dem der Balken besteht
E = 206000 n/mm^2 - Elastizitätsmodul des Stahlträgermaterials St3
[σi] = 250 n/mm^2 - zulässige Biegespannungen (Streckgrenze) für den Stahlträgerwerkstoff St3
Randbedingungen:
Мx (0) = 0 n*m – Moment am Punkt z = 0 m (erste Stütze)
Mx (1.2) = 0 n*m – Moment am Punkt z = 1,2 m (zweite Stütze)
V (0) = 0 mm – Durchbiegung im Punkt z = 0 m (erste Stütze)
V (1,2) = 0 mm – Durchbiegung im Punkt z = 1,2 m (zweite Stütze)
Berechnung:
1. Berechnen wir zunächst das Trägheitsmoment Ix und das Widerstandsmoment Wx des Balkenabschnitts. Sie werden uns bei weiteren Berechnungen nützlich sein. Für einen kreisförmigen Querschnitt (das ist der Querschnitt einer Stange):
Ix = (π*d^4)/64 = (3,14*(32/10)^4)/64 = 5,147 cm^4
Wx = (π*d^3)/32 = ((3,14*(32/10)^3)/32) = 3,217 cm^3
2. Wir erstellen Gleichgewichtsgleichungen, um die Reaktionen der Stützen R1 und R2 zu berechnen:
Qy = -R1+F1-R2 = 0
Mx (0) = F1*(0-b2) -R2*(0-b3) = 0
Aus der zweiten Gleichung: R2 = F1*b2/b3 = 900*0,6/1,2 = 450 n
Aus der ersten Gleichung: R1 = F1-R2 = 900-450 = 450 n
3. Ermitteln wir den Drehwinkel des Balkens im ersten Träger bei z = 0 aus der Durchbiegungsgleichung für den zweiten Abschnitt:
V (1.2) = V (0)+U (0)*1.2+(-R1*((1.2-b1)^3)/6+F1*((1.2-b2)^3)/6)/
U (0) = (R1*((1.2-b1)^3)/6 -F1*((1.2-b2)^3)/6)/(E*Ix)/1,2 =
= (450*((1.2-0)^3)/6 -900*((1.2-0.6)^3)/6)/
/(206000*5,147/100)/1,2 = 0,00764 rad = 0,44˚
4.
Wir stellen Gleichungen zur Erstellung von Diagrammen für den ersten Abschnitt auf (0 Scherkraft: Qy(z) = -R1 Biegemoment: Mx (z) = -R1*(z-b1) Drehwinkel: Ux (z) = U (0)+(-R1*((z-b1)^2)/2)/(E*Ix) Ablenkung: Vy (z) = V (0)+U (0)*z+(-R1*((z-b1)^3)/6)/(E*Ix) z = 0 m: Qy(0) = -R1 = -450 n Ux(0) = U(0) = 0,00764 rad Vy (0) = V (0) = 0 mm z = 0,6 m: Qy(0,6) = -R1 = -450 n Mx (0,6) = -R1*(0,6-b1) = -450*(0,6-0) = -270 n*m Ux (0,6) = U (0)+(-R1*((0,6-b1)^2)/2)/(E*Ix) = 0,00764+(-450*((0,6-0)^2)/2)/(206000*5,147/100) = 0 rad Vy (0,6) = V (0)+U (0)*0,6+(-R1*((0,6-b1)^3)/6)/(E*Ix) = 0+0,00764*0,6+(-450*((0,6-0)^3)/6)/ (206000*5,147/100) = 0,003 m Der Balken wird sich unter dem Gewicht meines Körpers in der Mitte um 3 mm biegen. Ich denke, das ist eine akzeptable Abweichung. 5.
Wir schreiben die Diagrammgleichungen für den zweiten Abschnitt (b2 Querkraft: Qy (z) = -R1+F1 Biegemoment: Mx (z) = -R1*(z-b1)+F1*(z-b2) Drehwinkel: Ux (z) = U (0)+(-R1*((z-b1)^2)/2+F1*((z-b2)^2)/2)/(E*Ix) Durchbiegung: Vy (z) = V (0)+U (0)*z+(-R1*((z-b1)^3)/6+F1*((z-b2)^3)/6)/( E*Ix) z = 1,2 m: Qy (1,2) = -R1+F1 = -450+900 = 450 n Mx (1.2) = 0 n*m Ux (1,2) = U (0)+(-R1*((1,2-b1)^2)/2+F1*((1,2-b2)^2)/2)/(E* Ix) = 0,00764+(-450*((1,2-0)^2)/2+900*((1,2-0,6)^2)/2)/ /(206000*5,147/100) = -0,00764 rad Vy (1,2) = V (1,2) = 0 m 6.
Wir erstellen Diagramme anhand der oben erhaltenen Daten. 7.
Wir berechnen die Biegespannungen im am stärksten belasteten Abschnitt – in der Mitte des Trägers – und vergleichen sie mit den zulässigen Spannungen: σi = Mx max/Wx = (270*1000)/(3,217*1000) = 84 n/mm^2 σi = 84 n/mm^2< [σи] = 250 н/мм^2 Bezüglich der Biegefestigkeit ergab die Berechnung einen dreifachen Sicherheitsspielraum – der Reck kann sicher aus einem vorhandenen Stab mit einem Durchmesser von zweiunddreißig Millimetern und einer Länge von eintausendzweihundert Millimetern hergestellt werden. So können Sie nun ganz einfach einen Balken zum Biegen „manuell“ berechnen und mit den Ergebnissen vergleichen, die Sie bei der Berechnung mit einem der zahlreichen im Internet vorgestellten Programme erhalten haben. Ich bitte diejenigen, die die Arbeit des Autors respektieren, Artikelankündigungen zu abonnieren.
88 Kommentare zu „Berechnung von Balken zum Biegen – „manuell“!“ Bei der Berechnung der Festigkeit von Biegeelementen von Bauwerken wird die Grenzzustandsberechnungsmethode verwendet. In den meisten Fällen sind Normalspannungen in Querschnitten von vorrangiger Bedeutung für die Beurteilung der Festigkeit von Trägern und Rahmen. In diesem Fall sollten die höchsten Normalspannungen, die in den äußersten Fasern des Trägers wirken, einen bestimmten zulässigen Wert für ein bestimmtes Material nicht überschreiten. Bei der Grenzzustandsberechnung wird dieser Wert gleich dem Bemessungswiderstand angenommen R, multipliziert mit dem Betriebsbedingungenkoeffizienten im Dorf Die Festigkeitsbedingung hat folgende Form: Werte R Und Ja für verschiedene Materialien sind im SNiP für Baukonstruktionen angegeben. Bei Trägern aus Kunststoff, die Zug und Druck gleichermaßen standhalten, empfiehlt sich die Verwendung von Profilen mit zwei Symmetrieachsen. In diesem Fall wird die Festigkeitsbedingung (7.33) unter Berücksichtigung der Formel (7.19) in das Formular geschrieben Manchmal werden aus statischen Gründen Träger mit asymmetrischem Querschnitt wie T-Träger, I-Träger mit mehreren Flanschen usw. verwendet. In diesen Fällen wird die Festigkeitsbedingung (7.33) unter Berücksichtigung von (7.17) in die Form geschrieben In den Formeln (7.34) und (7.35) W z Und WHM- Schnittwiderstandsmomente relativ zur neutralen Achse Oz„ Mnb ist das größte Biegemoment in absoluten Werten aufgrund der Einwirkung von Bemessungslasten, d. h. unter Berücksichtigung des Lastzuverlässigkeitskoeffizienten y^. Der Abschnitt des Balkens, in dem der größte Absolutwert des Biegemoments wirkt, wird aufgerufen gefährlicher Abschnitt. Bei der Berechnung der Festigkeit biegebeanspruchter Strukturelemente werden folgende Probleme gelöst: Überprüfung der Stärke des Balkens; Auswahl des Abschnitts; Bestimmung der Tragfähigkeit (Belastbarkeit) des Trägers, diese. Ermittlung von Belastungswerten, bei denen die höchsten Spannungen im gefährlichen Abschnitt des Trägers den Wert nicht überschreiten y c R. Die Lösung des ersten Problems besteht darin, die Einhaltung der Festigkeitsbedingungen bei bekannten Belastungen, die Form und Abmessungen des Abschnitts sowie die Eigenschaften des Materials zu überprüfen. Die Lösung des zweiten Problems besteht darin, die Abmessungen eines Abschnitts einer bestimmten Form unter bekannten Belastungen und Materialeigenschaften zu bestimmen. Zunächst wird aus den Festigkeitsbedingungen (7.34) bzw. (7.35) der Wert des erforderlichen Widerstandsmoments ermittelt und dann werden die Abschnittsabmessungen festgelegt. Bei Walzprofilen (I-Trägern, Kanälen) wird der Querschnitt nach Widerstandsmoment entsprechend dem Sortiment ausgewählt. Für nicht gewalzte Profile werden charakteristische Profilabmessungen festgelegt. Bei der Lösung des Problems, die Tragfähigkeit eines Balkens zu bestimmen, wird zunächst aus den Festigkeitsbedingungen (7.34) oder (7.35) der Wert des größten berechneten Biegemoments mithilfe der Formel ermittelt Anschließend wird das Biegemoment in einem gefährlichen Abschnitt durch die auf den Balken ausgeübten Lasten ausgedrückt und aus dem resultierenden Ausdruck werden die entsprechenden Lastwerte ermittelt. Zum Beispiel für einen Stahl-I-Träger 130, der in Abb. 7.47 Uhr, um R= 210 MPa, y c = 0,9, W z= 472 cm 3 finden wir Aus dem Diagramm der Biegemomente finden wir Reis. 7.47 Bei Balken, die mit großen konzentrierten Kräften belastet sind und sich in der Nähe der Stützen befinden (Abb. 7.48), kann das Biegemoment M nb relativ klein sein und die Querkraft 0 nb im Absolutwert erheblich sein. In diesen Fällen ist es notwendig, die Festigkeit des Balkens anhand der höchsten Tangentialspannungen tnb zu überprüfen. Die Festigkeitsbedingung für Tangentialspannungen kann in der Form geschrieben werden Wo R s - Bemessungswiderstand des Trägermaterials bei Scherung. Werte R s für grundlegende Baustoffe sind in den entsprechenden Abschnitten von SNiP angegeben. In den Stegen von I-Trägern, insbesondere in den dünnen Stegen von Verbundträgern, können Schubspannungen erhebliche Werte erreichen. Die Berechnung der Schubspannungsfestigkeit kann für Holzbalken von entscheidender Bedeutung sein, da Holz einem Abplatzen entlang der Faserrichtung nicht besonders gut standhält. So beträgt beispielsweise für Kiefer der berechnete Zug- und Druckwiderstand beim Biegen R= 13 MPa und beim Scheren entlang der Fasern RCK= 2,4 MPa. Eine solche Berechnung ist auch bei der Beurteilung der Festigkeit der Verbindungselemente von Verbundträgern – Schweißnähte, Bolzen, Nieten, Dübel usw. – erforderlich. Die Bedingung für die Scherfestigkeit entlang der Fasern für einen Holzbalken mit rechteckigem Querschnitt kann unter Berücksichtigung der Formel (7.27) in das Formular geschrieben werden Beispiel 7.15. Für den in Abb. 7,49, A, Lasst uns Diagramme erstellen Qy Und M v Wählen wir einen Trägerabschnitt in Form eines gewalzten I-Trägers aus Stahl aus und zeichnen wir Diagramme c x und t in Abschnitten mit dem größten Qy Und Mz. Ladungssicherheitsfaktor y f = 1.2, Bemessungswiderstand R= 210 MPa = 21 kN/cm 2, Koeffizient der Betriebsbedingungen y c = 1,0. Wir beginnen die Berechnung mit der Ermittlung der Stützreaktionen: Berechnen wir die Werte Qy Und Mz in charakteristischen Abschnitten des Balkens. Querkräfte innerhalb jedes Balkenabschnitts sind konstante Werte und weisen Sprünge in den Abschnitten unter der Kraft und an der Stütze auf IN. Biegemomente variieren linear. Diagramme Qy Und Mz sind in Abb. dargestellt. 7,49, b, c. Der gefährliche Abschnitt liegt in der Mitte der Trägerspannweite, wo das Biegemoment am größten ist. Berechnen wir den berechneten Wert des größten Biegemoments: Das erforderliche Widerstandsmoment beträgt Entsprechend dem Sortiment übernehmen wir Abschnitt 127 und schreiben die notwendigen geometrischen Eigenschaften des Abschnitts auf (Abb. 7.50, A): Berechnen wir die Werte der höchsten Normalspannungen im gefährlichen Abschnitt des Balkens und überprüfen wir seine Festigkeit: Die Festigkeit des Balkens ist gewährleistet. Tangentialspannungen haben die größten Werte in dem Abschnitt des Balkens, in dem die Querkraft mit der größten absoluten Größe wirkt (2 nb = 35 kN). Bemessungswert der Scherkraft Berechnen wir die Werte der Tangentialspannungen in der I-Trägerwand auf der Ebene der neutralen Achse und auf der Ebene der Schnittstelle zwischen Wand und Flanschen: Diagramme c x und x, im Abschnitt l: = 2,4 m (rechts) sind in Abb. dargestellt. 7,50, b, c. Das Vorzeichen der Tangentialspannungen wird als negativ angenommen, da es dem Vorzeichen der Scherkraft entspricht. Beispiel 7.16. Für einen Holzbalken mit rechteckigem Querschnitt (Abb. 7.51, A) Lasst uns Diagramme erstellen Q Und Mz, Bestimmen Sie die Höhe des Abschnitts H aus dem Kraftzustand, Einnahme R = = 14 MPa, yy= 1,4 und y c = 1,0 und überprüfen Sie die Festigkeit des Balkens auf Scherung auf der neutralen Schicht RCK= 2,4 MPa. Lassen Sie uns die Reaktionen der Unterstützung ermitteln: Berechnen wir die Werte Q v Und Mz Innerhalb des zweiten Abschnitts wird die Scherkraft Null. Die Position dieses Abschnitts ergibt sich aus der Ähnlichkeit der Dreiecke im Diagramm F y: Berechnen wir in diesem Abschnitt den Extremwert des Biegemoments: Diagramme Qy Und Mz sind in Abb. dargestellt. 7,51, b, c. Der Abschnitt des Trägers, in dem das maximale Biegemoment auftritt, ist gefährlich. Berechnen wir den berechneten Wert des Biegemoments in diesem Abschnitt: Erforderlicher Abschnittsmodul Mit der Formel (7.20) drücken wir das Widerstandsmoment durch die Höhe des Abschnitts aus H und setzen Sie es mit dem erforderlichen Widerstandsmoment gleich: Wir nehmen einen rechteckigen Abschnitt von 12x18 cm und berechnen die geometrischen Eigenschaften des Abschnitts: Lassen Sie uns die höchsten Normalspannungen im gefährlichen Abschnitt des Balkens ermitteln und dessen Festigkeit überprüfen: Die Festigkeitsbedingung ist erfüllt. Um die Scherfestigkeit eines Balkens entlang der Fasern zu überprüfen, müssen die Werte der maximalen Tangentialspannungen im Abschnitt mit dem größten Absolutwert der Querkraft 0 nb = 6 kN ermittelt werden. Der berechnete Wert der Scherkraft in diesem Abschnitt Die maximalen Schubspannungen im Querschnitt wirken auf der Ebene der neutralen Achse. Nach dem Paarungsgesetz wirken sie auch in der neutralen Schicht und bewirken tendenziell eine Verschiebung eines Teils des Strahls relativ zum anderen Teil. Mit der Formel (7.27) berechnen wir den Wert von mmax und prüfen die Scherfestigkeit des Balkens: Die Scherfestigkeitsbedingung ist erfüllt. Beispiel 7.17. Für einen runden Holzbalken (Abb. 7.52, A) Lasst uns Diagramme erstellen Q y n M z n Lassen Sie uns aus der Festigkeitsbedingung den erforderlichen Querschnittsdurchmesser ermitteln. In Berechnungen akzeptieren wir R= 14 MPa, yy = 1,4 und Ja = 1,0. Lassen Sie uns die Reaktionen der Unterstützung ermitteln: Berechnen wir die Werte Q Und M 7 in charakteristischen Abschnitten des Balkens. Diagramme Qy Und Mz sind in Abb. dargestellt. 7,52, b, c. Der Abschnitt über die Unterstützung ist gefährlich IN mit dem absolut größten Biegemoment Mnb = 4 kNm. Der berechnete Wert des Biegemoments in diesem Abschnitt Berechnen wir das erforderliche Widerstandsmoment des Abschnitts: Mit der Formel (7.21) für das Widerstandsmoment eines kreisförmigen Querschnitts ermitteln wir den erforderlichen Durchmesser: Akzeptieren wir D= 16 cm und bestimmen Sie die maximalen Normalspannungen im Balken: Beispiel 7.18.
Bestimmen wir die Tragfähigkeit eines Kastenträgers 120x180x10 mm, belastet gemäß dem Diagramm in Abb. 7,53, A. Lassen Sie uns Diagramme erstellen c x usw. in einem gefährlichen Abschnitt. Trägermaterial - Stahlsorte VStZ, R= 210 MPa = 21 kN/cm2, U/= Du, Wir =°’ 9 - Diagramme Qy Und Mz sind in Abb. dargestellt. 7,53, A. Gefährlich ist der Abschnitt des Trägers in der Nähe der Einbettung, wo das Biegemoment M nb in absoluten Werten am größten ist. - P1 = 3,2 R. Berechnen wir das Trägheitsmoment und das Widerstandsmoment des Kastenprofils: Unter Berücksichtigung der Formel (7.37) und des erhaltenen Wertes für L/nb ermitteln wir den berechneten Wert der Kraft R: Normativer Wert der Kraft Die höchsten Normalspannungen im Balken aufgrund der Bemessungskraft Berechnen wir das statische Moment des halben Abschnitts ^1/2 und das statische Moment der Querschnittsfläche des Flansches S n relativ zur neutralen Achse: Tangentialspannungen auf der Ebene der neutralen Achse und auf der Ebene der Flansch-Wand-Schnittstelle (Abb. 7.53, B) sind gleich: Diagramme Oh Und T äh im Querschnitt nahe der Einbettung sind in Abb. dargestellt. 7,53, in, g. Der Balken ist das Hauptelement der tragenden Struktur der Struktur. Während der Konstruktion ist es wichtig, die Durchbiegung des Balkens zu berechnen. Im realen Bauwesen wird dieses Element durch Windkraft, Belastung und Vibration beeinflusst. Bei Berechnungen ist es jedoch üblich, nur die Querlast oder die aufgebrachte Last zu berücksichtigen, die der Querlast entspricht. Balken im Haus Bei der Berechnung wird der Balken als starr befestigter Stab wahrgenommen, der auf zwei Stützen montiert ist. Bei einer Montage auf drei oder mehr Stützen ist die Berechnung der Durchbiegung aufwändiger und eine Selbstberechnung nahezu unmöglich. Die Hauptlast wird als Summe der Kräfte berechnet, die in Richtung des senkrechten Abschnitts der Struktur wirken. Zur Ermittlung der maximalen Verformung ist ein Bemessungsdiagramm erforderlich, das die Grenzwerte nicht überschreiten sollte. Auf diese Weise können Sie das optimale Material mit der erforderlichen Größe, Querschnitt, Flexibilität und anderen Indikatoren bestimmen. Für den Bau verschiedener Bauwerke werden Balken aus starken und langlebigen Materialien verwendet. Solche Strukturen können sich in Länge, Form und Querschnitt unterscheiden. Am häufigsten werden Holz- und Metallkonstruktionen verwendet. Für das Durchbiegungsberechnungsschema ist das Material des Elements von großer Bedeutung. Die Einzelheiten der Berechnung der Durchbiegung eines Balkens hängen in diesem Fall von der Homogenität und Struktur seines Materials ab. Für den Bau von Privathäusern, Ferienhäusern und anderen Einzelbauten werden am häufigsten Holzbalken verwendet. Für Decken und Böden können Holzkonstruktionen verwendet werden, die im Biegeverfahren arbeiten. Holzboden Berücksichtigen Sie zur Berechnung der maximalen Durchbiegung Folgendes: Die zulässige Durchbiegung des Trägers berücksichtigt die maximale tatsächliche Durchbiegung sowie mögliche zusätzliche Betriebslasten. Nadelholzstrukturen Metallträger haben einen komplexen oder sogar zusammengesetzten Querschnitt und bestehen meist aus mehreren Metallarten. Bei der Berechnung solcher Strukturen muss nicht nur deren Steifigkeit, sondern auch die Festigkeit der Verbindungen berücksichtigt werden. Stahlböden Metallkonstruktionen werden durch die Verbindung verschiedener Arten von gewalztem Metall hergestellt, wobei die folgenden Verbindungsarten verwendet werden: Stahlträger werden am häufigsten für mehrstöckige Gebäude und andere Bauarten verwendet, bei denen eine hohe strukturelle Festigkeit erforderlich ist. In diesem Fall ist bei Verwendung hochwertiger Verbindungen eine gleichmäßig verteilte Belastung des Trägers gewährleistet. Um den Strahl für die Durchbiegung zu berechnen, kann dieses Video helfen:
Um die Festigkeit, Haltbarkeit und Sicherheit der Struktur zu gewährleisten, ist es notwendig, den Durchbiegungswert der Träger bereits in der Entwurfsphase der Struktur zu berechnen. Daher ist es äußerst wichtig, die maximale Durchbiegung des Balkens zu kennen, deren Formel einen Rückschluss auf die Wahrscheinlichkeit der Nutzung einer bestimmten Gebäudestruktur ermöglicht. Mithilfe eines Steifigkeitsberechnungsschemas können Sie die maximalen Änderungen in der Geometrie des Teils ermitteln. Die Berechnung einer Struktur mithilfe experimenteller Formeln ist nicht immer effektiv. Es wird empfohlen, zusätzliche Koeffizienten zu verwenden, um den erforderlichen Sicherheitsspielraum hinzuzufügen. Das Nichtvorhandensein eines zusätzlichen Sicherheitsspielraums ist einer der größten Konstruktionsfehler, der zur Unmöglichkeit der Nutzung des Gebäudes oder sogar zu schwerwiegenden Folgen führt. Es gibt zwei Hauptmethoden zur Berechnung von Festigkeit und Steifigkeit: Die letzte Methode ist die genaueste und zuverlässigste, da sie hilft, genau zu bestimmen, welcher Belastung der Balken standhalten kann. Berechnung von Balken zur Durchbiegung Um die Biegefestigkeit eines Balkens zu berechnen, wird die Formel verwendet: M ist das maximale Moment, das im Balken auftritt; W n,min – Widerstandsmoment des Abschnitts, der ein Tabellenwert ist oder für jeden Profiltyp separat bestimmt wird. R y ist der Auslegungswiderstand von Stahl beim Biegen. Hängt von der Stahlsorte ab. γ c ist der Betriebszustandskoeffizient, bei dem es sich um einen Tabellenwert handelt. Die Berechnung der Steifigkeit oder Durchbiegung eines Balkens ist recht einfach, sodass auch ein unerfahrener Bauherr die Berechnungen durchführen kann. Um die maximale Durchbiegung genau zu bestimmen, müssen Sie jedoch die folgenden Schritte ausführen: Um ein Berechnungsschema zu erstellen, benötigen Sie folgende Daten: Wenn ein Träger mit zwei Stützen berechnet wird, gilt eine Stütze als starr und die zweite als gelenkig. Um die Steifigkeit zu berechnen, benötigen Sie das Trägheitsmoment des Abschnitts (J) und das Widerstandsmoment (W). Um das Widerstandsmoment eines Abschnitts zu berechnen, verwenden Sie am besten die Formel: Ein wichtiges Merkmal bei der Bestimmung des Trägheits- und Widerstandsmoments eines Abschnitts ist die Ausrichtung des Abschnitts in der Schnittebene. Mit zunehmendem Trägheitsmoment steigt auch der Steifigkeitsindex. Um die Durchbiegung eines Balkens genau zu bestimmen, verwenden Sie am besten diese Formel: q ist eine gleichmäßig verteilte Last; E – Elastizitätsmodul, ein Tabellenwert; l – Länge; I – Trägheitsmoment des Abschnitts. Zur Berechnung der maximalen Belastung müssen statische und periodische Belastungen berücksichtigt werden. Wenn es sich beispielsweise um eine zweistöckige Struktur handelt, ist der Holzbalken ständig der Belastung durch Gewicht, Ausrüstung und Personen ausgesetzt. Für alle Böden sind Durchbiegungsberechnungen erforderlich. Es ist äußerst wichtig, diesen Indikator bei erheblichen externen Belastungen genau zu berechnen. In diesem Fall ist die Verwendung komplexer Formeln nicht erforderlich. Wenn Sie die entsprechenden Koeffizienten verwenden, können die Berechnungen auf einfache Schemata reduziert werden: Wenn Sie diese Methode zur Berechnung der Durchbiegung verwenden, können Sie das Material ignorieren. Daher werden die Berechnungen nicht durch die Werte seiner Hauptmerkmale beeinflusst. Um den Prozess der Berechnung der Steifigkeit eines Balkens und seiner maximalen Durchbiegung zu verstehen, können Sie ein einfaches Berechnungsbeispiel verwenden. Diese Berechnung wird für einen Träger mit folgenden Eigenschaften durchgeführt: Zur Berechnung der maximal zulässigen Belastung wird das Gewicht von Balken, Böden und Stützen berücksichtigt. Es wird außerdem empfohlen, das Gewicht von Möbeln, Geräten, Dekorationen, Personen und anderen schweren Gegenständen zu berücksichtigen, die sich ebenfalls auf die Struktur auswirken. Für die Berechnung benötigen Sie folgende Daten: Um die Berechnung dieses Beispiels zu vereinfachen, können Sie die Masse des Bodens mit 60 kg/m², die Belastung jeder Etage mit 250 kg/m², die Belastung der Trennwände mit 75 kg/m² und das Gewicht eines Meters annehmen Balkengewicht: 18 kg. Bei einem Balkenabstand von 60 cm beträgt der Koeffizient k 0,6. Setzt man alle diese Werte in die Formel ein, erhält man: q = (60 + 250 + 75) * 0,6 + 18 = 249 kg/m. Um das Biegemoment zu berechnen, verwenden Sie die Formel f = (5 / 384) * [(qn * L4) / (E * J)] £ [¦]. Wenn wir die Daten darin einsetzen, erhalten wir f = (5 / 384) * [(qn * L4) / (E * J)] = (5 / 384) * [(249 * 44) / (100.000 * 10)] = 0,13020833 * [(249 * 256) / (100.000 * 10)] = 0,13020833 * (6,3744 / 10.000.000) = 0,13020833 * 0,0000063744 = 0,00083 m = 0,83 cm. Dies ist genau der Indikator für die Durchbiegung, wenn der Balken maximal belastet wird. Diese Berechnungen zeigen, dass es sich bei maximaler Belastung um 0,83 cm verbiegt. Wenn dieser Indikator kleiner als 1 ist, ist die Verwendung bei den angegebenen Belastungen zulässig. Die Verwendung solcher Berechnungen ist eine universelle Methode zur Berechnung der Steifigkeit einer Struktur und des Ausmaßes ihrer Durchbiegung. Es ist ganz einfach, diese Werte selbst zu berechnen. Es reicht aus, die notwendigen Formeln zu kennen und auch die Werte zu berechnen. Einige Daten müssen in einer Tabelle erfasst werden. Bei Berechnungen ist es äußerst wichtig, auf Maßeinheiten zu achten. Wenn der Wert in der Formel in Metern angegeben ist, muss er in diese Form umgerechnet werden. Einfache Fehler wie dieser können Berechnungen unbrauchbar machen. Um die Steifigkeit und maximale Durchbiegung eines Balkens zu berechnen, reicht es aus, die grundlegenden Eigenschaften und Abmessungen des Materials zu kennen. Diese Daten sollten in ein paar einfache Formeln eingefügt werden.Artikel mit ähnlichen Themen
Rezensionen
in charakteristischen Abschnitten des Balkens.
Hölzern
Stahl
Balkenstärke und Steifigkeit
Steifigkeitsberechnung
Berechnung von Trägheitsmomenten und Abschnittswiderständen
Ermittlung der maximalen Belastung und Durchbiegung
Merkmale der Durchbiegungsberechnungen
Beispiel für die Berechnung der Durchbiegung