Flexion transversale directe du sopromat. coude transversal
Lire aussi
Commençons par le cas le plus simple, celui dit flexion pure.
La flexion pure est un cas particulier de flexion, dans lequel dans les sections de la poutre force de cisaillement est égal à zéro. La flexion pure ne peut avoir lieu que lorsque le poids propre de la poutre est si petit que son influence peut être négligée. Pour les poutres sur deux appuis, des exemples de charges qui causent net
courbure, illustrée à la Fig. 88. Sur les sections de ces poutres, où Q \u003d 0 et, par conséquent, M \u003d const; il y a un virage pur.
Les forces dans n'importe quelle section de la poutre en flexion pure sont réduites à une paire de forces dont le plan d'action passe par l'axe de la poutre et le moment est constant.
Les contraintes peuvent être déterminées sur la base des considérations suivantes.
1. Les composantes tangentielles des efforts sur les surfaces élémentaires de la section transversale de la poutre ne peuvent être réduites à un couple d'efforts dont le plan d'action est perpendiculaire au plan de la section. Il s'ensuit que l'effort de flexion dans la section est le résultat d'une action sur des zones élémentaires
seules forces normales, et donc, avec une flexion pure, les contraintes ne sont réduites qu'aux forces normales.
2. Pour que les efforts sur les plates-formes élémentaires soient réduits à seulement quelques forces, il doit y avoir des forces positives et négatives parmi elles. Par conséquent, des fibres de faisceau tendues et comprimées doivent exister.

3. Du fait que les forces dans différentes sections sont les mêmes, les contraintes aux points correspondants des sections sont les mêmes.
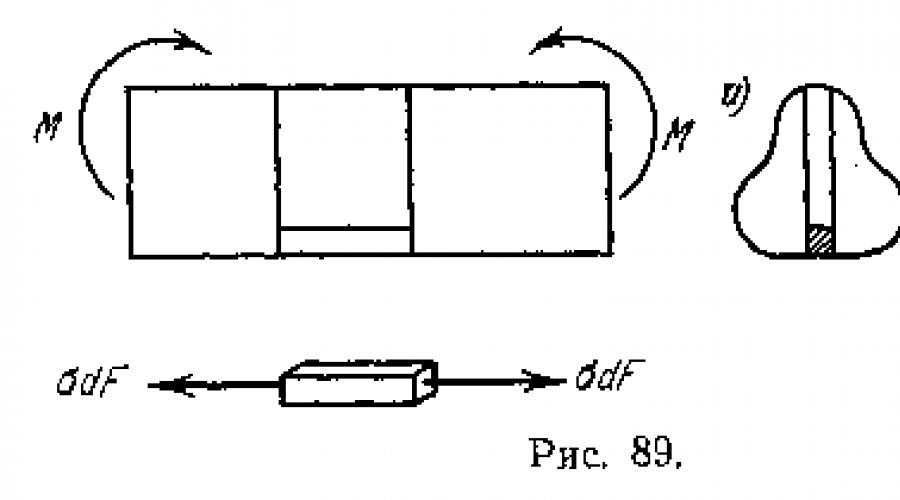
Considérez tout élément près de la surface (Fig. 89, a). Comme aucune force n'est appliquée le long de sa face inférieure, qui coïncide avec la surface de la poutre, il n'y a pas non plus de contraintes sur celle-ci. Par conséquent, il n'y a pas de contraintes sur la face supérieure de l'élément, car sinon l'élément ne serait pas en équilibre Considérant l'élément qui lui est adjacent en hauteur (Fig. 89, b), nous arrivons à

Même conclusion, etc. Il s'ensuit qu'il n'y a pas de contraintes le long des faces horizontales d'aucun élément. Considérant les éléments qui composent la couche horizontale, en commençant par l'élément près de la surface de la poutre (Fig. 90), nous arrivons à la conclusion qu'il n'y a pas de contraintes le long des faces verticales latérales d'aucun élément. Ainsi, l'état de contrainte de tout élément (Fig. 91, a), et à la limite de la fibre, doit être représenté comme indiqué sur la Fig. 91b, c'est-à-dire qu'il peut s'agir soit d'une traction axiale, soit d'une compression axiale.
4. En raison de la symétrie de l'application des forces externes, la section au milieu de la longueur de la poutre après déformation doit rester plate et normale à l'axe de la poutre (Fig. 92, a). Pour la même raison, les sections dans les quarts de la longueur de la poutre restent également plates et normales à l'axe de la poutre (Fig. 92, b), si seules les sections extrêmes de la poutre restent plates et normales à l'axe de la poutre pendant la déformation. Une conclusion similaire est également valable pour les sections en huitièmes de la longueur de la poutre (Fig. 92, c), etc. Par conséquent, si les sections extrêmes de la poutre restent plates pendant la flexion, alors pour toute section, il reste 
il est juste de dire qu'après déformation, il reste plat et normal à l'axe de la poutre courbe. Mais dans ce cas, il est évident que le changement d'allongement des fibres du faisceau le long de sa hauteur doit se produire non seulement de manière continue, mais également de manière monotone. Si nous appelons une couche un ensemble de fibres ayant les mêmes allongements, alors il résulte de ce qui a été dit que les fibres étirées et comprimées du faisceau doivent être situées sur des côtés opposés de la couche dans laquelle les allongements des fibres sont égaux à zéro. Nous appellerons fibres dont les allongements sont égaux à zéro, neutres ; une couche constituée de fibres neutres - une couche neutre ; ligne d'intersection de la couche neutre avec le plan la Coupe transversale poutres - la ligne neutre de cette section. Ensuite, sur la base des considérations précédentes, on peut affirmer qu'avec une flexion pure de la poutre dans chacune de ses sections il existe une ligne neutre qui divise cette section en deux parties (zones) : la zone des fibres tendues (zone tendue) et la zone des fibres comprimées (zone comprimée ). En conséquence, les contraintes de traction normales doivent agir aux points de la zone étirée de la section, les contraintes de compression aux points de la zone comprimée et aux points de la ligne neutre les contraintes sont égales à zéro.
Ainsi, avec une flexion pure d'une poutre de section constante :
1) seules les contraintes normales agissent dans les sections ;
2) toute la section peut être divisée en deux parties (zones) - étirées et comprimées; la limite des zones est la ligne neutre de la section, aux points de laquelle les contraintes normales sont égales à zéro ;
3) tout élément longitudinal de la poutre (à la limite, toute fibre) est soumis à une traction ou compression axiale, de sorte que les fibres adjacentes n'interagissent pas entre elles ;
4) si les sections extrêmes de la poutre lors de la déformation restent plates et normales à l'axe, alors toutes ses sections transversales restent plates et normales à l'axe de la poutre courbe.
Etat de contrainte d'une poutre en flexion pure
Considérons un élément de poutre soumis à une flexion pure, concluant  mesurée entre les sections m-m et n-n, qui sont espacées l'une de l'autre d'une distance dx infiniment petite (Fig. 93). En raison de la disposition (4) du paragraphe précédent, les sections m-m et n-n, qui étaient parallèles avant déformation, après flexion, restant planes, formeront un angle dQ et se couperont le long d'une droite passant par le point C, qui est le centre de fibre neutre en courbure NN. Ensuite, la partie de la fibre AB enserrée entre elles, située à une distance z de la fibre neutre (la direction positive de l'axe z est prise vers la convexité de la poutre lors de la flexion), se transformera en un arc A "B" après déformation Un segment de la fibre neutre O1O2, se transformant en un arc O1O2, il ne changera pas de longueur, tandis que la fibre AB recevra un allongement:
mesurée entre les sections m-m et n-n, qui sont espacées l'une de l'autre d'une distance dx infiniment petite (Fig. 93). En raison de la disposition (4) du paragraphe précédent, les sections m-m et n-n, qui étaient parallèles avant déformation, après flexion, restant planes, formeront un angle dQ et se couperont le long d'une droite passant par le point C, qui est le centre de fibre neutre en courbure NN. Ensuite, la partie de la fibre AB enserrée entre elles, située à une distance z de la fibre neutre (la direction positive de l'axe z est prise vers la convexité de la poutre lors de la flexion), se transformera en un arc A "B" après déformation Un segment de la fibre neutre O1O2, se transformant en un arc O1O2, il ne changera pas de longueur, tandis que la fibre AB recevra un allongement:
avant déformation

après déformation
![]()
où p est le rayon de courbure de la fibre neutre.
Par conséquent, l'allongement absolu du segment AB est
et allongement
Puisque, selon la position (3), la fibre AB est soumise à une traction axiale, puis à une déformation élastique

On en déduit que les contraintes normales sur la hauteur de la poutre sont réparties selon une loi linéaire (Fig. 94). Puisque la force égale de tous les efforts sur toutes les sections élémentaires de la section doit être égale à zéro, alors
d'où, en substituant la valeur de (5.8), on trouve

Mais la dernière intégrale est un moment statique autour de l'axe Oy, qui est perpendiculaire au plan d'action des forces de flexion.

Du fait de son égalité à zéro, cet axe doit passer par le centre de gravité O de la section. Ainsi, la ligne neutre de la section de la poutre est une droite yy, perpendiculaire au plan d'action des efforts de flexion. On l'appelle l'axe neutre de la section de poutre. Ensuite, de (5.8), il résulte que les contraintes aux points situés à la même distance de l'axe neutre sont les mêmes.
Le cas de la flexion pure, dans lequel les forces de flexion agissent dans un seul plan, provoquant une flexion dans ce plan uniquement, est une flexion pure plane. Si le plan nommé passe par l'axe Oz, alors le moment des efforts élémentaires par rapport à cet axe doit être égal à zéro, c'est-à-dire
En substituant ici la valeur de σ de (5.8), on trouve

L'intégrale du côté gauche de cette égalité, comme on le sait, est le moment d'inertie centrifuge de la section autour des axes y et z, de sorte que

Les axes par rapport auxquels le moment d'inertie centrifuge de la section est égal à zéro sont appelés axes principaux d'inertie de cette section. Si, en plus, ils passent par le centre de gravité de la section, alors ils peuvent être appelés les principaux axes centraux d'inertie de la section. Ainsi, avec une flexion pure plane, la direction du plan d'action des efforts de flexion et l'axe neutre de la section sont les principaux axes centraux d'inertie de cette dernière. En d'autres termes, pour obtenir une flexion pure plate d'une poutre, on ne peut lui appliquer arbitrairement une charge : il faut la réduire à des forces agissant dans un plan passant par l'un des axes centraux principaux d'inertie des sections de poutre ; dans ce cas, l'autre axe d'inertie central principal sera l'axe neutre de la section.
Comme on le sait, dans le cas d'une section symétrique par rapport à un axe quelconque, l'axe de symétrie est l'un de ses principaux axes centraux d'inertie. Ainsi, dans ce cas particulier, on obtiendra certainement une flexion pure en appliquant les anacharges appropriées dans le plan passant par l'axe longitudinal de la poutre et l'axe de symétrie de sa section. La droite, perpendiculaire à l'axe de symétrie et passant par le centre de gravité de la section, est l'axe neutre de cette section.
Après avoir établi la position de l'axe neutre, il n'est pas difficile de trouver l'amplitude de la contrainte en tout point de la section. En effet, puisque la somme des moments des forces élémentaires par rapport à l'axe neutre yy doit être égale au moment de flexion, alors
d'où, en substituant la valeur de σ de (5.8), on trouve

Depuis l'intégrale  est. moment d'inertie de la section autour de l'axe y, alors
est. moment d'inertie de la section autour de l'axe y, alors
et de l'expression (5.8) on obtient
Le produit EI Y est appelé raideur en flexion de la poutre.
La plus grande traction et la plus grande valeur absolue les contraintes de compression agissent aux points de la section pour lesquels la valeur absolue de z est la plus grande, c'est-à-dire aux points les plus éloignés de l'axe neutre. Avec les désignations, Fig. 95 ont

La valeur de Jy/h1 est appelée moment de résistance de la section à l'étirement et est notée Wyr ; de même, Jy/h2 est appelé moment de résistance de la section à la compression

et notons Wyc, donc

et donc

Si l'axe neutre est l'axe de symétrie de la section, alors h1 = h2 = h/2 et, par conséquent, Wyp = Wyc, il n'y a donc pas lieu de les distinguer, et ils utilisent la même désignation :
en appelant simplement le module de la section W y. Ainsi, dans le cas d'une section symétrique par rapport à l'axe neutre,
Toutes les conclusions ci-dessus sont obtenues sur la base de l'hypothèse que les sections transversales de la poutre, lorsqu'elles sont pliées, restent plates et normales à son axe (hypothèse des sections plates). Comme indiqué, cette hypothèse n'est valable que si les sections extrêmes (d'extrémité) de la poutre restent plates pendant la flexion. D'autre part, il résulte de l'hypothèse des sections planes que les efforts élémentaires dans de telles sections doivent être répartis selon une loi linéaire. Par conséquent, pour la validité de la théorie de flexion pure obtenue, il est nécessaire que les moments de flexion aux extrémités de la poutre soient appliqués sous la forme d'efforts élémentaires répartis sur la hauteur de la section selon une loi linéaire (Fig. 96), qui coïncide avec la loi de répartition des contraintes le long de la hauteur des poutres de section. Cependant, sur la base du principe de Saint-Venant, on peut affirmer qu'un changement de mode d'application des moments de flexion aux extrémités de la poutre ne provoquera que des déformations locales dont l'effet n'affectera qu'à une certaine distance de celles-ci. extrémités (approximativement égales à la hauteur de la section). Les sections situées dans le reste de la longueur de la poutre resteront planes. Par conséquent, la théorie énoncée de la flexion pure à plat, quelle que soit la méthode d'application des moments de flexion, n'est valable que dans la partie médiane de la longueur de la poutre, située à des distances de ses extrémités approximativement égales à la hauteur de la section. Il en ressort clairement que cette théorie est évidemment inapplicable si la hauteur de la section dépasse la moitié de la longueur ou de la portée de la poutre.
déformation en flexion consiste en la courbure de l'axe de la tige droite ou en la modification de la courbure initiale de la tige droite (Fig. 6.1). Familiarisons-nous avec les concepts de base utilisés lors de l'examen de la déformation en flexion.
Les tiges de flexion sont appelées poutres.
nettoyer appelé un coude, dans lequel le moment de flexion est le seul facteur de force interne qui se produit dans la section transversale de la poutre.
Le plus souvent, dans la section transversale de la tige, parallèlement au moment de flexion, une force transversale se produit également. Un tel virage est dit transversal.
plat (droit) appelé pli lorsque le plan d'action du moment de flexion dans la section transversale passe par l'un des axes centraux principaux de la section transversale.
À virage oblique le plan d'action du moment de flexion coupe la section transversale de la poutre le long d'une ligne qui ne coïncide avec aucun des axes centraux principaux de la section transversale.
Nous commençons l'étude de la déformation en flexion par le cas de la flexion plane pure.
Contraintes et déformations normales en flexion pure.
Comme déjà mentionné, avec une courbure plate pure dans la section transversale, des six facteurs de force internes, seul le moment de flexion est non nul (Fig. 6.1, c):
Des expériences réalisées sur des modèles élastiques montrent que si une grille de lignes est appliquée à la surface du modèle (Fig. 6.1, a), alors avec une flexion pure, elle se déforme comme suit (Fig. 6.1, b):
a) les lignes longitudinales sont courbées le long de la circonférence ;
b) les contours des sections transversales restent plats ;
c) les lignes des contours des sections se coupent partout avec les fibres longitudinales à angle droit.
Sur cette base, on peut supposer qu'en flexion pure, les sections transversales de la poutre restent planes et tournent de sorte qu'elles restent normales à l'axe de flexion de la poutre (hypothèse de section plane en flexion).

Riz. 6.1
En mesurant la longueur des lignes longitudinales (Fig. 6.1, b), on constate que les fibres supérieures s'allongent lors de la déformation en flexion de la poutre et que les fibres inférieures se raccourcissent. Bien entendu, il est possible de trouver de telles fibres dont la longueur reste inchangée. L'ensemble des fibres qui ne changent pas de longueur lorsque la poutre est pliée est appelé couche neutre (n.s.). La couche neutre coupe la section transversale du faisceau selon une droite appelée section de ligne neutre (n. l.).
Pour dériver une formule qui détermine l'amplitude des contraintes normales qui surviennent dans la section transversale, considérez la section de la poutre à l'état déformé et non déformé (Fig. 6.2).

Riz. 6.2
Par deux sections efficaces infinitésimales, on sélectionne un élément de longueur  . Avant de se déformer, la section qui délimite l'élément
. Avant de se déformer, la section qui délimite l'élément  , étaient parallèles les uns aux autres (Fig. 6.2, a), et après déformation, ils s'inclinaient quelque peu, formant un angle
, étaient parallèles les uns aux autres (Fig. 6.2, a), et après déformation, ils s'inclinaient quelque peu, formant un angle  . La longueur des fibres se trouvant dans la couche neutre ne change pas pendant la flexion
. La longueur des fibres se trouvant dans la couche neutre ne change pas pendant la flexion  . Désignons le rayon de courbure de la trace de la couche neutre sur le plan du dessin par la lettre
. Désignons le rayon de courbure de la trace de la couche neutre sur le plan du dessin par la lettre  . Déterminons la déformation linéaire d'une fibre arbitraire
. Déterminons la déformation linéaire d'une fibre arbitraire  , à une distance
, à une distance  de la couche neutre.
de la couche neutre.
La longueur de cette fibre après déformation (longueur d'arc  ) est égal à
) est égal à  . Considérant qu'avant la déformation toutes les fibres avaient la même longueur
. Considérant qu'avant la déformation toutes les fibres avaient la même longueur  , on obtient que l'allongement absolu de la fibre considérée
, on obtient que l'allongement absolu de la fibre considérée
Sa déformation relative 

Il est évident que  , puisque la longueur de la fibre située dans la couche neutre n'a pas changé. Puis après remplacement
, puisque la longueur de la fibre située dans la couche neutre n'a pas changé. Puis après remplacement  on a
on a
 (6.2)
(6.2)
Par conséquent, la déformation longitudinale relative est proportionnelle à la distance de la fibre à l'axe neutre.
Nous introduisons l'hypothèse que les fibres longitudinales ne se pressent pas lors de la flexion. Dans cette hypothèse, chaque fibre se déforme isolément, subissant une simple tension ou compression, dans laquelle  . En tenant compte de (6.2)
. En tenant compte de (6.2)
 , (6.3)
, (6.3)
c'est-à-dire que les contraintes normales sont directement proportionnelles aux distances des points considérés de la section à partir de l'axe neutre.
Nous substituons la dépendance (6.3) dans l'expression du moment de flexion  en coupe (6.1)
en coupe (6.1)
 .
.
Rappelons que l'intégrale  représente le moment d'inertie de la section autour de l'axe
représente le moment d'inertie de la section autour de l'axe 
 .
.
 (6.4)
(6.4)
La dépendance (6.4) est la loi de Hooke en flexion, puisqu'elle relie la déformation (courbure de la couche neutre  ) avec le moment agissant dans la section. Travailler
) avec le moment agissant dans la section. Travailler  est appelée la rigidité de la section en flexion, N m 2.
est appelée la rigidité de la section en flexion, N m 2.
Remplacer (6.4) par (6.3)
 (6.5)
(6.5)
C'est la formule recherchée pour déterminer les contraintes normales en flexion pure de la poutre en tout point de sa section.
Afin d'établir où se trouve la ligne neutre dans la section transversale, nous substituons la valeur des contraintes normales dans l'expression de la force longitudinale  et moment de flexion
et moment de flexion 

Parce que le  ,
,
 ;
;
 (6.6)
(6.6)
 (6.7)
(6.7)
L'égalité (6.6) indique que l'axe  - l'axe neutre de la section - passe par le centre de gravité de la section transversale.
- l'axe neutre de la section - passe par le centre de gravité de la section transversale.
L'égalité (6.7) montre que  et
et  - les grands axes centraux de la section.
- les grands axes centraux de la section.
D'après (6.5), les plus grandes contraintes sont atteintes dans les fibres les plus éloignées de la ligne neutre

Attitude  représente le module de section axiale
représente le module de section axiale  autour de son axe central
autour de son axe central  , moyens
, moyens

Sens  pour les sections les plus simples :
pour les sections les plus simples :
Pour section rectangulaire
 , (6.8)
, (6.8)
où  - côté de la section perpendiculaire à l'axe
- côté de la section perpendiculaire à l'axe  ;
;
 - côté de la section parallèle à l'axe
- côté de la section parallèle à l'axe  ;
;
Pour section ronde
 , (6.9)
, (6.9)
où  est le diamètre de la section circulaire.
est le diamètre de la section circulaire.
La condition de résistance pour les contraintes normales en flexion peut s'écrire
 (6.10)
(6.10)
Toutes les formules obtenues sont obtenues pour le cas de la flexion pure d'une tige droite. L'action de la force transversale conduit au fait que les hypothèses sous-jacentes aux conclusions perdent de leur force. Cependant, la pratique des calculs montre que dans le cas de la flexion transversale des poutres et des cadres, lorsqu'ils sont dans la section, en plus du moment de flexion  il y a aussi une force longitudinale
il y a aussi une force longitudinale  et force de cisaillement
et force de cisaillement  , vous pouvez utiliser les formules données pour la flexion pure. Dans ce cas, l'erreur s'avère insignifiante.
, vous pouvez utiliser les formules données pour la flexion pure. Dans ce cas, l'erreur s'avère insignifiante.
Classification des types de flexion de la tige
pliez appelé ce type de déformation, dans lequel des moments de flexion se produisent dans les sections transversales de la tige. Une tige travaillant en flexion s'appelle rayonner. Si les moments de flexion sont les seuls facteurs de force internes dans les sections transversales, alors la tige subit virage propre. Si des moments de flexion se produisent avec des forces transversales, alors un tel pli est appelé transversal.
Les poutres, les essieux, les arbres et autres détails structurels fonctionnent en flexion.
Introduisons quelques concepts. Le plan passant par l'un des axes centraux principaux de la section et l'axe géométrique de la tige est appelé avion principal. Le plan dans lequel agissent les charges externes, provoquant la flexion de la poutre, est appelé avion électrique. La ligne d'intersection du plan de force avec le plan de la section transversale de la tige est appelée ligne électrique. En fonction de la position relative les plans de puissance et principal du faisceau se distinguent par une courbure droite ou oblique. Si le plan de force coïncide avec l'un des plans principaux, alors la tige subit virage droit(Fig. 5.1, un), s'il ne correspond pas - oblique(Fig. 5.1, b).
Riz. 5.1. Courbure de tige : un- droit; b- oblique
D'un point de vue géométrique, la flexion de la tige s'accompagne d'une modification de la courbure de l'axe de la tige. L'axe initialement rectiligne de la tige devient curviligne lorsqu'elle est pliée. En flexion directe, l'axe de flexion de la tige se situe dans le plan d'effort, en flexion oblique, dans un plan autre que le plan d'effort.
En observant la flexion d'une tige de caoutchouc, on peut remarquer qu'une partie de ses fibres longitudinales est étirée, tandis que l'autre partie est comprimée. Évidemment, entre les fibres étirées et comprimées de la tige, il y a une couche de fibres qui ne subit ni tension ni compression, la soi-disant couche neutre. La ligne d'intersection de la couche neutre de la tige avec le plan de sa section transversale est appelée ligne de section neutre.
En règle générale, les charges agissant sur la poutre peuvent être attribuées à l'un des trois types suivants : forces concentrées R, instants concentrés M intensité des charges réparties c(Fig. 5.2). La partie I de la poutre, située entre les appuis, est appelée envergure, partie II de la poutre, située d'un côté de l'appui, - console.
Lors de la flexion, les tiges sont soumises à un effort transversal ou un moment de flexion. La flexion est dite pure si seul le moment de flexion agit, et transversale si la charge est perpendiculaire à l'axe de la tige. Une poutre (tige) travaillant en flexion est généralement appelée poutre. Les poutres sont les éléments les plus courants des structures et des machines qui prennent les charges d'autres éléments structurels et les transfèrent aux parties qui supportent la poutre (le plus souvent des supports).
Dans les structures de construction et les structures de construction de machines, on trouve le plus souvent les cas suivants de poutres de fixation: porte-à-faux - avec une extrémité pincée (avec un joint rigide), à deux roulements - avec un support articulé-fixe et un support articulé-mobile et poutres multisupports. Si les réactions de support peuvent être trouvées à partir des seules équations statiques, alors les poutres sont dites statiquement déterminées. Si le nombre de réactions de support inconnues est supérieur au nombre d'équations de la statique, alors ces poutres sont dites statiquement indéterminées. Pour déterminer les réactions dans de telles poutres, il est nécessaire de composer des équations supplémentaires - des équations de déplacement. En flexion transversale à plat, toutes les charges externes sont perpendiculaires à l'axe de la poutre.
La détermination des facteurs de force internes agissant dans les sections transversales de la poutre doit commencer par la détermination des réactions d'appui. Après cela, nous utilisons la méthode des sections, coupons mentalement la poutre en deux parties et considérons l'équilibre d'une partie. Nous remplaçons l'interaction des parties de la poutre par des facteurs internes : le moment fléchissant et l'effort transversal.
La force transversale dans la section est égale à la somme algébrique des projections de toutes les forces et le moment de flexion est égal à la somme algébrique des moments de toutes les forces situées d'un côté de la section. Les signes des forces et moments agissants doivent être déterminés conformément aux règles acceptées. Il est nécessaire d'apprendre à déterminer correctement la force résultante et le moment de flexion à partir d'une charge uniformément répartie sur la longueur de la poutre.
Il convient de garder à l'esprit que lors de la détermination des contraintes survenant lors de la flexion, les hypothèses suivantes sont faites: les sections plates avant la flexion restent plates après la flexion (hypothèse des sections plates); les fibres adjacentes longitudinales ne se pressent pas les unes sur les autres ; la relation entre contraintes et déformations est linéaire.
Lors de l'étude de la flexion, il convient de prêter attention à la répartition inégale des contraintes normales dans la section transversale de la poutre. Contraintes normales modification de la hauteur de la section transversale proportionnellement à la distance à l'axe neutre. Vous devriez être en mesure de déterminer les contraintes de flexion, qui dépendent de l'amplitude du moment de flexion effectif M je et module de section en flexion W O(module de section axiale).
Condition de résistance à la flexion : σ = М È / W О £ [σ]. Sens W O dépend de la taille, de la forme et de l'emplacement de la section transversale par rapport à l'axe.
La présence d'un effort transversal agissant sur une poutre est associée à l'apparition de contraintes de cisaillement dans les sections transversales, et, selon la loi d'appariement des contraintes de cisaillement, dans les sections longitudinales. Les contraintes de cisaillement sont déterminées par la formule de D. I. Zhuravsky.
L'effort transversal déplace la section considérée par rapport à la section adjacente. Le moment de flexion, qui consiste en des forces normales élémentaires apparaissant dans la section transversale de la poutre, fait tourner la section par rapport à la section adjacente, ce qui provoque la courbure de l'axe de la poutre, c'est-à-dire sa flexion.
Lorsqu'une poutre subit une flexion pure, un moment de flexion agit sur toute la longueur de la poutre ou dans une section distincte de celle-ci dans chaque section valeur constante, et la force transversale dans n'importe quelle section de cette section est égale à zéro. Dans ce cas, seules les contraintes normales apparaissent dans les sections transversales de la poutre.
Afin d'approfondir phénomènes physiques flexion et dans la méthodologie de résolution des problèmes lors du calcul de la résistance et de la rigidité, il est nécessaire de bien maîtriser les caractéristiques géométriques des sections plates, à savoir: les moments statiques des sections, les moments d'inertie des sections la forme la plus simple et sections complexes, détermination du centre de gravité des figures, moments d'inertie principaux des sections et axes principaux d'inertie, moment d'inertie centrifuge, changement des moments d'inertie lors de la rotation des axes, théorèmes sur le transfert des axes.
Lors de l'étude de cette section, vous devez apprendre à construire correctement des diagrammes de moments de flexion et d'efforts tranchants, à déterminer les sections dangereuses et les contraintes qui y agissent. En plus de déterminer les contraintes, il faut apprendre à déterminer les déplacements (flèches des poutres) lors de la flexion. Pour cela, il est utilisé équation différentielle axe plié de la poutre (ligne élastique), écrit en termes généraux.
Pour déterminer les flèches, l'équation de la droite élastique est intégrée. Dans ce cas, il est nécessaire de déterminer correctement les constantes d'intégration DE et réà partir des conditions d'appui de la poutre (conditions aux limites). Connaître les quantités DE et ré, vous pouvez déterminer l'angle de rotation et de déviation de n'importe quelle section de la poutre. L'étude de la résistance complexe commence généralement par une courbure oblique.
Le phénomène de flexion oblique est particulièrement dangereux pour les tronçons dont les moments d'inertie principaux sont sensiblement différents ; les poutres avec une telle section fonctionnent bien pour la flexion dans le plan de plus grande rigidité, mais même à de petits angles d'inclinaison du plan des forces externes par rapport au plan de plus grande rigidité, des contraintes et des déformations supplémentaires importantes apparaissent dans les poutres. Pour un faisceau section ronde la flexion oblique est impossible, car tous les axes centraux d'une telle section sont principaux et la couche neutre sera toujours perpendiculaire au plan des forces extérieures. La flexion oblique est également impossible pour une poutre carrée.
Lors de la détermination des contraintes en cas de traction ou de compression excentrée, il est nécessaire de connaître la position des axes centraux principaux de la section ; c'est à partir de ces axes que sont mesurées les distances du point d'application de la force et du point de détermination des contraintes.
La force de compression excentrique appliquée peut provoquer des contraintes de traction dans la section transversale de la tige. A cet égard, la compression excentrique est particulièrement dangereuse pour les tiges en matériaux fragiles, qui résistent faiblement aux efforts de traction.
En conclusion, il convient d'étudier le cas de la résistance complexe, lorsque le corps subit plusieurs déformations simultanément : par exemple, flexion avec torsion, traction-compression avec flexion, etc. Il faut garder à l'esprit que les moments de flexion agissant dans des plans différents peuvent s'additionner en tant que vecteurs.
virage droit- il s'agit d'un type de déformation dans lequel deux facteurs de force internes apparaissent dans les sections transversales de la tige : un moment de flexion et une force transversale.
Courbure pure est un cas particulier virage droit, auquel seul un moment de flexion se produit dans les sections transversales de la tige, et la force transversale est égale à zéro.
Exemple de courbure pure - Tracé CD sur la tige UN B. Moment de flexion est la valeur Pennsylvanie paire de forces externes provoquant la flexion. De l'équilibre de la partie de la tige à gauche de la section transversale mn il s'ensuit que les efforts internes répartis sur cette section sont statiquement équivalents au moment M, égal et opposé au moment de flexion Pennsylvanie.
Pour trouver la répartition de ces efforts internes sur la section transversale, il est nécessaire de considérer la déformation de la barre.
Dans le cas le plus simple, la tige présente un plan de symétrie longitudinal et est soumise à l'action de couples d'efforts de flexion extérieurs situés dans ce plan. Ensuite, le virage se produira dans le même plan.
axe de tige nn 1 est une droite passant par les centres de gravité de ses sections transversales.
Soit la section transversale de la tige soit un rectangle. Tracez deux lignes verticales sur ses faces millimètre et pp. Lorsqu'elles sont pliées, ces lignes restent droites et tournent de manière à rester perpendiculaires aux fibres longitudinales de la tige.
Une autre théorie de la flexion est basée sur l'hypothèse que non seulement les lignes millimètre et pp, mais toute la section plane du jonc reste plane après flexion et normale aux fibres longitudinales du jonc. Par conséquent, lors de la flexion, les sections transversales millimètre et pp tourner les uns par rapport aux autres autour d'axes perpendiculaires au plan de pliage (plan de dessin). Dans ce cas, les fibres longitudinales du côté convexe subissent une tension et les fibres du côté concave subissent une compression.
surface neutre est une surface qui ne subit pas de déformation lors de la flexion. (Maintenant, il est situé perpendiculairement au dessin, l'axe déformé de la tige nn 1 appartient à cette surface).
Axe de coupe neutre- c'est l'intersection d'une surface neutre avec n'importe quelle section transversale (maintenant également située perpendiculairement au dessin).
Soit une fibre arbitraire à une distance y d'une surface neutre. ρ est le rayon de courbure de l'axe courbe. Point O est le centre de courbure. Traçons une ligne n 1 s 1 parallèle millimètre.ss 1 est l'allongement absolu de la fibre.
Extension relative ε x fibres
Il s'ensuit que déformation des fibres longitudinales proportionnel à la distance y de la surface neutre et inversement proportionnel au rayon de courbure ρ .
L'allongement longitudinal des fibres du côté convexe de la tige s'accompagne de constriction latérale, et le raccourcissement longitudinal du côté concave - extension latérale, comme dans le cas d'un étirement et d'une contraction simples. De ce fait, l'apparence de toutes les coupes transversales change, les côtés verticaux du rectangle deviennent inclinés. Déformation latérale z:
μ - Coefficient de Poisson.
En raison de cette distorsion, toutes les lignes droites en coupe parallèles à l'axe z, sont courbés de manière à rester perpendiculaires aux côtés de la section. Le rayon de courbure de cette courbe R sera plus que ρ de la même façon que ε x est supérieur en valeur absolue à ε z , et on obtient
Ces déformations des fibres longitudinales correspondent à des contraintes
La tension dans toute fibre est proportionnelle à sa distance par rapport à l'axe neutre. n 1 n 2. Position de l'axe neutre et rayon de courbure ρ sont deux inconnues dans l'équation de σ x - peut être déterminé à partir de la condition que les forces réparties sur toute section transversale forment une paire de forces qui équilibre le moment externe M.
Tout ce qui précède est également vrai si la tige n'a pas de plan de symétrie longitudinal dans lequel le moment de flexion agit, tant que le moment de flexion agit dans le plan axial, qui contient l'un des deux axes principaux la Coupe transversale. Ces avions sont appelés plans de flexion principaux.
Lorsqu'il existe un plan de symétrie et que le moment de flexion agit dans ce plan, la déviation se produit dans celui-ci. Moments d'efforts internes autour de l'axe zéquilibrer le moment extérieur M. Moments d'effort par rapport à l'axe y sont mutuellement détruits.