Courbe transversale plate à courbure droite. Flexion transversale de la tige Détermination des réactions d'appui
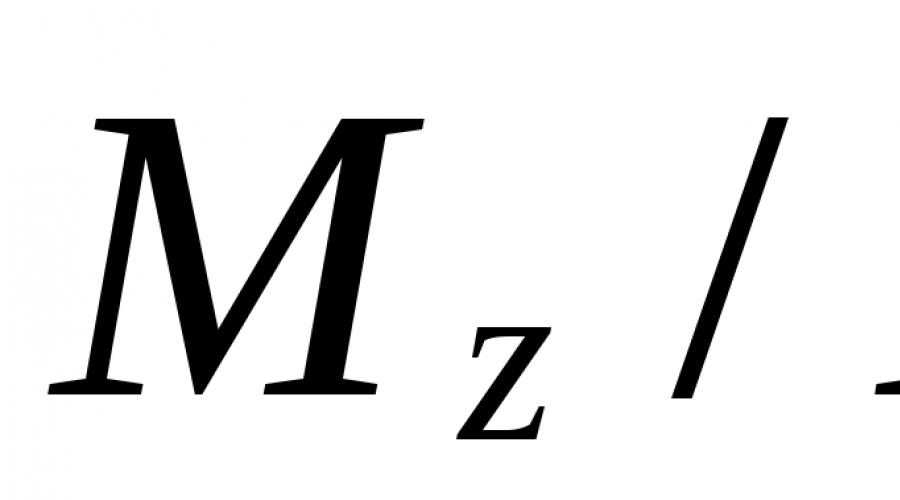
Lire aussi
Courbe transversale droite se produit lorsque toutes les charges sont appliquées perpendiculairement à l'axe de la tige, se trouvent dans le même plan et, de plus, le plan de leur action coïncide avec l'un des principaux axes centraux d'inertie de la section. La flexion transversale droite fait référence à un type simple de résistance et est état de contrainte plat, c'est à dire. deux contraintes principales sont non nulles. Avec ce type de déformation, des efforts internes apparaissent : effort tranchant et moment fléchissant. Un cas particulier de direct flexion transversale est pur virage, avec une telle résistance, il existe des zones de charge à l'intérieur desquelles la force transversale devient nulle et le moment de flexion est non nul. Dans les sections transversales des tiges lors de la flexion transversale directe, des contraintes normales et tangentielles apparaissent. Les contraintes sont fonction de la force interne, dans ce cas les contraintes normales sont fonction du moment de flexion et les contraintes tangentielles sont fonction de la force de cisaillement. Pour la flexion transversale directe, plusieurs hypothèses sont introduites :
1) Les sections transversales de la poutre, plates avant déformation, restent plates et orthogonales à la couche neutre après déformation (hypothèse des sections planes ou hypothèse de J. Bernoulli). Cette hypothèse est satisfaite en flexion pure et est violée lorsque des forces de cisaillement, des contraintes de cisaillement et une déformation angulaire se produisent.
2) Il n'y a pas de pression mutuelle entre les couches longitudinales (hypothèse de non-pression des fibres). De cette hypothèse, il s'ensuit que les fibres longitudinales subissent une tension ou une compression uniaxiale ; par conséquent, en flexion pure, la loi de Hooke est valide.
Une tige en flexion est appelée faisceau. Lors de la flexion, une partie des fibres s'étire, l'autre partie se contracte. La couche de fibres située entre les fibres étirées et comprimées est appelée couche neutre, il passe par le centre de gravité des sections. La ligne de son intersection avec la section transversale de la poutre est appelée axe neutre. Sur la base des hypothèses introduites pour la flexion pure, une formule a été obtenue pour déterminer stress normal, qui est également utilisé pour le pliage transversal direct. La contrainte normale peut être trouvée à l'aide de la relation linéaire (1), dans laquelle le rapport entre le moment de flexion et le moment d'inertie axial (  ) dans une section particulière est une valeur constante et la distance ( oui) le long de l'axe des ordonnées depuis le centre de gravité de la section jusqu'au point de détermination de la contrainte varie de 0 à
) dans une section particulière est une valeur constante et la distance ( oui) le long de l'axe des ordonnées depuis le centre de gravité de la section jusqu'au point de détermination de la contrainte varie de 0 à
 .
.
 .
(1)
.
(1)
Déterminer la contrainte de cisaillement lors de la flexion en 1856. Ingénieur russe et constructeur de ponts D.I. Zhuravsky est devenu accro
 .
(2)
.
(2)
La contrainte de cisaillement dans une section particulière ne dépend pas du rapport entre la force transversale et le moment d'inertie axial (  ), parce que cette valeur ne change pas au sein d'une section, mais dépend du rapport du moment statique de la surface de la partie coupée à la largeur de la section au niveau de la partie coupée (
), parce que cette valeur ne change pas au sein d'une section, mais dépend du rapport du moment statique de la surface de la partie coupée à la largeur de la section au niveau de la partie coupée (  ).
).
En cas de flexion transversale droite mouvements : déviations (v
) et les angles de rotation (Θ
)
. Pour les déterminer, utiliser les équations de la méthode des paramètres initiaux (3), qui sont obtenues en intégrant l'équation différentielle de l'axe courbe de la poutre (  ).
).
Ici v 0 , Θ 0 ,M 0 , Q 0 – les paramètres initiaux, X – distance entre l'origine et la section dans laquelle le déplacement est déterminé , un– la distance entre l'origine des coordonnées et le lieu d'application ou le début du chargement.
Les calculs de résistance et de rigidité sont effectués en utilisant les conditions de résistance et de rigidité. En utilisant ces conditions, vous pouvez résoudre des tâches de vérification (vérifier le respect d'une condition), déterminer la taille coupe transversale ou sélectionnez une valeur acceptable pour le paramètre de charge. Il existe plusieurs conditions de résistance, dont certaines sont indiquées ci-dessous. Condition normale de résistance à la contrainte a la forme :
 ,
(4)
,
(4)
Ici  –
moment résistant de la section par rapport à l'axe z, R – résistance de conception basée sur les contraintes normales.
–
moment résistant de la section par rapport à l'axe z, R – résistance de conception basée sur les contraintes normales.
Condition de résistance pour les contraintes tangentielles ressemble à:
 ,
(5)
,
(5)
ici les notations sont les mêmes que dans la formule de Zhuravsky, et R. s – résistance calculée au cisaillement ou résistance calculée aux contraintes tangentielles.
Condition de force selon la troisième hypothèse de force soit l'hypothèse des plus grandes contraintes tangentielles peut s'écrire sous la forme suivante :
 .
(6)
.
(6)
Conditions de gravité peut être écrit pour déflexions (v ) Et angles de rotation (Θ ) :
où les valeurs de déplacement entre crochets sont valables.
Exemple de réalisation de la tâche individuelle n°4 (terme 2-8 semaines)
Déformation en flexion consiste en une courbure de l'axe d'une tige droite ou en une modification de la courbure initiale d'une tige droite (Fig. 6.1). Faisons connaissance avec les concepts de base utilisés lors de la prise en compte de la déformation par flexion.
Les tiges qui se plient sont appelées poutres.
Faire le ménage appelée flexion, dans laquelle le moment de flexion est le seul facteur de force interne apparaissant dans la section transversale de la poutre.
Le plus souvent, dans la section transversale de la tige, parallèlement au moment de flexion, une force transversale apparaît également. Cette flexion est dite transversale.
Plat (droit) appelée flexion lorsque le plan d'action du moment fléchissant dans la section transversale passe par l'un des axes centraux principaux de la section transversale.
À courbure oblique le plan d'action du moment fléchissant coupe la section transversale de la poutre le long d'une ligne qui ne coïncide avec aucun des axes centraux principaux de la section transversale.
Nous commençons notre étude de la déformation en flexion avec le cas de courbure plate.
Contraintes et déformations normales lors d'une flexion pure.
Comme déjà mentionné, avec une flexion plane pure dans la section transversale, parmi les six facteurs de force internes, seul le moment de flexion est non nul (Fig. 6.1, c) :
Des expériences réalisées sur des modèles élastiques montrent que si une grille de lignes est appliquée à la surface du modèle (Fig. 6.1, a), alors en flexion pure, elle se déforme comme suit (Fig. 6.1, b) :
a) les lignes longitudinales sont courbes le long de la circonférence ;
b) les contours des sections transversales restent plats ;
c) les courbes de niveau des sections coupent partout les fibres longitudinales à angle droit.
Sur cette base, on peut supposer qu'en flexion pure, les sections transversales de la poutre restent plates et tournent de manière à rester normales à l'axe courbe de la poutre (sections plates dans l'hypothèse de flexion).

Riz. 6.1
En mesurant la longueur des lignes longitudinales (Fig. 6.1, b), vous pouvez constater que les fibres supérieures s'allongent lorsque la poutre se plie et que les fibres inférieures se raccourcissent. Bien évidemment, il est possible de trouver des fibres dont la longueur reste inchangée. Un ensemble de fibres qui ne changent pas de longueur lorsqu'une poutre est pliée est appelé couche neutre (n.s.). La couche neutre coupe la section transversale du faisceau en ligne droite, appelée section de ligne neutre (n.l.).
Pour dériver une formule qui détermine l'ampleur des contraintes normales apparaissant dans la section transversale, considérons une section de la poutre dans un état déformé et non déformé (Fig. 6.2).

Riz. 6.2
A l’aide de deux sections efficaces infinitésimales, on sélectionne un élément de longueur  . Avant déformation, sections délimitant l'élément
. Avant déformation, sections délimitant l'élément  , étaient parallèles les uns aux autres (Fig. 6.2, a), et après déformation ils se pliaient légèrement, formant un angle
, étaient parallèles les uns aux autres (Fig. 6.2, a), et après déformation ils se pliaient légèrement, formant un angle  . La longueur des fibres situées dans la couche neutre ne change pas lors du pliage
. La longueur des fibres situées dans la couche neutre ne change pas lors du pliage  . Notons le rayon de courbure de la trace de la couche neutre sur le plan de dessin par la lettre
. Notons le rayon de courbure de la trace de la couche neutre sur le plan de dessin par la lettre  . Déterminons la déformation linéaire d'une fibre arbitraire
. Déterminons la déformation linéaire d'une fibre arbitraire  , situé à distance
, situé à distance  de la couche neutre.
de la couche neutre.
La longueur de cette fibre après déformation (longueur d'arc  ) est égal à
) est égal à  . Considérant qu'avant déformation toutes les fibres avaient la même longueur
. Considérant qu'avant déformation toutes les fibres avaient la même longueur  , on constate que l'allongement absolu de la fibre considérée
, on constate que l'allongement absolu de la fibre considérée
Sa déformation relative 

Il est évident que  , puisque la longueur de la fibre située dans la couche neutre n'a pas changé. Puis après substitution
, puisque la longueur de la fibre située dans la couche neutre n'a pas changé. Puis après substitution  on a
on a
 (6.2)
(6.2)
Par conséquent, la déformation longitudinale relative est proportionnelle à la distance entre la fibre et l’axe neutre.
Introduisons l'hypothèse selon laquelle lors de la flexion, les fibres longitudinales ne se pressent pas les unes sur les autres. Dans cette hypothèse, chaque fibre est déformée isolément, subissant une simple tension ou compression, dans laquelle  . Prise en compte (6.2)
. Prise en compte (6.2)
 , (6.3)
, (6.3)
c'est-à-dire que les contraintes normales sont directement proportionnelles aux distances des points de section considérés par rapport à l'axe neutre.
Remplaçons la dépendance (6.3) dans l'expression du moment fléchissant  en section transversale (6.1)
en section transversale (6.1)
 .
.
Rappelons que l'intégrale  représente le moment d'inertie de la section par rapport à l'axe
représente le moment d'inertie de la section par rapport à l'axe 
 .
.
 (6.4)
(6.4)
La dépendance (6.4) représente la loi de Hooke pour la flexion, puisqu'elle relie la déformation (courbure de la couche neutre  ) avec un moment agissant dans la section. Travail
) avec un moment agissant dans la section. Travail  est appelée rigidité de section en flexion, N m 2.
est appelée rigidité de section en flexion, N m 2.
Remplaçons (6.4) par (6.3)
 (6.5)
(6.5)
Il s'agit de la formule requise pour déterminer les contraintes normales lors de la flexion pure d'une poutre en tout point de sa section transversale.
Afin d'établir où se situe la ligne neutre dans la section transversale, nous substituons la valeur des contraintes normales dans l'expression de la force longitudinale  et moment de flexion
et moment de flexion 

Parce que le  ,
,
 ;
;
 (6.6)
(6.6)
 (6.7)
(6.7)
L'égalité (6.6) indique que l'axe  – axe neutre de la section – passe par le centre de gravité de la section transversale.
– axe neutre de la section – passe par le centre de gravité de la section transversale.
L'égalité (6.7) montre que  Et
Et  - les grands axes centraux du tronçon.
- les grands axes centraux du tronçon.
D'après (6.5), la tension la plus élevée est atteinte dans les fibres les plus éloignées de la ligne neutre

Attitude  représente le moment résistant axial de la section
représente le moment résistant axial de la section  par rapport à son axe central
par rapport à son axe central  , Moyens
, Moyens

Signification  pour les sections transversales les plus simples, ce qui suit :
pour les sections transversales les plus simples, ce qui suit :
Pour section rectangulaire
 , (6.8)
, (6.8)
Où  - côté de la section perpendiculaire à l'axe
- côté de la section perpendiculaire à l'axe  ;
;
 - côté de la section parallèle à l'axe
- côté de la section parallèle à l'axe  ;
;
Pour section ronde
 , (6.9)
, (6.9)
Où  - diamètre de la section circulaire.
- diamètre de la section circulaire.
La condition de résistance pour les contraintes de flexion normales peut être écrite sous la forme
 (6.10)
(6.10)
Toutes les formules obtenues sont obtenues pour le cas flexion pure tige droite. L'action de la force transversale conduit au fait que les hypothèses qui sous-tendent les conclusions perdent de leur force. Cependant, la pratique du calcul montre que même lors de la flexion transversale des poutres et des cadres, lorsqu'ils sont en section, en plus du moment de flexion  il y a aussi une force longitudinale
il y a aussi une force longitudinale  et force de cisaillement
et force de cisaillement  , vous pouvez utiliser les formules données pour le pliage pur. L'erreur est insignifiante.
, vous pouvez utiliser les formules données pour le pliage pur. L'erreur est insignifiante.
Courbe droite- c'est un type de déformation dans lequel deux internes facteurs de puissance: moment de flexion et effort tranchant.
Courbe propre- il s'agit d'un cas particulier de flexion directe, dans lequel seul un moment de flexion se produit dans les sections transversales de la tige, et la force transversale est nulle.
Un exemple de virage pur - une section CD sur la tige UN B. Moment de flexion est la quantité Pennsylvanie une paire de forces externes provoquant une flexion. De l'équilibre de la partie de la tige à gauche de la section transversale minute il s'ensuit que les efforts internes répartis sur cette section sont statiquement équivalents au moment M, égal et opposé au moment de flexion Pennsylvanie.
Pour connaître la répartition de ces efforts internes sur la section, il faut considérer la déformation de la tige.
Dans le cas le plus simple, la tige présente un plan de symétrie longitudinal et est soumise à l'action de couples de forces de flexion externes situés dans ce plan. Ensuite, la flexion se fera dans le même plan.
Axe de tige nn 1 est une ligne passant par les centres de gravité de ses sections transversales.
Soit la section transversale de la tige un rectangle. Traçons deux lignes verticales sur ses bords mm Et pp. Lors du pliage, ces lignes restent droites et tournent de manière à rester perpendiculaires aux fibres longitudinales de la tige.
Une autre théorie de la flexion est basée sur l'hypothèse que non seulement les lignes mm Et pp, mais toute la section transversale plate de la tige reste, après pliage, plate et normale aux fibres longitudinales de la tige. Ainsi, lors du pliage, les sections transversales mm Et pp tourner les uns par rapport aux autres autour d'axes perpendiculaires au plan de pliage (plan de dessin). Dans ce cas, les fibres longitudinales du côté convexe subissent une tension et les fibres du côté concave subissent une compression.
Surface neutre- Il s'agit d'une surface qui ne subit pas de déformation lors de la flexion. (Maintenant il est situé perpendiculairement au dessin, l'axe déformé de la tige nn 1 appartient à cette surface).
Axe neutre de section- il s'agit de l'intersection d'une surface neutre avec n'importe quelle section transversale (désormais également située perpendiculairement au dessin).
Soit une fibre arbitraire à distance ouià partir d'une surface neutre. ρ – rayon de courbure de l'axe courbe. Point Ô– centre de courbure. Traçons une ligne n 1 s 1 parallèle mm.article 1– allongement absolu des fibres.
Extension relative εx fibres
Il s'ensuit que déformation des fibres longitudinales proportionnel à la distance oui de la surface neutre et inversement proportionnel au rayon de courbure ρ .
L'allongement longitudinal des fibres du côté convexe de la tige s'accompagne de rétrécissement latéral, et le raccourcissement longitudinal du côté concave est expansion latérale, comme dans le cas d’un simple étirement et compression. De ce fait, l'apparence de toutes les sections change, les côtés verticaux du rectangle deviennent inclinés. Déformation latérale z:
μ - Coefficient de Poisson.
En raison de cette distorsion, toutes les lignes droites de section parallèles à l'axe z, sont courbés de manière à rester normaux aux côtés latéraux de la section. Le rayon de courbure de cette courbe R. sera plus que ρ au même titre que ε x par valeur absolue plus que ε z et on obtient
Ces déformations des fibres longitudinales correspondent à des contraintes
La tension dans n'importe quelle fibre est proportionnelle à sa distance par rapport à l'axe neutre n 1 n 2. Position de l'axe neutre et rayon de courbure ρ – deux inconnues dans l'équation de σ x - peut être déterminé à partir de la condition selon laquelle les forces réparties sur n'importe quelle section transversale forment une paire de forces qui équilibrent le moment externe M.
Tout ce qui précède est également vrai si la tige ne possède pas de plan de symétrie longitudinal dans lequel agit le moment de flexion, à condition que le moment de flexion agisse dans le plan axial qui contient l'un des deux axes principaux coupe transversale. Ces avions sont appelés plans de pliage principaux.
Lorsqu'il existe un plan de symétrie et que le moment fléchissant agit dans ce plan, la déflexion se produit précisément dans celui-ci. Moments d'efforts internes par rapport à l'axe zéquilibrer le moment extérieur M. Moments d'effort autour de l'axe oui sont mutuellement détruits.
Nous commencerons par le cas le plus simple, celui que l’on appelle le virage pur.
La flexion pure est un cas particulier de flexion dans lequel l'effort transversal dans les sections de la poutre est nul. La flexion pure ne peut se produire que lorsque le poids propre de la poutre est si faible que son influence peut être négligée. Pour les poutres sur deux appuis, exemples de charges provoquant des
flexion, illustrée à la Fig. 88. Dans les sections de ces poutres, où Q = 0 et donc M = const ; une flexion pure a lieu.
Les forces dans n'importe quelle section de la poutre lors de la flexion pure sont réduites à une paire de forces dont le plan d'action passe par l'axe de la poutre et le moment est constant.
Les tensions peuvent être déterminées sur la base des considérations suivantes.
1. Les composantes tangentielles des forces le long des zones élémentaires de la section transversale d'une poutre ne peuvent être réduites à un couple de forces dont le plan d'action est perpendiculaire au plan de section. Il s'ensuit que l'effort de flexion dans la section est le résultat d'une action le long des zones élémentaires
uniquement les forces normales, et donc en flexion pure, les contraintes sont réduites uniquement à la normale.
2. Pour que les efforts sur les sites élémentaires soient réduits à seulement quelques forces, parmi elles il faut qu'il y ait à la fois du positif et du négatif. Par conséquent, les fibres de tension et de compression de la poutre doivent exister.

3. Du fait que les forces dans différentes sections sont les mêmes, les contraintes aux points correspondants des sections sont les mêmes.
Considérons un élément proche de la surface (Fig. 89, a). Puisqu’aucune force n’est appliquée le long de son bord inférieur, qui coïncide avec la surface de la poutre, aucune contrainte n’est exercée sur celle-ci. Il n'y a donc aucune contrainte sur le bord supérieur de l'élément, car sinon l'élément ne serait pas en équilibre. En considérant l'élément qui lui est adjacent en hauteur (Fig. 89, b), on arrive à.

La même conclusion, etc. Il s'ensuit qu'il n'y a aucune contrainte le long des bords horizontaux d'un élément. En considérant les éléments qui composent la couche horizontale, en commençant par l'élément proche de la surface de la poutre (Fig. 90), nous arrivons à la conclusion qu'il n'y a aucune contrainte le long des bords verticaux latéraux d'aucun élément. Ainsi, l'état de contrainte de tout élément (Fig. 91, a) et, à la limite, des fibres, doit être représenté comme le montre la Fig. 91,b, c'est-à-dire qu'il peut s'agir soit d'une traction axiale, soit d'une compression axiale.
4. En raison de la symétrie de l'application des forces externes, la section au milieu de la longueur de la poutre après déformation doit rester plate et normale à l'axe de la poutre (Fig. 92, a). Pour la même raison, les sections en quarts de longueur de la poutre restent également plates et normales à l'axe de la poutre (Fig. 92, b), à moins que les sections extrêmes de la poutre lors de la déformation restent plates et normales à l'axe de le rayon. Une conclusion similaire est valable pour les sections en huitièmes de la longueur de la poutre (Fig. 92, c), etc. Par conséquent, si pendant la flexion les sections extérieures de la poutre restent plates, alors pour toute section, il reste 
Il est juste d’affirmer qu’après déformation, elle reste plate et normale à l’axe de la poutre incurvée. Mais dans ce cas, il est évident que le changement d'allongement des fibres de la poutre le long de sa hauteur doit se produire non seulement de manière continue, mais également de manière monotone. Si l'on appelle une couche un ensemble de fibres ayant les mêmes allongements, alors il résulte de ce qui a été dit que les fibres étirées et comprimées de la poutre doivent être situées sur les côtés opposés de la couche dans laquelle les allongements des fibres sont égaux à zéro. On appellera neutres les fibres dont les allongements sont nuls ; une couche constituée de fibres neutres est une couche neutre ; la ligne d'intersection de la couche neutre avec le plan de section transversale du faisceau - la ligne neutre de cette section. Ensuite, sur la base du raisonnement précédent, on peut affirmer qu'avec la flexion pure d'une poutre, dans chaque section il y a une ligne neutre qui divise cette section en deux parties (zones) : une zone de fibres étirées (zone étirée) et une zone de fibres compressées (zone compressée). En conséquence, aux points de la zone étirée de la section, des contraintes de traction normales doivent agir, aux points de la zone comprimée - des contraintes de compression, et aux points de la ligne neutre les contraintes sont égales à zéro.
Ainsi, en flexion pure d'une poutre de section constante :
1) seules les contraintes normales agissent par sections ;
2) la section entière peut être divisée en deux parties (zones) - étirées et comprimées ; la limite des zones est la ligne de section neutre, aux points de laquelle les contraintes normales sont égales à zéro ;
3) tout élément longitudinal de la poutre (à la limite, toute fibre) est soumis à une tension ou une compression axiale, de sorte que les fibres adjacentes n'interagissent pas entre elles ;
4) si les sections extrêmes de la poutre lors de la déformation restent plates et normales à l'axe, alors toutes ses sections transversales restent plates et normales à l'axe de la poutre courbe.
Etat de contrainte d'une poutre en flexion pure
Considérons un élément d'une poutre soumis à une flexion pure, en concluant  situé entre les sections m-m et n-n, qui sont espacées les unes des autres d'une distance infinitésimale dx (Fig. 93). En raison de la position (4) du paragraphe précédent, les sections m- m et n - n, qui étaient parallèles avant déformation, restant plates après pliage, formeront un angle dQ et se couperont selon une droite passant par le point C, qui est le centre de courbure de la fibre neutre NN. Alors la partie AB de la fibre enfermée entre elles, située à une distance z de la fibre neutre (la direction positive de l'axe z est prise vers la convexité de la poutre lors de la flexion), se transformera après déformation en un arc AB. morceau de fibre neutre O1O2, s'étant transformé en arc, O1O2 ne changera pas de longueur, tandis que la fibre AB recevra un allongement :
situé entre les sections m-m et n-n, qui sont espacées les unes des autres d'une distance infinitésimale dx (Fig. 93). En raison de la position (4) du paragraphe précédent, les sections m- m et n - n, qui étaient parallèles avant déformation, restant plates après pliage, formeront un angle dQ et se couperont selon une droite passant par le point C, qui est le centre de courbure de la fibre neutre NN. Alors la partie AB de la fibre enfermée entre elles, située à une distance z de la fibre neutre (la direction positive de l'axe z est prise vers la convexité de la poutre lors de la flexion), se transformera après déformation en un arc AB. morceau de fibre neutre O1O2, s'étant transformé en arc, O1O2 ne changera pas de longueur, tandis que la fibre AB recevra un allongement :
avant déformation

après déformation
![]()
où p est le rayon de courbure de la fibre neutre.
L’allongement absolu du segment AB est donc égal à
et allongement relatif
Puisque, selon la position (3), la fibre AB est soumise à une tension axiale, alors lors de la déformation élastique

Cela montre que les contraintes normales le long de la hauteur de la poutre sont réparties selon une loi linéaire (Fig. 94). Puisque la force égale de toutes les forces sur toutes les zones de section élémentaire doit être égale à zéro, alors
d'où, en substituant la valeur de (5.8), on trouve

Mais la dernière intégrale est un moment statique autour de l'axe Oy, perpendiculaire au plan d'action des forces de flexion.

Du fait de son égalité à zéro, cet axe doit passer par le centre de gravité O de la section. Ainsi, la ligne neutre de la section de la poutre est une droite y, perpendiculaire au plan d'action des forces de flexion. C'est ce qu'on appelle l'axe neutre de la section de la poutre. Il résulte ensuite de (5.8) que les contraintes en des points situés à la même distance de l'axe neutre sont les mêmes.
Le cas de flexion pure, dans lequel les forces de flexion agissent dans un seul plan, provoquant une flexion uniquement dans ce plan, est une flexion pure plane. Si ledit plan passe par l'axe Oz, alors le moment des forces élémentaires par rapport à cet axe doit être égal à zéro, c'est-à-dire
En substituant ici la valeur de σ de (5.8), nous trouvons

L'intégrale du côté gauche de cette égalité, comme on le sait, est le moment d'inertie centrifuge de la section par rapport aux axes y et z, donc

Les axes autour desquels le moment d'inertie centrifuge de la section est nul sont appelés axes principaux d'inertie de cette section. S'ils traversent en outre le centre de gravité de la section, ils peuvent alors être appelés les principaux axes centraux d'inertie de la section. Ainsi, en flexion pure à plat, la direction du plan d'action des efforts de flexion et l'axe neutre de la section sont les principaux axes centraux d'inertie de cette dernière. Autrement dit, pour obtenir une courbure plate et pure d'une poutre, une charge ne peut lui être appliquée arbitrairement : elle doit être réduite à des forces agissant dans un plan passant par l'un des principaux axes centraux d'inertie des sections de la poutre. faisceau; dans ce cas, l'autre axe central principal d'inertie sera l'axe neutre de la section.
Comme on le sait, dans le cas d'une section symétrique par rapport à un axe quelconque, l'axe de symétrie est l'un de ses principaux axes centraux d'inertie. Par conséquent, dans ce cas particulier on obtiendra certainement une flexion pure en appliquant des charges appropriées dans un plan passant par l'axe longitudinal de la poutre et l'axe de symétrie de sa section. Une droite perpendiculaire à l'axe de symétrie et passant par le centre de gravité de la section est l'axe neutre de cette section.
Après avoir établi la position de l'axe neutre, il n'est pas difficile de trouver l'ampleur de la contrainte en tout point de la section. En effet, puisque la somme des moments des forces élémentaires par rapport à l'axe neutre yy doit être égale au moment fléchissant, alors
d'où, en substituant la valeur de σ de (5.8), nous trouvons

Puisque l'intégrale  est. moment d'inertie de la section par rapport à l'axe yy, alors
est. moment d'inertie de la section par rapport à l'axe yy, alors
et de l’expression (5.8) on obtient
Le produit EI Y est appelé rigidité en flexion de la poutre.
Les contraintes de traction et de compression les plus grandes en valeur absolue agissent aux points de la section pour lesquels la valeur absolue de z est la plus grande, c'est-à-dire aux points les plus éloignés de l'axe neutre. Avec la notation Fig. 95 nous avons

La valeur Jy/h1 est appelée moment de résistance de la section à la traction et est notée Wyr ; de même, Jy/h2 est appelé moment résistant de la section à la compression

et désignent Wyc, donc

et donc

Si l'axe neutre est l'axe de symétrie de la section, alors h1 = h2 = h/2 et donc Wyp = Wyc, il n'y a donc pas besoin de les distinguer, et ils utilisent la même notation :
appelant W y simplement le moment résistant de la section. Par conséquent, dans le cas d'une section symétrique par rapport à l'axe neutre,
Toutes les conclusions ci-dessus ont été obtenues sur la base de l'hypothèse selon laquelle les sections transversales de la poutre, lorsqu'elle est courbée, restent plates et normales à son axe (hypothèse des sections plates). Comme cela a été montré, cette hypothèse n'est valable que dans le cas où les sections extrêmes (d'extrémité) de la poutre restent plates pendant la flexion. En revanche, de l'hypothèse des sections planes, il résulte que les forces élémentaires dans de telles sections doivent être réparties selon une loi linéaire. Par conséquent, pour la validité de la théorie résultante de flexion pure à plat, il est nécessaire que les moments de flexion aux extrémités de la poutre soient appliqués sous la forme d'efforts élémentaires répartis sur la hauteur de la section selon une loi linéaire (Fig. 96), coïncidant avec la loi de répartition des contraintes sur la hauteur des poutres profilées. Cependant, sur la base du principe de Saint-Venant, on peut affirmer que changer la méthode d'application des moments fléchissants aux extrémités de la poutre n'entraînera que des déformations locales dont l'effet n'affectera qu'une certaine distance de ces extrémités (approximativement égale à la hauteur de la section). Les sections situées sur le reste de la longueur de la poutre resteront plates. Par conséquent, la théorie énoncée de la flexion pure à plat pour toute méthode d'application des moments de flexion n'est valable que dans la partie médiane de la longueur de la poutre, située à partir de ses extrémités à des distances approximativement égales à la hauteur de la section. Il est donc clair que cette théorie est évidemment inapplicable si la hauteur de la section dépasse la moitié de la longueur ou de l'envergure de la poutre.
Lors de la construction diagrammes de moments fléchissantsM à constructeurs accepté : ordonnées exprimant sur une certaine échelle positif valeurs des moments fléchissants, mises de côté étiré fibres, c'est-à-dire - vers le bas, UN négatif - vers le haut de l'axe du faisceau. Par conséquent, on dit que les constructeurs construisent des diagrammes sur des fibres étirées. Chez la mécanique les valeurs positives de l'effort tranchant et du moment de flexion sont reportées en haut. Les mécaniciens dessinent des diagrammes comprimé fibres.
Principales contraintes lors de la flexion. Tensions équivalentes.
Dans le cas général de flexion directe dans les sections transversales d'une poutre, normale Et tangentes![]() tension. Ces tensions varient à la fois sur la longueur et la hauteur de la poutre.
tension. Ces tensions varient à la fois sur la longueur et la hauteur de la poutre.
Ainsi, dans le cas de la flexion, il y a état de contrainte plane.
Considérons un diagramme où la poutre est chargée d'une force P

La plus grande normale des tensions apparaissent dans extrême, points les plus éloignés de la ligne neutre, et Il n'y a aucune contrainte de cisaillement en eux. Ainsi, pour extrême fibres les contraintes principales non nulles sont des contraintes normales en coupe transversale.
Au niveau de la ligne neutre dans la section transversale de la poutre il y a contrainte de cisaillement la plus élevée, UN les contraintes normales sont nulles. signifie dans les fibres neutre couche les contraintes principales sont déterminées par les valeurs des contraintes tangentielles.
Dans ce schéma de conception les fibres supérieures de la poutre seront étirées et les fibres inférieures seront comprimées. Pour déterminer les contraintes principales on utilise l'expression bien connue : 
Complet analyse des contraintes Imaginons-le sur la photo.

Analyse des contraintes de flexion
Contrainte principale maximale σ 1 est situé supérieur fibres extrêmes et est égal à zéro sur les fibres inférieures les plus externes. Contrainte principale σ 3 Il a la plus grande valeur absolue se situe sur les fibres inférieures.
Trajectoire des principales contraintes dépend de type de charge Et méthode de fixation de la poutre.


Pour résoudre des problèmes, il suffit séparément vérifier normale Et contraintes tangentielles séparément. Cependant, parfois le plus stressant s'avère être intermédiaire fibres dans lesquelles il existe à la fois des contraintes normales et des contraintes de cisaillement. Cela se produit dans les sections où simultanément, le moment de flexion et la force de cisaillement atteignent grandes valeurs - cela peut être dans l'encastrement d'une poutre en porte-à-faux, sur le support d'une poutre avec un porte-à-faux, dans des sections sous force concentrée, ou dans des sections avec des largeurs fortement changeantes. Par exemple, dans une section en I, le plus dangereux la jonction du mur et de l'étagère- il y a des contraintes normales et de cisaillement importantes.
Le matériau est dans un état de contrainte plane et est requis vérifiez les tensions équivalentes.
Conditions de résistance des poutres en matières plastiques Par troisième(théorie des contraintes tangentielles maximales) ![]() Et quatrième(théorie de l'énergie des changements de forme)
Et quatrième(théorie de l'énergie des changements de forme) ![]() théories de la force.
théories de la force.
En règle générale, dans les poutres laminées, les contraintes équivalentes ne dépassent pas les contraintes normales dans les fibres les plus externes et aucun essai spécial n'est requis. Autre chose - poutres métalliques composites, lequel le mur est plus fin que pour les profilés laminés de même hauteur. Les poutres composites soudées en tôles d'acier sont plus souvent utilisées. Calcul de la résistance de ces poutres : a) sélection de la section - hauteur, épaisseur, largeur et épaisseur des membrures de la poutre ; b) vérifier la résistance par contraintes normales et tangentielles ; c) vérifier la résistance à l'aide de contraintes équivalentes.
Détermination des contraintes de cisaillement dans une section en I. Considérons la section Je rayonne S x =96,9 cm3 ; Yx=2030 cm 4 ; Q=200kN

Pour déterminer la contrainte de cisaillement, on utilise formule![]() ,où Q est l'effort tranchant dans la section, S x 0 est le moment statique de la partie de la section située d'un côté de la couche dans laquelle les contraintes tangentielles sont déterminées, I x est le moment d'inertie de l'ensemble section transversale, b est la largeur de la section à l'endroit où la contrainte de cisaillement est déterminée
,où Q est l'effort tranchant dans la section, S x 0 est le moment statique de la partie de la section située d'un côté de la couche dans laquelle les contraintes tangentielles sont déterminées, I x est le moment d'inertie de l'ensemble section transversale, b est la largeur de la section à l'endroit où la contrainte de cisaillement est déterminée
Calculons maximum contrainte de cisaillement :
Calculons le moment statique pour étagère supérieure: 
Maintenant calculons contrainte de cisaillement : 
Nous construisons diagramme de contrainte de cisaillement :

Considérons la section transversale d'un profil standard sous la forme Je rayonne et définir contrainte de cisaillement, agissant parallèlement à la force de cisaillement :

Calculons moments statiques chiffres simples : 
Cette valeur peut être calculée et sinon, en utilisant le fait que pour les sections de poutre en I et de creux, le moment statique de la moitié de la section est donné. Pour ce faire, il faut soustraire de la valeur connue du moment statique la valeur du moment statique à la ligne A 1 B 1 : 
Les contraintes tangentielles à la jonction de la bride et du mur changent spasmodiquement, parce que pointu l'épaisseur de la paroi varie de t st avant b.
Les diagrammes des contraintes tangentielles dans les parois des sections en auge, rectangulaires creuses et autres ont la même forme que dans le cas d'une section en I. La formule inclut le moment statique de la partie ombrée de la section par rapport à l'axe X, et le dénominateur inclut la largeur de la section (nette) dans la couche où la contrainte de cisaillement est déterminée.


Déterminons les contraintes tangentielles pour une section circulaire.


Étant donné que les contraintes de cisaillement au niveau du contour de la section doivent être dirigées tangent au contour, puis aux points UN Et DANS aux extrémités de toute corde parallèle au diamètre UN B, les contraintes de cisaillement sont dirigées perpendiculaire aux rayons OA Et VO. Ainsi, directions contraintes tangentielles aux points UN, Capital-risque converger à un moment donné N sur l'axe Y.
Moment statique de la pièce coupée : 
Autrement dit, les contraintes de cisaillement changent en fonction parabolique loi et sera maximum au niveau de la ligne neutre, lorsque oui 0 =0

Formule pour déterminer la contrainte de cisaillement (formule) 
Considérons une section rectangulaire

À distance oui 0à partir de l'axe central, nous dessinons article 1-1 et déterminer les contraintes tangentielles. Moment statique zone partie coupée :
Il ne faut pas oublier qu'il est fondamental indifférent, prenons le moment statique de l'aire partie ombrée ou restante coupe transversale. Les deux moments statiques signe égal et opposé, donc leur somme, qui représente moment statique de l'aire de toute la section par rapport à la ligne neutre, à savoir l'axe central des x, sera égal à zéro.
Moment d'inertie d'une section rectangulaire :

Alors contrainte de cisaillement selon la formule

La variable y 0 est incluse dans la formule dans deuxième degrés, c'est-à-dire les contraintes tangentielles dans une section rectangulaire varient en fonction loi d'une parabole carrée.
Contrainte de cisaillement atteinte maximum au niveau de la ligne neutre, c'est à dire Quand oui 0 =0 :
 ,
Où A est l'aire de toute la section.
,
Où A est l'aire de toute la section.
Condition de résistance pour les contraintes tangentielles a la forme :
![]() , Où S x 0– moment statique de la partie de la section située d'un côté de la couche dans laquelle les contraintes de cisaillement sont déterminées, je x– moment d'inertie de toute la section transversale, b– largeur de section à l'endroit où la contrainte de cisaillement est déterminée, Q-force latérale, τ
- la contrainte de cisaillement, [τ]
— contrainte tangentielle admissible.
, Où S x 0– moment statique de la partie de la section située d'un côté de la couche dans laquelle les contraintes de cisaillement sont déterminées, je x– moment d'inertie de toute la section transversale, b– largeur de section à l'endroit où la contrainte de cisaillement est déterminée, Q-force latérale, τ
- la contrainte de cisaillement, [τ]
— contrainte tangentielle admissible.
Cette condition de résistance nous permet de produire trois type de calcul (trois types de problèmes lors du calcul de la résistance) :
1. Calcul de vérification ou essai de résistance basé sur les contraintes tangentielles : ![]()
2. Sélection de la largeur de section (pour une section rectangulaire) : ![]()
3. Détermination de la force latérale admissible (pour une section rectangulaire) :
![]()
Pour déterminer tangentes contraintes, considérons une poutre chargée de forces.

La tâche de déterminer les contraintes est toujours statiquement indéterminé et nécessite une implication géométrique Et physiqueéquations. Il est cependant possible d'accepter une telle hypothèses sur la nature de la répartition du stress que la tâche deviendra définissable statiquement.
Par deux sections transversales infiniment proches 1-1 et 2-2 on sélectionne élément dz, Représentons-le à grande échelle, puis dessinons une coupe longitudinale 3-3.
Dans les sections 1-1 et 2-2, contraintes normales σ 1, σ 2, qui sont déterminés par les formules bien connues :
Où M - moment de flexion en coupe transversale, dM - incrément moment de flexion en longueur dz
Force latérale dans les sections 1–1 et 2–2 est dirigé le long de l’axe central principal Y et représente évidemment la somme des composantes verticales des contraintes tangentielles internes réparties sur la section. En termes de résistance des matériaux, il est généralement pris hypothèse de leur répartition uniforme sur toute la largeur de la section.
Pour déterminer l'ampleur des contraintes de cisaillement en tout point de la section transversale situé à une distance oui 0à partir de l'axe neutre X, tracez un plan parallèle à la couche neutre (3-3) passant par ce point et retirez l'élément clipsé. Nous déterminerons la tension agissant aux bornes de la zone ABCD. 
Projetons toutes les forces sur l'axe Z

La résultante des efforts longitudinaux internes le long du côté droit sera égale à :
Où A 0 – aire du bord de la façade, S x 0 – moment statique de la partie coupée par rapport à l'axe X. De même sur le côté gauche :
![]() Les deux résultats Dirigé vers l'un l'autre,
puisque l'élément est dans comprimé zone du faisceau. Leur différence est compensée par les forces tangentielles sur le bord inférieur de 3-3.
Les deux résultats Dirigé vers l'un l'autre,
puisque l'élément est dans comprimé zone du faisceau. Leur différence est compensée par les forces tangentielles sur le bord inférieur de 3-3.
Faisons comme si contrainte de cisaillement τ réparti sur toute la largeur de la section transversale de la poutre b uniformément. Cette hypothèse est d’autant plus probable que la largeur de la section est petite par rapport à la hauteur. Alors résultante des forces tangentielles dTégale à la valeur de contrainte multipliée par la surface du visage : ![]()
Composons maintenant équation d'équilibre Σz=0 : ![]()
ou d'où
![]()
Souvenons-nous dépendances différentielles
, selon lequel ![]() On obtient alors la formule :
On obtient alors la formule :
![]()
Cette formule s'appelle formules. Cette formule a été obtenue en 1855. Ici S x 0 – moment statique d'une partie de la section transversale, situé d'un côté de la couche dans laquelle sont déterminées les contraintes de cisaillement, I x – moment d'inertie toute la section transversale, b – largeur de sectionà l'endroit où est déterminée la contrainte de cisaillement, Q - force de cisaillement en coupe transversale.
![]() — condition de résistance à la flexion, Où
— condition de résistance à la flexion, Où
- moment maximum (modulo) du diagramme des moments fléchissants ; ![]() - moment résistant axial de la section, géométrique caractéristique; - contrainte admissible (σ adm)
- moment résistant axial de la section, géométrique caractéristique; - contrainte admissible (σ adm)
- tension normale maximale.
Si le calcul est effectué selon méthode des états limites, puis au lieu de la tension admissible, nous entrons dans le calcul résistance de calcul du matériau R.
Types de calculs de résistance à la flexion
1. Vérifier calcul ou vérification de la résistance à l'aide de contraintes normales ![]()
2. Conception calcul ou sélection de rubrique ![]()
3. Définition permis charge (définition capacité de levage et/ou opérationnel transporteur capacités) ![]()
Lors de la dérivation de la formule de calcul des contraintes normales, nous considérons le cas de la flexion, lorsque les efforts internes dans les sections de la poutre sont réduits uniquement à moment de flexion, UN la force de cisaillement s'avère nulle. Ce cas de flexion est appelé flexion pure. Considérons la section médiane de la poutre, qui est soumise à une pure flexion.
 Lorsqu'elle est chargée, la poutre se plie de sorte qu'elle Les fibres inférieures s'allongent et les supérieures se raccourcissent.
Lorsqu'elle est chargée, la poutre se plie de sorte qu'elle Les fibres inférieures s'allongent et les supérieures se raccourcissent.
Puisqu'une partie des fibres de la poutre est étirée et une partie est comprimée, et la transition de la tension à la compression se produit en douceur, sans sauts, V moyenne une partie de la poutre est située une couche dont les fibres ne font que se plier, mais ne subissent ni tension ni compression. Cette couche est appelée neutre couche. La ligne le long de laquelle la couche neutre coupe la section transversale du faisceau est appelée ligne neutre ou axe neutre sections. Des lignes neutres sont enfilées sur l'axe du faisceau. Ligne neutre est la ligne dans laquelle les contraintes normales sont nulles.
Les lignes tracées sur la surface latérale de la poutre perpendiculairement à l'axe restent plat lors de la flexion. Ces données expérimentales permettent de fonder les conclusions des formules hypothèse de sections planes (conjecture). Selon cette hypothèse, les sections de la poutre sont plates et perpendiculaires à son axe avant pliage, restent plates et s'avèrent perpendiculaires à l'axe courbe de la poutre lorsqu'elle est pliée.
Hypothèses pour dériver les formules de contrainte normale : 1) L'hypothèse des sections planes est vérifiée. 2) Les fibres longitudinales ne s'appuient pas les unes sur les autres (hypothèse de non-pression) et, par conséquent, chacune des fibres est dans un état de tension ou de compression uniaxiale. 3) Les déformations des fibres ne dépendent pas de leur position le long de la largeur de la section transversale. Par conséquent, les contraintes normales, changeant sur la hauteur de la section, restent les mêmes sur la largeur. 4) La poutre a au moins un plan de symétrie et toutes les forces externes se situent dans ce plan. 5) Le matériau de la poutre obéit à la loi de Hooke, et le module d'élasticité en traction et en compression est le même. 6) La relation entre les dimensions de la poutre est telle qu'elle fonctionne dans des conditions de flexion plane sans déformation ni torsion.
Considérons une poutre de section arbitraire, mais ayant un axe de symétrie.  Moment de flexion représente moment résultant des forces normales internes, apparaissant sur des zones infiniment petites et peut être exprimé en intégral formulaire:
Moment de flexion représente moment résultant des forces normales internes, apparaissant sur des zones infiniment petites et peut être exprimé en intégral formulaire: ![]() (1), où y est le bras de la force élémentaire par rapport à l'axe x
(1), où y est le bras de la force élémentaire par rapport à l'axe x
Formule (1) exprime statique côté du problème de la flexion d'une poutre droite, mais le long de celle-ci à un moment de flexion connu Il est impossible de déterminer les contraintes normales tant que la loi de leur répartition n'est pas établie.
Sélectionnons les poutres de la section médiane et considérons section de longueur dz, sujet à la flexion. Représentons-le à une échelle agrandie.

Sections délimitant la zone dz, parallèles les uns aux autres jusqu'à déformation, et après avoir appliqué la charge tourner autour de leurs lignes neutres d'un angle . La longueur du segment de fibre de couche neutre ne changera pas. et sera égal à : ![]() , où est-il rayon de courbure l'axe courbe de la poutre. Mais toute autre fibre ment inférieur ou supérieur couche neutre, va changer sa longueur. Calculons allongement relatif des fibres situées à une distance y de la couche neutre. L'allongement relatif est le rapport entre la déformation absolue et la longueur d'origine, alors :
, où est-il rayon de courbure l'axe courbe de la poutre. Mais toute autre fibre ment inférieur ou supérieur couche neutre, va changer sa longueur. Calculons allongement relatif des fibres situées à une distance y de la couche neutre. L'allongement relatif est le rapport entre la déformation absolue et la longueur d'origine, alors :
Réduisons de et ramenons des termes similaires, nous obtenons alors : (2) Cette formule exprime géométrique côté du problème de flexion pure : Les déformations des fibres sont directement proportionnelles à leurs distances à la couche neutre.
Passons maintenant à stresser, c'est à dire. nous allons le prendre en compte physique côté de la tâche. conformément à hypothèse de non-pression on utilise des fibres sous tension-compression axiale : alors, en tenant compte de la formule (2)
nous avons ![]() (3),
ceux. stress normal lors d'une flexion le long de la hauteur de la section distribué linéairement. Sur les fibres les plus externes, les contraintes normales atteignent leur valeur maximale, et au centre de gravité de la section elles sont égales à zéro. Remplaçons (3)
dans l'équation (1)
et retirez la fraction du signe intégral comme valeur constante, ensuite nous avons
(3),
ceux. stress normal lors d'une flexion le long de la hauteur de la section distribué linéairement. Sur les fibres les plus externes, les contraintes normales atteignent leur valeur maximale, et au centre de gravité de la section elles sont égales à zéro. Remplaçons (3)
dans l'équation (1)
et retirez la fraction du signe intégral comme valeur constante, ensuite nous avons ![]() . Mais l'expression est moment d'inertie axial de la section par rapport à l'axe x - je x.
Sa dimension cm 4, m 4
. Mais l'expression est moment d'inertie axial de la section par rapport à l'axe x - je x.
Sa dimension cm 4, m 4
Alors ![]() ,où
,où ![]() (4), où est la courbure de l'axe incurvé de la poutre, et est la rigidité de la section de poutre pendant la flexion.
(4), où est la courbure de l'axe incurvé de la poutre, et est la rigidité de la section de poutre pendant la flexion.
Remplaçons l'expression résultante courbure (4) en expression (3)
et nous obtenons formule pour calculer les contraintes normales en tout point de la section transversale : ![]() (5)
(5)
Que. maximum des tensions surgissent aux points les plus éloignés de la ligne neutre. Attitude ![]() (6)
appelé moment axial de résistance de section. Sa dimension cm 3, m 3. Le moment résistant caractérise l'influence de la forme et des dimensions de la section sur l'ampleur des contraintes.
(6)
appelé moment axial de résistance de section. Sa dimension cm 3, m 3. Le moment résistant caractérise l'influence de la forme et des dimensions de la section sur l'ampleur des contraintes.
Alors tensions maximales : ![]() (7)
(7)
Condition de résistance à la flexion : ![]() (8)
(8)
En cas de flexion transversale non seulement normales, mais aussi contraintes de cisaillement, parce que disponible force de cisaillement. Contrainte de cisaillement compliquer l'image de la déformation, ils conduisent à courbure sections transversales de la poutre, ce qui entraîne l'hypothèse des sections planes est violée. Cependant, les recherches montrent que les distorsions introduites par les contraintes de cisaillement légèrement affecter les contraintes normales calculées par la formule (5) . Ainsi, lors de la détermination des contraintes normales en cas de flexion transversale La théorie de la flexion pure est tout à fait applicable.
Ligne neutre. Question sur la position de la ligne neutre.
Absent en flexion force longitudinale, pour que nous puissions écrire ![]() Remplaçons ici la formule des contraintes normales (3)
et nous obtenons
Remplaçons ici la formule des contraintes normales (3)
et nous obtenons ![]() Puisque le module d'élasticité longitudinale du matériau de la poutre n'est pas égal à zéro et que l'axe incurvé de la poutre a un rayon de courbure fini, il reste à supposer que cette intégrale est moment statique de l'aire section transversale du faisceau par rapport à l'axe de la ligne neutre x
Puisque le module d'élasticité longitudinale du matériau de la poutre n'est pas égal à zéro et que l'axe incurvé de la poutre a un rayon de courbure fini, il reste à supposer que cette intégrale est moment statique de l'aire section transversale du faisceau par rapport à l'axe de la ligne neutre x ![]() , et depuis elle est égale à zéro, alors la ligne neutre passe par le centre de gravité de la section.
, et depuis elle est égale à zéro, alors la ligne neutre passe par le centre de gravité de la section.
La condition (absence de moment d'efforts internes par rapport à la ligne de champ) donnera ![]() ou en tenant compte (3)
ou en tenant compte (3)
![]() . Pour les mêmes raisons (voir ci-dessus)
. Pour les mêmes raisons (voir ci-dessus) ![]() . En intégrande - le moment d'inertie centrifuge de la section par rapport aux axes x et y est nul, ce qui signifie que ces axes sont principal et central et maquiller droit coin. Ainsi, La force et les lignes neutres dans un virage droit sont mutuellement perpendiculaires.
. En intégrande - le moment d'inertie centrifuge de la section par rapport aux axes x et y est nul, ce qui signifie que ces axes sont principal et central et maquiller droit coin. Ainsi, La force et les lignes neutres dans un virage droit sont mutuellement perpendiculaires.
Après avoir installé position de la ligne neutre, facile à construire diagramme de contrainte normale le long de la hauteur de la section. Son linéaire le caractère est déterminé équation du premier degré.

La nature du diagramme σ pour les sections symétriques par rapport à la ligne neutre, M<0