Comment trouver la plus petite valeur de la fonction racine. A quel point la valeur de la dérivée est-elle la plus grande ?

Parfois dans les problèmes B14 il y a de "mauvaises" fonctions pour lesquelles il est difficile de trouver la dérivée. Auparavant, ce n'était que sur les sondes, mais maintenant ces tâches sont si courantes qu'elles ne peuvent plus être ignorées lors de la préparation de cet examen. Dans ce cas, d'autres astuces fonctionnent, dont l'une est la monotonie. Définition La fonction f (x) est dite monotone croissante sur le segment si pour tous les points x 1 et x 2 de ce segment on a : x 1

Définition. La fonction f (x) est dite monotone décroissante sur le segment si pour tous les points x 1 et x 2 de ce segment on a : x 1 f (x 2). Autrement dit, pour une fonction croissante, plus x est grand, plus f(x) est grand. Pour une fonction décroissante, l'inverse est vrai : plus x est grand, plus f(x) est petit.

Exemples. Le logarithme croît de façon monotone si la base a > 1 et décroît de façon monotone si 0 0. f (x) = log a x (a > 0 ; a 1 ; x > 0) 1, et diminue de façon monotone si 0 0. f (x) = log a x (a > 0; a 1; x > 0)"> 1, et diminue de façon monotone si 0 0. f (x) = log a x (a > 0 ; a 1; x > 0)"> 1, et décroît de façon monotone si 0 0. f (x) = log a x (a > 0; a 1; x > 0)" title="(!LANG:Examples Le logarithme est monotone croissante si la base a > 1 et monotone décroissante si 0 0. f (x) = log a x (a > 0 ; a 1 ; x > 0)"> title="Exemples. Le logarithme croît de façon monotone si la base a > 1 et décroît de façon monotone si 0 0. f (x) = log a x (a > 0 ; a 1 ; x > 0)"> !}

Exemples. Fonction exponentielle se comporte comme le logarithme : il augmente pour a > 1 et diminue pour 0 0 : 1 et décroissante à 0 0 :"> 1 et décroissante à 0 0 :"> 1 et décroissante à 0 0 :" title="(!LANG:Examples. La fonction exponentielle se comporte comme un logarithme : elle croît pour a > 1 et diminue pour 0 0 :"> title="Exemples. La fonction exponentielle se comporte comme le logarithme : elle croît pour a > 1 et décroît pour 0 0 :"> !}

0) ou bas (a 0) ou bas (a 9 Coordonnées du sommet de la parabole Le plus souvent, l'argument de la fonction est remplacé par un trinôme carré de la forme Son graphe est une parabole standard dont on s'intéresse aux branches : Les branches de la parabole peuvent monter (pour a > 0) ou descendre (a 0) ou le plus grand (a 0) ou vers le bas (a 0) ou vers le bas (a 0) ou le plus grand (a 0) ou vers le bas (a 0) ou vers le bas (a title="(!LANG : Coordonnées du sommet de la parabole Le plus souvent, l'argument de la fonction est remplacé par un trinôme carré de la forme Son graphe est une parabole standard, dont on s'intéresse aux branches : Les branches d'une parabole peuvent monter (pour a > 0) ou descendre (a

Il n'y a pas de segment dans l'état du problème. Par conséquent, il n'est pas nécessaire de calculer f(a) et f(b). Il ne reste plus qu'à considérer les points extrêmes ; Mais il n'y a qu'un seul point de ce type - c'est le sommet de la parabole x 0, dont les coordonnées sont calculées littéralement verbalement et sans aucune dérivée.

Ainsi, la solution du problème est grandement simplifiée et réduite à seulement deux étapes : Écrivez l'équation de la parabole et trouvez son sommet en utilisant la formule : Trouvez la valeur de la fonction d'origine en ce point : f (x 0). Si aucun conditions additionnelles non, ce serait la réponse.

0. Sommet de la parabole : x 0 = b/(2a) = 6/(2 1) = 6/2 = 3" title="(!LANG:Find plus petite valeur fonctions : Solution : sous la racine se dresse fonction quadratique Le graphe de cette fonction est une parabole à branches vers le haut, puisque le coefficient a = 1 > 0. Le sommet de la parabole : x 0 = b/(2a) = 6/(2 1) = 6/2 = classe 3" ="lien_pouce"> 18 Trouver la plus petite valeur de la fonction : Solution : Il y a une fonction quadratique sous la racine. Le graphique de cette fonction est une parabole avec des branches vers le haut, puisque le coefficient a \u003d 1\u003e 0. Sommet de la parabole : x 0 \ u003d b / (2a) \u003d 6 / (2 1) \u003d 6/2 = 3 0. Sommet de la parabole : x 0 = b/(2a) = 6/(2 1) = 6/2 = 3"> 0. Sommet de la parabole : x 0 = b/(2a) = 6/(2 1) = 6/2 = 3"> 0. Sommet de la parabole : x 0 = b/(2a) = 6/(2 1) = 6/2 = 3" title="(!LANG : Trouver la plus petite valeur de la fonction : Solution : Sous la racine se trouve une fonction quadratique. Le graphique de cette fonction est une parabole avec des branches vers le haut, puisque le coefficient a \u003d 1\u003e 0. Le sommet de la parabole : x 0 \u003d b / ( 2a) \u003d 6 / (2 1) \u003d 6/2 \u003d 3"> title="Trouver la plus petite valeur de la fonction : Solution : Il y a une fonction quadratique sous la racine. Le graphique de cette fonction est une parabole avec des branches vers le haut, puisque le coefficient a \u003d 1\u003e 0. Sommet de la parabole : x 0 \ u003d b / (2a) \u003d 6 / (2 1) \u003d 6/2 = 3"> !}

Trouver la plus petite valeur de la fonction : Solution Sous le logarithme se trouve à nouveau une fonction quadratique. a = 1 > 0. Sommet de la parabole : x 0 = b/(2a) = 2/(2 1) = 2/2 = 1 0. Sommet de la parabole : x 0 = b/(2a) = 2/(2 1) = 2/2 = 1"> 0. Sommet de la parabole : x 0 = b/(2a) = 2/(2 1) = 2/2 = 1"> 0. Sommet de la parabole : x 0 = b/(2a) = 2/(2 1) = 2/2 = 1" title="(!LANG : Trouver la plus petite valeur de la fonction : Solution Sous le logarithme est à nouveau une fonction quadratique.Graphique de la parabole avec des branches vers le haut, car a \u003d 1\u003e 0. Sommet de la parabole : x 0 \u003d b / (2a) \u003d 2 / ( 2 1) \u003d 2/2 \u003d 1"> title="Trouver la plus petite valeur de la fonction : Solution Sous le logarithme se trouve à nouveau une fonction quadratique. a = 1 > 0. Sommet de la parabole : x 0 = b/(2a) = 2/(2 1) = 2/2 = 1"> !}

Trouver valeur la plus élevée fonctions : Solution : L'exposant contient une fonction quadratique Réécrivons-la sous forme normale : Il est évident que le graphe de cette fonction est une parabole, branche vers le bas (a = 1

Conséquences sur le domaine de la fonction Parfois, pour résoudre le problème B14, il ne suffit pas de trouver le sommet de la parabole. La valeur souhaitée peut se situer à la fin du segment, et pas du tout au point extrême. Si un segment n'est pas spécifié du tout dans le problème, on regarde la zone des valeurs admissibles de la fonction d'origine. À savoir:

0 2. Arithmétique Racine carrée n'existe qu'à partir de nombres non négatifs : 3. Le dénominateur de la fraction ne doit pas être nul :" title="(!LANG:1. L'argument du logarithme doit être positif : y = log a f (x) f (x) > 0 2. La racine carrée arithmétique n'existe qu'à partir de nombres non négatifs : 3. Le dénominateur de la fraction ne doit pas être égal à zéro :" class="link_thumb"> 26 !} 1. L'argument du logarithme doit être positif : y = log a f (x) f (x) > 0 2. La racine carrée arithmétique n'existe qu'à partir de nombres non négatifs : 3. Le dénominateur de la fraction ne doit pas être égal à zéro: 0 2. La racine carrée arithmétique n'existe qu'à partir de nombres non négatifs : 3. Le dénominateur de la fraction ne doit pas être égal à zéro : "> 0 2. La racine carrée arithmétique n'existe qu'à partir de nombres non négatifs : 3. Le dénominateur de la la fraction ne doit pas être égale à zéro :"> 0 2. Arithmétique, la racine carrée n'existe qu'à partir de nombres non négatifs : 3. Le dénominateur de la fraction ne doit pas être égal à zéro :" titre="(!LANG:1. L'argument logarithme doit être positif : y = log a f (x) f (x) > 0 2. Carré arithmétique la racine n'existe qu'à partir de nombres non négatifs : 3. Le dénominateur de la fraction ne doit pas être égal à zéro :"> title="1. L'argument du logarithme doit être positif : y = log a f (x) f (x) > 0 2. La racine carrée arithmétique n'existe qu'à partir de nombres non négatifs : 3. Le dénominateur de la fraction ne doit pas être égal à zéro:"> !}

Solution La racine carrée est encore une fonction quadratique. Son graphique est une parabole, mais les branches sont descendantes car a = 1
Trouvons maintenant le sommet de la parabole : x 0 = b/(2a) = (2)/(2 · (1)) = 2/(2) = 1 Le point x 0 = 1 appartient au segment ODZ et c'est bien. Considérons maintenant la valeur de la fonction au point x 0, ainsi qu'aux extrémités de l'ODZ: ​​y (3) \u003d y (1) \u003d 0 Ainsi, nous avons obtenu les nombres 2 et 0. On nous demande pour trouver le plus grand nombre 2. Réponse : 2

Attention : l'inégalité est stricte, donc les extrémités n'appartiennent pas à l'ODZ. De cette façon, le logarithme diffère de la racine, où les extrémités du segment nous conviennent assez bien. On cherche le sommet de la parabole : x 0 \u003d b / (2a) \u003d 6 / (2 (1)) \u003d 6 / (2) = 3 Mais comme les extrémités du segment ne nous intéressent pas, on considère la valeur de la fonction uniquement au point x 0 :

Y min = y(3) = log 0,5 (6 ) = = log 0,5 (18 9 5) = log 0,5 4 = 2 Réponse : -2

Le processus de recherche des valeurs les plus petites et les plus grandes d'une fonction sur un segment rappelle un vol fascinant autour d'un objet (un graphique d'une fonction) sur un hélicoptère avec tir à partir d'un canon à longue portée à certains points et en choisissant parmi ces points sont des points très spéciaux pour les coups de contrôle. Les points sont sélectionnés d'une certaine manière et selon certaines règles. Selon quelles règles ? Nous en reparlerons plus loin.

Si la fonction y = F(X) continue sur l'intervalle [ un, b] , alors il atteint sur ce segment moins et valeurs les plus élevées . Cela peut se produire soit dans points extrêmes ou aux extrémités du segment. Par conséquent, pour trouver moins et les plus grandes valeurs de la fonction , continue sur l'intervalle [ un, b] , vous devez calculer ses valeurs en tout points critiques et aux extrémités du segment, puis choisissez le plus petit et le plus grand d'entre eux.

Supposons, par exemple, qu'il soit nécessaire de déterminer la valeur maximale de la fonction F(X) sur le segment [ un, b] . Pour ce faire, trouvez tous ses points critiques se trouvant sur [ un, b] .

point critique est appelé le point auquel fonction définie, et elle dérivé est nul ou n'existe pas. Ensuite, vous devez calculer les valeurs de la fonction aux points critiques. Et, enfin, il faut comparer les valeurs de la fonction aux points critiques et aux extrémités du segment ( F(un) et F(b) ). Le plus grand de ces nombres sera la plus grande valeur de la fonction sur l'intervalle [un, b] .

Le problème de trouver les plus petites valeurs de la fonction .

On cherche ensemble les plus petites et les plus grandes valeurs de la fonction

Exemple 1. Trouver les plus petites et les plus grandes valeurs d'une fonction sur la tranche [-1, 2] .

La solution. On trouve la dérivée de cette fonction. Égalez la dérivée à zéro () et obtenez deux points critiques : et . Pour trouver les plus petites et les plus grandes valeurs d'une fonction sur un segment donné, il suffit de calculer ses valeurs aux extrémités du segment et au point , puisque le point n'appartient pas au segment [-1, 2] . Ces valeurs de fonction sont les suivantes : , , . Il s'ensuit que plus petite valeur de fonction(marqué en rouge sur le graphique ci-dessous), égal à -7, est atteint à l'extrémité droite du segment - au point , et le plus grand(également rouge sur le graphique), est égal à 9, - au point critique .

Si la fonction est continue dans un certain intervalle et que cet intervalle n'est pas un segment (mais est, par exemple, un intervalle ; la différence entre un intervalle et un segment : les points limites de l'intervalle ne sont pas inclus dans l'intervalle, mais les les points limites du segment sont inclus dans le segment), alors parmi les valeurs de la fonction, il peut ne pas y avoir la plus petite et la plus grande. Ainsi, par exemple, la fonction représentée dans la figure ci-dessous est continue sur ]-∞, +∞[ et n'a pas la plus grande valeur.

Cependant, pour tout intervalle (fermé, ouvert ou infini), la propriété suivante des fonctions continues est valable.

Exemple 4. Trouver les plus petites et les plus grandes valeurs d'une fonction sur la tranche [-1, 3] .

La solution. On trouve la dérivée de cette fonction comme la dérivée du quotient :

.

On égalise la dérivée à zéro, ce qui nous donne un point critique : . Il appartient à l'intervalle [-1, 3] . Pour trouver les plus petites et les plus grandes valeurs d'une fonction sur un segment donné, on trouve ses valeurs aux extrémités du segment et au point critique trouvé :

Comparons ces valeurs. Conclusion : égal à -5/13, au point et la plus grande valeurégal à 1 au point .

Nous continuons à rechercher ensemble les plus petites et les plus grandes valeurs de la fonction

Il y a des enseignants qui, au sujet de la recherche des valeurs les plus petites et les plus grandes d'une fonction, ne donnent pas aux élèves des exemples plus compliqués que ceux que nous venons de considérer, c'est-à-dire ceux dans lesquels la fonction est un polynôme ou une fraction, le numérateur et dont le dénominateur sont des polynômes. Mais nous ne nous limiterons pas à de tels exemples, car parmi les enseignants, il y a des amateurs de faire réfléchir les élèves en entier (tableau des dérivés). Par conséquent, le logarithme et la fonction trigonométrique seront utilisés.

Exemple 6. Trouver les plus petites et les plus grandes valeurs d'une fonction sur la tranche .

La solution. On trouve la dérivée de cette fonction comme dérivé du produit :

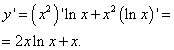
On égalise la dérivée à zéro, ce qui donne un point critique : . Il appartient au segment. Pour trouver les plus petites et les plus grandes valeurs d'une fonction sur un segment donné, on trouve ses valeurs aux extrémités du segment et au point critique trouvé :

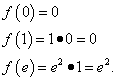
Le résultat de toutes les actions : la fonction atteint sa valeur minimale, égal à 0, en un point et en un point et la plus grande valeurégal à e² , au point .

Exemple 7. Trouver les plus petites et les plus grandes valeurs d'une fonction sur la tranche .

La solution. On trouve la dérivée de cette fonction :

Égalez la dérivée à zéro :

Le seul point critique appartient au segment . Pour trouver les plus petites et les plus grandes valeurs d'une fonction sur un segment donné, on trouve ses valeurs aux extrémités du segment et au point critique trouvé :

Conclusion: la fonction atteint sa valeur minimale, égal à , au point et la plus grande valeur, égal à , au point .

Dans les problèmes extrémaux appliqués, trouver les plus petites (plus grandes) valeurs de fonction, en règle générale, se réduit à trouver le minimum (maximum). Mais ce ne sont pas les minima ou les maxima eux-mêmes qui présentent le plus grand intérêt pratique, mais les valeurs de l'argument auquel ils sont atteints. Lors de la résolution de problèmes appliqués, une difficulté supplémentaire se pose - la compilation de fonctions décrivant le phénomène ou le processus considéré.

Exemple 8 Un réservoir d'une capacité de 4, ayant la forme d'un parallélépipède à base carrée et ouvert au sommet, doit être étamé. Quelles doivent être les dimensions du réservoir pour qu'il prenne moindre montant Matériel?

La solution. Laisser X- côté socle h- hauteur du réservoir, S- sa superficie hors couverture, V- son volume. La surface du réservoir est exprimée par la formule , c'est-à-dire est une fonction de deux variables. Exprimer S en fonction d'une variable, on utilise le fait que , d'où . Remplacer l'expression trouvée h dans la formule de S:

Examinons cette fonction pour un extremum. Elle est définie et différentiable partout dans ]0, +∞[ , et

.

Nous assimilons la dérivée à zéro () et trouvons le point critique. De plus, en , la dérivée n'existe pas, mais cette valeur n'est pas comprise dans le domaine de définition et ne peut donc pas être un point extremum. Donc, - le seul point critique. Vérifions la présence d'un extremum en utilisant le deuxième critère suffisant. Trouvons la dérivée seconde. Lorsque la dérivée seconde est supérieure à zéro (). Cela signifie que lorsque la fonction atteint un minimum . Car ce minimum - le seul extremum de cette fonction, c'est sa plus petite valeur. Ainsi, le côté de la base du réservoir doit être égal à 2 m et sa hauteur.

Exemple 9 Du paragraphe UN, situé sur la voie ferrée, jusqu'au point DE, à distance de celui-ci je, les marchandises doivent être transportées. Le coût de transport d'une unité de poids par unité de distance par chemin de fer est égal à , et par route il est égal à . Jusqu'à quel point M lignes chemin de fer une autoroute devrait être construite pour que le transport des marchandises MAIS dans DEétait le plus économique UN B chemin de fer est supposé être droit) ?

Comment trouver les plus grandes et les plus petites valeurs d'une fonction sur un segment ?

Pour ça nous suivons l'algorithme bien connu:

1 . On retrouve les fonctions ODZ.

2 . Trouver la dérivée d'une fonction

3 . Égaliser la dérivée à zéro

4 . Nous trouvons les intervalles auxquels la dérivée conserve son signe, et à partir d'eux nous déterminons les intervalles d'augmentation et de diminution de la fonction :

Si sur l'intervalle I la dérivée de la fonction 0" title="(!LANG:f^(prime)(x)>0">, то функция !} augmente sur cet intervalle.

Si sur l'intervalle I la dérivée de la fonction , alors la fonction diminue sur cet intervalle.

5 . Nous trouvons points maximum et minimum de la fonction.

À le point maximum de la fonction, la dérivée change de signe de "+" à "-".

À point minimum de la fonctionla dérivée change de signe de "-" à "+".

6 . On trouve la valeur de la fonction aux extrémités du segment,

• puis on compare la valeur de la fonction aux extrémités du segment et aux points maximaux, et choisissez la plus grande d'entre elles si vous avez besoin de trouver la plus grande valeur de la fonction
• soit on compare la valeur de la fonction aux extrémités du segment et aux points minimaux, et choisissez la plus petite d'entre elles si vous avez besoin de trouver la plus petite valeur de la fonction

Cependant, selon le comportement de la fonction sur l'intervalle, cet algorithme peut être considérablement réduit.

Considérez la fonction . Le graphique de cette fonction ressemble à ceci :

Considérons plusieurs exemples de résolution de problèmes de l'Open Task Bank pour

une . Tâche B15 (#26695)

Sur la coupe.

1. La fonction est définie pour toutes les valeurs réelles de x

Évidemment, cette équation n'a pas de solutions, et la dérivée est positive pour toutes les valeurs de x. Par conséquent, la fonction augmente et prend la plus grande valeur à l'extrémité droite de l'intervalle, c'est-à-dire à x=0.

Réponse : 5.

2 . Tâche B15 (n° 26702)

Trouver la plus grande valeur d'une fonction sur la tranche.

Fonction 1.ODZ title="(!LANG:x(pi)/2+(pi)k, k(in)(bbZ)">!}

La dérivée est nulle en , cependant, en ces points, elle ne change pas de signe :

Par conséquent, title="(!LANG:3/(cos^2(x))>=3">, значит, title="3/(cos^2(x))-3>=0">, то есть производная при всех допустимых значених х неотрицательна, следовательно, функция !} augmente et prend la plus grande valeur à l'extrémité droite de l'intervalle, à .

Pour bien comprendre pourquoi la dérivée ne change pas de signe, nous transformons l'expression de la dérivée comme suit :

Titre="(!LANG:y^(prime)=3/(cos^2(x))-3=(3-3cos^2(x))/(cos^2(x))=(3sin^2 (x))/(cos^2(x))=3tg^2(x)>=0">!}

Réponse : 5.

3 . Tâche B15 (#26708)

Trouver la plus petite valeur de la fonction sur l'intervalle .

1. Fonctions ODZ : title="(!LANG:x(pi)/2+(pi)k, k(in)(bbZ)">!}

Plaçons les racines de cette équation sur un cercle trigonométrique.

L'intervalle contient deux nombres : et

Mettons les signes. Pour cela, on détermine le signe de la dérivée au point x=0 : . En passant par les points et la dérivée change de signe.

Représentons le changement de signe de la dérivée de la fonction sur la ligne de coordonnées :

Évidemment, le point est un point minimum (où la dérivée change de signe de "-" à "+"), et pour trouver la plus petite valeur de la fonction sur l'intervalle, vous devez comparer les valeurs de la fonction au point minimum et à l'extrémité gauche du segment, .

En pratique, il est assez courant d'utiliser la dérivée pour calculer la plus grande et la plus petite valeur d'une fonction. Nous effectuons cette action lorsque nous découvrons comment minimiser les coûts, augmenter les bénéfices, calculer la charge optimale sur la production, etc., c'est-à-dire dans les cas où il est nécessaire de déterminer la valeur optimale d'un paramètre. Pour résoudre correctement de tels problèmes, il faut bien comprendre ce que sont la plus grande et la plus petite valeur d'une fonction.

Yandex.RTB R-A-339285-1

Habituellement, nous définissons ces valeurs dans un certain intervalle x , qui à son tour peut correspondre à toute la portée de la fonction ou à une partie de celle-ci. Il peut s'agir soit d'un segment [ a ; b ] , et intervalle ouvert (a ; b) , (a ; b ] , [ a ; b) , intervalle infini (a ; b) , (a ; b ] , [ a ; b) ou intervalle infini - ∞ ; une , (- ∞ ; une ] , [ une ; + ∞) , (- ∞ ; + ∞) .

Dans cet article, nous décrirons comment la plus grande et la plus petite valeur d'une fonction explicitement donnée avec une variable y=f(x) y = f (x) est calculée.

Définitions basiques

Nous commençons, comme toujours, par la formulation des principales définitions.

Définition 1

La plus grande valeur de la fonction y = f (x) sur un intervalle x est la valeur m a x y = f (x 0) x ∈ X , qui, pour toute valeur x x ∈ X , x ≠ x 0, rend l'inégalité f (x ) ≤ f (x 0) .

Définition 2

La plus petite valeur de la fonction y = f (x) sur un intervalle x est la valeur m i n x ∈ X y = f (x 0) , ce qui, pour toute valeur x ∈ X , x ≠ x 0, rend l'inégalité f(X f (x) ≥ f(x0) .

Ces définitions sont assez évidentes. Il peut être encore plus simple de dire ceci : la plus grande valeur d'une fonction est sa plus grande valeur dans un intervalle connu à l'abscisse x 0, et la plus petite est la plus petite valeur acceptée dans le même intervalle à x 0.

Définition 3

Les points stationnaires sont les valeurs de l'argument de la fonction auxquelles sa dérivée devient 0.

Pourquoi avons-nous besoin de savoir ce que sont les points stationnaires ? Pour répondre à cette question, rappelons le théorème de Fermat. Il en résulte qu'un point stationnaire est un point où se situe l'extremum d'une fonction différentiable (c'est-à-dire son minimum ou maximum local). Par conséquent, la fonction prendra la valeur la plus petite ou la plus grande sur un certain intervalle exactement à l'un des points stationnaires.

Une autre fonction peut prendre la valeur la plus grande ou la plus petite aux points où la fonction elle-même est définie et sa première dérivée n'existe pas.

La première question qui se pose lors de l'étude de ce sujet est : dans tous les cas, peut-on déterminer la valeur maximale ou minimale d'une fonction sur un intervalle donné ? Non, nous ne pouvons pas le faire lorsque les frontières de l'intervalle donné coïncideront avec les frontières du domaine de définition, ou si nous avons affaire à un intervalle infini. Il arrive aussi qu'une fonction dans un intervalle donné ou à l'infini prenne des valeurs infiniment petites ou infiniment grandes. Dans ces cas, il n'est pas possible de déterminer la valeur la plus grande et/ou la plus petite.

Ces moments deviendront plus compréhensibles après l'image sur les graphiques :

La première figure nous montre une fonction qui prend les plus grandes et les plus petites valeurs (m a x y et m i n y) aux points stationnaires situés sur l'intervalle [ - 6 ; 6].

Examinons en détail le cas indiqué dans le second graphique. Changeons la valeur du segment en [ 1 ; 6] et nous obtenons que la plus grande valeur de la fonction sera atteinte au point avec l'abscisse dans la limite droite de l'intervalle, et la plus petite - au point stationnaire.

Sur la troisième figure, les abscisses des points représentent les points frontières du segment [ - 3 ; 2]. Ils correspondent à la plus grande et à la plus petite valeur de la fonction donnée.

Regardons maintenant la quatrième image. Dans celui-ci, la fonction prend m a x y (la plus grande valeur) et m i n y (la plus petite valeur) aux points stationnaires de l'intervalle ouvert (- 6 ; 6) .

Si l'on prend l'intervalle [ 1 ; 6) , alors on peut dire que la plus petite valeur de la fonction sur celle-ci sera atteinte en un point stationnaire. Nous ne connaîtrons pas la valeur maximale. La fonction pourrait prendre la plus grande valeur à x égale à 6 si x = 6 appartenait à l'intervalle. C'est ce cas qui est représenté sur la figure 5.

Sur le graphique 6, cette fonction acquiert la plus petite valeur dans le bord droit de l'intervalle (- 3 ; 2 ] , et nous ne pouvons pas tirer de conclusions définitives sur la plus grande valeur.

Sur la figure 7, on voit que la fonction aura m a x y au point stationnaire, d'abscisse égale à 1 . La fonction atteint sa valeur minimale à la limite de l'intervalle avec côté droit. A moins l'infini, les valeurs de la fonction approcheront asymptotiquement y = 3 .

Si on prend un intervalle x ∈ 2 ; + ∞ , alors nous verrons que la fonction donnée ne prendra sur elle ni la plus petite ni la plus grande valeur. Si x tend vers 2, alors les valeurs de la fonction tendront vers moins l'infini, puisque la droite x = 2 est une asymptote verticale. Si l'abscisse tend vers plus l'infini, alors les valeurs de la fonction approcheront asymptotiquement y = 3. C'est le cas illustré à la figure 8.

Dans ce paragraphe, nous donnerons une séquence d'actions qui doivent être effectuées pour trouver la plus grande ou la plus petite valeur d'une fonction sur un certain intervalle.

1. Trouvons d'abord le domaine de la fonction. Vérifions si le segment spécifié dans la condition y est inclus.
2. Calculons maintenant les points contenus dans ce segment où la dérivée première n'existe pas. On les trouve le plus souvent dans des fonctions dont l'argument est écrit sous le signe module, ou dans fonctions de puissance, dont l'exposant est un nombre fractionnairement rationnel.
3. Ensuite, nous découvrons quels points stationnaires appartiennent à un segment donné. Pour ce faire, vous devez calculer la dérivée de la fonction, puis l'assimiler à 0 et résoudre l'équation résultante, puis choisir les racines appropriées. Si nous n'obtenons pas un seul point stationnaire ou qu'ils ne tombent pas dans un segment donné, nous passons à l'étape suivante.
4. Déterminons quelles valeurs la fonction prendra aux points stationnaires donnés (le cas échéant), ou aux points où la première dérivée n'existe pas (le cas échéant), ou nous calculons les valeurs pour x = a et x = b.
5. 5. Nous avons une série de valeurs de fonction, parmi lesquelles nous devons maintenant choisir la plus grande et la plus petite. Ce seront les valeurs les plus grandes et les plus petites de la fonction que nous devons trouver.

Voyons comment appliquer correctement cet algorithme lors de la résolution de problèmes.

Exemple 1

Condition: la fonction y = x 3 + 4 x 2 est donnée. Déterminer sa plus grande et sa plus petite valeur sur les segments [ 1 ; 4 ] et [ - 4 ; - une ] .

La solution:

Commençons par trouver le domaine de cette fonction. Dans ce cas, ce sera l'ensemble de tous les nombres réels sauf 0 . Autrement dit, D (y) : x ∈ (- ∞ ; 0) ∪ 0 ; +∞ . Les deux segments spécifiés dans la condition seront à l'intérieur de la zone de définition.

On calcule maintenant la dérivée de la fonction selon la règle de différenciation d'une fraction :

y "= x 3 + 4 x 2" = x 3 + 4 " x 2 - x 3 + 4 x 2" x 4 = = 3 x 2 x 2 - (x 3 - 4) 2 x x 4 = x 3 - 8 x3

Nous avons appris que la dérivée de la fonction existera en tout point des segments [ 1 ; 4 ] et [ - 4 ; - une ] .

Maintenant, nous devons déterminer les points stationnaires de la fonction. Faisons cela avec l'équation x 3 - 8 x 3 = 0. Il n'a qu'une seule racine réelle, qui est 2. Ce sera un point stationnaire de la fonction et tombera dans le premier segment [ 1 ; quatre ] .

Calculons les valeurs de la fonction aux extrémités du premier segment et au point donné, c'est-à-dire pour x = 1 , x = 2 et x = 4 :

y(1) = 1 3 + 4 1 2 = 5 y(2) = 2 3 + 4 2 2 = 3 y(4) = 4 3 + 4 4 2 = 4 1 4

Nous avons obtenu que la plus grande valeur de la fonction m a x y x ∈ [ 1 ; 4 ] = y (2) = 3 sera atteint à x = 1 , et le plus petit m i n y x ∈ [ 1 ; 4 ] = y (2) = 3 – à x = 2 .

Le deuxième segment ne comprend aucun point stationnaire, nous devons donc calculer les valeurs de la fonction uniquement aux extrémités du segment donné :

y (- 1) = (- 1) 3 + 4 (- 1) 2 = 3

Par conséquent, m une x y x ∈ [ - 4 ; - 1 ] = y (- 1) = 3 , m je n y X ∈ [ - 4 ; - 1 ] = y (- 4) = - 3 3 4 .

Réponse: Pour le segment [ 1 ; 4 ] - m une X y X ∈ [ 1 ; 4 ] = y (2) = 3 , m je n y X ∈ [ 1 ; 4 ] = y (2) = 3 , pour le segment [ - 4 ; - 1 ] - m une X y X ∈ [ - 4 ; - 1 ] = y (- 1) = 3 , m je n y X ∈ [ - 4 ; - 1 ] = y (- 4) = - 3 3 4 .

Voir l'image:

Avant d'étudier Par ici, nous vous conseillons de répéter comment calculer correctement la limite unilatérale et la limite à l'infini, ainsi que d'apprendre les méthodes de base pour les trouver. Pour trouver la plus grande et/ou la plus petite valeur d'une fonction sur un intervalle ouvert ou infini, nous effectuons les étapes suivantes dans l'ordre.

1. Vous devez d'abord vérifier si l'intervalle donné sera un sous-ensemble du domaine de la fonction donnée.
2. Déterminons tous les points contenus dans l'intervalle requis et pour lesquels la dérivée première n'existe pas. Habituellement, ils se produisent dans les fonctions où l'argument est enfermé dans le signe du module et dans les fonctions de puissance avec un exposant fractionnellement rationnel. Si ces points manquent, vous pouvez passer à l'étape suivante.
3. Maintenant, nous déterminons quels points stationnaires tombent dans un intervalle donné. Tout d'abord, nous assimilons la dérivée à 0, résolvons l'équation et trouvons des racines appropriées. Si nous n'avons pas un seul point stationnaire ou qu'ils ne se situent pas dans l'intervalle spécifié, nous procédons immédiatement à d'autres actions. Ils sont déterminés par le type d'intervalle.

• Si l'intervalle ressemble à [ a ; b) , alors nous devons calculer la valeur de la fonction au point x = a et la limite unilatérale lim x → b - 0 f (x) .
• Si l'intervalle a la forme (a ; b ] , alors nous devons calculer la valeur de la fonction au point x = b et la limite unilatérale lim x → a + 0 f (x) .
• Si l'intervalle a la forme (a ; b) , alors nous devons calculer les limites unilatérales lim x → b - 0 f (x) , lim x → a + 0 f (x) .
• Si l'intervalle ressemble à [ a ; + ∞) , alors il faut calculer la valeur au point x = a et la limite à plus l'infini lim x → + ∞ f (x) .
• Si l'intervalle ressemble à (- ∞ ; b ] , on calcule la valeur au point x = b et la limite à moins l'infini lim x → - ∞ f (x) .
• Si - ∞ ; b , alors on considère la limite unilatérale lim x → b - 0 f (x) et la limite à moins l'infini lim x → - ∞ f (x)
• Si - ∞ ; + ∞ , alors on considère les limites à moins et plus l'infini lim x → + ∞ f (x) , lim x → - ∞ f (x) .

1. À la fin, vous devez tirer une conclusion basée sur les valeurs obtenues de la fonction et des limites. Il existe de nombreuses options ici. Ainsi, si la limite unilatérale est égale à moins l'infini ou plus l'infini, alors il est immédiatement clair que rien ne peut être dit sur la plus petite et la plus grande valeur de la fonction. Ci-dessous, nous allons considérer un exemple typique. Descriptifs détaillés vous aider à comprendre ce qui est quoi. Si nécessaire, vous pouvez revenir aux figures 4 à 8 dans la première partie du matériel.

Condition : étant donné une fonction y = 3 e 1 x 2 + x - 6 - 4 . Calculer sa plus grande et sa plus petite valeur dans les intervalles - ∞ ; - 4 , - ∞ ; - 3 , (- 3 ; 1 ] , (- 3 ; 2) , [ 1 ; 2) , 2 ; + ∞ , [ 4 ; +∞) .

La solution

Tout d'abord, nous trouvons le domaine de la fonction. Le dénominateur de la fraction est un trinôme carré, qui ne doit pas tendre vers 0 :

x 2 + x - 6 = 0 ré = 1 2 - 4 1 (- 6) = 25 x 1 = - 1 - 5 2 = - 3 x 2 = - 1 + 5 2 = 2 ⇒ ré (y) : x ∈ (- ∞ ; - 3) ∪ (- 3 ; 2) ∪ (2 ; + ∞)

Nous avons obtenu la portée de la fonction, à laquelle appartiennent tous les intervalles spécifiés dans la condition.

Maintenant, différencions la fonction et obtenons :

y "= 3 e 1 X 2 + X - 6 - 4" = 3 e 1 X 2 + X - 6 " = 3 e 1 X 2 + X - 6 1 X 2 + X - 6 " == 3 e 1 X 2 + x - 6 1 "x 2 + x - 6 - 1 x 2 + x - 6" (x 2 + x - 6) 2 = - 3 (2 x + 1) e 1 x 2 + x - 6 x 2 + x - 6 2

Par conséquent, les dérivées d'une fonction existent sur tout le domaine de sa définition.

Passons à la recherche de points fixes. La dérivée de la fonction devient 0 à x = - 1 2 . C'est un point stationnaire qui est dans les intervalles (- 3 ; 1 ] et (- 3 ; 2) .

Calculons la valeur de la fonction à x = - 4 pour l'intervalle (- ∞ ; - 4 ] , ainsi que la limite à moins l'infini :

y (- 4) \u003d 3 e 1 (- 4) 2 + (- 4) - 6 - 4 \u003d 3 e 1 6 - 4 ≈ - 0. 456 lim X → - ∞ 3 e 1 X 2 + X - 6 = 3 e 0 - 4 = - 1

Puisque 3 e 1 6 - 4 > - 1 , alors m a x y x ∈ (- ∞ ; - 4 ] = y (- 4) = 3 e 1 6 - 4 . Cela ne permet pas de déterminer de manière unique la plus petite valeur de la fonction. On ne peut que conclure qu'il y a une limite en dessous de -1 , puisque c'est à cette valeur que la fonction s'approche asymptotiquement à moins l'infini.

Une caractéristique du deuxième intervalle est qu'il n'a pas un seul point stationnaire et pas une seule limite stricte. Par conséquent, nous ne pouvons pas calculer la plus grande ou la plus petite valeur de la fonction. En définissant la limite à moins l'infini et comme l'argument tend vers - 3 sur le côté gauche, on obtient uniquement la plage de valeurs :

lim x → - 3 - 0 3 e 1 x 2 + x - 6 - 4 = lim x → - 3 - 0 3 e 1 (x + 3) (x - 3) - 4 = 3 e 1 (- 3 - 0 + 3) (- 3 - 0 - 2) - 4 = = 3 e 1 (+ 0) - 4 = 3 e + ∞ - 4 = + ∞ lim X → - ∞ 3 e 1 X 2 + x - 6 - 4 = 3 et 0 - 4 = - 1

Cela signifie que les valeurs de la fonction seront situées dans l'intervalle - 1 ; +∞

Pour trouver la valeur maximale de la fonction dans le troisième intervalle, on détermine sa valeur au point stationnaire x = - 1 2 si x = 1 . Nous avons également besoin de connaître la limite unilatérale pour le cas où l'argument tend vers - 3 du côté droit :

y - 1 2 = 3 e 1 - 1 2 2 + - 1 2 - 6 - 4 = 3 e 4 25 - 4 ≈ - 1 . 444 y (1) = 3 e 1 1 2 + 1 - 6 - 4 ≈ - 1 . 644 lim X → - 3 + 0 3 e 1 x 2 + x - 6 - 4 = lim X → - 3 + 0 3 e 1 (x + 3) (x - 2) - 4 = 3 e 1 - 3 + 0 + 3 (- 3 + 0 - 2) - 4 = = 3 e 1 (- 0) - 4 = 3 e - ∞ - 4 = 3 0 - 4 = - 4

Il s'est avéré que la fonction prendra la plus grande valeur en un point stationnaire m a x y x ∈ (3 ; 1 ] = y - 1 2 = 3 e - 4 25 - 4. Quant à la plus petite valeur, nous ne pouvons pas la déterminer. Tout ce que nous savoir , est la présence d' une borne inférieure à - 4 .

Pour l'intervalle (- 3 ; 2), reprenons les résultats du calcul précédent et calculons à nouveau ce à quoi la limite unilatérale est égale lorsqu'elle tend vers 2 depuis le côté gauche :

y - 1 2 = 3 e 1 - 1 2 2 + - 1 2 - 6 - 4 = 3 e - 4 25 - 4 ≈ - 1 . 444 lim X → - 3 + 0 3 e 1 x 2 + x - 6 - 4 = - 4 lim X → 2 - 0 3 e 1 x 2 + x - 6 - 4 = lim X → - 3 + 0 3 e 1 (x + 3) (x - 2) - 4 = 3 e 1 (2 - 0 + 3) (2 - 0 - 2) - 4 = = 3 e 1 - 0 - 4 = 3 e - ∞ - 4 = 3 0 - 4 = - 4

Par conséquent, m a x y x ∈ (- 3 ; 2) = y - 1 2 = 3 e - 4 25 - 4 , et la plus petite valeur ne peut pas être déterminée, et les valeurs de la fonction sont délimitées par le bas par le nombre - 4 .

Sur la base de ce que nous avons fait dans les deux calculs précédents, nous pouvons affirmer que sur l'intervalle [ 1 ; 2) la fonction prendra la plus grande valeur à x = 1, et il est impossible de trouver la plus petite.

Sur l'intervalle (2 ; + ∞), la fonction n'atteindra ni la plus grande ni la plus petite valeur, c'est-à-dire il prendra des valeurs de l'intervalle - 1 ; +∞ .

lim x → 2 + 0 3 e 1 x 2 + x - 6 - 4 = lim x → - 3 + 0 3 e 1 (x + 3) (x - 2) - 4 = 3 e 1 (2 + 0 + 3 ) (2 + 0 - 2) - 4 = = 3 e 1 (+ 0) - 4 = 3 e + ∞ - 4 = + ∞ lim X → + ∞ 3 e 1 X 2 + X - 6 - 4 = 3 e 0 - 4 = - 1

Après avoir calculé à quoi la valeur de la fonction sera égale à x = 4 , nous découvrons que m a x y x ∈ [ 4 ; + ∞) = y (4) = 3 e 1 14 - 4 , et la fonction donnée à plus l'infini s'approchera asymptotiquement de la ligne y = - 1 .

Comparons ce que nous avons obtenu dans chaque calcul avec le graphique de la fonction donnée. Sur la figure, les asymptotes sont représentées par des pointillés.

C'est tout ce dont nous voulions parler pour trouver la plus grande et la plus petite valeur d'une fonction. Ces séquences d'actions que nous avons données vous aideront à effectuer les calculs nécessaires aussi rapidement et simplement que possible. Mais rappelez-vous qu'il est souvent utile de savoir d'abord sur quels intervalles la fonction va diminuer et sur lesquels elle va augmenter, après quoi d'autres conclusions peuvent être tirées. Ainsi, vous pouvez déterminer plus précisément la valeur la plus grande et la plus petite de la fonction et justifier les résultats.

Si vous remarquez une erreur dans le texte, veuillez le mettre en surbrillance et appuyer sur Ctrl+Entrée

Chers amis! Le groupe de tâches liées à la dérivée comprend des tâches - dans la condition, le graphe de la fonction est donné, plusieurs points sur ce graphe et la question est :

À quel point la valeur de la dérivée est-elle la plus grande (la plus petite) ?

Répétons brièvement :

La dérivée en un point est coefficient angulaire tangente passant parce point sur le graphique.

Àle coefficient global de la tangente à son tour égal à la tangente la pente de cette tangente.

*Il s'agit de l'angle entre la tangente et l'axe des x.

1. Sur des intervalles de fonction croissante, la dérivée a valeur positive.

2. Sur les intervalles de sa décroissance, la dérivée a Sens négatif.

Considérez le croquis suivant :

Aux points 1,2,4, la dérivée de la fonction a une valeur négative, puisque ces points appartiennent aux intervalles décroissants.

Aux points 3,5,6, la dérivée de la fonction a une valeur positive, puisque ces points appartiennent aux intervalles d'augmentation.

Comme vous pouvez le voir, tout est clair avec la valeur de la dérivée, c'est-à-dire qu'il n'est pas difficile de déterminer son signe (positif ou négatif) à un certain point du graphique.

De plus, si nous construisons mentalement des tangentes en ces points, nous verrons que les droites passant par les points 3, 5 et 6 forment des angles avec l'axe oX compris entre 0 et 90°, et les droites passant par les points 1, 2 et 4 forment avec l'axe oX, des angles allant de 90 o à 180 o.

* La relation est claire : les tangentes passant par des points appartenant à des intervalles de fonctions croissantes forment des angles aigus avec l'axe oX, les tangentes passant par des points appartenant à des intervalles de fonctions décroissantes forment des angles obtus avec l'axe oX.

Maintenant la question importante !

Comment évolue la valeur de la dérivée ? Après tout, la tangente points différents arts graphiques fonction continue forme des angles différents, selon le point du graphique par lequel il passe.

*Ou, parlant langage clair, la tangente est située, pour ainsi dire, "plus horizontalement" ou "plus verticalement". Voir:

Les lignes droites forment des angles avec l'axe oX allant de 0 à 90 o

Les lignes droites forment des angles avec l'axe oX allant de 90 o à 180 o

Donc s'il y a des questions :

- Auquel des points donnés sur le graphique la valeur de la dérivée a-t-elle la plus petite valeur ?

- Auquel des points donnés du graphique la valeur de la dérivée a-t-elle la plus grande valeur ?

alors pour la réponse il faut comprendre comment la valeur de la tangente de l'angle de la tangente change dans la plage de 0 à 180 o.

*Comme déjà mentionné, la valeur de la dérivée de la fonction en un point est égale à la tangente de la pente de la tangente à l'axe des abscisses.

La valeur de la tangente change comme suit :

Lorsque la pente de la droite passe de 0 o à 90 o, la valeur de la tangente, et donc de la dérivée, passe de 0 à +∞, respectivement ;

Lorsque la pente de la droite passe de 90 o à 180 o, la valeur de la tangente, et donc de la dérivée, change en conséquence –∞ en 0.

Cela peut être clairement vu sur le graphique de la fonction tangente :

En termes simples :

Lorsque l'angle d'inclinaison de la tangente est de 0 o à 90 o

Plus il est proche de 0 o, plus la valeur de la dérivée sera proche de zéro (du côté positif).

Plus l'angle est proche de 90°, plus la valeur de la dérivée augmentera vers +∞.

Lorsque l'angle d'inclinaison de la tangente est de 90 o à 180 o

Plus il est proche de 90 o, plus la valeur de la dérivée va décroître vers –∞.

Plus l'angle est proche de 180°, plus la valeur de la dérivée sera proche de zéro (du côté négatif).

317543. La figure montre un graphique de la fonction y = F(X) et points marqués–2, –1, 1, 2. Auquel de ces points la valeur de la dérivée est-elle la plus grande ? Veuillez indiquer ce point dans votre réponse.

Nous avons quatre points : deux d'entre eux appartiennent aux intervalles sur lesquels la fonction décroît (ce sont les points –1 et 1) et deux aux intervalles sur lesquels la fonction augmente (ce sont les points –2 et 2).

Nous pouvons immédiatement conclure qu'aux points -1 et 1 la dérivée a une valeur négative, aux points -2 et 2 elle a une valeur positive. Par conséquent, dans ce cas, il est nécessaire d'analyser les points -2 et 2 et de déterminer lequel d'entre eux aura la plus grande valeur. Construisons des tangentes passant par les points indiqués :

La valeur de la tangente de l'angle entre la droite a et l'axe des abscisses sera plus de valeur la tangente de l'angle entre la ligne b et cet axe. Cela signifie que la valeur de la dérivée au point -2 sera la plus grande.

Répondons à la question suivante : en quel point -2, -1, 1 ou 2 la valeur de la dérivée est-elle la plus grande négative ? Veuillez indiquer ce point dans votre réponse.

La dérivée aura une valeur négative aux points appartenant aux intervalles décroissants, donc considérons les points -2 et 1. Construisons les tangentes qui les traversent :

On voit ça angle obtus entre la droite b et l'axe oX est "plus proche" de 180 sur , donc sa tangente sera supérieure à la tangente de l'angle formé par la droite a et l'axe des abscisses.

Ainsi, au point x = 1, la valeur de la dérivée sera la plus grande négative.

317544. La figure montre un graphique de la fonction y = F(X) et points marqués–2, –1, 1, 4. Auquel de ces points la valeur de la dérivée est-elle la plus petite ? Veuillez indiquer ce point dans votre réponse.

Nous avons quatre points : deux d'entre eux appartiennent aux intervalles sur lesquels la fonction décroît (ce sont les points –1 et 4) et deux aux intervalles sur lesquels la fonction croît (ce sont les points –2 et 1).

Nous pouvons immédiatement conclure qu'aux points -1 et 4 la dérivée a une valeur négative, aux points -2 et 1 elle a une valeur positive. Par conséquent, dans ce cas, il est nécessaire d'analyser les points -1 et 4 et de déterminer lequel d'entre eux aura la plus petite valeur. Construisons des tangentes passant par les points indiqués :

La valeur de la tangente de l'angle entre la droite a et l'axe des abscisses sera supérieure à la valeur de la tangente de l'angle entre la droite b et cet axe. Cela signifie que la valeur de la dérivée au point x = 4 sera la plus petite.

Réponse : 4

J'espère que je ne vous "surcharge" pas avec la quantité d'écriture. En fait, tout est très simple, il suffit de comprendre les propriétés de la dérivée, sa signification géométrique et comment la valeur de la tangente de l'angle passe de 0 à 180°.

1. Tout d'abord, déterminez les signes de la dérivée en ces points (+ ou -) et sélectionnez les points nécessaires (selon la question posée).

2. Construisez des tangentes en ces points.

3. À l'aide du tracé tangésoïde, marquez schématiquement les coins et affichezAlexandre.

P.S: Je vous serais reconnaissant de parler du site dans les réseaux sociaux.