Gerader Bogen, flacher Querbogen. Querbiegung des Stabes Ermittlung der Auflagerreaktionen
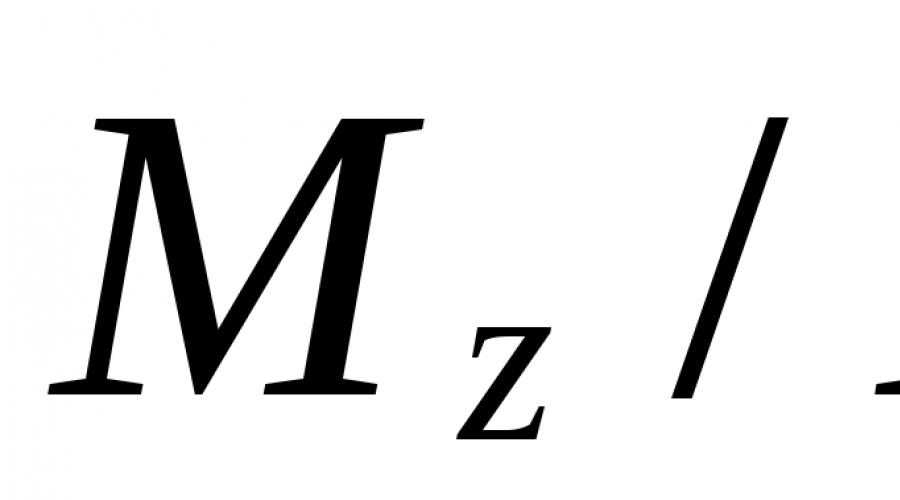
Lesen Sie auch
Gerader Querbogen tritt auf, wenn alle Lasten senkrecht zur Achse der Stange wirken, in derselben Ebene liegen und außerdem die Ebene ihrer Wirkung mit einer der zentralen Hauptträgheitsachsen des Abschnitts zusammenfällt. Die gerade Querbiegung ist eine einfache Widerstandsart flacher Spannungszustand, d.h. zwei Hauptspannungen sind ungleich Null. Bei dieser Art der Verformung entstehen innere Kräfte: Querkraft und Biegemoment. Ein Sonderfall von direkt Querbiegung Ist reine Biegung Bei einem solchen Widerstand gibt es Belastungsbereiche, in denen die Querkraft Null wird und das Biegemoment ungleich Null ist. In den Querschnitten der Stäbe entstehen bei direkter Querbiegung Normal- und Tangentialspannungen. Spannungen sind eine Funktion der inneren Kraft, in diesem Fall sind Normalspannungen eine Funktion des Biegemoments und Tangentialspannungen eine Funktion der Scherkraft. Für die direkte Querbiegung werden mehrere Hypothesen aufgestellt:
1) Die vor der Verformung flachen Querschnitte des Balkens bleiben nach der Verformung flach und orthogonal zur neutralen Schicht (Hypothese der ebenen Querschnitte oder Hypothese von J. Bernoulli). Diese Hypothese ist bei reiner Biegung erfüllt und wird verletzt, wenn Scherkräfte, Scherspannungen und Winkelverformungen auftreten.
2) Es besteht kein gegenseitiger Druck zwischen den Längsschichten (Hypothese des Nichtdrucks der Fasern). Aus dieser Hypothese folgt, dass Längsfasern einer einachsigen Spannung oder Kompression ausgesetzt sind, daher gilt bei reiner Biegung das Hookesche Gesetz.
Ein Stab, der sich einer Biegung unterzieht, wird genannt Strahl. Beim Biegen dehnt sich ein Teil der Fasern, der andere Teil zieht sich zusammen. Die zwischen den gestreckten und komprimierten Fasern liegende Faserschicht wird als bezeichnet neutrale Schicht, es verläuft durch den Schwerpunkt der Abschnitte. Die Schnittlinie mit dem Querschnitt des Balkens wird aufgerufen neutrale Achse. Basierend auf den eingeführten Hypothesen zur reinen Biegung wurde eine Formel zur Bestimmung erstellt normaler Stress, das auch zum direkten Querbiegen verwendet wird. Die Normalspannung kann mithilfe der linearen Beziehung (1) ermittelt werden, bei der das Verhältnis des Biegemoments zum axialen Trägheitsmoment (  ) in einem bestimmten Abschnitt ist ein konstanter Wert und der Abstand ( j) entlang der Ordinatenachse vom Schwerpunkt des Abschnitts bis zum Punkt, an dem die Spannung bestimmt wird, variiert von 0 bis
) in einem bestimmten Abschnitt ist ein konstanter Wert und der Abstand ( j) entlang der Ordinatenachse vom Schwerpunkt des Abschnitts bis zum Punkt, an dem die Spannung bestimmt wird, variiert von 0 bis
 .
.
 .
(1)
.
(1)
Zur Bestimmung der Schubspannung beim Biegen im Jahr 1856. Russischer Ingenieur und Brückenbauer D.I. Zhuravsky wurde süchtig
 .
(2)
.
(2)
Die Schubspannung in einem bestimmten Abschnitt hängt nicht vom Verhältnis der Querkraft zum axialen Trägheitsmoment ab (  ), Weil Dieser Wert ändert sich nicht innerhalb eines Abschnitts, sondern hängt vom Verhältnis des statischen Moments der Fläche des abgeschnittenen Teils zur Breite des Abschnitts auf Höhe des abgeschnittenen Teils ab (
), Weil Dieser Wert ändert sich nicht innerhalb eines Abschnitts, sondern hängt vom Verhältnis des statischen Moments der Fläche des abgeschnittenen Teils zur Breite des Abschnitts auf Höhe des abgeschnittenen Teils ab (  ).
).
Wenn eine gerade Querbiegung auftritt Bewegungen: Auslenkungen (v
) und Drehwinkel (Θ
)
. Um sie zu bestimmen, verwenden Sie die Gleichungen der Anfangsparametermethode (3), die durch Integration der Differentialgleichung der gekrümmten Achse des Strahls erhalten werden (  ).
).
Hier v 0 , Θ 0 ,M 0 , Q 0 – Anfangsparameter, X – Abstand vom Ursprung zum Abschnitt, in dem die Verschiebung bestimmt wird , A– der Abstand vom Koordinatenursprung bis zum Angriffsort bzw. Beginn der Belastung.
Festigkeits- und Steifigkeitsberechnungen werden anhand der Festigkeits- und Steifigkeitsbedingungen durchgeführt. Anhand dieser Bedingungen können Sie Verifizierungsaufgaben lösen (die Erfüllung einer Bedingung prüfen) und die Größe bestimmen Querschnitt oder wählen Sie einen akzeptablen Wert für den Lastparameter. Es gibt mehrere Festigkeitsbedingungen, von denen einige unten aufgeführt sind. Normaler Spannungsfestigkeitszustand hat die Form:
 ,
(4)
,
(4)
Hier  –
Widerstandsmoment des Abschnitts relativ zur Z-Achse, R – Bemessungswiderstand basierend auf Normalspannungen.
–
Widerstandsmoment des Abschnitts relativ zur Z-Achse, R – Bemessungswiderstand basierend auf Normalspannungen.
Festigkeitsbedingung für Tangentialspannungen sieht aus wie:
 ,
(5)
,
(5)
hier sind die Notationen die gleichen wie in Zhuravskys Formel und R S – berechneter Scherwiderstand oder berechneter Widerstand gegen Tangentialspannungen.
Kraftzustand gemäß der dritten Krafthypothese oder die Hypothese der größten Tangentialspannungen kann in folgender Form geschrieben werden:
 .
(6)
.
(6)
Schwere Bedingungen geschrieben werden kann Auslenkungen (v ) Und Drehwinkel (Θ ) :
wobei die Verschiebungswerte in eckigen Klammern gelten.
Beispiel für die Erledigung der Einzelaufgabe Nr. 4 (Laufzeit 2-8 Wochen)
Biegeverformung besteht in einer Krümmung der Achse eines geraden Stabes oder in einer Änderung der anfänglichen Krümmung eines geraden Stabes (Abb. 6.1). Machen wir uns mit den Grundkonzepten vertraut, die bei der Betrachtung der Biegeverformung verwendet werden.
Man nennt Stäbe, die sich biegen Balken.
Sauber Dies wird als Biegung bezeichnet, bei der das Biegemoment der einzige innere Kraftfaktor ist, der im Querschnitt des Balkens auftritt.
Häufiger entsteht im Querschnitt des Stabes neben dem Biegemoment auch eine Querkraft. Diese Biegung wird Querbiegung genannt.
Flach (gerade) Man nennt es Biegung, wenn die Wirkungsebene des Biegemoments im Querschnitt durch eine der Hauptmittelachsen des Querschnitts verläuft.
Bei schräge Biegung Die Wirkungsebene des Biegemoments schneidet den Querschnitt des Balkens entlang einer Linie, die mit keiner der Hauptmittelachsen des Querschnitts zusammenfällt.
Wir beginnen unsere Untersuchung der Biegeverformung mit dem Fall der reinen Verformung flache Biegung.
Normale Spannungen und Dehnungen beim reinen Biegen.
Wie bereits erwähnt, ist bei reiner ebener Biegung im Querschnitt von den sechs Schnittgrößenfaktoren nur das Biegemoment ungleich Null (Abb. 6.1, c):
An elastischen Modellen durchgeführte Experimente zeigen, dass sich, wenn ein Liniengitter auf die Oberfläche des Modells aufgetragen wird (Abb. 6.1, a), dieses bei reiner Biegung wie folgt verformt (Abb. 6.1, b):
a) Längslinien sind entlang des Umfangs gekrümmt;
b) die Konturen der Querschnitte bleiben flach;
c) Die Höhenlinien der Abschnitte schneiden sich überall mit den Längsfasern im rechten Winkel.
Auf dieser Grundlage kann davon ausgegangen werden, dass bei reiner Biegung die Querschnitte des Balkens flach bleiben und sich so drehen, dass sie normal zur gekrümmten Achse des Balkens bleiben (flache Abschnitte in der Biegehypothese).

Reis. 6.1
Durch Messen der Länge der Längslinien (Abb. 6.1, b) können Sie feststellen, dass sich die oberen Fasern bei der Biegung des Balkens verlängern und die unteren kürzer werden. Offensichtlich ist es möglich, Fasern zu finden, deren Länge unverändert bleibt. Ein Satz Fasern, deren Länge sich beim Biegen eines Balkens nicht ändert, wird als bezeichnet neutrale Schicht (n.s.). Die neutrale Schicht schneidet den Querschnitt des Balkens in einer geraden Linie, die man nennt Abschnitt der Neutralleitung (n.l.)..
Um eine Formel abzuleiten, die die Größe der im Querschnitt auftretenden Normalspannungen bestimmt, betrachten wir einen Abschnitt des Balkens im verformten und unverformten Zustand (Abb. 6.2).

Reis. 6.2
Unter Verwendung zweier infinitesimaler Querschnitte wählen wir ein Längenelement aus  . Vor der Verformung die das Element begrenzenden Abschnitte
. Vor der Verformung die das Element begrenzenden Abschnitte  , waren parallel zueinander (Abb. 6.2, a) und nach der Verformung bogen sie sich leicht und bildeten einen Winkel
, waren parallel zueinander (Abb. 6.2, a) und nach der Verformung bogen sie sich leicht und bildeten einen Winkel  . Die Länge der in der Neutralschicht liegenden Fasern verändert sich beim Biegen nicht
. Die Länge der in der Neutralschicht liegenden Fasern verändert sich beim Biegen nicht  . Bezeichnen wir den Krümmungsradius der Spur der neutralen Schicht auf der Zeichenebene mit dem Buchstaben
. Bezeichnen wir den Krümmungsradius der Spur der neutralen Schicht auf der Zeichenebene mit dem Buchstaben  . Bestimmen wir die lineare Verformung einer beliebigen Faser
. Bestimmen wir die lineare Verformung einer beliebigen Faser  , in einiger Entfernung gelegen
, in einiger Entfernung gelegen  aus der neutralen Schicht.
aus der neutralen Schicht.
Die Länge dieser Faser nach der Verformung (Bogenlänge).  ) ist gleich
) ist gleich  . Bedenkt man, dass vor der Verformung alle Fasern die gleiche Länge hatten
. Bedenkt man, dass vor der Verformung alle Fasern die gleiche Länge hatten  , finden wir, dass die absolute Dehnung der betrachteten Faser ist
, finden wir, dass die absolute Dehnung der betrachteten Faser ist
Seine relative Verformung 

Es ist klar, dass  , da sich die Länge der in der Neutralschicht liegenden Faser nicht verändert hat. Dann nach der Auswechslung
, da sich die Länge der in der Neutralschicht liegenden Faser nicht verändert hat. Dann nach der Auswechslung  wir bekommen
wir bekommen
 (6.2)
(6.2)
Daher ist die relative Längsdehnung proportional zum Abstand der Faser von der neutralen Achse.
Nehmen wir an, dass die Längsfasern beim Biegen nicht aufeinander drücken. Unter dieser Annahme verformt sich jede Faser isoliert und erfährt dabei eine einfache Spannung oder Kompression  . Unter Berücksichtigung von (6.2)
. Unter Berücksichtigung von (6.2)
 , (6.3)
, (6.3)
das heißt, Normalspannungen sind direkt proportional zu den Abständen der betrachteten Querschnittspunkte von der neutralen Achse.
Ersetzen wir die Abhängigkeit (6.3) in den Ausdruck für das Biegemoment  im Querschnitt (6.1)
im Querschnitt (6.1)
 .
.
Denken Sie daran, dass das Integral  stellt das Trägheitsmoment des Abschnitts relativ zur Achse dar
stellt das Trägheitsmoment des Abschnitts relativ zur Achse dar 
 .
.
 (6.4)
(6.4)
Die Abhängigkeit (6.4) stellt das Hookesche Gesetz für die Biegung dar, da sie die Verformung (Krümmung der neutralen Schicht) in Beziehung setzt  ) mit einem im Abschnitt wirkenden Moment. Arbeiten
) mit einem im Abschnitt wirkenden Moment. Arbeiten  wird als Querschnittssteifigkeit beim Biegen bezeichnet, N m 2.
wird als Querschnittssteifigkeit beim Biegen bezeichnet, N m 2.
Ersetzen wir (6.4) durch (6.3)
 (6.5)
(6.5)
Dies ist die erforderliche Formel zur Bestimmung der Normalspannungen bei reiner Biegung eines Balkens an jedem Punkt seines Querschnitts.
Um festzustellen, wo sich die Neutrallinie im Querschnitt befindet, setzen wir den Wert der Normalspannungen in den Ausdruck für die Längskraft ein  und Biegemoment
und Biegemoment 

Weil das  ,
,
 ;
;
 (6.6)
(6.6)
 (6.7)
(6.7)
Gleichheit (6.6) zeigt an, dass die Achse  – neutrale Achse des Querschnitts – verläuft durch den Schwerpunkt des Querschnitts.
– neutrale Achse des Querschnitts – verläuft durch den Schwerpunkt des Querschnitts.
Gleichheit (6.7) zeigt das  Und
Und  - die Hauptmittelachsen des Abschnitts.
- die Hauptmittelachsen des Abschnitts.
Nach (6.5) wird die höchste Spannung in den Fasern erreicht, die am weitesten vom Neutralleiter entfernt sind

Attitüde  stellt das axiale Widerstandsmoment des Abschnitts dar
stellt das axiale Widerstandsmoment des Abschnitts dar  relativ zu seiner Mittelachse
relativ zu seiner Mittelachse  , Bedeutet
, Bedeutet

Bedeutung  für die einfachsten Querschnitte gilt:
für die einfachsten Querschnitte gilt:
Für rechteckigen Querschnitt
 , (6.8)
, (6.8)
Wo  - Seite des Abschnitts senkrecht zur Achse
- Seite des Abschnitts senkrecht zur Achse  ;
;
 - Seite des Abschnitts parallel zur Achse
- Seite des Abschnitts parallel zur Achse  ;
;
Für runden Querschnitt
 , (6.9)
, (6.9)
Wo  - Durchmesser des kreisförmigen Querschnitts.
- Durchmesser des kreisförmigen Querschnitts.
Der Festigkeitszustand für normale Biegebeanspruchungen kann in das Formular geschrieben werden
 (6.10)
(6.10)
Alle erhaltenen Formeln werden für den Fall erhalten reines Biegen gerader Stab. Die Wirkung der Querkraft führt dazu, dass die den Schlussfolgerungen zugrunde liegenden Hypothesen ihre Kraft verlieren. Die Berechnungspraxis zeigt jedoch, dass auch bei Querbiegungen von Trägern und Rahmen im Querschnitt zusätzlich das Biegemoment auftritt  es gibt auch eine Längskraft
es gibt auch eine Längskraft  und Scherkraft
und Scherkraft  , können Sie die angegebenen Formeln für die reine Biegung verwenden. Der Fehler ist unbedeutend.
, können Sie die angegebenen Formeln für die reine Biegung verwenden. Der Fehler ist unbedeutend.
Gerade Kurve- Dies ist eine Art Verformung, bei der zwei interne Leistungsfaktoren: Biegemoment und Scherkraft.
Saubere Biegung- Dies ist ein Sonderfall der direkten Biegung, bei der in den Stabquerschnitten nur ein Biegemoment auftritt und die Querkraft Null ist.
Ein Beispiel für eine reine Kurve – ein Abschnitt CD auf der Stange AB. Biegemoment ist die Menge Pa ein Paar äußerer Kräfte, die eine Biegung verursachen. Aus dem Gleichgewicht des Stabteils links vom Querschnitt mn Daraus folgt, dass die über diesen Abschnitt verteilten Schnittgrößen statisch dem Moment äquivalent sind M, gleich und entgegengesetzt zum Biegemoment Pa.
Um die Verteilung dieser Schnittgrößen über den Querschnitt zu ermitteln, muss die Verformung des Stabes berücksichtigt werden.
Im einfachsten Fall hat der Stab eine Längssymmetrieebene und unterliegt der Einwirkung äußerer Biegekraftpaare, die in dieser Ebene liegen. Dann erfolgt die Biegung in derselben Ebene.
Stabachse nn 1 ist eine Linie, die durch die Schwerpunkte seiner Querschnitte verläuft.
Der Querschnitt des Stabes sei ein Rechteck. Zeichnen wir zwei vertikale Linien an den Rändern mm Und S. Beim Biegen bleiben diese Linien gerade und drehen sich, sodass sie senkrecht zu den Längsfasern des Stabes bleiben.
Die weitere Biegetheorie basiert auf der Annahme, dass es sich nicht nur um Linien handelt mm Und S, aber der gesamte flache Querschnitt des Stabes bleibt nach dem Biegen flach und normal zu den Längsfasern des Stabes. Daher verändern sich beim Biegen die Querschnitte mm Und S relativ zueinander um Achsen drehen, die senkrecht zur Biegeebene (Zeichenebene) stehen. Dabei erfahren die Längsfasern auf der konvexen Seite eine Spannung und die Fasern auf der konkaven Seite eine Kompression.
Neutrale Oberfläche- Dies ist eine Oberfläche, die beim Biegen keine Verformung erfährt. (Jetzt liegt sie senkrecht zur Zeichnung, der verformten Achse des Stabes nn 1 gehört zu dieser Fläche).
Neutrale Schnittachse- Dies ist der Schnittpunkt einer neutralen Fläche mit einem beliebigen Querschnitt (der nun auch senkrecht zur Zeichnung liegt).
Lassen Sie eine beliebige Faser einen Abstand haben j von einer neutralen Oberfläche. ρ – Krümmungsradius der gekrümmten Achse. Punkt Ö– Krümmungsmittelpunkt. Lasst uns eine Linie ziehen n 1 s 1 parallel mm.SS 1– absolute Faserdehnung.
Relative Erweiterung ε x Fasern
Es folgt dem Verformung von Längsfasern proportional zur Entfernung j von der neutralen Oberfläche und umgekehrt proportional zum Krümmungsradius ρ .
Mit der Längsdehnung der Fasern der konvexen Seite des Stabes geht einher seitliche Verengung und die Längsverkürzung der konkaven Seite ist seitliche Ausdehnung, wie im Fall einer einfachen Dehnung und Kompression. Dadurch verändert sich das Aussehen aller Querschnitte, die vertikalen Seiten des Rechtecks werden geneigt. Seitliche Verformung z:
μ - Poissonzahl.
Aufgrund dieser Verzerrung verlaufen alle geraden Querschnittslinien parallel zur Achse z werden so gebogen, dass sie senkrecht zu den Seiten des Abschnitts bleiben. Der Krümmungsradius dieser Kurve R wird mehr sein als ρ im gleichen Sinne wie ε x von Absolutwert mehr als ε z und wir bekommen
Diese Verformungen der Längsfasern entsprechen Spannungen
Die Spannung in jeder Faser ist proportional zu ihrem Abstand von der neutralen Achse n 1 n 2. Neutrale Achsenposition und Krümmungsradius ρ – zwei Unbekannte in der Gleichung für σ x – kann aus der Bedingung bestimmt werden, dass über einen beliebigen Querschnitt verteilte Kräfte ein Kräftepaar bilden, das das äußere Moment ausgleicht M.
Das alles gilt auch dann, wenn der Stab keine Längssymmetrieebene hat, in der das Biegemoment wirkt, solange das Biegemoment in der Axialebene wirkt, die eine der beiden enthält Hauptachsen Querschnitt. Diese Flugzeuge heißen Hauptbiegeebenen.
Wenn es eine Symmetrieebene gibt und das Biegemoment in dieser Ebene wirkt, erfolgt die Durchbiegung genau in dieser Ebene. Momente der Schnittgrößen relativ zur Achse z das äußere Moment ausgleichen M. Kraftmomente um die Achse j werden gegenseitig zerstört.
Wir beginnen mit dem einfachsten Fall, der sogenannten reinen Biegung.
Die reine Biegung ist ein Sonderfall der Biegung, bei der die Querkraft in den Balkenabschnitten Null ist. Eine reine Biegung kann nur dann auftreten, wenn das Eigengewicht des Balkens so gering ist, dass sein Einfluss vernachlässigt werden kann. Für Balken auf zwei Stützen, Beispiele für Lasten, die rein sind
Biegen, dargestellt in Abb. 88. In Abschnitten dieser Balken, in denen Q = 0 und daher M = const; Es findet reines Biegen statt.
Die Kräfte in jedem Abschnitt des Balkens werden beim reinen Biegen auf ein Kräftepaar reduziert, dessen Wirkungsebene durch die Achse des Balkens verläuft und das Moment konstant ist.
Spannungen können anhand der folgenden Überlegungen ermittelt werden.
1. Die Tangentialkomponenten der Kräfte entlang der Elementarflächen im Querschnitt eines Balkens lassen sich nicht auf ein Kräftepaar reduzieren, dessen Wirkungsebene senkrecht zur Schnittebene steht. Daraus folgt, dass die Biegekraft im Querschnitt das Ergebnis der Einwirkung entlang von Elementarflächen ist
nur Normalkräfte, und daher reduzieren sich die Spannungen bei reiner Biegung nur auf Normalkräfte.
2. Damit die Bemühungen an elementaren Standorten auf nur ein paar Kräfte reduziert werden können, müssen unter ihnen sowohl positive als auch negative Kräfte vorhanden sein. Daher müssen sowohl Zug- als auch Druckfasern des Balkens vorhanden sein.

3. Aufgrund der Tatsache, dass die Kräfte in verschiedenen Abschnitten gleich sind, sind die Spannungen an den entsprechenden Punkten der Abschnitte gleich.
Betrachten wir ein Element in der Nähe der Oberfläche (Abb. 89, a). Da entlang seiner Unterkante, die mit der Oberfläche des Balkens zusammenfällt, keine Kräfte wirken, entsteht keine Spannung auf ihn. Daher treten keine Spannungen an der Oberkante des Elements auf, da sich das Element sonst nicht im Gleichgewicht befände. Betrachtet man das benachbarte Element in der Höhe (Abb. 89, b), kommen wir zu

Die gleiche Schlussfolgerung usw. Daraus folgt, dass an den horizontalen Kanten eines Elements keine Spannungen auftreten. Betrachtet man die Elemente, aus denen die horizontale Schicht besteht, beginnend mit dem Element nahe der Oberfläche des Balkens (Abb. 90), kommen wir zu dem Schluss, dass es an den seitlichen vertikalen Kanten eines Elements keine Spannungen gibt. Daher sollte der Spannungszustand eines beliebigen Elements (Abb. 91, a) und im Grenzfall auch der Fasern wie in Abb. dargestellt dargestellt werden. 91,b, d. h. es kann entweder eine axiale Spannung oder eine axiale Kompression sein.
4. Aufgrund der Symmetrie der Einwirkung äußerer Kräfte sollte der Abschnitt in der Mitte der Balkenlänge nach der Verformung flach und normal zur Balkenachse bleiben (Abb. 92, a). Aus dem gleichen Grund bleiben auch Abschnitte in Vierteln der Balkenlänge flach und normal zur Balkenachse (Abb. 92, b), es sei denn, die äußersten Balkenabschnitte bleiben während der Verformung flach und normal zur Balkenachse der Balken. Eine ähnliche Schlussfolgerung gilt für Abschnitte in Achtellänge des Balkens (Abb. 92, c) usw. Wenn also beim Biegen die äußeren Abschnitte des Balkens flach bleiben, bleibt dies für jeden Abschnitt der Fall 
Es ist eine berechtigte Aussage, dass es nach der Verformung flach und normal zur Achse des gebogenen Balkens bleibt. In diesem Fall ist es jedoch offensichtlich, dass die Änderung der Dehnung der Fasern des Balkens entlang seiner Höhe nicht nur kontinuierlich, sondern auch monoton erfolgen sollte. Wenn wir eine Schicht als einen Satz von Fasern bezeichnen, die die gleichen Dehnungen haben, dann folgt aus dem Gesagten, dass sich die gestreckten und komprimierten Fasern des Balkens auf gegenüberliegenden Seiten der Schicht befinden sollten, in denen die Dehnungen der Fasern gleich sind bis Null. Wir nennen Fasern, deren Dehnung Null ist, neutral; eine Schicht aus neutralen Fasern ist eine neutrale Schicht; die Schnittlinie der neutralen Schicht mit der Querschnittsebene des Balkens – die neutrale Linie dieses Abschnitts. Basierend auf der vorherigen Überlegung kann dann argumentiert werden, dass es bei reiner Biegung eines Balkens in jedem Abschnitt eine neutrale Linie gibt, die diesen Abschnitt in zwei Teile (Zonen) unterteilt: eine Zone aus gestreckten Fasern (gestreckte Zone) und eine Zone komprimierter Fasern (komprimierte Zone). ). Dementsprechend sollten an den Punkten der gestreckten Zone des Abschnitts normale Zugspannungen wirken, an den Punkten der komprimierten Zone Druckspannungen und an den Punkten der Neutrallinie sind die Spannungen gleich Null.
Somit gilt bei reiner Biegung eines Balkens mit konstantem Querschnitt:
1) abschnittsweise wirken nur Normalspannungen;
2) der gesamte Abschnitt kann in zwei Teile (Zonen) unterteilt werden – gestreckt und gestaucht; die Grenze der Zonen ist die neutrale Schnittlinie, an deren Punkten die Normalspannungen gleich Null sind;
3) jedes Längselement des Balkens (im Grenzfall jede Faser) wird einer axialen Spannung oder Kompression ausgesetzt, so dass benachbarte Fasern nicht miteinander interagieren;
4) Wenn die äußersten Abschnitte des Balkens während der Verformung flach und normal zur Achse bleiben, bleiben alle seine Querschnitte flach und normal zur Achse des gebogenen Balkens.
Spannungszustand eines Balkens bei reiner Biegung
Betrachten wir abschließend ein Element eines Balkens, das einer reinen Biegung ausgesetzt ist  befindet sich zwischen den Abschnitten m-m und n-n, die einen unendlich kleinen Abstand dx voneinander haben (Abb. 93). Aufgrund der Position (4) des vorherigen Absatzes bilden die Abschnitte m-m und n-n, die vor der Verformung parallel waren, nach dem Biegen flach bleiben, einen Winkel dQ und schneiden sich entlang einer geraden Linie, die durch den Punkt C verläuft der Mittelpunkt der Krümmung der neutralen Faser NN. Dann verwandelt sich der zwischen ihnen eingeschlossene Teil AB der Faser, der sich im Abstand z von der neutralen Faser befindet (die positive Richtung der z-Achse wird beim Biegen in Richtung der Konvexität des Balkens genommen), nach der Verformung in einen Bogen AB. A Nachdem sich ein Stück neutrale Faser O1O2 in einen Bogen verwandelt hat, ändert O1O2 seine Länge nicht, während die Faser AB eine Verlängerung erhält:
befindet sich zwischen den Abschnitten m-m und n-n, die einen unendlich kleinen Abstand dx voneinander haben (Abb. 93). Aufgrund der Position (4) des vorherigen Absatzes bilden die Abschnitte m-m und n-n, die vor der Verformung parallel waren, nach dem Biegen flach bleiben, einen Winkel dQ und schneiden sich entlang einer geraden Linie, die durch den Punkt C verläuft der Mittelpunkt der Krümmung der neutralen Faser NN. Dann verwandelt sich der zwischen ihnen eingeschlossene Teil AB der Faser, der sich im Abstand z von der neutralen Faser befindet (die positive Richtung der z-Achse wird beim Biegen in Richtung der Konvexität des Balkens genommen), nach der Verformung in einen Bogen AB. A Nachdem sich ein Stück neutrale Faser O1O2 in einen Bogen verwandelt hat, ändert O1O2 seine Länge nicht, während die Faser AB eine Verlängerung erhält:
vor der Verformung

nach Verformung
![]()
wobei p der Krümmungsradius der neutralen Faser ist.
Daher ist die absolute Verlängerung des Segments AB gleich
und relative Dehnung
Da gemäß Position (3) die Faser AB einer axialen Spannung ausgesetzt ist, dann bei elastischer Verformung

Dies zeigt, dass die Normalspannungen entlang der Balkenhöhe nach einem linearen Gesetz verteilt sind (Abb. 94). Da dann die gleiche Kraft aller Kräfte über alle Elementarquerschnittsflächen gleich Null sein muss
von wo aus wir durch Ersetzen des Wertes aus (5.8) finden

Das letzte Integral ist jedoch ein statisches Moment um die Oy-Achse, senkrecht zur Wirkungsebene der Biegekräfte.

Aufgrund ihrer Nullgleichheit muss diese Achse durch den Schwerpunkt O des Abschnitts verlaufen. Somit ist die neutrale Linie des Balkenabschnitts eine gerade Linie y, senkrecht zur Wirkungsebene der Biegekräfte. Sie wird als neutrale Achse des Strahlabschnitts bezeichnet. Aus (5.8) folgt dann, dass die Spannungen an Punkten, die im gleichen Abstand von der neutralen Achse liegen, gleich sind.
Der Fall der reinen Biegung, bei der die Biegekräfte nur in einer Ebene wirken und eine Biegung nur in dieser Ebene verursachen, ist eine ebene reine Biegung. Wenn diese Ebene durch die Oz-Achse verläuft, sollte das Moment der Elementarkräfte relativ zu dieser Achse gleich Null sein, d.h.
Wenn wir hier den Wert von σ aus (5.8) einsetzen, finden wir

Das Integral auf der linken Seite dieser Gleichheit ist bekanntlich das Zentrifugalträgheitsmoment des Abschnitts relativ zur y- und z-Achse, also

Die Achsen, um die das Zentrifugalträgheitsmoment des Abschnitts Null ist, werden als Hauptträgheitsachsen dieses Abschnitts bezeichnet. Wenn sie zusätzlich durch den Schwerpunkt des Abschnitts verlaufen, können sie als Hauptmittelträgheitsachsen des Abschnitts bezeichnet werden. Somit sind bei flacher reiner Biegung die Richtung der Wirkungsebene der Biegekräfte und die neutrale Achse des Abschnitts die Hauptmittelträgheitsachsen des letzteren. Mit anderen Worten: Um eine flache, reine Biegung eines Balkens zu erhalten, kann eine Last nicht willkürlich auf ihn ausgeübt werden: Sie muss auf Kräfte reduziert werden, die in einer Ebene wirken, die durch eine der Hauptmittelträgheitsachsen der Abschnitte verläuft Strahl; In diesem Fall ist die andere zentrale Hauptträgheitsachse die neutrale Achse des Abschnitts.
Bekanntlich ist bei einem Querschnitt, der um eine beliebige Achse symmetrisch ist, die Symmetrieachse eine seiner zentralen Hauptträgheitsachsen. Folglich werden wir in diesem speziellen Fall mit Sicherheit eine reine Biegung erreichen, indem wir geeignete Lasten in einer Ebene anwenden, die durch die Längsachse des Balkens und die Symmetrieachse seines Querschnitts verläuft. Eine gerade Linie senkrecht zur Symmetrieachse, die durch den Schwerpunkt des Abschnitts verläuft, ist die neutrale Achse dieses Abschnitts.
Nachdem die Position der neutralen Achse ermittelt wurde, ist es nicht schwierig, die Größe der Spannung an jedem Punkt des Abschnitts zu ermitteln. Tatsächlich muss die Summe der Momente der Elementarkräfte relativ zur neutralen Achse yy gleich dem Biegemoment sein
woraus, indem wir den Wert von σ aus (5.8) ersetzen, finden wir

Da das Integral  Ist. Trägheitsmoment des Abschnitts relativ zur yy-Achse
Ist. Trägheitsmoment des Abschnitts relativ zur yy-Achse
und aus Ausdruck (5.8) erhalten wir
Das Produkt EI Y wird als Biegesteifigkeit des Balkens bezeichnet.
Die größten Zug- und Druckspannungen im Absolutwert wirken an den Punkten des Abschnitts, für die der Absolutwert von z am größten ist, d. h. an den Punkten, die am weitesten von der neutralen Achse entfernt sind. Mit der Notation Abb. 95 haben wir

Der Wert Jy/h1 wird als Widerstandsmoment des Abschnitts gegen Zug bezeichnet und mit Wyr bezeichnet; In ähnlicher Weise wird Jy/h2 als Widerstandsmoment des Abschnitts gegen Druck bezeichnet

und bezeichnen Wyc, also

Und deswegen

Wenn die neutrale Achse die Symmetrieachse des Abschnitts ist, dann ist h1 = h2 = h/2 und daher Wyp = Wyc, es besteht also keine Notwendigkeit, sie zu unterscheiden, und sie verwenden dieselbe Notation:
Man nennt W y einfach das Widerstandsmoment des Abschnitts. Folglich gilt im Fall eines Abschnitts, der symmetrisch um die neutrale Achse ist,
Alle oben genannten Schlussfolgerungen wurden auf der Grundlage der Annahme gezogen, dass die Querschnitte des Balkens im gebogenen Zustand flach und normal zu seiner Achse bleiben (Hypothese flacher Abschnitte). Wie gezeigt wurde, ist diese Annahme nur dann gültig, wenn die äußersten (End-)Abschnitte des Trägers beim Biegen flach bleiben. Andererseits folgt aus der Hypothese ebener Abschnitte, dass die Elementarkräfte in solchen Abschnitten nach einem linearen Gesetz verteilt sein sollten. Für die Gültigkeit der resultierenden Theorie der flachen reinen Biegung ist es daher notwendig, dass die Biegemomente an den Enden des Balkens in Form von Elementarkräften aufgebracht werden, die nach einem linearen Gesetz über die Höhe des Abschnitts verteilt sind (Abb. 96), was mit dem Gesetz der Spannungsverteilung entlang der Höhe der Profilträger zusammenfällt. Basierend auf dem Saint-Venant-Prinzip kann jedoch argumentiert werden, dass eine Änderung der Methode zur Aufbringung von Biegemomenten an den Enden des Trägers nur lokale Verformungen verursacht, deren Wirkung sich nur auf einen bestimmten Abstand von diesen Enden auswirkt (ungefähr gleich). auf die Höhe des Abschnitts). Die über die restliche Länge des Trägers verteilten Abschnitte bleiben flach. Folglich gilt die dargelegte Theorie der flachen reinen Biegung für jede Methode zur Anwendung von Biegemomenten nur innerhalb des mittleren Teils der Länge des Trägers, der von seinen Enden in Abständen liegt, die ungefähr der Höhe des Abschnitts entsprechen. Daraus wird deutlich, dass diese Theorie offensichtlich nicht anwendbar ist, wenn die Höhe des Abschnitts die Hälfte der Länge oder Spannweite des Trägers überschreitet.
Beim Bauen Diagramme der BiegemomenteM bei Bauherren akzeptiert: Ordinaten, die in einem bestimmten Maßstab ausgedrückt werden positiv Werte der Biegemomente, beiseite legen gestreckt Fasern, d.h. - runter, A negativ - oben von der Strahlachse. Daher sagen sie, dass Bauherren Diagramme auf gedehnten Fasern erstellen. Bei den Mechanikern Positive Werte sowohl der Querkraft als auch des Biegemoments werden verschoben hoch. Mechaniker zeichnen Diagramme auf komprimiert Fasern.
Hauptbetonungen beim Biegen. Äquivalente Spannungen.
Im allgemeinen Fall einer direkten Biegung in den Querschnitten eines Trägers gilt: normal Und Tangenten![]() Stromspannung. Diese Spannungen variieren sowohl entlang der Länge als auch der Höhe des Balkens.
Stromspannung. Diese Spannungen variieren sowohl entlang der Länge als auch der Höhe des Balkens.
Im Falle einer Biegung ist dies der Fall ebener Spannungszustand.
Betrachten wir ein Diagramm, in dem der Balken mit der Kraft P belastet wird

Größter Normalwert Spannungen entstehen in extrem, Punkte, die am weitesten von der neutralen Linie entfernt sind, und In ihnen treten keine Scherspannungen auf. Also z extrem Fasern Hauptspannungen ungleich Null sind Normalspannungen im Querschnitt.
Auf der Ebene der neutralen Linie im Querschnitt des Balkens gibt es höchste Scherbeanspruchung, A Normalspannungen sind Null. bedeutet in den Fasern neutral Schicht die Hauptspannungen werden durch die Werte der Tangentialspannungen bestimmt.
In diesem Entwurfsschema Die oberen Fasern des Balkens werden gedehnt und die unteren werden gestaucht. Zur Bestimmung der Hauptspannungen verwenden wir den bekannten Ausdruck: 
Voll Spannungsanalyse Stellen wir es uns auf dem Bild vor.

Biegespannungsanalyse
Maximale Hauptspannung σ 1 befindet sich Oberer, höher extreme Fasern und ist auf den unteren äußersten Fasern gleich Null. Hauptspannung σ 3 Es hat Der größte absolute Wert liegt in den unteren Fasern.
Verlauf der Hauptspannungen hängt von der Lasttyp Und Methode zur Befestigung des Balkens.


Beim Lösen von Problemen reicht es separatüberprüfen normal Und getrennt Tangentialspannungen. Allerdings manchmal am stressigsten erweisen sich als dazwischenliegend Fasern, in denen sowohl Normal- als auch Scherspannungen auftreten. Dies geschieht in Abschnitten, in denen Gleichzeitig erreichen sowohl das Biegemoment als auch die Querkraft große Werte - Dies kann bei der Einbettung eines Kragarms, bei der Auflage eines Balkens mit Kragarm, in Abschnitten unter konzentrierter Krafteinwirkung oder in Abschnitten mit stark wechselnden Breiten der Fall sein. Zum Beispiel in einem I-Abschnitt am gefährlichsten die Verbindung von Wand und Regal- es gibt Sowohl Normal- als auch Scherspannungen sind erheblich.
Das Material befindet sich in einem ebenen Spannungszustand und ist erforderlich Überprüfen Sie, ob entsprechende Spannungen vorhanden sind.
Festigkeitsbedingungen für Träger aus Kunststoffmaterialien Von dritte(Theorie maximaler Tangentialspannungen) ![]() Und vierte(Theorie der Energie von Formänderungen)
Und vierte(Theorie der Energie von Formänderungen) ![]() Theorien der Stärke.
Theorien der Stärke.
In gewalzten Trägern übersteigen die äquivalenten Spannungen in der Regel nicht die Normalspannungen in den äußersten Fasern und es sind keine besonderen Prüfungen erforderlich. Etwas anderes - Verbundmetallträger, welche Die Wand ist dünner als bei Walzprofilen auf gleicher Höhe. Häufiger werden geschweißte Verbundträger aus Stahlblechen verwendet. Berechnung der Festigkeit solcher Balken: a) Auswahl des Abschnitts – Höhe, Dicke, Breite und Dicke der Balkensehnen; b) Überprüfung der Festigkeit durch Normal- und Tangentialspannungen; c) Überprüfung der Festigkeit anhand von Vergleichsspannungen.
Bestimmung der Schubspannungen in einem I-Profil. Betrachten wir den Abschnitt Ich glänze S x =96,9 cm 3 ; Yх=2030 cm 4 ; Q=200 kN

Zur Bestimmung der Schubspannung wird diese verwendet Formel![]() ,wobei Q die Scherkraft im Abschnitt ist, S x 0 das statische Moment des Teils des Querschnitts ist, der sich auf einer Seite der Schicht befindet, in der die Tangentialspannungen bestimmt werden, I x das Trägheitsmoment des Ganzen Querschnitt, b ist die Breite des Abschnitts an der Stelle, an der die Scherspannung bestimmt wird
,wobei Q die Scherkraft im Abschnitt ist, S x 0 das statische Moment des Teils des Querschnitts ist, der sich auf einer Seite der Schicht befindet, in der die Tangentialspannungen bestimmt werden, I x das Trägheitsmoment des Ganzen Querschnitt, b ist die Breite des Abschnitts an der Stelle, an der die Scherspannung bestimmt wird
Rechnen wir maximal Schubspannung:
Berechnen wir das statische Moment für obersten Regal: 
Nun lasst uns rechnen Schubspannung: 
Wir bauen Schubspannungsdiagramm:

Betrachten wir den Querschnitt eines Standardprofils in der Form Ich glänze und definieren Scherbeanspruchung, parallel zur Scherkraft wirkend:

Rechnen wir statische Momente einfache Zahlen: 
Dieser Wert kann berechnet werden und ansonsten, unter Ausnutzung der Tatsache, dass für die I-Träger- und Trogabschnitte das statische Moment der Hälfte des Abschnitts angegeben ist. Dazu ist es notwendig, vom bekannten Wert des statischen Moments den Wert des statischen Moments zur Geraden abzuziehen A 1 B 1: 
Die Tangentialspannungen an der Verbindungsstelle zwischen Flansch und Wand ändern sich krampfhaft, als scharf Wandstärke variiert von t st Vor B.
Diagramme der Tangentialspannungen in den Wänden von Trog-, Hohl-Rechteck- und anderen Profilen haben die gleiche Form wie im Fall eines I-Profils. Die Formel umfasst das statische Moment des schattierten Teils des Abschnitts relativ zur X-Achse und der Nenner enthält die Breite des Abschnitts (netto) in der Schicht, in der die Scherspannung bestimmt wird.


Bestimmen wir die Tangentialspannungen für einen Kreisabschnitt.


Da die Schubspannungen auf die Profilkontur gerichtet sein müssen tangential zur Kontur, dann punktuell A Und IN an den Enden einer beliebigen Sehne parallel zum Durchmesser AB, Schubspannungen werden gerichtet senkrecht zu den Radien OA Und OV. Somit, Richtungen Tangentialspannungen an Punkten A, VC irgendwann zusammenlaufen N auf der Y-Achse.
Statisches Moment des abgeschnittenen Teils: 
Das heißt, die Schubspannungen ändern sich entsprechend parabolisch Gesetz und wird auf der Ebene der neutralen Linie maximal sein, wenn y 0 =0

Formel zur Bestimmung der Schubspannung (Formel) 
Betrachten Sie einen rechteckigen Abschnitt

Auf Distanz y 0 Von der Mittelachse zeichnen wir Abschnitt 1-1 und bestimmen Sie die Tangentialspannungen. Statischer Moment Bereich abgeschnittenes Teil:
Es sollte bedacht werden, dass es von grundlegender Bedeutung ist gleichgültig, nimm das statische Moment der Fläche schattierter oder verbleibender Teil Querschnitt. Beides statische Momente gleich und entgegengesetzt im Vorzeichen, also ihre Summe, was darstellt statisches Flächenmoment des gesamten Abschnitts relativ zur neutralen Linie, nämlich der zentralen x-Achse, gleich sein null.
Trägheitsmoment eines rechteckigen Abschnitts:

Dann Scherbeanspruchung nach der Formel

Die Variable y 0 ist in der Formel enthalten zweite Grad, d.h. Tangentialspannungen in einem rechteckigen Abschnitt variieren je nach Gesetz einer quadratischen Parabel.
Schubspannung erreicht maximal auf der Ebene der neutralen Linie, d.h. Wann y 0 =0:
 ,
Wo A ist die Fläche des gesamten Abschnitts.
,
Wo A ist die Fläche des gesamten Abschnitts.
Festigkeitsbedingung für Tangentialspannungen hat die Form:
![]() , Wo S x 0– statisches Moment des Teils des Querschnitts, der sich auf einer Seite der Schicht befindet, in dem die Schubspannungen bestimmt werden, Ix– Trägheitsmoment des gesamten Querschnitts, B– Abschnittsbreite an der Stelle, an der die Schubspannung bestimmt wird, Q-Seitenkraft, τ
- Scherbeanspruchung, [τ]
— zulässige Tangentialspannung.
, Wo S x 0– statisches Moment des Teils des Querschnitts, der sich auf einer Seite der Schicht befindet, in dem die Schubspannungen bestimmt werden, Ix– Trägheitsmoment des gesamten Querschnitts, B– Abschnittsbreite an der Stelle, an der die Schubspannung bestimmt wird, Q-Seitenkraft, τ
- Scherbeanspruchung, [τ]
— zulässige Tangentialspannung.
Dieser Festigkeitszustand ermöglicht es uns zu produzieren drei Art der Berechnung (drei Arten von Problemen bei der Berechnung der Festigkeit):
1. Nachweisrechnung bzw. Festigkeitsprüfung anhand von Tangentialspannungen: ![]()
2. Auswahl der Abschnittsbreite (für einen rechteckigen Abschnitt): ![]()
3. Bestimmung der zulässigen Querkraft (für einen rechteckigen Querschnitt):
![]()
Zur Bestimmung Tangenten Betrachten Sie bei Spannungen einen mit Kräften belasteten Balken.

Die Aufgabe, Spannungen zu ermitteln, ist immer statisch unbestimmt und erfordert Engagement geometrisch Und körperlich Gleichungen. Es ist jedoch möglich, dies zu akzeptieren Hypothesen über die Natur der Stressverteilung dass die Aufgabe wird statisch definierbar.
Durch zwei unendlich nahe beieinander liegende Querschnitte 1-1 und 2-2 selektieren wir dz-Element, Lassen Sie uns es im großen Maßstab darstellen und dann einen Längsschnitt 3-3 zeichnen.
In den Abschnitten 1–1 und 2–2, Normalspannungen σ 1, σ 2, die durch die bekannten Formeln bestimmt werden:
Wo M - Biegemoment im Querschnitt, dM - Inkrement Biegemoment bei der Länge dz
Seitenkraft in den Abschnitten 1–1 und 2–2 ist entlang der Hauptmittelachse Y gerichtet und stellt offensichtlich dar die Summe der vertikalen Komponenten der über den Abschnitt verteilten inneren Tangentialspannungen. In der Regel wird auf die Festigkeit der Materialien geachtet Annahme ihrer gleichmäßigen Verteilung über die Breite des Abschnitts.
Zur Bestimmung der Größe der Scherspannungen an einem beliebigen Punkt im Querschnitt, der sich in einiger Entfernung befindet y 0 Zeichnen Sie von der neutralen X-Achse aus eine Ebene parallel zur neutralen Ebene (3-3) durch diesen Punkt und entfernen Sie das abgeschnittene Element. Wir werden die Spannung bestimmen, die über den ABCD-Bereich wirkt. 
Projizieren wir alle Kräfte auf die Z-Achse

Die Resultierende der inneren Längskräfte entlang der rechten Seite ist gleich:
Wo A 0 – Fläche der Fassadenkante, S x 0 – statisches Moment des abgeschnittenen Teils relativ zur X-Achse. Ebenso auf der linken Seite:
![]() Beide Ergebnisse gerichtet auf gegenseitig,
da das Element in ist komprimiert Strahlbereich. Ihr Unterschied wird durch die Tangentialkräfte am unteren Rand von 3-3 ausgeglichen.
Beide Ergebnisse gerichtet auf gegenseitig,
da das Element in ist komprimiert Strahlbereich. Ihr Unterschied wird durch die Tangentialkräfte am unteren Rand von 3-3 ausgeglichen.
Tun wir mal so Schubspannung τüber die Breite des Balkenquerschnitts verteilt b gleichmäßig. Diese Annahme ist umso wahrscheinlicher, je kleiner die Breite im Vergleich zur Höhe des Abschnitts ist. Dann Resultierende der Tangentialkräfte dT gleich dem Spannungswert multipliziert mit der Gesichtsfläche: ![]()
Lasst uns jetzt komponieren Gleichgewichtsgleichung Σz=0: ![]()
oder woher
![]()
Lass uns erinnern unterschiedliche Abhängigkeiten
, wonach ![]() Dann erhalten wir die Formel:
Dann erhalten wir die Formel:
![]()
Diese Formel heißt Formeln. Diese Formel wurde 1855 erhalten. Hier S x 0 – statisches Moment eines Teils des Querschnitts, auf einer Seite der Schicht liegen, in der die Schubspannungen bestimmt werden, I x – Trägheitsmoment der gesamte Querschnitt, b – Abschnittsbreite an der Stelle, an der die Schubspannung bestimmt wird, Q – Scherkraft im Querschnitt.
![]() — Biegefestigkeitszustand, Wo
— Biegefestigkeitszustand, Wo
- maximales Moment (Modulo) aus dem Diagramm der Biegemomente; ![]() - axiales Widerstandsmoment des Abschnitts, geometrisch charakteristisch; - zulässige Spannung (σ zul)
- axiales Widerstandsmoment des Abschnitts, geometrisch charakteristisch; - zulässige Spannung (σ zul)
- maximale Normalspannung.
Erfolgt die Berechnung gem Grenzzustandsmethode, dann gehen wir statt der zulässigen Spannung in die Berechnung ein Bemessungswiderstand des Materials R.
Arten von Biegefestigkeitsberechnungen
1. Überprüfen Berechnung oder Prüfung der Festigkeit unter Verwendung von Normalspannungen ![]()
2. Design Berechnung bzw Auswahl des Abschnitts ![]()
3. Definition zulässig laden (Definition Tragfähigkeit und/oder betriebsbereit Träger Fähigkeiten) ![]()
Bei der Ableitung der Formel zur Berechnung der Normalspannungen berücksichtigen wir den Biegefall, bei dem die Schnittgrößen in den Balkenabschnitten nur auf reduziert werden Biegemoment, A Die Scherkraft ist Null. Dieser Biegefall wird aufgerufen reines Biegen. Betrachten Sie den mittleren Abschnitt des Trägers, der einer reinen Biegung unterliegt.
 Bei Belastung biegt sich der Balken so, dass er Die unteren Fasern verlängern sich und die oberen Fasern verkürzen sich.
Bei Belastung biegt sich der Balken so, dass er Die unteren Fasern verlängern sich und die oberen Fasern verkürzen sich.
Da ein Teil der Fasern des Balkens gedehnt und ein Teil komprimiert wird, kommt es zum Übergang von Spannung zu Kompression reibungslos, ohne Sprünge, V Durchschnitt Ein Teil des Balkens befindet sich eine Schicht, deren Fasern sich nur biegen, aber weder Zug noch Druck erfahren. Diese Schicht heißt neutral Schicht. Die Linie, entlang der die neutrale Schicht den Querschnitt des Balkens schneidet, wird aufgerufen neutrale Linie oder neutrale Achse Abschnitte. Auf der Achse des Balkens sind neutrale Linien aufgereiht. Neutrale Linie ist die Zeile, in der Normalspannungen sind Null.
Die auf der Seitenfläche des Strahls senkrecht zur Achse gezeichneten Linien bleiben erhalten Wohnung beim Biegen. Diese experimentellen Daten ermöglichen es, die Schlussfolgerungen der Formeln zu begründen Hypothese ebener Schnitte (Vermutung). Nach dieser Hypothese sind die Abschnitte des Balkens vor dem Biegen flach und senkrecht zu seiner Achse, bleiben flach und verlaufen beim Biegen senkrecht zur gekrümmten Achse des Balkens.
Annahmen zur Ableitung von Normalspannungsformeln: 1) Die Hypothese ebener Schnitte ist erfüllt. 2) Längsfasern drücken nicht aufeinander (Nicht-Druck-Hypothese) und daher befindet sich jede der Fasern in einem Zustand einachsiger Spannung oder Kompression. 3) Verformungen von Fasern hängen nicht von ihrer Position entlang der Querschnittsbreite ab. Folglich bleiben die Normalspannungen, die sich entlang der Höhe des Abschnitts ändern, entlang der Breite gleich. 4) Der Balken hat mindestens eine Symmetrieebene und alle äußeren Kräfte liegen in dieser Ebene. 5) Das Material des Balkens gehorcht dem Hookeschen Gesetz und der Elastizitätsmodul bei Zug und Druck ist gleich. 6) Das Verhältnis zwischen den Abmessungen des Trägers ist so, dass er unter ebenen Biegebedingungen ohne Verformung oder Verdrehung funktioniert.
Betrachten wir einen Balken mit beliebigem Querschnitt, aber einer Symmetrieachse.  Biegemoment repräsentiert resultierendes Moment der inneren Normalkräfte, entsteht auf unendlich kleinen Flächen und kann ausgedrückt werden in Integral bilden:
Biegemoment repräsentiert resultierendes Moment der inneren Normalkräfte, entsteht auf unendlich kleinen Flächen und kann ausgedrückt werden in Integral bilden: ![]() (1), wobei y der Arm der Elementarkraft relativ zur x-Achse ist
(1), wobei y der Arm der Elementarkraft relativ zur x-Achse ist
Formel (1) drückt aus statisch Seite des Problems der Biegung eines geraden Balkens, jedoch entlang dieser mit einem bekannten Biegemoment Es ist unmöglich, Normalspannungen zu bestimmen, bis das Gesetz ihrer Verteilung festgelegt ist.
Wählen wir die Balken im Mittelteil aus und überlegen wir Abschnitt der Länge dz, unterliegen einer Biegung. Lassen Sie es uns im vergrößerten Maßstab darstellen.

Abschnitte, die den Bereich dz begrenzen, parallel zueinander, bis sie verformt werden, und nach Aufbringen der Last drehen sich um einen Winkel um ihre neutralen Linien . Die Länge des Fasersegments der neutralen Schicht ändert sich nicht. und wird gleich sein: ![]() , wo ist es Krümmungsradius die gekrümmte Achse des Balkens. Aber jede andere Faser liegt niedriger oder höher neutrale Schicht, wird seine Länge ändern. Rechnen wir relative Dehnung von Fasern, die sich im Abstand y von der neutralen Schicht befinden. Die relative Dehnung ist das Verhältnis der absoluten Verformung zur ursprünglichen Länge, dann:
, wo ist es Krümmungsradius die gekrümmte Achse des Balkens. Aber jede andere Faser liegt niedriger oder höher neutrale Schicht, wird seine Länge ändern. Rechnen wir relative Dehnung von Fasern, die sich im Abstand y von der neutralen Schicht befinden. Die relative Dehnung ist das Verhältnis der absoluten Verformung zur ursprünglichen Länge, dann:
Reduzieren wir um und bringen ähnliche Begriffe mit, dann erhalten wir: (2) Diese Formel drückt aus geometrisch Seite des reinen Biegeproblems: Die Verformungen der Fasern sind direkt proportional zu ihren Abständen zur neutralen Schicht.
Kommen wir nun zu betont, d.h. wir werden darüber nachdenken körperlich Seite der Aufgabe. gemäß Annahme ohne Druck Wir verwenden Fasern unter axialem Zug-Druck: dann unter Berücksichtigung der Formel (2)
wir haben ![]() (3),
diese. normaler Stress beim Biegen entlang der Profilhöhe linear verteilt. An den äußersten Fasern erreichen die Normalspannungen ihren Maximalwert und im Schwerpunkt des Abschnitts sind sie gleich Null. Lasst uns ersetzen (3)
in die Gleichung ein (1)
und nimm den Bruch aus dem Integralzeichen als konstanter Wert, dann haben wir
(3),
diese. normaler Stress beim Biegen entlang der Profilhöhe linear verteilt. An den äußersten Fasern erreichen die Normalspannungen ihren Maximalwert und im Schwerpunkt des Abschnitts sind sie gleich Null. Lasst uns ersetzen (3)
in die Gleichung ein (1)
und nimm den Bruch aus dem Integralzeichen als konstanter Wert, dann haben wir ![]() . Aber der Ausdruck ist axiales Trägheitsmoment des Abschnitts relativ zur x-Achse - Ich x.
Seine Dimension cm 4, m 4
. Aber der Ausdruck ist axiales Trägheitsmoment des Abschnitts relativ zur x-Achse - Ich x.
Seine Dimension cm 4, m 4
Dann ![]() ,Wo
,Wo ![]() (4) ,wo ist die Krümmung der gekrümmten Achse des Balkens und die Steifigkeit des Balkenabschnitts beim Biegen.
(4) ,wo ist die Krümmung der gekrümmten Achse des Balkens und die Steifigkeit des Balkenabschnitts beim Biegen.
Ersetzen wir den resultierenden Ausdruck Krümmung (4) in den Ausdruck bringen (3)
und wir bekommen Formel zur Berechnung der Normalspannungen an jedem Punkt im Querschnitt: ![]() (5)
(5)
Das. maximal Spannungen entstehen an den Punkten, die am weitesten von der neutralen Linie entfernt sind. Attitüde ![]() (6)
angerufen axiales Moment des Abschnittswiderstands. Seine Dimension cm 3, m 3. Das Widerstandsmoment charakterisiert den Einfluss der Form und Abmessungen des Querschnitts auf die Größe der Spannungen.
(6)
angerufen axiales Moment des Abschnittswiderstands. Seine Dimension cm 3, m 3. Das Widerstandsmoment charakterisiert den Einfluss der Form und Abmessungen des Querschnitts auf die Größe der Spannungen.
Dann maximale Spannungen: ![]() (7)
(7)
Biegefestigkeitsbedingung: ![]() (8)
(8)
Wenn eine Querbiegung auftritt nicht nur Normal-, sondern auch Schubspannungen, Weil verfügbar Scherkraft. Scherbeanspruchung erschweren das Bild der Verformung, sie führen zu Krümmung Querschnitte des Balkens, was zu die Hypothese der ebenen Schnitte wird verletzt. Untersuchungen zeigen jedoch, dass durch Scherspannungen Verformungen entstehen leicht wirken sich auf die nach der Formel berechneten Normalspannungen aus (5) . Daher bei der Ermittlung der Normalspannungen bei Querbiegung Die Theorie der reinen Biegung ist durchaus anwendbar.
Neutrale Linie. Frage zur Position der neutralen Linie.
Fehlt beim Biegen Längskraft, damit wir schreiben können ![]() Ersetzen wir hier die Formel für Normalspannungen (3)
und wir bekommen
Ersetzen wir hier die Formel für Normalspannungen (3)
und wir bekommen ![]() Da der Längselastizitätsmodul des Balkenmaterials ungleich Null ist und die gekrümmte Achse des Balkens einen endlichen Krümmungsradius aufweist, bleibt die Annahme, dass dieses Integral gleich Null ist statisches Flächenmoment Querschnitt des Strahls relativ zur neutralen Linienachse x
Da der Längselastizitätsmodul des Balkenmaterials ungleich Null ist und die gekrümmte Achse des Balkens einen endlichen Krümmungsradius aufweist, bleibt die Annahme, dass dieses Integral gleich Null ist statisches Flächenmoment Querschnitt des Strahls relativ zur neutralen Linienachse x ![]() , und da ist sie gleich Null, dann verläuft die Neutrallinie durch den Schwerpunkt des Abschnitts.
, und da ist sie gleich Null, dann verläuft die Neutrallinie durch den Schwerpunkt des Abschnitts.
Die Bedingung (Fehlen eines Moments der Schnittgrößen relativ zur Feldlinie) ergibt ![]() oder unter Berücksichtigung (3)
oder unter Berücksichtigung (3)
![]() . Aus den gleichen Gründen (siehe oben)
. Aus den gleichen Gründen (siehe oben) ![]() . Im Integranden - Das Zentrifugalträgheitsmoment des Abschnitts relativ zur x- und y-Achse ist Null, was bedeutet, dass diese Achsen sind Haupt und Zentral und schminken gerade Ecke. Somit, Die Kraft- und Neutrallinien in einer geraden Biegung stehen senkrecht zueinander.
. Im Integranden - Das Zentrifugalträgheitsmoment des Abschnitts relativ zur x- und y-Achse ist Null, was bedeutet, dass diese Achsen sind Haupt und Zentral und schminken gerade Ecke. Somit, Die Kraft- und Neutrallinien in einer geraden Biegung stehen senkrecht zueinander.
Nach der Installation neutrale Linienposition, einfach zu bauen Normalspannungsdiagramm entlang der Abschnittshöhe. Ihr linear Charakter wird bestimmt Gleichung ersten Grades.

Die Art des Diagramms σ für symmetrische Abschnitte relativ zur Neutrallinie, M<0