Relativer Fehler der ungefähren Zahl. Absoluter und relativer Berechnungsfehler
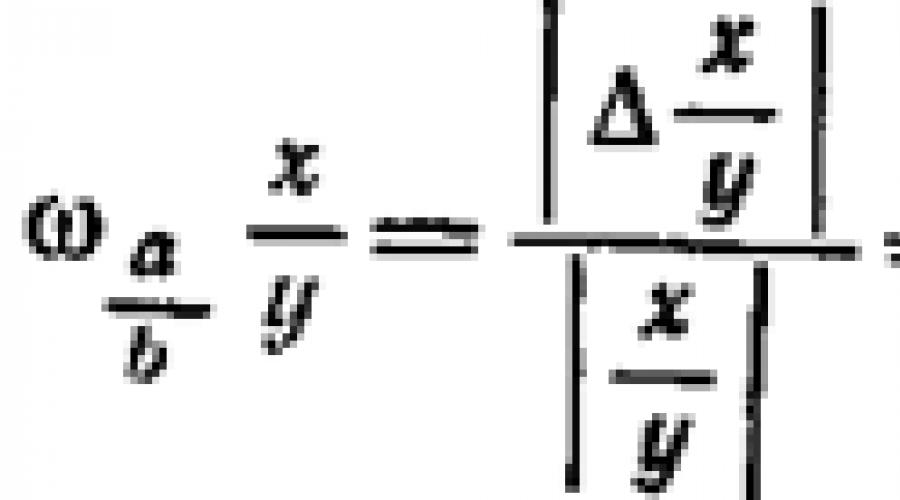
Lesen Sie auch
Bei Berechnungen ist es oft erforderlich, Zahlen zu runden, d. h. indem man sie durch Zahlen mit weniger ersetzt bedeutende Zahlen.
Es gibt drei Möglichkeiten, Zahlen zu runden:
Abrunden auf k Die th-signifikante Ziffer besteht darin, alle Ziffern ab zu verwerfen (k+1) Th.
Das Aufrunden unterscheidet sich vom Abwärtsrunden dadurch, dass die letzte gespeicherte Ziffer um eins erhöht wird.
Eine engere Rundung unterscheidet sich von einer Überrundung dadurch, dass die letzte zu behaltende Ziffer nur dann um eins erhöht wird, wenn die erste zu verwerfende Ziffer größer als 4 ist.
Ausnahme: Wenn das Runden mit dem kleinsten Fehler auf das Verwerfen nur einer Ziffer 5 reduziert wird, wird die letzte beibehaltene Ziffer nicht geändert, wenn sie gerade ist, und um 1 erhöht, wenn sie ungerade ist.
Aus den oben genannten Regeln zum Runden von Näherungszahlen folgt, dass der Fehler, der durch das Runden mit dem kleinsten Fehler entsteht, eine halbe Einheit der letzten beibehaltenen Ziffer nicht überschreitet, und dass der Fehler beim Runden mit einem Defizit oder Überschuss mehr als eine halbe Einheit betragen kann der letzten beibehaltenen Ziffer, jedoch nicht mehr als eine ganze Einheit dieser Entladung.
Schauen wir uns das anhand der folgenden Beispiele an.
1. Summenfehler. Lassen X A, bei-- eine gewisse Annäherung an den Wert B. Lassen X Und bei-- absolute Fehler der entsprechenden Näherungen X Und bei. Lassen Sie uns die absolute Fehlergrenze ermitteln H a+b Beträge x+y, was eine Näherung der Summe ist a+b.
a = x + x,
b = y + y.
Addieren wir diese beiden Gleichheiten und erhalten wir
a + b = x + y + x + y.
Offensichtlich liegt der Fehler in der Summe der Näherungen X Und bei gleich der Summe der Fehler der Terme, d.h.
(x + y) = x + y
Es ist bekannt, dass der Modul der Summe kleiner oder gleich der Summe der Module der Terme ist. Deshalb
(x + y) = x + y X + j
Daraus folgt, dass der absolute Fehler der Summe der Näherungen die Summe der absoluten Fehler der Terme nicht überschreitet. Folglich kann die Summe der Grenzen der absoluten Fehler der Terme als Grenze des absoluten Fehlers der Summe angesehen werden.
Nachdem die Grenze des absoluten Fehlers des Wertes festgelegt wurde A durch H A, und die Werte von b bis H B werde haben
H a+b = H A + H B
2. Differenzfehler. Seien x und y die Fehler der Näherungen x bzw. y der Größen a und b.
a = x + x,
b = y + y.
Subtrahieren wir die zweite von der ersten Gleichheit, erhalten wir
a - b = (x - y) + (x - y)
Offensichtlich ist der Fehler der Differenz zwischen den Näherungen gleich der Differenz zwischen den Fehlern von Minuend und Subtrahend, d.h.
(x - y) = x - y),
(x - y) = x + (-y)
Und dann werden wir auf die gleiche Weise argumentieren wie im Fall der Addition
(x - y) = x + (-y) X + j
Daraus folgt, dass der absolute Fehler der Differenz die Summe der absoluten Fehler von Minuend und Subtrahend nicht überschreitet.
Die Grenze des absoluten Fehlers der Differenz kann als Summe der Grenzen der absoluten Fehler von Minuend und Subtrahend angenommen werden. Auf diese Weise.
H a-b = h A + h B (9)
Aus Formel (9) folgt, dass die Grenze des absoluten Fehlers der Differenz nicht kleiner sein kann als die Grenze des absoluten Fehlers jeder Näherung. Daraus ergibt sich die Regel zum Subtrahieren von Näherungen, die manchmal in Berechnungen verwendet wird.
Beim Subtrahieren von Zahlen, die Annäherungen an bestimmte Größen darstellen, sollte das Ergebnis so viele Nachkommastellen übrig lassen wie die Näherung mit der geringsten Anzahl an Dezimalstellen.
3. Produktfehler. Betrachten Sie das Produkt der Zahlen X Und bei, die Näherungen der Mengen sind A Und B. Bezeichnen wir mit X Näherungsfehler X, Und durch bei-- Näherungsfehler bei,
a = x + x,
b = y + y.
Wenn wir diese beiden Gleichungen multiplizieren, erhalten wir
Absoluter Produktfehler xy gleich
Und deswegen
Division beider Seiten der resultierenden Ungleichung durch xy, wir bekommen
Wenn man bedenkt, dass der Modul des Produkts gleich dem Produkt der Module der Faktoren ist, erhalten wir
Hier stellt die linke Seite der Ungleichung den relativen Fehler des Produkts dar xy, – relativer Näherungsfehler X und ist der relative Näherungsfehler bei. Wenn wir hier also den kleinen Wert verwerfen, erhalten wir die Ungleichung
Somit übersteigt der relative Fehler des Approximationsprodukts nicht die Summe der relativen Fehler der Faktoren. Daraus folgt, dass die Summe der Grenzen der relativen Fehler der Faktoren die Grenze des relativen Fehlers des Produkts ist, d.h.
E ab = E A + E B (10)
Aus Formel (10) folgt, dass die Grenze des relativen Fehlers des Produkts nicht kleiner sein kann als die Grenze des relativen Fehlers des am wenigsten genauen Faktors. Daher macht es hier, wie auch in den vorherigen Schritten, keinen Sinn, zu viele signifikante Zahlen in den Faktoren zu hinterlegen.
Manchmal ist es bei Berechnungen sinnvoll, die folgende Regel zu verwenden, um den Arbeitsaufwand zu reduzieren: Bei der Multiplikation von Näherungen mit unterschiedlicher Anzahl signifikanter Stellen sollte das Ergebnis so viele signifikante Stellen enthalten wie die Näherung mit der geringsten Anzahl signifikanter Stellen.
4. Fehler des Quotienten. Wenn x eine Näherung der Größe a ist, deren Fehler x ist, und y eine Näherung der Größe b mit einem Fehler von y ist, dann
Berechnen wir zunächst den absoluten Fehler des Quotienten:
und dann der relative Fehler:

Unter Berücksichtigung dessen j wenig im Vergleich zu j, der Absolutwert des Bruchs kann als gleich eins betrachtet werden. Dann
Aus der letzten Formel folgt, dass der relative Fehler des Quotienten die Summe der relativen Fehler von Dividend und Divisor nicht überschreitet. Folglich können wir davon ausgehen, dass die Grenze des relativen Fehlers des Quotienten gleich der Summe der Grenzen der relativen Fehler von Dividend und Divisor ist, d.h.
5. Grad- und Wurzelfehler. 1) Lass u = a N, Wo N -- natürliche Zahl, und sei ein x. Dann wenn E A– Grenze des relativen Approximationsfehlers X Mengen A, Das
Und deswegen
Somit ist die Grenze des relativen Fehlers des Grades gleich dem Produkt aus der Grenze des relativen Fehlers der Basis und des Exponenten, d.h.
E u = n E A (11)
2) Lass wo N– eine natürliche Zahl, und sei Oh.
Nach Formel (11)
und deshalb
Fehler subtrahierte Berechnung
Somit ist die Grenze des relativen Fehlers der Wurzel N Abschluss in N mal kleiner als die Grenze des relativen Fehlers der Wurzelzahl.
6. Inverses Problem der Näherungsberechnungen. Im direkten Problem ist es erforderlich, den Näherungswert der Funktion u=f(x,y,...,n) anhand der angegebenen Näherungswerte der Argumente zu ermitteln
und Fehlergrenze H A, was durch die Fehler der Argumente einer bestimmten Funktion ausgedrückt wird
H u = (h X , H j , …, H z ) (12)
In der Praxis ist es oft notwendig, das Umkehrproblem zu lösen, bei dem es darum geht, herauszufinden, mit welcher Genauigkeit die Werte der Argumente angegeben werden sollen x, y, …, z um die entsprechenden Funktionswerte zu berechnen u = f(x, y, …, z) mit einer vorgegebenen Genauigkeit h u .
Bei der Lösung des inversen Problems sind die gesuchten Grenzen also die Fehlergrenzen der Argumente, die der gegebenen Fehlergrenze der Funktion zugeordnet sind H u Gleichung (12) und die Lösung des inversen Problems reduziert sich auf das Zusammenstellen und Lösen der Gleichung H u = (h X , H j , …, H z ) verhältnismäßig H X , H j , …, H z. Eine solche Gleichung hat entweder unendlich viele Lösungen oder überhaupt keine Lösungen. Das Problem gilt als gelöst, wenn mindestens eine Lösung für eine solche Gleichung gefunden wird.
Um das oft unsichere inverse Problem zu lösen, ist es notwendig, zusätzliche Bedingungen über die Verhältnisse der gesuchten Fehler einzuführen, beispielsweise diese als gleich zu betrachten und dadurch das Problem auf eine Gleichung mit einer Unbekannten zu reduzieren.
Wenn Sie in Berechnungen mit unendlichen Dezimalbrüchen arbeiten, müssen Sie diese Zahlen der Einfachheit halber annähern, d. h. runden. Nähere Zahlen werden auch aus verschiedenen Messungen ermittelt.
Es kann hilfreich sein zu wissen, um wie viel der ungefähre Wert einer Zahl von ihrem genauen Wert abweicht. Es ist klar, dass die Messung bzw. Berechnung umso genauer erfolgt, je kleiner dieser Unterschied ist.
Um die Genauigkeit von Messungen (Berechnungen) zu bestimmen, kann ein Konzept wie z Näherungsfehler. Sie nennen es anders Absoluter Fehler. Der Näherungsfehler ist die Modulo-Differenz zwischen dem genauen Wert einer Zahl und ihrem Näherungswert.
Wenn a ist genauer Wert Zahl und b ihr Näherungswert ist, wird der Näherungsfehler durch die Formel |a – b| bestimmt.
Nehmen wir an, dass als Ergebnis der Messungen die Zahl 1,5 erhalten wurde. Als Ergebnis der Berechnung mit der Formel beträgt der genaue Wert dieser Zahl jedoch 1,552. In diesem Fall beträgt der Näherungsfehler |1,552 – 1,5| = 0,052.
Bei unendlichen Brüchen wird der Näherungsfehler nach der gleichen Formel bestimmt. Anstelle der genauen Zahl wird der unendliche Bruch selbst geschrieben. Zum Beispiel |π – 3,14| = |3,14159... – 3,14| = 0,00159... . Hier stellt sich heraus, dass der Näherungsfehler durch eine irrationale Zahl ausgedrückt wird.
Bekanntermaßen kann die Annäherung sowohl durch Mangel als auch durch Überschuss erfolgen. Die gleiche Zahl π beträgt bei Näherung durch den Mangel mit einer Genauigkeit von 0,01 3,14 und bei Näherung durch den Überschuss mit einer Genauigkeit von 0,01 3,15. Der Grund dafür, dass bei der Berechnung die Defizitnäherung verwendet wird, ist die Anwendung von Rundungsregeln. Wenn nach diesen Regeln die erste zu verwerfende Ziffer fünf oder größer als fünf ist, wird eine übermäßige Näherung durchgeführt. Wenn weniger als fünf, liegt ein Mangel vor. Da die dritte Nachkommastelle der Zahl π 1 ist, erfolgt die Näherung mit einer Genauigkeit von 0,01 durch Defizit.
Wenn wir tatsächlich die Fehler der Annäherung an 0,01 der Zahl π durch Mangel und Überschuss berechnen, erhalten wir:
|3,14159... – 3,14| = 0,00159...
|3,14159... – 3,15| = 0,0084...
Seit 0,00159...
Wenn vom Näherungsfehler die Rede ist, wie auch im Fall der Näherung selbst (durch Überschuss oder Mangel), wird auf deren Genauigkeit hingewiesen. Im obigen Beispiel mit der Zahl π sollte also gesagt werden, dass sie mit einer Genauigkeit von 0,01 gleich der Zahl 3,14 ist. Schließlich überschreitet der Modul der Differenz zwischen der Zahl selbst und ihrem Näherungswert nicht 0,01 (0,00159... ≤ 0,01).
Ebenso ist π gleich 3,15 mit einer Genauigkeit von 0,01, da 0,0084... ≤ 0,01. Wenn wir jedoch von einer höheren Genauigkeit sprechen, beispielsweise bis zu 0,005, dann können wir sagen, dass π gleich 3,14 mit einer Genauigkeit von 0,005 ist (da 0,00159... ≤ 0,005). Wir können dies nicht in Bezug auf die Näherung von 3,15 sagen (da 0,0084... > 0,005).
Der absolute Berechnungsfehler ergibt sich aus der Formel:
Das Modulzeichen zeigt, dass es uns egal ist, welcher Wert größer und welcher kleiner ist. Wichtig, wie weit das ungefähre Ergebnis weicht in der einen oder anderen Richtung vom genauen Wert ab.
Der relative Berechnungsfehler wird durch die Formel ermittelt:
, oder dasselbe: ![]()
Der relative Fehler wird angezeigt um wie viel Prozent das ungefähre Ergebnis weicht vom genauen Wert ab. Es gibt eine Version der Formel ohne Multiplikation mit 100 %, aber in der Praxis sehe ich fast immer die obige Version mit Prozentsätzen.
Kehren wir nach einer kurzen Referenz zu unserem Problem zurück, bei dem wir den Näherungswert der Funktion berechnet haben ![]() mit einem Differenzial.
mit einem Differenzial.
Berechnen wir den genauen Wert der Funktion mit einem Mikrorechner:
Genau genommen ist der Wert immer noch ungefähr, wir werden ihn jedoch als korrekt betrachten. Solche Probleme kommen vor.
Berechnen wir den absoluten Fehler:
Berechnen wir den relativen Fehler:
, Tausendstel Prozent wurden erhalten, sodass das Differential nur eine hervorragende Näherung darstellte.
Antwort: ![]() , absoluter Rechenfehler, relativer Rechenfehler
, absoluter Rechenfehler, relativer Rechenfehler
Das folgende Beispiel ist für unabhängige Entscheidung:
Beispiel 4
![]() am Punkt . Berechnen Sie einen genaueren Wert der Funktion an einem bestimmten Punkt und schätzen Sie den absoluten und relativen Fehler der Berechnungen.
am Punkt . Berechnen Sie einen genaueren Wert der Funktion an einem bestimmten Punkt und schätzen Sie den absoluten und relativen Fehler der Berechnungen.
Ein ungefähres Muster des endgültigen Entwurfs und eine Antwort am Ende der Lektion.
Vielen ist aufgefallen, dass in allen betrachteten Beispielen Wurzeln auftauchen. Dies ist kein Zufall; in den meisten Fällen bietet das betrachtete Problem tatsächlich Funktionen mit Wurzeln.
Aber für leidende Leser habe ich ausgegraben kleines Beispiel mit Arkussinus:
Beispiel 5
Berechnen Sie ungefähr den Wert einer Funktion mithilfe eines Differentials ![]() am Punkt
am Punkt
Dieses kurze, aber informative Beispiel können Sie auch selbst lösen. Und ich habe mich ein wenig ausgeruht, um mit neuem Elan die besondere Aufgabe in Angriff nehmen zu können:
Beispiel 6
Berechnen Sie näherungsweise mithilfe einer Differenzialrechnung und runden Sie das Ergebnis auf zwei Dezimalstellen.
Lösung: Was ist neu an der Aufgabe? Die Bedingung erfordert, dass das Ergebnis auf zwei Dezimalstellen gerundet wird. Aber das ist nicht der Punkt; ich denke, das Schulrundungsproblem ist für Sie nicht schwierig. Tatsache ist, dass uns ein Tangens mit einem Argument gegeben wird, das in Grad ausgedrückt wird. Was sollten Sie tun, wenn Sie aufgefordert werden, eine trigonometrische Funktion mit Graden zu lösen? Zum Beispiel , usw.
Der Lösungsalgorithmus ist grundsätzlich derselbe, das heißt, es ist wie in den vorherigen Beispielen erforderlich, die Formel anzuwenden
Schreiben wir eine offensichtliche Funktion
Der Wert muss im Formular dargestellt werden. Werde ernsthafte Hilfe leisten Wertetabelle trigonometrischer Funktionen . Für diejenigen, die es noch nicht ausgedruckt haben, empfehle ich übrigens, dies zu tun, da man während des gesamten Studiums der Höheren Mathematik dort nachschauen muss.
Bei der Analyse der Tabelle bemerken wir einen „guten“ Tangentenwert, der nahe bei 47 Grad liegt:
Auf diese Weise: ![]()
Nach Voruntersuchung Grad müssen in Bogenmaß umgerechnet werden. Ja, und nur so!
IN in diesem Beispiel direkt von trigonometrische Tabelle Sie können herausfinden, was. Verwendung der Formel zur Umrechnung von Grad in Bogenmaß: ![]() (Formeln finden Sie in derselben Tabelle).
(Formeln finden Sie in derselben Tabelle).
Was folgt, ist formelhaft:
Auf diese Weise: ![]() (Wir verwenden den Wert für Berechnungen). Das Ergebnis wird, je nach Bedingung, auf zwei Dezimalstellen gerundet.
(Wir verwenden den Wert für Berechnungen). Das Ergebnis wird, je nach Bedingung, auf zwei Dezimalstellen gerundet.
Antwort:
Beispiel 7
Rechnen Sie näherungsweise mit einem Differenzial, runden Sie das Ergebnis auf drei Dezimalstellen.
Dies ist ein Beispiel, das Sie selbst lösen können. Komplette Lösung und die Antwort am Ende der Lektion.
Wie Sie sehen, gibt es nichts Kompliziertes, wir rechnen Grad in Bogenmaß um und halten uns an den üblichen Lösungsalgorithmus.
Näherungsberechnungen unter Verwendung des Gesamtdifferentials einer Funktion zweier Variablen
Alles wird sehr, sehr ähnlich sein. Wenn Sie also speziell für diese Aufgabe auf diese Seite gekommen sind, empfehle ich Ihnen, sich zunächst mindestens ein paar Beispiele des vorherigen Absatzes anzusehen.
Um einen Absatz zu studieren, muss man ihn finden können Partielle Ableitungen zweiter Ordnung , wo wären wir ohne sie? In der obigen Lektion habe ich eine Funktion zweier Variablen mit dem Buchstaben bezeichnet. In Bezug auf die betrachtete Aufgabe ist es bequemer, die äquivalente Notation zu verwenden.
Wie im Fall einer Funktion einer Variablen kann der Zustand des Problems auf unterschiedliche Weise formuliert werden, und ich werde versuchen, alle angetroffenen Formulierungen zu berücksichtigen.
Beispiel 8
![]()
Lösung: Unabhängig davon, wie die Bedingung geschrieben ist, ist es in der Lösung selbst zur Bezeichnung der Funktion, ich wiederhole, besser, nicht den Buchstaben „zet“ zu verwenden, sondern .
Und hier ist die Arbeitsformel:
Was wir vor uns haben, ist eigentlich die ältere Schwester der Formel des vorherigen Absatzes. Die Variable hat nur zugenommen. Was soll ich selbst sagen Der Lösungsalgorithmus wird grundsätzlich derselbe sein!
Je nach Bedingung ist es erforderlich, den Näherungswert der Funktion an dem Punkt zu ermitteln.
Stellen wir die Zahl 3,04 in der Form dar. Das Brötchen selbst möchte gegessen werden:
,
Stellen wir uns die Zahl 3,95 als vor. Die zweite Hälfte von Kolobok ist an der Reihe:
,
Und schauen Sie sich nicht alle Tricks des Fuchses an, es gibt einen Kolobok – den müssen Sie essen.
Berechnen wir den Wert der Funktion an der Stelle:
Wir ermitteln das Differential einer Funktion an einem Punkt mit der Formel:
Aus der Formel folgt, was wir finden müssen partielle Ableitungen erste Ordnung und berechnen Sie ihre Werte am Punkt .
Berechnen wir die partiellen Ableitungen erster Ordnung an der Stelle:
![]()

Gesamtdifferenz zum Zeitpunkt:
Somit ist nach der Formel der Näherungswert der Funktion an der Stelle:
Berechnen wir den genauen Wert der Funktion an der Stelle:
Dieser Wert ist absolut korrekt.
Fehler werden anhand von Standardformeln berechnet, die bereits in diesem Artikel besprochen wurden.
Absoluter Fehler:
Relativer Fehler:![]()
Antwort: , absoluter Fehler: , relativer Fehler:
Beispiel 9
Berechnen Sie den Näherungswert einer Funktion ![]() Schätzen Sie an einem Punkt mithilfe eines Gesamtdifferentials den absoluten und relativen Fehler.
Schätzen Sie an einem Punkt mithilfe eines Gesamtdifferentials den absoluten und relativen Fehler.
Dies ist ein Beispiel, das Sie selbst lösen können. Wer sich dieses Beispiel genauer anschaut, wird feststellen, dass die Rechenfehler sehr, sehr auffällig ausgefallen sind. Dies geschah aus folgendem Grund: Im vorgeschlagenen Problem sind die Argumentzuwächse ziemlich groß: .
Das allgemeine Muster ist folgendes a - je größer diese Inkremente sind Absolutwert, desto geringer ist die Genauigkeit der Berechnungen. So werden beispielsweise für einen ähnlichen Punkt die Inkremente klein sein: und die Genauigkeit der Näherungsberechnungen wird sehr hoch sein.
Diese Funktion gilt auch für den Fall einer Funktion einer Variablen (erster Teil der Lektion).
Beispiel 10
![]()
Lösung: Berechnen wir diesen Ausdruck näherungsweise anhand des Gesamtdifferentials einer Funktion zweier Variablen:
Der Unterschied zu den Beispielen 8–9 besteht darin, dass wir zunächst eine Funktion aus zwei Variablen konstruieren müssen: ![]() . Ich denke, jeder versteht intuitiv, wie die Funktion aufgebaut ist.
. Ich denke, jeder versteht intuitiv, wie die Funktion aufgebaut ist.
Der Wert 4,9973 liegt nahe bei „fünf“, daher: , .
Der Wert 0,9919 liegt nahe bei „eins“, daher gehen wir davon aus: , .
Berechnen wir den Wert der Funktion an der Stelle:
Wir ermitteln das Differential an einem Punkt mit der Formel:
Dazu berechnen wir die partiellen Ableitungen erster Ordnung an der Stelle.
Die Ableitungen hier sind nicht die einfachsten, und Sie sollten vorsichtig sein:  ;
;![]()

![]() .
.
Gesamtdifferenz zum Zeitpunkt:
Somit ist der ungefähre Wert dieses Ausdrucks:
Berechnen wir mit einem Mikrorechner einen genaueren Wert: 2,998899527
Finden wir den relativen Berechnungsfehler:
Antwort: , ![]()
Nur zur Veranschaulichung des oben Gesagten: Bei dem betrachteten Problem sind die Argumentzuwächse sehr klein und der Fehler erwies sich als fantastisch winzig.
Beispiel 11
Berechnen Sie anhand des vollständigen Differentials einer Funktion zweier Variablen ungefähr den Wert dieses Ausdrucks. Berechnen Sie denselben Ausdruck mit einem Mikrorechner. Schätzen Sie den relativen Berechnungsfehler in Prozent. ![]()
Dies ist ein Beispiel, das Sie selbst lösen können. Ein ungefähres Muster des endgültigen Entwurfs am Ende der Lektion.
Wie bereits erwähnt, ist der häufigste Gast bei dieser Art von Aufgabe eine Art Wurzel. Aber von Zeit zu Zeit gibt es auch andere Funktionen. Und ein letztes einfaches Beispiel zur Entspannung:
Beispiel 12
Berechnen Sie anhand des Gesamtdifferentials einer Funktion zweier Variablen ungefähr den Wert der Funktion if ![]()
Die Lösung befindet sich weiter unten auf der Seite. Achten Sie noch einmal auf die Formulierung der Unterrichtsaufgaben verschiedene Beispiele In der Praxis können die Formulierungen unterschiedlich sein, was jedoch nichts Grundsätzliches am Wesen und am Algorithmus der Lösung ändert.
Ehrlich gesagt war ich etwas müde, weil der Stoff etwas langweilig war. Es war nicht pädagogisch, dies am Anfang des Artikels zu sagen, aber jetzt ist es bereits möglich =) Tatsächlich sind Probleme in der Computermathematik normalerweise nicht sehr komplex, nicht sehr interessant, das Wichtigste ist vielleicht, keinen Fehler zu machen in gewöhnlichen Berechnungen.
Mögen die Tasten Ihres Rechners nicht gelöscht werden!
Lösungen und Antworten:
Beispiel 2:
Lösung: Wir verwenden die Formel:
In diesem Fall: , ,

Auf diese Weise: ![]()
Antwort:
Beispiel 4:
Lösung: Wir verwenden die Formel:
In diesem Fall: ![]() , ,
, ,

Auf diese Weise:
Berechnen wir einen genaueren Wert der Funktion mit einem Mikrorechner:
Absoluter Fehler:
Relativer Fehler:
Antwort: ![]() , absoluter Rechenfehler, relativer Rechenfehler
, absoluter Rechenfehler, relativer Rechenfehler
Beispiel 5:
Lösung: Wir verwenden die Formel:
In diesem Fall: ![]() , ,
, ,

Auf diese Weise:
Antwort: ![]()
Beispiel 7:
Lösung: Wir verwenden die Formel:
In diesem Fall: , , ![]()
Absoluter und relativer Zahlenfehler.
Als Merkmale der Genauigkeit von Näherungsgrößen jeglichen Ursprungs werden die Konzepte der absoluten und relativen Fehler dieser Größen eingeführt.
Bezeichnen wir mit a die Annäherung an die genaue Zahl A.
Definieren. Die Menge wird als Fehler der ungefähren Zahla bezeichnet.
Definition.
Absoluter Fehler  Die ungefähre Zahl a heißt Menge
Die ungefähre Zahl a heißt Menge  .
.
Die praktisch genaue Zahl A ist normalerweise unbekannt, wir können jedoch immer die Grenzen angeben, innerhalb derer der absolute Fehler variiert.
Definition.
Maximaler absoluter Fehler  Die ungefähre Zahl a wird als kleinste der oberen Grenzen für die Menge bezeichnet
Die ungefähre Zahl a wird als kleinste der oberen Grenzen für die Menge bezeichnet  , die mit dieser Methode zur Ermittlung der Zahla ermittelt werden kann.
, die mit dieser Methode zur Ermittlung der Zahla ermittelt werden kann.
In der Praxis, wie  Wählen Sie eine der oberen Grenzen für
Wählen Sie eine der oberen Grenzen für  , ganz nah am Kleinsten.
, ganz nah am Kleinsten.
Weil das  , Das
, Das  . Manchmal schreiben sie:
. Manchmal schreiben sie:  .
.
Absoluter Fehler ist die Differenz zwischen dem Messergebnis
und wahrer (echter) Wert gemessene Größe.
Der absolute Fehler und der maximale absolute Fehler reichen nicht aus, um die Genauigkeit einer Messung oder Berechnung zu charakterisieren. Qualitativ ist die Größe des relativen Fehlers bedeutsamer.
Definition.
Relativer Fehler  Wir nennen die ungefähre Zahl a die Menge:
Wir nennen die ungefähre Zahl a die Menge:

Definition.
Maximaler relativer Fehler  ungefähre Zahl a nennen wir die Menge
ungefähre Zahl a nennen wir die Menge

Als  .
.
Somit bestimmt der relative Fehler tatsächlich die Größe des absoluten Fehlers pro Einheit der gemessenen oder berechneten Näherungszahl a.
Beispiel. Bestimmen Sie, indem Sie die genauen Zahlen A auf drei signifikante Ziffern runden
absolute D- und relative δ-Fehler der erhaltenen Näherungswerte
Gegeben:
Finden:
∆-absoluter Fehler
δ – relativer Fehler
Lösung:
=|-13.327-(-13.3)|=0.027
 ,A
,A  0
0
 *100%=0.203%
*100%=0.203%
Antwort:=0,027; δ=0,203 %
2. Dezimalschreibweise einer ungefähren Zahl. Signifikante Figur. Korrekte Ziffern von Zahlen (Definition korrekter und signifikanter Ziffern, Beispiele; Theorie des Zusammenhangs zwischen relativem Fehler und Anzahl korrekter Ziffern).
Wahre Zeichen Zahlen.
Definition. Die signifikante Ziffer einer Näherungszahl a ist jede Ziffer außer Null und Null, wenn sie zwischen signifikanten Ziffern liegt oder eine gespeicherte Dezimalstelle darstellt.
Zum Beispiel in der Zahl 0,00507 =  wir haben 3 signifikante Zahlen und in der Zahl 0,005070=
wir haben 3 signifikante Zahlen und in der Zahl 0,005070=  bedeutende Zahlen, d.h. Die Null auf der rechten Seite, wobei die Dezimalstelle erhalten bleibt, ist signifikant.
bedeutende Zahlen, d.h. Die Null auf der rechten Seite, wobei die Dezimalstelle erhalten bleibt, ist signifikant.
Von nun an stimmen wir zu, Nullen auf die rechte Seite zu schreiben, wenn sie nur von Bedeutung sind. Dann, mit anderen Worten,
Alle Ziffern von a sind von Bedeutung, mit Ausnahme der Nullen auf der linken Seite.
Im dezimalen Zahlensystem kann jede Zahl a als endliche oder unendliche Summe (Dezimalbruch) dargestellt werden:
Wo  ,
,
 - die erste signifikante Ziffer, m - eine ganze Zahl, die als führende Dezimalstelle der Zahl a bezeichnet wird.
- die erste signifikante Ziffer, m - eine ganze Zahl, die als führende Dezimalstelle der Zahl a bezeichnet wird.
Beispiel: 518,3 =, m=2.
Mithilfe der Notation führen wir das Konzept der korrekten Dezimalstellen (in signifikanten Ziffern) ein, ungefähr –
am 1. Tag.
Definition.
Sie sagen, dass in einer ungefähren Zahl a die Form n ist – erste signifikante Ziffern  ,
,
wobei i= m, m-1,..., m-n+1 korrekt sind, wenn der absolute Fehler dieser Zahl eine halbe Zifferneinheit, ausgedrückt durch die n-te signifikante Ziffer, nicht überschreitet:

Ansonsten die letzte Ziffer  als zweifelhaft bezeichnet.
als zweifelhaft bezeichnet.
Beim Schreiben einer ungefähren Zahl ohne Angabe des Fehlers ist es erforderlich, dass alle geschriebenen Zahlen angegeben werden
waren treu. Diese Anforderung wird in allen mathematischen Tabellen erfüllt.
Der Begriff „n richtige Ziffern“ charakterisiert nur den Grad der Genauigkeit der Näherungszahl und ist nicht so zu verstehen, dass die ersten n signifikanten Ziffern der Näherungszahl a mit den entsprechenden Ziffern der genauen Zahl A übereinstimmen. Beispielsweise z die Zahlen A = 10, a = 9,997, alle signifikanten Ziffern sind unterschiedlich, aber die Zahl a hat 3 gültige signifikante Ziffern. Tatsächlich ist hier m=0 und n=3 (wir finden es durch Auswahl).
Messergebnis
Der Fehler des Messergebnisses ermöglicht es uns, zuverlässige Ergebnisse zu ermitteln. Bei der Berechnung des Fehlerwerts, insbesondere mit Hilfe von Taschenrechnern, erhält man den Fehlerwert mit einer großen Anzahl von Vorzeichen. Dadurch entsteht der Eindruck einer hohen Messgenauigkeit, was nicht stimmt, da die Ausgangsdaten für die Berechnung meist die normierten Fehlerwerte des verwendeten SI sind, die nur mit einer oder zwei signifikanten Ziffern angegeben werden. Daher sollte der Endwert des berechneten Fehlers nicht mehr als zwei signifikante Ziffern enthalten. In der Messtechnik gelten folgende Regeln:
1. Der Fehler des Messergebnisses wird durch zwei signifikante Ziffern angezeigt, wenn die erste davon 3 oder weniger beträgt, und durch eine, wenn die erste Ziffer 4 oder mehr beträgt.
Die signifikanten Ziffern einer Zahl sind alle Ziffern von der ersten Ziffer links, die nicht Null ist, bis zur letzten Ziffer rechts, wobei mit dem Faktor 10 n geschriebene Nullen nicht berücksichtigt werden.
2. Das Messergebnis wird auf die gleiche Dezimalstelle gerundet, mit der der gerundete absolute Fehlerwert endet. (Beispiel: Das Ergebnis ist 85,6342, Fehler 0,01. Das Ergebnis wird auf 85,63 gerundet. Das gleiche Ergebnis mit einem Fehler innerhalb von 0,012 sollte auf 85,634 gerundet werden.)
3. Die Rundung erfolgt nur in der endgültigen Antwort und alle vorläufigen Berechnungen werden mit einer oder zwei zusätzlichen Ziffern durchgeführt.
4. Das Runden sollte sofort auf die gewünschte Anzahl signifikanter Stellen erfolgen; schrittweises Runden führt zu Fehlern.
Beim Runden von numerischen Fehlerwerten und Messergebnissen sind die folgenden allgemeinen Rundungsregeln zu beachten.
Überschüssige Ziffern in ganzen Zahlen werden durch Nullen ersetzt und in Dezimalzahlen werden verworfen. (Zum Beispiel wird die Zahl 165245, wenn vier signifikante Ziffern beibehalten werden, auf 165200 gerundet, und die Zahl 165,245 wird auf 165,2 gerundet.)
Wenn ein Dezimalbruch mit Nullen endet, werden sie nur bis zu der Ziffer verworfen, die der Fehlerziffer entspricht. (Beispiel: Das Messergebnis ist 235,200, Fehler 0,05. Das Ergebnis wird auf 235,20 gerundet. Das gleiche Ergebnis mit einem Fehler innerhalb von 0,015 sollte auf 235,200 gerundet werden.)
Wenn die erste (von links nach rechts gezählte) der durch Nullen ersetzten oder verworfenen Ziffern kleiner als 5 ist, werden die übrigen Ziffern angezeigt verändere dich nicht .
Wenn die erste dieser Ziffern 5 ist und keine Ziffern oder Nullen folgen, dann Wenn die letzte Ziffer der zu rundenden Zahl gerade oder Null ist, bleibt sie unverändert , Wenn ungerade – erhöht sich um eins . (Zum Beispiel wird die Zahl 1234,50 auf 1234 gerundet und die Zahl 8765,50 wird auf 8766 gerundet.)
Wenn die erste durch Nullen zu ersetzende oder zu verwerfende Ziffer größer als 5 oder gleich 5 ist, ihr aber eine signifikante Ziffer folgt, dann wird die letzte verbleibende Ziffer um eins erhöht . (Zum Beispiel wird die Zahl 6783,6 unter Beibehaltung von vier signifikanten Ziffern auf 6784 gerundet, und die Zahl 12,34520 wird auf 12,35 gerundet.)
Besondere Vorsicht ist bei der Aufzeichnung des Messergebnisses ohne Angabe des Fehlers geboten, da die Aufzeichnung des Ergebnisses 2,4 · 10 3 V und 2400 V beträgt sind nicht identisch . Der erste Eintrag bedeutet dass die Tausender- und Hundertstel-Volt-Zahlen korrekt sind und der wahre Wert kann im Bereich von 2,351 kV bis 2,449 kV liegen. Die Angabe 2400 bedeutet, dass auch die Einheit Volt korrekt ist, der wahre Spannungswert kann also im Bereich von 2399,51 V bis 2400,49 V liegen.
Daher wird das Ergebnis ohne Angabe des Fehlers aufgezeichnet höchst unerwünscht .
Abschließend lassen sich die Regeln zur Erfassung von Messergebnissen wie folgt formulieren.
1) Bei Zwischenberechnungen werden die Fehlerwerte auf drei oder vier signifikante Stellen beschränkt.
2) Der endgültige Fehlerwert und der Ergebniswert werden gemäß den oben genannten Regeln gerundet.
3) Bei einzelnen technischen Messungen, wenn nur der Haupt-SI-Fehler berücksichtigt wird (SI werden unter normalen Betriebsbedingungen verwendet), wird das Ergebnis in der Form geschrieben:
(Zum Beispiel das Ergebnis einer Spannungsmessung  B, Fehler
B, Fehler  B. Das Ergebnis kann wie folgt geschrieben werden:)
B. Das Ergebnis kann wie folgt geschrieben werden:)

4) Bei einzelnen technischen Messungen unter Betriebsbedingungen wird das Ergebnis unter Berücksichtigung der Haupt- und Zusatzfehler gemäß den Standarddaten des SI und der Ermittlung des resultierenden Fehlers nach Formel (1.35) in der Form geschrieben:

5) Wenn bei statistischen Messungen nur der Wert des Zufallsfehlers normalverteilter Daten in Form eines Konfidenzintervalls bestimmt wird, wird das Ergebnis gemäß (1.31) geschrieben:

Wenn die Grenzen des Konfidenzintervalls asymmetrisch sind, werden sie separat angegeben.
Zum Beispiel,

6) Bei statistischen Messungen, wenn die Grenzen nicht ausgeschlossener systematischer Fehler des Ergebnisses (NSE) und das Konfidenzintervall des Zufallsfehlers normalverteilter Daten geschätzt werden, das Ergebnis jedoch als Zwischenergebnis verwendet wird, um andere Werte zu ermitteln (zum Beispiel bei statistischen indirekten Messungen) oder soll es mit anderen Ergebnissen ähnlicher Messexperimente verglichen werden, wird das Ergebnis gemäß (1.39) geschrieben:
Wenn  , dann wird dies wie in Abschnitt 5 zusätzlich angegeben.
, dann wird dies wie in Abschnitt 5 zusätzlich angegeben.
Wenn die Grenzen des NSP oder die Grenzen des Konfidenzintervalls asymmetrisch sind, werden sie separat angegeben:
7) Wenn während der Messung Fehlerschätzungen unter den in Abschnitt 6 genannten Bedingungen erhalten werden, das Ergebnis jedoch endgültig ist und nicht für eine weitere Analyse und einen Vergleich mit anderen Ergebnissen vorgesehen ist, wird es gemäß (1.41) geschrieben:

Wo  bestimmt durch Formel (1.40),
bestimmt durch Formel (1.40),
Wenn  , wird dies zusätzlich wie in Absatz 5 angegeben.
, wird dies zusätzlich wie in Absatz 5 angegeben.
8) Bei statistischen Messungen, wenn die Grenzen des NSP und das Konfidenzintervall des Zufallsfehlers geschätzt werden, bei der Verarbeitung der Ergebnisse jedoch ein anderes als das normale Verteilungsgesetz festgestellt wird, werden Schätzungen des Werts des Messergebnisses und des Konfidenzintervalls vorgenommen Werden die Zufallsfehler anhand der entsprechenden Formeln ermittelt, wird das Ergebnis in der Form dargestellt, die der Darstellung des Ergebnisses in S. 6 ähnelt, jedoch werden zusätzlich Informationen zur Art des Verteilungsgesetzes der experimentellen Daten bereitgestellt.
9) Wenn, wie in Absatz 8, die Ergebnisse statischer Messungen verarbeitet werden und im Voraus bekannt ist, dass das Verteilungsgesetz der experimentellen Daten vom Normalwert abweicht, aber keine Maßnahmen ergriffen werden, um die Art des tatsächlichen Gesetzes zu ermitteln Aus irgendeinem Grund kann das Ergebnis in einer ähnlichen Form wie das Darstellungsergebnis in Absatz 6 dargestellt werden, das Konfidenzintervall des Zufallsfehlers wird jedoch gemäß den Empfehlungen von GOST 11.001-73 bestimmt  mit Konfidenzwahrscheinlichkeit
mit Konfidenzwahrscheinlichkeit  .
.
Das Ergebnis könnte beispielsweise so aussehen:

 (bei
(bei  );
);
 ;
;
 ;
;
 .
.
Konfidenzwahrscheinlichkeit, mit der das Gesamt-ERP bestimmt wird -  , kann in diesem Fall abweichen
, kann in diesem Fall abweichen  .
.