Bezeichnung von Schnittlinien. Grenzen überschreiten

In diesem Artikel definieren wir zunächst den Winkel zwischen sich kreuzenden Linien und stellen eine grafische Darstellung bereit. Als nächstes beantworten wir die Frage: „Wie findet man den Winkel zwischen sich kreuzenden Linien, wenn die Koordinaten der Richtungsvektoren dieser Linien in einem rechtwinkligen Koordinatensystem bekannt sind“? Abschließend üben wir das Ermitteln des Winkels zwischen sich schneidenden Linien beim Lösen von Beispielen und Problemen.

Seitennavigation.

Winkel zwischen sich schneidenden Geraden - Definition.

Wir werden uns schrittweise der Bestimmung des Winkels zwischen sich schneidenden Geraden nähern.

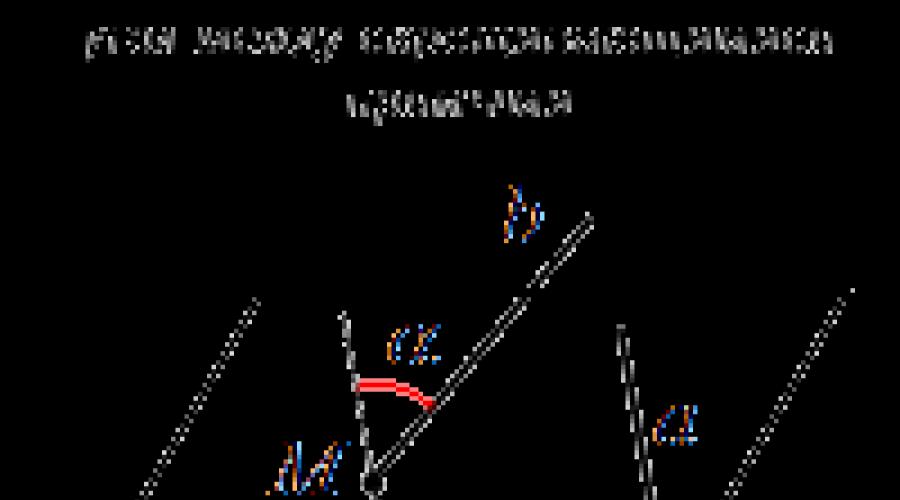
Erinnern wir uns zunächst an die Definition von Schräglinien: Man nennt zwei Linien im dreidimensionalen Raum Kreuzung, wenn sie nicht in derselben Ebene liegen. Aus dieser Definition folgt, dass sich schneidende Linien nicht schneiden, nicht parallel sind und darüber hinaus nicht zusammenfallen, da sie sonst beide in einer bestimmten Ebene liegen würden.

Lassen Sie uns weitere Hilfsbegründungen anführen.

Gegeben seien zwei Schnittlinien a und b im dreidimensionalen Raum. Konstruieren wir gerade Linien a 1 und b 1 so, dass sie parallel zu den Schräglinien a bzw. b verlaufen und durch einen Punkt im Raum M 1 verlaufen. Somit erhalten wir zwei Schnittlinien a 1 und b 1. Sei der Winkel zwischen den Schnittlinien a 1 und b 1 gleich Winkel. Konstruieren wir nun die Linien a 2 und b 2 parallel zu den Schräglinien a bzw. b, die durch einen Punkt M 2 verlaufen, der sich vom Punkt M 1 unterscheidet. Der Winkel zwischen den Schnittlinien a 2 und b 2 ist ebenfalls gleich dem Winkel. Diese Aussage ist wahr, da die Geraden a 1 und b 1 mit den Geraden a 2 bzw. b 2 zusammenfallen, wenn eine parallele Übertragung durchgeführt wird, bei der sich Punkt M 1 zu Punkt M 2 bewegt. Somit hängt das Maß des Winkels zwischen zwei Geraden, die sich in einem Punkt M schneiden, bzw. parallel zu den gegebenen Schnittlinien sind, nicht von der Wahl des Punktes M ab.

Jetzt können wir den Winkel zwischen sich schneidenden Linien definieren.

Definition.

Winkel zwischen sich schneidenden Linien ist der Winkel zwischen zwei Schnittlinien, die jeweils parallel zu den gegebenen Schnittlinien sind.

Aus der Definition folgt, dass der Winkel zwischen sich kreuzenden Linien auch nicht von der Wahl des Punktes M abhängt. Daher können wir als Punkt M jeden Punkt annehmen, der zu einer der Schnittlinien gehört.

Lassen Sie uns die Bestimmung des Winkels zwischen sich schneidenden Linien veranschaulichen.

Ermitteln des Winkels zwischen sich schneidenden Linien.

Da der Winkel zwischen sich schneidenden Linien durch den Winkel zwischen sich schneidenden Linien bestimmt wird, reduziert sich die Bestimmung des Winkels zwischen sich schneidenden Linien auf die Ermittlung des Winkels zwischen den entsprechenden sich schneidenden Linien im dreidimensionalen Raum.

Zweifellos sind die im Geometrieunterricht erlernten Methoden in weiterführende Schule. Das heißt, nachdem Sie die erforderlichen Konstruktionen abgeschlossen haben, können Sie den gewünschten Winkel mit jedem aus der Bedingung bekannten Winkel verbinden, basierend auf der Gleichheit oder Ähnlichkeit der Figuren. In einigen Fällen hilft dies Kosinussatz, und führt manchmal zum Ergebnis Definition von Sinus, Cosinus und Tangens eines Winkels rechtwinkliges Dreieck.

Es ist jedoch sehr praktisch, das Problem der Ermittlung des Winkels zwischen sich kreuzenden Linien mithilfe der Koordinatenmethode zu lösen. Das werden wir berücksichtigen.

Lassen Sie Oxyz im dreidimensionalen Raum einführen (obwohl Sie ihn bei vielen Problemen selbst eingeben müssen).

Stellen wir uns eine Aufgabe: Finden Sie den Winkel zwischen den sich kreuzenden Linien a und b, die einigen Gleichungen einer Raumlinie im rechtwinkligen Koordinatensystem Oxyz entsprechen.

Lass es uns lösen.

Nehmen wir einen beliebigen Punkt im dreidimensionalen Raum M und gehen davon aus, dass durch ihn die Geraden a 1 und b 1 verlaufen, parallel zu den sich kreuzenden Geraden a bzw. b. Dann ist der erforderliche Winkel zwischen den Schnittlinien a und b per Definition gleich dem Winkel zwischen den Schnittlinien a 1 und b 1.

Wir müssen also nur den Winkel zwischen den Schnittlinien a 1 und b 1 ermitteln. Um die Formel zum Ermitteln des Winkels zwischen zwei sich schneidenden Linien im Raum anzuwenden, müssen wir die Koordinaten der Richtungsvektoren der Linien a 1 und b 1 kennen.

Wie können wir sie bekommen? Und es ist ganz einfach. Die Definition des Richtungsvektors einer Geraden erlaubt uns die Behauptung, dass die Mengen der Richtungsvektoren paralleler Geraden zusammenfallen. Daher können die Richtungsvektoren der Geraden a 1 und b 1 als Richtungsvektoren angenommen werden Und Geraden a bzw. b.

Also, Der Winkel zwischen zwei Schnittlinien a und b wird nach der Formel berechnet
, Wo Und sind die Richtungsvektoren der Geraden a bzw. b.

Formel zum Ermitteln des Kosinus des Winkels zwischen sich kreuzenden Linien a und b haben die Form .

Ermöglicht die Ermittlung des Sinus des Winkels zwischen sich kreuzenden Linien, wenn der Kosinus bekannt ist: .

Es bleibt die Analyse der Lösungen zu den Beispielen.

Beispiel.

Ermitteln Sie den Winkel zwischen den Schnittlinien a und b, die im rechtwinkligen Oxyz-Koordinatensystem durch die Gleichungen definiert werden Und .

Lösung.

Mit den kanonischen Gleichungen einer Geraden im Raum können Sie sofort die Koordinaten des Richtungsvektors dieser Geraden bestimmen – sie werden durch die Zahlen im Nenner der Brüche gegeben, also . Parametrische Gleichungen einer Geraden im Raum ermöglichen es auch, die Koordinaten des Richtungsvektors sofort aufzuschreiben – sie sind gleich den Koeffizienten vor dem Parameter, also - direkter Vektor . Somit verfügen wir über alle notwendigen Daten, um die Formel anzuwenden, nach der der Winkel zwischen sich schneidenden Linien berechnet wird:

Antwort:

Der Winkel zwischen den angegebenen Schnittlinien ist gleich.

Beispiel.

Finden Sie den Sinus und Cosinus des Winkels zwischen den Schnittlinien, auf denen die Kanten AD und BC der Pyramide ABCD liegen, wenn die Koordinaten ihrer Scheitelpunkte bekannt sind: .

Lösung.

Die Richtungsvektoren der Kreuzungslinien AD und BC sind die Vektoren und . Berechnen wir ihre Koordinaten als Differenz zwischen den entsprechenden Koordinaten der End- und Anfangspunkte des Vektors:

Nach der Formel Wir können den Kosinus des Winkels zwischen den angegebenen Schnittlinien berechnen:

Berechnen wir nun den Sinus des Winkels zwischen den sich kreuzenden Linien:

Antwort:

Abschließend betrachten wir die Lösung eines Problems, bei dem der Winkel zwischen sich kreuzenden Linien ermittelt werden muss und das rechteckige Koordinatensystem unabhängig eingegeben werden muss.

Beispiel.

Gegeben sei ein rechteckiges Parallelepiped ABCDA 1 B 1 C 1 D 1, das AB = 3, AD = 2 und AA 1 = 7 Einheiten hat. Punkt E liegt auf der Kante AA 1 und teilt diese im Verhältnis 5 zu 2, gezählt von Punkt A. Finden Sie den Winkel zwischen den Schnittlinien BE und A 1 C.

Lösung.

Da die Rippen rechteckiges Parallelepiped Wenn ein Scheitelpunkt senkrecht zueinander steht, ist es zweckmäßig, ein rechtwinkliges Koordinatensystem einzuführen und den Winkel zwischen den angegebenen Kreuzungslinien mit der Koordinatenmethode durch den Winkel zwischen den Richtungsvektoren dieser Linien zu bestimmen.

Führen wir das rechtwinklige Koordinatensystem Oxyz ein auf die folgende Weise: Lassen Sie den Ursprung mit dem Scheitelpunkt A zusammenfallen, die Ox-Achse mit der Geraden AD, die Oy-Achse mit der Geraden AB und die Oz-Achse mit der Geraden AA 1.

Dann hat Punkt B Koordinaten, Punkt E - (siehe ggf. den Artikel), Punkt A 1 - und Punkt C -. Aus den Koordinaten dieser Punkte können wir die Koordinaten der Vektoren und berechnen. Wir haben , .

Es bleibt die Formel anzuwenden, um den Winkel zwischen sich schneidenden Linien anhand der Koordinaten der Richtungsvektoren zu ermitteln:

Antwort:

Referenzliste.

• Atanasyan L.S., Butuzov V.F., Kadomtsev S.B., Kiseleva L.S., Poznyak E.G. Geometrie. Lehrbuch für die Klassen 10-11 der Sekundarschule.
• Pogorelov A.V., Geometrie. Lehrbuch für die Klassen 7-11 in allgemeinbildenden Einrichtungen.
• Bugrov Ya.S., Nikolsky S.M. Höhere Mathematik. Band eins: Elemente der linearen Algebra und der analytischen Geometrie.
• Ilyin V.A., Poznyak E.G. Analytische Geometrie.

Wenn zwei Geraden im Raum einen gemeinsamen Punkt haben, dann spricht man von einem Schnittpunkt dieser beiden Geraden. In der folgenden Abbildung schneiden sich die Linien a und b im Punkt A. Die Linien a und c schneiden sich nicht.

Zwei beliebige Geraden haben entweder nur einen gemeinsamen Punkt oder keine gemeinsamen Punkte.

Parallele Linien

Zwei Geraden im Raum heißen parallel, wenn sie in derselben Ebene liegen und sich nicht schneiden. Um parallele Linien zu kennzeichnen, verwenden Sie ein spezielles Symbol – ||.

Die Notation a||b bedeutet, dass Linie a parallel zu Linie b ist. In der oben dargestellten Abbildung sind die Linien a und c parallel.

Satz über parallele Linien

Durch jeden Punkt im Raum, der nicht auf einer gegebenen Geraden liegt, geht eine Gerade parallel zu dieser, und zwar nur eine.

Grenzen überschreiten

Zwei Linien, die in derselben Ebene liegen, können sich entweder schneiden oder parallel sein. Aber im Raum gehören zwei Geraden nicht unbedingt zu dieser Ebene. Sie können in zwei verschiedenen Ebenen liegen.

Es ist offensichtlich, dass Linien, die in verschiedenen Ebenen liegen, sich nicht schneiden und keine parallelen Linien sind. Zwei Geraden, die nicht in derselben Ebene liegen, werden aufgerufen Gerade Linien kreuzen.

Die folgende Abbildung zeigt zwei sich schneidende Geraden a und b, die in unterschiedlichen Ebenen liegen.

Test und Satz über schiefe Linien

Wenn eine von zwei Geraden in einer bestimmten Ebene liegt und die andere Gerade diese Ebene an einem Punkt schneidet, der nicht auf der ersten Geraden liegt, dann schneiden sich diese Geraden.

Satz über Schräglinien: Durch jede der beiden Schnittlinien verläuft eine Ebene parallel zur anderen Linie, und zwar nur eine.

Daher haben wir alle möglichen Fälle berücksichtigt relative Position gerade Linien im Raum. Es gibt nur drei davon.

1. Linien schneiden sich. (Das heißt, sie haben nur einen gemeinsamen Punkt.)

2. Linien sind parallel. (Das heißt, sie haben keine gemeinsamen Punkte und liegen in derselben Ebene.)

3. Gerade Linien kreuzen sich. (Das heißt, sie befinden sich in verschiedenen Ebenen.)

Die Linien l1 und l2 heißen schief, wenn sie nicht in derselben Ebene liegen. Seien a und b die Richtungsvektoren dieser Geraden und die Punkte M1 und M2 gehören zu den Geraden l1 bzw. l2

Dann sind die Vektoren a, b, M1M2> nicht koplanar und daher ist ihr gemischtes Produkt nicht gleich Null, d. h. (a, b, M1M2>) =/= 0. Die umgekehrte Aussage gilt auch: if (a, b , M1M2> ) =/= 0, dann sind die Vektoren a, b, M1M2> nicht koplanar und daher liegen die Geraden l1 und l2 nicht in derselben Ebene, d. h. sie schneiden sich. Somit schneiden sich zwei Geraden genau dann, wenn Bedingung(a, b, M1M2>) =/= 0 ist, wobei a und b die Richtungsvektoren der Geraden sind und M1 und M2 die zu diesen Geraden gehörenden Punkte sind. Die Bedingung (a, b, M1M2>) = 0 ist eine notwendige und hinreichende Bedingung dafür, dass die Geraden in derselben Ebene liegen. Wenn die Linien durch ihre kanonischen Gleichungen gegeben sind

dann a = (a1; a2; a3), b = (b1; b2; b3), M1 (x1; y1; z1), M2(x2; y2; z2) und Bedingung (2) wird wie folgt geschrieben:

Abstand zwischen sich kreuzenden Linien

Dies ist der Abstand zwischen einer der Schnittlinien und einer Ebene parallel dazu, die durch eine andere Linie verläuft. Der Abstand zwischen Schnittlinien ist der Abstand von einem Punkt einer der Schnittlinien zu einer Ebene, die durch eine andere Linie parallel zur ersten verläuft Linie.

26.Definition einer Ellipse, kanonische Gleichung. Herleitung der kanonischen Gleichung. Eigenschaften.

Eine Ellipse ist der geometrische Ort von Punkten auf einer Ebene, für die die Summe der Abstände zu zwei fokussierten Punkten F1 und F2 dieser Ebene, Brennpunkte genannt, ein konstanter Wert ist. In diesem Fall ist die Koinzidenz der Brennpunkte der Ellipse nicht ausgeschlossen. Wenn die Geschmacksrichtungen übereinstimmen, ist die Ellipse ein Kreis. Für jede Ellipse können Sie ein kartesisches Koordinatensystem finden, sodass die Ellipse durch die Gleichung (die kanonische Gleichung der Ellipse) beschrieben wird:

Es beschreibt eine im Ursprung zentrierte Ellipse, deren Achsen mit den Koordinatenachsen zusammenfallen.

Wenn auf der rechten Seite eine Einheit mit einem Minuszeichen steht, dann lautet die resultierende Gleichung:

beschreibt eine imaginäre Ellipse. Es ist unmöglich, eine solche Ellipse in der realen Ebene darzustellen. Bezeichnen wir die Brennpunkte mit F1 und F2, den Abstand zwischen ihnen mit 2c und die Summe der Abstände von einem beliebigen Punkt der Ellipse zu den Brennpunkten mit 2a

Um die Gleichung der Ellipse abzuleiten, wählen wir das Koordinatensystem Oxy so, dass die Brennpunkte F1 und F2 auf der Ox-Achse liegen und der Ursprung mit der Mitte des Segments F1F2 zusammenfällt. Dann haben die Brennpunkte die folgenden Koordinaten: und Sei M(x;y) ein beliebiger Punkt der Ellipse. Dann gilt gemäß der Definition einer Ellipse, d.h.

Dies ist im Wesentlichen die Gleichung einer Ellipse.

27. Definition einer Hyperbel, kanonische Gleichung. Herleitung der kanonischen Gleichung. Eigenschaften

Eine Hyperbel ist ein geometrischer Ort von Punkten auf einer Ebene, für den der Absolutwert der Abstandsdifferenz zu zwei festen Punkten F1 und F2 dieser Ebene, Brennpunkte genannt, ein konstanter Wert ist. Sei M(x;y) ein beliebiger Wert Punkt der Hyperbel. Dann gilt gemäß der Definition der Hyperbel |MF 1 – MF 2 |=2a bzw. MF 1 – MF 2 =±2a,

28. Definition einer Parabel, kanonische Gleichung. Herleitung der kanonischen Gleichung. Eigenschaften. Eine Parabel ist die HMT einer Ebene, für die der Abstand zu einem festen Punkt F dieser Ebene gleich dem Abstand zu einer festen Geraden ist, die sich ebenfalls in der betrachteten Ebene befindet. F – Fokus der Parabel; Die feste Linie ist die Leitlinie der Parabel. r=d,

r=; d=x+p/2; (x-p/2) 2 +y 2 =(x+p/2) 2 ; x 2 -xp+p 2 /4+y 2 =x 2 +px+p 2 /4; j 2 =2px;

Eigenschaften: 1. Eine Parabel hat eine Symmetrieachse (Parabelachse); 2.Alle

Die Parabel liegt bei p>0 in der rechten Halbebene der Oxy-Ebene und in der linken

wenn P<0. 3.Директриса параболы, определяемая каноническим уравнением, имеет уравнение x= -p/2.

Sich kreuzende Linien sind an diesen Merkmalen leicht zu erkennen. Zeichen 1. Wenn es auf zwei Geraden vier Punkte gibt, die nicht in derselben Ebene liegen, dann schneiden sich diese Geraden (Abb. 1.21).

Wenn sich diese Linien tatsächlich schneiden würden oder parallel wären, dann würden sie in derselben Ebene liegen, und dann würden die gegebenen Punkte in derselben Ebene liegen, was der Bedingung widerspricht.

Zeichen 2. Wenn die Gerade O in der Ebene liegt und die Gerade b die Ebene a irgendwann schneidet

Liegt M nicht auf der Geraden a, dann schneiden sich die Geraden a und b (Abb. 1.22).

Tatsächlich gelangen wir, wenn wir zwei beliebige Punkte auf der Geraden a und zwei beliebige Punkte auf der Geraden b nehmen, zu Kriterium 1, d. h. a und b sind gekreuzt.

Reale Beispiele für Kreuzungslinien sind Verkehrsknotenpunkte (Abb. 1.23).

Im Raum gibt es gewissermaßen mehr Paare sich schneidender Linien als Paare paralleler oder sich schneidender Linien. Das lässt sich so erklären.

Nehmen wir im Raum einen Punkt A und eine Linie a, die nicht durch Punkt A geht. Um eine Linie parallel zu Linie a durch Punkt A zu zeichnen, müssen wir eine Ebene a durch Punkt A und Linie a zeichnen (Satz 2 von Abschnitt 1.1). ) und dann in der Ebene und zeichne eine Linie b parallel zur Linie a (Abb. 1.24).

Es gibt nur eine solche Zeile b. Alle Geraden, die durch den Punkt A gehen und die Gerade O schneiden, liegen ebenfalls in der Ebene a und füllen diese mit Ausnahme der Geraden b vollständig aus. Alle anderen Linien, die durch A gehen und den gesamten Raum außer der Ebene a ausfüllen, schneiden sich mit der Linie a. Wir können sagen, dass sich schneidende Linien im Raum ein allgemeiner Fall sind und sich schneidende und parallele Linien Sonderfälle sind. „Kleine Bewegungen“ sich kreuzender Linien führen dazu, dass sie sich kreuzen. Aber die Eigenschaften, parallel zu sein oder sich mit „kleinen Bewegungen“ im Raum zu überschneiden, bleiben nicht erhalten.

Vorlesung: Sich kreuzende, parallele und sich kreuzende Linien; Rechtwinkligkeit von Linien

Schnittlinien

Liegen in einer Ebene mehrere Geraden, so schneiden sie sich früher oder später entweder beliebig oder im rechten Winkel oder verlaufen parallel. Schauen wir uns jeden einzelnen Fall an.

Diejenigen Linien, die mindestens einen Schnittpunkt haben, können als Schnittpunkte bezeichnet werden.

Sie fragen sich vielleicht, warum sich mindestens eine Gerade nicht zwei- oder dreimal mit einer anderen Geraden schneiden kann. Sie haben Recht! Aber gerade Linien können vollständig miteinander übereinstimmen. In diesem Fall wird es unendlich viele gemeinsame Punkte geben.

Parallelität

Parallel Sie können die Linien benennen, die sich selbst im Unendlichen niemals schneiden werden.

Mit anderen Worten, parallel sind solche, die keinen einzigen gemeinsamen Punkt haben. Bitte beachten Sie, dass diese Definition nur gültig ist, wenn die Linien in derselben Ebene liegen. Wenn sie jedoch keine gemeinsamen Punkte haben und in verschiedenen Ebenen liegen, gelten sie als sich schneidend.

Beispiele für parallele Linien im Leben: zwei gegenüberliegende Kanten eines Monitorbildschirms, Linien in Notizbüchern sowie viele andere Teile von Dingen, die quadratische, rechteckige und andere Formen haben.

Wenn sie schriftlich zeigen wollen, dass eine Linie parallel zu einer anderen ist, verwenden sie die folgende Notation a||b. Dieser Eintrag besagt, dass Linie a parallel zu Linie b ist.

Beim Studium dieses Themas ist es wichtig, eine weitere Aussage zu verstehen: Durch einen bestimmten Punkt auf der Ebene, der nicht zu einer bestimmten Linie gehört, kann man eine einzelne parallele Linie zeichnen. Aber aufgepasst, auch hier liegt die Korrektur im Plan. Wenn wir den dreidimensionalen Raum betrachten, können wir unendlich viele Linien zeichnen, die sich nicht schneiden, sondern schneiden.

Die oben beschriebene Anweisung heißt Axiom paralleler Geraden.

Rechtwinkligkeit

Direktleitungen können nur angerufen werden, wenn aufrecht, wenn sie sich in einem Winkel von 90 Grad schneiden.

Im Raum können durch einen bestimmten Punkt auf einer Linie unendlich viele senkrechte Linien gezeichnet werden. Wenn wir jedoch von einer Ebene sprechen, können Sie durch einen Punkt auf einer Linie eine einzelne senkrechte Linie zeichnen.

Gekreuzte gerade Linien. Sekante

Wenn sich einige Geraden an einem bestimmten Punkt in einem beliebigen Winkel schneiden, können sie aufgerufen werden Kreuzung.

Alle Schnittlinien haben vertikale und benachbarte Winkel.

Wenn Winkel, die durch zwei sich schneidende Geraden gebildet werden, eine gemeinsame Seite haben, werden sie als benachbart bezeichnet:

Benachbarte Winkel addieren sich zu 180 Grad.