Wenn die Ableitung einer Funktion im Diagramm positiv ist. An welchem ​​Punkt ist die Ableitung am größten?

Aufgabe B9 gibt einen Graphen einer Funktion oder Ableitung an, aus dem Sie eine der folgenden Größen bestimmen müssen:

1. Der Wert der Ableitung an einem Punkt x 0,
2. Maximale oder minimale Punkte (Extrempunkte),
3. Intervalle steigender und fallender Funktionen (Intervalle der Monotonie).

Die in diesem Problem vorgestellten Funktionen und Ableitungen sind immer stetig, was die Lösung erheblich erleichtert. Trotz der Tatsache, dass die Aufgabe zum Abschnitt gehört mathematische Analyse, es liegt durchaus im Leistungsvermögen selbst der schwächsten Studierenden, da hier keine tiefen theoretischen Kenntnisse erforderlich sind.

Um den Wert der Ableitung, der Extrempunkte und der Monotonieintervalle zu ermitteln, gibt es einfache und universelle Algorithmen – alle werden im Folgenden besprochen.

Lesen Sie die Bedingungen der Aufgabe B9 sorgfältig durch, um dumme Fehler zu vermeiden: Manchmal stößt man auf ziemlich lange Texte, aber wichtige Bedingungen, die den Verlauf der Entscheidung beeinflussen, gibt es nur wenige.

Berechnung des Ableitungswertes. Zwei-Punkte-Methode

Wenn dem Problem ein Graph einer Funktion gegeben ist f(x), tangential zu diesem Graphen an einem Punkt x 0, und es erforderlich ist, den Wert der Ableitung an diesem Punkt zu finden, wird der folgende Algorithmus angewendet:

1. Finden Sie zwei „geeignete“ Punkte im Tangentendiagramm: Ihre Koordinaten müssen ganzzahlig sein. Bezeichnen wir diese Punkte als A (x 1 ; y 1) und B (x 2 ; y 2). Schreiben Sie die Koordinaten richtig auf – das ist ein zentraler Punkt der Lösung, und jeder Fehler hier führt zu einer falschen Antwort.
2. Wenn man die Koordinaten kennt, ist es einfach, das Inkrement des Arguments Δx = x 2 − x 1 und das Inkrement der Funktion Δy = y 2 − y 1 zu berechnen.
3. Schließlich finden wir den Wert der Ableitung D = Δy/Δx. Mit anderen Worten: Sie müssen das Inkrement der Funktion durch das Inkrement des Arguments dividieren – und das ist die Antwort.

Beachten wir noch einmal: Die Punkte A und B müssen genau auf der Tangente gesucht werden und nicht auf dem Graphen der Funktion f(x), wie es oft der Fall ist. Die Tangente muss unbedingt mindestens zwei solcher Punkte enthalten, sonst wird das Problem nicht richtig formuliert.

Betrachten Sie die Punkte A (−3; 2) und B (−1; 6) und ermitteln Sie die Inkremente:
Δx = x 2 − x 1 = −1 − (−3) = 2; Δy = y 2 − y 1 = 6 − 2 = 4.

Finden wir den Wert der Ableitung: D = Δy/Δx = 4/2 = 2.

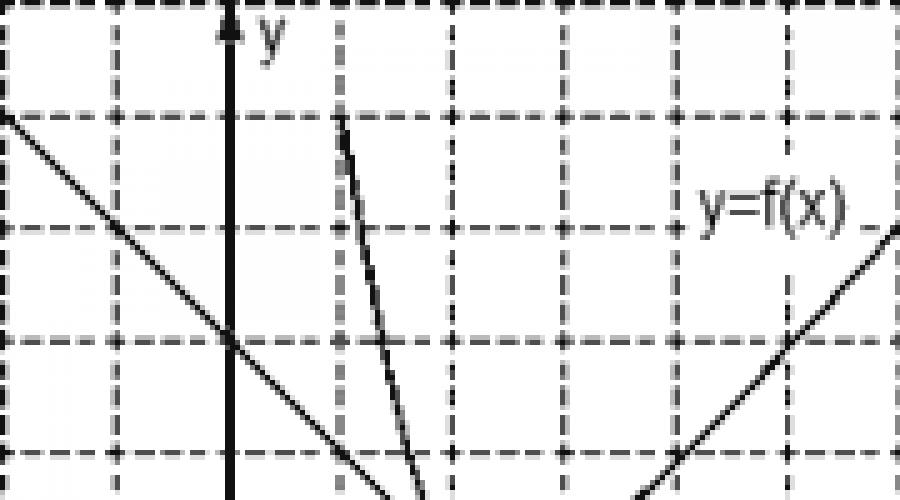
Aufgabe. Die Abbildung zeigt einen Graphen der Funktion y = f(x) und eine Tangente daran am Punkt mit der Abszisse x 0. Finden Sie den Wert der Ableitung der Funktion f(x) am Punkt x 0 .

Betrachten Sie die Punkte A (0; 3) und B (3; 0) und ermitteln Sie die Inkremente:
Δx = x 2 − x 1 = 3 − 0 = 3; Δy = y 2 − y 1 = 0 − 3 = −3.

Nun ermitteln wir den Wert der Ableitung: D = Δy/Δx = −3/3 = −1.

Aufgabe. Die Abbildung zeigt einen Graphen der Funktion y = f(x) und eine Tangente daran am Punkt mit der Abszisse x 0. Finden Sie den Wert der Ableitung der Funktion f(x) am Punkt x 0 .

Betrachten Sie die Punkte A (0; 2) und B (5; 2) und ermitteln Sie die Inkremente:
Δx = x 2 − x 1 = 5 − 0 = 5; Δy = y 2 − y 1 = 2 − 2 = 0.

Es bleibt noch der Wert der Ableitung zu finden: D = Δy/Δx = 0/5 = 0.

Aus dem letzten Beispiel können wir eine Regel formulieren: Wenn die Tangente parallel zur OX-Achse verläuft, ist die Ableitung der Funktion am Tangentialpunkt Null. In diesem Fall müssen Sie nicht einmal etwas zählen – schauen Sie sich einfach die Grafik an.

Berechnung der maximalen und minimalen Punkte

Manchmal gibt Problem B9 anstelle eines Graphen einer Funktion einen Graphen der Ableitung an und erfordert die Ermittlung des Maximal- oder Minimalpunkts der Funktion. In dieser Situation ist die Zwei-Punkte-Methode nutzlos, aber es gibt einen anderen, noch einfacheren Algorithmus. Definieren wir zunächst die Terminologie:

1. Der Punkt x 0 heißt Maximalpunkt der Funktion f(x), wenn in einer Umgebung dieses Punktes die folgende Ungleichung gilt: f(x 0) ≥ f(x).
2. Der Punkt x 0 heißt Minimalpunkt der Funktion f(x), wenn in einer Umgebung dieses Punktes die folgende Ungleichung gilt: f(x 0) ≤ f(x).

Um die maximalen und minimalen Punkte aus dem Ableitungsdiagramm zu ermitteln, befolgen Sie einfach diese Schritte:

1. Zeichnen Sie den Ableitungsgraphen neu und entfernen Sie alle unnötigen Informationen. Wie die Praxis zeigt, beeinträchtigen unnötige Daten nur die Entscheidung. Deshalb markieren wir die Nullstellen der Ableitung auf der Koordinatenachse – und das war’s.
2. Finden Sie die Vorzeichen der Ableitung der Intervalle zwischen Nullen heraus. Wenn für einen Punkt x 0 bekannt ist, dass f'(x 0) ≠ 0, dann sind nur zwei Optionen möglich: f'(x 0) ≥ 0 oder f'(x 0) ≤ 0. Das Vorzeichen der Ableitung ist aus der Originalzeichnung leicht zu ermitteln: Wenn der Ableitungsgraph oberhalb der OX-Achse liegt, dann ist f'(x) ≥ 0. Und umgekehrt, wenn der Ableitungsgraph unterhalb der OX-Achse liegt, dann ist f'(x) ≤ 0.
3. Wir überprüfen noch einmal die Nullstellen und Vorzeichen der Ableitung. Wo das Vorzeichen von Minus zu Plus wechselt, ist der Mindestpunkt. Ändert sich umgekehrt das Vorzeichen der Ableitung von Plus nach Minus, ist dies der Maximalpunkt. Gezählt wird immer von links nach rechts.

Dieses Schema funktioniert nur für kontinuierliche Funktionen – andere gibt es in Aufgabe B9 nicht.

Aufgabe. Die Abbildung zeigt einen Graphen der Ableitung der Funktion f(x), definiert auf dem Intervall [−5; 5]. Finden Sie den Minimalpunkt der Funktion f(x) auf diesem Segment.

Lassen Sie uns unnötige Informationen loswerden und nur die Grenzen [−5; 5] und Nullstellen der Ableitung x = −3 und x = 2,5. Wir beachten auch die Zeichen:

Offensichtlich ändert sich am Punkt x = −3 das Vorzeichen der Ableitung von Minus nach Plus. Dies ist die Mindestpunktzahl.

Aufgabe. Die Abbildung zeigt einen Graphen der Ableitung der Funktion f(x), definiert auf dem Intervall [−3; 7]. Finden Sie den Maximalpunkt der Funktion f(x) auf diesem Segment.

Zeichnen wir den Graphen neu und lassen nur die Grenzen [−3; 7] und Nullstellen der Ableitung x = −1,7 und x = 5. Beachten wir die Vorzeichen der Ableitung im resultierenden Diagramm. Wir haben:

Offensichtlich ändert sich am Punkt x = 5 das Vorzeichen der Ableitung von Plus nach Minus – dies ist der Maximalpunkt.

Aufgabe. Die Abbildung zeigt einen Graphen der Ableitung der Funktion f(x), definiert auf dem Intervall [−6; 4]. Finden Sie die Anzahl der Maximalpunkte der Funktion f(x), die zum Segment [−4; 3].

Aus den Bedingungen des Problems folgt, dass es ausreicht, nur den durch das Segment [−4; 3]. Deshalb erstellen wir einen neuen Graphen, auf dem wir nur die Grenzen markieren [−4; 3] und Nullstellen der darin enthaltenen Ableitung. Nämlich die Punkte x = −3,5 und x = 2. Wir erhalten:

In diesem Diagramm gibt es nur einen Maximalpunkt x = 2. An diesem Punkt ändert sich das Vorzeichen der Ableitung von Plus nach Minus.

Eine kleine Anmerkung zu Punkten mit nicht ganzzahligen Koordinaten. Beispielsweise wurde im letzten Problem der Punkt x = −3,5 berücksichtigt, aber mit dem gleichen Erfolg können wir x = −3,4 annehmen. Bei richtiger Problemstellung dürften solche Änderungen keinen Einfluss auf die Lösung haben, da die Punkte „ohne festen Wohnsitz“ keinen unmittelbaren Beitrag zur Lösung des Problems leisten. Natürlich funktioniert dieser Trick nicht mit ganzzahligen Punkten.

Finden von Intervallen steigender und fallender Funktionen

Bei einem solchen Problem wie den Maximal- und Minimalpunkten wird vorgeschlagen, den Ableitungsgraphen zu verwenden, um Bereiche zu finden, in denen die Funktion selbst zunimmt oder abnimmt. Definieren wir zunächst, was Zunahme und Abnahme sind:

1. Eine Funktion f(x) heißt auf einem Segment wachsend, wenn für zwei beliebige Punkte x 1 und x 2 aus diesem Segment die folgende Aussage gilt: x 1 ≤ x 2 ⇒ f(x 1) ≤ f(x 2) . Mit anderen Worten: Je größer der Argumentwert, desto größer der Funktionswert.
2. Eine Funktion f(x) heißt auf einem Segment abnehmend, wenn für zwei beliebige Punkte x 1 und x 2 aus diesem Segment die folgende Aussage gilt: x 1 ≤ x 2 ⇒ f(x 1) ≥ f(x 2) . Diese. höherer Wert Das Argument entspricht dem kleineren Wert der Funktion.

Lassen Sie uns ausreichende Bedingungen für die Erhöhung und Verringerung formulieren:

1. Damit kontinuierliche Funktion f(x) auf dem Segment zunimmt, reicht es aus, dass seine Ableitung innerhalb des Segments positiv ist, d. h. f’(x) ≥ 0.
2. Damit eine stetige Funktion f(x) auf dem Segment abnimmt, reicht es aus, dass ihre Ableitung innerhalb des Segments negativ ist, d. h. f’(x) ≤ 0.

Akzeptieren wir diese Aussagen ohne Beweise. Somit erhalten wir ein Schema zum Finden von Anstiegs- und Abfallintervallen, das in vielerlei Hinsicht dem Algorithmus zur Berechnung von Extrempunkten ähnelt:

1. Entfernen Sie alle unnötigen Informationen. Im Originalgraphen der Ableitung interessieren uns vor allem die Nullstellen der Funktion, daher belassen wir nur diese.
2. Markieren Sie die Vorzeichen der Ableitung in den Abständen zwischen den Nullen. Wenn f’(x) ≥ 0, nimmt die Funktion zu, und wenn f’(x) ≤ 0, nimmt sie ab. Wenn das Problem Einschränkungen für die Variable x vorsieht, markieren wir diese zusätzlich in einem neuen Diagramm.
3. Nachdem wir nun das Verhalten der Funktion und die Einschränkungen kennen, müssen wir noch die für das Problem erforderliche Menge berechnen.

Aufgabe. Die Abbildung zeigt einen Graphen der Ableitung der Funktion f(x), definiert auf dem Intervall [−3; 7.5]. Finden Sie die Abnahmeintervalle der Funktion f(x). Geben Sie in Ihrer Antwort die Summe der in diesen Intervallen enthaltenen ganzen Zahlen an.

Zeichnen wir wie üblich den Graphen neu und markieren die Grenzen [−3; 7.5], sowie Nullstellen der Ableitung x = −1.5 und x = 5.3. Dann notieren wir die Vorzeichen der Ableitung. Wir haben:

Da die Ableitung im Intervall (− 1,5) negativ ist, ist dies das Intervall der abnehmenden Funktion. Es müssen noch alle ganzen Zahlen summiert werden, die innerhalb dieses Intervalls liegen:
−1 + 0 + 1 + 2 + 3 + 4 + 5 = 14.

Aufgabe. Die Abbildung zeigt einen Graphen der Ableitung der Funktion f(x), definiert im Intervall [−10; 4]. Finden Sie die Anstiegsintervalle der Funktion f(x). Geben Sie in Ihrer Antwort die Länge des größten davon an.

Lassen Sie uns unnötige Informationen loswerden. Lassen wir nur die Grenzen [−10; 4] und Nullstellen der Ableitung, von denen es diesmal vier gab: x = −8, x = −6, x = −3 und x = 2. Markieren wir die Vorzeichen der Ableitung und erhalten das folgende Bild:

Uns interessieren die Intervalle zunehmender Funktion, d.h. So ist f’(x) ≥ 0. Es gibt zwei solcher Intervalle im Diagramm: (−8; −6) und (−3; 2). Berechnen wir ihre Längen:
l 1 = − 6 − (−8) = 2;
l 2 = 2 − (−3) = 5.

Da wir die Länge des größten Intervalls ermitteln müssen, schreiben wir als Antwort den Wert l 2 = 5.

Untersuchen einer Funktion anhand ihrer Ableitung. In diesem Artikel analysieren wir einige Aufgaben im Zusammenhang mit der Untersuchung des Funktionsgraphen. Bei solchen Problemen wird ein Graph der Funktion y = f (x) angegeben und es werden Fragen zur Bestimmung der Anzahl der Punkte, an denen die Ableitung der Funktion positiv (oder negativ) ist, sowie zu anderen Fragen aufgeworfen. Sie werden als Aufgaben zur Anwendung von Ableitungen auf das Studium von Funktionen klassifiziert.

Die Lösung solcher Probleme und allgemeiner Probleme im Zusammenhang mit der Forschung ist nur mit einem vollständigen Verständnis der Eigenschaften der Ableitung zum Studium der Funktionsgraphen und der Ableitung möglich. Daher empfehle ich Ihnen dringend, die entsprechende Theorie zu studieren. Man kann es studieren und auch anschauen (aber es enthält eine kurze Zusammenfassung).

Wir werden in zukünftigen Artikeln auch Probleme berücksichtigen, bei denen der Ableitungsgraph angegeben ist. Verpassen Sie ihn nicht! Also die Aufgaben:

Die Abbildung zeigt einen Graphen der Funktion y = f (x), definiert auf dem Intervall (−6; 8). Definieren:

1. Die Anzahl der ganzzahligen Punkte, an denen die Ableitung der Funktion negativ ist;

2. Die Anzahl der Punkte, an denen die Tangente an den Funktionsgraphen parallel zur Geraden y = 2 verläuft;

1. Die Ableitung einer Funktion ist negativ auf Intervallen, auf denen die Funktion abnimmt, also auf den Intervallen (−6; –3), (0; 4.2), (6.9; 8). Sie enthalten die ganzzahligen Punkte −5, −4, 1, 2, 3, 4 und 7. Wir erhalten 7 Punkte.

2. Direkt j= 2 parallel zur AchseOhj= 2 nur an Extrempunkten (an Punkten, an denen der Graph sein Verhalten von zunehmend zu fallend oder umgekehrt ändert). Es gibt vier solcher Punkte: –3; 0; 4,2; 6.9

Entscheide dich selbst:

Bestimmen Sie die Anzahl der ganzzahligen Punkte, an denen die Ableitung der Funktion positiv ist.

Die Abbildung zeigt einen Graphen der Funktion y = f (x), definiert auf dem Intervall (−5; 5). Definieren:

2. Die Anzahl der ganzzahligen Punkte, an denen die Tangente an den Funktionsgraphen parallel zur Geraden y = 3 verläuft;

3. Die Anzahl der Punkte, an denen die Ableitung Null ist;

1. Aus den Eigenschaften der Ableitung einer Funktion weiß man, dass sie in den Intervallen positiv ist, in denen die Funktion zunimmt, d. h. in den Intervallen (1,4; 2,5) und (4,4; 5). Sie enthalten nur einen ganzzahligen Punkt x = 2.

2. Direkt j= 3 parallel zur AchseOh. Die Tangente verläuft parallel zur Liniej= 3 nur an Extrempunkten (an Punkten, an denen der Graph sein Verhalten von zunehmend zu fallend oder umgekehrt ändert).

Es gibt vier solcher Punkte: –4,3; 1,4; 2,5; 4.4

3. Die Ableitung ist an vier Punkten (an den Extrempunkten) gleich Null, wir haben sie bereits angegeben.

Entscheide dich selbst:

Bestimmen Sie die Anzahl der ganzzahligen Punkte, an denen die Ableitung der Funktion f(x) negativ ist.

Die Abbildung zeigt einen Graphen der Funktion y = f (x), definiert auf dem Intervall (−2; 12). Finden:

1. Die Anzahl der ganzzahligen Punkte, an denen die Ableitung der Funktion positiv ist;

2. Die Anzahl der ganzzahligen Punkte, an denen die Ableitung der Funktion negativ ist;

3. Die Anzahl der ganzzahligen Punkte, an denen die Tangente an den Funktionsgraphen parallel zur Geraden y = 2 verläuft;

4. Die Anzahl der Punkte, an denen die Ableitung Null ist.

1. Aus den Eigenschaften der Ableitung einer Funktion weiß man, dass sie auf Intervallen positiv ist, auf denen die Funktion zunimmt, d. h. auf den Intervallen (–2; 1), (2; 4), (7; 9) und ( 10; 11). Sie enthalten ganzzahlige Punkte: –1, 0, 3, 8. Insgesamt gibt es vier davon.

2. Die Ableitung einer Funktion ist in Intervallen negativ, in denen die Funktion abnimmt, d. h. in den Intervallen (1; 2), (4; 7), (9; 10), (11; 12). Sie enthalten die Ganzzahlpunkte 5 und 6. Wir erhalten 2 Punkte.

3. Direkt j= 2 parallel zur AchseOh. Die Tangente verläuft parallel zur Liniej= 2 nur an Extrempunkten (an Punkten, an denen der Graph sein Verhalten von zunehmend zu fallend oder umgekehrt ändert). Es gibt sieben solcher Punkte: 1; 2; 4; 7; 9; 10; elf.

4. Die Ableitung ist an sieben Punkten (an Extrempunkten) gleich Null, wir haben sie bereits angegeben.

Zeigt den Zusammenhang zwischen dem Vorzeichen der Ableitung und der Art der Monotonie der Funktion.

Bitte seien Sie bei den folgenden Punkten äußerst vorsichtig. Schauen Sie, der Zeitplan dessen, WAS Ihnen gegeben wird! Funktion oder ihre Ableitung

Wenn ein Diagramm der Ableitung gegeben ist, dann interessieren uns nur die Funktionszeichen und Nullstellen. An irgendwelchen „Hügeln“ oder „Senken“ sind wir grundsätzlich nicht interessiert!

Aufgabe 1.

Die Abbildung zeigt einen Graphen einer auf dem Intervall definierten Funktion. Bestimmen Sie die Anzahl der ganzzahligen Punkte, an denen die Ableitung der Funktion negativ ist.

Lösung:

In der Abbildung sind die Bereiche abnehmender Funktion farblich hervorgehoben:

Diese abnehmenden Bereiche der Funktion enthalten 4 ganzzahlige Werte.

Aufgabe 2.

Die Abbildung zeigt einen Graphen einer auf dem Intervall definierten Funktion. Ermitteln Sie die Anzahl der Punkte, an denen die Tangente an den Funktionsgraphen parallel zur Geraden verläuft oder mit ihr zusammenfällt.

Lösung:

Sobald die Tangente an den Graphen einer Funktion parallel zu einer Geraden (oder, was dasselbe ist) ist (oder mit ihr zusammenfällt), hat Neigung, gleich Null, dann hat die Tangente einen Winkelkoeffizienten .

Dies bedeutet wiederum, dass die Tangente parallel zur Achse verläuft, da die Steigung der Tangens des Neigungswinkels der Tangente zur Achse ist.

Daher finden wir Extrempunkte (Maximum- und Minimumpunkte) im Diagramm – an diesen Punkten verlaufen die tangentialen Funktionen zum Diagramm parallel zur Achse.

Es gibt 4 solcher Punkte.

Aufgabe 3.

Die Abbildung zeigt einen Graphen der Ableitung einer auf dem Intervall definierten Funktion. Ermitteln Sie die Anzahl der Punkte, an denen die Tangente an den Funktionsgraphen parallel zur Geraden verläuft oder mit ihr zusammenfällt.

Lösung:

Da die Tangente an den Graphen einer Funktion parallel zu einer Geraden mit Steigung ist (oder mit dieser übereinstimmt), hat auch die Tangente eine Steigung.

Das bedeutet wiederum, dass an den Berührungspunkten.

Daher schauen wir uns an, wie viele Punkte im Diagramm eine Ordinate haben, die gleich ist.

Wie Sie sehen, gibt es vier solcher Punkte.

Aufgabe 4.

Die Abbildung zeigt einen Graphen einer auf dem Intervall definierten Funktion. Finden Sie die Anzahl der Punkte, an denen die Ableitung der Funktion 0 ist.

Lösung:

An Extrempunkten ist die Ableitung gleich Null. Wir haben 4 davon:

Aufgabe 5.

Die Abbildung zeigt einen Graphen einer Funktion und elf Punkte auf der x-Achse:. An wie vielen dieser Punkte ist die Ableitung der Funktion negativ?

Lösung:

In Intervallen mit abnehmender Funktion nimmt die Ableitung negative Werte an. Und die Funktion nimmt punktuell ab. Es gibt 4 solcher Punkte.

Aufgabe 6.

Die Abbildung zeigt einen Graphen einer auf dem Intervall definierten Funktion. Ermitteln Sie die Summe der Extrempunkte der Funktion.

Lösung:

Extremumpunkte– Dies sind die Höchstpunkte (-3, -1, 1) und Mindestpunkte (-2, 0, 3).

Summe der Extrempunkte: -3-1+1-2+0+3=-2.

Aufgabe 7.

Die Abbildung zeigt einen Graphen der Ableitung einer auf dem Intervall definierten Funktion. Finden Sie die Anstiegsintervalle der Funktion. Geben Sie in Ihrer Antwort die Summe der in diesen Intervallen enthaltenen ganzzahligen Punkte an.

Lösung:

Die Abbildung hebt die Intervalle hervor, in denen die Ableitung der Funktion nicht negativ ist.

Auf dem kleinen ansteigenden Intervall gibt es keine ganzzahligen Punkte; auf dem ansteigenden Intervall gibt es vier ganzzahlige Werte: , , und .

Ihre Summe:

Aufgabe 8.

Die Abbildung zeigt einen Graphen der Ableitung einer auf dem Intervall definierten Funktion. Finden Sie die Anstiegsintervalle der Funktion. Geben Sie in Ihrer Antwort die Länge des größten davon an.

Lösung:

In der Abbildung sind alle Intervalle, in denen die Ableitung positiv ist, farblich hervorgehoben, was bedeutet, dass die Funktion selbst in diesen Intervallen zunimmt.

Die Länge des größten von ihnen beträgt 6.

Aufgabe 9.

Die Abbildung zeigt einen Graphen der Ableitung einer auf dem Intervall definierten Funktion. An welchem ​​Punkt des Segments erfolgt dies? Höchster Wert.

Lösung:

Sehen wir uns an, wie sich der Graph auf dem Segment verhält, was uns interessiert nur das Vorzeichen der Ableitung .

Das Vorzeichen der Ableitung ist negativ, da der Graph auf diesem Segment unterhalb der Achse liegt.

Erste Ableitung Wenn die Ableitung einer Funktion in einem bestimmten Intervall positiv (negativ) ist, dann nimmt die Funktion in diesem Intervall monoton zu (monoton ab). Wenn die Ableitung einer Funktion in einem bestimmten Intervall positiv (negativ) ist, dann nimmt die Funktion in diesem Intervall monoton zu (monoton ab). Weiter

Definition Eine Kurve heißt in einem Punkt konvex, wenn sie in einer Umgebung dieses Punktes unter ihrer Tangente in einem Punkt liegt. Eine Kurve heißt in einem Punkt konvex, wenn sie in einer Umgebung dieses Punktes unter ihrer Tangente in einem Punkt liegt Eine Kurve heißt an einem Punkt konkav, wenn sie in einer Umgebung dieses Punktes über ihrer Tangente an einem Punkt liegt. Eine Kurve heißt an einem Punkt konkav, wenn sie in einer Umgebung dieses Punktes über ihrer Tangente an einem Punkt Next liegt

Vorzeichen von Konkavität und Konvexität. Wenn die zweite Ableitung einer Funktion in einem bestimmten Intervall positiv ist, dann ist die Kurve in diesem Intervall konkav, und wenn sie negativ ist, ist sie in diesem Intervall konvex. Wenn die zweite Ableitung einer Funktion in einem bestimmten Intervall positiv ist, ist die Kurve in diesem Intervall konkav, und wenn sie negativ ist, ist sie in diesem Intervall konvex. Definition

Planen Sie die Untersuchung einer Funktion und die Erstellung ihres Graphen. 1. Finden Sie den Definitionsbereich der Funktion und bestimmen Sie die Diskontinuitätspunkte, falls vorhanden. 1. Finden Sie den Definitionsbereich der Funktion und bestimmen Sie die Diskontinuitätspunkte, falls vorhanden. 2. Finden Sie herauszufinden, ob die Funktion gerade oder ungerade ist; Überprüfen Sie die Periodizität. 2. Finden Sie heraus, ob die Funktion gerade oder ungerade ist. Überprüfen Sie seine Periodizität. 3. Bestimmen Sie die Schnittpunkte des Funktionsgraphen mit den Koordinatenachsen. 3. Bestimmen Sie die Schnittpunkte des Funktionsgraphen mit den Koordinatenachsen. 4. Finden Sie kritische Punkte der 1. Art. 4. Finden Sie kritisch Punkte 1. Art 5. Bestimmen Sie die Intervalle der Monotonie und Extrema der Funktion. 5. Bestimmen Sie die Intervalle der Monotonie und Extrema der Funktion. 6. Bestimmen Sie die Intervalle der Konvexität und Konkavität und finden Sie Wendepunkte. 6. Bestimmen Sie die Intervalle der Konvexität und Konkavität und finden Sie Wendepunkte. 7. Verbinden Sie mithilfe der Forschungsergebnisse die erhaltenen Punkte mit einer glatten Kurve. 7. Verbinden Sie mithilfe der Forschungsergebnisse die erhaltenen Punkte mit einer glatten Kurve. Ausgabe

(Abb.1)

Abbildung 1. Ableitungsdiagramm

Eigenschaften von Ableitungsgraphen

1. In zunehmenden Abständen ist die Ableitung positiv. Wenn die Ableitung an einem bestimmten Punkt ein bestimmtes Intervall hat positiver Wert, dann wächst der Graph der Funktion über dieses Intervall.
2. In abnehmenden Abständen ist die Ableitung negativ (mit Minuszeichen). Wenn die Ableitung an einem bestimmten Punkt aus einem bestimmten Intervall einen negativen Wert hat, dann nimmt der Graph der Funktion in diesem Intervall ab.
3. Die Ableitung am Punkt x ist gleich Neigung Tangente, die am gleichen Punkt an den Graphen der Funktion gezogen wird.
4. An den Maximal- und Minimalpunkten der Funktion ist die Ableitung gleich Null. Die Tangente an den Funktionsgraphen verläuft an diesem Punkt parallel zur OX-Achse.

Beispiel 1

Bestimmen Sie anhand des Diagramms (Abb. 2) der Ableitung, an welchem ​​Punkt des Segments [-3; 5] Funktion ist maximal.

Abbildung 2. Ableitungsdiagramm

Lösung: Auf diesem Segment ist die Ableitung negativ, was bedeutet, dass die Funktion von links nach rechts abnimmt und der größte Wert auf der linken Seite am Punkt -3 liegt.

Beispiel 2

Bestimmen Sie anhand des Diagramms (Abb. 3) der Ableitung die Anzahl der maximalen Punkte auf dem Segment [-11; 3].

Abbildung 3. Ableitungsdiagramm

Lösung: Die maximalen Punkte entsprechen den Punkten, an denen das Vorzeichen der Ableitung von positiv nach negativ wechselt. In diesem Intervall ändert die Funktion zweimal das Vorzeichen von Plus nach Minus – am Punkt -10 und am Punkt -1. Dies bedeutet, dass die maximale Punktzahl zwei beträgt.

Beispiel 3

Bestimmen Sie anhand des Diagramms (Abb. 3) der Ableitung die Anzahl der Mindestpunkte im Segment [-11; -1].

Lösung: Die Mindestpunkte entsprechen den Punkten, an denen das Vorzeichen der Ableitung von negativ nach positiv wechselt. Auf diesem Segment beträgt ein solcher Punkt nur -7. Dies bedeutet, dass die Anzahl der Mindestpunkte in einem bestimmten Segment eins beträgt.

Beispiel 4

Bestimmen Sie anhand des Diagramms (Abb. 3) der Ableitung die Anzahl der Extrempunkte.

Lösung: Die Extrempunkte sind sowohl die Minimal- als auch die Maximalpunkte. Lassen Sie uns die Anzahl der Punkte ermitteln, an denen die Ableitung das Vorzeichen ändert.