So finden Sie die Wertemenge einer Funktion anhand ihrer Ableitung. Funktionsumfang (Satz von Funktionswerten)
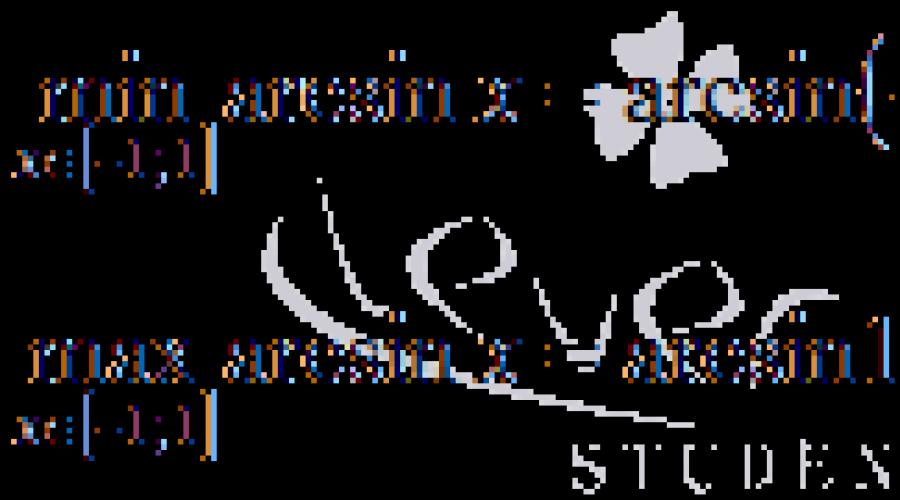
Lesen Sie auch
Funktion ist eines der wichtigsten mathematischen Konzepte.
Definition: Wenn jeder Zahl aus einer bestimmten Menge x eine einzelne Zahl y zugeordnet ist, dann sagt man, dass auf dieser Menge eine Funktion y(x) definiert ist. In diesem Fall wird x als unabhängige Variable oder Argument bezeichnet und y als abhängige Variable oder als Wert einer Funktion oder einfach als Funktion.
Die Variable y soll auch eine Funktion der Variablen x sein.
Nachdem eine Übereinstimmung mit einem Buchstaben, zum Beispiel f, gekennzeichnet wurde, ist es praktisch, zu schreiben: y=f (x), d. h. der Wert y wird aus dem Argument x unter Verwendung der Übereinstimmung f ermittelt. (Lesen Sie: y ist gleich f von x.) Das Symbol f (x) bezeichnet den Wert der Funktion, der dem Wert des Arguments gleich x entspricht.
Beispiel 1 Die Funktion sei durch die Formel y=2x 2 –6 gegeben. Dann können wir schreiben, dass f(x)=2x 2 –6. Finden wir die Werte der Funktion für Werte von x, die beispielsweise gleich 1 sind; 2,5;–3; d.h. wir finden f(1), f(2,5), f(–3):
f(1)=2 1 2 –6=–4;
f(2,5)=2 2,5 2 –6=6,5;
f(–3)=2 (–3) 2 –6= 12.
Beachten Sie, dass in der Notation der Form y=f (x) andere Buchstaben anstelle von f verwendet werden: g usw.
Definition: Der Definitionsbereich einer Funktion sind alle Werte von x, für die die Funktion existiert.
Wenn eine Funktion durch eine Formel angegeben wird und ihr Definitionsbereich nicht angegeben ist, wird davon ausgegangen, dass der Definitionsbereich der Funktion aus allen Werten des Arguments besteht, für die die Formel sinnvoll ist.
Mit anderen Worten: Der Definitionsbereich einer durch eine Formel gegebenen Funktion umfasst alle Werte des Arguments mit Ausnahme derjenigen, die zu Aktionen führen, die wir nicht ausführen können. An dieser Moment wir kennen nur zwei solcher Aktionen. Wir können nicht durch Null dividieren und wir können nicht extrahieren Quadratwurzel von einer negativen Zahl.
Definition: Alle Werte, die die abhängige Variable annimmt, bilden den Bereich der Funktion.
Der Definitionsbereich einer Funktion, die einen realen Prozess beschreibt, hängt von den spezifischen Bedingungen seines Auftretens ab. Beispielsweise wird die Abhängigkeit der Länge l eines Eisenstabs von der Heiztemperatur t durch die Formel ausgedrückt, wobei l 0 die Anfangslänge des Stabs und der lineare Ausdehnungskoeffizient ist. Diese Formel ist für alle Werte von t sinnvoll. Der Definitionsbereich der Funktion l=g(t) ist jedoch ein Intervall von mehreren zehn Grad, für das das Gesetz der linearen Expansion gilt.
Beispiel.
Geben Sie den Funktionsumfang an y = arcsinx.
Lösung.
Der Definitionsbereich des Arkussinus ist das Segment [-1; 1]
. Suchen wir den größten und kleinsten Wert der Funktion in diesem Segment.
Die Ableitung ist für alle positiv X aus dem Intervall (-1; 1)
, das heißt, die Arkussinusfunktion nimmt über den gesamten Definitionsbereich zu. Daher nimmt es den kleinsten Wert an, wenn x = -1, und das Größte bei x = 1.
Wir haben den Bereich der Arkussinusfunktion erhalten  .
.
Finden Sie die Menge der Funktionswerte ![]() auf dem Segment
.
auf dem Segment
.
Lösung.
Lassen Sie uns den größten und kleinsten Wert der Funktion in einem bestimmten Segment ermitteln.
Bestimmen wir die zum Segment gehörenden Extrempunkte
:
Viele Probleme führen dazu, dass wir in einem bestimmten Segment oder im gesamten Definitionsbereich nach einer Reihe von Funktionswerten suchen. Zu diesen Aufgaben gehören verschiedene Auswertungen von Ausdrücken und das Lösen von Ungleichungen.
In diesem Artikel definieren wir den Wertebereich einer Funktion, betrachten Methoden zu ihrer Suche und analysieren die Lösung von Beispielen von einfach bis komplexer im Detail. Alle Materialien werden zur Verdeutlichung mit grafischen Illustrationen versehen. Dieser Artikel ist also eine ausführliche Antwort auf die Frage, wie man den Bereich einer Funktion ermittelt.
Definition.
Die Wertemenge der Funktion y = f(x) im Intervall X ist die Menge aller Werte einer Funktion, die sie bei der Iteration über alles annimmt.
Definition.
Funktionsumfang y = f(x) ist die Menge aller Werte einer Funktion, die sie annimmt, wenn sie über alle x aus dem Definitionsbereich iteriert.
Der Bereich der Funktion wird als E(f) bezeichnet.
Der Bereich einer Funktion und die Wertemenge einer Funktion sind nicht dasselbe. Wir betrachten diese Konzepte als äquivalent, wenn das Intervall X beim Finden der Wertemenge der Funktion y = f(x) mit dem Definitionsbereich der Funktion übereinstimmt.
Verwechseln Sie außerdem nicht den Bereich der Funktion mit der Variablen x für den Ausdruck auf der rechten Seite der Gleichung y=f(x) . Der Bereich zulässiger Werte der Variablen x für den Ausdruck f(x) ist der Definitionsbereich der Funktion y=f(x) .
Die Abbildung zeigt mehrere Beispiele.
Funktionsgraphen werden mit dicken blauen Linien dargestellt, dünne rote Linien sind Asymptoten, rote Punkte und Linien auf der Oy-Achse zeigen den Wertebereich der entsprechenden Funktion.

Wie Sie sehen, erhält man den Wertebereich einer Funktion, indem man den Graphen der Funktion auf die y-Achse projiziert. Sie könnte die Richtige sein Singular(erster Fall), eine Menge von Zahlen (zweiter Fall), ein Segment (dritter Fall), ein Intervall (vierter Fall), ein offener Strahl (fünfter Fall), eine Vereinigung (sechster Fall) usw.
Was müssen Sie also tun, um den Wertebereich einer Funktion zu ermitteln?
Beginnen wir mit dem einfachsten Fall: Wir zeigen, wie man die Wertemenge einer stetigen Funktion y = f(x) auf dem Segment bestimmt.
Es ist bekannt, dass eine in einem Intervall kontinuierliche Funktion darauf ihre Maximal- und Minimalwerte erreicht. Somit ist die Menge der Werte der ursprünglichen Funktion auf dem Segment das Segment ![]() . Folglich besteht unsere Aufgabe darin, den größten und kleinsten Wert der Funktion im Segment zu finden.
. Folglich besteht unsere Aufgabe darin, den größten und kleinsten Wert der Funktion im Segment zu finden.
Lassen Sie uns zum Beispiel den Wertebereich der Arkussinusfunktion ermitteln.
Beispiel.
Geben Sie den Bereich der Funktion y = arcsinx an.
Lösung.
Der Definitionsbereich des Arkussinus ist das Segment [-1; 1] . Suchen wir den größten und kleinsten Wert der Funktion in diesem Segment. 
Die Ableitung ist für alle x aus dem Intervall (-1; 1) positiv, d. h. die Arkussinusfunktion nimmt über den gesamten Definitionsbereich zu. Folglich nimmt es den kleinsten Wert bei x = -1 und den größten bei x = 1 an. 
Wir haben den Bereich der Arkussinusfunktion erhalten  .
.
Beispiel.
Finden Sie die Menge der Funktionswerte ![]() auf dem Segment.
auf dem Segment.
Lösung.
Lassen Sie uns den größten und kleinsten Wert der Funktion in einem bestimmten Segment ermitteln.
Bestimmen wir die zum Segment gehörenden Extrempunkte: 
Wir berechnen die Werte der Originalfunktion an den Enden des Segments und an Punkten ![]() :
:
Daher ist die Menge der Werte einer Funktion in einem Intervall das Intervall  .
.
Jetzt zeigen wir, wie man die Wertemenge einer stetigen Funktion y = f(x) in den Intervallen (a; b) , findet.
Zuerst bestimmen wir die Extrempunkte, Extrema der Funktion, Anstiegs- und Abfallintervalle der Funktion in einem bestimmten Intervall. Als nächstes berechnen wir die Enden des Intervalls und (oder) die Grenzen im Unendlichen (das heißt, wir untersuchen das Verhalten der Funktion an den Grenzen des Intervalls oder im Unendlichen). Diese Informationen reichen aus, um die Menge der Funktionswerte in solchen Intervallen zu finden.
Beispiel.
Definieren Sie die Menge der Funktionswerte im Intervall (-2; 2).
Lösung.
Suchen wir die Extrempunkte der Funktion, die auf das Intervall (-2; 2) fallen: 
Punkt x = 0 ist ein Maximalpunkt, da die Ableitung beim Durchlaufen das Vorzeichen von Plus nach Minus ändert und der Graph der Funktion von zunehmend nach fallend übergeht. 
![]() es gibt ein entsprechendes Maximum der Funktion.
es gibt ein entsprechendes Maximum der Funktion.
Lassen Sie uns das Verhalten der Funktion herausfinden, wenn x rechts zu -2 tendiert und wenn x links zu 2 tendiert, das heißt, wir finden einseitige Grenzen: 
Was wir bekommen haben: Wenn sich das Argument von -2 auf Null ändert, erhöhen sich die Funktionswerte von minus Unendlich auf minus ein Viertel (das Maximum der Funktion bei x = 0), wenn sich das Argument von Null auf 2 ändert Funktionswerte verringern sich auf minus unendlich. Somit ist die Menge der Funktionswerte im Intervall (-2; 2).
Beispiel.
Geben Sie die Wertemenge der Tangensfunktion y = tgx im Intervall an.
Lösung.
Die Ableitung der Tangensfunktion nach dem Intervall ist positiv ![]() , was auf eine Funktionssteigerung hinweist. Lassen Sie uns das Verhalten der Funktion an den Grenzen des Intervalls untersuchen:
, was auf eine Funktionssteigerung hinweist. Lassen Sie uns das Verhalten der Funktion an den Grenzen des Intervalls untersuchen: 
Wenn sich also das Argument von zu ändert, steigen die Funktionswerte von minus Unendlich auf plus Unendlich, d. h. die Menge der Tangentenwerte in diesem Intervall ist die Menge aller reellen Zahlen.
Beispiel.
Finden Sie den Bereich der natürlichen Logarithmusfunktion y = lnx.
Lösung.
Die natürliche Logarithmusfunktion ist für positive Werte des Arguments definiert ![]() . In diesem Intervall ist die Ableitung positiv
. In diesem Intervall ist die Ableitung positiv ![]() Dies weist auf eine Erhöhung der Funktion hin. Finden wir den einseitigen Grenzwert der Funktion, wenn das Argument rechts gegen Null tendiert, und den Grenzwert, wenn x gegen plus Unendlich tendiert:
Dies weist auf eine Erhöhung der Funktion hin. Finden wir den einseitigen Grenzwert der Funktion, wenn das Argument rechts gegen Null tendiert, und den Grenzwert, wenn x gegen plus Unendlich tendiert: 
Wir sehen, dass die Werte der Funktion von minus Unendlich auf plus Unendlich ansteigen, wenn sich x von Null auf plus Unendlich ändert. Daher ist der Bereich der natürlichen Logarithmusfunktion die gesamte Menge der reellen Zahlen.
Beispiel.
Lösung.
Diese Funktion ist für alle reellen Werte von x definiert. Bestimmen wir die Extrempunkte sowie die Anstiegs- und Abfallintervalle der Funktion. 
Folglich nimmt die Funktion bei ab, steigt bei an, x = 0 ist der Maximalpunkt, ![]() das entsprechende Maximum der Funktion.
das entsprechende Maximum der Funktion.
Schauen wir uns das Verhalten der Funktion im Unendlichen an: 
Somit nähern sich die Werte der Funktion im Unendlichen asymptotisch Null.
Wir haben herausgefunden, dass, wenn sich das Argument von minus Unendlich auf Null (den Maximalpunkt) ändert, die Funktionswerte von Null auf Neun (bis zum Maximum der Funktion) ansteigen und wenn x von Null auf Plus Unendlich wechselt, die Funktion Werte sinken von neun auf null.
Schauen Sie sich die schematische Zeichnung an.

Nun ist deutlich zu erkennen, dass der Wertebereich der Funktion beträgt.
Das Finden der Wertemenge der Funktion y = f(x) in Intervallen erfordert ähnliche Untersuchungen. Wir werden uns jetzt nicht im Detail mit diesen Fällen befassen. Wir werden sie in den folgenden Beispielen wieder treffen.
Der Definitionsbereich der Funktion y = f(x) sei die Vereinigung mehrerer Intervalle. Bei der Ermittlung des Wertebereichs einer solchen Funktion werden die Wertemengen in jedem Intervall bestimmt und deren Vereinigung gebildet.
Beispiel.
Finden Sie den Bereich der Funktion.
Lösung.
Der Nenner unserer Funktion sollte nicht Null werden, also .
Suchen wir zunächst die Menge der Funktionswerte auf dem offenen Strahl.
Ableitung einer Funktion  ist in diesem Intervall negativ, d. h. die Funktion nimmt in diesem Intervall ab.
ist in diesem Intervall negativ, d. h. die Funktion nimmt in diesem Intervall ab. 
Wir haben festgestellt, dass sich die Funktionswerte asymptotisch der Eins nähern, wenn das Argument gegen minus Unendlich tendiert. Wenn sich x von minus Unendlich auf zwei ändert, nehmen die Werte der Funktion von eins auf minus Unendlich ab, d. h. im betrachteten Intervall nimmt die Funktion eine Reihe von Werten an. Wir schließen die Einheit nicht ein, da die Werte der Funktion diese nicht erreichen, sondern nur asymptotisch bei minus Unendlich dazu tendieren.
Für den offenen Balken gehen wir ähnlich vor.
In diesem Intervall nimmt auch die Funktion ab. 
Die Menge der Funktionswerte auf diesem Intervall ist die Menge.
Somit ist der gewünschte Wertebereich der Funktion die Vereinigung der Mengen und .
Grafische Illustration.

Besonderes Augenmerk sollte auf periodische Funktionen gelegt werden. Der Wertebereich periodischer Funktionen stimmt mit der Wertemenge auf dem Intervall überein, das der Periode dieser Funktion entspricht.
Beispiel.
Finden Sie den Bereich der Sinusfunktion y = sinx.
Lösung.
Diese Funktion ist periodisch mit einer Periode von zwei pi. Nehmen wir ein Segment und definieren die Wertemenge darauf. 
Das Segment enthält zwei Extrempunkte und .
Wir berechnen die Werte der Funktion an diesen Punkten und wählen an den Grenzen des Segments die kleinsten und aus Höchster Wert:
Somit, ![]() .
.
Beispiel.
Finden Sie den Bereich einer Funktion ![]() .
.
Lösung.
Wir wissen, dass der Arcuskosinusbereich das Segment von Null bis Pi ist, d. h. ![]() oder in einem anderen Beitrag. Funktion
oder in einem anderen Beitrag. Funktion ![]() kann aus arccosx durch Verschiebung und Streckung entlang der Abszissenachse erhalten werden. Solche Transformationen haben keinen Einfluss auf den Wertebereich, daher
kann aus arccosx durch Verschiebung und Streckung entlang der Abszissenachse erhalten werden. Solche Transformationen haben keinen Einfluss auf den Wertebereich, daher ![]() . Funktion
. Funktion ![]() erhalten von
erhalten von ![]() dreimal entlang der Oy-Achse strecken, das heißt,
dreimal entlang der Oy-Achse strecken, das heißt, ![]() . Und die letzte Transformationsstufe ist eine Verschiebung um vier Einheiten nach unten entlang der Ordinate. Dies führt uns zu einer doppelten Ungleichheit
. Und die letzte Transformationsstufe ist eine Verschiebung um vier Einheiten nach unten entlang der Ordinate. Dies führt uns zu einer doppelten Ungleichheit 
Somit beträgt der erforderliche Wertebereich ![]() .
.
Lassen Sie uns die Lösung für ein anderes Beispiel geben, jedoch ohne Erklärungen (sie sind nicht erforderlich, da sie völlig ähnlich sind).
Beispiel.
Funktionsumfang definieren ![]() .
.
Lösung.
Schreiben wir die ursprüngliche Funktion in das Formular ![]() . Wertebereich Power-Funktion ist Intervall. Also, . Dann
. Wertebereich Power-Funktion ist Intervall. Also, . Dann 
Somit, ![]() .
.
Um das Bild zu vervollständigen, sollten wir darüber sprechen, den Wertebereich einer Funktion zu finden, die im Definitionsbereich nicht stetig ist. In diesem Fall unterteilen wir den Definitionsbereich durch Haltepunkte in Intervalle und finden für jedes von ihnen Wertemengen. Durch die Kombination der resultierenden Wertemengen erhalten wir den Wertebereich der ursprünglichen Funktion. Wir empfehlen, sich 3 auf der linken Seite zu merken, die Werte der Funktion tendieren zu minus eins, und da x auf der rechten Seite zu 3 tendiert, tendieren die Werte der Funktion zu plus Unendlich.
Daher unterteilen wir den Definitionsbereich der Funktion in drei Intervalle.
Auf dem Intervall haben wir die Funktion ![]() . Seit damals
. Seit damals 
Somit beträgt die Wertemenge der ursprünglichen Funktion im Intervall [-6;2] .
Auf dem Halbintervall haben wir eine konstante Funktion y = -1. Das heißt, die Wertemenge der ursprünglichen Funktion im Intervall besteht aus einem einzigen Element.
Die Funktion ist für alle gültigen Argumentwerte definiert. Lassen Sie uns die Intervalle der Zunahme und Abnahme der Funktion herausfinden.
Die Ableitung verschwindet bei x=-1 und x=3. Markieren wir diese Punkte auf dem Zahlenstrahl und bestimmen wir die Vorzeichen der Ableitung der resultierenden Intervalle. 
Die Funktion nimmt um ab ![]() , erhöht sich um [-1; 3], x=-1 minimaler Punkt, x=3 maximaler Punkt.
, erhöht sich um [-1; 3], x=-1 minimaler Punkt, x=3 maximaler Punkt.
Berechnen wir das entsprechende Minimum und Maximum der Funktion: 
Lassen Sie uns das Verhalten der Funktion im Unendlichen überprüfen: 
Der zweite Grenzwert wurde mit berechnet.
Lassen Sie uns eine schematische Zeichnung erstellen.
Wenn sich das Argument von minus Unendlich auf -1 ändert, verringern sich die Funktionswerte von plus Unendlich auf -2e, wenn sich das Argument von -1 auf 3 ändert, erhöhen sich die Funktionswerte von -2e auf, wenn sich das Argument von ändert 3 bis plus unendlich, die Funktionswerte nehmen von auf Null ab, erreichen aber nicht Null.

Die Abhängigkeit einer Variablen von einer anderen heißt funktionale Abhängigkeit. Abhängigkeitsvariable j aus Variable X angerufen Funktion, wenn jeder Wert X entspricht einem einzelnen Wert j.
Bezeichnung:
Variable X heißt die unabhängige Variable oder Streit, und die Variable j- abhängig. Sie sagen, dass j ist eine Funktion von X. Bedeutung j, entsprechend dem angegebenen Wert X, angerufen Funktionswert.
Alle Werte, die es akzeptiert X, bilden Domäne einer Funktion; alle Werte, die es braucht j, bilden Satz von Funktionswerten.
Bezeichnungen: 
D(f)- Argumentwerte. E(f)- Funktionswerte. Wenn eine Funktion durch eine Formel gegeben ist, dann besteht der Definitionsbereich aus allen Werten der Variablen, für die diese Formel sinnvoll ist.
Funktionsgraph ist die Menge aller Punkte auf der Koordinatenebene, deren Abszissen gleich den Werten des Arguments sind und deren Ordinaten gleich den entsprechenden Werten der Funktion sind. Wenn irgendein Wert x=x 0 stimmt mit mehreren Werten überein (nicht nur mit einem) j, dann ist eine solche Korrespondenz keine Funktion. Damit eine Menge von Punkten auf einer Koordinatenebene ein Graph einer bestimmten Funktion ist, ist es notwendig und ausreichend, dass jede gerade Linie parallel zur Oy-Achse den Graphen in nicht mehr als einem Punkt schneidet.

Methoden zur Angabe einer Funktion
1) Funktion einstellbar analytisch in Form einer Formel. Zum Beispiel, ![]()
2) Die Funktion kann durch eine Tabelle mit vielen Paaren angegeben werden (x; y).
3) Die Funktion kann grafisch spezifiziert werden. Wertepaare (x; y) werden auf der Koordinatenebene dargestellt.
Monotonie der Funktion
Funktion f(x) angerufen zunehmend auf einem gegebenen numerischen Intervall, wenn höherer Wert Das Argument entspricht dem größeren Wert der Funktion. Stellen Sie sich vor, ein bestimmter Punkt bewegt sich entlang des Diagramms von links nach rechts. Dann scheint der Punkt im Diagramm nach oben zu „klettern“.
Funktion f(x) angerufen abnehmend auf einem gegebenen numerischen Intervall, wenn ein größerer Wert des Arguments einem kleineren Wert der Funktion entspricht. Stellen Sie sich vor, ein bestimmter Punkt bewegt sich entlang des Diagramms von links nach rechts. Dann scheint der Punkt im Diagramm nach unten zu „rollen“.
Eine Funktion, die in einem bestimmten numerischen Intervall nur zunimmt oder nur abnimmt, wird aufgerufen eintönig in diesem Intervall.

Nullstellen der Funktion und Intervalle mit konstantem Vorzeichen
Werte X, bei welchem y=0, angerufen Funktionsnullstellen. Dies sind die Abszissen der Schnittpunkte des Funktionsgraphen mit der Ox-Achse.

Solche Wertebereiche X, auf dem die Funktionswerte liegen j entweder nur positiv oder nur negativ genannt werden Intervalle mit konstantem Vorzeichen der Funktion.

Gerade und ungerade Funktionen
Gleiche Funktion
1) Der Definitionsbereich ist symmetrisch in Bezug auf den Punkt (0; 0), das heißt, wenn der Punkt A gehört zum Definitionsbereich, dann der Punkt -A gehört ebenfalls zum Bereich der Definition.
2) Für jeden Wert X f(-x)=f(x)
3) Der Graph einer geraden Funktion ist symmetrisch um die Oy-Achse.
Komische Funktion hat die folgenden Eigenschaften:
1) Der Definitionsbereich ist symmetrisch um den Punkt (0; 0).
2) für jeden Wert X, zum Definitionsbereich gehörend, die Gleichheit f(-x)=-f(x)
3) Der Graph einer ungeraden Funktion ist symmetrisch bezüglich des Ursprungs (0; 0).
Nicht jede Funktion ist gerade oder ungerade. Funktionen Gesamtansicht sind weder gerade noch ungerade.



Periodische Funktionen
Funktion F heißt periodisch, wenn es für jede eine solche Zahl gibt X aus dem Definitionsbereich die Gleichheit f(x)=f(x-T)=f(x+T). T ist die Periode der Funktion.
Jede periodische Funktion hat unendlich viele Perioden. In der Praxis wird üblicherweise die kleinste positive Periode berücksichtigt.
Die Werte einer periodischen Funktion wiederholen sich nach einem Intervall, das der Periode entspricht. Dies wird beim Erstellen von Diagrammen verwendet.

Im Rahmen der Lösung von Problemen müssen wir häufig nach vielen Werten einer Funktion in einem Definitionsbereich oder einem Segment suchen. Dies sollte beispielsweise beim Lösen erfolgen verschiedene Typen Ungleichungen, Bewertungen von Ausdrücken usw.
In diesem Material erklären wir Ihnen den Wertebereich einer Funktion, geben die wichtigsten Methoden an, mit denen sie berechnet werden kann, und analysieren Probleme unterschiedlicher Komplexität. Aus Gründen der Übersichtlichkeit sind einzelne Bestimmungen mit Grafiken dargestellt. Nach der Lektüre dieses Artikels erhalten Sie ein umfassendes Verständnis für den Umfang einer Funktion.
Beginnen wir mit grundlegenden Definitionen.
Definition 1
Die Wertemenge einer Funktion y = f(x) auf einem bestimmten Intervall x ist die Menge aller Werte, die diese Funktion annimmt, wenn sie über alle Werte x ∈ X iteriert.
Definition 2
Der Wertebereich einer Funktion y = f (x) ist die Menge aller ihrer Werte, die sie annehmen kann, wenn sie die Werte von x aus dem Bereich x ∈ (f) durchsucht.
Der Wertebereich einer bestimmten Funktion wird üblicherweise mit E(f) bezeichnet.
Bitte beachten Sie, dass der Begriff der Wertemenge einer Funktion nicht immer mit ihrem Wertebereich identisch ist. Diese Konzepte sind nur dann äquivalent, wenn der Wertebereich von x beim Finden der Menge vorliegt Werte werden übereinstimmen mit dem Definitionsbereich der Funktion.
Es ist auch wichtig, zwischen dem Wertebereich und dem Bereich akzeptabler Werte der Variablen x für den Ausdruck auf der rechten Seite y = f (x) zu unterscheiden. Der Bereich der zulässigen Werte x für den Ausdruck f (x) ist der Definitionsbereich dieser Funktion.
Nachfolgend finden Sie eine Abbildung mit einigen Beispielen. Blaue Linien sind Funktionsgraphen, rote Linien sind Asymptoten, rote Punkte und Linien auf der Ordinatenachse sind Funktionsbereiche.
Offensichtlich kann der Wertebereich einer Funktion erhalten werden, indem der Graph der Funktion auf die O-y-Achse projiziert wird. Darüber hinaus kann es entweder eine einzelne Zahl oder eine Menge von Zahlen, ein Segment, ein Intervall, einen offenen Strahl, eine Vereinigung numerischer Intervalle usw. darstellen.
Schauen wir uns die wichtigsten Möglichkeiten an, den Wertebereich einer Funktion zu ermitteln.
Beginnen wir mit der Definition der Wertemenge der stetigen Funktion y = f (x) auf einem bestimmten Segment mit der Bezeichnung [ a ; B ] . Wir wissen, dass eine Funktion, die auf einem bestimmten Segment stetig ist, dort ihr Minimum und Maximum erreicht, also das größte m a x x ∈ a ; b f (x) und der kleinste Wert m i n x ∈ a ; b f (x) . Das bedeutet, dass wir ein Segment m i n x ∈ a erhalten; bf(x); m a x x ∈ a ; b f (x) , das die Wertemengen der ursprünglichen Funktion enthält. Dann müssen wir nur noch die angegebenen Mindest- und Höchstpunkte auf diesem Segment finden.
Nehmen wir ein Problem, bei dem wir den Bereich der Arkussinuswerte bestimmen müssen.
Beispiel 1
Zustand: Finden Sie den Wertebereich y = a r c sin x .
Lösung
Im allgemeinen Fall liegt der Definitionsbereich des Arkussinus auf der Strecke [ - 1 ; 1 ] . Wir müssen den größten und kleinsten Wert der angegebenen Funktion darauf bestimmen.
y " = a r c sin x " = 1 1 - x 2
Wir wissen, dass die Ableitung der Funktion für alle Werte von x im Intervall [ - 1 ; 1 ], das heißt, im gesamten Definitionsbereich nimmt die Arkussinusfunktion zu. Das bedeutet, dass es den kleinsten Wert annimmt, wenn x gleich -1 ist, und den größten Wert, wenn x gleich 1 ist.
m ich n x ∈ - 1 ; 1 a r c sin x = a r c sin - 1 = - π 2 m a x x ∈ - 1 ; 1 a r c sin x = a r c sin 1 = π 2
Somit ist der Wertebereich der Arkussinusfunktion gleich E (a r c sin x) = - π 2; π 2.
Antwort: E (a r c sin x) = - π 2 ; π 2
Beispiel 2
Zustand: Berechnen Sie den Wertebereich y = x 4 - 5 x 3 + 6 x 2 im angegebenen Intervall [ 1 ; 4 ] .
Lösung
Wir müssen lediglich den größten und kleinsten Wert der Funktion in einem bestimmten Intervall berechnen.
Um Extrempunkte zu bestimmen, müssen folgende Berechnungen durchgeführt werden:
y " = x 4 - 5 x 3 + 6 x 2 " = 4 x 3 + 15 x 2 + 12 x = x 4 x 2 - 15 x + 12 y " = 0 ⇔ x (4 x 2 - 15 x + 12 ) = 0 x 1 = 0 ∉ 1; 4 und l und 4 x 2 - 15 x + 12 = 0 D = - 15 2 - 4 4 12 = 33 x 2 = 15 - 33 8 ≈ 1. 16 ∈ 1 ; 4 ; x 3 = 15 + 33 8 ≈ 2 , 59 ∈ 1 ; 4
Suchen wir nun die Werte der gegebenen Funktion an den Enden des Segments und an den Punkten x 2 = 15 - 33 8; x 3 = 15 + 33 8:
y (1) = 1 4 - 5 1 3 + 6 1 2 = 2 y 15 - 33 8 = 15 - 33 8 4 - 5 15 - 33 8 3 + 6 15 - 33 8 2 = = 117 + 165 33 512 ≈ 2. 08 y 15 + 33 8 = 15 + 33 8 4 - 5 · 15 + 33 8 3 + 6 · 15 + 33 8 2 = = 117 - 165 33 512 ≈ - 1 . 62 Jahre (4) = 4 4 - 5 4 3 + 6 4 2 = 32
Dies bedeutet, dass die Menge der Funktionswerte durch das Segment 117 - 165 33 512 bestimmt wird; 32.
Antwort: 117 - 165 33 512 ; 32 .
Fahren wir mit der Ermittlung der Wertemenge der stetigen Funktion y = f (x) in den Intervallen (a ; b) und a ; + ∞ , - ∞ ; b , - ∞ ; + ∞ .
Beginnen wir mit der Bestimmung der größten und kleinsten Punkte sowie der Anstiegs- und Abfallintervalle in einem bestimmten Intervall. Danach müssen wir einseitige Grenzen an den Enden des Intervalls und/oder Grenzen im Unendlichen berechnen. Mit anderen Worten: Wir müssen das Verhalten der Funktion unter bestimmten Bedingungen bestimmen. Dafür liegen uns alle notwendigen Daten vor.
Beispiel 3
Zustand: Berechnen Sie den Bereich der Funktion y = 1 x 2 - 4 auf dem Intervall (- 2 ; 2) .
Lösung
Bestimmen Sie den größten und kleinsten Wert einer Funktion auf einem bestimmten Segment
y " = 1 x 2 - 4 " = - 2 x (x 2 - 4) 2 y " = 0 ⇔ - 2 x (x 2 - 4) 2 = 0 ⇔ x = 0 ∈ (- 2 ; 2)
Wir haben einen Maximalwert von 0 erhalten, da sich an diesem Punkt das Vorzeichen der Funktion ändert und der Graph abzunehmen beginnt. Siehe Abbildung:

Das heißt, y (0) = 1 0 2 - 4 = - 1 4 ist der Maximalwert der Funktion.
Bestimmen wir nun das Verhalten der Funktion für ein x, das gegen – 2 s tendiert rechte Seite und k + 2 auf der linken Seite. Mit anderen Worten: Wir finden einseitige Grenzen:
lim x → - 2 + 0 1 x 2 - 4 = lim x → - 2 + 0 1 (x - 2) (x + 2) = = 1 - 2 + 0 - 2 - 2 + 0 + 2 = - 1 4 · 1 + 0 = - ∞ lim x → 2 + 0 1 x 2 - 4 = lim x → 2 + 0 1 (x - 2) (x + 2) = = 1 2 - 0 - 2 2 - 0 + 2 = 1 4 1 - 0 = - ∞
Es stellt sich heraus, dass die Funktionswerte von minus Unendlich auf – 1 4 ansteigen, wenn sich das Argument von – 2 auf 0 ändert. Und wenn sich das Argument von 0 auf 2 ändert, nehmen die Funktionswerte in Richtung minus Unendlich ab. Folglich ist die Menge der Werte einer gegebenen Funktion in dem von uns benötigten Intervall (- ∞ ; - 1 4 ] .
Antwort: (- ∞ ; - 1 4 ] .
Beispiel 4
Zustand: Geben Sie die Wertemenge y = t g x in einem bestimmten Intervall an - π 2; π 2.
Lösung
Wir wissen, dass im allgemeinen Fall die Ableitung der Tangente - π 2 ist; π 2 wird positiv sein, das heißt, die Funktion wird zunehmen. Lassen Sie uns nun bestimmen, wie sich die Funktion innerhalb der angegebenen Grenzen verhält:
lim x → π 2 + 0 t g x = t g - π 2 + 0 = - ∞ lim x → π 2 - 0 t g x = t g π 2 - 0 = + ∞
Wir haben eine Zunahme der Werte der Funktion von minus Unendlich auf plus Unendlich erhalten, wenn sich das Argument von - π 2 auf π 2 ändert, und wir können sagen, dass die Menge der Lösungen dieser Funktion die Menge aller reellen Zahlen sein wird .
Antwort: - ∞ ; + ∞ .
Beispiel 5
Zustand: Bestimmen Sie den Bereich der natürlichen Logarithmusfunktion y = ln x.
Lösung
Wir wissen, dass diese Funktion definiert ist positive Werte Argument D (y) = 0 ; + ∞ . Die Ableitung in einem bestimmten Intervall ist positiv: y " = ln x " = 1 x . Dies bedeutet, dass die Funktion darauf zunimmt. Als nächstes müssen wir einen einseitigen Grenzwert für den Fall definieren, dass das Argument gegen 0 geht (auf der rechten Seite) und wenn x gegen Unendlich geht:
lim x → 0 + 0 ln x = ln (0 + 0) = - ∞ lim x → ∞ ln x = ln + ∞ = + ∞
Wir haben festgestellt, dass die Werte der Funktion von minus Unendlich auf plus Unendlich ansteigen, wenn sich die Werte von x von Null auf plus Unendlich ändern. Das bedeutet, dass die Menge aller reellen Zahlen der Wertebereich der natürlichen Logarithmusfunktion ist.
Antwort: Die Menge aller reellen Zahlen ist der Wertebereich der natürlichen Logarithmusfunktion.
Beispiel 6
Zustand: Bestimmen Sie den Bereich der Funktion y = 9 x 2 + 1 .
Lösung
Diese Funktion ist definiert, vorausgesetzt, dass x eine reelle Zahl ist. Berechnen wir den größten und kleinsten Wert der Funktion sowie die Intervalle ihrer Zunahme und Abnahme:
y " = 9 x 2 + 1 " = - 18 x (x 2 + 1) 2 y " = 0 ⇔ x = 0 y " ≤ 0 ⇔ x ≥ 0 y " ≥ 0 ⇔ x ≤ 0
Als Ergebnis haben wir festgestellt, dass diese Funktion abnimmt, wenn x ≥ 0; erhöhen, wenn x ≤ 0 ; Es hat einen Maximalpunkt y (0) = 9 0 2 + 1 = 9 mit einer Variablen gleich 0.
Sehen wir uns an, wie sich die Funktion im Unendlichen verhält:
lim x → - ∞ 9 x 2 + 1 = 9 - ∞ 2 + 1 = 9 1 + ∞ = + 0 lim x → + ∞ 9 x 2 + 1 = 9 + ∞ 2 + 1 = 9 1 + ∞ = + 0
Aus der Aufzeichnung geht klar hervor, dass sich die Funktionswerte in diesem Fall asymptotisch 0 nähern.
Zusammenfassend lässt sich sagen: Wenn sich das Argument von minus unendlich auf Null ändert, erhöhen sich die Funktionswerte von 0 auf 9. Wenn sich die Argumentwerte von 0 auf plus unendlich ändern, verringern sich die entsprechenden Funktionswerte von 9 auf 0. Wir haben dies in der Abbildung gezeigt:

Es zeigt, dass der Wertebereich der Funktion das Intervall E (y) = (0 ; 9 ] sein wird
Antwort: E (y) = (0 ; 9 ]
Wenn wir die Wertemenge der Funktion y = f (x) in den Intervallen [ a ; b) , (a ; b ] , [ a ; + ∞) , (- ∞ ; b ] , dann müssen wir genau die gleichen Studien durchführen. Wir werden diese Fälle vorerst nicht analysieren: Wir werden ihnen später in begegnen Probleme.
Was aber, wenn der Definitionsbereich einer bestimmten Funktion eine Vereinigung mehrerer Intervalle ist? Dann müssen wir die Wertesätze für jedes dieser Intervalle berechnen und sie kombinieren.
Beispiel 7
Zustand: Bestimmen Sie den Wertebereich y = x x - 2 .
Lösung
Da der Nenner der Funktion nicht auf 0 gedreht werden sollte, gilt D (y) = - ∞; 2 ∪ 2 ; + ∞ .
Beginnen wir mit der Definition der Menge der Funktionswerte im ersten Segment – ∞; 2, das ist ein offener Balken. Wir wissen, dass die Funktion darauf abnimmt, das heißt, die Ableitung dieser Funktion wird negativ sein.
lim x → 2 - 0 x x - 2 = 2 - 0 2 - 0 - 2 = 2 - 0 = - ∞ lim x → - ∞ x x - 2 = lim x → - ∞ x - 2 + 2 x - 2 = lim x → - ∞ 1 + 2 x - 2 = 1 + 2 - ∞ - 2 = 1 - 0
Dann nähern sich die Funktionswerte in Fällen, in denen sich das Argument in Richtung minus Unendlich ändert, asymptotisch 1. Wenn sich die Werte von x von minus Unendlich auf 2 ändern, dann sinken die Werte von 1 auf minus Unendlich, d.h. die Funktion in diesem Segment nimmt Werte aus dem Intervall - ∞; 1 . Wir schließen die Einheit aus unseren Betrachtungen aus, da die Werte der Funktion diese nicht erreichen, sondern sich ihr nur asymptotisch nähern.
Für offenen Balken 2; + ∞ führen wir genau die gleichen Aktionen aus. Die Funktion darauf nimmt ebenfalls ab:
lim x → 2 + 0 x x - 2 = 2 + 0 2 + 0 - 2 = 2 + 0 = + ∞ lim x → + ∞ x x - 2 = lim x → + ∞ x - 2 + 2 x - 2 = lim x → + ∞ 1 + 2 x - 2 = 1 + 2 + ∞ - 2 = 1 + 0
Die Werte der Funktion in einem bestimmten Segment werden durch die Menge 1 bestimmt; + ∞ . Dies bedeutet, dass der Wertebereich, den wir für die in der Bedingung angegebene Funktion benötigen, die Vereinigung von Mengen ist - ∞ ; 1 und 1; + ∞ .
Antwort: E(y) = - ∞ ; 1 ∪ 1 ; + ∞ .
Dies ist in der Grafik zu sehen:

Ein Sonderfall sind periodische Funktionen. Ihr Wertebereich stimmt mit der Wertemenge auf dem Intervall überein, das der Periode dieser Funktion entspricht.
Beispiel 8
Zustand: Bestimmen Sie den Wertebereich von Sinus y = sin x.
Lösung
Sinus ist eine periodische Funktion und ihre Periode beträgt 2 pi. Nehmen Sie das Segment 0; 2 π und sehen Sie, wie die Wertemenge darauf aussehen wird.
y " = (sin x) " = cos x y " = 0 ⇔ cos x = 0 ⇔ x = π 2 + πk , k ∈ Z
Innerhalb von 0; 2 π Die Funktion hat Extrempunkte π 2 und x = 3 π 2 . Berechnen wir, wie hoch die Funktionswerte in ihnen sowie an den Grenzen des Segments sein werden, und wählen dann den größten und kleinsten Wert aus.
y (0) = sin 0 = 0 y π 2 = sin π 2 = 1 y 3 π 2 = sin 3 π 2 = - 1 y (2 π) = sin (2 π) = 0 ⇔ min x ∈ 0 ; 2 π sin x = sin 3 π 2 = - 1, max x ∈ 0; 2 π sin x = sin π 2 = 1
Antwort: E (sin x) = - 1 ; 1 .
Wenn Sie die Bereiche von Funktionen wie Potenz, Exponential, Logarithmus, Trigonometrie, Umkehrtrigonometrie kennen müssen, empfehlen wir Ihnen, den Artikel über grundlegende Elementarfunktionen noch einmal zu lesen. Die hier vorgestellte Theorie ermöglicht es uns, die dort angegebenen Werte zu überprüfen. Es empfiehlt sich, sie zu erlernen, da sie häufig bei der Lösung von Problemen benötigt werden. Wenn Sie die Bereiche der Grundfunktionen kennen, können Sie mithilfe einer geometrischen Transformation leicht die Bereiche von Funktionen ermitteln, die aus Elementarfunktionen erhalten werden.
Beispiel 9
Zustand: Bestimmen Sie den Wertebereich y = 3 a r c cos x 3 + 5 π 7 - 4 .
Lösung
Wir wissen, dass das Segment von 0 bis Pi der Arcus-Cosinus-Bereich ist. Mit anderen Worten: E (a r c cos x) = 0; π oder 0 ≤ a r c cos x ≤ π . Wir können die Funktion a r c cos x 3 + 5 π 7 aus dem Arkuskosinus erhalten, indem wir ihn entlang der O x-Achse verschieben und strecken, aber solche Transformationen werden uns nichts bringen. Dies bedeutet 0 ≤ a r c cos x 3 + 5 π 7 ≤ π .
Die Funktion 3 a r c cos x 3 + 5 π 7 kann aus dem Arcuskosinus a r c cos x 3 + 5 π 7 durch Streckung entlang der Ordinatenachse erhalten werden, d.h. 0 ≤ 3 a r c cos x 3 + 5 π 7 ≤ 3 π . Die letzte Transformation ist eine Verschiebung entlang der Oy-Achse um 4 Werte. Als Ergebnis erhalten wir eine doppelte Ungleichung:
0 - 4 ≤ 3 a r c cos x 3 + 5 π 7 - 4 ≤ 3 π - 4 ⇔ - 4 ≤ 3 arccos x 3 + 5 π 7 - 4 ≤ 3 π - 4
Wir haben festgestellt, dass der von uns benötigte Wertebereich gleich E (y) = - 4 ist; 3 π - 4 .
Antwort: E(y) = - 4 ; 3 π - 4 .
Wir werden ein weiteres Beispiel ohne Erklärung aufschreiben, weil es ist dem vorherigen völlig ähnlich.
Beispiel 10
Zustand: Berechnen Sie, wie groß der Bereich der Funktion y = 2 2 x - 1 + 3 sein wird.
Lösung
Schreiben wir die in der Bedingung angegebene Funktion als y = 2 · (2 x - 1) - 1 2 + 3 um. Für eine Potenzfunktion y = x - 1 2 wird der Wertebereich auf dem Intervall 0 definiert; + ∞, d.h. x - 1 2 > 0 . In diesem Fall:
2 x - 1 - 1 2 > 0 ⇒ 2 (2 x - 1) - 1 2 > 0 ⇒ 2 (2 x - 1) - 1 2 + 3 > 3
Also E(y) = 3; + ∞ .
Antwort: E(y) = 3; + ∞ .
Schauen wir uns nun an, wie man den Wertebereich einer Funktion ermittelt, die nicht stetig ist. Dazu müssen wir den gesamten Bereich in Intervalle unterteilen und in jedem von ihnen Wertemengen finden und dann das Ergebnis kombinieren. Um dies besser zu verstehen, empfehlen wir Ihnen, sich die wichtigsten Arten von Funktionshaltepunkten anzusehen.
Beispiel 11
Zustand: gegeben die Funktion y = 2 sin x 2 - 4 , x ≤ - 3 - 1 , - 3< x ≤ 3 1 x - 3 , x >3. Berechnen Sie den Wertebereich.
Lösung
Diese Funktion ist für alle Werte von x definiert. Analysieren wir es auf Kontinuität mit den Werten des Arguments gleich - 3 und 3:
lim x → - 3 - 0 f (x) = lim x → - 3 2 sin x 2 - 4 = 2 sin - 3 2 - 4 = - 2 sin 3 2 - 4 lim x → - 3 + 0 f (x) = lim x → - 3 (1) = - 1 ⇒ lim x → - 3 - 0 f (x) ≠ lim x → - 3 + 0 f (x)
Wir haben eine unentfernbare Diskontinuität erster Art, wenn der Wert des Arguments -3 ist. Wenn wir uns dem nähern, tendieren die Werte der Funktion zu - 2 sin 3 2 - 4 , und wenn x auf der rechten Seite zu - 3 tendiert, tendieren die Werte zu - 1 .
lim x → 3 - 0 f (x) = lim x → 3 - 0 (- 1) = 1 lim x → 3 + 0 f (x) = lim x → 3 + 0 1 x - 3 = + ∞
Im Punkt 3 haben wir eine unauflösbare Diskontinuität zweiter Art. Wenn eine Funktion dazu tendiert, nähern sich ihre Werte - 1, wenn sie zum gleichen Punkt rechts tendiert - minus Unendlich.
Dies bedeutet, dass der gesamte Definitionsbereich dieser Funktion in 3 Intervalle (- ∞ ; - 3 ], (- 3 ; 3 ], (3 ; + ∞) unterteilt ist.
Im ersten von ihnen haben wir die Funktion y = 2 sin x 2 - 4 erhalten. Da - 1 ≤ sin x ≤ 1, erhalten wir:
1 ≤ sin x 2< 1 ⇒ - 2 ≤ 2 sin x 2 ≤ 2 ⇒ - 6 ≤ 2 sin x 2 - 4 ≤ - 2
Das bedeutet, dass in einem gegebenen Intervall (- ∞ ; - 3 ] die Menge der Funktionswerte [ - 6 ; 2 ] ist.
Auf dem halben Intervall (- 3; 3 ] ist das Ergebnis eine konstante Funktion y = - 1. Folglich wird die gesamte Menge ihrer Werte in diesem Fall auf eine Zahl reduziert - 1.
Im zweiten Intervall 3 ; + ∞ haben wir die Funktion y = 1 x - 3 . Sie nimmt ab, weil y " = - 1 (x - 3) 2< 0 . Она будет убывать от плюс бесконечности до 0 , но самого 0 не достигнет, потому что:
lim x → 3 + 0 1 x - 3 = 1 3 + 0 - 3 = 1 + 0 = + ∞ lim x → + ∞ 1 x - 3 = 1 + ∞ - 3 = 1 + ∞ + 0
Dies bedeutet, dass die Wertemenge der Originalfunktion für x > 3 die Menge 0 ist; + ∞ . Nun kombinieren wir die Ergebnisse: E (y) = - 6 ; - 2 ∪ - 1 ∪ 0 ; + ∞ .
Antwort: E(y) = - 6 ; - 2 ∪ - 1 ∪ 0 ; + ∞ .
Die Lösung ist in der Grafik dargestellt:

Beispiel 12
Bedingung: Es gibt eine Funktion y = x 2 - 3 e x. Bestimmen Sie die Menge seiner Werte.
Lösung
Es ist für alle Argumentwerte definiert, die reelle Zahlen sind. Bestimmen wir, in welchen Intervallen diese Funktion zunimmt und in welchen sie abnimmt:
y " = x 2 - 3 e x " = 2 x e x - e x (x 2 - 3) e 2 x = - x 2 + 2 x + 3 e x = - (x + 1) (x - 3) e x
Wir wissen, dass die Ableitung 0 wird, wenn x = - 1 und x = 3. Platzieren wir diese beiden Punkte auf der Achse und finden wir heraus, welche Vorzeichen die Ableitung in den resultierenden Intervallen haben wird.

Die Funktion verringert sich um (- ∞ ; - 1 ] ∪ [ 3 ; + ∞) und erhöht sich um [ - 1 ; 3]. Die Mindestpunktzahl beträgt -1, die Höchstpunktzahl -3.
Suchen wir nun die entsprechenden Funktionswerte:
y (- 1) = - 1 2 - 3 e - 1 = - 2 e y (3) = 3 2 - 3 e 3 = 6 e - 3
Schauen wir uns das Verhalten der Funktion im Unendlichen an:
lim x → - ∞ x 2 - 3 e x = - ∞ 2 - 3 e - ∞ = + ∞ + 0 = + ∞ lim x → + ∞ x 2 - 3 e x = + ∞ 2 - 3 e + ∞ = + ∞ + ∞ = = lim x → + ∞ x 2 - 3 " e x " = lim x → + ∞ 2 x e x = + ∞ + ∞ = = lim x → + ∞ 2 x " (e x) " = 2 lim x → + ∞ 1 e x = 2 1 + ∞ = + 0
Zur Berechnung der zweiten Grenze wurde die Regel von L'Hopital verwendet. Lassen Sie uns den Fortschritt unserer Lösung in einem Diagramm darstellen.

Es zeigt, dass die Funktionswerte von plus Unendlich auf – 2 e sinken, wenn sich das Argument von minus Unendlich auf – 1 ändert. Ändert er sich von 3 auf plus unendlich, dann sinken die Werte von 6 e – 3 auf 0, 0 wird jedoch nicht erreicht.
Somit ist E(y) = [ - 2 e ; + ∞) .
Antwort: E(y) = [ - 2 e ; + ∞)
Wenn Sie einen Fehler im Text bemerken, markieren Sie ihn bitte und drücken Sie Strg+Eingabetaste
D(f)- jene Werte, die das Argument annehmen kann, d.h. Domäne einer Funktion.
E(f)- jene Werte, die die Funktion annehmen kann, d.h. Satz von Funktionswerten.
Methoden zum Finden der Funktionsbereiche.
sequentielles Finden der Werte komplexer Funktionsargumente;
Schätz-/Grenzmethode;
Verwendung der Eigenschaften der Stetigkeit und Monotonie einer Funktion;
Verwendung von Derivaten;
Verwenden der größten und kleinsten Werte einer Funktion;
grafische Methode;
Parametereingabemethode;
Umkehrfunktionsmethode.
Schauen wir uns einige davon an.
Ableitung verwenden
Allgemeiner Ansatz Um die Wertemenge einer stetigen Funktion f(x) zu finden, besteht darin, den größten und kleinsten Wert der Funktion f(x) in ihrem Definitionsbereich zu finden (oder zu beweisen, dass einer oder beide nicht existieren).
Für den Fall, dass Sie Mengen von Funktionswerten finden müssen auf dem Segment:
Finden Sie die Ableitung der gegebenen Funktion f "(x);
Finden Sie die kritischen Punkte der Funktion f(x) und wählen Sie diejenigen aus, die zu diesem Segment gehören;
Berechnen Sie die Funktionswerte an den Enden des Segments und an ausgewählten kritischen Punkten;
Wählen Sie unter den gefundenen Werten den kleinsten und den größten Wert aus;
Zwischen diesen Werten ist die Menge der Funktionswerte eingeschlossen.
Wenn der Definitionsbereich einer Funktion ist Intervall, dann wird das gleiche Schema verwendet, aber anstelle der Werte an den Enden werden die Grenzen der Funktion verwendet, da das Argument zu den Enden des Intervalls tendiert. Grenzwerte von sind nicht im Wertesatz enthalten.
Grenzen/Scores-Methode
Um die Menge der Funktionswerte zu finden, suchen Sie zuerst die Menge der Argumentwerte und dann die entsprechenden kleinsten und größten Werte der Funktion. Mithilfe von Ungleichungen werden Grenzen bestimmt.
Das Wesentliche besteht darin, eine kontinuierliche Funktion von unten und oben abzuschätzen und zu beweisen, dass die Funktion die Unter- und Obergrenzen der Schätzungen erreicht. In diesem Fall wird die Übereinstimmung der Menge der Funktionswerte mit dem Intervall von der Untergrenze der Schätzung zur Obergrenze durch die Kontinuität der Funktion und das Fehlen anderer Werte dafür bestimmt.
Eigenschaften einer stetigen Funktion
Eine andere Möglichkeit besteht darin, die Funktion in eine kontinuierliche monotone Funktion umzuwandeln und dann anhand der Eigenschaften von Ungleichungen die Wertemenge der neu erhaltenen Funktion zu schätzen.
Sequentielles Ermitteln der Werte komplexer Funktionsargumente
Basierend auf der sequentiellen Suche nach einer Menge von Werten von Zwischenfunktionen, aus denen die Funktion besteht
Wertebereiche grundlegender Elementarfunktionen
| Funktion | Mehrere Bedeutungen |
|---|---|
| $y = kx+ b$ | E(y) = (-∞;+∞) |
| $y = x^(2n)$ | E(y) = |
| $y = \cos(x)$ | E(y) = [-1;1] |
| $y = (\rm tg)\, x$ | E(y) = (-∞;+∞) |
| $y = (\rm ctg)\, x$ | E(y) = (-∞;+∞) |
| $y = \arcsin(x)$ | E(y) = [-π/2; π/2] |
| $y = \arccos(x)$ | E(y) = |
| $y = (\rm arctan)\, x$ | E(y) = (-π/2; π/2) |
| $y = (\rm arcctg)\, x$ | E(y) = (0; π) |
Beispiele
Finden Sie die Menge der Funktionswerte:
Ableitung verwenden
Wir finden den Definitionsbereich: D(f)=[-3;3], weil $9-x^(2)\geq 0$
Finden Sie die Ableitung: $f"(x)=-\frac(x)(\sqrt(9-x^(2)))$
f"(x) = 0, wenn x = 0. f"(x) existiert nicht, wenn $\sqrt(9-x^(2))=0$, also für x = ±3. Wir erhalten drei kritische Punkte: x 1 = –3, x 2 = 0, x 3 = 3, von denen zwei mit den Enden des Segments zusammenfallen. Berechnen wir: f(–3) = 0, f(0) = 3, f(3) = 0. Der kleinste Wert von f(x) ist also 0, der größte Wert ist 3.
Antwort: E(f) = .
KEINE Ableitung verwenden
Finden Sie das Größte und kleinster Wert Merkmale:
Seit $
f(x) = 1-\cos^(2)(x)+\cos(x)-\frac(1)(2) =
= 1-\frac(1)(2)+\frac(1)(4)-(\cos^(2)(x)-2\cdot\cos(x)\cdot\frac(1)(2) +(\frac(1)(2))^2) =
= \frac(3)(4)-(\cos(x)-\frac(1)(2))^(2) $ , dann:
$f(x)\leq \frac(3)(4)$ für alle x;
$f(x)\geq \frac(3)(4)-(\frac(3)(2))^(2)=-\frac(3)(2)$ für alle x(da $|\cos (x)|\leq 1$);
$f(\frac(\pi)(3))= \frac(3)(4)-(\cos(\frac(\pi)(3))-\frac(1)(2))^(2 )=\frac(3)(4)$;
$f(\pi)= \frac(3)(4)-(\cos(\pi)-\frac(1)(2))^(2)=-\frac(3)(2)$;
Antwort: $\frac(3)(4)$ und $-\frac(3)(2)$
Wenn Sie dieses Problem mithilfe von Ableitungen lösen, müssen Sie Hindernisse überwinden, die damit zusammenhängen, dass die Funktion f(x) nicht auf einem Segment, sondern auf der gesamten Zahlengeraden definiert ist.
Verwendung der Grenzen/Schätzungen-Methode
Aus der Sinusdefinition folgt $-1\leq\sin(x)\leq 1$. Als nächstes verwenden wir die Eigenschaften numerischer Ungleichungen.
$-4\leq - 4\sin(x)\leq 4$, (alle drei Teile der doppelten Ungleichung mit -4 multipliziert);
$1\leq 5 - 4\sin(x)\leq 9$ (addiert zu den drei Teilen der doppelten Ungleichung 5);
Da diese Funktion über den gesamten Definitionsbereich stetig ist, liegt die Menge ihrer Werte zwischen ihrem kleinsten und ihrem größten Wert über den gesamten Definitionsbereich, sofern vorhanden.
In diesem Fall ist die Menge der Werte der Funktion $y = 5 - 4\sin(x)$ die Menge.
Aus den Ungleichungen $$ \\ -1\leq\cos(7x)\leq 1 \\ -5\leq 5\cos(x)\leq 5 $$ erhalten wir die Schätzung $$\\ -6\leq y\ leq 6$ $
Bei x = p und x = 0 nimmt die Funktion die Werte -6 und 6 an, d.h. die untere und obere Grenze der Schätzung erreicht. Als Linearkombination der stetigen Funktionen cos(7x) und cos(x) ist die Funktion y auf der gesamten Zahlengeraden stetig, daher nimmt sie aufgrund der Eigenschaft einer stetigen Funktion alle Werte von -6 bis einschließlich 6 an , und nur sie, da seine anderen Werte aufgrund der Ungleichungen $- 6\leq y\leq 6$ unmöglich sind.
Daher ist E(y) = [-6;6].
$$ \\ -1\leq\sin(x)\leq 1 \\ 0\leq\sin^(2)(x)\leq 1 \\ 0\leq2\sin^(2)(x)\leq 2 \\ 1\leq1+2\sin^(2)(x)\leq 3 $$ Antwort: E(f) = .
$$ \\ -\infty< {\rm tg}\, x < +\infty \\ 0 \leq {\rm tg}^{2}\, x < +\infty \\ 3 \leq 3+{\rm tg}^{2}\, x < +\infty \\ 2^{3} \leq 2^{3+{\rm tg}^{2}\, x} < +\infty \\ -\infty < -2^{3+{\rm tg}^{2}\, x} \leq -8 \\ -\infty < 3-2^{3+{\rm tg}^{2}\, x} \leq -5 $$ Ответ: E(f) = (–∞; -5].
$$ \\ -\infty< \lg{x} < +\infty \\ 0 \leq \lg^{2}{x} < +\infty \\ -\infty < -\lg^{2}{x} \leq 0 \\ -\infty < 16-\lg^{2}{x} \leq 16 \\ 0 \leq \sqrt{16-\lg^{2}{x}} \leq 4 \\ 2 \leq 2+\sqrt{16-\lg^{2}{x}} \leq 6 $$ Ответ: E(f) = .
Transformieren wir den Ausdruck $$ \\ \sin(x) + \cos(x) = \sin(x) + \sin(\frac(\pi)(2) - x) = \\ 2\sin\left ( (\ frac(x + \frac(\pi)(2) - x)(2)) \right)\cos\left ((\frac(x + \frac(\pi)(2) + x)(2 )) \right) \\ = 2\sin(\frac(\pi)(4))cos(x +\frac(\pi)(4)) = \sqrt(2)cos(x +\frac(\ pi) (4)) $$.
Aus der Definition des Kosinus folgt $$ \\ -1\leq\cos(x)\leq 1; \\ -1\leq \cos((x + \frac(\pi)(4)))\leq 1; \\ -\sqrt(2)\leq \sqrt(2)\cos((x +\frac(\pi)(4)))\leq\sqrt(2); $$
Da diese Funktion über den gesamten Definitionsbereich stetig ist, liegt die Menge ihrer Werte zwischen ihrem kleinsten und ihrem größten Wert, falls vorhanden, der Menge der Funktionswerte $y =\sqrt(2)\cos((x +\frac(\pi)(4 )))$ ist die Menge $[-\sqrt(2);\sqrt(2)]$.
$$\\ E(3^(x)) = (0;+∞), \\ E(3^(x)+ 1) = (1;+∞), \\ E(-(3^(x )+ 1)^(2) = (-∞;-1), \\ E(5 – (3^(x)+1)^(2)) = (-∞;4) $$
Bezeichnen wir $t = 5 – (3^(x)+1)^(2)$, wobei -∞≤t≤4. Somit reduziert sich das Problem darauf, die Wertemenge der Funktion $y = \log_(0,5)(t)$ auf dem Strahl (-∞;4) zu finden. Da die Funktion $y = \log_(0,5)(t)$ nur für t > 0 definiert ist, dann stimmt ihre Wertemenge auf dem Strahl (-∞;4) mit der Menge der Funktionswerte überein auf dem Intervall (0;4), was den Schnittpunkt des Strahls (-∞;4) mit dem Definitionsbereich (0;+∞) der logarithmischen Funktion darstellt. Im Intervall (0;4) ist diese Funktion stetig und abnehmend. Bei t > 0 tendiert es zu +∞ und bei t = 4 nimmt es den Wert -2 an, also E(y) = (-2, +∞).
Wir verwenden eine Technik, die auf einer grafischen Darstellung einer Funktion basiert.
Nach der Transformation der Funktion gilt: y 2 + x 2 = 25 und y ≥ 0, |x| ≤ 5.
Es sei daran erinnert, dass $x^(2)+y^(2)=r^(2)$ die Gleichung eines Kreises mit dem Radius r ist.
Mit diesen Einschränkungen ist der Zeitplan gegebene Gleichung ist der obere Halbkreis mit Mittelpunkt im Ursprung und Radius gleich 5. Offensichtlich ist E(y) = .
Antwort: E(y) = .
Verweise
Bedeutungsbereich der Funktionen bei Problemen des Einheitlichen Staatsexamens, Irina Borisovna Minyuk
Tipps zum Finden der Wertemenge einer Funktion, Belyaeva I., Fedorova S.
Finden der Menge von Funktionswerten
Wie man Probleme in Mathematik bei Aufnahmeprüfungen löst, I.I.Melnikov, I.N.Sergeev