Teorema inversă este mai mică. Teoremele lui Ceva și Menelaus

A.V. Shevkin

FMS № 2007

Teoremele lui Ceva și Menelaus privind examenul de stat unificat

Un articol detaliat „În jurul teoremelor lui Ceva și Menelaus” este publicat pe site-ul nostru în secțiunea ARTICOLE. Se adresează profesorilor de matematică și liceenilor care sunt motivați să aibă bune cunoștințe de matematică. Puteți reveni la el dacă doriți să înțelegeți problema mai detaliat. În această notă, vom face informatie scurta din articolul menționat și analizați soluțiile la problemele din colecția de pregătire pentru Examenul Unificat de Stat-2016.

teorema lui Ceva

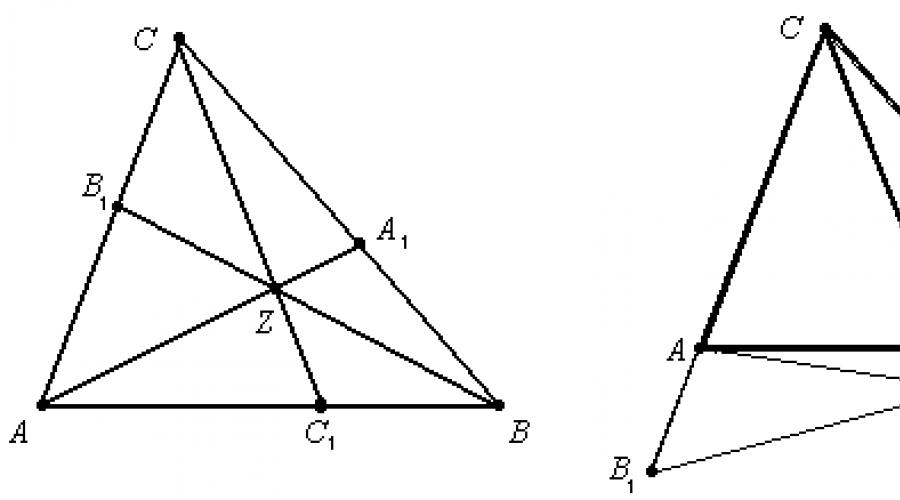
Să fie dat un triunghi ABC iar pe laturile ei AB, î.HrȘi AC punctele sunt marcate C 1 , A 1 Și B 1 respectiv (fig. 1).

a) Dacă segmentele AA 1 , BB 1 și CC 1 se intersectează la un punct, atunci

b) Dacă egalitatea (1) este adevărată, atunci segmentele AA 1 , BB 1 și CC 1 se intersectează într-un punct.

Figura 1 prezintă cazul în care segmentele AA 1 , BB 1 și CC 1 se intersectează într-un punct din interiorul triunghiului. Acesta este așa-numitul caz punct interior. Teorema lui Ceva este valabilă și în cazul unui punct exterior, când unul dintre puncte A 1 , B 1 sau CU 1 aparține laturii triunghiului, iar celelalte două aparțin prelungirilor laturilor triunghiului. În acest caz, punctul de intersecție al segmentelor AA 1 , BB 1 și CC 1 se află în afara triunghiului (Fig. 2).

Cum să ne amintim ecuația lui Cheva?

Să fim atenți la metoda de memorare a egalității (1). Vârfurile triunghiului din fiecare relație și relațiile în sine sunt scrise în direcția de ocolire a vârfurilor triunghiului ABC, pornind de la punct A. din punct A mergi la subiect B, întâlnim un punct CU 1, notează fracția
. Mai departe de punct ÎN mergi la subiect CU, întâlnim un punct A 1, notează fracția
. În fine, din punct de vedere CU mergi la subiect A, întâlnim un punct ÎN 1, notează fracția
. În cazul unui punct exterior se păstrează ordinea scrierii fracțiilor, deși cele două „puncte de împărțire” ale segmentului se află în afara segmentelor lor. În astfel de cazuri, spunem că punctul împarte segmentul în exterior.

Rețineți că orice segment de linie care leagă vârful unui triunghi cu orice punct de pe dreapta care conține latura opusă a triunghiului se numește ceviana.

Să luăm în considerare câteva modalități de demonstrare a aserției a) a teoremei lui Ceva pentru cazul unui punct interior. Pentru a demonstra teorema lui Ceva, trebuie să demonstrăm afirmația a) prin oricare dintre metodele propuse mai jos și, de asemenea, să demonstrăm afirmația b). Dovada afirmaţiei b) este dată după prima metodă de demonstrare a aserţiei a). Demonstrațiile teoremei lui Ceva pentru cazul unui punct extern sunt realizate în mod similar.

Demonstrarea aserției a) a teoremei lui Ceva folosind teorema pe segmente proporționale

Lasă trei cevian AA 1 , BB 1 și CC 1 se intersectează într-un punct Zîn interiorul triunghiului ABC.

Ideea demonstrației este de a înlocui rapoartele segmentelor din egalitatea (1) cu rapoartele segmentelor aflate pe aceeași linie dreaptă.

Prin punct ÎN trage o linie paralelă cu ceviana SS 1 . Drept AA 1 intersectează linia construită în punct M, iar linia care trece prin punct Cși paralel AA 1 , - la punct T. prin puncte AȘi CU trage linii drepte paralele cu cevianele BB 1 . Vor trece linia VM la puncte NȘi R respectiv (fig. 3).

P despre teorema despre segmente proporționale avem:

,
Și
.

Apoi egalitățile

.

În paralelograme ZCTMȘi ZCRB segmente TM, СZȘi BR egale ca laturile opuse ale unui paralelogram. Prin urmare,
iar egalitatea este adevărată

.

Pentru a demonstra afirmația b) folosim următoarea aserțiune. Orez. 3

Lema 1. Dacă punctele CU 1 și CU 2 împărțiți tăietura AB imagine internă (sau externă) în același sens, numărând din același punct, atunci aceste puncte coincid.

Să demonstrăm lema pentru cazul în care punctele CU 1 și CU 2 împărțiți tăietura AB intern în același sens:
.

Dovada. Din egalitate
urmate de egalităţi
Și
. Ultima dintre ele este îndeplinită numai cu condiția ca CU 1 BȘi CU 2 B sunt egale, adică cu condiția ca punctele CU 1 și CU 2 meci.

Dovada lemei pentru cazul în care punctele CU 1 și CU 2 împărțiți tăietura AB desfășurată în exterior într-un mod similar.

Dovada afirmaţiei b) a teoremei lui Ceva

Acum să fie adevărată egalitatea (1). Să demonstrăm că segmentele AA 1 , BB 1 și CC 1 se intersectează într-un punct.

Lasă cevianele AA 1 și BB 1 se intersectează într-un punct Z, trageți un segment prin acest punct CC 2 (CU 2 se află pe segment AB). Apoi, pe baza afirmației a), obținem egalitatea corectă

. (2)

ȘI Comparând egalitățile (1) și (2), concluzionăm că
, adică puncte CU 1 și CU 2 împărțiți tăietura ABîn același raport, numărând din același punct. Lema 1 implică faptul că punctele CU 1 și CU 2 meci. Aceasta înseamnă că segmentele AA 1 , BB 1 și CC 1 se intersectează la un punct, ceea ce trebuia demonstrat.

Se poate dovedi că procedura de scriere a egalității (1) nu depinde de ce punct și în ce direcție sunt ocolite vârfurile triunghiului.

Exercitiul 1. Aflați lungimea segmentului ANîn figura 4, care arată lungimile altor segmente.

Răspuns. 8.

Sarcina 2. cevianele A.M, BN, CK se intersectează într-un punct din interiorul triunghiului ABC. Găsiți o atitudine
, Dacă
,
. Orez. 4

Răspuns.
.

P prezentam dovada teoremei lui Ceva din articol. Ideea demonstrației este de a înlocui rapoartele segmentelor din egalitate (1) cu rapoartele segmentelor aflate pe drepte paralele.

Lasă drept AA 1 , BB 1 , CC 1 se intersectează într-un punct Oîn interiorul triunghiului ABC(Fig. 5). Prin vârf CU triunghi ABC trage o linie paralelă AB, și punctele sale de intersecție cu liniile AA 1 , BB 1 denotă, respectiv A 2 , B 2 .

Din asemănarea a două perechi de triunghiuri CB 2 B 1 Și ABB 1 , BAA 1 Și CA 2 A 1, Fig. 5

avem egalitățile

,
. (3)

Din asemănarea triunghiurilor î.Hr 1 OȘi B 2 CO, ACU 1 OȘi A 2 CO avem egalitățile
, din care rezultă că

. (4)

P înmulțind egalitățile (3) și (4), obținem egalitatea (1).

Se dovedește aserția a) a teoremei lui Ceva.

Se consideră dovezile aserției a) ale teoremei lui Ceva cu ajutorul ariilor pentru un punct interior. Se precizează în cartea lui A.G. Myakishev și se bazează pe enunțurile pe care le vom formula sub formă de sarcini 3 Și 4 .

Sarcina 3. Raportul dintre ariile a două triunghiuri cu un vârf comun și baze situate pe aceeași linie este egal cu raportul lungimilor acestor baze. Demonstrează această afirmație.

Sarcina 4. Demonstrează că dacă
, Acea
Și
. Orez. 6

Lasă segmentele AA 1 , BB 1 și CC 1 se intersectează într-un punct Z(Fig. 6), atunci

,
. (5)

ȘI din egalităţi (5) şi al doilea enunţ al sarcinii 4 urmează că
sau
. În mod similar, obținem asta
Și
. Înmulțind ultimele trei egalități, obținem:

,

adică egalitatea (1) este adevărată, ceea ce trebuia demonstrat.

Se dovedește aserția a) a teoremei lui Ceva.

Sarcina 15. Lăsați cevianele să se intersecteze într-un punct din interiorul triunghiului și împărțiți-l în 6 triunghiuri, ale căror zone sunt egale cu S 1 , S 2 , S 3 , S 4 , S 5 , S 6 (Fig. 7). Demonstrează că. Orez. 7

Sarcina 6. Găsiți zona S triunghi CNZ(ariile altor triunghiuri sunt prezentate în Figura 8).

Răspuns. 15.

Sarcina 7. Găsiți zona S triunghi CNO dacă aria triunghiului ANU este 10 și
,
(Fig. 9).

Răspuns. 30.

Sarcina 8. Găsiți zona S triunghi CNO dacă aria triunghiului Aî.Hr este egal cu 88 și ,
(Fig. 9).

R soluţie. Din moment ce , notăm
,
. Deoarece , atunci notăm
,
. Din teorema lui Ceva rezultă că
, și apoi
. Dacă
, Acea
(Fig. 10). Avem trei necunoscute ( X, y Și S), deci pentru a găsi S Să facem trei ecuații.

Deoarece
, Acea
= 88. Din moment ce
, Acea
, Unde
. Deoarece
, Acea
.

Asa de,
, Unde
. Orez. 10

Sarcina 9. Într-un triunghi ABC puncte KȘi L aparțin, respectiv, părților AB Și BC.
,
. P ALȘi CK. Aria unui triunghi PBC este egal cu 1. Aflați aria triunghiului ABC.

Răspuns. 1,75.

T Teorema lui Menelaus

Să fie dat un triunghi ABC iar pe laturile ei ACȘi CB punctele sunt marcate B 1 și A 1 respectiv, şi pe continuarea laturii AB punct marcat C 1 (Fig. 11).

a) Dacă punctele A 1 , B 1 și CU Mă întind pe aceeași linie, atunci

. (6)

b) Dacă egalitatea (7) este adevărată, atunci punctele A 1 , B 1 și CU 1 se află pe aceeași linie. Orez. unsprezece

Cum să ne amintim egalitatea lui Menelaus?

Tehnica de memorare a egalității (6) este aceeași cu cea a egalității (1). Vârfurile triunghiului din fiecare relație și relațiile în sine sunt scrise în direcția de ocolire a vârfurilor triunghiului ABC- de la vârf la vârf, trecând prin puncte de diviziune (interne sau externe).

Sarcina 10. Demonstrați că atunci când scrieți egalitatea (6) de la orice vârf al triunghiului în orice direcție, se obține același rezultat.

Pentru a demonstra teorema lui Menelaus, trebuie să se demonstreze afirmația a) prin oricare dintre metodele propuse mai jos și, de asemenea, să se demonstreze afirmația b). Dovada afirmaţiei b) este dată după prima metodă de demonstrare a aserţiei a).

Demonstrarea afirmaţiei a) folosind teorema segmentelor proporţionale

eucale. a) Ideea demonstrației este de a înlocui rapoartele lungimilor segmentelor în egalitate (6) cu rapoartele lungimilor segmentelor aflate pe o singură dreaptă.

Lasă punctele A 1 , B 1 și CU 1 se află pe aceeași linie. Prin punct C hai sa tragem o linie dreapta l, paralel cu linia A 1 B 1, intersectează linia AB la punct M(Fig. 12).

R
este. 12

Conform teoremei segmentelor proporționale, avem:
Și
.

Apoi egalitățile
.

Dovada afirmaţiei b) a teoremei lui Menelaus

Acum, dacă egalitatea (6) este adevărată, vom demonstra că punctele A 1 , B 1 și CU 1 se află pe aceeași linie. Lasă drept ABȘi A 1 B 1 se intersectează într-un punct CU 2 (Fig. 13).

Din moment ce punctele A 1 B 1 și CU 2 se află pe aceeași linie, apoi prin afirmația a) a teoremei Menelaus

. (7)

Dintr-o comparație a egalităților (6) și (7) avem
, de unde rezultă că egalitățile

,
,
.

Ultima egalitate este adevărată numai cu condiția
, adică dacă punctele CU 1 și CU 2 meci.

Se dovedește aserția b) a teoremei lui Menelaus. Orez. 13

Dovada afirmaţiei a) folosind asemănarea triunghiurilor

Ideea demonstrației este de a înlocui rapoartele lungimilor segmentelor din egalitate (6) cu rapoartele lungimilor segmentelor aflate pe linii paralele.

Lasă punctele A 1 , B 1 și CU 1 se află pe aceeași linie. Din puncte A, BȘi C trage perpendiculare AA 0 , BB 0 și SS 0 la această linie dreaptă (Fig. 14).

R
este. 14

Din asemănarea a trei perechi de triunghiuri AA 0 B 1 Și CC 0 B 1 , CC 0 A 1 Și BB 0 A 1 , C 1 B 0 BȘi C 1 A 0 A(în două colțuri) avem egalitățile corecte

,
,
,

înmulțindu-le, obținem:

.

Se dovedește aserția a) a teoremei lui Menelaus.

Dovada afirmaţiei a) folosirea zonelor

Ideea demonstrației este de a înlocui raportul dintre lungimile segmentelor din egalitate (7) cu rapoartele ariilor triunghiurilor.

Lasă punctele A 1 , B 1 și CU 1 se află pe aceeași linie. Uneste punctele CȘi C 1 . Indicați ariile triunghiurilor S 1 , S 2 , S 3 , S 4 , S 5 (Fig. 15).

Apoi egalitățile

,
,
. (8)

Înmulțind egalitățile (8), obținem:

Se dovedește aserția a) a teoremei lui Menelaus.

R
este. 15

Așa cum teorema lui Ceva rămâne valabilă dacă punctul de intersecție al lui Cevian este în afara triunghiului, teorema lui Menelaus rămâne valabilă dacă secanta intersectează doar prelungirile laturilor triunghiului. În acest caz, putem vorbi despre intersecția laturilor triunghiului în puncte externe.

Dovada afirmaţiei a) pentru cazul punctelor externe

P gura secantei intersectează laturile triunghiului ABCîn puncte externe, adică intersectează prelungirile laturilor AB,î.HrȘi AC la puncte C 1 , A 1 și B 1, respectiv, iar aceste puncte se află pe aceeași linie dreaptă (Fig. 16).

Conform teoremei segmentelor proporționale, avem:

Și .

Apoi egalitățile

Se dovedește aserția a) a teoremei lui Menelaus. Orez. 16

Rețineți că demonstrația de mai sus coincide cu demonstrația teoremei lui Menelaus pentru cazul în care secanta intersectează două laturi ale triunghiului în punctele interne și una în cel extern.

Dovada aserției b) a teoremei lui Menelaus pentru cazul punctelor externe este similară cu demonstrația dată mai sus.

W iad11. Într-un triunghi ABC puncte A 1 , ÎN 1 culcat respectiv pe laterale SoareȘi ACU. P- punctul de intersecție al segmentelor AA 1 Și BB 1 .
,
. Găsiți o atitudine
.

Soluţie. Denota
,
,
,
(Fig. 17). După teorema lui Menelaus pentru un triunghi î.HrÎN 1 și secante PA 1 scrieți egalitatea corectă:

,

de unde rezultă că

. Orez. 17

Răspuns. .

W iad12 (Universitatea de Stat din Moscova, cursuri pregătitoare prin corespondență). Într-un triunghi ABC, a cărui suprafață este 6, pe lateral AB punct luat LA, împărțind această latură în raport cu
, iar pe lateral AC- punct L, împărțind ACîntr-o relație
. Punct P intersecții de linii SCȘi ÎNL scos din linie AB la o distanta de 1,5. Aflați lungimea laturii AB.

Soluţie. Din puncte RȘi CU să scăpăm perpendicularele relatii cu publiculȘi CM direct AB. Denota
,
,
,
(Fig. 18). După teorema lui Menelaus pentru un triunghi AKC si secante PL scrie ecuația corectă:
, de unde obținem asta
,
. Orez. 18

Din asemănarea triunghiurilor LAMCȘi LARP(pe două colțuri) obținem asta
, de unde rezultă că
.

Acum, știind lungimea înălțimii trase în lateral AB triunghi ABSși aria acestui triunghi, calculăm lungimea laturii:
.

Răspuns. 4.

W iad13. Trei cercuri cu centre A,ÎN,CU, ale căror raze sunt legate ca
, atingeți unul pe celălalt în exterior la puncte X, Y, Z după cum se arată în figura 19. Segmente TOPORȘi DE se intersectează într-un punct O. În ce raport, numărând de la punct B, segment de linie czîmparte segmentul DE?

Soluţie. Denota
,
,
(Fig. 19). Deoarece
, apoi prin afirmația b) a teoremei lui Ceva, segmentele AX, DEȘi CUZ se intersectează la un punct O. Apoi segmentul czîmparte segmentul DEîntr-o relație
. Să găsim această relație. Orez. 19

După teorema lui Menelaus pentru un triunghi BCY si secante BOU avem:
, de unde rezultă că
.

Răspuns. .

Sarcina 14 (USE-2016).

puncte ÎN 1 și CU ACȘi AB triunghi ABC, în plus AB 1:B 1 CU =
= AC 1:CU 1 B. Direct BB 1 Și SS 1 se intersectează într-un punct DESPRE.

A ) Demonstrați că linia SA traversează partea laterală Soare.

AB 1 OC 1 la aria unui triunghi ABC dacă se ştie că AB 1:B 1 CU = 1:4.

Soluţie. a) Lasă linia AO traversează lateral î.Hr la punct A 1 (Fig. 20). După teorema lui Ceva, avem:

. (9)

Deoarece AB 1:B 1 CU = AC 1:CU 1 B, atunci din egalitate (9) rezultă că
, acesta este CA 1 = A 1 B, ceea ce urma să fie dovedit. Orez. 20

b) Fie aria triunghiului AB 1 O este egal cu S. Deoarece AB 1:B 1 CU CB 1 O este egal cu 4 S, și aria triunghiului AOC este egal cu 5 S. Apoi aria triunghiului AOB este de asemenea egal cu 5 S, din moment ce triunghiurile AOB Și AOC au un teren comun AO, și vârfurile lor BȘi C echidistant de linie AO. Și aria triunghiului AOC 1 este egal S, deoarece AC 1:CU 1 B = 1:4. Apoi aria triunghiului ABB 1 este egal cu 6 S. Deoarece AB 1:B 1 CU= 1:4, apoi aria triunghiului CB 1 O este egal cu 24 S, și aria triunghiului ABC este egal cu 30 S. Acum să găsim raportul dintre aria patrulaterului AB 1 OC 1 (2S) la aria triunghiului ABC (30S), este egal cu 1:15.

Răspuns. 1:15.

Sarcina 15 (USE-2016).

puncte ÎN 1 și CU 1 întins pe laterale ACȘi AB triunghi ABC, în plus AB 1:B 1 CU =
= AC 1:CU 1 B. Direct BB 1 Și SS 1 se intersectează într-un punct DESPRE.

a) Demonstrați că linia SA traversează partea laterală Soare.

b) Aflați raportul dintre aria patrulaterului AB 1 OC 1 la aria unui triunghi ABC dacă se ştie că AB 1:B 1 CU = 1:3.

Răspuns. 1:10.

W sarcina 16 (USE-2016). Pe segment BD punct luat CU. Bisectoare BL ABC cu baza Soare BLD cu baza BD.

a) Demonstrați că triunghiul DCL isoscel.

b) Se ştie că cos
ABC DL, adică triunghiul BD punct luat CU. Bisectoare BL triunghi isoscel ABC cu baza Soare este o latură laterală a unui triunghi isoscel BLD cu baza BD.

a) Demonstrați că triunghiul DCL isoscel.

b) Se ştie că cos ABC= . În ce fel este direct DL desparte partea AB?

Răspuns. 4:21.

Literatură

1. Smirnova I.M., Smirnov V.A. Minunate puncte și linii triunghiulare. M.: Matematică, 2006, nr. 17.

2. Miakishev A.G. Elemente de geometrie triunghiulară. (Seria „Biblioteca „Educația matematică””). M.: MTsNMO, 2002. - 32 p.

3. Geometrie. Capitole suplimentare pentru manualul de clasa a VIII-a: Manual pentru elevii școlilor și claselor cu studiu aprofundat / L.S. Atanasyan, V.F. Butozov, S.B. Kadomtsev și alții - M.: Vita-Press, 2005. - 208 p.

4. Erdniev P., Mantsaev N. Cheva și teoremele lui Menelaus. M.: Kvant, 1990, nr. 3, p. 56–59.

5. Sharygin I.F. Teoremele lui Ceva și Menelaus. Moscova: Kvant, 1976, nr. 11, p. 22–30.

6. Vavilov V.V. Medianele și liniile mediane ale unui triunghi. M.: Matematică, 2006, nr. 1.

7. Efremov Dm. Noua geometrie a triunghiului. Odesa, 1902. - 334 p.

8. Matematică. 50 de variante de sarcini tipice de testare / I.V. Iascenko, M.A. Volkevici, I.R. Vysotsky și alții; ed. I.V. Iascenko. - M .: Editura „Examen”, 2016. - 247 p.

În cursul geometriei există teoreme care nu sunt studiate în detaliu la școală, dar care pot fi utile pentru rezolvarea celor mai multe sarcini provocatoare OGE și EGE. Acestea includ, de exemplu, teorema lui Menelaus. În mod tradițional, se studiază în clase cu studiu aprofundat al matematicii în clasa a VIII-a, iar în programul obișnuit (conform manualului lui Atanasyan), teorema lui Menelaus este inclusă în manualul claselor 10-11.
Între timp, rezultatul studierii resurselor de pe Internet care menționează teorema Menelaus arată că aceasta este de obicei formulată incomplet și deci inexact, iar toate cazurile de utilizare a acesteia, precum și demonstrația teoremei inverse, nu sunt date. Scopul acestui articol este de a înțelege ce este teorema Menelaus, cum și de ce este utilizată și, de asemenea, de a împărtăși metodologia de predare a acestei teoreme pe lecții individuale tutore cu elevii.
Considera sarcină tipică(Sarcina nr. 26, OGE), care apare la examene într-o varietate de opțiuni care diferă numai în număr în stare.

Soluția problemei în sine este simplă - o puteți citi mai jos. În acest articol, însă, ne interesează mai ales un punct ușor diferit, care este adesea omis, înțeles ca de la sine înțeles, ca evident. Dar evident este ceea ce se poate dovedi. Și acest lucru poate fi demonstrat în diverse moduri - de obicei o dovedesc exclusiv cu ajutorul asemănării - dar este posibil și cu ajutorul teoremei lui Menelaus.
Rezultă din condiția că, deoarece unghiurile de la baza inferioară a trapezului se adună până la 90 °, atunci dacă extindem laturile, obținem triunghi dreptunghic. În plus, din punctul de intersecție rezultat al prelungirilor laturilor laterale, este trasat un segment care trece prin punctele medii ale bazelor. Și de ce acest segment trece prin toate aceste trei puncte? De obicei, nu se spune un cuvânt despre asta în soluțiile problemei găsite pe Internet. Nu există nici măcar o referire la teorema trapezului în patru puncte, cu atât mai puțin o dovadă a acestei afirmații. Între timp, poate fi demonstrat folosind teorema Menelaus, care este o condiție de apartenență trei puncte la o linie dreaptă.

Enunțuri ale teoremei lui Menelaus
Este timpul să formulăm teorema. Trebuie remarcat faptul că în diverse manuale și manuale există formulări destul de diferite ale acestuia, deși esența rămâne neschimbată. În manualul lui Atanasyan și alții pentru clasele 10-11, este dată următoarea formulare a teoremei Menelaus, să o numim „vector”:

În manualul „Geometrie clasa 10-11” Alexandrov și colab., precum și în ghid de studiu aceiaşi autori „Geometrie. Gradul 8 ”este dată o formulare ușor diferită a teoremei Menelaus, iar pentru clasele 10-11 și pentru clasa a 8-a este aceeași:
Aici trebuie făcute trei observații.
Nota 1. La examene, nu există probleme care să fie rezolvate doar cu ajutorul vectorilor, pentru care se folosește exact „minus unu”. Prin urmare, pentru uz practic formularea cea mai convenabilă este, de fapt, o consecință a teoremei intervalului (aceasta este a doua formulare cu litere aldine). Ne vom limita la el pentru a studia în continuare teorema Menelaus, deoarece scopul nostru este să învățăm cum să o aplicăm pentru a rezolva probleme.
Nota 2. În ciuda faptului că toate manualele prevăd în mod clar cazul când toate cele trei puncte A 1 , B 1 și C 1 se pot întinde pe prelungirile laturilor triunghiului (sau pe linii care conțin laturile triunghiului), pe mai multe Site-urile de tutorat pe Internet doar cazul este formulat când două puncte se află pe două laturi, iar al treilea se află pe prelungirea celei de-a treia laturi. Acest lucru cu greu poate fi justificat prin faptul că doar probleme de primul tip sunt întâlnite la examene și probleme nu pot fi întâlnite atunci când toate aceste puncte se află pe prelungirile a trei laturi.
Nota 3. Teorema inversă, adică condiția ca trei puncte să se afle pe aceeași linie dreaptă, de obicei, nu este luată în considerare deloc, iar unii tutori chiar sfătuiesc (???) să se ocupe doar de teorema directă și să nu ia în considerare teorema inversă. Între timp, demonstrația afirmației inverse este destul de instructivă și permite să se demonstreze enunțuri similare cu cele date în soluția problemei 1. Experiența de a demonstra teorema inversă va oferi, fără îndoială, un beneficiu tangibil studentului în rezolvarea problemelor.

Desene și modele

Pentru a-l învăța pe student să vadă teorema Menelaus în probleme și să o folosească în rezolvare, este important să acorde atenție desenelor și modelelor din înregistrarea teoremei pentru un anumit caz. Și întrucât teorema în sine este în forma ei „pură”, i.e. fără a fi înconjurate de alte segmente, laturile diferitelor figuri în probleme nu apar de obicei, atunci este mai oportun să se arate teorema pe probleme specifice. Și dacă arătați imagini ca explicație, atunci faceți-le multivariate. În același timp, evidențiați cu o singură culoare (de exemplu, roșu) linia dreaptă, care este formată din trei puncte, și albastru - segmentele triunghiului implicate în înregistrarea teoremei lui Menelaus. În același timp, acele elemente care nu participă rămân negre:

La prima vedere, poate părea că formularea teoremei este destul de complicată și nu întotdeauna clară; deoarece implică trei fracții. Într-adevăr, dacă studentul nu are suficientă experiență, atunci poate face cu ușurință o greșeală în scris și, ca urmare, poate rezolva incorect problema. Și aici, uneori, încep problemele. Faptul este că manualele nu se concentrează, de obicei, pe cum să „fai ocolul” atunci când scrii o teoremă. Nu se spune nimic despre regularitățile scrierii teoremei în sine. Prin urmare, unii tutori chiar desenează diferite săgeți, în ce ordine să scrie formula. Și le cer elevilor să respecte cu strictețe aceste îndrumări. Acest lucru este parțial corect, dar este mult mai important să înțelegeți esența teoremei decât să o scrieți pur mecanic folosind „regula de ocolire” și săgețile.
De fapt, este important să înțelegeți doar logica „ocolirii”, și este atât de precis încât este imposibil să faceți o greșeală în scrierea formulei. În ambele cazuri a) și b) scriem formula pentru triunghiul AMC.
Pentru început, determinăm noi înșine trei puncte - vârfurile triunghiului. Avem aceste puncte A, M, C. Apoi determinăm punctele situate pe linia de intersectare (linia roșie), acestea sunt B, P, K. Începem „mișcarea” din vârful triunghiului, de exemplu, de la punctul C. Din acest punct „mergem „în punctul care este format prin intersecția, de exemplu, a laturii AC și a dreptei de intersectare - avem acest punct K. Scriem în numărătorul primei fracții - SK. Mai departe de la punctul K „mergem” la punctul rămas de pe dreapta AC - la punctul A. În numitorul primei fracții scriem - KA. Deoarece punctul A aparține și dreptei AM, procedăm la fel cu segmentele de pe dreapta AM. Și aici din nou, pornim de la vârf, apoi „mergem” la un punct de pe dreapta de intersectare, după care mergem la vârful M. „Ne-am găsit” pe dreapta BC, facem același lucru cu segmentele de pe aceasta. linia. Desigur, „mergem” de la M la B, după care revenim la C. Acest „bypass” se poate face atât în ​​sensul acelor de ceasornic, cât și în sens invers acelor de ceasornic. Este important doar să înțelegeți regula de ocolire - de la un vârf la un punct pe o linie dreaptă și de la un punct pe o dreaptă la un alt vârf. Așa ceva se explică de obicei prin regula de scriere a produsului fracțiilor. Rezultatul este:
Să acordăm atenție faptului că întregul „bypass” este reflectat în înregistrare și este afișat prin săgeți pentru comoditate.
Cu toate acestea, înregistrarea rezultată poate fi preluată fără a efectua nicio „traversare”. După ce sunt scrise punctele - vârfurile triunghiului (A, M, C) și punctele - situate pe dreapta de intersectare (B, P, K), ele notează și triple de litere care denotă puncte situate pe fiecare dintre trei rânduri. În cazurile noastre, acestea sunt I) B , M , C ; II) A , P , M și III) A , C , K . După aceea, partea stângă corectă a formulei poate fi scrisă fără să se uite măcar la desen și în orice ordine. Este suficient să scriem fracții adevărate din fiecare triplu de litere, care respectă regula - condiționat, literele „de mijloc” sunt punctele liniei de intersectare (roșu). În mod convențional, literele „extreme” sunt punctele vârfurilor triunghiului (albastru). Când scrieți o formulă în acest fel, trebuie doar să vă asigurați că orice literă „albastru” (vârful triunghiului) lovește atât numărătorul, cât și numitorul o dată. De exemplu.
Această metodă este utilă în special pentru cazuri precum b) și, de asemenea, pentru autotestare.

Teorema lui Menelaus. Dovada
Sunt câteva diferite căi dovada teoremei lui Menelaus. Uneori se dovedesc folosind asemănarea triunghiurilor, pentru care din punctul M este trasat un segment paralel cu AC (ca în acest desen). Alții desenează o linie suplimentară care nu este paralelă cu linia de intersectare și apoi, cu linii paralele cu linia de intersectare, par să „proiecteze” toate segmentele necesare pe această dreaptă și, folosind o generalizare a teoremei Thales (adică, teoremă asupra segmentelor proporționale), deduceți o formulă. Cu toate acestea, poate cel mai simplu mod de a demonstra aceasta se obține prin trasarea unei drepte din punctul M paralel cu cel care se intersectează. Să demonstrăm teorema lui Menelaus în acest fel.
Dat: Triunghiul ABC. Linia PK intersectează laturile triunghiului și prelungirea laturii MC în punctul B.
Demonstrați că egalitatea este valabilă:
Dovada. Să desenăm o grindă MM 1 paralelă cu BK. Să notăm relațiile în care participă segmentele care sunt incluse în formula teoremei Menelaus. Într-un caz, luați în considerare liniile care se intersectează în punctul A, iar în celălalt caz, care se intersectează în punctul C. Să înmulțim părțile din stânga și din dreapta acestor ecuații:

Teorema a fost demonstrată.
Teorema este demonstrată în mod similar pentru cazul b).

Din punctul C trasăm un segment CC 1 paralel cu dreapta BK. Să notăm relațiile în care participă segmentele care sunt incluse în formula teoremei Menelaus. Într-un caz, considerăm drepte care se intersectează în punctul A, iar în celălalt caz, care se intersectează în punctul M. Deoarece teorema Thales nu spune nimic despre locația segmentelor pe două drepte care se intersectează, segmentele pot fi amplasate și pe laturi opuse. a punctului M. Prin urmare

Teorema a fost demonstrată.

Acum demonstrăm teorema inversă.
Dat:
Demonstrați că punctele B, P, K se află pe aceeași dreaptă.
Dovada. Fie ca dreapta BP să intersecteze AC într-un punct K 2 care nu coincide cu punctul K. Deoarece BP este o dreaptă care conține punctul K 2 , teorema lui Menelaus tocmai demonstrată este valabilă pentru aceasta. Deci, pentru asta scriem
Cu toate acestea, tocmai am arătat asta
Rezultă că punctele K și K 2 coincid, deoarece au latura AC în același raport.
Pentru cazul b) teorema se demonstrează în mod similar.

Rezolvarea problemelor folosind teorema Menelaus

Mai întâi, să revenim la problema 1 și să o rezolvăm. Să o citim din nou. Hai sa facem un desen:

Dat un trapez ABCD. ST - linia de mijloc a trapezului, adică una dintre aceste distante. Unghiurile A și D se adună până la 90°. Extindem laturile AB și CD și la intersecția lor obținem punctul K. Să conectăm punctul K cu punctul N - mijlocul lui BC. Acum să demonstrăm că punctul P, care este mijlocul bazei lui AD, aparține de asemenea dreptei KN. Luați în considerare triunghiurile ABD și ACD în succesiune. Linia KP intersectează două laturi ale fiecărui triunghi. Să presupunem că dreapta KN intersectează baza AD într-un punct X. Conform teoremei lui Menelaus:
Deoarece triunghiul AKD este dreptunghic, punctul P, care este punctul de mijloc al ipotenuzei AD, este echidistant de A, D și K. În mod similar, punctul N este echidistant de punctele B, C și K. De unde o bază este 36 și cealaltă este 2.
Soluţie. Luați în considerare triunghiul BCD. Este străbătută de raza AX, unde X este punctul de intersecție al acestei raze cu prelungirea laturii BC. Conform teoremei lui Menelaus:
Înlocuind (1) în (2) obținem:

Soluţie. Fie S 1 , S 2 , S 3 și S 4 ariile triunghiurilor AOB, AOM, BOK și, respectiv, patrulaterul MOKC.

Deoarece BM este mediana, atunci S ABM = S BMC .
Deci S 1 + S 2 = S 3 + S 4 .
Deoarece trebuie să găsim raportul dintre zonele S 1 și S 4, împărțim ambele părți ale ecuației la S 4:
Să înlocuim aceste valori în formula (1): Din triunghiul BMC cu secanta AK, conform teoremei lui Menelaus, avem: Din triunghiul AKC cu secanta BM, conform teoremei lui Menelaus, avem: Toate rapoartele necesare sunt exprimate în termeni de k, iar acum le putem înlocui în expresia (2):
Soluția acestei probleme folosind teorema Menelaus este considerată pe pagină.

Nota profesorului de matematică. Aplicarea teoremei Menelaus în această problemă este chiar cazul în care această metodă poate economisi timp semnificativ la examen. Această sarcină este oferită în versiunea demo a examenului de admitere la liceu la Școala Superioară de Științe Economice pentru clasa a IX-a (2019).

© Tutor de matematică la Moscova, Alexander Anatolyevich, 8-968-423-9589.

Decide pentru tine

1) Sarcina este mai rapidă. Un punct M este marcat pe mediana BD a triunghiului ABC astfel încât BM: MD = m: n. Linia AM intersectează latura BC în punctul K.
Găsiți raportul BK:KC.
2) Sarcina este mai dificilă. Bisectoarea unghiului A a paralelogramului ABCD intersectează latura BC în punctul P și diagonala BD în punctul T. Se știe că AB: AD = k (0 3) Sarcina numărul 26 OGE. În triunghiul ABC, bisectoarea BE și mediana AD sunt perpendiculare și au aceeași lungime egală cu 36. Aflați laturile triunghiului ABC.
Sugestie pentru profesor de matematică. Pe Internet, există o soluție la o astfel de problemă cu ajutorul construcției suplimentare și apoi fie asemănarea, fie găsirea de zone și numai după aceea laturile triunghiului. Acestea. ambele metode necesită construcție suplimentară. Cu toate acestea, rezolvarea unei astfel de probleme folosind proprietatea bisectoare și teorema Menelaus nu necesită construcții suplimentare. Este mult mai simplu și mai rațional.

Clasă: 9

Obiectivele lecției:

1. generalizarea, extinderea și sistematizarea cunoștințelor și aptitudinilor elevilor; să învețe cum să folosească cunoștințele în rezolvarea unor probleme complexe;
2. promovează dezvoltarea abilităților de aplicare independentă a cunoștințelor în rezolvarea problemelor;
3. dezvoltarea gândirii logice și a vorbirii matematice a elevilor, capacitatea de a analiza, compara și generaliza;
4. educa elevii în încredere în sine, sârguință; capacitatea de a lucra în echipă.

Obiectivele lecției:

• Educational: repetă teoremele lui Menelaus și Ceva; aplicați-le la rezolvarea problemelor.
• În curs de dezvoltare: a învăța să prezinte o ipoteză și să-și apere cu pricepere opinia cu dovezi; testarea capacităţii de generalizare şi sistematizare a cunoştinţelor lor.
• Educational: creste interesul pentru subiect si pregateste-te pentru rezolvarea unor probleme mai complexe.

Tip de lecție: lectie de generalizare si sistematizare a cunostintelor.

Echipament: fișe pentru lucrul în grup în cadrul lecției pe o anumită temă, fișe individuale pt muncă independentă, computer, proiector multimedia, ecran.

În timpul orelor

Eu pun în scenă. Moment organizatoric (1 min.)

Profesorul explică tema și scopul lecției.

etapa a II-a. Actualizarea cunoștințelor și abilităților de bază (10 min.)

Profesor:În lecție, ne amintim teoremele lui Menelaus și Ceva pentru a trece cu succes la rezolvarea problemelor. Să aruncăm o privire la ecran cu tine. Pentru ce teoremă este această imagine? (teorema lui Menelaus). Încercați să enunțați clar teorema.

Poza 1

Fie punctul A 1 să se afle pe latura BC a triunghiului ABC, punctul C 1 pe latura AB, punctul B 1 pe prelungirea laturii AC dincolo de punctul C. Punctele A 1 , B 1 și C 1 se află pe aceeași dreaptă dacă şi numai dacă egalitate

Profesor: Să aruncăm o privire la următoarea poză împreună. Formulați o teoremă pentru această figură.

Figura 2

Linia AD intersectează două laturi și prelungirea celei de-a treia laturi a triunghiului BMC.

Conform teoremei lui Menelaus

Linia MB intersectează două laturi și prelungirea celei de-a treia laturi a triunghiului ADC.

Conform teoremei lui Menelaus

Profesor: Cărei teoreme îi corespunde imaginea? (teorema lui Ceva). Formulați o teoremă.

Figura 3

Fie în triunghiul ABC punctul A 1 se află pe latura BC, punctul B 1 pe latura AC, punctul C 1 pe latura AB. Segmentele AA 1 , BB 1 și CC 1 se intersectează într-un punct dacă și numai dacă egalitatea

etapa a III-a. Rezolvarea problemelor. (22 min.)

Clasa este împărțită în 3 echipe, fiecare primește un cartonaș cu două diverse sarcini. Se acordă timp pentru rezolvare, apoi se afișează ecranul<Рисунки 4-9>. Conform desenelor gata făcute pentru sarcini, reprezentanții echipelor își explică pe rând soluția. Fiecare explicație este urmată de o discuție, răspunsuri la întrebări și verificarea corectitudinii soluției pe ecran. La discuție participă toți membrii echipei. Cu cât echipa este mai activă, cu atât este mai bine evaluată la rezumat.

Cardul 1.

1. În triunghiul ABC pe latura BC se ia punctul N astfel încât NC = 3BN; pe prelungirea laturii AC, punctul M este luat drept punct A astfel încât MA = AC. Linia MN intersectează latura AB în punctul F. Aflați raportul

2. Demonstrați că medianele unui triunghi se intersectează într-un punct.

Soluția 1

Figura 4

După starea problemei, MA = AC, NC = 3BN. Fie MA = AC =b, BN = k, NC = 3k. Linia MN intersectează două laturi ale triunghiului ABC și prelungirea celui de-al treilea.

Conform teoremei lui Menelaus

Răspuns:

Dovada 2

Figura 5

Fie AM 1 , BM 2 , CM 3 medianele triunghiului ABC. Pentru a demonstra că aceste segmente se intersectează la un moment dat, este suficient să arătăm că

Apoi, după teorema (inversa) Ceva, segmentele AM ​​1 , BM 2 și CM 3 se intersectează într-un punct.

Avem:

Deci, se dovedește că medianele unui triunghi se intersectează într-un punct.

Cardul 2.

1. Punctul N este luat pe latura PQ a triunghiului PQR, iar punctul L este luat pe latura PR, iar NQ = LR. Punctul de intersecție al segmentelor QL și NR împarte QL în raportul m:n, numărând din punctul Q. Aflați

2. Demonstrați că bisectoarele unui triunghi se intersectează într-un punct.

Soluția 1

Figura 6

Prin ipoteza NQ = LR, Fie NA = LR =a, QF = km, LF = kn. Linia NR intersectează două laturi ale triunghiului PQL și prelungirea celui de-al treilea.

Conform teoremei lui Menelaus

Răspuns:

Dovada 2

Figura 7

Să arătăm asta

Apoi, după teorema (inversa) Ceva, AL 1 , BL 2 , CL 3 se intersectează într-un punct. După proprietatea bisectoarelor unui triunghi

Înmulțind egalitățile obținute termen cu termen, obținem

Pentru bisectoarele unui triunghi, egalitatea lui Ceva este satisfăcută, prin urmare, ele se intersectează într-un punct.

Cardul 3.

1. În triunghiul ABC AD este mediana, punctul O este mijlocul medianei. Linia BO intersectează latura AC în punctul K. În ce raport punctul K împarte AC, numărând din punctul A?

2. Demonstrați că, dacă un cerc este înscris într-un triunghi, atunci segmentele care leagă vârfurile triunghiului cu punctele de contact ale laturilor opuse se intersectează într-un punct.

Soluția 1

Figura 8

Fie BD = DC = a, AO = OD = m. Linia VC intersectează două laturi și prelungirea celei de-a treia laturi a triunghiului ADC.

Conform teoremei lui Menelaus

Răspuns:

Dovada 2

Figura 9

Fie A 1 , B 1 și C 1 punctele tangente ale cercului înscris al triunghiului ABC. Pentru a demonstra că segmentele AA 1 , BB 1 și CC 1 se intersectează într-un punct, este suficient să arătăm că egalitatea lui Ceva este valabilă:

Folosind proprietatea tangentelor trasate la un cerc dintr-un punct, introducem notatia: C 1 B = BA 1 = x, AC 1 = CB 1 = y, BA 1 = AC 1 = z.

Egalitatea lui Ceva este valabilă, ceea ce înseamnă că bisectoarele triunghiului se intersectează într-un punct.

stadiul IV. Rezolvarea problemelor (muncă independentă) (8 min.)

Profesor: Munca echipelor s-a încheiat și acum vom începe lucrul independent pe cartonașe individuale pentru 2 opțiuni.

Materiale pentru lecția pentru munca independentă a elevilor

Opțiunea 1.Într-un triunghi ABC, a cărui aria este 6, pe latura AB, se ia un punct K, împărțind această latură în raportul AK:BK = 2:3, iar pe latura AC - punctul L, împărțind AC în raportul AL:LC = 5:3. Punctul Q de intersecție a dreptelor СК și BL este îndepărtat de pe dreapta AB la o distanță . Aflați lungimea laturii AB. (Răspuns: 4.)

Opțiunea 2. Punctul K este luat pe latura AC în triunghiul ABC.AK = 1, KS = 3. Punctul L este luat pe latura AB. AL:LВ = 2:3, Q este punctul de intersecție al dreptelor BK și CL. Aflați lungimea înălțimii triunghiului ABC, coborâtă de la vârful B. (Răspuns: 1.5.)

Lucrarea este transmisă profesorului pentru revizuire.

etapa V. Rezumatul lecției (2 min.)

Se analizează greșelile, se notează răspunsurile și comentariile originale. Rezultatele muncii fiecărei echipe sunt însumate și se acordă note.

etapa a VI-a. Tema pentru acasă (1 min.)

Tema pentru acasă este alcătuită din sarcinile nr. 11, 12 p. 289-290, nr. 10 p. 301.

Ultimul cuvânt al profesorului (1 min).

Astăzi v-ați auzit reciproc discursul matematic și v-ați evaluat capacitățile. Pe viitor, vom folosi astfel de discuții pentru a înțelege mai bine subiectul. Argumentele din lecție erau prietene cu faptele, iar teoria cu practica. Va multumesc tuturor.

Literatură:

1. Tkachuk V.V. Matematică pentru un solicitant. – M.: MTsNMO, 2005.

— Ce au în comun teorema lui Menelaus și medicamentele?
Toată lumea știe despre ele, dar nimeni nu vorbește despre ele.
Conversație tipică cu un student

Aceasta este o teoremă cool care te va ajuta în momentul în care pare că nimic nu te va ajuta. În lecție, vom formula teorema în sine, vom lua în considerare mai multe opțiuni pentru utilizarea sa și, ca desert, veți găsi un sever teme pentru acasă. Merge!

Pentru început, formularea. Poate voi oferi nu cea mai „frumoasă” versiune a teoremei, ci cea mai înțeleasă și mai convenabilă.

Teorema lui Menelaus. Luați în considerare un triunghi arbitrar $ABC$ și o dreaptă $l$ care intersectează două laturi ale triunghiului nostru în interior și o latură în continuare. Să notăm punctele de intersecție ale lui $M$, $N$ și $K$:

Triunghi $ABC$ și secanta $l$

Atunci următoarea relație este adevărată:

\[\frac(AM)(MB)\cdot \frac(BN)(NC)\cdot \frac(CK)(KA)=1\]

Vreau să notez: nu înghesuiți locația literelor în această formulă rea! Acum vă voi spune un algoritm prin care puteți restaura oricând toate cele trei fracții literalmente din mers. Chiar și în timpul examenului sub stres. Chiar dacă stai la geometrie la 3 dimineața și nu înțelegi absolut nimic. :)

Schema este simplă:

1. Desenăm un triunghi și o secanta. De exemplu, așa cum se arată în teoremă. Desemnăm vârfurile și punctele cu câteva litere. Poate fi un triunghi arbitrar $ABC$ și o linie dreaptă cu puncte $M$, $N$, $K$ sau altele - nu acesta este ideea.
2. Punem un pix (creion, marker, pix) la orice vârf al triunghiului și începem să ocolim laturile acestui triunghi cu abordarea obligatorie a punctelor de intersecţie cu dreapta. De exemplu, dacă mergem mai întâi de la punctul $A$ la punctul $B$, atunci obținem segmente: $AM$ și $MB$, apoi $BN$ și $NC$ și apoi (atenție!) $CK$ și $KA$ . Deoarece punctul $K$ se află pe extensia laturii $AC$, atunci când treceți de la $C$ la $A$, va trebui să părăsiți temporar triunghiul.
3. Și acum împărțim segmentele adiacente unele în altele exact în ordinea în care le-am obținut în timpul bypass-ului: $AM/MB$, $BN/NC$, $CK/KA$ - obținem trei fracții, produsul lui care ne va da unitate .

Pe desen va arăta astfel:

circuit simplu, permițându-vă să restabiliți formula de la t. Menelaus

Și doar câteva comentarii. Mai precis, acestea nu sunt nici măcar comentarii, ci răspunsuri la întrebări tipice:

• Ce se întâmplă dacă linia $l$ trece prin vârful triunghiului? Răspuns: nimic. Teorema lui Menelaus nu funcționează în acest caz.
• Ce se întâmplă dacă alegi un alt vârf pentru a începe sau mergi în altă direcție? Răspuns: va fi la fel. Schimbă doar ordinea fracțiilor.

Cred că am înțeles corect formularea. Să vedem cum se folosește tot acest joc pentru a rezolva probleme geometrice complexe.

De ce sunt necesare toate acestea?

Avertizare. Folosirea excesivă a teoremei Menelaus pentru rezolvarea problemelor planimetrice poate provoca vătămări ireparabile psihicului tău, deoarece această teoremă accelerează semnificativ calculele și te face să-ți amintești alte fapte importante de la cursul de geometrie a școlii.

Dovada

Nu voi dovedi. :)

Bine, lasă-mă să dovedesc.

Acum rămâne să comparăm cele două valori obținute pentru segmentul $CT$:

\[\frac(AM\cdot BN\cdot CK)(BM\cdot CN\cdot AK)=1;\]

\[\frac(AM)(BM)\cdot \frac(BN)(CN)\cdot \frac(CK)(AK)=1;\]

OK, totul sa terminat acum. Rămâne doar să „pieptănăm” această formulă, plasând corect literele în interiorul segmentelor - și formula este gata. :)

Teorema lui Menelaus sau teorema completă cu patru laturi este cunoscută încă de atunci Grecia antică. A fost numit după autorul său, un matematician și astronom grec antic. Menelau al Alexandriei(aproximativ 100 d.Hr.). Această teoremă este foarte frumoasă și simplă, dar, din păcate, nu i se acordă atenția cuvenită în cursul școlar modern. Și, între timp, în multe cazuri ajută la rezolvarea problemelor geometrice destul de complexe foarte ușor și grațios.

Teorema 1 (teorema lui Menelaus). Fie ∆ABC intersectat de o dreaptă care nu este paralelă cu latura AB și care intersectează două dintre laturile sale AC și BC, respectiv, în punctele F și E, dar de dreapta AB în punctul D (Fig. 1),

apoi A F FC * CE EB * BD DA = 1

Notă. Pentru a reține cu ușurință această formulă, puteți folosi următoarea regulă: deplasați-vă de-a lungul conturului triunghiului de la vârf la punctul de intersecție cu linia și de la punctul de intersecție la următorul vârf.

Dovada. Din vârfurile A, B, C ale triunghiului trasăm trei drepte paralele, respectiv, până se intersectează cu linia secante. Vom primi trei perechi triunghiuri asemănătoare(semn de asemănare în două colțuri). Următoarele egalități rezultă din asemănarea triunghiurilor

Și acum înmulțim egalitățile datelor obținute:

Teorema a fost demonstrată.

Pentru a simți frumusețea acestei teoreme, să încercăm să rezolvăm problema geometrică propusă mai jos cu două căi diferite: folosind un helper build si cu ajutorul teoremele lui Menelaus.

Sarcina 1.

În ∆ABC, bisectoarea AD împarte latura BC într-un raport de 2: 1. În ce raport mediana CE împarte această bisectoare?

Soluţie.

Cu ajutorul unei constructii auxiliare:

Fie S punctul de intersecție al bisectoarei AD și medianei CE. Completam ∆ASB la paralelogramul ASBK. (Fig. 2)

Este evident că SE = EK, deoarece punctul de intersecție al paralelogramului bisectează diagonalele. Considerăm acum triunghiurile ∆CBK și ∆CDS. Este ușor de observat că sunt asemănătoare (un semn de similitudine în două unghiuri: și ca unghiuri interne unilaterale cu drepte paralele AD și KB și secante CB). Asemănarea unui triunghi implică următoarele:

Folosind condiția, obținem:

CB CD = CD + DB CD = CD + 2CD CB = 3CD CD = 3

Acum rețineți că KB = AS, ca laturi opuse ale unui paralelogram. Apoi

AS SD = KB SD = CB CD = 3

Folosind teorema lui Menelaus.

Se consideră ∆ABD și se aplică teorema lui Menelaus (dreapta care trece prin punctele C, S, E este o dreaptă secantă):

BE EA * AS SD * DC CB = 1

După condiția teoremei, avem BE/EA = 1, deoarece CE este mediana și DC/CB = 1/3, așa cum am calculat deja mai devreme.

1*AS SD*1 3=1

De aici obținem AS/SD = 3 La prima vedere, ambele soluții sunt destul de compacte și aproximativ echivalente. Cu toate acestea, ideea unei construcții suplimentare pentru școlari se dovedește adesea a fi foarte complicată și deloc evidentă, în timp ce, cunoscând teorema lui Menelaus, este suficient pentru el să o aplice corect.

Luați în considerare o altă problemă în care teorema lui Menelaus funcționează foarte grațios.

Sarcina 2.

Pe laturile AB și BC ∆ABC, punctele M și N sunt date, respectiv, astfel încât să fie valabile următoarele egalități:

AM MB = CN NA = 1 2

În ce raport punctul de intersecție S al segmentelor BN și CM împarte fiecare dintre aceste segmente (fig. 3)?

Soluţie.

Luați în considerare ∆ABN. Aplicăm teorema lui Menelaus pentru acest triunghi (dreapta care trece prin punctele M, S, C este linia secantă)

AM MB * BC SN * CN CA = 1

Din starea problemei avem: AM MB = 1 2

NC CA = NC CN + NA = NC CN + 2NC = NC 3 NC = 1 3

Conectând aceste rezultate, obținem:

1 2 * BS SN * 1 3 = 1

Prin urmare, BS / SN = 6. Și, prin urmare, punctul S de intersecție a segmentelor BN și CM împarte segmentul BN în raportul 6: 1.

Luați în considerare ∆ACM. Aplicăm teorema lui Menelaus pentru acest triunghi (dreapta care trece prin punctele N, S, B este linia secantă):

AN NC * CS SM * MB BA = 1

Din starea problemei avem: AN NC = 2

MB BA = MB BM + MA = 2MA 2MA + MA = 2MB 3MA = 2 3

Conectând aceste rezultate, obținem:

2*CS-SM*2 3=1

Prin urmare CS/SM = 3/4

Și, prin urmare, punctul S al intersecției segmentelor BN și CM împarte segmentul CM în raportul 3: 4.

Teorema inversă la teorema lui Menelaus este de asemenea valabilă. De multe ori se dovedește a fi și mai util. Funcționează bine mai ales în problemele cu dovezi. Adesea, cu ajutorul lui, chiar și problemele olimpiadelor sunt rezolvate frumos, ușor și rapid.

Teorema 2(Teorema inversă a lui Menelaus). Fie dat triunghiul ABC și punctele D, E, F aparțin, respectiv, dreptelor BC, AC, AB (rețineți că ele pot fi situate atât pe laturile triunghiului ABC, cât și pe prelungirile lor) (Fig. 4).

Atunci dacă AF FC * CE EB * BD DA = 1

atunci punctele D, E, F se află pe aceeași dreaptă.

Dovada. Să demonstrăm teorema prin contradicție. Să presupunem că relația din condiția teoremei este satisfăcută, dar punctul F nu se află pe dreapta DE (Fig. 5).

Să notăm punctul de intersecție al dreptelor DE și AB cu litera O. Acum aplicăm teorema lui Menelaus și obținem: AE EC * CD DB * BO OA = 1

Dar, pe de altă parte, egalitatea BF FA = BO OA

nu poate fi executat.

Prin urmare, relația din condiția teoremei nu poate fi satisfăcută. Avem o contradicție.

Teorema a fost demonstrată.

site-ul, cu copierea integrală sau parțială a materialului, este necesară un link către sursă.