Teorema lui Pitagora spune:

Într-un triunghi dreptunghic, suma pătratelor catetelor este egală cu pătratul ipotenuzei:

a 2 + b 2 = c 2,

• Ași b- picioarele formând un unghi drept.
• Cu este ipotenuza triunghiului.

Formule ale teoremei lui Pitagora

• a = \sqrt(c^(2) - b^(2))
• b = \sqrt (c^(2) - a^(2))
• c = \sqrt (a^(2) + b^(2))

Dovada teoremei lui Pitagora

Aria unui triunghi dreptunghic se calculează cu formula:

S = \frac(1)(2)ab

Pentru a calcula aria unui triunghi arbitrar, formula ariei este:

• p- semiperimetrul. p=\frac(1)(2)(a+b+c),
• r este raza cercului înscris. Pentru un dreptunghi r=\frac(1)(2)(a+b-c).

Apoi echivalăm părțile drepte ale ambelor formule pentru aria unui triunghi:

\frac(1)(2) ab = \frac(1)(2)(a+b+c) \frac(1)(2)(a+b-c)

2 ab = (a+b+c) (a+b-c)

2 ab = \left((a+b)^(2) -c^(2) \right)

2ab = a^(2)+2ab+b^(2)-c^(2)

0=a^(2)+b^(2)-c^(2)

c^(2) = a^(2)+b^(2)

Teorema inversă a lui Pitagora:

Dacă pătratul unei laturi a unui triunghi este egal cu suma pătratelor celorlalte două laturi, atunci triunghiul este un triunghi dreptunghic. Adică pentru orice triplu de numere pozitive a, bși c, astfel încât

a 2 + b 2 = c 2,

există un triunghi dreptunghic cu catete Ași b si ipotenuza c.

teorema lui Pitagora- una dintre teoremele fundamentale ale geometriei euclidiene, stabilind relaţia dintre laturile unui triunghi dreptunghic. A fost dovedit de savantul matematician și filozoful Pitagora.

Sensul teoremei prin aceea că poate fi folosit pentru a demonstra alte teoreme și pentru a rezolva probleme.

Material suplimentar:

Este remarcabil faptul că proprietatea indicată în teorema lui Pitagora este o proprietate caracteristică unui triunghi dreptunghic. Aceasta rezultă dintr-o teoremă inversă la teorema lui Pitagora.

Teoremă: Dacă pătratul unei laturi a unui triunghi este egal cu suma pătratelor celorlalte două laturi, atunci triunghiul este un triunghi dreptunghic.

Formula lui Heron

Obținem o formulă care exprimă planul unui triunghi în funcție de lungimile laturilor sale. Această formulă este asociată cu numele de Heron din Alexandria, un matematician și mecanic grec antic care probabil a trăit în secolul I d.Hr. Heron a acordat multă atenție aplicațiilor practice ale geometriei.

Teorema. Aria S a unui triunghi ale cărui laturi sunt a, b, c se calculează prin formula S=, unde p este semiperimetrul triunghiului.

Dovada.

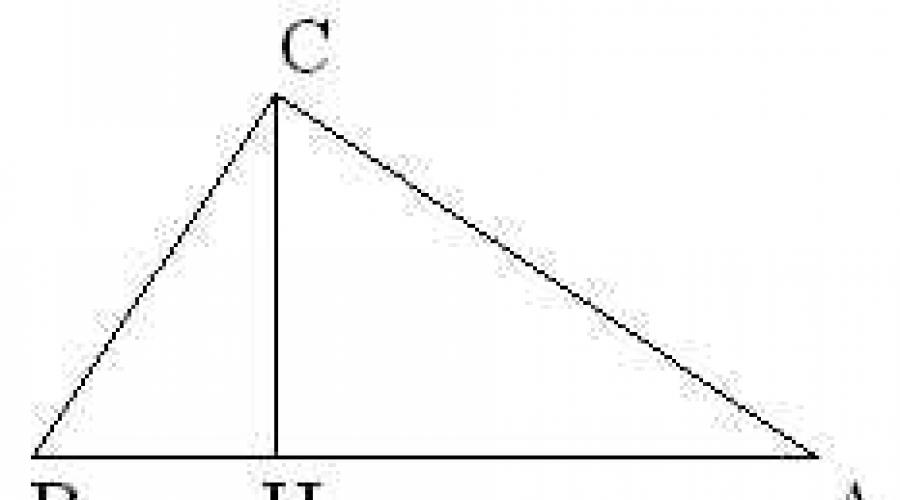
Dat: ?ABC, AB=c, BC=a, AC=b. Unghiurile A si B sunt acute. CH - înălțime.

Dovedi:

Dovada:

Să considerăm un triunghi ABC în care AB=c , BC=a, AC=b. Fiecare triunghi are cel puțin două unghiuri ascuțite. Fie A și B unghiuri ascuțite ale triunghiului ABC. Atunci baza H a înălțimii CH a triunghiului se află pe latura AB. Să introducem notația: CH = h, AH=y, HB=x. conform teoremei lui Pitagora a 2 - x 2 \u003d h 2 \u003d b 2 -y 2, de unde

Y 2 - x 2 \u003d b 2 - a 2 sau (y - x) (y + x) \u003d b 2 - a 2, iar din moment ce y + x \u003d c, atunci y- x \u003d (b2 - a2).

Adunând ultimele două egalități, obținem:

2y = +c, de unde

y \u003d și, prin urmare, h 2 \u003d b 2 -y 2 \u003d (b - y) (b + y) \u003d

Obiectivele lecției:

educatie generala:

• verificarea cunoștințelor teoretice ale elevilor (proprietățile unui triunghi dreptunghic, teorema lui Pitagora), capacitatea de a le folosi în rezolvarea problemelor;
• după ce a creat o situație problemă, aduceți elevii la „descoperirea” teoremei lui Pitagora inversă.

în curs de dezvoltare:

• dezvoltarea abilităților de aplicare a cunoștințelor teoretice în practică;
• dezvoltarea capacității de a formula concluzii în timpul observațiilor;
• dezvoltarea memoriei, a atenției, a observației:
• dezvoltarea motivaţiei învăţării prin satisfacţia emoţională din descoperiri, prin introducerea unor elemente de istorie a dezvoltării conceptelor matematice.

educational:

• să cultive un interes constant pentru subiect prin studiul vieții lui Pitagora;
• promovarea asistenței reciproce și a evaluării obiective a cunoștințelor colegilor de clasă prin evaluarea colegilor.

Forma lecție: clasă-lecție.

Planul lecției:

• Organizarea timpului.
• Verificarea temelor. Actualizare de cunoștințe.
• Rezolvarea problemelor practice folosind teorema lui Pitagora.
• Subiect nou.
• Consolidarea primară a cunoștințelor.
• Teme pentru acasă.
• Rezultatele lecției.
• Muncă independentă (conform cardurilor individuale cu ghicirea aforismelor lui Pitagora).

În timpul orelor.

Organizarea timpului.

Verificarea temelor. Actualizare de cunoștințe.

Profesor: Ce sarcină ai făcut acasă?

Elevi: Având în vedere două laturi ale unui triunghi dreptunghic, găsiți a treia latură, aranjați răspunsurile sub forma unui tabel. Repetați proprietățile unui romb și ale unui dreptunghi. Repetați ceea ce se numește condiție și care este concluzia teoremei. Pregătiți rapoarte despre viața și opera lui Pitagora. Aduceți o frânghie cu 12 noduri legate de ea.

Profesor: Verificați răspunsurile la teme conform tabelului

(datele sunt cu negru, răspunsurile sunt cu roșu).

Profesor: Declarațiile sunt scrise pe tablă. Dacă sunteți de acord cu ei pe foile de hârtie vizavi de numărul de întrebare corespunzător, puneți „+”, dacă nu sunteți de acord, puneți „-”.

Declarațiile sunt scrise pe tablă.

1. Ipotenuza este mai mare decât catetul.
2. Suma unghiurilor ascuțite ale unui triunghi dreptunghic este 180 0 .
3. Aria unui triunghi dreptunghic cu catete Ași în calculat prin formula S=ab/2.
4. Teorema lui Pitagora este valabilă pentru toate triunghiurile isoscele.
5. Într-un triunghi dreptunghic, catetul opus unghiului 30 0 este egal cu jumătate din ipotenuză.
6. Suma pătratelor catetelor este egală cu pătratul ipotenuzei.
7. Pătratul catetei este egal cu diferența dintre pătratele ipotenuzei și al doilea catet.
8. Latura unui triunghi este egală cu suma celorlalte două laturi.

Lucrările sunt verificate prin evaluarea colegială. Se discută declarații controversate.

Cheia întrebărilor teoretice.

Elevii se evaluează reciproc conform următorului sistem:

8 răspunsuri corecte „5”;
6-7 răspunsuri corecte „4”;
4-5 răspunsuri corecte „3”;
mai puțin de 4 răspunsuri corecte „2”.

Profesor: Despre ce am vorbit în ultima lecție?

Student: Despre Pitagora și teorema lui.

Profesor: Formulați teorema lui Pitagora. (mai mulți elevi citesc formularea, în acest moment 2-3 elevi o dovedesc la tablă, 6 elevi la primele mese de pe foi).

Pe tablă magnetică de pe carduri sunt scrise formule matematice. Alegeți-le pe cele care reflectă sensul teoremei lui Pitagora, unde A și în - catetere, Cu - ipotenuza.

În timp ce studenții care demonstrează teorema la tablă și pe teren nu sunt pregătiți, cuvântul este dat celor care au pregătit rapoarte despre viața și opera lui Pitagora.

Școlarii care lucrează la câmp predau pliante și ascultă dovezile celor care au lucrat la tablă.

Profesor: Vă ofer sarcini practice folosind teorema studiată. Vom vizita mai întâi pădurea, după furtună, apoi în mediul rural.

Sarcina 1. După furtună, molidul s-a rupt. Înălțimea părții rămase este de 4,2 m. Distanța de la bază până la vârful căzut este de 5,6 m. Aflați înălțimea molidului înainte de furtună.

Sarcina 2. Înălțimea casei este de 4,4 m. Lățimea gazonului din jurul casei este de 1,4 m. Cât de lungă trebuie făcută scara astfel încât să nu calce pe gazon și să ajungă pe acoperișul casei?

Profesor:(se aude muzica)Închideți ochii, pentru câteva minute ne vom cufunda în istorie. Suntem cu tine în Egiptul Antic. Aici, în șantierele navale, egiptenii își construiesc faimoasele corăbii. Dar topografii măsoară loturi de pământ ale căror limite au fost spălate după inundația Nilului. Constructorii construiesc piramide grandioase care încă ne uimesc prin măreția lor. În toate aceste activități, egiptenii trebuiau să folosească unghiuri drepte. Au știut să le construiască folosind o frânghie cu 12 noduri legate la aceeași distanță unul de celălalt. Încearcă și tu, certându-te ca vechii egipteni, construiești triunghiuri dreptunghiulare cu ajutorul funiilor tale. (Rezolvând această problemă, băieții lucrează în grupuri de 4 persoane. După un timp, cineva arată construcția unui triunghi pe tabletă la tablă).

Laturile triunghiului rezultat sunt 3, 4 și 5. Dacă mai legați un nod între aceste noduri, atunci laturile sale vor deveni 6, 8 și 10. Dacă două fiecare - 9, 12 și 15. Toate aceste triunghiuri sunt dreptunghiulare deoarece .

5 2 \u003d 3 2 + 4 2, 10 2 \u003d 6 2 + 8 2, 15 2 \u003d 9 2 + 12 2 etc.

Ce proprietate trebuie să aibă un triunghi pentru a fi un triunghi dreptunghic? (Elevii încearcă să formuleze ei înșiși teorema lui Pitagora inversă, în cele din urmă, cineva reușește).

Cum este această teoremă diferită de teorema lui Pitagora?

Student: Condiția și concluzia sunt inversate.

Profesor: Acasă, ai repetat cum se numesc astfel de teoreme. Deci ce facem acum?

Student: Cu teorema inversă a lui Pitagora.

Profesor: Notează subiectul lecției în caiet. Deschideți manualele de la pagina 127, citiți din nou această afirmație, notați-o în caiet și analizați dovada.

(După câteva minute de lucru independent cu manualul, dacă se dorește, o persoană de la tablă dă o dovadă a teoremei).

1. Cum se numește un triunghi cu laturile 3, 4 și 5? De ce?
2. Ce triunghiuri se numesc triunghiuri pitagorice?
3. Cu ce ​​triunghiuri ai lucrat la teme? Și în probleme cu un pin și o scară?

Această teoremă ajută la rezolvarea problemelor în care este necesar să se afle dacă triunghiurile sunt triunghiuri dreptunghiulare.

Sarcini:

1) Aflați dacă un triunghi este dreptunghic dacă laturile sale sunt egale:

a) 12,37 și 35; b) 21, 29 și 24.

2) Calculați înălțimile unui triunghi cu laturile de 6, 8 și 10 cm.

Pagina 127: Teorema lui Pitagora inversă. Nr. 498 (a, b, c) Nr. 497.

Muncă independentă (desfășurată pe carduri individuale).

Profesor: Acasă, ai repetat proprietățile unui romb și ale unui dreptunghi. Enumerați-le (există o conversație cu clasa). În ultima lecție, am vorbit despre faptul că Pitagora era o persoană versatilă. S-a angajat în medicină, muzică și astronomie, a fost, de asemenea, un atlet și a participat la Jocurile Olimpice. Pitagora a fost și filosof. Multe dintre aforismele sale sunt și astăzi relevante pentru noi. Acum îți vei face singur treaba. Pentru fiecare sarcină se dau mai multe răspunsuri, lângă care sunt scrise fragmente de aforisme pitagorice. Sarcina ta este să rezolvi toate sarcinile, să faci o declarație din fragmentele primite și să o notezi.

Obiectivele lecției:

Educativ: formulați și demonstrați teorema lui Pitagora și inversul teoremei lui Pitagora. Arătați semnificația lor istorică și practică.

Dezvoltare: pentru a dezvolta atenția, memoria, gândirea logică a elevilor, capacitatea de a raționa, de a compara, de a trage concluzii.

Educativ: pentru a cultiva interesul și dragostea pentru subiect, acuratețea, capacitatea de a asculta camarazi și profesori.

Dotare: Portretul lui Pitagora, postere cu sarcini de consolidare, manual „Geometrie” clasele 7-9 (I.F. Sharygin).

Planul lecției:

I. Moment organizatoric - 1 min.

II. Verificarea temelor - 7 min.

III. Discurs introductiv al profesorului, context istoric - 4-5 min.

IV. Formularea și demonstrarea teoremei lui Pitagora - 7 min.

V. Formularea și demonstrarea teoremei inverse la teorema lui Pitagora - 5 min.

Fixarea materialului nou:

a) orală - 5-6 minute.
b) scris - 7-10 min.

VII. Tema pentru acasă - 1 min.

VIII. Rezumatul lecției - 3 min.

În timpul orelor

I. Moment organizatoric.

II. Verificarea temelor.

p.7.1, Nr.3 (la tablă conform desenului finit).

Condiție: Înălțimea unui triunghi dreptunghic împarte ipotenuza în segmente de lungime 1 și 2. Aflați catetele acestui triunghi.

BC = a; CA=b; BA=c; BD = a 1 ; DA = b 1 ; CD = hC

Întrebare suplimentară: notează rapoartele într-un triunghi dreptunghic.

itemul 7.1, nr. 5. Tăiați triunghiul dreptunghic în trei triunghiuri asemănătoare unul cu celălalt.

Explica.

ASN ~ ABC ~ SVN

(atrageți atenția elevilor asupra înregistrării corecte a vârfurilor corespunzătoare ale triunghiurilor similare)

Adevărul va rămâne etern, de îndată ce o persoană slabă îl va ști!

Și acum teorema lui Pitagora este adevărată, ca în epoca lui îndepărtată.

Nu întâmplător mi-am început lecția cu cuvintele romancierului german Chamisso. Lecția noastră de astăzi este despre teorema lui Pitagora. Să scriem subiectul lecției.

În fața ta este un portret al marelui Pitagora. Născut în 576 î.Hr. După ce a trăit 80 de ani, a murit în 496 î.Hr. Cunoscut ca filozof și profesor grec antic. Era fiul negustorului Mnesarchus, care îl ducea adesea în călătoriile sale, datorită cărora băiatul a dezvoltat curiozitatea și dorința de a învăța lucruri noi. Pitagora este o poreclă dată lui pentru elocvența sa („Pythagoras” înseamnă „vorbire persuasivă”). El însuși nu a scris nimic. Toate gândurile lui au fost înregistrate de studenții săi. Ca urmare a primei prelegeri pe care a ținut-o, Pitagora a dobândit 2.000 de elevi care, împreună cu soțiile și copiii lor, au format o școală uriașă și au creat un stat numit „Marea Grecie”, care se bazează pe legile și regulile lui Pitagora, venerat ca porunci divine. El a fost primul care a numit raționamentul său despre sensul vieții filozofie (filosofie). Era predispus la mistificare și comportament demonstrativ. Odată, Pitagora s-a ascuns în subteran și a aflat despre tot ce se întâmpla de la mama lui. Apoi, ofilit ca un schelet, el a declarat în adunarea publică că a fost în Hades și a arătat o conștientizare uimitoare a evenimentelor pământești. Pentru aceasta, locuitorii atinși l-au recunoscut drept Dumnezeu. Pitagora nu a plâns niciodată și era în general inaccesibil pasiunilor și entuziasmului. El credea că provine dintr-o sămânță care este mai bună în comparație cu umanul. Întreaga viață a lui Pitagora este o legendă care a ajuns până la vremea noastră și ne-a vorbit despre cel mai talentat om al lumii antice.

Formularea teoremei lui Pitagora vă este cunoscută din cursul de algebră. Să ne amintim de ea.

Într-un triunghi dreptunghic, pătratul ipotenuzei este egal cu suma pătratelor catetelor.

Cu toate acestea, această teoremă era cunoscută cu mulți ani înainte de Pitagora. Cu 1500 de ani înainte de Pitagora, vechii egipteni știau că un triunghi cu laturile 3, 4 și 5 este dreptunghiular și au folosit această proprietate pentru a construi unghiuri drepte atunci când planificau terenuri și construiau clădiri. În cea mai veche lucrare chineză de matematică și astronomie care a ajuns până la noi, „Zhiu-bi”, scrisă cu 600 de ani înainte de Pitagora, printre alte propoziții legate de un triunghi dreptunghic, este conținută și teorema lui Pitagora. Chiar și mai devreme, această teoremă era cunoscută hindușilor. Astfel, Pitagora nu a descoperit această proprietate a unui triunghi dreptunghic; el a fost probabil primul care a generalizat-o și a dovedit-o, care a transferat-o din domeniul practicii în domeniul științei.

Din cele mai vechi timpuri, matematicienii au găsit din ce în ce mai multe dovezi ale teoremei lui Pitagora. Sunt peste o sută cincizeci cunoscute. Să ne amintim demonstrația algebrică a teoremei lui Pitagora, cunoscută nouă din cursul algebrei. („Matematică. Algebră. Funcții. Analiza datelor” G.V. Dorofeev, M., „Bubblehead”, 2000).

Invitați elevii să-și amintească dovada desenului și să o scrie pe tablă.

(a + b) 2 \u003d 4 1/2 a * b + c 2 b a

a 2 + 2a * b + b 2 \u003d 2a * b + c 2

a 2 + b 2 = c 2 a a b

Vechii hinduși, cărora le aparține acest raționament, de obicei nu l-au notat, ci au însoțit desenul cu un singur cuvânt: „Uite”.

Să considerăm într-o prezentare modernă una dintre dovezile aparținând lui Pitagora. La începutul lecției, ne-am amintit teorema raporturilor într-un triunghi dreptunghic:

h 2 \u003d a 1 * b 1 a 2 \u003d a 1 * c b 2 \u003d b 1 * c

Adăugăm ultimele două egalități termen cu termen:

b 2 + a 2 \u003d b 1 * c + a 1 * c \u003d (b 1 + a 1) * c 1 \u003d c * c \u003d c 2; a 2 + b 2 = c 2

În ciuda simplității aparente a acestei dovezi, este departe de a fi cea mai simplă. La urma urmei, pentru aceasta a fost necesar să se deseneze o înălțime într-un triunghi dreptunghic și să se ia în considerare triunghiuri similare. Vă rugăm să notați această dovadă în caiet.

Care este inversul acestei teoreme? (... dacă condiția și concluzia sunt inversate.)

Să încercăm acum să formulăm teorema, inversul teoremei lui Pitagora.

Dacă într-un triunghi cu laturile a, b și c egalitatea cu 2 \u003d a 2 + b 2 este adevărată, atunci acest triunghi este dreptunghic, iar unghiul drept este opus laturii c.

(Demonstrarea teoremei inverse pe un afiș)

ABC, BC = a,

AC = b, BA = c.

a 2 + b 2 = c 2

Dovedi:

ABC - dreptunghiular,

Dovada:

Considerăm un triunghi dreptunghic A 1 B 1 C 1,

unde C 1 \u003d 90 °, A 1 C 1 \u003d a, A 1 C 1 \u003d b.

Apoi, conform teoremei lui Pitagora, B 1 A 1 2 \u003d a 2 + b 2 \u003d c 2.

Adică B 1 A 1 \u003d c A 1 B 1 C 1 \u003d ABC pe trei laturi ale ABC - dreptunghiular

C = 90°, ceea ce trebuia demonstrat.

1. Conform afișului cu desene gata făcute.

Fig.1: găsiți AD dacă BD = 8, BDA = 30°.

Fig. 2: găsiți CD dacă BE = 5, BAE = 45°.

Fig. 3: găsiți BD dacă BC = 17, AD = 16.

2. Este un triunghi dreptunghic dacă laturile sale sunt exprimate prin numere:

Cum se numesc triplele numerelor din ultimele două cazuri? (Pitagorean).

Nr. 9. Latura unui triunghi echilateral este egală cu a. Aflați înălțimea acestui triunghi, raza cercului circumscris, raza cercului înscris.

№ 14. Demonstrați că într-un triunghi dreptunghic raza cercului circumscris este egală cu mediana trasată la ipotenuză și egală cu jumătate din ipotenuză.

Punctul 7.1, pp. 175-177, analiza Teorema 7.4 (teorema lui Pitagora generalizată), nr. 1 (oral), nr. 2, nr. 4.

Ce nou ai învățat la lecția de astăzi? …………

Pitagora a fost în primul rând un filozof. Acum vreau să vă citesc câteva dintre spusele lui, care sunt relevante în timpul nostru pentru tine și pentru mine.

• Nu ridicați praf pe calea vieții.
• Fă doar ceea ce în viitor nu te va supăra și nu te va forța să te pocăiești.
• Nu face niciodată ceea ce nu știi, ci învață tot ce trebuie să știi și atunci vei duce o viață liniștită.
• Nu închide ochii când vrei să dormi fără să înțelegi toate acțiunile tale din ziua precedentă.
• Învață să trăiești simplu și fără lux.