Somme des angles opposés d'un quadrilatère inscrit dans un cercle. Quadrilatère inscrit

Un quadrilatère est inscrit dans un cercle si tous ses sommets se trouvent sur le cercle. Un tel cercle est circonscrit à un quadrilatère.

Tout comme tous les quadrilatères ne peuvent pas être décrits autour d’un cercle, tous les quadrilatères ne peuvent pas non plus être inscrits dans un cercle.

Un quadrilatère convexe inscrit dans un cercle a la propriété que ses angles opposés totalisent 180°. Ainsi, si l’on donne un quadrilatère ABCD, dans lequel l’angle A est opposé à l’angle C et l’angle B est opposé à l’angle D, alors ∠A + ∠C = 180° et ∠B + ∠D = 180°.

En général, si une paire d’angles opposés d’un quadrilatère totalise 180°, alors l’autre paire totalise le même montant. Cela découle du fait que dans un quadrilatère convexe la somme des angles est toujours égale à 360°. Ce fait découle à son tour du fait que pour les polygones convexes, la somme des angles est déterminée par la formule 180° * (n – 2), où n est le nombre d'angles (ou de côtés).

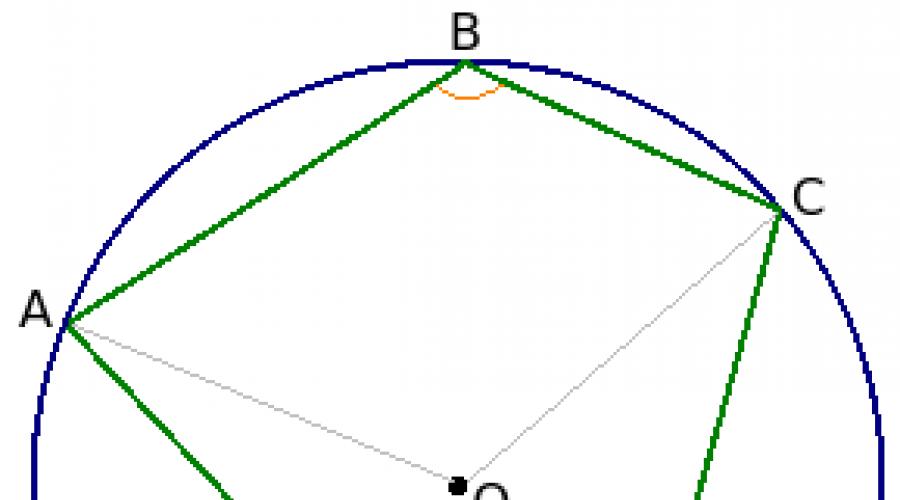
Vous pouvez prouver la propriété d'un quadrilatère inscrit de la manière suivante. Soit un quadrilatère ABCD inscrit dans le cercle O. Nous devons prouver que ∠B + ∠D = 180°.

L'angle B est inscrit dans un cercle. Comme vous le savez, un tel angle est égal à la moitié de l'arc sur lequel il repose. Dans ce cas, l'angle B est supporté par l'arc ADC, ce qui signifie ∠B = ½◡ADC. (Puisque l'arc est égal à l'angle entre les rayons qui le forment, on peut écrire que ∠B = ½∠AOC, dont la région intérieure contient le point D.)

Par contre, l'angle D du quadrilatère repose sur l'arc ABC, c'est-à-dire ∠D = ½◡ABC.

Puisque les côtés des angles B et D coupent le cercle aux mêmes points (A et C), ils divisent le cercle en seulement deux arcs - ◡ADC et ◡ABC. Puisqu’un cercle complet totalise 360°, alors ◡ADC + ◡ABC = 360°.

Ainsi, les égalités suivantes ont été obtenues :

∠B = ½◡ADC
∠D = ½◡ABC
◡ADC + ◡ABC = 360°

Exprimons la somme des angles :

∠B + ∠D = ½◡ADC + ½◡ABC

Mettons ½ entre parenthèses :

∠B + ∠D = ½(◡ADC + ◡ABC)

Remplaçons la somme des arcs par leur valeur numérique :

∠B + ∠D = ½ * 360° = 180°

Nous avons constaté que la somme des angles opposés d’un quadrilatère inscrit est de 180°. C’était ce qu’il fallait prouver.

Le fait qu'un quadrilatère inscrit possède cette propriété (la somme des angles opposés est de 180°) ne signifie pas que tout quadrilatère dont la somme des angles opposés est de 180° peut être inscrit dans un cercle. Même si en réalité cela est vrai. Ce fait est appelé test du quadrilatère inscrit et se formule ainsi : si la somme des angles opposés d'un quadrilatère convexe est de 180°, alors un cercle peut être décrit autour de lui (ou inscrit dans un cercle).

Vous pouvez prouver le test d’un quadrilatère inscrit par contradiction. Soit un quadrilatère ABCD dont les angles opposés B et D totalisent 180°. Dans ce cas, l’angle D ne se trouve pas sur le cercle. Prenez ensuite un point E sur la droite contenant le segment CD tel qu'il repose sur le cercle. Le résultat est un quadrilatère cyclique ABCE. Ce quadrilatère a des angles opposés B et E, ce qui signifie qu'ils totalisent 180°. Cela découle de la propriété d’un quadrilatère inscrit.

Il s’avère que ∠B + ∠D = 180° et ∠B + ∠E = 180°. Or l'angle D du quadrilatère ABCD par rapport au triangle AED est extérieur, et donc supérieur à l'angle E de ce triangle. Nous sommes donc arrivés à une contradiction. Cela signifie que si la somme des angles opposés d’un quadrilatère totalise 180°, alors il peut toujours être inscrit dans un cercle.

Le cours vidéo « Obtenez un A » comprend tous les sujets nécessaires pour réussir l'examen d'État unifié en mathématiques avec 60 à 65 points. Complètement tous les problèmes 1-13 Profil Examen d'État unifié mathématiques. Convient également pour réussir l'examen d'État unifié de base en mathématiques. Si vous souhaitez réussir l'examen d'État unifié avec 90 à 100 points, vous devez résoudre la partie 1 en 30 minutes et sans erreurs !

Cours de préparation à l'examen d'État unifié pour les classes 10-11, ainsi que pour les enseignants. Tout ce dont vous avez besoin pour résoudre la partie 1 de l'examen d'État unifié en mathématiques (les 12 premiers problèmes) et le problème 13 (trigonométrie). Et cela représente plus de 70 points à l'examen d'État unifié, et ni un étudiant de 100 points ni un étudiant en sciences humaines ne peuvent s'en passer.

Toute la théorie nécessaire. Moyens rapides solutions, pièges et secrets de l'examen d'État unifié. Toutes les tâches actuelles de la partie 1 de la banque de tâches FIPI ont été analysées. Le cours est entièrement conforme aux exigences de l'examen d'État unifié 2018.

Le cours contient 5 grands sujets de 2,5 heures chacun. Chaque sujet est donné de toutes pièces, simplement et clairement.

Des centaines de tâches d'examen d'État unifié. Problèmes de mots et théorie des probabilités. Algorithmes simples et faciles à retenir pour résoudre des problèmes. Géométrie. Théorie, matériel de référence, analyse de tous types de tâches d'examen d'État unifié. Stéréométrie. Astuces délicates solutions, aide-mémoire utiles, développement de l'imagination spatiale. Trigonométrie de zéro au problème 13. Comprendre au lieu de bachoter. Explications claires de concepts complexes. Algèbre. Racines, puissances et logarithmes, fonction et dérivée. Base de solution tâches complexes 2 parties de l'examen d'État unifié.

Matériel de Wikipédia - l'encyclopédie gratuite

• En géométrie euclidienne, quadrilatère inscrit est un quadrilatère dont les sommets se trouvent tous sur le même cercle. Ce cercle s'appelle cercle circonscrit quadrilatère, et on dit que les sommets se trouvent sur le même cercle. Le centre de ce cercle et son rayon sont appelés respectivement centre Et rayon cercle circonscrit. Autres termes pour ce quadrilatère : un quadrilatère repose sur un cercle, les côtés du dernier quadrilatère sont des cordes du cercle. Un quadrilatère convexe est généralement considéré comme un quadrilatère convexe. Les formules et propriétés données ci-dessous sont valables dans le cas convexe.
• Ils disent que si un cercle peut être tracé autour d'un quadrilatère, Que le quadrilatère est inscrit dans ce cercle, et vice versa.

Critères généraux pour l'inscription d'un quadrilatère

• Autour d'un quadrilatère convexe $\backslash pi$ radians), soit :

$\backslash angle\; A+\backslash angle\; C\; =\; \backslash angle\; B\; +\; \backslash angle\; D\; =\; 180^\backslash circ$

ou dans la notation des figures :

$\backslash alpha\; +\; \backslash gamma\; =\; \backslash beta\; +\; \backslash delta\; =\; \backslash pi\; =\; 180^(\backslash circ).$

• Il est possible de décrire un cercle autour de n'importe quel quadrilatère dans lequel les quatre bissectrices perpendiculaires de ses côtés se coupent en un point (ou médiatrices de ses côtés, c'est-à-dire les perpendiculaires aux côtés passant par leurs milieux).
• Vous pouvez décrire un cercle autour de n’importe quel quadrilatère qui en possède un coin extérieur, adjacente à angle interne donné, est exactement égal à l’autre angle intérieur opposé coin interne donné. Essentiellement, cette condition est la condition d’antiparallélisme de deux côtés opposés du quadrilatère. En figue. Ci-dessous se trouvent les coins extérieurs et intérieurs adjacents d’un pentagone vert.

$\backslash displaystyle\; AX\backslash cdot\; XC\; =\; BX\backslash cdot\; XD.$

• Intersection X peut être interne ou externe au cercle. Dans le premier cas, on obtient le quadrilatère cyclique soit A B C D, et dans ce dernier cas on obtient un quadrilatère inscrit ABDC. Lors d'une intersection à l'intérieur d'un cercle, l'égalité indique que le produit des longueurs des segments dans lesquels le point X divise une diagonale, est égal au produit des longueurs des segments dans lesquels le point X divise une autre diagonale. Cette condition est connue sous le nom de « théorème des accords d’intersection ». Dans notre cas, les diagonales du quadrilatère inscrit sont les cordes du cercle.
• Un autre critère d'inclusion. Quadrilatère convexe A B C D un cercle est inscrit si et seulement si

$\backslash tan(\backslash frac(\backslash alpha)(2))\backslash tan(\backslash frac(\backslash gamma)(2))=\backslash tan(\backslash frac(\backslash beta)(2))\backslash tan(\backslash frac(\backslash delta)(\; 2))=1.$

Critères particuliers pour l'inscription d'un quadrilatère

Un quadrilatère simple inscrit (sans auto-intersection) est convexe. Un cercle peut être décrit autour d'un quadrilatère convexe si et seulement si la somme de ses angles opposés est égale à 180° ( $\backslash pi$ radian). Vous pouvez décrire un cercle autour de :

• tout antiparallélogramme
• n'importe quel rectangle (un cas particulier est un carré)
• tout trapèze isocèle
• tout quadrilatère qui a deux angles droits opposés.

Propriétés

Formules avec diagonales

$ef=ac+bd$; $\backslash frac(e)(f)\; =\; \backslash frac(a\backslash cdot\; d+b\backslash cdot\; c)(a\backslash cdot\; b+c\backslash cdot\; d).$

Dans la dernière formule du couple côtés adjacents numérateur un Et d, b Et c reposent leurs extrémités sur une longueur diagonale e. Une affirmation similaire vaut pour le dénominateur.

• Formules pour les longueurs diagonales(conséquences ):

$e\; =\; \backslash sqrt(\backslash frac((ac+bd)(ad+bc))(ab+cd))$ Et $f\; =\; \backslash sqrt(\backslash frac((ac+bd)(ab+cd))(ad+bc))$

Formules avec angles

Pour un quadrilatère cyclique avec une séquence de côtés un , b , c , d, avec demi-périmètre p et angle UN entre les parties un Et d, fonctions d'angle trigonométrique UN sont donnés par des formules

$\backslash cos\; A\; =\; \backslash frac(a^2\; +\; d^2\; -\; b^2\; -\; c^2)(2(ad\; +\; bc)),$ $\backslash sin\; A\; =\; \backslash frac(2\backslash sqrt((p-a)(p-b)(p-c)(p-d)))((ad+bc)),$ $\backslash tan\; \backslash frac(A)(2)\; =\; \backslash sqrt(\backslash frac((p-a)(p-d))((p-b)(p-c))).$

Coin θ entre les diagonales il y a :p.26

$\backslash tan\; \backslash frac(\backslash theta)(2)\; =\; \backslash sqrt(\backslash frac((p-b)(p-d))((p-a)(p-c))).$

• Si côtés opposés un Et c se croisent sous un angle φ , alors c'est égal

$\backslash cos(\backslash frac(\backslash varphi)(2))=\backslash sqrt(\backslash frac((p-b)(p-d)(b+d)^2)((ab+cd)(ad+bc))),$

Où p il y a un demi-périmètre. :p.31

Rayon d'un cercle circonscrit à un quadrilatère

Formule Parameshvara

Si un quadrilatère avec des côtés consécutifs un , b , c , d et demi-périmètre p inscrit dans un cercle, alors son rayon est égal à La formule de Parameshwar:p. 84

$R=\; \backslash frac(1)(4)\; \backslash sqrt(\backslash frac((ab+cd)(ad+bc)(ac+bd))((p-a)(p-b)(p-c)(p-d))).$

Il a été dérivé par le mathématicien indien Parameshwar au XVe siècle (vers 1380-1460).

• Quadrilatère convexe (voir figure de droite) formé de quatre données Les lignes droites de Mikel, est inscrit dans un cercle si et seulement si le point Mikel M d'un quadrilatère se trouve sur une ligne reliant deux des six points d'intersection des lignes (ceux qui ne sont pas des sommets du quadrilatère). C'est quand M se trouve sur E.F..

Un critère selon lequel un quadrilatère composé de deux triangles est inscrit dans un certain cercle

$f^2\; =\; \backslash frac((ac+bd)(ad+bc))((ab+cd)).$

• La dernière condition donne l'expression de la diagonale F un quadrilatère inscrit dans un cercle par la longueur de ses quatre côtés ( un, b, c, d). Cette formule suit immédiatement en multipliant et en assimilant les parties gauche et droite des formules exprimant l'essence Premier et deuxième théorèmes de Ptolémée(voir au dessus).

Un critère selon lequel un quadrilatère coupé par une droite à partir d'un triangle est inscrit dans un certain cercle

• Une ligne droite antiparallèle au côté du triangle et le coupant en coupe un quadrilatère, autour duquel un cercle peut toujours être décrit.
• Conséquence. Autour d'un antiparallélogramme, dans lequel deux côtés opposés sont antiparallèles, il est toujours possible de décrire un cercle.

Aire d'un quadrilatère inscrit dans un cercle

Variations de la formule de Brahmagupta

$S=\backslash sqrt((p-a)(p-b)(p-c)(p-d)),$ où p est le demi-périmètre du quadrilatère. $S=\; \backslash frac(1)(4)\; \backslash sqrt(-\; \backslash begin(vmatrix)$

a & b & c & -d \\ b & a & -d & c \\ c & -d & a & b \\ -d & c & b & a \end(vmatrix))

Autres formules de zones

$S\; =\; \backslash tfrac(1)(2)(ab+cd)\backslash sin(B)$ $S\; =\; \backslash tfrac(1)(2)(ac+bd)\backslash sin(\backslash theta),$

Où θ n'importe lequel des angles entre les diagonales. À condition que l'angle UN n'est pas une ligne droite, l'aire peut aussi être exprimée comme suit :p.26

$S\; =\; \backslash tfrac(1)(4)(a^2-b^2-c^2+d^2)\backslash tan(A).$ $\backslash \; displaystyle\; S\; =\; 2R\; ^\; 2\; \backslash \; sin\; (A)\; \backslash \; sin\; (B)\; \backslash \; sin\; (\backslash \; theta),$

Où R. est le rayon du cercle circonscrit. En conséquence directe, nous avons l'inégalité

$S\backslash le\; 2R^2,$

où l’égalité est possible si et seulement si ce quadrilatère est un carré.

Quadrangles de Brahmagupta

Quadrangle Brahmagupta est un quadrilatère inscrit dans un cercle avec des longueurs de côtés entières, des diagonales entières et une aire entière. Tous les quadrilatères Brahmagupta possibles avec côtés un , b , c , d, avec des diagonales e , F, avec aire S, et le rayon du cercle circonscrit R. peut être obtenu en supprimant les dénominateurs des expressions suivantes impliquant des paramètres rationnels t , toi, Et v :

$une\; =$ $b=(1+u^2)(vt)(1+tv)$ $c=t(1+u^2)(1+v^2)$ $d=(1+v^2)(u-t)(1+tu)$ $e=u(1+t^2)(1+v^2)$ $f=v(1+t^2)(1+u^2)$ $S\; =\; uv$ $4R=(1+u^2)(1+v^2)(1+t^2).$

Exemples

• Les quadrilatères particuliers inscrits dans un cercle sont : rectangle, carré, trapèze isocèle ou isocèle, antiparallélogramme.

Quadrilatères inscrits dans un cercle à diagonales perpendiculaires (quadrilatères orthodiagonaux inscrits)

Propriétés des quadrilatères inscrits dans un cercle à diagonales perpendiculaires

Circonstance et superficie

Pour un quadrilatère inscrit dans un cercle à diagonales perpendiculaires, supposons que l'intersection des diagonales divise une diagonale en segments de longueur p 1 et p 2, et divise l'autre diagonale en segments de longueur q 1 et q 2. Alors (La première égalité est la proposition 11 d'Archimède" Livre des lemmes)

$D^2=p\_1^2+p\_2^2+q\_1^2+q\_2^2=a^2+c^2=b^2+d^2,$

Où D- diamètre du cercle. Cela est vrai car les diagonales sont perpendiculaires à la corde du cercle. De ces équations il résulte que le rayon du cercle circonscrit R. peut s'écrire comme

$R=\backslash tfrac(1)(2)\backslash sqrt(p\_1^2+p\_2^2+q\_1^2+q\_2^2)$

ou en termes de côtés d'un quadrilatère sous la forme

$R=\backslash tfrac(1)(2)\backslash sqrt(a^2+c^2)=\backslash tfrac(1)(2)\backslash sqrt(b^2+d^2).$

Il s'ensuit également que

$a^2+b^2+c^2+d^2=8R^2.$

• Pour les quadrilatères ordiagonaux inscrits, le théorème de Brahmagupta est valable :

Si un quadrilatère cyclique a des diagonales perpendiculaires se coupant en un point $M$, puis deux paires antimédiatre passer par un point $M$.

Commentaire. Dans ce théorème sous anti-médiatrice comprendre le segment $F.E.$ quadrilatère sur la figure de droite (par analogie avec la médiatrice perpendiculaire au côté du triangle). Il est perpendiculaire à un côté et passe en même temps par le milieu du côté opposé du quadrilatère.

Donnez votre avis sur l'article "Quadrilatères inscrits dans un cercle"

Remarques

1. Bradley, Christopher J. (2007), L'algèbre de la géométrie : coordonnées cartésiennes, surfaciques et projectives,Haute perception, p. 179, ISBN 1906338000, OCLC
2. . Quadrilatères inscrits.
3. Siddons, AW et Hughes, RT (1929) Trigonométrie, La Presse de l'Universite de Cambridge, p. 202, O.C.L.C.
4. Durell, CV et Robson, A. (2003), , Courrier Douvres, ISBN 978-0-486-43229-8 ,
5. Alsina, Claudi et Nelsen, Roger B. (2007), "", Forum Géométrique T. 7 : 147-9 ,
6. Johnson, Roger A., Géométrie euclidienne avancée, Dover Publ., 2007 (orig. 1929).
7. Hoehn, Larry (mars 2000), "Circonradius of a cyclic quadrilatère", Gazette mathématique T. 84 (499) : 69-70
8. .
9. Altshiller-Cour, Nathan (2007), Géométrie universitaire : une introduction à la géométrie moderne du triangle et du cercle(2e éd.), Courier Dover, p. 131, 137-8, ISBN 978-0-486-45805-2, OCLC
10. Honsberger, Ross (1995), , Épisodes de la géométrie euclidienne des XIXe et XXe siècles, vol. 37, Nouvelle bibliothèque mathématique, Cambridge University Press, pp. 35-39, ISBN978-0-88385-639-0
11. Weisstein, Éric W.(anglais) sur le site Web de Wolfram MathWorld.
12. Bradley, Christophe (2011), ,
13. .
14. Coxeter, Harold Scott MacDonald et Greitzer, Samuel L. (1967), , La géométrie revisitée, Association mathématique d'Amérique, pp. 57, 60, ISBN978-0-88385-619-2
15. .
16. Andreescu, Titu et Enescu, Bogdan (2004), , Trésors de l'Olympiade mathématique, Springer, p. 44-46, 50, ISBN978-0-8176-4305-8
17. .
18. Buchholz, RH et MacDougall, JA (1999), "", Bulletin de la Société mathématique australienne T. 59 (2) : 263-9 , DOI 10.1017/S0004972700032883
19. .
20. Johnson, Roger A., Géométrie euclidienne avancée, Douvres Pub. Cie, 2007
21. , Avec. 74.
22. .
23. .
24. .
25. Peter, Thomas (septembre 2003), "Maximiser l'aire d'un quadrilatère", Le journal de mathématiques du Collège T. 34 (4) : 315-6
26. Prasolov, Viktor, ,
27. Alsina, Claudi et Nelsen, Roger (2009), , , Association mathématique d'Amérique, p. 64, ISBN978-0-88385-342-9 ,
28. Sastry, K.R.S. (2002). "" (PDF). Forum Géométrique 2 : 167–173.
29. Posamentier, Alfred S. et Salkind, Charles T. (1970), , Problèmes difficiles en géométrie(2e éd.), Courier Dover, p. 104-5, ISBN978-0-486-69154-1
30. .
31. .
32. .

voir également

Par nombre de côtés Correct Triangles Quadrilatères voir également

L'article contient de courtes références (« Harvard ») à des publications qui ne sont pas répertoriées ou mal décrites dans la section bibliographique. Liste des liens rompus : , , , , , , , , , – Eh bien, quoi, mon cosaque ? (Marya Dmitrievna a appelé Natasha une cosaque) - a-t-elle dit en caressant Natasha avec sa main, qui s'est approchée de sa main sans crainte et joyeusement. - Je sais que la potion est une fille, mais je l'aime. Elle sortit de son énorme réticule des boucles d'oreilles yakhon en forme de poire et, les offrant à Natasha, qui rayonnait et rougissait pour son anniversaire, se détourna immédiatement d'elle et se tourna vers Pierre. - Eh, hein ! gentil! "Viens ici," dit-elle d'une voix feinte et mince. - Allez, ma chérie... Et elle a retroussé ses manches encore plus haut, d'un air menaçant. Pierre s'approcha, la regardant naïvement à travers ses lunettes. - Viens, viens, ma chérie ! J'étais le seul à avoir dit la vérité à ton père quand il en avait l'occasion, mais Dieu te l'ordonne. Elle fit une pause. Tout le monde était silencieux, attendant ce qui allait se passer et sentant qu'il n'y avait qu'une préface. - Bon, rien à dire ! bon garçon !... Le père est allongé sur son lit, et il s'amuse à mettre le policier sur un ours. C'est dommage, père, c'est dommage ! Il vaudrait mieux faire la guerre. Elle se détourna et tendit la main au comte, qui ne put s'empêcher de rire. - Bon, viens à table, je vais prendre le thé, c'est l'heure ? - a déclaré Marya Dmitrievna. Le comte marchait en avant avec Marya Dmitrievna ; puis la comtesse, qui était dirigée par un colonel hussard, la bonne personne, avec qui Nikolai était censé rattraper le régiment. Anna Mikhailovna - avec Shinshin. Berg serra la main de Vera. Julie Karagina, souriante, accompagna Nikolaï à table. Derrière eux venaient d'autres couples, s'étendant dans toute la salle, et derrière eux, un à un, se trouvaient des enfants, des précepteurs et des gouvernantes. Les serveurs ont commencé à bouger, les chaises ont claqué, la musique a commencé à jouer dans la chorale et les invités ont pris place. Les sons de la musique familiale du comte ont été remplacés par les sons des couteaux et des fourchettes, les bavardages des invités et les pas silencieux des serveurs. A un bout de la table, la comtesse était assise en tête. À droite se trouve Marya Dmitrievna, à gauche Anna Mikhailovna et d'autres invités. A l'autre bout étaient assis le comte, à gauche le colonel hussard, à droite Shinshin et d'autres invités masculins. D'un côté de la longue table se trouvent des jeunes plus âgés : Vera à côté de Berg, Pierre à côté de Boris ; d'autre part, les enfants, les tuteurs et les gouvernantes. Derrière les cristaux, les bouteilles et les vases de fruits, le comte regardait sa femme et son grand bonnet à rubans bleus et versait assidûment du vin à ses voisins, sans s'oublier lui-même. La comtesse aussi, derrière les ananas, sans oublier ses devoirs de ménagère, jetait des regards significatifs sur son mari, dont la tête chauve et le visage, lui semblait-il, différaient plus nettement de ses cheveux gris dans leur rougeur. Il y avait un bavardage constant du côté des dames ; dans les toilettes des hommes, les voix se faisaient de plus en plus fortes, notamment celle du colonel hussard, qui mangeait et buvait tellement, rougissant de plus en plus, que le comte le donnait déjà en exemple aux autres invités. Berg, avec un doux sourire, a dit à Vera que l'amour n'est pas un sentiment terrestre, mais céleste. Boris a nommé son nouvel ami Pierre les invités à table et a échangé des regards avec Natasha, assise en face de lui. Pierre parlait peu, regardait de nouveaux visages et mangeait beaucoup. A partir de deux soupes, parmi lesquelles il a choisi à la tortue, [tortue,] et kulebyaki et au tétras des noisettes, il n'a manqué aucun plat ni un seul vin, que le majordome a mystérieusement mis dans une bouteille enveloppée dans une serviette. derrière l'épaule de son voisin, en disant ou "drey Madère", ou "hongrois" ou "vin du Rhin". Il plaça le premier des quatre verres en cristal avec le monogramme du comte qui se trouvaient devant chaque appareil, et but avec plaisir, en regardant les convives avec une expression de plus en plus agréable. Natasha, assise en face de lui, regardait Boris comme des filles de treize ans regardent un garçon qu'elles viennent de s'embrasser pour la première fois et dont elles sont amoureuses. Ce même regard se tournait parfois vers Pierre, et sous le regard de cette fille drôle et vive, il avait envie de rire lui-même, sans savoir pourquoi. Nikolai s'est assis loin de Sonya, à côté de Julie Karagina, et encore une fois avec le même sourire involontaire, il lui a parlé. Sonya sourit grandiosement, mais apparemment tourmentée par la jalousie : elle pâlit, puis rougit et écouta de toutes ses forces ce que se disaient Nikolaï et Julie. La gouvernante regardait autour d'elle avec inquiétude, comme si elle se préparait à riposter si quelqu'un décidait d'offenser les enfants. Le tuteur allemand a essayé de mémoriser toutes sortes de plats, desserts et vins afin de tout décrire en détail dans une lettre à sa famille en Allemagne, et a été très offensé par le fait que le majordome, avec une bouteille enveloppée dans une serviette, portait lui autour. L'Allemand fronça les sourcils, essaya de montrer qu'il ne voulait pas recevoir ce vin, mais fut offensé car personne ne voulait comprendre qu'il avait besoin de ce vin non pas pour étancher sa soif, non par cupidité, mais par curiosité consciencieuse. Du côté masculin de la table, la conversation devenait de plus en plus animée. Le colonel a déclaré que le manifeste de déclaration de guerre avait déjà été publié à Saint-Pétersbourg et que l'exemplaire qu'il avait lui-même vu avait été remis par courrier au commandant en chef. - Et pourquoi nous est-il difficile de combattre Bonaparte ? - dit Shinshin. – II a deja rabattu le caquet a l "Autriche. Je crins, que cette fois ce ne soit notre tour. [Il a déjà renversé l'arrogance de l'Autriche. J'ai peur que notre tour ne vienne pas maintenant.] Le colonel était un Allemand trapu, grand et optimiste, visiblement un serviteur et un patriote. Il a été offensé par les paroles de Shinshin. "Et puis, nous sommes un bon souverain", dit-il en prononçant e au lieu de e et ъ au lieu de ь. "Ensuite, l'empereur le sait. Il a déclaré dans son manifeste qu'il pouvait regarder avec indifférence les dangers qui menacent la Russie et que la sécurité de l'empire, sa dignité et le caractère sacré de ses alliances", a-t-il déclaré, en insistant particulièrement pour une raison quelconque. le mot «syndicats», comme si c'était là toute l'essence du problème. Et avec sa mémoire officielle, infaillible et caractéristique, il répétait les premiers mots du manifeste... « et le désir, seul et indispensable objectif du souverain : établir la paix en Europe sur des bases solides - ils ont décidé d'envoyer maintenant une partie de l’armée à l’étranger et faire de nouveaux efforts pour réaliser cet objectif ». "C'est pourquoi nous sommes un bon souverain", a-t-il conclu en buvant un verre de vin de manière édifiante et en regardant le comte pour l'encourager. – Connaissez vous le proverbe : [Vous connaissez le proverbe :] « Erema, Erema, tu devrais t'asseoir à la maison, affûter tes fuseaux », dit Shinshin en grimaçant et en souriant. – Cela nous convient à merveille. [Cela nous est utile.] Pourquoi Souvorov - ils l'ont découpé en morceaux, une plaque de couture, [sur sa tête,] et où sont nos Souvorov maintenant ? Je vous demande un peu, [Je vous demande,] - sautant constamment du russe au Français, il a dit. "Nous devons nous battre jusqu'à la dernière goutte de sang", dit le colonel en frappant la table, "et mourir pour notre empereur, et alors tout ira bien." Et pour argumenter le plus possible (il a surtout étiré la voix sur le mot « possible »), le moins possible », termina-t-il en se tournant de nouveau vers le comte. "C'est comme ça qu'on juge les vieux hussards, c'est tout." Comment jugez-vous, jeune homme et jeune hussard ? - ajouta-t-il en se tournant vers Nikolaï, qui, ayant entendu dire qu'il s'agissait de guerre, quitta son interlocuteur et regarda de tous ses yeux et écouta de toutes ses oreilles le colonel. "Je suis tout à fait d'accord avec vous", répondit Nikolaï tout rouge en faisant tourner l'assiette et en réarrangeant les verres avec un regard si décisif et désespéré, comme s'il était à ce moment exposé à un grand danger, "je suis convaincu que les Russes doivent mourir ou gagner », a-t-il déclaré, ressentant comme les autres, après que le mot ait déjà été prononcé, que c'était trop enthousiaste et pompeux pour l'occasion présente et donc gênant. "C"est bien beau ce que vous venez de dire, [Merveilleux ! Ce que vous avez dit est merveilleux]", dit Julie, qui était assise à côté de lui en soupirant. Sonya tremblait de partout et rougit jusqu'aux oreilles, derrière les oreilles et jusqu'au cou et aux épaules, en Pendant que Nikolaï parlait, Pierre écoutait les discours du colonel et hochait la tête avec approbation. "C'est sympa", dit-il. « Un vrai hussard, jeune homme », cria le colonel en frappant à nouveau la table. -Pourquoi fais-tu du bruit là ? – La voix basse de Marya Dmitrievna s’est soudainement fait entendre de l’autre côté de la table. - Pourquoi tu frappes sur la table ? - elle se tourna vers le hussard, - pour qui t'excites-tu ? hein, tu penses que les Français sont devant toi ? "Je dis la vérité", dit le hussard en souriant. « Tout sur la guerre », cria le comte à travers la table. - Après tout, mon fils arrive, Marya Dmitrievna, mon fils arrive. - Et j'ai quatre fils dans l'armée, mais ça ne me dérange pas. Tout est la volonté de Dieu : vous mourrez allongé sur le poêle, et au combat, Dieu aura pitié », résonnait sans aucun effort la voix épaisse de Marya Dmitrievna à l'autre bout de la table. - C'est vrai. Et la conversation se concentra à nouveau – les dames à leur bout de table, les hommes à lui. "Mais tu ne demanderas pas", dit le petit frère à Natasha, "mais tu ne demanderas pas !" "Je vais demander", répondit Natasha. Son visage rougit soudainement, exprimant une détermination désespérée et joyeuse. Elle se leva, invitant Pierre, assis en face d'elle, à l'écouter, et se tourna vers sa mère : - Mère! – sa voix enfantine et corpulente résonnait à travers la table. - Que veux-tu? – a demandé la comtesse avec peur, mais, voyant sur le visage de sa fille qu'il s'agissait d'une farce, elle a agité la main sévèrement, faisant un geste de tête menaçant et négatif. La conversation s'est calmée. - Mère! quel genre de gâteau sera-ce ? – La voix de Natasha était encore plus décisive, sans s'effondrer. La comtesse voulait froncer les sourcils, mais elle n'y parvenait pas. Marya Dmitrievna secoua son gros doigt. « Cosaque », dit-elle d'un ton menaçant. La plupart des invités regardaient les aînés, ne sachant pas comment prendre cette astuce. - Me voici! - dit la comtesse. - Mère! quel genre de gâteau y aura-t-il ? - Natasha a crié joyeusement et capricieusement, confiante d'avance que sa farce serait bien reçue. Sonya et le gros Petya se cachaient du rire. "C'est pour ça que j'ai demandé", murmura Natasha à son petit frère et à Pierre, qu'elle regarda à nouveau. "De la glace, mais ils ne vous la donneront pas", a déclaré Marya Dmitrievna. Natasha a vu qu'il n'y avait rien à craindre et elle n'avait donc pas peur de Marya Dmitrievna. - Marie Dmitrievna ? quelle glace ! Je n'aime pas la crème. - Carotte. - Non, lequel ? Marya Dmitrievna, laquelle ? – elle a presque crié. - Je veux savoir! Marya Dmitrievna et la comtesse ont ri et tous les invités les ont suivies. Tout le monde n'a pas ri de la réponse de Marya Dmitrievna, mais du courage et de la dextérité incompréhensibles de cette fille, qui savait et a osé traiter Marya Dmitrievna comme ça. Natasha n'a pris du retard que lorsqu'on lui a dit qu'il y aurait de l'ananas. Le champagne était servi avant la glace. La musique recommença, le comte embrassa la comtesse, et les invités se levèrent et félicitèrent la comtesse, trinquant autour de la table avec le comte, les enfants et entre eux. Les serveurs accoururent à nouveau, les chaises claquèrent, et dans le même ordre, mais avec des visages plus rouges, les invités retournèrent au salon et au bureau du comte. Les tables de Boston furent écartées, les fêtes furent dressées et les invités du comte s'installèrent dans deux salons, un salon avec canapé et une bibliothèque. Le comte, déployant ses cartes, pouvait difficilement résister à l'habitude de faire une sieste l'après-midi et se moquait de tout. La jeunesse, excitée par la comtesse, se rassembla autour du clavicorde et de la harpe. Julie a été la première, à la demande de tous, à jouer un morceau avec des variations sur la harpe et, avec d'autres filles, a commencé à demander à Natasha et Nikolai, connus pour leur musicalité, de chanter quelque chose. Natasha, qu'on appelait une grande fille, en était apparemment très fière, mais en même temps elle était timide. - Qu'est-ce qu'on va chanter ? - elle a demandé. "La clé", répondit Nikolaï. - Eh bien, dépêchons-nous. Boris, viens ici », dit Natasha. - Où est Sonya ? Elle regarda autour d'elle et, voyant que son amie n'était pas dans la pièce, courut après elle. Courant dans la chambre de Sonya et n'y trouvant pas son amie, Natasha a couru dans la crèche - et Sonya n'était pas là. Natasha réalisa que Sonya était dans le couloir sur la poitrine. Le coffre dans le couloir était le lieu des chagrins de la jeune génération féminine de la maison de Rostov. En effet, Sonya dans sa robe rose aérienne, l'écrasant, s'allongea face contre terre sur le lit de plumes rayées sale de sa nounou, sur la poitrine et, se couvrant le visage de ses doigts, pleura amèrement en secouant ses épaules nues. Le visage de Natasha, animé, avec un anniversaire toute la journée, changea soudain : ses yeux s'arrêtèrent, puis son large cou frémit, les commissures de ses lèvres tombèrent. - Sonya ! qu'est-ce que tu es ?... Quoi, qu'est-ce qui ne va pas chez toi ? Wow Wow!… Et Natasha, ouvrant sa grande bouche et devenant complètement stupide, se mit à rugir comme une enfant, sans en connaître la raison et uniquement parce que Sonya pleurait. Sonya voulait lever la tête, voulait répondre, mais elle ne pouvait pas et se cachait encore plus. Cria Natasha en s'asseyant sur le lit de plumes bleues et en serrant son amie dans ses bras. Ayant rassemblé ses forces, Sonya se leva, commença à essuyer ses larmes et à raconter l'histoire. - Nikolenka part dans une semaine, son... journal... est sorti... il me l'a dit lui-même... Oui, je ne pleurerais toujours pas... (elle montra le morceau de papier qu'elle tenait dans sa main : c'était de la poésie écrite par Nikolai) Je ne pleurerais toujours pas, mais tu ne l'as pas fait, tu peux... personne ne peut comprendre... quel genre d'âme il a. Et elle se remit à pleurer parce que son âme était si bonne. "Tu te sens bien... Je ne t'envie pas... Je t'aime, et Boris aussi", dit-elle en rassemblant un peu de force, "il est mignon... il n'y a pas d'obstacles pour toi." Et Nikolaï est mon cousin... J'ai besoin... du métropolite lui-même... et c'est impossible. Et puis, si maman... (Sonya considéra la comtesse et appela sa mère), elle dira que je ruine la carrière de Nikolaï, que je n'ai pas de cœur, que je suis ingrate, mais vraiment... pour l'amour de Dieu... (elle se signa) Je l'aime tellement aussi, et vous tous, seulement Vera... Pour quoi ? Qu'est-ce que je lui ai fait ? Je vous suis tellement reconnaissant que je serais heureux de tout sacrifier, mais je n'ai rien... Sonya ne pouvait plus parler et cacha à nouveau sa tête dans ses mains et dans le lit de plumes. Natasha a commencé à se calmer, mais son visage montrait qu'elle comprenait l'importance du chagrin de son amie. - Sonya ! - dit-elle soudain, comme si elle avait deviné la véritable raison du chagrin de son cousin. – C'est vrai, Vera t'a parlé après le dîner ? Oui? – Oui, Nicolas lui-même a écrit ces poèmes, et j'en ai copié d'autres ; Elle les a trouvés sur ma table et a dit qu'elle les montrerait à maman, et elle a aussi dit que j'étais ingrat, que maman ne lui permettrait jamais de m'épouser et qu'il épouserait Julie. Tu vois comme il est avec elle toute la journée... Natasha ! Pour quoi?… Et encore une fois, elle pleura plus amèrement qu'auparavant. Natasha la souleva, la serra dans ses bras et, souriant à travers ses larmes, commença à la calmer. - Sonya, ne la crois pas, chérie, ne la crois pas. Vous souvenez-vous de la façon dont nous avons discuté tous les trois avec Nikolenka dans le salon du canapé ; tu te souviens après le dîner ? Après tout, nous avons décidé de tout comment cela se passerait. Je ne me souviens pas comment, mais vous vous souvenez à quel point tout était bien et tout était possible. Voici le frère de l'oncle Shinshin, il est marié à cousin, et nous sommes cousins ​​​​germains. Et Boris a dit que c'était tout à fait possible. Tu sais, je lui ai tout dit. Et il est si intelligent et si bon", a déclaré Natasha... "Toi, Sonya, ne pleure pas, ma chère chérie, Sonya." - Et elle l'embrassa en riant. - La foi est mauvaise, que Dieu la bénisse ! Mais tout ira bien, et elle ne le dira pas à maman ; Nikolenka le dira lui-même, et il n'a même pas pensé à Julie. Et elle l'embrassa sur la tête. Sonya s'est levée et le chaton s'est redressé, ses yeux brillaient et il semblait prêt à agiter sa queue, à sauter sur ses pattes douces et à jouer à nouveau avec le ballon, comme il convenait. - Tu penses? Droite? Par Dieu? – dit-elle en redressant rapidement sa robe et ses cheveux. - Vraiment, par Dieu ! – répondit Natasha en redressant une mèche de cheveux grossiers sous la tresse de son amie. Et ils rirent tous les deux. - Eh bien, allons chanter "The Key". - Allons à. "Tu sais, ce gros Pierre qui était assis en face de moi est tellement drôle !" – dit soudain Natasha en s'arrêtant. - Je m'amuse beaucoup ! Et Natasha a couru dans le couloir. Sonya, se débarrassant des peluches et cachant les poèmes dans sa poitrine, jusqu'à son cou avec les os de la poitrine saillants, d'un pas léger et joyeux, le visage rouge, courut après Natasha le long du couloir jusqu'au canapé. A la demande des invités, les jeunes ont chanté le quatuor « Key », qui a beaucoup plu à tout le monde ; puis Nicolas chanta la chanson qu'il avait réappris. Par une agréable nuit, au clair de lune, Imaginez-vous heureux Qu'il y a encore quelqu'un dans le monde, Qui pense à toi aussi ! Comme elle, de sa belle main, Marchant le long de la harpe d'or, Avec son harmonie passionnée S'appelant à lui-même, vous appelant ! Encore un jour ou deux, et le paradis viendra... Mais ah ! ton ami ne vivra pas ! Et il n'a pas encore fini de chanter derniers mots, lorsque les jeunes dans la salle se préparaient à danser et que les musiciens commençaient à se cogner les pieds et à tousser dans la chorale. Pierre était assis dans le salon, où Shinshin, comme avec un visiteur de l'étranger, entama avec lui une conversation politique ennuyeuse pour Pierre, à laquelle d'autres se joignirent. Lorsque la musique commença à jouer, Natasha entra dans le salon et, s'approchant directement de Pierre, en riant et en rougissant, lui dit : - Maman m'a dit de t'inviter à danser. "J'ai peur de confondre les chiffres", dit Pierre, "mais si tu veux être mon professeur..." Et il tendit sa grosse main, en la baissant très bas, à la fille maigre. Pendant que les couples s'installaient et que les musiciens faisaient la queue, Pierre s'assit avec sa petite dame. Natasha était complètement heureuse ; elle dansait avec un grand, avec quelqu'un qui venait de l'étranger. Elle s'asseyait devant tout le monde et lui parlait comme une grande fille. Elle avait à la main un éventail qu'une jeune femme lui avait donné de tenir. Et, prenant la pose la plus laïque (Dieu sait où et quand elle l'a appris), elle, s'éventant et souriant à travers l'éventail, s'adressa à son monsieur. - Qu'est-ce que c'est, qu'est-ce que c'est ? Regardez, regardez, dit la vieille comtesse en traversant le couloir et en désignant Natasha. Natasha rougit et rit. - Et toi, maman ? Eh bien, quel genre de chasse recherchez-vous ? Qu'est-ce qui est surprenant ici ? Au milieu de la troisième éco-séance, les chaises du salon, où jouaient le comte et Marya Dmitrievna, ont commencé à bouger, et la plupart des invités d'honneur et des personnes âgées, s'étirant après une longue séance et mettant leurs portefeuilles et leurs sacs à main dans leurs poches, sortirent par les portes du hall. Marya Dmitrievna marchait devant le comte, tous deux avec des visages joyeux. Le comte, avec une politesse enjouée, comme un ballet, offrit sa main ronde à Marya Dmitrievna. Il se redressa et son visage s'éclaira d'un sourire particulièrement courageux et narquois, et aussitôt que la dernière figure de l'écosaise fut dansée, il battit des mains vers les musiciens et cria au chœur en s'adressant au premier violon : - Semyon ! Connaissez-vous Danila Kupor ? C'était la danse préférée du comte, qu'il dansait dans sa jeunesse. (Danilo Kupor était en fait une figure des Angles.) "Regarde papa", a crié Natasha à toute la salle (oubliant complètement qu'elle dansait avec un grand), penchant sa tête bouclée jusqu'à ses genoux et éclatant de rire dans toute la salle. En effet, tout le monde dans la salle regardait avec un sourire de joie le joyeux vieil homme qui, à côté de sa digne dame, Marya Dmitrievna, qui était plus grande que lui, arrondissait ses bras, les secouait au rythme, redressait ses épaules, tordait son jambes, tapant légèrement du pied, et avec un sourire de plus en plus épanoui sur son visage rond, il préparait le public à ce qui allait arriver. Dès que les sons joyeux et provocants de Danila Kupor, semblables à un bavard joyeux, ont été entendus, toutes les portes de la salle se sont soudainement remplies de visages d'hommes d'un côté et de visages de femmes souriantes de servantes de l'autre, qui sont sorties pour regarde le joyeux maître. - Père est à nous ! Aigle! – a dit la nounou à voix haute depuis une porte. Le comte dansait bien et le savait, mais sa dame ne savait pas comment et ne voulait pas bien danser. Son énorme corps se tenait droit, les bras baissés avec des mains puissantes(elle tendit le réticule à la comtesse) ; une seule chose stricte, mais Beau visage elle dansait. Ce qui s'exprimait dans toute la silhouette ronde du comte, chez Marya Dmitrievna, ne s'exprimait que par un visage de plus en plus souriant et un nez tremblant. Mais si le comte, devenant de plus en plus insatisfait, captivait le public par la surprise des torsions adroites et des légers sauts de ses jambes douces, Marya Dmitrievna, avec le moindre zèle à bouger les épaules ou à arrondir ses bras à tour de rôle et à piétiner, ne faisait aucun moins une impression de mérite, dont chacun appréciait son obésité et sa sévérité omniprésente. La danse devenait de plus en plus animée. Les homologues n’ont pas pu attirer l’attention pendant une minute et n’ont même pas essayé de le faire. Tout était occupé par le comte et Marya Dmitrievna. Natasha a tiré les manches et les robes de toutes les personnes présentes, qui gardaient déjà les yeux rivés sur les danseurs, et a exigé qu'elles regardent papa. Pendant les intervalles de la danse, le comte respirait profondément, saluait et criait aux musiciens de jouer vite. De plus en plus vite, de plus en plus vite, de plus en plus vite, le décompte s'est déroulé, tantôt sur la pointe des pieds, tantôt sur les talons, se précipitant autour de Marya Dmitrievna et, enfin, tournant sa dame vers sa place, a fait le dernier pas, levant sa jambe douce de derrière, penchant sa tête en sueur avec un visage souriant et agitant rondement main droite au milieu d'un tonnerre d'applaudissements et de rires, notamment de la part de Natasha. Les deux danseurs s'arrêtèrent, haletant lourdement et s'essuyant avec des mouchoirs en batiste. « C'est ainsi qu'on dansait à notre époque, ma chère, dit le comte. - Oh oui Danila Kupor ! - dit Marya Dmitrievna, laissant échapper l'esprit lourdement et longuement, retroussant ses manches. Pendant que les Rostov dansaient dans la salle la sixième anglaise au son de musiciens fatigués désaccordés, et que les serveurs et les cuisiniers fatigués préparaient le dîner, le sixième coup frappa le comte Bezukhy. Les médecins déclarèrent qu'il n'y avait aucun espoir de guérison ; le patient a reçu une confession silencieuse et la communion ; On se préparait pour l'onction, et dans la maison régnait l'agitation et l'anxiété de l'attente, habituelles dans de tels moments. A l'extérieur de la maison, derrière les grilles, les croque-morts se pressaient, se cachant des voitures qui approchaient, attendant une riche commande pour les funérailles du comte. Le commandant en chef de Moscou, qui envoyait constamment des adjudants pour s'enquérir de la position du comte, vint lui-même ce soir-là dire au revoir au célèbre noble de Catherine, le comte Bezukhim. La magnifique salle de réception était pleine. Tout le monde se leva respectueusement lorsque le commandant en chef, après avoir été seul avec le patient pendant environ une demi-heure, sortit de là, rendant légèrement les arcs et essayant le plus rapidement possible de passer sous le regard des médecins, du clergé et des proches. fixé sur lui. Le prince Vasily, qui avait perdu du poids et pâli au cours de ces jours, accompagna le commandant en chef et lui répéta doucement quelque chose à plusieurs reprises. Après avoir accompagné le commandant en chef, le prince Vasily s'assit seul sur une chaise dans le hall, croisant les jambes haut, posant son coude sur son genou et fermant les yeux avec sa main. Après être resté assis ainsi pendant un certain temps, il se leva et, d'un pas inhabituellement précipité, regardant autour de lui avec des yeux effrayés, il traversa le long couloir jusqu'à la moitié arrière de la maison, jusqu'à la princesse aînée. Ceux qui se trouvaient dans la pièce faiblement éclairée se parlaient à voix basse et se taisaient à chaque fois et, les yeux pleins de questions et d'attentes, se retournaient vers la porte qui menait aux appartements du mourant et émettaient un léger bruit lorsque quelqu'un sortait. de celui-ci ou y est entré. "La limite humaine", dit le vieil homme, ecclésiastique, à la dame qui s'assit à côté de lui et l'écoutait naïvement, "la limite est fixée, mais vous ne pouvez pas la dépasser". "Je me demande s'il est trop tard pour accomplir l'onction ?" - en ajoutant le titre spirituel, a demandé la dame, comme si elle n'avait pas d'opinion personnelle à ce sujet.

Retour avant

Attention! Les aperçus des diapositives sont fournis à titre informatif uniquement et peuvent ne pas représenter toutes les fonctionnalités de la présentation. Si tu es intéressé ce travail, veuillez télécharger la version complète.

Objectifs.

Éducatif. Créer les conditions d'une maîtrise réussie du concept du quadrilatère décrit, de ses propriétés, de ses caractéristiques et maîtriser les compétences nécessaires pour les appliquer dans la pratique.

Du développement. Développement des capacités mathématiques, création de conditions pour la capacité de généraliser et d'appliquer une pensée avancée et rétrospective.

Éducatif. Cultiver le sens de la beauté à travers l'esthétique des dessins, s'étonner de l'insolite

décision, formation de l’organisation, responsabilité des résultats de son travail.

1. Étudiez la définition d’un quadrilatère circonscrit.

2. Démontrer la propriété des côtés du quadrilatère circonscrit.

3. Introduire la dualité des propriétés des sommes des côtés opposés et des angles opposés des quadrilatères inscrits et circonscrits.

4. Fournir une expérience dans l'application pratique des théorèmes considérés lors de la résolution de problèmes.

5. Effectuer un suivi initial du niveau d'assimilation du nouveau matériel.

Équipement:

• ordinateur, projecteur;
• manuel « Géométrie. 10-11 années » pour l’enseignement général. institutions : base et profil. niveaux automatiques UN V. Pogorelov.

Logiciel : Microsoft Word, Puissance Microsoft Indiquer.

Utiliser un ordinateur pour préparer un enseignant à une leçon.

À l'aide d'un programme standard du système d'exploitation Windows, les éléments suivants ont été créés pour la leçon :

1. Présentation.
2. Les tables.
3. Plans.
4. Polycopié.

Plan de cours

Organisation du temps. (2 minutes.)

Vérification des devoirs. (5 minutes.)

Apprendre du nouveau matériel. (28 minutes)

Travail indépendant. (7 minutes)

Devoirs.(1 minute.)

Résumé de la leçon. (2 minutes.)

Pendant les cours

1. Moment organisationnel. Salutations. Énoncez le sujet et le but de la leçon. Notez la date et le sujet de la leçon dans votre cahier.

2. Vérification des devoirs.

3. Étudier du nouveau matériel.

Travail sur la notion de polygone circonscrit.

Définition. Le polygone s'appelle décrit sur un cercle, si Tous ses côtés préoccupation un cercle.

Question. Lesquels des polygones proposés sont décrits et lesquels ne le sont pas et pourquoi ?

<Презентация. Слайд №2>

Preuve des propriétés du quadrilatère circonscrit.

<Презентация. Слайд №3>

Théorème. Dans un quadrilatère circonscrit, les sommes des côtés opposés sont égales.

Les élèves travaillent avec un manuel et notent la formulation du théorème dans un cahier.

1. Présentez la formulation du théorème sous la forme d'une phrase avec sursis.

2. Quelle est la condition du théorème ?

3. Quelle est la conclusion du théorème ?

Répondre. Si un quadrilatère est circonscrit à un cercle, Que les sommes des côtés opposés sont égales.

La preuve est effectuée, les élèves prennent des notes dans leurs cahiers.

<Презентация. Слайд №4>

Professeur. Note dualité situations pour les côtés et les angles des quadrilatères circonscrits et inscrits.

Consolidation des connaissances acquises.

Tâches.

Les côtés opposés du quadrilatère décrit mesurent 8 m et 12 m. Est-il possible de trouver le périmètre ?

Tâches basées sur des dessins finis.<Презентация. Слайд №5>

Répondre. 1. 10 m. 2. 20 m. 3. 21 m

Preuve de la caractéristique d'un quadrilatère circonscrit.

Énoncez le théorème inverse.

Répondre. Si dans un quadrilatère les sommes des côtés opposés sont égales, alors un cercle peut y être inscrit. (Retournez à la diapositive 2, fig. 7) <Презентация. Слайд №2>

Professeur. Clarifier la formulation du théorème.

Théorème. Si les sommes des côtés opposés convexe quadrilatères sont égaux, alors un cercle peut y être inscrit.

Travailler avec le manuel. Familiarisez-vous avec la preuve du test pour un quadrilatère circonscrit à l'aide du manuel.

Application des connaissances acquises.

3. Tâches basées sur des dessins finis.

1. Est-il possible d'inscrire un cercle dans un quadrilatère dont les côtés opposés sont 9 m et 4 m, 10 m et 3 m ?

2. Est-il possible d'inscrire un cercle dans un trapèze isocèle de bases 1 m et 9 m et de hauteur 3 m ?

<Презентация. Слайд №6>

Travail écrit dans des cahiers

.

Tâche. Trouvez le rayon d'un cercle inscrit dans un losange de diagonales 6 m et 8 m.

<Презентация. Слайд № 7>

4. Travail indépendant.

1 possibilité

1. Est-il possible d'inscrire un cercle

1) en un rectangle de 7 m et 10 m de côté,

2. Les côtés opposés d'un quadrilatère circonscrit à un cercle mesurent 7 m et 10 m.

Trouvez le périmètre du quadrilatère.

3. Un trapèze équilatéral de bases 4 m et 16 m est décrit autour d'un cercle.

1) rayon du cercle inscrit,

Option 2

1. Est-il possible d'inscrire un cercle :

1) dans un parallélogramme de côtés 6 m et 13 m,

2) au carré ?

2. Les côtés opposés d'un quadrilatère circonscrit à un cercle mesurent 9 m et 11 m. Trouvez le périmètre du quadrilatère.

3. Un trapèze équilatéral d'un côté de 5 m est circonscrit à un cercle de rayon de 2 m.

1) la base du trapèze,

2) rayon du cercle circonscrit.

5. Devoirs. P.86, n° 28, 29, 30.

6. Résumé de la leçon. Le travail indépendant est vérifié et des notes sont attribuées.

<Презентация. Слайд № 8>

"Cercle" Nous avons vu qu'un cercle peut être circonscrit autour de n'importe quel triangle. Autrement dit, pour chaque triangle, il existe un cercle tel que les trois sommets du triangle « reposent » dessus. Comme ça:

Question : peut-on en dire autant d’un quadrilatère ? Est-il vrai qu’il y aura toujours un cercle sur lequel les quatre sommets du quadrilatère « reposeront » ?

Il s'avère que ce n'est PAS VRAI ! Un quadrilatère ne peut PAS TOUJOURS être inscrit dans un cercle. Il y a une condition très importante :

Sur notre photo :

.

Regardez, les angles et se font face, ce qui signifie qu'ils sont opposés. Qu'en est-il alors des angles et ? Ils semblent également être opposés ? Est-il possible de prendre des angles et au lieu d'angles et ?

Bien sûr vous pouvez! L'essentiel est que le quadrilatère ait deux angles opposés dont la somme sera. Les deux angles restants s’additionneront alors également d’eux-mêmes. Ne crois pas? Assurons-nous-en. Regarder:

Laisser être. Vous souvenez-vous de la somme des quatre angles d’un quadrilatère ? Certainement, . C'est-à-dire - toujours ! . Mais, → .

De la magie là-bas !

Alors souvenez-vous bien de ceci :

Si un quadrilatère est inscrit dans un cercle, alors la somme de deux de ses angles opposés est égale à

et vice versa:

Si un quadrilatère a deux angles opposés dont la somme est égale, alors le quadrilatère est cyclique.

Nous ne prouverons pas tout cela ici (si cela vous intéresse, renseignez-vous sur les niveaux de théorie suivants). Mais voyons à quoi conduit ce fait remarquable : que dans un quadrilatère inscrit la somme des angles opposés est égale.

Par exemple, la question vient à l’esprit : est-il possible de décrire un cercle autour d’un parallélogramme ? Essayons d'abord la « méthode poke ».

D'une manière ou d'une autre, ça ne marche pas.

Appliquons maintenant les connaissances :

Supposons que nous ayons réussi à faire correspondre un cercle sur un parallélogramme. Alors il doit certainement y avoir : , c'est-à-dire.

Rappelons maintenant les propriétés d'un parallélogramme :

Tout parallélogramme a des angles opposés égaux.

Il s'est avéré que

Qu'en est-il des angles et ? Eh bien, c'est la même chose bien sûr.

Inscrit → →

Parallélogramme → →

Incroyable, non ?

Il s'avère que si un parallélogramme est inscrit dans un cercle, alors tous ses angles sont égaux, c'est-à-dire que c'est un rectangle !

Et en même temps - le centre du cercle coïncide avec le point d'intersection des diagonales de ce rectangle. Ceci est inclus en bonus, pour ainsi dire.

Eh bien, cela signifie que nous avons découvert qu'un parallélogramme inscrit dans un cercle est rectangle.

Parlons maintenant du trapèze. Que se passe-t-il si un trapèze est inscrit dans un cercle ? Mais il s'avère qu'il y aura trapèze isocèle . Pourquoi?

Laissez le trapèze s'inscrire dans un cercle. Là encore, mais à cause du parallélisme des lignes et.

Cela signifie que nous avons : → → trapèze isocèle.

Encore plus simple qu’avec un rectangle, non ? Mais vous devez vous en souvenir fermement - cela vous sera utile :

Listons le plus principales déclarations tangent à un quadrilatère inscrit dans un cercle :

1. Un quadrilatère est inscrit dans un cercle si et seulement si la somme de ses deux angles opposés est égale à
2. Un parallélogramme inscrit dans un cercle - certainement rectangle et le centre du cercle coïncide avec le point d'intersection des diagonales
3. Un trapèze inscrit dans un cercle est équilatéral.

Quadrilatère inscrit. Niveau moyen

On sait que pour chaque triangle il existe un cercle circonscrit (nous l'avons prouvé dans le thème « Le cercle circonscrit »). Que peut-on dire du quadrilatère ? Il se trouve que TOUS les quadrilatères ne peuvent pas être inscrits dans un cercle, et il existe un tel théorème :

Un quadrilatère est inscrit dans un cercle si et seulement si la somme de ses angles opposés est égale à.

Dans notre dessin -

Essayons de comprendre pourquoi il en est ainsi ? En d’autres termes, nous allons maintenant démontrer ce théorème. Mais avant de le prouver, vous devez comprendre comment fonctionne la déclaration elle-même. Avez-vous remarqué les mots « alors et seulement alors » dans la déclaration ? De tels mots signifient que des mathématiciens nuisibles ont regroupé deux affirmations en une seule.

Décryptons :

1. « Alors » signifie : Si un quadrilatère est inscrit dans un cercle, alors la somme de deux de ses angles opposés est égale.
2. « Alors seulement » signifie : si un quadrilatère a deux angles opposés dont la somme est égale, alors un tel quadrilatère peut être inscrit dans un cercle.

Tout comme Alice : « Je pense ce que je dis » et « Je dis ce que je pense ».

Voyons maintenant pourquoi 1 et 2 sont vrais ?

Premier 1.

Soit un quadrilatère inscrit dans un cercle. Marquons son centre et traçons les rayons et. Que va-t-il se passer ? Vous souvenez-vous qu'un angle inscrit est la moitié de la taille de l'angle central correspondant ? Si vous vous en souvenez, nous l'appliquerons maintenant, et sinon, jetez un œil au sujet "Cercle. Angle inscrit".

Inscrit

Inscrit

Mais regarde: .

Nous obtenons que si - est inscrit, alors

Eh bien, il est clair que cela s’additionne aussi. (nous devons également considérer).

Maintenant « vice versa », c'est-à-dire 2.

Il s'avère que dans un quadrilatère la somme de deux angles opposés est égale. Disons que

Nous ne savons pas encore si nous pouvons décrire un cercle autour d'elle. Mais nous savons avec certitude que nous sommes assurés de pouvoir décrire un cercle autour d'un triangle. Alors faisons-le.

Si un point ne « repose » pas sur le cercle, il finit inévitablement soit à l’extérieur, soit à l’intérieur.

Considérons les deux cas.

Que le point soit d'abord à l'extérieur. Ensuite, le segment coupe le cercle à un moment donné. Connectons-nous et. Le résultat est un quadrilatère inscrit (!).

Nous savons déjà que la somme de ses angles opposés est égale, c'est-à-dire et selon notre condition.

Il s'avère qu'il devrait en être ainsi.

Mais cela ne peut pas être le cas puisque - est un angle extérieur pour et un moyen.

Et à l'intérieur ? Faisons des choses similaires. Que le point soit à l'intérieur.

Ensuite, la continuation du segment coupe le cercle en un point. Encore une fois - un quadrilatère inscrit, et selon la condition il doit être satisfait, mais - un angle extérieur pour et un moyen, c'est-à-dire encore une fois, cela ne peut pas être cela.

Autrement dit, un point ne peut être ni à l'extérieur ni à l'intérieur du cercle - cela signifie qu'il est sur le cercle !

Tout le théorème a été prouvé !

Voyons maintenant quelles bonnes conséquences donne ce théorème.

Corollaire 1

Un parallélogramme inscrit dans un cercle ne peut être qu'un rectangle.

Comprenons pourquoi il en est ainsi. Soit un parallélogramme inscrit dans un cercle. Alors cela devrait être fait.

Mais grâce aux propriétés d’un parallélogramme, nous le savons.

Et la même chose, bien entendu, en ce qui concerne les angles et.

Il s'avère donc que c'est un rectangle - tous les coins sont alignés.

Mais il y a en outre un fait supplémentaire agréable : le centre du cercle circonscrit au rectangle coïncide avec le point d'intersection des diagonales.

Comprenons pourquoi. J'espère que vous vous souvenez très bien que l'angle sous-tendu par le diamètre est une ligne droite.

Diamètre,

Diamètre

ce qui veut dire que c'est le centre. C'est tout.

Corollaire 2

Un trapèze inscrit dans un cercle est isocèle.

Laissez le trapèze s'inscrire dans un cercle. Alors.

Et aussi.

Avons-nous discuté de tout ? Pas vraiment. En fait, il existe une autre façon « secrète » de reconnaître un quadrilatère inscrit. Nous ne formulerons pas cette méthode de manière très stricte (mais claire), mais la prouverons seulement au dernier niveau de la théorie.

Si dans un quadrilatère on peut observer une image telle qu'ici sur la figure (ici les angles « regardant » du côté des points et sont égaux), alors un tel quadrilatère est inscrit.

C'est un dessin très important - dans les problèmes, il est souvent plus facile à trouver angles égaux, que la somme des angles et.

Malgré le manque total de rigueur dans notre formulation, elle est correcte, et de plus, elle est toujours acceptée par les examinateurs de l'Examen d'État unifié. Vous devriez écrire quelque chose comme ceci :

"- inscrit" - et tout ira bien !

N'oubliez pas ce signe important - souvenez-vous de l'image, et peut-être qu'elle attirera votre attention à temps lorsque vous résoudrez le problème.

Quadrilatère inscrit. Brève description et formules de base

Si un quadrilatère est inscrit dans un cercle, alors la somme de deux de ses angles opposés est égale à

et vice versa:

Si un quadrilatère a deux angles opposés dont la somme est égale, alors le quadrilatère est cyclique.

Un quadrilatère est inscrit dans un cercle si et seulement si la somme de ses deux angles opposés est égale.

Parallélogramme inscrit dans un cercle- certainement un rectangle, et le centre du cercle coïncide avec le point d'intersection des diagonales.

Un trapèze inscrit dans un cercle est isocèle.