Proportionale Segmente in einem rechtwinkligen Dreieck. Proportionale Segmente in einem rechtwinkligen Dreieck. Proportionale Segmente in einer rechtwinkligen Dreieckslösung
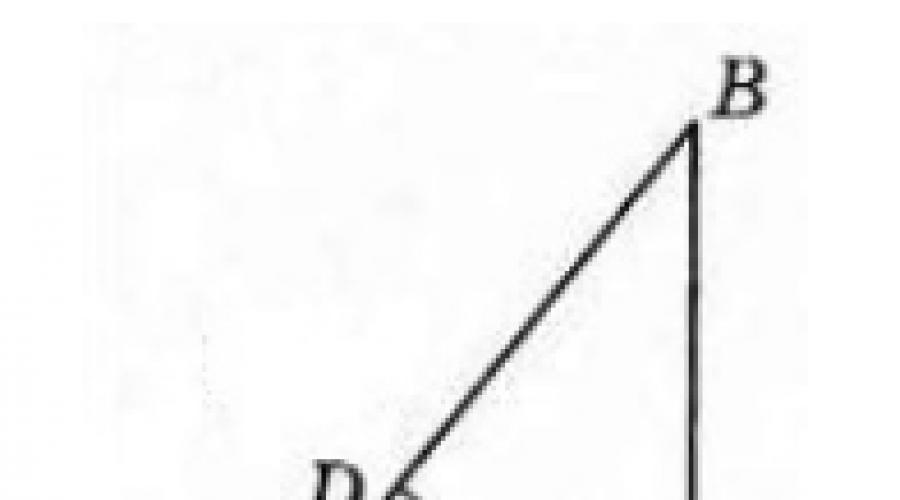
Lesen Sie auch
Ähnlichkeitstest für rechtwinklige Dreiecke
Zunächst führen wir das Ähnlichkeitskriterium für rechtwinklige Dreiecke ein.
Satz 1
Ähnlichkeitstest für rechtwinklige Dreiecke: Zwei rechtwinklige Dreiecke sind ähnlich, wenn eines gleich ist scharfe Ecke(Abb. 1).
Abbildung 1. Ähnliche rechtwinklige Dreiecke
Nachweisen.
Gegeben sei $\angle B=\angle B_1$. Da die Dreiecke rechtwinklig sind, gilt $\angle A=\angle A_1=(90)^0$. Daher sind sie nach dem ersten Kriterium der Ähnlichkeit von Dreiecken ähnlich.
Der Satz ist bewiesen.
Höhensatz im rechtwinkligen Dreieck
Satz 2
Höhe eines rechtwinkligen Dreiecks, das vom Scheitelpunkt aus gezeichnet wird rechter Winkel, teilt ein Dreieck in zwei ähnliche rechtwinklige Dreiecke, von denen jedes dem gegebenen Dreieck ähnlich ist.
Nachweisen.
Gegeben sei ein rechtwinkliges Dreieck $ABC$ mit einem rechten Winkel $C$. Zeichnen wir die Höhe $CD$ ein (Abb. 2).

Abbildung 2. Illustration von Satz 2
Lassen Sie uns beweisen, dass die Dreiecke $ACD$ und $BCD$ dem Dreieck $ABC$ ähnlich sind und dass die Dreiecke $ACD$ und $BCD$ einander ähnlich sind.
Da $\angle ADC=(90)^0$ ist, ist das Dreieck $ACD$ rechtwinklig. Die Dreiecke $ACD$ und $ABC$ haben einen gemeinsamen Winkel $A$, daher sind die Dreiecke $ACD$ und $ABC$ nach Satz 1 ähnlich.
Da $\angle BDC=(90)^0$ ist, ist das Dreieck $BCD$ rechtwinklig. Die Dreiecke $BCD$ und $ABC$ haben einen gemeinsamen Winkel $B$, daher sind die Dreiecke $BCD$ und $ABC$ nach Satz 1 ähnlich.
Betrachten wir nun die Dreiecke $ACD$ und $BCD$
\[\angle A=(90)^0-\angle ACD\] \[\angle BCD=(90)^0-\angle ACD=\angle A\]
Daher sind nach Satz 1 die Dreiecke $ACD$ und $BCD$ ähnlich.
Der Satz ist bewiesen.
Durchschnittlich proportional
Satz 3
Die Höhe eines rechtwinkligen Dreiecks, das vom Scheitelpunkt eines rechten Winkels gezogen wird, ist der Durchschnitt proportional zu den Segmenten, in die die Höhe die Hypotenuse des gegebenen Dreiecks unterteilt.
Nachweisen.
Nach Satz 2 haben wir also, dass die Dreiecke $ACD$ und $BCD$ ähnlich sind
Der Satz ist bewiesen.
Satz 4
Der Schenkel eines rechtwinkligen Dreiecks ist der mittlere Proportionalwert zwischen der Hypotenuse und dem Abschnitt der Hypotenuse, der zwischen dem Schenkel und der vom Scheitelpunkt des Winkels ausgehenden Höhe eingeschlossen ist.
Nachweisen.
Im Beweis des Theorems verwenden wir die Notation aus Abbildung 2.
Nach Satz 2 haben wir daher, dass die Dreiecke $ACD$ und $ABC$ ähnlich sind
Der Satz ist bewiesen.
Lernziele:
Lehrreich:
1.Schaffen Sie Bedingungen für die unabhängige Ableitung von Beziehungen, die proportionale Segmente verbinden rechtwinkliges Dreieck.
- Sorgen Sie dafür, dass das erworbene Wissen bei der Lösung von Problemen gefestigt wird.
Lehrreich:
1. Sorgen Sie für die Entwicklung der Unabhängigkeit bei der Ausführung von Aufgaben.
Lehrreich :
1. Fördern Sie eine Kommunikationskultur in einer Mikrogruppe.
- Entwickeln Sie die Fähigkeit, Entscheidungen zu treffen und Verantwortung dafür zu übernehmen.
Während des Unterrichts.
Leute, hört zu, wie still es ist!
Der Unterricht begann in der Schule.
Wir werden unsere Zeit nicht verschwenden
Und machen wir uns alle an die Arbeit.
Wir kamen hierher, um zu lernen
Seien Sie nicht faul, sondern arbeiten Sie.
Wir arbeiten fleißig
Hören wir aufmerksam zu.
- Unterrichtsmotivation.
Hallo Leute!
Ich hoffe, dass diese Lektion für alle interessant und von großem Nutzen sein wird. Ich möchte wirklich, dass diejenigen, denen die Königin aller Wissenschaften immer noch gleichgültig gegenübersteht, unsere Lektion mit der tiefen Überzeugung verlassen, dass Geometrie ein interessantes und notwendiges Fach ist.
Der französische Schriftsteller Anatole France aus dem 19. Jahrhundert bemerkte einmal: „Man kann nur durch Spaß lernen … Um Wissen zu verdauen, muss man es mit Appetit aufnehmen.“
Befolgen wir in der heutigen Lektion den Rat des Autors: Seien Sie aktiv, aufmerksam und nehmen Sie eifrig Wissen auf, das Ihnen im späteren Leben nützlich sein wird.
3. Wissen aktualisieren. Überprüfung von d/z.
Frontale Befragung:
- Wie nennt man das Verhältnis zweier Segmente?
- In welchem Fall sagen sie, dass die Segmente AB und CD proportional zu den Segmenten A 1 B 1 und C 1 D 1 sind?
- Definieren ähnliche Dreiecke
- So lesen Sie das erste Zeichen der Ähnlichkeit von Dreiecken
- So lesen Sie das zweite Ähnlichkeitszeichen von Dreiecken
- So lesen Sie das dritte Ähnlichkeitszeichen von Dreiecken
- Welche Figuren werden als ähnlich bezeichnet? Was ist ein Ähnlichkeitskoeffizient?
- Rechtwinkliges Dreieck. Beine. Hypotenuse.
Entscheidung Nr. 570 (mündlich), 573(1) (schriftlich).
- Neues Material lernen.
Bei der Lösung von Problemen haben wir am häufigsten spitze und stumpfe Dreiecke berücksichtigt. Die Elemente eines rechtwinkligen Dreiecks stehen in etwas unterschiedlicher Weise zueinander in Beziehung. Schauen wir uns die Zeichnung an.
Eigenschaften proportionaler Segmente in einem rechtwinkligen Dreieck:
1) ein Schenkel eines rechtwinkligen Dreiecks, es besteht ein proportionaler Mittelwert zwischen der Hypotenuse und der Projektion dieses Schenkels auf die Hypotenuse;
2) Die Höhe eines rechtwinkligen Dreiecks, das vom Scheitelpunkt eines rechten Winkels gezogen wird, ist das durchschnittliche Verhältnis zwischen den Projektionen der Schenkel auf die Hypotenuse.
Historische Referenz.Zur Entwicklung der praktischen Geometrie im antiken Russland.
Bereits im 16. Jahrhundert. Die Bedürfnisse der Vermessungs-, Bau- und Militärangelegenheiten führten zur Erstellung handschriftlicher Handbücher mit geometrischem Inhalt. Das erste Werk dieser Art, das uns überliefert ist, heißt „Über das Anlegen der Erde, wie man die Erde anlegt“. Es ist Teil des „Buches der Soshnogo-Briefe“, das vermutlich 1556 unter Iwan IV. geschrieben wurde. Die erhaltene Kopie stammt aus dem Jahr 1629.
Beim Abbau der Waffenkammer in Moskau im Jahr 1775 wurde die Anweisung „Charta des Militärs, der Kanonen und „anderer Angelegenheiten im Zusammenhang mit der Militärwissenschaft““ entdeckt, die 1607 und 1621 veröffentlicht wurde und einige geometrische Informationen enthielt, die auf bestimmte Methoden für reduziert wurden Lösung von Problemen beim Finden von Entfernungen Hier ist ein Beispiel.
Um den Abstand von Punkt I zu Punkt B (siehe Abbildung) zu messen, empfiehlt es sich, einen etwa menschengroßen Stab in Punkt I zu treiben. Die Spitze des rechten Winkels des Quadrats wird am oberen Ende der Stange C befestigt, sodass eines der Beine (oder seine Verlängerung) durch Punkt B verläuft. Punkt 3 des Schnittpunkts des anderen Beins (oder seiner Verlängerung) mit Der Boden ist markiert. Dann verhält sich der Abstand BYA genauso zur Stablänge TsYa wie die Stablänge zum Abstand YAZ. Zur Vereinfachung von Berechnungen und Messungen wurde der Stab in 1000 gleiche Teile geteilt.
- Konsolidierung von neuem Material.
Beschließen Sie mündlich Nr. 601, schriftlich Nr. 610, 600, 604(1), 607(2), 620.
- Übung für die Augen.
Schauen Sie sich, ohne den Kopf zu drehen, im Uhrzeigersinn um die Wand des Klassenzimmers herum, um die Tafel um den Umfang gegen den Uhrzeigersinn, um das auf dem Ständer abgebildete Dreieck im Uhrzeigersinn und das gleichförmige Dreieck gegen den Uhrzeigersinn. Drehen Sie Ihren Kopf nach links und schauen Sie auf die Horizontlinie und nun auf Ihre Nasenspitze. Schließe deine Augen, zähle bis 5, öffne deine Augen und...
Wir werden unsere Handflächen an unsere Augen legen,
Spreizen wir unsere starken Beine.
Nach rechts abbiegen
Schauen wir uns majestätisch um.
Und du musst auch nach links gehen
Schauen Sie unter Ihren Handflächen hervor.
Und – nach rechts! Und weiter
Über deine linke Schulter!
Jetzt lasst uns weiterarbeiten.
- Selbstständige Arbeit.
Arbeiten Sie zu zweit: Lösen Sie Nr. 604(2) (schriftlich)
8. Zusammenfassung der Lektion. Betrachtung.
- Woran erinnern Sie sich am meisten von der Lektion?
- Was hat Sie überrascht?
- Was mochtest du am Meisten?
- Wie soll die nächste Lektion aussehen?
Hausaufgabe: Paragraph 14 lernen, Nr. 604(3), 607(3), 573(2) lösen.
Abschnitte: Mathematik
Klasse: 8
Unterrichtsart: kombiniert.
Didaktisches Ziel: Schaffung von Bedingungen für das Bewusstsein und Verständnis des Konzepts des „proportionalen Durchschnitts“, Verbesserung der Fähigkeiten zum Finden proportionaler Segmente basierend auf der Ähnlichkeit von Dreiecken, Überprüfung des Niveaus der Assimilation von Wissen und Fähigkeiten zu diesem Thema.
Aufgaben:
- Stellen Sie eine Entsprechung zwischen den Seiten eines rechtwinkligen Dreiecks, der Höhe der Hypotenuse und den Segmenten der Hypotenuse her.
- das Konzept des durchschnittlichen Proportionalitätsfaktors einführen;
- die Fähigkeit entwickeln, erworbenes Wissen zur Lösung praktischer Probleme anzuwenden;
Lehrmaterial: Lehrbuch „Geometrie 7-9“ von L. S. Atanasyan, Präsentation „Proportionale Segmente in einem rechtwinkligen Dreieck“. Anhang 1 .
Erwartete Ergebnisse:
persönlich
- Die Fähigkeit, die Grenze zwischen Wissen und Unwissenheit zu bestimmen.
- Fähigkeit, Gedanken mathematisch korrekt auszudrücken.
- Fähigkeit, falsche Aussagen zu erkennen.
Metasubjekt
- Die Fähigkeit, Ihre Aktivitäten zur Lösung eines Lernproblems zu planen.
- Die Fähigkeit, eine Kette logischen Denkens aufzubauen.
- Die Fähigkeit, eine in Form einer Formel geschriebene Tatsache verbal zu formulieren.
Thema
- Die Fähigkeit, ähnliche Dreiecke zu finden und ihre Ähnlichkeit zu beweisen.
- Die Fähigkeit, die Schenkel eines rechtwinkligen Dreiecks und die Höhe darzustellen, die vom Scheitelpunkt eines rechten Winkels durch Segmente der Hypotenuse gezogen werden.
- Fähigkeit, mathematische Notationen unter Verwendung des Konzepts des „proportionalen Durchschnitts“ zu lesen.
Unterrichtsübersichtsplan.
1. Organisatorischer Moment. Aufmerksamkeitsorganisation; freiwillige Selbstregulierung. (Jeder Schüler erhält Arbeitsblätter für die Lektion für zwei Optionen). Anlage 2 , Anhang 3 .
2. Wiederholung: Wiederholen wir die grundlegenden Informationen zum Thema „Ähnliche Dreiecke“ Folie 1
- Definieren Sie ähnliche Dreiecke
- So lesen Sie das erste Zeichen der Ähnlichkeit von Dreiecken
- So lesen Sie das zweite Ähnlichkeitszeichen von Dreiecken
- So lesen Sie das dritte Ähnlichkeitszeichen von Dreiecken
- Was ist ein Ähnlichkeitskoeffizient?
- Rechtwinkliges Dreieck. Beine. Hypotenuse.
Ein Test zur Feststellung der Wahrheit oder Falschheit von Aussagen (Antwort „Ja“ oder „Nein“). Folie 2
- Zwei Dreiecke sind ähnlich, wenn ihre Winkel jeweils gleich sind und ihre ähnlichen Seiten proportional sind.
- Zwei gleichseitige Dreiecke sind immer ähnlich.
- Wenn drei Seiten eines Dreiecks jeweils proportional zu drei Seiten eines anderen Dreiecks sind, dann sind solche Dreiecke ähnlich.
- Die Seiten des einen Dreiecks haben eine Länge von 3, 4, 6 cm, die Seiten des anderen Dreiecks sind 9, 14, 18 cm lang. Sind diese Dreiecke ähnlich?
- Die Umfänge ähnlicher Dreiecke sind gleich.
- Wenn zwei Winkel eines Dreiecks 60° und 50° betragen und zwei Winkel eines anderen Dreiecks 50° und 80° betragen, dann sind die Dreiecke ähnlich.
- Zwei rechtwinklige Dreiecke sind ähnlich, wenn sie gleiche spitze Winkel haben.
- Zwei gleichschenkligen Dreiecksähnlich.
- Wenn zwei Winkel eines Dreiecks jeweils gleich zwei Winkeln eines anderen Dreiecks sind, dann sind diese Dreiecke ähnlich.
- Wenn zwei Seiten eines Dreiecks jeweils proportional zu zwei Seiten eines anderen Dreiecks sind, dann sind die Dreiecke ähnlich.
Schlüssel zum Test: 1. ja; 2. ja; 3. ja; 4. nein; 5. nein; 6. nein; 7. ja; 8. nein; 9. ja; 10. nein.
Das Testverifizierungsformular ist eine gegenseitige Verifizierung. Antworten und Überprüfung erfolgen im Arbeitsblatt zur Lektion.
3. Theoretische Aufgabe in Gruppen. Die Klasse ist in drei Gruppen aufgeteilt. Jede Gruppe erhält eine Aufgabe. Anhang 4 .
Gruppe Nr. 1
- Beweisen Sie die Ähnlichkeit der „linken“ und „rechten“ rechtwinkligen Dreiecke.
- Notieren Sie die Proportionalität der Beine.
- Drücken Sie die Höhe anhand der Proportionen aus.
Gruppe Nr. 2
Nach einer vorbereiteten Zeichnung eines rechtwinkligen Dreiecks (Abbildung 1)
- Beweisen Sie die Ähnlichkeit des „linken“ und des „großen“ rechtwinkligen Dreiecks.
- Ausdrücken aus dem Verhältnis BC.
Gruppe Nr. 3
Nach einer vorbereiteten Zeichnung eines rechtwinkligen Dreiecks (Abbildung 1)
- Beweisen Sie die Ähnlichkeit des „rechten“ und des „großen“ rechtwinkligen Dreiecks.
- Notieren Sie die Verhältnismäßigkeit ähnlicher Seiten.
- Aus dem Verhältnis AC ausdrücken.
Schreiben Sie den Beweis dieser Aussagen anhand vorgefertigter Zeichnungen und in Notizbüchern an die Tafel. Eine Person aus der Gruppe wird an die Tafel gerufen.
4. Formulierung des Unterrichtsthemas. In allen drei Aufgaben haben wir einige Beziehungen hergestellt. Wie kann man die Elemente nennen, die in diesen Beziehungen enthalten sind? Antwort: Proportionale Segmente. Lassen Sie uns die proportionalen Segmente in ... klären? Antwort: in einem rechtwinkligen Dreieck. Also, Leute, das Thema unserer Lektion? Antwort: „Proportionale Segmente in einem rechtwinkligen Dreieck.“ Folie 3
5. Formulierung bewiesener Aussagen
Bevor wir weiterarbeiten, stellen wir einige neue Konzepte und Notationen vor.
Was ist das arithmetische Mittel zweier Zahlen?
Antwort: Das arithmetische Mittel der Zahlen m und n ist die Zahl a, die der Hälfte der Summe der Zahlen m und n entspricht
Schreiben Sie die Formel für das arithmetische Mittel der Zahlen m und n auf.
Formulieren wir die Definition des geometrischen Mittels zweier Zahlen: Die Zahl a heißt geometrisches Mittel (oder Proportionalmittel) für die Zahlen m und n, wenn die Gleichheit erfüllt ist Folie 4
Lassen Sie uns mehrere Übungen lösen, um diese Definitionen zu festigen. Folie 5
1. Ermitteln Sie das arithmetische Mittel und das geometrische Mittel der Zahlen 3 und 12.
2. Ermitteln Sie die Länge der durchschnittlichen proportionalen (geometrischen) Segmente MN und KP, wenn MN = 9 cm, KP = 27 cm
Lassen Sie uns das Konzept der Projektion eines Beins auf die Hypotenuse einführen. Folie 6.
Nun werden wir versuchen, anhand neuer Konzepte die in der Gruppenarbeit bewährten Schlussfolgerungen zu formulieren.
Versuchen Sie anhand dieser Folie eine Aussage zu formulieren, die von der zweiten und dritten Gruppe bewiesen wurde. Folie 7
Schreiben Sie diese Aussage mit der neuen Notation (Projektion eines Schenkels auf die Hypotenuse) auf und formulieren Sie sie dann mit der Definition der Projektion eines Schenkels auf die Hypotenuse. Folie 8
Versuchen Sie, auf der Grundlage dieser Folie eine Aussage zu formulieren, die von Schülern der dritten Gruppe bewiesen wurde. Folie 9
Schreiben Sie diese Aussage mit der neuen Notation (Projektion eines Schenkels auf die Hypotenuse) auf und formulieren Sie sie dann mit der Definition der Projektion eines Schenkels auf die Hypotenuse. Folie 10
6. Blitzumfrage zur Konsolidierung der untersuchten Formeln. Folie 11-12
- In einem rechtwinkligen Dreieck ABC wird die Höhe CD vom Scheitelpunkt des rechten Winkels C gezeichnet. AD = 16, DB = 9. Finden Sie AC, AB, CB und CD. Folie 11
- In einem rechtwinkligen Dreieck ABC wird die Höhe CD vom Scheitelpunkt des rechten Winkels C gezeichnet. AD = 18, DB = 2. Finden Sie AC, AB, CB und CD. Folie 12
- In einem rechtwinkligen Dreieck ABC wird die Höhe CH vom Scheitelpunkt des rechten Winkels C aus gezeichnet. CA = 6, AN = 2. Finden Sie NV. Folie 13
Testen Sie, um die anfängliche Beherrschung des Materials zu überprüfen
Öffnen Sie in der Präsentation die Folie mit den abgeleiteten Formeln (Folie 14). Auf den Arbeitsblättern ist ein Test aufgedruckt: Schließen Sie den Test ab, indem Sie die richtigen Antworten in die Tabelle schreiben. Anschließend gegenseitige Überprüfung (Folie 15) anhand vorgefertigter Antworten in der Präsentation.
Hausaufgaben
Jeder Schüler erhält ein Memo mit Formeln und dem Text der Hausaufgaben mit Tipps (einen Plan für die schrittweise Erledigung jeder Aufgabe). Anhang 5 .
9. Reflexion
Fassen Sie die Lektion zusammen. Sammeln Sie Arbeitsblätter und benoten Sie die Lektion jedes Schülers.
Literatur.
- http://gorkunova.ucoz.ru/ Handouts zum Workshop zum Thema „Proportionale Segmente in einem rechtwinkligen Dreieck“
- Präsentation „Proportionale Segmente in einem rechtwinkligen Dreieck“ Savchenko E.M. Polyarnye Zori, Region Murmansk.
Um Präsentationsvorschauen zu nutzen, erstellen Sie ein Google-Konto und melden Sie sich an: https://accounts.google.com
Folienunterschriften:
Proportionale Segmente in einem rechtwinkligen Dreieck, Geometrieklasse 8
Hausaufgaben
1. Aufgabe 3, 5 A B C N M 3 4 Gegeben: MN || A.C. Fundort: Р∆АВС
A B C D M N P Q MNPQ ist ein Parallelogramm? 2. Problem
Ähnlichkeit rechtwinkliger Dreiecke A B C A 1 B 1 C 1 Wenn ein spitzer Winkel eines rechtwinkligen Dreiecks gleich einem spitzen Winkel eines anderen rechtwinkligen Dreiecks ist, dann sind solche rechtwinkligen Dreiecke ähnlich
Proportionaler Mittelwert A B C D X Y Das Segment XY wird als Proportionalmittelwert (geometrisches Mittel) für die Segmente AB und CD bezeichnet, wenn
Lösen Sie die Aufgaben: 1. Ist ein Segment mit einer Länge von 8 cm das durchschnittliche Verhältnis zwischen Segmenten mit einer Länge von 16 cm und 4 cm? 2. Ist ein Segment mit einer Länge von 9 cm das durchschnittliche Verhältnis zwischen Segmenten mit einer Länge von 15 cm und 6 cm? 3. Ist ein Segment mit einer Länge von cm das durchschnittliche Verhältnis zwischen Segmenten mit einer Länge von 5 cm und 4 cm? ja nein ja
Proportionale Segmente in einem rechtwinkligen Dreieck A B C H Die Höhe eines rechtwinkligen Dreiecks, das vom Scheitelpunkt eines rechten Winkels gezogen wird, ist der Durchschnitt proportional zu den Segmenten, in die die Hypotenuse durch diese Höhe geteilt wird
Proportionale Segmente in einem rechtwinkligen Dreieck A B C H 9 4? Aufgabe 1.
Proportionale Segmente in einem rechtwinkligen Dreieck A B C H 9 7? Aufgabe 2.
Proportionale Segmente in einem rechtwinkligen Dreieck A B C N Ein Schenkel eines rechtwinkligen Dreiecks ist der Mittelwert proportional zur Hypotenuse und der Projektion dieses Schenkels auf die Hypotenuse.
Proportionale Segmente in einem rechtwinkligen Dreieck A B C H 21 4? Aufgabe 3.
A B C N 20 30 ? Aufgabe 4.
Hausaufgaben
Aufgabe 5 lösen 2 ? ? ? Problem 9 lösen 4 ? ? ? Dreieck lösen
A B C N 20 15 ? Aufgabe. In einem Dreieck mit den Seitenlängen 15, 20 und 25 wird die Höhe auf der längeren Seite dargestellt. Finden Sie die Segmente, in die die Höhe diese Seite 25 teilt
A B C N 20 15 ? Aufgabe 5. In einem Dreieck mit den Seitenlängen 15, 20 und 25 wird die Höhe auf der längeren Seite dargestellt. Finden Sie die Segmente, in die die Höhe diese Seite 25 teilt