Die Mantelfläche des Kegels ist zusätzlich. Fläche der Mantel- und Gesamtfläche des Kegels

Die in der Schule untersuchten Rotationskörper sind Zylinder, Kegel und Kugel.

Wenn Sie bei einer Aufgabe im Einheitlichen Staatsexamen in Mathematik das Volumen eines Kegels oder die Fläche einer Kugel berechnen müssen, können Sie sich glücklich schätzen.

Wenden Sie Formeln für Volumen und Oberfläche eines Zylinders, Kegels und einer Kugel an. Alle davon sind in unserer Tabelle. Auswendig lernen. Hier beginnt das Wissen über Stereometrie.

Manchmal ist es gut, die Ansicht von oben zu zeichnen. Oder, wie in diesem Problem, von unten.

2. Wie oft wird das Volumen eines Kegels um das Richtige herum beschrieben? viereckige Pyramide, ist größer als das Volumen des Kegels, der in diese Pyramide eingeschrieben ist?

Es ist ganz einfach: Zeichnen Sie die Ansicht von unten. Wir sehen, dass der Radius des größeren Kreises um ein Vielfaches größer ist als der Radius des kleineren. Die Höhe beider Kegel ist gleich. Daher ist das Volumen des größeren Kegels doppelt so groß.

Noch eins wichtiger Punkt. Denken Sie daran, dass in den Problemen von Teil B Optionen für das einheitliche Staatsexamen In der Mathematik wird die Antwort als ganze Zahl oder endliche Zahl geschrieben Dezimal. Daher sollte Ihre Antwort in Teil B kein oder enthalten. Es besteht auch keine Notwendigkeit, den ungefähren Wert der Zahl zu ersetzen! Es muss unbedingt schrumpfen! Zu diesem Zweck wird bei einigen Problemen die Aufgabe beispielsweise wie folgt formuliert: „Finden Sie die Fläche der Mantelfläche des Zylinders geteilt durch.“

Wo sonst werden die Formeln für Volumen und Oberfläche von Rotationskörpern verwendet? Natürlich in Aufgabe C2 (16). Wir werden Ihnen auch davon erzählen.

Zurück vorwärts

Aufmerksamkeit! Folienvorschauen dienen nur zu Informationszwecken und stellen möglicherweise nicht alle Funktionen der Präsentation dar. Wenn Sie interessiert sind diese Arbeit Bitte laden Sie die Vollversion herunter.

Unterrichtsart: eine Lektion zum Erlernen neuer Materialien unter Verwendung von Elementen einer problembasierten Entwicklungslehrmethode.

Lernziele:

• lehrreich:
  • Kennenlernen eines neuen mathematischen Konzepts;
  • Gründung neuer Ausbildungszentren;
  • Ausbildung praktischer Problemlösungsfähigkeiten.
• Entwicklung:
  • Entwicklung des unabhängigen Denkens der Studierenden;
  • Kompetenzentwicklung richtige Rede Schulkinder.
• lehrreich:
  • Teamfähigkeit entwickeln.

Unterrichtsausrüstung: Magnettafel, Computer, Leinwand, Multimediaprojektor, Kegelmodell, Unterrichtspräsentation, Handouts.

Unterrichtsziele (für Studierende):

• lernen Sie ein neues geometrisches Konzept kennen - Kegel;
• Leiten Sie eine Formel zur Berechnung der Oberfläche eines Kegels ab.
• lernen, das erworbene Wissen bei der Lösung praktischer Probleme anzuwenden.

Während des Unterrichts

Stufe I. Organisatorisch.

Abgabe von Heften mit Heimtestarbeiten zum behandelten Thema.

Die Schüler sind eingeladen, durch Lösen des Rätsels das Thema der kommenden Unterrichtsstunde herauszufinden (Folie 1):

Bild 1.

Bekanntgabe des Themas und der Ziele des Unterrichts an die Schüler (Folie 2).

Stufe II. Erläuterung des neuen Materials.

1) Vortrag des Lehrers.

Auf der Tafel befindet sich eine Tabelle mit dem Bild eines Kegels. Neues Material wird mit dem Programmmaterial „Stereometrie“ erläutert. Auf dem Bildschirm erscheint ein dreidimensionales Bild eines Kegels. Der Lehrer gibt die Definition eines Kegels und spricht über seine Elemente. (Folie 3). Man sagt, ein Kegel sei ein Körper, der durch die Drehung eines rechtwinkligen Dreiecks relativ zu einem Bein entsteht. (Folien 4, 5). Es erscheint ein Bild eines Scans der Seitenfläche des Kegels. (Folie 6)

2) Praktische Arbeit.

Grundkenntnisse aktualisieren: Wiederholen Sie die Formeln zur Berechnung der Fläche eines Kreises, der Fläche eines Sektors, der Länge eines Kreises, der Länge eines Kreisbogens. (Folien 7–10)

Die Klasse wird in Gruppen eingeteilt. Jede Gruppe erhält einen Scan der Mantelfläche des aus Papier ausgeschnittenen Kegels (ein Kreissektor mit einer zugewiesenen Nummer). Die Studierenden nehmen die notwendigen Messungen vor und berechnen die Fläche des resultierenden Sektors. Anweisungen zur Arbeitsausführung, Fragen – Problemstellungen – erscheinen auf dem Bildschirm (Folien 11–14). Ein Vertreter jeder Gruppe schreibt die Ergebnisse der Berechnungen in eine an der Tafel vorbereitete Tabelle. Die Teilnehmer jeder Gruppe kleben aus der Vorlage, die sie haben, ein Modell eines Kegels zusammen. (Folie 15)

3) Darstellung und Lösung des Problems.

Wie berechnet man die Mantelfläche eines Kegels, wenn nur der Radius der Grundfläche und die Länge der Mantellinie des Kegels bekannt sind? (Folie 16)

Jede Gruppe nimmt die notwendigen Messungen vor und versucht anhand der verfügbaren Daten eine Formel zur Berechnung der benötigten Fläche abzuleiten. Bei dieser Arbeit sollten die Schüler beachten, dass der Umfang der Kegelbasis gleich der Länge des Sektorbogens ist – der Entwicklung der Mantelfläche dieses Kegels. (Folien 17–21) Anhand der notwendigen Formeln wird die gewünschte Formel abgeleitet. Die Argumente der Studierenden sollten etwa so aussehen:

Der Sektor-Sweep-Radius ist gleich lch, Gradmaß des Bogens – φ. Die Fläche des Sektors wird nach der Formel berechnet: Die Länge des diesen Sektor begrenzenden Bogens ist gleich dem Radius der Kegelbasis R. Die Länge des an der Kegelbasis liegenden Kreises beträgt C = 2πR . Beachten Sie, dass die Fläche der Seitenfläche des Kegels gleich der Entwicklungsfläche seiner Seitenfläche ist

Die Fläche der Mantelfläche des Kegels wird also nach der Formel berechnet S BSB = πRl.

Nach der Berechnung der Fläche der Mantelfläche des Kegelmodells anhand einer unabhängig abgeleiteten Formel schreibt ein Vertreter jeder Gruppe das Ergebnis der Berechnungen entsprechend den Modellnummern in eine Tabelle an die Tafel. Die Berechnungsergebnisse in jeder Zeile müssen gleich sein. Auf dieser Grundlage bestimmt der Lehrer die Richtigkeit der Schlussfolgerungen jeder Gruppe. Die Ergebnistabelle sollte so aussehen:

Modellparameter:

1. l=12 cm, φ =120°
2. l=10 cm, φ =150°
3. l=15 cm, φ =120°
4. l=10 cm, φ =170°
5. l=14 cm, φ =110°

Die Annäherung von Berechnungen ist mit Messfehlern verbunden.

Nach Überprüfung der Ergebnisse erscheint die Ausgabe der Formeln für die Flächen der Mantel- und Gesamtflächen des Kegels auf dem Bildschirm (Folien 22–26), Schüler machen Notizen in Notizbüchern.

Stufe III. Konsolidierung des untersuchten Materials.

1) Studenten werden angeboten Probleme zur mündlichen Lösung anhand vorgefertigter Zeichnungen.

Ermitteln Sie die Flächen der vollständigen Oberflächen der in den Abbildungen gezeigten Kegel (Folien 27–32).

2) Frage: Sind die Oberflächenflächen von Kegeln, die durch die Drehung eines rechtwinkligen Dreiecks um verschiedene Schenkel entstehen, gleich? Die Schüler stellen eine Hypothese auf und testen diese. Die Hypothese wird durch das Lösen von Problemen überprüft und vom Schüler an die Tafel geschrieben.

Gegeben:Δ ABC, ∠C=90°, AB=c, AC=b, BC=a;

ВАА", АВВ" – Rotationskörper.

Finden: S PPK 1, S PPK 2.

Abbildung 5. (Folie 33)

Lösung:

1) R=BC = a; S PPK 1 = S BSB 1 + S Haupt 1 = π a c + π a 2 = π a (a + c).

2) R=AC = b; S PPK 2 = S BSB 2 + S Basis 2 = π b c+π b 2 = π b (b + c).

Wenn S PPK 1 = S PPK 2, dann a 2 +ac = b 2 + bc, a 2 - b 2 + ac - bc = 0, (a-b)(a+b+c) = 0. Weil a, b, c – positive Zahlen (die Längen der Seiten des Dreiecks), die Gleichheit ist nur dann wahr, wenn a =B.

Abschluss: Die Oberflächen zweier Kegel sind nur dann gleich, wenn die Seiten des Dreiecks gleich sind. (Folie 34)

3) Lösung des Problems aus dem Lehrbuch: Nr. 565.

Stufe IV. Zusammenfassung der Lektion.

Hausaufgaben: Absätze 55, 56; Nr. 548, Nr. 561. (Folie 35)

Bekanntgabe der vergebenen Noten.

Schlussfolgerungen während des Unterrichts, Wiederholung der wichtigsten während des Unterrichts erhaltenen Informationen.

Literatur (Folie 36)

1. Geometrieklassen 10–11 – Atanasyan, V.F. Butuzov, S.B. Kadomtsev et al., M., „Prosveshchenie“, 2008.
2. „Mathematische Rätsel und Scharaden“ – N.V. Udaltsova, Bibliothek „Erster September“, Reihe „MATHEMATIK“, Ausgabe 35, M., Chistye Prudy, 2010.

Wir wissen, was ein Kegel ist. Versuchen wir, seine Oberfläche zu ermitteln. Warum müssen Sie ein solches Problem lösen? Sie möchten zum Beispiel wissen, wie viel Teig für die Herstellung einer Waffelwaffel benötigt wird? Oder wie viele Steine ​​braucht man, um das Dach einer gemauerten Burg zu bauen?

Die Messung der Mantelfläche eines Kegels ist einfach nicht möglich. Aber stellen wir uns das gleiche Horn vor, das in Stoff gehüllt ist. Um die Fläche eines Stoffstücks zu ermitteln, müssen Sie es ausschneiden und auf dem Tisch auslegen. Das Ergebnis ist eine flache Figur, deren Fläche wir ermitteln können.

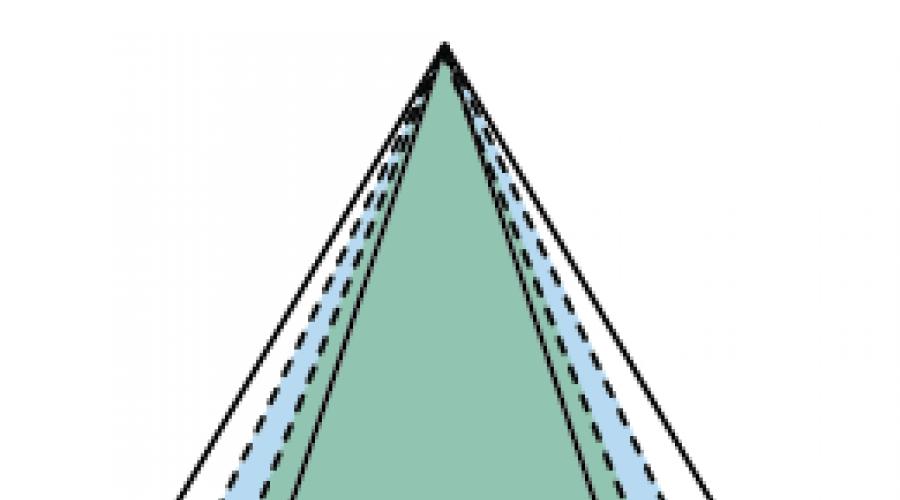
Reis. 1. Schnitt eines Kegels entlang der Mantellinie

Machen wir dasselbe mit dem Kegel. Lassen Sie uns seine Seitenfläche zum Beispiel entlang einer beliebigen Mantellinie „schneiden“ (siehe Abb. 1).

Lassen Sie uns nun die Seitenfläche auf eine Ebene „abwickeln“. Wir bekommen einen Sektor. Der Mittelpunkt dieses Sektors ist die Spitze des Kegels, der Radius des Sektors ist gleich der Erzeugenden des Kegels und die Länge seines Bogens stimmt mit dem Umfang der Basis des Kegels überein. Dieser Sektor wird als Entwicklung der Mantelfläche des Kegels bezeichnet (siehe Abb. 2).

Reis. 2. Entwicklung der Seitenfläche

Reis. 3. Winkelmessung im Bogenmaß

Versuchen wir, anhand der verfügbaren Daten die Fläche des Sektors zu ermitteln. Lassen Sie uns zunächst die Notation einführen: Der Winkel am Scheitelpunkt des Sektors sei im Bogenmaß angegeben (siehe Abb. 3).

Bei Problemen müssen wir uns oft mit dem Winkel am oberen Ende des Sweeps auseinandersetzen. Versuchen wir zunächst, die Frage zu beantworten: Kann dieser Winkel nicht mehr als 360 Grad betragen? Das heißt, würde sich nicht herausstellen, dass sich der Sweep überlappen würde? Natürlich nicht. Lassen Sie uns dies mathematisch beweisen. Lassen Sie den Scan sich selbst „überlagern“. Dies bedeutet, dass die Länge des Sweep-Bogens größer ist als die Länge des Kreises mit dem Radius. Aber wie bereits erwähnt, ist die Länge des Sweep-Bogens die Länge des Kreises mit dem Radius. Und der Radius der Kegelbasis ist natürlich kleiner als die Erzeugende, weil zum Beispiel der Schenkel eines rechtwinkligen Dreiecks kleiner ist als die Hypotenuse

Dann erinnern wir uns an zwei Formeln aus dem Planimetriekurs: Bogenlänge. Branchengebiet: .

In unserem Fall übernimmt der Generator die Rolle , und die Länge des Bogens ist gleich dem Umfang der Kegelbasis, das heißt. Wir haben:

Schließlich erhalten wir: .

Neben der Fläche der Mantelfläche findet man auch die Fläche Vollflächig. Dazu muss die Fläche der Basis zur Fläche der Mantelfläche addiert werden. Aber die Basis ist ein Kreis mit einem Radius, dessen Fläche gemäß der Formel gleich ist.

Endlich haben wir: , Wo ist der Radius der Basis des Zylinders, ist die Generatrix.

Lassen Sie uns ein paar Probleme mit den angegebenen Formeln lösen.

Reis. 4. Erforderlicher Winkel

Beispiel 1. Die Entwicklung der Mantelfläche des Kegels ist ein Sektor mit einem Winkel an der Spitze. Finden Sie diesen Winkel, wenn die Höhe des Kegels 4 cm und der Radius der Basis 3 cm beträgt (siehe Abb. 4).

Reis. 5. Rechtwinkliges Dreieck, das einen Kegel bildet

Durch die erste Aktion ermitteln wir nach dem Satz des Pythagoras den Generator: 5 cm (siehe Abb. 5). Als nächstes wissen wir das .

Beispiel 2. Die axiale Querschnittsfläche des Kegels ist gleich, die Höhe ist gleich. Ermitteln Sie die Gesamtoberfläche (siehe Abb. 6).