Funcții cuadratice, proprietățile și grafica lor. Funcția pătratică și graficul acesteia

O funcție de forma unde este numită funcţie pătratică.

Graficul unei funcții pătratice – parabolă.

Să luăm în considerare cazurile:

I CAZ, PARABOLA CLASICA

Acesta este , ,

Pentru a construi, completați tabelul înlocuind valorile x în formula:

Marcați punctele (0;0); (1;1); (-1;1), etc. pe planul de coordonate (cu cât este mai mic pasul luăm valorile x (în acest caz, pasul 1), și cu cât luăm mai multe valori x, cu atât curba va fi mai netedă), obținem o parabolă:

Este ușor de observat că dacă luăm cazul , , , adică, atunci obținem o parabolă care este simetrică față de axa (oh). Este ușor să verificați acest lucru completând un tabel similar:

II CAZUL, „a” ESTE DIFERIT DE UNITATEA

Ce se va întâmpla dacă luăm , , ? Cum se va schimba comportamentul parabolei? Cu title="Redată de QuickLaTeX.com" height="20" width="55" style="vertical-align: -5px;"> парабола изменит форму, она “похудеет” по сравнению с параболой (не верите – заполните соответствующую таблицу – и убедитесь сами):!}

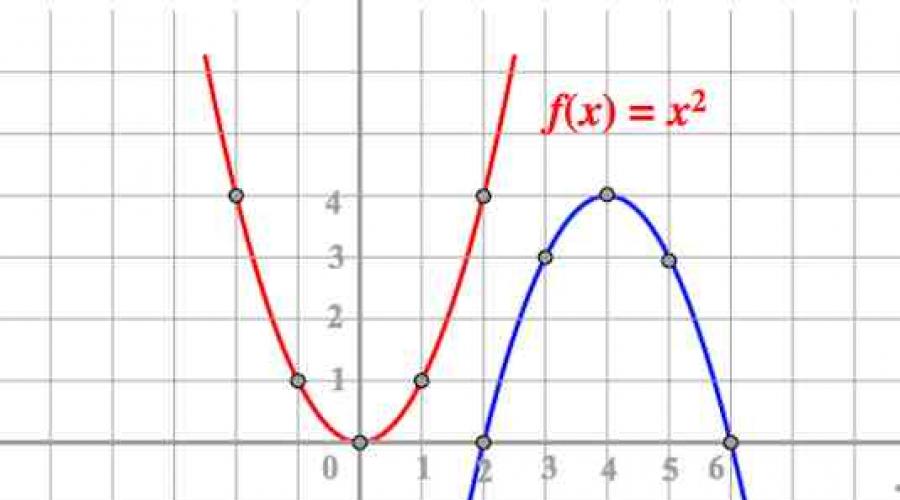
În prima imagine (vezi mai sus) se vede clar că punctele din tabel pentru parabolă (1;1), (-1;1) au fost transformate în puncte (1;4), (1;-4), adică, cu aceleași valori, ordonata fiecărui punct este înmulțită cu 4. Acest lucru se va întâmpla cu toate punctele cheie ale tabelului original. Raționăm în mod similar în cazurile imaginilor 2 și 3.

Și când parabola „devine mai lată” decât parabola:

Să rezumăm:

1)Semnul coeficientului determină direcția ramurilor. Cu title="Redată de QuickLaTeX.com" height="14" width="47" style="vertical-align: 0px;"> ветви направлены вверх, при - вниз. !}

2) Valoare absolută coeficientul (modulul) este responsabil pentru „expansiunea” și „compresia” parabolei. Cu cât este mai mare, cu atât parabola este mai îngustă; cu cât |a| este mai mic, cu atât parabola este mai largă.

CAZUL III, APARE „C”.

Acum să introducem în joc (adică să luăm în considerare cazul când), vom lua în considerare parabole de forma . Nu este greu să ghiciți (vă puteți referi întotdeauna la tabel) că parabola se va deplasa în sus sau în jos de-a lungul axei, în funcție de semn:

CAZUL IV, AARE „b”.

Când se va „desprinde” parabola de axă și, în cele din urmă, „se va plimba” de-a lungul întregului plan de coordonate? Când va înceta să mai fie egal?

Aici avem nevoie pentru a construi o parabolă formula pentru calcularea vârfului: , .

Deci, în acest moment (ca la punctul (0;0) sistem nou coordonate) vom construi o parabolă, ceea ce o putem face deja. Dacă avem de-a face cu cazul, atunci din vârf punem un segment de unitate la dreapta, unul în sus, - punctul rezultat este al nostru (în mod similar, un pas la stânga, un pas în sus este punctul nostru); dacă avem de-a face cu, de exemplu, atunci de la vârf punem un segment de unitate la dreapta, două - în sus etc.

De exemplu, vârful unei parabole:

Acum, principalul lucru de înțeles este că la acest vârf vom construi o parabolă conform modelului parabolei, deoarece în cazul nostru.

La construirea unei parabole după ce s-au găsit coordonatele vârfului foarteEste convenabil să luați în considerare următoarele puncte:

1) parabolă va trece cu siguranță prin punct . Într-adevăr, înlocuind x=0 în formulă, obținem că . Adică, ordonata punctului de intersecție al parabolei cu axa (oy) este . În exemplul nostru (mai sus), parabola intersectează ordonata în punctul , deoarece .

2) axa de simetrie parabole este o linie dreaptă, deci toate punctele parabolei vor fi simetrice față de ea. În exemplul nostru, luăm imediat punctul (0; -2) și îl construim simetric față de axa de simetrie a parabolei, obținem punctul (4; -2) prin care va trece parabola.

3) Echivalând cu , aflăm punctele de intersecție ale parabolei cu axa (oh). Pentru a face acest lucru, rezolvăm ecuația. În funcție de discriminant, vom obține unul (, ), doi ( title="Rendered by QuickLaTeX.com)" height="14" width="54" style="vertical-align: 0px;">, ) или нИсколько () точек пересечения с осью (ох) !} . În exemplul anterior, rădăcina noastră a discriminantului nu este un număr întreg; atunci când construim, nu prea are sens să găsim rădăcinile, dar vedem clar că vom avea două puncte de intersecție cu axa (oh) (din moment ce title="Redată de QuickLaTeX.com" height="14" width="54" style="vertical-align: 0px;">), хотя, в общем, это видно и без дискриминанта.!}

Deci hai să rezolvăm

Algoritm pentru construirea unei parabole dacă este dat sub forma

1) determinați direcția ramurilor (a>0 – sus, a<0 – вниз)

2) găsim coordonatele vârfului parabolei folosind formula , .

3) găsim punctul de intersecție al parabolei cu axa (oy) folosind termenul liber, construim un punct simetric față de acest punct față de axa de simetrie a parabolei (de remarcat că se întâmplă ca nu este rentabil să se marcheze acest punct, de exemplu, pentru că valoarea este mare... sărim peste acest punct...)

4) În punctul găsit - vârful parabolei (ca și în punctul (0;0) al noului sistem de coordonate) construim o parabolă. Dacă title="Redată de QuickLaTeX.com" height="20" width="55" style="vertical-align: -5px;">, то парабола становится у’же по сравнению с , если , то парабола расширяется по сравнению с !}

5) Găsim punctele de intersecție ale parabolei cu axa (oy) (dacă nu au „ieșit la suprafață”) rezolvând ecuația

Exemplul 1

Exemplul 2

Nota 1. Dacă parabola ne este dată inițial sub forma , unde sunt unele numere (de exemplu, ), atunci va fi și mai ușor să o construim, deoarece ni s-au dat deja coordonatele vârfului . De ce?

Să luăm un trinom pătratic și să izolăm pătratul complet din el: Uite, am obținut că , . Tu și cu mine anterior numiam vârful unei parabole, adică acum,.

De exemplu, . Marcam vârful parabolei pe plan, înțelegem că ramurile sunt îndreptate în jos, parabola este extinsă (în raport cu ). Adică realizăm punctele 1; 3; 4; 5 din algoritmul pentru construirea unei parabole (vezi mai sus).

Nota 2. Dacă parabola este dată într-o formă similară cu aceasta (adică prezentată ca un produs al doi factori liniari), atunci vedem imediat punctele de intersecție ale parabolei cu axa (bou). În acest caz – (0;0) și (4;0). În rest, acționăm conform algoritmului, deschizând parantezele.

După cum arată practica, sarcinile privind proprietățile și graficele unei funcții pătratice provoacă dificultăți serioase. Acest lucru este destul de ciudat, deoarece ei studiază funcția pătratică în clasa a 8-a, iar apoi pe parcursul primului trimestru al clasei a IX-a „chinuiază” proprietățile parabolei și își construiesc grafice pentru diferiți parametri.

Acest lucru se datorează faptului că atunci când îi forțează pe elevi să construiască parabole, practic nu dedică timp „citirii” graficelor, adică nu exersează înțelegerea informațiilor primite din imagine. Aparent, se presupune că, după construirea unei duzini sau două grafice, un student inteligent va descoperi însuși și va formula relația dintre coeficienții din formulă și aspect Arte grafice. În practică, acest lucru nu funcționează. Pentru o astfel de generalizare, este necesară o experiență serioasă în mini-cercetare matematică, pe care, desigur, majoritatea elevilor de clasa a IX-a nu o posedă. Între timp, Inspectoratul de Stat propune să se determine semnele coeficienților folosind graficul.

Nu vom cere imposibilul de la școlari și vom oferi pur și simplu unul dintre algoritmii pentru rezolvarea unor astfel de probleme.

Deci, o funcție a formei y = ax 2 + bx + c numit pătratic, graficul său este o parabolă. După cum sugerează și numele, termenul principal este toporul 2. Acesta este A nu trebuie să fie egal cu zero, coeficienții rămași ( bȘi Cu) poate fi egal cu zero.

Să vedem cum semnele coeficienților săi afectează aspectul unei parabole.

Cea mai simplă dependență pentru coeficient A. Majoritatea școlarilor răspund cu încredere: „dacă A> 0, atunci ramurile parabolei sunt îndreptate în sus, iar dacă A < 0, - то вниз". Совершенно верно. Ниже приведен график квадратичной функции, у которой A > 0.

y = 0,5x 2 - 3x + 1

În acest caz A = 0,5

Și acum pentru A < 0:

y = - 0,5x2 - 3x + 1

În acest caz A = - 0,5

Impactul coeficientului Cu De asemenea, este destul de ușor de urmărit. Să ne imaginăm că vrem să găsim valoarea unei funcții într-un punct X= 0. Înlocuiți zero în formula:

y = A 0 2 + b 0 + c = c. Se pare că y = c. Acesta este Cu este ordonata punctului de intersecție al parabolei cu axa y. De obicei, acest punct este ușor de găsit pe grafic. Și stabiliți dacă se află peste zero sau mai jos. Acesta este Cu> 0 sau Cu < 0.

Cu > 0:

y = x 2 + 4x + 3

Cu < 0

y = x 2 + 4x - 3

În consecință, dacă Cu= 0, atunci parabola va trece neapărat prin origine:

y = x 2 + 4x

Mai dificil cu parametrul b. Punctul în care îl vom găsi depinde nu numai de b dar si din A. Acesta este vârful parabolei. Abscisa sa (coordonatele axei X) se găsește prin formula x în = - b/(2a). Prin urmare, b = - 2ax in. Adică acționăm în felul următor: pe grafic găsim vârful parabolei, determinați semnul abscisei acesteia, adică priviți în dreapta lui zero ( x in> 0) sau la stânga ( x in < 0) она лежит.

Cu toate acestea, asta nu este tot. Trebuie să fim atenți și la semnul coeficientului A. Adică, uită-te la locul în care sunt îndreptate ramurile parabolei. Și numai după aceea, după formula b = - 2ax in determina semnul b.

Să ne uităm la un exemplu:

Ramurile sunt îndreptate în sus, ceea ce înseamnă A> 0, parabola intersectează axa la sub zero, adică Cu < 0, вершина параболы лежит правее нуля. Следовательно, x in> 0. Deci b = - 2ax in = -++ = -. b < 0. Окончательно имеем: A > 0, b < 0, Cu < 0.

Menținerea confidențialității dvs. este importantă pentru noi. Din acest motiv, am dezvoltat o Politică de confidențialitate care descrie modul în care folosim și stocăm informațiile dumneavoastră. Vă rugăm să examinați practicile noastre de confidențialitate și să ne comunicați dacă aveți întrebări.

Colectarea și utilizarea informațiilor personale

Informațiile personale se referă la date care pot fi folosite pentru a identifica sau contacta o anumită persoană.

Vi se poate cere să furnizați informațiile dumneavoastră personale în orice moment când ne contactați.

Mai jos sunt câteva exemple de tipuri de informații personale pe care le putem colecta și cum putem folosi aceste informații.

Ce informații personale colectăm:

• Când trimiteți o cerere pe site, este posibil să colectăm diverse informații, inclusiv numele, numărul de telefon, adresa de e-mail etc.

Cum folosim informațiile dumneavoastră personale:

• Informațiile personale pe care le colectăm ne permit să vă contactăm cu oferte unice, promoții și alte evenimente și evenimente viitoare.
• Din când în când, putem folosi informațiile dumneavoastră personale pentru a trimite notificări și comunicări importante.
• De asemenea, putem folosi informații personale în scopuri interne, cum ar fi efectuarea de audituri, analize de date și diverse cercetări pentru a îmbunătăți serviciile pe care le oferim și pentru a vă oferi recomandări cu privire la serviciile noastre.
• Dacă participați la o tragere la sorți, la un concurs sau la o promoție similară, este posibil să folosim informațiile pe care le furnizați pentru a administra astfel de programe.

Dezvăluirea informațiilor către terți

Nu dezvăluim informațiile primite de la dumneavoastră către terți.

Excepții:

• Daca este necesar, in conditiile legii, procedura judiciara, în proceduri judiciare și/sau pe baza unor solicitări publice sau solicitări din partea agențiilor guvernamentale din Federația Rusă - de a vă dezvălui informațiile personale. De asemenea, putem dezvălui informații despre dumneavoastră dacă stabilim că o astfel de dezvăluire este necesară sau adecvată pentru securitate, aplicarea legii sau alte scopuri de importanță publică.
• În cazul unei reorganizări, fuziuni sau vânzări, este posibil să transferăm informațiile personale pe care le colectăm terței părți succesoare aplicabile.

Protecția informațiilor personale

Luăm măsuri de precauție - inclusiv administrative, tehnice și fizice - pentru a vă proteja informațiile personale împotriva pierderii, furtului și utilizării greșite, precum și împotriva accesului, dezvăluirii, modificării și distrugerii neautorizate.

Respectarea vieții private la nivelul companiei

Pentru a ne asigura că informațiile dumneavoastră personale sunt în siguranță, comunicăm angajaților noștri standarde de confidențialitate și securitate și aplicăm strict practicile de confidențialitate.

La lecțiile de matematică de la școală, v-ați familiarizat deja cu cele mai simple proprietăți și graficul unei funcții y = x 2. Să ne extindem cunoștințele funcţie pătratică.

Exercitiul 1.

Reprezentați grafic funcția y = x 2. Scara: 1 = 2 cm.Marcați un punct pe axa Oy F(0; 1/4). Folosind o busolă sau o bandă de hârtie, măsurați distanța de la punct F până la un moment dat M parabole. Apoi fixați banda în punctul M și rotiți-o în jurul acelui punct până când devine verticală. Capătul benzii va cădea ușor sub axa x (Fig. 1). Marcați pe bandă cât de departe se extinde dincolo de axa x. Acum luați un alt punct de pe parabolă și repetați măsurarea din nou. Cât de departe a căzut marginea benzii sub axa x?

Rezultat: indiferent de punctul de pe parabola y = x 2 pe care îl luați, distanța de la acest punct la punctul F(0; 1/4) va fi mai mare decât distanța de la același punct la axa absciselor cu același număr - 1/4.

O putem spune altfel: distanța de la orice punct al parabolei la punctul (0; 1/4) este egală cu distanța de la același punct al parabolei la dreapta y = -1/4. Acest punct minunat F(0; 1/4) se numește se concentreze parabole y = x 2, iar linia dreaptă y = -1/4 – directoare această parabolă. Fiecare parabolă are o directrice și un focar.

Proprietăți interesante ale unei parabole:

1. Orice punct al parabolei este echidistant de un punct, numit focar al parabolei, și o linie dreaptă, numită directrice.

2. Dacă rotiți o parabolă în jurul axei de simetrie (de exemplu, parabola y = x 2 în jurul axei Oy), veți obține o suprafață foarte interesantă numită paraboloid de revoluție.

Suprafața lichidului dintr-un vas rotativ are forma unui paraboloid de revoluție. Puteți vedea această suprafață dacă amestecați energic cu o lingură într-un pahar incomplet de ceai, apoi scoateți lingura.

3. Dacă arunci o piatră în gol la un anumit unghi față de orizont, aceasta va zbura într-o parabolă (Fig. 2).

4. Dacă intersectați suprafața unui con cu un plan paralel cu oricare dintre generatoarele sale, atunci secțiunea transversală va avea ca rezultat o parabolă (Fig. 3).

5. Parcurile de distracție au uneori o plimbare distractivă numită Paraboloid of Wonders. Tuturor celor care stau în interiorul paraboloidului rotativ li se pare că stă pe podea, în timp ce restul oamenilor se țin cumva miraculos de pereți.

6. În telescoapele reflectorizante se folosesc și oglinzi parabolice: lumina unei stele îndepărtate, venită într-un fascicul paralel, căzând pe oglinda telescopului, este adunată în focalizare.

7. Spoturile au de obicei o oglindă în formă de paraboloid. Dacă plasați o sursă de lumină în focarul unui paraboloid, atunci razele, reflectate de oglinda parabolică, formează un fascicul paralel.

Reprezentarea grafică a unei funcții pătratice

La lecțiile de matematică, ați studiat cum să obțineți grafice ale funcțiilor de forma din graficul funcției y = x 2:

1) y = ax 2– întinderea graficului y = x 2 de-a lungul axei Oy în |a| ori (cu |a|< 0 – это сжатие в 1/|a| раз, orez. 4).

2) y = x 2 + n– deplasarea graficului cu n unități de-a lungul axei Oy, iar dacă n > 0, atunci deplasarea este în sus, iar dacă n< 0, то вниз, (или же можно переносить ось абсцисс).

3) y = (x + m) 2– deplasarea graficului cu m unități de-a lungul axei Ox: dacă m< 0, то вправо, а если m >0, apoi la stânga, (Fig. 5).

4) y = -x 2– afișare simetrică față de axa Ox a graficului y = x 2 .

Să aruncăm o privire mai atentă la trasarea funcției y = a(x – m) 2 + n.

O funcție pătratică de forma y = ax 2 + bx + c poate fi întotdeauna redusă la forma

y = a(x – m) 2 + n, unde m = -b/(2a), n = -(b 2 – 4ac)/(4a).

Să demonstrăm.

Într-adevăr,

y = ax 2 + bx + c = a(x 2 + (b/a) x + c/a) =

A(x 2 + 2x · (b/a) + b 2 /(4a 2) – b 2 /(4a 2) + c/a) =

A((x + b/2a) 2 – (b 2 – 4ac)/(4a 2)) = a(x + b/2a) 2 – (b 2 – 4ac)/(4a).

Să introducem notații noi.

Lăsa m = -b/(2a), A n = -(b 2 – 4ac)/(4a),

atunci obținem y = a(x – m) 2 + n sau y – n = a(x – m) 2.

Să mai facem câteva substituții: fie y – n = Y, x – m = X (*).

Apoi obținem funcția Y = aX 2, al cărei grafic este o parabolă.

Vârful parabolei este la origine. X = 0; Y = 0.

Înlocuind coordonatele vârfului în (*), obținem coordonatele vârfului graficului y = a(x – m) 2 + n: x = m, y = n.

Astfel, pentru a reprezenta grafic o funcție pătratică reprezentată ca

y = a(x – m) 2 + n

prin transformări, puteți proceda după cum urmează:

A) reprezentaţi grafic funcţia y = x 2 ;

b) prin translație paralelă de-a lungul axei Ox cu m unități și de-a lungul axei Oy cu n unități - transferați vârful parabolei de la origine la punctul cu coordonatele (m; n) (Fig. 6).

Înregistrarea transformărilor:

y = x 2 → y = (x – m) 2 → y = a(x – m) 2 → y = a(x – m) 2 + n.

Exemplu.

Folosind transformări, construiți un grafic al funcției y = 2(x – 3) 2 în sistemul de coordonate carteziene – 2.

Soluţie.

Lanț de transformări:

y = x 2 (1) → y = (x – 3) 2 (2) → y = 2(x – 3) 2 (3) → y = 2(x – 3) 2 – 2 (4) .

Graficul este afișat în orez. 7.

Puteți exersa singuri reprezentarea grafică a funcțiilor pătratice. De exemplu, construiți un grafic al funcției y = 2(x + 3) 2 + 2 într-un sistem de coordonate folosind transformări. Dacă aveți întrebări sau doriți să obțineți sfaturi de la un profesor, atunci aveți ocazia să conduceți lecție gratuită de 25 de minute cu un tutor online după . Pentru a lucra în continuare cu un profesor, îl puteți alege pe cel care vi se potrivește

Mai ai întrebări? Nu știi cum să grafici o funcție pătratică?
Pentru a primi ajutor de la un tutor -.
Prima lecție este gratuită!

blog.site, atunci când copiați materialul integral sau parțial, este necesar un link către sursa originală.