Berechnung von T-Trägern aus Stahlbeton. Berechnung von T-Trägern aus Stahlbeton. Schwerpunkt des T-Profils

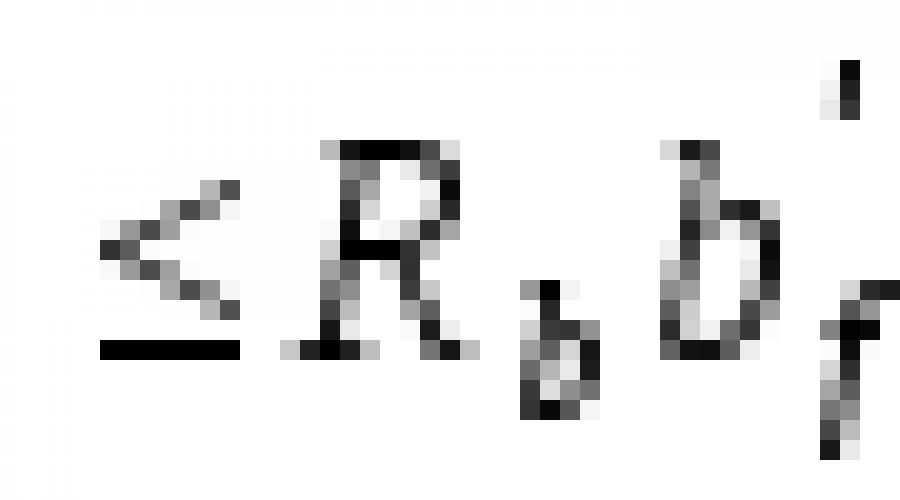
Die Berechnungen sind die gleichen wie für einen rechteckigen Balken. Sie umfassen die Ermittlung der Kräfte im Balken und an den Ecken der Platte. Die Anstrengungen führen dann zum Schwerpunkt des Neuen T-Abschnitt.

Die Achse verläuft durch den Schwerpunkt der Platte.

Ein vereinfachter Ansatz zur Berücksichtigung von Plattenkräften besteht darin, die Kräfte an Plattenknoten (gemeinsame Platten- und Balkenknoten) mit der Entwurfsbreite der Platte zu multiplizieren. Bei der Positionierung eines Trägers relativ zu einer Platte werden Verschiebungen (auch relative Verschiebungen) berücksichtigt. Die resultierenden abgekürzten Ergebnisse sind die gleichen, als ob das T-Profil von der Plattenebene um einen Verschiebungsbetrag angehoben würde, der dem Abstand vom Schwerpunkt der Platte zum Schwerpunkt des T-Profils entspricht (siehe Abbildung unten).

Die Einleitung der Kräfte in den Schwerpunkt des T-Profils erfolgt wie folgt:

M = Mb + Mp * B + Np * B * e1 + Nb * e2

B = beff1+b+beff2

Bestimmung des Schwerpunkts eines T-Stücks

Statisches Moment, berechnet im Schwerpunkt der Platte

S = b*h*(Offset)

A = (beff1+b+beff2)*hpl + b*h

Schwerpunkt gegenüber dem Plattenschwerpunkt erhöht:

b - Strahlbreite;

h - Balkenhöhe;

beff1, beff2 – berechnete Plattenbreiten;

hpl – Plattenhöhe (Plattendicke);

Verschiebung ist die Verschiebung des Balkens relativ zur Platte.

NOTIZ.

1. Es ist zu berücksichtigen, dass es gemeinsame Bereiche von Platte und Balken geben kann, die leider doppelt berechnet werden, was zu einer Erhöhung der Steifigkeit des Plattenbalkens führt. Dadurch werden Kräfte und Auslenkungen reduziert.
2. Die Plattenergebnisse werden aus den Finite-Elemente-Knoten gelesen; Die Netzverfeinerung wirkt sich auf die Ergebnisse aus.
3. Im Modell verläuft die Achse des T-Profils durch den Schwerpunkt der Platte.
4. Die Multiplikation der entsprechenden Kräfte mit der angenommenen Auslegungsbreite der Platte stellt eine Vereinfachung dar, die zu ungefähren Ergebnissen führt.

Biegbar Stahlbetonkonstruktionen Rechteckige Querschnitte sind aus wirtschaftlicher Sicht nicht sinnvoll. Dies liegt daran, dass normaler Stress Die Höhe der Abschnitte ist beim Biegen des Elements ungleichmäßig verteilt. Im Vergleich zu rechteckigen Profilen sind T-Profile wesentlich rentabler, weil Bei gleicher Tragfähigkeit ist der Betonverbrauch bei T-Profil-Elementen geringer.

Das T-Profil weist in der Regel eine Einzelbewehrung auf.

Bei Festigkeitsberechnungen von Normalquerschnitten von Biege-T-Profilelementen gibt es zwei Bemessungsfälle.

Der Algorithmus für den ersten Bemessungsfall basiert auf der Annahme, dass die neutrale Achse des Biegeelements innerhalb des komprimierten Flansches liegt.

Der Algorithmus für den zweiten Bemessungsfall basiert auf der Annahme, dass die neutrale Achse des Biegeelements außerhalb des komprimierten Flansches liegt (entlang der Kante des T-Profils des Elements verläuft).

Die Berechnung der Festigkeit des Normalquerschnitts eines Biegeelements aus Stahlbeton mit Einzelbewehrung für den Fall, dass die neutrale Achse innerhalb des komprimierten Flansches liegt, ist identisch mit dem Algorithmus zur Berechnung eines rechteckigen Querschnitts mit Einzelbewehrung und einer Querschnittsbreite gleich Breite des T-Flansches.

Das Designdiagramm für diesen Fall ist in Abb. 3.3 dargestellt.

Reis. 3.3. Berechnung der Festigkeit des Normalquerschnitts eines sich biegenden Stahlbetonelements für den Fall, dass die neutrale Achse innerhalb des komprimierten Flansches liegt.

Geometrisch bedeutet der Fall, dass die neutrale Achse innerhalb des komprimierten Flansches liegt, dass die Höhe der komprimierten Zone des Abschnitts des T-Stücks () nicht größer ist als die Höhe des komprimierten Flansches und wird durch die Bedingung ausgedrückt: .

Unter dem Gesichtspunkt der wirkenden Kräfte aus der äußeren Last und den inneren Kräften bedeutet diese Bedingung, dass die Festigkeit des Abschnitts gewährleistet ist, wenn der berechnete Wert des Biegemoments aus der äußeren Last erreicht wird (M ) den berechneten Wert des Schnittgrößenmoments relativ zum Schwerpunkt des Zugbewehrungsabschnitts bei Werten nicht überschreiten .

M (3.25)

Wenn Bedingung (3.25) erfüllt ist, liegt die Neutralachse tatsächlich innerhalb des komprimierten Flansches. In diesem Fall muss geklärt werden, welche Breite des komprimierten Flansches bei der Berechnung berücksichtigt werden soll. Die Normen legen folgende Regeln fest:

Bedeutung B " F , in die Berechnung eingeflossen; vorausgesetzt, dass die Breite des Regalüberstands in jede Richtung von der Rippe nicht größer sein sollte 1 / 6 Elementspanne und nicht mehr:

a) bei Vorhandensein von Querrippen oder wenn H " F ≥ 0,1 H - 1 / 2 lichte Abstände zwischen Längsrippen;

b) wenn keine Querrippen vorhanden sind (oder wenn die Abstände zwischen ihnen größer sind als die Abstände zwischen den Längsrippen) und H " F < 0,1 H - 6 H " F

c) bei auskragenden Regalüberständen:

bei H " F ≥ 0,1 H - 6 H " F ;

bei 0,05 H ≤ H " F < 0,1 H - 3 H " F ;

bei H " F < 0,05 H - Überhänge werden nicht berücksichtigt.

Schreiben wir den Festigkeitszustand relativ zum Schwerpunkt der Zuglängsbewehrung auf

M (3.26)

Lassen Sie uns Gleichung (3.26) ähnlich wie die Transformationen der Ausdrücke (3.3) umwandeln. (3.4) erhalten wir den Ausdruck

M (3.27)

Von hier aus ermitteln wir den Wert

= (3.28)

Nach Wert aus der Tabelle Bestimmen wir die Werte von 𝛈.

Vergleichen wir den Wert . Elementabschnitte. Wenn die Bedingung 𝛏 erfüllt ist, handelt es sich um eine Festigkeitsbedingung relativ zum Schwerpunkt der komprimierten Zone des Abschlags.

M (3.29)

Nachdem wir die Transformation des Ausdrucks (3.29) ähnlich der Transformation des Ausdrucks (3.12) durchgeführt haben, erhalten wir:

= (3.30)

Es ist notwendig, die Flächenwerte der gestreckten Längsarbeitsbewehrung auszuwählen.

Die Berechnung der Festigkeit des Normalquerschnitts eines Biegeelements aus Stahlbeton mit Einzelbewehrung für den Fall, dass sich die neutrale Achse außerhalb des komprimierten Flansches befindet (entlang der Kante des T-Stücks verläuft), unterscheidet sich etwas von der oben diskutierten.

Das Designdiagramm für diesen Fall ist in Abb. 3.4 dargestellt.

Reis. 3.4. Zur Berechnung der Festigkeit des Normalquerschnitts eines sich biegenden Stahlbetonelements für den Fall, dass die neutrale Achse außerhalb des komprimierten Flansches liegt.

Betrachten wir den Querschnitt der komprimierten Zone des T-Stücks als eine Summe bestehend aus zwei Rechtecken (Flanschüberständen) und einem Rechteck, das sich auf den komprimierten Teil der Rippe bezieht.

Festigkeitszustand relativ zum Schwerpunkt der Zugbewehrung.

M + (3.31)

Wo – Kraft in komprimierten Regalüberhängen;

Schulter vom Schwerpunkt der gespannten Bewehrung bis zum Schwerpunkt der Regalüberstände;

– Kraft im komprimierten Teil der T-Rippe;

- Schulter vom Schwerpunkt der Zugbewehrung zum Schwerpunkt des komprimierten Teils der Rippe.

= (3.32)

= (3.33)

= B (3.34)

= (3.35)

Ersetzen wir die Ausdrücke (3.32 – 3.35) in der Formel (3.31).

M + B (3.36)

Lassen Sie uns den zweiten Term auf der rechten Seite der Gleichung in Ausdruck (3.36) transformieren, ähnlich wie die oben durchgeführten Transformationen (Formeln 3.3; 3.4; 3.5).

Wir erhalten den folgenden Ausdruck:

M + (3.37)

Von hier aus ermitteln wir den Zahlenwert .

= (3.38)

Nach Wert aus der Tabelle Bestimmen wir die Werte von 𝛈.

Vergleichen wir den Wert mit dem Grenzwert der relativen Höhe der komprimierten Zone . Elementabschnitte. Ist die Bedingung 𝛏 erfüllt, so entsteht die Gleichgewichtsbedingung für die Kraftprojektionen auf die Längsachse des Elements. Σ N=0

--=0 (3.39)

=+ B (3.40)

Von hier aus ermitteln wir die erforderliche Querschnittsfläche der gestreckten Längsarbeitsbewehrung.

= (3.41)

Durch Sortiment an Stabverstärkungen Es ist notwendig, die Flächenwerte der gestreckten Längsarbeitsbewehrung auszuwählen.

Der Schwerpunkt zeichnet sich dadurch aus, dass diese Kraft nicht an einem Punkt auf den Körper einwirkt, sondern sich über das gesamte Körpervolumen verteilt. Die auf einzelne Elemente des Körpers (die als materielle Punkte betrachtet werden können) wirkenden Schwerkraftkräfte sind auf den Erdmittelpunkt gerichtet und nicht streng parallel. Da aber die Größe der meisten Körper auf der Erde viel kleiner ist als ihr Radius, werden diese Kräfte als parallel betrachtet.

Bestimmung des Schwerpunktes

Definition

Der Punkt, durch den die Resultierende aller parallelen Schwerkraftkräfte verläuft, die an jedem Ort des Körpers im Raum auf die Elemente des Körpers einwirken, wird genannt Schwerpunkt.

Mit anderen Worten: Der Schwerpunkt ist der Punkt, an dem die Schwerkraft an jeder Stelle des Körpers im Raum angreift. Wenn die Position des Schwerpunkts bekannt ist, können wir davon ausgehen, dass die Schwerkraft eine Kraft ist und im Schwerpunkt wirkt.

Die Aufgabe, den Schwerpunkt zu finden, ist eine bedeutende Aufgabe in der Technik, da die Stabilität aller Bauwerke von der Lage des Schwerpunkts abhängt.

Methode zur Ermittlung des Schwerpunkts eines Körpers

Wenn Sie die Position des Schwerpunkts eines Körpers mit komplexer Form bestimmen, können Sie den Körper zunächst gedanklich in Teile mit einfacher Form zerlegen und die Schwerpunkte für diese ermitteln. Bei Körpern einfacher Form lässt sich der Schwerpunkt aus Symmetrieüberlegungen sofort bestimmen. Die Schwerkraft einer homogenen Scheibe und Kugel liegt in ihrem Mittelpunkt, bei einem homogenen Zylinder in einem Punkt in der Mitte seiner Achse; ein homogenes Parallelepiped am Schnittpunkt seiner Diagonalen usw. Bei allen homogenen Körpern fällt der Schwerpunkt mit dem Symmetriezentrum zusammen. Der Schwerpunkt kann außerhalb des Körpers liegen, beispielsweise bei einem Ring.

Lassen Sie uns die Lage der Schwerpunkte von Körperteilen und die Lage des Schwerpunkts des gesamten Körpers herausfinden. Dazu wird der Körper als Ansammlung materieller Punkte dargestellt. Jeder dieser Punkte liegt im Schwerpunkt seines Körperteils und hat die Masse dieses Teils.

Schwerpunktkoordinaten

Im dreidimensionalen Raum werden die Koordinaten des Angriffspunkts der Resultierenden aller parallelen Schwerkraftkräfte (Koordinaten des Schwerpunkts) für einen starren Körper wie folgt berechnet:

\[\left\( \begin(array)(c) x_c=\frac(\sum\limits_i(\Delta m_ix_i))(m);; \\ y_c=\frac(\sum\limits_i(\Delta m_iy_i) )(m);; \\ z_c=\frac(\sum\limits_i(\Delta m_iz_i))(m) \end(array) \right.\left(1\right),\]

wobei $m$ die Masse des Körpers ist.$;;x_i$ ist die Koordinate auf der X-Achse der Elementarmasse $\Delta m_i$; $y_i$ - Koordinate auf der Y-Achse der Elementarmasse $\Delta m_i$; ; $z_i$ ist die Koordinate auf der Z-Achse der Elementarmasse $\Delta m_i$.

In der Vektorschreibweise wird ein System aus drei Gleichungen (1) wie folgt geschrieben:

\[(\overline(r))_c=\frac(1)(m)\sum\limits_i(m_i(\overline(r))_i\left(2\right),)\]

$(\overline(r))_c$ – Radius – ein Vektor, der die Position des Schwerpunkts bestimmt; $(\overline(r))_i$ sind Radiusvektoren, die die Positionen von Elementarmassen bestimmen.

Schwerpunkt, Massenschwerpunkt und Trägheitszentrum des Körpers

Formel (2) stimmt mit den Ausdrücken überein, die den Schwerpunkt des Körpers bestimmen. Wenn die Abmessungen des Körpers im Vergleich zur Entfernung zum Erdmittelpunkt klein sind, wird davon ausgegangen, dass der Schwerpunkt mit dem Massenschwerpunkt des Körpers zusammenfällt. Bei den meisten Problemen fällt der Schwerpunkt mit dem Schwerpunkt des Körpers zusammen.

Die Trägheitskraft in translatorisch bewegten, nicht inertialen Bezugssystemen wirkt auf den Schwerpunkt des Körpers.

Es ist jedoch zu berücksichtigen, dass die Zentrifugalkraft der Trägheit (im allgemeinen Fall) nicht auf den Schwerpunkt wirkt, da in einem nicht trägen Bezugssystem unterschiedliche Zentrifugalkräfte der Trägheit auf die Elemente des Körpers wirken (gerade). wenn die Massen der Elemente gleich sind), da die Abstände zur Rotationsachse unterschiedlich sind.

Beispiele für Probleme mit Lösungen

Beispiel 1

Übung. Das System besteht aus vier kleinen Kugeln (Abb. 1). Welche Koordinaten hat sein Schwerpunkt?

Lösung. Schauen wir uns Abb. 1 an. Der Schwerpunkt hat in diesem Fall eine Koordinate $x_c$, die wir wie folgt definieren:

Die Körpermasse ist in unserem Fall gleich:

Der Zähler des Bruchs auf der rechten Seite des Ausdrucks (1.1) im Fall (1(a)) hat die Form:

\[\sum\limits_(i=4)(\Delta m_ix_i=m\cdot 0+2m\cdot a+3m\cdot 2a+4m\cdot 3a=20m\cdot a).\]

Wir bekommen:

Antwort.$x_c=2a;$

Beispiel 2

Übung. Das System besteht aus vier kleinen Kugeln (Abb. 2). Welche Koordinaten hat sein Schwerpunkt?

Lösung. Schauen wir uns Abb. 2 an. Der Schwerpunkt des Systems liegt in der Ebene, daher hat es zwei Koordinaten ($x_c,y_c$). Finden wir sie mithilfe der Formeln:

\[\left\( \begin(array)(c) x_c=\frac(\sum\limits_i(\Delta m_ix_i))(m);; \\ y_с=\frac(\sum\limits_i(\Delta m_iy_i) )(m).\end(array)\right.\]

Systemgewicht:

Finden wir die Koordinate $x_c$:

Koordinate $y_с$:

Antwort.$x_c=0,5\ a$; $y_с=0,3\ a$