Das Konzept der Beschleunigung. Bewegung mit konstanter Beschleunigung in einer geraden Linie

Unterrichtsplan zum Thema „Geschwindigkeit bei linearer Bewegung mit konstanter Beschleunigung“

Datum :

Thema: „Geschwindigkeit bei Geradeausfahrt mit konstanter Beschleunigung“

Ziele:

Lehrreich : Sicherstellung und Bildung einer bewussten Aneignung des Wissens über die Geschwindigkeit bei geradliniger Bewegung mit konstanter Beschleunigung;

Entwicklung : Entwickeln Sie Ihre Fähigkeiten weiter selbständige Tätigkeit, Gruppenarbeitsfähigkeiten.

Lehrreich : Kognitives Interesse an neuem Wissen wecken; Verhaltensdisziplin entwickeln.

Unterrichtsart: Lektion im Erlernen neuen Wissens

Ausstattung und Informationsquellen:

Isachenkova, L. A. Physik: Lehrbuch. für die 9. Klasse. öffentliche Einrichtungen Durchschn. Unterricht mit Russisch Sprache Ausbildung / L. A. Isachenkova, G. V. Palchik, A. A. Sokolsky; bearbeitet von A. A. Sokolsky. Minsk: Volks-Asweta, 2015

Isachenkova, L. A. Sammlung physikalischer Probleme. 9. Klasse: Ein Handbuch für Studierende allgemeinbildender Institutionen. Durchschn. Unterricht mit Russisch Sprache Ausbildung / L. A. Isachenkova, G. V. Palchik, V. V. Dorofeychik. Minsk: Aversev, 2016, 2017.

Unterrichtsaufbau:

Organisatorischer Moment (5 Min.)

Grundkenntnisse aktualisieren (5 Min.)

Neues Material lernen (15 Min.)

Sportunterrichtsminute (2 Min.)

Festigung des Wissens (13min)

Zusammenfassung der Lektion (5 Min.)

Zeit organisieren

Hallo, setz dich! (Überprüft die Anwesenden).Heute müssen wir in der Lektion die Geschwindigkeit einer linearen Bewegung mit konstanter Beschleunigung verstehen. Und das bedeutet dasUnterrichtsthema : Geschwindigkeit bei geradliniger Bewegung mit konstanter Beschleunigung

Aktualisierung des Referenzwissens

Die einfachste aller ungleichmäßigen Bewegungen - geradlinige Bewegung mit konstanter Beschleunigung. Man nennt es gleich variabel.

Wie verändert sich die Geschwindigkeit eines Körpers bei gleichförmiger Bewegung?

Neues Material lernen

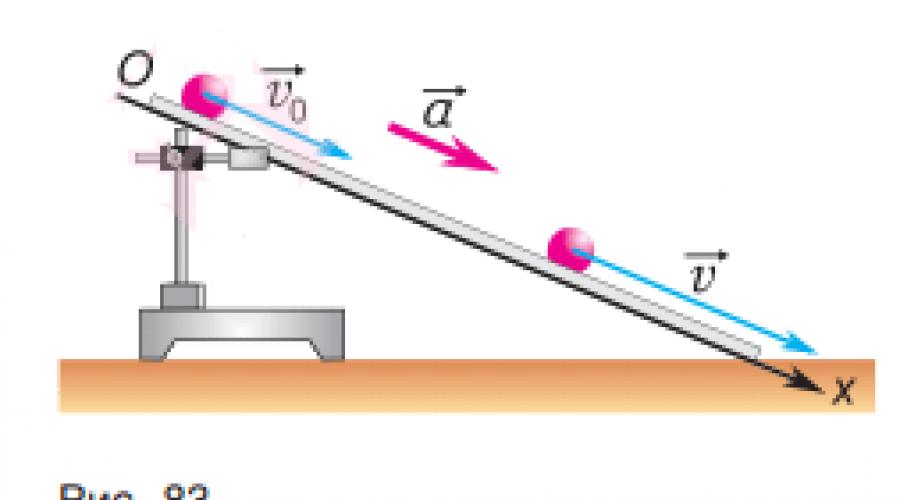
Betrachten Sie die Bewegung einer Stahlkugel entlang einer geneigten Rutsche. Die Erfahrung zeigt, dass seine Beschleunigung nahezu konstant ist:

Lassen V Moment der Zeit T = 0 Der Ball hatte eine Anfangsgeschwindigkeit (Abb. 83).

Wie findet man die Abhängigkeit der Ballgeschwindigkeit von der Zeit?

BallbeschleunigungA = . In unserem BeispielΔt = T , Δ - . Bedeutet,

, Wo

Bei einer Bewegung mit konstanter Beschleunigung hängt die Geschwindigkeit eines Körpers linear davon ab Zeit.

Aus den Gleichheiten ( 1 ) und (2) die Formeln für Projektionen lauten:

Lassen Sie uns Abhängigkeitsdiagramme erstellenA X ( T ) Und v X ( T ) (Reis. 84, a, b).

Reis. 84

Gemäß Abbildung 83A X = A > 0, = v 0 > 0.

Dann Abhängigkeiten A X ( T ) entspricht dem Zeitplan1 (siehe Abb. 84, A). DasGerade parallel zur Zeitachse. Abhängigkeitenv X ( T ) entspricht dem Zeitplan, Beschreibung einer Erhöhung der Projektionsko wachsen (siehe Abb. 84, B). Es ist klar, dass es wächstModulGeschwindigkeit. Der Ball bewegt sichgleichmäßig beschleunigt.

Betrachten wir das zweite Beispiel (Abb. 85). Nun ist die Anfangsgeschwindigkeit des Balls entlang der Rille nach oben gerichtet. Beim Aufwärtsbewegen verliert der Ball allmählich an Geschwindigkeit. Am PunktA Er AnDer Moment wird aufhören undwird beginnenherunterrutschen. PunktA angerufenWendepunkt.

Entsprechend Zeichnung 85 A X = - a< 0, = v 0 > 0 und Formeln (3) und (4) passend zur Grafik2 Und 2" (cm. Reis. 84, A , B).

Zeitplan 2" zeigt, dass am Anfang, während sich der Ball nach oben bewegte, die Geschwindigkeitsprojektionv X war positiv. Gleichzeitig nahm sie abT= wurde gleich Null. In diesem Moment hat der Ball den Wendepunkt erreichtA (siehe Abb. 85). Zu diesem Zeitpunkt hat sich die Geschwindigkeitsrichtung des Balls in die entgegengesetzte Richtung geändertT> Die Geschwindigkeitsprojektion wurde negativ.

Aus der Grafik 2" (siehe Abb. 84, B) Es ist auch klar, dass vor dem Moment der Drehung das Geschwindigkeitsmodul abnahm – die Kugel bewegte sich mit gleicher Geschwindigkeit nach oben. BeiT > T N das Geschwindigkeitsmodul steigt – der Ball bewegt sich gleichmäßig beschleunigt nach unten.

Erstellen Sie für beide Beispiele Ihre eigenen Diagramme des Geschwindigkeitsmoduls über der Zeit.

Welche anderen Gesetze der gleichförmigen Bewegung müssen bekannt sein?

In § 8 haben wir bewiesen, dass für eine gleichmäßige geradlinige Bewegung die Fläche der Figur zwischen dem Diagrammv X und die Zeitachse (siehe Abb. 57) ist numerisch gleich der Verschiebungsprojektion ΔR X . Es kann nachgewiesen werden, dass diese Regel auch für ungleichmäßige Bewegungen gilt. Dann ergibt sich gemäß Abbildung 86 die Verschiebungsprojektion ΔR X bei gleichmäßig wechselnder Bewegung wird durch die Fläche des Trapezes bestimmtA B C D . Diese Fläche entspricht der Hälfte der Summe der BasenTrapez multipliziert mit seiner HöheANZEIGE .

Ergebend:

Da der Durchschnittswert der Geschwindigkeitsprojektion der Formel (5)

folgt:

Während der Fahrt MitBei konstanter Beschleunigung ist die Beziehung (6) nicht nur für die Projektion, sondern auch für die Geschwindigkeitsvektoren erfüllt:

Die durchschnittliche Bewegungsgeschwindigkeit bei konstanter Beschleunigung entspricht der Hälfte der Summe aus Anfangs- und Endgeschwindigkeit.

Die Formeln (5), (6) und (7) können nicht verwendet werdenFür Bewegung Mitinkonsistente Beschleunigung. Das kann dazu führenZu grobe Fehler.

Festigung des Wissens

Schauen wir uns ein Beispiel zur Lösung des Problems von Seite 57 an:

Das Auto bewegte sich mit einer Geschwindigkeit, deren Modul = 72 war. Der Fahrer sieht eine rote Ampel auf dem StraßenabschnittS= 50 m gleichmäßig reduzierte Geschwindigkeit auf = 18 . Bestimmen Sie die Art der Bewegung des Autos. Ermitteln Sie die Richtung und Größe der Beschleunigung, mit der sich das Auto beim Bremsen bewegte.

Gegeben: Reshe tion:

72 = 20 Die Bewegung des Autos war gleichmäßig langsam. Usko-

Autofahrenentgegengesetzten Richtung

18 = 5 Geschwindigkeit seiner Bewegung.

Beschleunigungsmodul:

S= 50 m

Bremszeit:

A - ? Δ t =

Dann

Antwort:

Zusammenfassung der Lektion

Während der Fahrt MitBei konstanter Beschleunigung hängt die Geschwindigkeit linear von der Zeit ab.

Bei gleichmäßig beschleunigter Bewegung fallen die Richtungen von Momentangeschwindigkeit und Beschleunigung zusammen, bei gleichmäßig langsamer Bewegung sind sie entgegengesetzt.

Durchschnittliche FahrgeschwindigkeitMitDie konstante Beschleunigung entspricht der Hälfte der Summe aus Anfangs- und Endgeschwindigkeit.

Organisation Hausaufgaben

§ 12, Bsp. 7 Nr. 1, 5

Betrachtung.

Setzen Sie die Sätze fort:

Heute im Unterricht habe ich gelernt...

Es war interessant…

Das Wissen, das ich in der Lektion erworben habe, wird nützlich sein

Für gleichmäßig beschleunigte Bewegung gelten folgende Gleichungen, die wir ohne Herleitung darstellen:

Wie Sie wissen, sind die Vektorformel links und die beiden Skalarformeln rechts gleich. Aus algebraischer Sicht bedeuten Skalarformeln, dass bei gleichmäßig beschleunigter Bewegung Verschiebungsprojektionen nach einem quadratischen Gesetz von der Zeit abhängen. Vergleichen Sie dies mit der Natur von Mome(siehe § 12-h).

Da wir wissen, dass  sx = x – xo  und  sy = y – yo  (siehe § 12), erhalten wir aus den beiden Skalarformeln aus der oberen rechten Spalte Gleichungen für die Koordinaten:

Da die Beschleunigung bei gleichmäßig beschleunigter Bewegung eines Körpers konstant ist, können die Koordinatenachsen immer so positioniert werden, dass der Beschleunigungsvektor parallel zu einer Achse, beispielsweise der Y-Achse, gerichtet ist. Folglich lautet die Bewegungsgleichung entlang der X-Achse deutlich vereinfacht:

x  =  xo + υox t  + (0) und y  =  yo + υoy t  + ½ ay t²

Bitte beachten Sie, dass die linke Gleichung mit der Gleichung der gleichmäßigen geradlinigen Bewegung übereinstimmt (siehe § 12-g). Dies bedeutet, dass sich eine gleichmäßig beschleunigte Bewegung aus einer gleichmäßigen Bewegung entlang einer Achse und einer gleichmäßig beschleunigten Bewegung entlang der anderen „zusammensetzen“ kann. Dies wird durch die Erfahrung mit dem Kern auf einer Yacht bestätigt (siehe § 12-b).

Aufgabe. Das Mädchen streckte die Arme aus und warf den Ball. Er stieg 80 cm hoch und fiel bald vor den Füßen des Mädchens nieder, wobei er 180 cm weit flog. Mit welcher Geschwindigkeit wurde der Ball geworfen und welche Geschwindigkeit hatte der Ball, als er den Boden berührte?

Quadrieren wir beide Seiten der Gleichung für die Projektion der Momentangeschwindigkeit auf die Y-Achse: υy = υoy + ay t (siehe § 12). Wir erhalten die Gleichheit:

υy²  = ( υoy + ay t )²  = υoy² + 2 υoy ay t + ay² t²

Nehmen wir aus Klammern den Faktor 2 ay nur für die beiden rechten Terme:

υy²  = υoy² + 2 ay ( υoy t + ½ ay t² )

Beachten Sie, dass wir in Klammern die Formel zur Berechnung der Verschiebungsprojektion erhalten:  sy = υoy t + ½ ay t². Wenn wir es durch sy ersetzen, erhalten wir:

Lösung. Machen wir eine Zeichnung: Richten Sie die Y-Achse nach oben und platzieren Sie den Koordinatenursprung auf dem Boden zu Füßen des Mädchens. Wenden wir die Formel, die wir für das Quadrat der Geschwindigkeitsprojektion abgeleitet haben, zunächst am höchsten Punkt des Ballaufstiegs an:

0 = υoy² + 2·(–g)·(+h) ⇒ υoy = ±√¯2gh = +4 m/s

Wenn Sie dann beginnen, sich vom oberen Punkt nach unten zu bewegen:

υy² = 0 + 2·(–g)·(–H) ⇒ υy = ±√¯2gh = –6 m/s

Antwort: Der Ball wurde mit einer Geschwindigkeit von 4 m/s nach oben geschleudert und hatte im Moment der Landung eine Geschwindigkeit von 6 m/s, gerichtet gegen die Y-Achse.

Notiz. Wir hoffen, dass Sie verstehen, dass die Formel für die quadratische Projektion der Momentangeschwindigkeit analog für die X-Achse korrekt ist:

Wenn die Bewegung eindimensional ist, also nur entlang einer Achse erfolgt, können Sie eine der beiden Formeln im Framework verwenden.

§ 12. Bewegung mit konstanter Beschleunigung

Für gleichmäßig beschleunigte Bewegung gelten folgende Gleichungen, die wir ohne Herleitung darstellen:

Wie Sie wissen, sind die Vektorformel links und die beiden Skalarformeln rechts gleich. Aus algebraischer Sicht bedeuten Skalarformeln das Bei gleichmäßig beschleunigter Bewegung hängen die Verschiebungsprojektionen nach einem quadratischen Gesetz von der Zeit ab. Vergleichen Sie dies mit der Natur von Mome(siehe § 12-h).

Wissend, dass s x = x – x o Und s y = y – y o(siehe § 12), aus den beiden Skalarformeln aus der oberen rechten Spalte erhalten wir Gleichungen für Koordinaten:

Da die Beschleunigung bei gleichmäßig beschleunigter Bewegung eines Körpers konstant ist, können die Koordinatenachsen immer so positioniert werden, dass der Beschleunigungsvektor parallel zu einer Achse, beispielsweise der Y-Achse, gerichtet ist. Folglich lautet die Bewegungsgleichung entlang der X-Achse deutlich vereinfacht:

x  = x o + υ ox  t  + (0) Und y  = y o + υ oy  t  + ½ a y  t²

Bitte beachten Sie, dass die linke Gleichung mit der Gleichung der gleichmäßigen geradlinigen Bewegung übereinstimmt (siehe § 12-g). Das bedeutet es Eine gleichmäßig beschleunigte Bewegung kann aus einer gleichmäßigen Bewegung entlang einer Achse und einer gleichmäßig beschleunigten Bewegung entlang der anderen „zusammensetzen“. Dies wird durch die Erfahrung mit dem Kern auf einer Yacht bestätigt (siehe § 12-b).

Aufgabe. Das Mädchen streckte die Arme aus und warf den Ball. Er stieg 80 cm hoch und fiel bald vor den Füßen des Mädchens nieder, wobei er 180 cm weit flog. Mit welcher Geschwindigkeit wurde der Ball geworfen und welche Geschwindigkeit hatte der Ball, als er den Boden berührte?

Quadrieren wir beide Seiten der Gleichung, um die Momentangeschwindigkeit auf die Y-Achse zu projizieren: υ y  =  υ oy + a y  t(siehe § 12). Wir erhalten die Gleichheit:

υ y ²  = ( υ oy + a y  t )²  =  υ oy ² + 2 υ oy  a y  t + a y ² t²

Nehmen wir den Faktor aus der Klammer 2 Jahre alt nur für die beiden rechten Terme:

υ y ²  =  υ oy ² + 2 a y  ( υ oy  t + ½ a y  t² )

Beachten Sie, dass wir in Klammern die Formel zur Berechnung der Verschiebungsprojektion erhalten: s y = υ oy  t + ½ a y  t². Ersetzen Sie es durch s y, wir bekommen:

Lösung. Machen wir eine Zeichnung: Richten Sie die Y-Achse nach oben und platzieren Sie den Koordinatenursprung auf dem Boden zu Füßen des Mädchens. Wenden wir die Formel, die wir für das Quadrat der Geschwindigkeitsprojektion abgeleitet haben, zunächst am höchsten Punkt des Ballaufstiegs an:

0 = υ oy ² + 2·(–g)·(+h) ⇒ υ oy = ±√¯2gh = +4 m/s

Wenn Sie dann beginnen, sich vom oberen Punkt nach unten zu bewegen:

υ y² = 0 + 2·(–g)·(–H) ⇒ υ y = ±√¯2gh = –6 m/s

Antwort: Der Ball wurde mit einer Geschwindigkeit von 4 m/s nach oben geschleudert und hatte im Moment der Landung eine Geschwindigkeit von 6 m/s, gerichtet gegen die Y-Achse.

Notiz. Wir hoffen, dass Sie verstehen, dass die Formel für das Quadrat der Projektion der Momentangeschwindigkeit analog für die X-Achse korrekt ist.

Eine Bewegung mit konstanter Beschleunigung ist eine Bewegung, bei der der Beschleunigungsvektor sowohl im Betrag als auch in der Richtung konstant bleibt. Ein Beispiel für diese Art von Bewegung ist die Bewegung eines Punktes in einem Schwerefeld (sowohl vertikal als auch schräg zum Horizont).

Mit der Definition der Beschleunigung erhalten wir die folgende Beziehung

Nach der Integration haben wir die Gleichheit
.

Unter Berücksichtigung der Tatsache, dass der momentane Geschwindigkeitsvektor ist
, wir werden den folgenden Ausdruck haben

Die Integration des letzten Ausdrucks ergibt die folgende Beziehung

. Daraus erhalten wir die Bewegungsgleichung eines Punktes mit konstanter Beschleunigung

.

Beispiele für Vektorgleichungen der Bewegung eines materiellen Punktes

Gleichmäßige lineare Bewegung (
):

. (1.7)

Bewegung mit konstanter Beschleunigung (
):

. (1.8)

Die Geschwindigkeitsabhängigkeit von der Zeit, wenn sich ein Punkt mit konstanter Beschleunigung bewegt, hat die Form:

. (1.9)

Fragen zur Selbstkontrolle.

Formulieren Sie eine Definition mechanisches Uhrwerk.

Geben Sie die Definition eines materiellen Punktes an.

Wie wird bei der vektoriellen Bewegungsbeschreibung die Position eines materiellen Punktes im Raum bestimmt?

Was ist das Wesentliche an der Vektormethode zur Beschreibung mechanischer Bewegung? Mit welchen Merkmalen wird diese Bewegung beschrieben?

Geben Sie Definitionen der Vektoren der Durchschnitts- und Momentangeschwindigkeit an. Wie wird die Richtung dieser Vektoren bestimmt?

Definieren Sie die Vektoren der durchschnittlichen und momentanen Beschleunigungen.

Welche der Beziehungen ist die Bewegungsgleichung eines Punktes mit konstanter Beschleunigung? Welcher Zusammenhang bestimmt die Abhängigkeit des Geschwindigkeitsvektors von der Zeit?

§1.2. Koordinatenmethode zur Beschreibung von Bewegung

Bei der Koordinatenmethode wird zur Beschreibung der Bewegung ein Koordinatensystem (z. B. kartesisch) gewählt. Der Referenzpunkt ist fest mit dem ausgewählten Körper verbunden ( Referenzstelle). Lassen
Einheitsvektoren, die jeweils auf die positiven Seiten der OX-, OY- und OZ-Achsen gerichtet sind. Die Position des Punktes wird durch die Koordinaten angegeben
.

Der momentane Geschwindigkeitsvektor wird wie folgt bestimmt:

Wo
Projektionen des Geschwindigkeitsvektors auf die Koordinatenachsen und
Ableitungen von Koordinaten nach der Zeit.

Die Länge des Geschwindigkeitsvektors hängt mit seinen Projektionen durch die Beziehung zusammen:

. (1.11)

Für den momentanen Beschleunigungsvektor gilt folgende Beziehung:

Wo
Projektionen des Beschleunigungsvektors auf die Koordinatenachsen und
Zeitableitungen von Geschwindigkeitsvektorprojektionen.

Die Länge des momentanen Beschleunigungsvektors wird durch die Formel ermittelt:

. (1.13)

Beispiele für Bewegungsgleichungen eines Punktes in einem kartesischen Koordinatensystem

. (1.14)

Bewegungsgleichungen:
. (1.15)

Abhängigkeiten der Projektionen des Geschwindigkeitsvektors auf die Koordinatenachsen von der Zeit:

(1.16)

Fragen zur Selbstkontrolle.

Was ist das Wesentliche an der Koordinatenmethode zur Beschreibung von Bewegungen?

Welche Beziehung bestimmt den momentanen Geschwindigkeitsvektor? Mit welcher Formel wird der Betrag des Geschwindigkeitsvektors berechnet?

Welche Beziehung bestimmt den momentanen Beschleunigungsvektor? Mit welcher Formel wird der Betrag des momentanen Beschleunigungsvektors berechnet?

Welche Beziehungen werden als Gleichungen der gleichförmigen Bewegung eines Punktes bezeichnet?

Welche Beziehungen nennt man Bewegungsgleichungen mit konstanter Beschleunigung? Welche Formeln werden verwendet, um die Projektion der Momentangeschwindigkeit eines Punktes auf der Koordinatenachse zu berechnen?

Die Position von Körpern relativ zum gewählten Koordinatensystem wird üblicherweise durch einen zeitabhängigen Radiusvektor charakterisiert. Dann kann die Position des Körpers im Raum zu jedem Zeitpunkt mit der Formel ermittelt werden:

.

(Denken Sie daran, dass dies die Hauptaufgabe der Mechanik ist.)

Unter den vielen verschiedene Arten Die einfachste Bewegung ist Uniform– Bewegung mit konstanter Geschwindigkeit (Beschleunigung Null), und der Geschwindigkeitsvektor () muss unverändert bleiben. Offensichtlich kann eine solche Bewegung nur geradlinig sein. Genau wann gleichmäßige Bewegung Die Bewegung wird nach der Formel berechnet:

Manchmal bewegt sich ein Körper entlang einer gekrümmten Bahn, sodass der Geschwindigkeitsmodul konstant bleibt () (eine solche Bewegung kann nicht als gleichmäßig bezeichnet werden und die Formel kann nicht darauf angewendet werden). In diesem Fall zurückgelegte Strecke kann mit einer einfachen Formel berechnet werden:

Ein Beispiel für eine solche Bewegung ist Bewegung im Kreis mit konstanter absoluter Geschwindigkeit.

Schwieriger ist gleichmäßig beschleunigte Bewegung– Bewegung mit konstanter Beschleunigung (). Für eine solche Bewegung gelten zwei kinematische Formeln:

Daraus können zwei zusätzliche Formeln abgeleitet werden, die häufig bei der Lösung von Problemen nützlich sein können:

;

Gleichmäßig beschleunigte Bewegung muss nicht einfach sein. Es ist nur notwendig, dass Vektor Beschleunigung blieb konstant. Ein Beispiel für eine gleichmäßig beschleunigte, aber nicht immer geradlinige Bewegung ist die Bewegung mit freier Fallbeschleunigung ( G= 9,81 m/s 2), senkrecht nach unten gerichtet.

Eine komplexere Bewegung kennt man auch aus dem Schulphysikkurs – harmonische Schwingungen eines Pendels, für die die Formeln nicht gelten.

Bei Bewegung eines Körpers im Kreis mit konstanter absoluter Geschwindigkeit es bewegt sich mit dem sogenannten normal (zentripetal) Beschleunigung

auf den Mittelpunkt des Kreises gerichtet und senkrecht zur Bewegungsgeschwindigkeit.

Im allgemeineren Fall der Bewegung entlang einer krummlinigen Flugbahn mit unterschiedlicher Geschwindigkeit kann die Beschleunigung eines Körpers in zwei zueinander senkrechte Komponenten zerlegt und als Summe aus tangentialer (tangentialer) und normaler (senkrechter, zentripetaler) Beschleunigung dargestellt werden:

,

wo ist der Einheitsvektor des Geschwindigkeitsvektors und die Einheitseinheit normal zur Flugbahn; R– Krümmungsradius der Flugbahn.

Die Bewegung von Körpern wird immer relativ zu einem Bezugssystem (FR) beschrieben. Bei der Lösung von Problemen ist es notwendig, das bequemste SO zu wählen. Für sich fortschreitend bewegende COs lautet die Formel

ermöglicht Ihnen den einfachen Wechsel von einem CO zum anderen. In der Formel – die Geschwindigkeit des Körpers relativ zu einem CO; – Körpergeschwindigkeit relativ zum zweiten Referenzpunkt; – Geschwindigkeit des zweiten CO relativ zum ersten.

Fragen und Aufgaben zum Selbsttest

1) Modell eines materiellen Punktes: Was ist sein Wesen und seine Bedeutung?

2) Formulieren Sie die Definition einer gleichmäßigen, gleichmäßig beschleunigten Bewegung.

3) Formulieren Sie die Definitionen der grundlegenden kinematischen Größen (Radiusvektor, Verschiebung, Geschwindigkeit, Beschleunigung, Tangential- und Normalbeschleunigung).

4) Schreiben Sie die Formeln für die Kinematik einer gleichmäßig beschleunigten Bewegung und leiten Sie sie ab.

5) Formulieren Sie Galileis Relativitätsprinzip.

2.1.1. Geradlinige Bewegung

Aufgabe 22.(1) Das Auto fährt weiter gerader Abschnitt Straßen mit einer konstanten Geschwindigkeit von 90. Finden Sie die Verschiebung des Autos in 3,3 Minuten und seine Position zum gleichen Zeitpunkt, wenn sich das Auto zum ersten Zeitpunkt an einem Punkt befand, dessen Koordinate 12,23 km und die Achse beträgt Ochse gerichtet 1) entlang der Bewegung des Autos; 2) gegen die Bewegung des Autos.

Aufgabe 23.(1) Ein Radfahrer fährt mit der Geschwindigkeit 12 8,5 Minuten lang auf einer Landstraße nach Norden, biegt dann an der Kreuzung rechts ab und fährt weitere 4,5 km. Finden Sie die Verschiebung des Radfahrers während seiner Bewegung.

Aufgabe 24.(1) Ein Skater bewegt sich geradlinig mit einer Beschleunigung von 2,6 und in 5,3 s erhöht sich seine Geschwindigkeit auf 18. Finden Sie die Anfangsgeschwindigkeit des Skaters. Wie weit wird der Sportler in dieser Zeit laufen?

Aufgabe 25.(1) Das Auto bewegt sich geradlinig und bremst vor einem Tempolimit-Schild von 40 mit einer Beschleunigung von 2,3 ab. Wie lange dauerte diese Bewegung, wenn die Geschwindigkeit des Autos vor dem Bremsen 70 betrug? In welchem ​​Abstand zum Schild begann der Fahrer zu bremsen?

Aufgabe 26.(1) Mit welcher Beschleunigung bewegt sich der Zug, wenn seine Geschwindigkeit auf einer Strecke von 1200 m von 10 auf 20 zunimmt? Wie lange hat der Zug für diese Fahrt gebraucht?

Aufgabe 27.(1) Ein senkrecht nach oben geworfener Körper kehrt nach 3 s zu Boden zurück. Wie groß war die Anfangsgeschwindigkeit des Körpers? Wie hoch war die maximale Höhe?

Aufgabe 28.(2) Ein Körper an einem Seil wird aus dem Ruhezustand mit einer Beschleunigung von 2,7 m/s 2 senkrecht nach oben von der Erdoberfläche gehoben. Nach 5,8 s riss das Seil. Wie lange brauchte der Körper, um den Boden zu erreichen, nachdem das Seil gerissen war? Luftwiderstand vernachlässigen.

Aufgabe 29.(2) Der Körper beginnt sich ohne Anfangsgeschwindigkeit mit einer Beschleunigung von 2,4 zu bewegen. Bestimmen Sie den Weg, den der Körper in den ersten 16 s ab Beginn der Bewegung zurückgelegt hat, und den Weg, den er in den nächsten 16 s zurückgelegt hat. Von was Durchschnittsgeschwindigkeit Hat sich der Körper während dieser 32 Sekunden bewegt?

2.1.2. Gleichmäßig beschleunigte Bewegung in einer Ebene

Aufgabe 30.(1) Ein Basketballspieler wirft einen Ball mit einer Geschwindigkeit von 8,5 in einem Winkel von 63° zur Horizontalen in einen Korb. Mit welcher Geschwindigkeit traf der Ball den Korb, wenn er ihn in 0,93 s erreichte?

Aufgabe 31.(1) Ein Basketballspieler wirft den Ball in den Korb. Im Moment des Wurfs befindet sich der Ball in einer Höhe von 2,05 m und nach 0,88 s fällt er in den Ring, der sich in einer Höhe von 3,05 m befindet. Aus welcher Entfernung vom Ring (horizontal) wurde der Ball geworfen wurde in einem Winkel von 56° zum Horizont geworfen?

Aufgabe 32.(2) Der Ball wird horizontal mit einer Geschwindigkeit von 13 geworfen, nach einiger Zeit stellt sich heraus, dass seine Geschwindigkeit gleich 18 ist. Finden Sie die Bewegung des Balls während dieser Zeit. Luftwiderstand vernachlässigen.

Aufgabe 33.(2) Ein Körper wird mit einer Anfangsgeschwindigkeit von 17 m/s in einem bestimmten Winkel zum Horizont geschleudert. Ermitteln Sie den Wert dieses Winkels, wenn die Flugreichweite des Körpers 4,3-mal größer ist als die maximale Auftriebshöhe.

Aufgabe 34.(2) Ein Bomber, der mit einer Geschwindigkeit von 360 km/h abstürzt, wirft eine Bombe aus einer Höhe von 430 m horizontal in einer Entfernung von 250 m vom Ziel ab. In welchem ​​Winkel sollte ein Bomber tauchen? In welcher Höhe wird sich die Bombe 2 Sekunden nach Beginn ihres Falls befinden? Welche Geschwindigkeit wird es zu diesem Zeitpunkt haben?

Aufgabe 35.(2) Ein Flugzeug, das in einer Höhe von 2940 m mit einer Geschwindigkeit von 410 km/h flog, warf eine Bombe ab. Wie lange muss das Flugzeug vor dem Überflug über das Ziel und in welcher Entfernung davon die Bombe abfeuern, um das Ziel zu treffen? Ermitteln Sie die Größe und Richtung der Geschwindigkeit der Bombe 8,5 s nach Beginn ihres Falls. Luftwiderstand vernachlässigen.

Aufgabe 36.(2) Ein in einem Winkel von 36,6 Grad zur Horizontalen abgefeuertes Projektil befand sich zweimal auf derselben Höhe: 13 und 66 Sekunden nach dem Abflug. Bestimmen Sie die Anfangsgeschwindigkeit, die maximale Hubhöhe und die Reichweite des Projektils. Luftwiderstand vernachlässigen.

2.1.3. Kreisbewegung

Aufgabe 37.(2) Ein Senkkörper, der sich an einer Angelschnur im Kreis mit konstanter Tangentialbeschleunigung bewegt, hatte am Ende der achten Umdrehung eine Geschwindigkeit von 6,4 m/s und nach 30 Sekunden Bewegung betrug seine normale Beschleunigung 92 m/s 2 . Finden Sie den Radius dieses Kreises.

Aufgabe 38.(2) Ein Junge, der auf einem Karussell fährt, bewegt sich, wenn das Karussell anhält, entlang eines Kreises mit einem Radius von 9,5 m und legt einen Weg von 8,8 m zurück, wobei er am Anfang dieses Bogens eine Geschwindigkeit von 3,6 m/s und 1,4 m/s hat am Ende. Mit. Bestimmen Sie die Gesamtbeschleunigung des Jungen am Anfang und Ende des Bogens sowie die Zeit seiner Bewegung entlang dieses Bogens.

Aufgabe 39.(2) Eine Fliege, die auf der Kante eines Ventilatorflügels sitzt, bewegt sich beim Einschalten auf einem Kreis mit einem Radius von 32 cm mit einer konstanten Tangentialbeschleunigung von 4,6 cm/s 2 . Wie lange nach Beginn der Bewegung wird die Normalbeschleunigung doppelt so groß sein wie die Tangentialbeschleunigung und wie groß wird die lineare Geschwindigkeit der Fliege zu diesem Zeitpunkt sein? Wie viele Umdrehungen wird die Fliege in dieser Zeit machen?

Aufgabe 40.(2) Beim Öffnen der Tür bewegt sich der Griff aus dem Ruhezustand auf einem Kreis mit einem Radius von 68 cm mit einer konstanten Tangentialbeschleunigung von 0,32 m/s 2 . Finden Sie die Abhängigkeit der Gesamtbeschleunigung des Griffs von der Zeit.

Aufgabe 41.(3) Um Platz zu sparen, ist der Eingang zu einer der höchsten Brücken Japans in Form einer Schraubenlinie angeordnet, die sich um einen Zylinder mit einem Radius von 65 m windet. Das Straßenbett bildet mit der horizontalen Ebene einen Winkel von 4,8 Grad. Finden Sie die Beschleunigung eines Autos, das sich mit einer konstanten absoluten Geschwindigkeit von 85 km/h auf dieser Straße bewegt?

2.1.4. Relativität der Bewegung

Aufgabe 42.(2) Zwei Schiffe bewegen sich relativ zur Küste mit einer Geschwindigkeit von 9,00 bzw. 12,0 Knoten (1 Knoten = 0,514 m/s) und sind in einem Winkel von 30 bzw. 60 ° zum Meridian ausgerichtet. Mit welcher Geschwindigkeit bewegt sich das zweite Schiff relativ zum ersten?

Aufgabe 43.(3) Ein Junge, der mit einer Geschwindigkeit schwimmen kann, die 2,5-mal langsamer ist als die Geschwindigkeit der Flussströmung, möchte diesen Fluss so überqueren, dass er möglichst wenig flussabwärts getragen wird. In welchem ​​Winkel zum Ufer sollte der Junge schwimmen? Wie weit wird es transportiert, wenn die Flussbreite 190 m beträgt?

Aufgabe 44.(3) Zwei Körper beginnen sich gleichzeitig von einem Punkt im Schwerkraftfeld aus mit der gleichen Geschwindigkeit von 2,6 m/s zu bewegen. Die Geschwindigkeit eines Körpers ist in einem Winkel π/4 und die des anderen – in einem Winkel –π/4 zum Horizont gerichtet. Bestimmen Sie die Relativgeschwindigkeit dieser Körper 2,9 s nach Beginn ihrer Bewegung.