Suma unghiurilor opuse ale unui patrulater înscris într-un cerc. Patrulaterul înscris

Un patrulater este înscris într-un cerc dacă toate vârfurile lui se află pe cerc. Un astfel de cerc este circumscris unui patrulater.

Așa cum nu orice patrulater poate fi circumscris unui cerc, la fel nu orice patrulater poate fi înscris într-un cerc.

Un patrulater convex înscris într-un cerc are proprietatea că unghiurile sale opuse însumează 180°. Deci, având în vedere un patrulater ABCD al cărui unghi A este opus unghiului C și unghiul B este opus unghiului D, atunci ∠A + ∠C = 180° și ∠B + ∠D = 180°.

În general, dacă o pereche de unghiuri opuse ale unui patrulater se adună până la 180°, atunci cealaltă pereche se va aduna la aceeași sumă. Aceasta rezultă din faptul că pentru un patrulater convex suma unghiurilor este întotdeauna 360°. La rândul său, acest fapt rezultă din faptul că pentru poligoane convexe, suma unghiurilor este determinată de formula 180 ° * (n - 2), unde n este numărul de unghiuri (sau laturi).

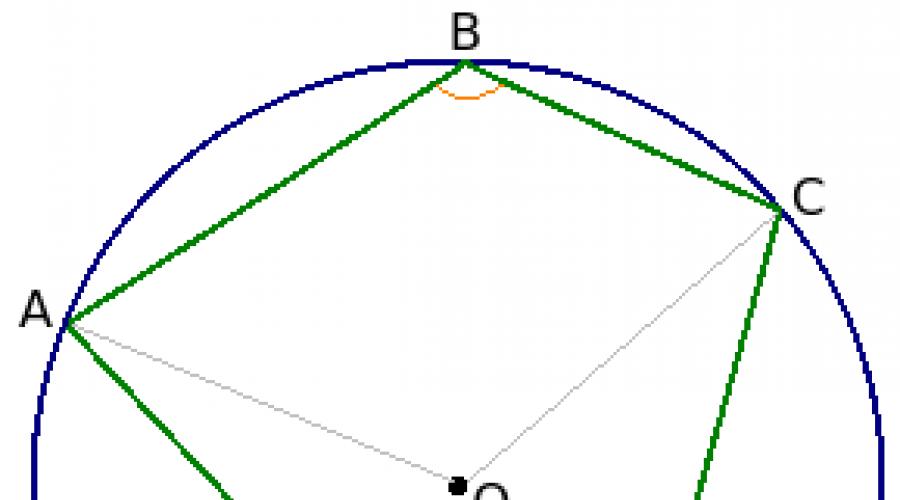
Puteți demonstra proprietatea unui patrulater înscris în felul următor. Fie înscris patrulaterul ABCD în cercul O. Se cere să se demonstreze că ∠B + ∠D = 180°.

Unghiul B este înscris într-un cerc. După cum știți, un astfel de unghi este egal cu jumătate din arcul pe care se sprijină. În acest caz, unghiul B se sprijină pe arcul ADC, deci ∠B = ½◡ADC. (Deoarece arcul este egal cu unghiul dintre razele care îl formează, putem scrie că ∠B = ½∠AOC, al cărui interior conține punctul D.)

Pe de altă parte, unghiul D al patrulaterului se sprijină pe arcul ABC, adică ∠D = ½◡ABC.

Deoarece laturile unghiurilor B și D intersectează cercul în aceleași puncte (A și C), ele împart cercul numai în două arce - ◡ADC și ◡ABC. Deoarece cercul total este de 360°, atunci ◡ADC + ◡ABC = 360°.

Astfel, se obțin următoarele egalități:

∠B = ½◡ADC
∠D = ½◡ABC
◡ADC + ◡ABC = 360°

Exprimați suma unghiurilor:

∠B + ∠D = ½◡ADC + ½◡ABC

Să scoatem ½ din paranteză:

∠B + ∠D = ½(◡ADC + ◡ABC)

Să înlocuim suma arcurilor cu valoarea lor numerică:

∠B + ∠D = ½ * 360° = 180°

Am constatat că suma unghiurilor opuse ale unui patrulater înscris este de 180°. Acesta este ceea ce trebuia dovedit.

Faptul că un patrulater înscris are această proprietate (suma unghiurilor opuse este 180°) nu înseamnă că orice patrulater a cărui sumă a unghiurilor opuse este 180° poate fi înscris într-un cerc. Deși de fapt este. Acest fapt se numește semnul unui patrulater înscrisși se formulează astfel: dacă suma unghiurilor opuse ale unui patrulater convex este de 180 °, atunci un cerc poate fi descris în jurul lui (sau înscris într-un cerc).

Puteți demonstra criteriul pentru un patrulater înscris prin contradicție. Fie ca ABCD să aibă un patrulater ale cărui unghiuri opuse B și D însumează 180°. În acest caz, unghiul D nu se află pe cerc. Apoi luăm pe dreapta care conține segmentul CD un punct E astfel încât să se afle pe cerc. Obțineți un patrulater inscripționat ABCE. Acest patrulater are unghiuri opuse B și E, ceea ce înseamnă că adună până la 180°. Aceasta rezultă din proprietatea unui patrulater înscris.

Rezultă că ∠B + ∠D = 180° și ∠B + ∠E = 180°. Totuși, unghiul D al patrulaterului ABCD față de triunghiul AED este extern și, prin urmare, mai mare decât unghiul E al acestui triunghi. Astfel, am ajuns la o contradicție. Deci, dacă suma unghiurilor opuse ale unui patrulater este de 180°, atunci acesta poate fi întotdeauna înscris într-un cerc.

Cursul video „Obțineți A” include toate subiectele necesare promovării cu succes a examenului la matematică cu 60-65 de puncte. Complet toate sarcinile 1-13 examen de profil matematică. De asemenea, potrivit pentru promovarea USE de bază în matematică. Dacă vrei să treci examenul cu 90-100 de puncte, trebuie să rezolvi partea 1 în 30 de minute și fără greșeli!

Curs de pregătire pentru examen pentru clasele 10-11, precum și pentru profesori. Tot ce ai nevoie pentru a rezolva partea 1 a examenului la matematică (primele 12 probleme) și problema 13 (trigonometrie). Și asta înseamnă mai mult de 70 de puncte la examenul de stat unificat și nici un student de o sută de puncte, nici un umanist nu se pot descurca fără ele.

Toată teoria necesară. Căi rapide soluții, capcane și secrete ale examenului. Au fost analizate toate sarcinile relevante din partea 1 din sarcinile Băncii FIPI. Cursul respectă pe deplin cerințele USE-2018.

Cursul conține 5 subiecte mari, câte 2,5 ore fiecare. Fiecare subiect este dat de la zero, simplu și clar.

Sute de sarcini de examen. Probleme de text și teoria probabilității. Algoritmi simpli și ușor de reținut pentru rezolvarea problemelor. Geometrie. Teorie, material de referință, analiza tuturor tipurilor de sarcini USE. Stereometrie. Trucuri complicate soluții, cheat sheets utile, dezvoltarea imaginației spațiale. Trigonometrie de la zero - la sarcina 13. Înțelegerea în loc de înghesuială. Explicarea vizuală a conceptelor complexe. Algebră. Rădăcini, puteri și logaritmi, funcție și derivată. Baza pentru solutie sarcini provocatoare 2 părți ale examenului.

De la Wikipedia, enciclopedia liberă

• În geometria euclidiană, patrulater înscris este un patrulater în care toate vârfurile se află pe același cerc. Acest cerc se numește cerc circumscris patrulater și se spune că vârfurile se află pe același cerc. Centrul acestui cerc și, respectiv, raza lui se numesc centruȘi rază cerc circumscris. Alți termeni pentru acest patrulater: patrulaterul se află pe același cerc, laturile ultimului patrulater sunt coardele cercului. De obicei, se presupune că un patrulater convex este un patrulater convex. Formulele și proprietățile prezentate mai jos sunt valabile în cazul convex.
• Ei spun că dacă un cerc poate fi circumscris în jurul unui patrulater, Acea patrulaterul este înscris în acest cerc, si invers.

Criterii generale pentru înscrierea unui patrulater

• Despre un patrulater convex $\backslash pi$ radian), adică:

$\backslash unghi\; A+\backslash unghi\; C\; =\; \backslash unghi\; B\; +\; \backslash unghi\; D\; =\; 180^\backslash circ$

sau în notația figurii:

$\backslash alpha\; +\; \backslash gamma\; =\; \backslash beta\; +\; \backslash delta\; =\; \backslash pi\; =\; 180^(\backslash circ).$

• Este posibil să descriem un cerc în jurul oricărui patrulater, în care patru bisectoare perpendiculare ale laturilor sale (sau mediatrice ale laturilor sale, adică perpendiculare pe laturile care trec prin punctele mijlocii ale acestora) se intersectează într-un punct.
• Este posibil să descrii un cerc despre orice patrulater cu unul colțul exterior, adiacent la unghiul intern dat, exact egal cu un alt unghi interior opus dat colțul interior. De fapt, această condiție este condiția de antiparalelism a două laturi opuse ale patrulaterului. Pe fig. colțurile exterioare și interioare adiacente ale pentagonului verde sunt prezentate mai jos.

$\backslash displaystyle\; AX\backslash cdot\; XC\; =\; BX\backslash cdot\; XD.$

• intersecție X poate fi intern sau extern cercului. În primul caz, obținem patrulaterul înscris este ABCD, iar în acest din urmă caz ​​obținem un patrulater înscris ABDC. La traversarea în interiorul unui cerc, ecuația spune că produsul lungimilor segmentelor în care punctul Xîmparte o diagonală este egală cu produsul lungimilor segmentelor în care punctul Xîmparte cealaltă diagonală. Această condiție este cunoscută sub numele de „teorema acordurilor care se intersectează”. În cazul nostru, diagonalele patrulaterului înscris sunt coardele cercului.
• Un alt criteriu de eligibilitate. Patrulaterul convex ABCD se înscrie un cerc dacă şi numai dacă

$\backslash tan(\backslash frac(\backslash alpha)(2))\backslash tan(\backslash frac(\backslash gamma)(2))=\backslash tan(\backslash frac(\backslash beta)(2))\backslash tan(\backslash frac(\backslash delta)(\; 2))=1.$

Criterii speciale pentru înscrierea unui patrulater

Un patrulater simplu (fără auto-intersecții) înscris este convex. Un cerc poate fi circumscris unui patrulater convex dacă și numai dacă suma unghiurilor sale opuse este de 180° ( $\backslash pi$ radian). Puteți descrie un cerc în jurul:

• orice antiparalelogram
• orice dreptunghi (un caz special de pătrat)
• orice trapez isoscel
• orice patrulater cu două unghiuri opuse drepte.

Proprietăți

Formule cu diagonale

$ef=ac+bd$; $\backslash frac(e)(f)\; =\; \backslash frac(a\backslash cdot\; d+b\backslash cdot\; c)(a\backslash cdot\; b+c\backslash cdot\; d).$

În ultima formulă a perechii partidele adiacente numărător AȘi d, bȘi c sprijină capetele lor pe o diagonală de lungime e. O afirmație similară este valabilă pentru numitor.

• Formule pentru lungimi diagonale(consecințe ):

$e\; =\; \backslash sqrt(\backslash frac((ac+bd)(ad+bc))(ab+cd))$Și $f\; =\; \backslash sqrt(\backslash frac((ac+bd)(ab+cd))(ad+bc))$

Formule cu colțuri

Pentru un patrulater înscris cu o succesiune de laturi A , b , c , d, cu semiperimetru pși unghi A intre parti AȘi d, funcții trigonometrice ale unghiului A sunt date prin formule

$\backslash cos\; A\; =\; \backslash frac(a^2\; +\; d^2\; -\; b^2\; -\; c^2)(2(ad\; +\; bc)),$ $\backslash sin\; A\; =\; \backslash frac(2\backslash sqrt((p-a)(p-b)(p-c)(p-d)))((ad+bc)),$ $\backslash tan\; \backslash frac(A)(2)\; =\; \backslash sqrt(\backslash frac((p-a)(p-d))((p-b)(p-c))).$

Colţ θ intre diagonale este :p.26

$\backslash tan\; \backslash frac(\backslash theta)(2)\; =\; \backslash sqrt(\backslash frac((p-b)(p-d))((p-a)(p-c))).$

• Dacă părți opuse AȘi c se intersectează într-un unghi φ , atunci este egal cu

$\backslash cos(\backslash frac(\backslash varphi)(2))=\backslash sqrt(\backslash frac((p-b)(p-d)(b+d)^2)((ab+cd)(ad+bc))),$

Unde p este un semiperimetru. :p.31

Raza unui cerc circumscris unui patrulater

Formula lui Parameshvara (Parameshvara)

Dacă un patrulater cu laturile consecutive A , b , c , dși semiperimetrul p este înscris un cerc, apoi raza lui este Formula Parameswar:p. 84

$R=\; \backslash frac(1)(4)\; \backslash sqrt(\backslash frac((ab+cd)(ad+bc)(ac+bd))((p-a)(p-b)(p-c)(p-d))).$

A fost dezvoltat de matematicianul indian Parameswar în secolul al XV-lea (c. 1380-1460)

• Un patrulater convex (vezi figura din dreapta) format din patru date direct Mikel, este înscris într-un cerc dacă și numai dacă punctul Miquel M al patrulaterului se află pe dreapta care unește două dintre cele șase puncte de intersecție ale dreptelor (cele care nu sunt vârfuri ale patrulaterului). Adică când M se întinde pe EF.

Criteriul conform căruia un patrulater compus din două triunghiuri este înscris într-un cerc

$f^2\; =\; \backslash frac((ac+bd)(ad+bc))((ab+cd)).$

• Ultima condiție oferă o expresie pentru diagonală f un patrulater înscris într-un cerc, prin lungimile celor patru laturi ale sale ( A, b, c, d). Această formulă urmează imediat atunci când se înmulțesc și se echivalează unele cu altele părțile din stânga și din dreapta ale formulelor care exprimă esența Prima și a doua teoremă a lui Ptolemeu(Vezi deasupra).

Criteriul conform căruia un patrulater tăiat printr-o linie dreaptă dintr-un triunghi este înscris într-un cerc

• O linie dreaptă, antiparalelă cu latura triunghiului și care îl intersectează, decupează din acesta un patrulater, în jurul căruia poate fi întotdeauna circumscris un cerc.
• Consecinţă. În apropierea unui antiparalelogram, în care două laturi opuse sunt antiparalele, este întotdeauna posibil să descrii un cerc.

Aria unui patrulater înscris într-un cerc

Variante ale formulei Brahmagupta

$S=\backslash sqrt((p-a)(p-b)(p-c)(p-d)),$ unde p este semiperimetrul patrulaterului. $S=\; \backslash frac(1)(4)\; \backslash sqrt(-\; \backslash begin(vmatrix)$

a & b & c & -d \\ b & a & -d & c \\ c & -d & a & b \\ -d & c & b & a \end(vmatrix))

Alte formule de zonă

$S\; =\; \backslash tfrac(1)(2)(ab+cd)\backslash sin(B)$ $S\; =\; \backslash tfrac(1)(2)(ac+bd)\backslash sin(\backslash theta),$

Unde θ oricare dintre unghiurile dintre diagonale. Cu condiția ca unghiul A nu este drept, aria poate fi exprimată și ca :p.26

$S\; =\; \backslash tfrac(1)(4)(a^2-b^2-c^2+d^2)\backslash tan(A).$ $\backslash displaystyle\; S=2R^2\backslash sin(A)\backslash sin(B)\backslash sin(\backslash theta),$

Unde R este raza cercului circumscris. Ca o consecință directă, avem inegalitatea

$S\backslash le\; 2R^2,$

unde egalitatea este posibilă dacă și numai dacă acest patrulater este un pătrat.

Patraunghiuri ale lui Brahmagupta

Quadrunghiul Brahmagupta este un patrulater înscris într-un cerc cu lungimi laturi întregi, diagonale întregi și zonă întreagă. Toate patrulaterele Brahmagupta posibile cu laturi A , b , c , d, cu diagonale e , f, cu suprafata S, și raza cercului circumscris R poate fi obținut prin eliminarea numitorilor următoarelor expresii care implică parametri raționali t , u, Și v :

$a=$ $b=(1+u^2)(v-t)(1+tv)$ $c=t(1+u^2)(1+v^2)$ $d=(1+v^2)(u-t)(1+tu)$ $e=u(1+t^2)(1+v^2)$ $f=v(1+t^2)(1+u^2)$ $S=uv$ $4R=(1+u^2)(1+v^2)(1+t^2).$

Exemple

• Patrulaterele private înscrise într-un cerc sunt: ​​dreptunghi, pătrat, trapez isoscel sau isoscel, antiparalelogram.

Patrulatere înscrise într-un cerc cu diagonale perpendiculare (patralatere ortodiagonale înscrise)

Proprietățile patrulaterelor înscrise într-un cerc cu diagonale perpendiculare

Raza cercului circumscris și aria

Pentru un patrulater înscris într-un cerc cu diagonale perpendiculare, să presupunem că intersecția diagonalelor împarte o diagonală în segmente de lungime p 1 și p 2 și împarte cealaltă diagonală în segmente de lungime q 1 și q 2. Atunci (prima egalitate este Propunerea 11 din Arhimede " Cartea Lemelor)

$D^2=p\_1^2+p\_2^2+q\_1^2+q\_2^2=a^2+c^2=b^2+d^2,$

Unde D- diametrul cercului. Acest lucru este adevărat deoarece diagonalele sunt perpendiculare pe coarda cercului. Din aceste ecuaţii rezultă că raza cercului circumscris R poate fi scris sub forma

$R=\backslash tfrac(1)(2)\backslash sqrt(p\_1^2+p\_2^2+q\_1^2+q\_2^2)$

sau în ceea ce privește laturile unui patrulater în formă

$R=\backslash tfrac(1)(2)\backslash sqrt(a^2+c^2)=\backslash tfrac(1)(2)\backslash sqrt(b^2+d^2).$

De asemenea, rezultă din aceasta că

$a^2+b^2+c^2+d^2=8R^2.$

• Pentru patrulaterele ortodiagonale înscrise, teorema lui Brahmagupta este valabilă:

Dacă un patrulater înscris are diagonale perpendiculare care se intersectează într-un punct $M$, apoi două perechi de antimediatris trece prin punct $M$.

cometariu. În această teoremă, antimediatrisînțelegeți segmentul $F.E.$ patrulater din figura din dreapta (prin analogie cu bisectoarea perpendiculară (mediatria) pe latura triunghiului). Este perpendicular pe o latură și trece simultan prin mijlocul părții opuse a patrulaterului.

Scrieți o recenzie despre articolul „Cadunghiuri înscrise într-un cerc”

Note

1. Bradley, Christopher J. (2007), Algebra geometriei: coordonate carteziene, ariale și proiective, Highperception, p. 179, ISBN 1906338000, OCLC
2. . Patrulatere înscrise.
3. Siddons, A. W. & Hughes, R. T. (1929), Trigonometrie, Cambridge University Press, p. 202, OCLC
4. Durell, C.V. & Robson, A. (2003), Courier Dover, ISBN 978-0-486-43229-8 ,
5. Alsina, Claudi & Nelsen, Roger B. (2007), "", Forum Geometricorum T. 7: 147–9 ,
6. Johnson, Roger A., Geometrie Euclidiană Avansată, Dover Publ., 2007 (orig. 1929).
7. Hoehn, Larry (martie 2000), „Circumradius of a cyclic quadrilateral”, Gazeta Matematică T. 84 (499): 69–70
8. .
9. Altshiller-Court, Nathan (2007), Geometria colegiului: o introducere în geometria modernă a triunghiului și a cercului(ed. a II-a), Courier Dover, ss. 131, 137–8, ISBN 978-0-486-45805-2, OCLC
10. Honsberger, Ross (1995), . Episoade din geometria euclidiană din secolul al XIX-lea și al XX-lea, vol. 37, New Mathematical Library, Cambridge University Press, pp. 35–39, ISBN 978-0-88385-639-0
11. Weisstein, Eric W.(engleză) pe site-ul web Wolfram MathWorld.
12. Bradley, Christopher (2011), ,
13. .
14. Coxeter, Harold Scott MacDonald & Greitzer, Samuel L. (1967), . Geometrie Revizuită, Asociația de matematică din America, pp. 57, 60, ISBN 978-0-88385-619-2
15. .
16. Andreescu, Titu & Enescu, Bogdan (2004), . Comori ale Olimpiadei de Matematică, Springer, ss. 44–46, 50, ISBN 978-0-8176-4305-8
17. .
18. Buchholz, R. H. & MacDougall, J. A. (1999), „”, Buletinul Societății Australiane de Matematică T. 59(2): 263–9 , DOI 10.1017/S0004972700032883
19. .
20. Johnson, Roger A., Geometrie Euclidiană Avansată, Dover Publ. co., 2007
21. , Cu. 74.
22. .
23. .
24. .
25. Peter, Thomas (septembrie 2003), „Maximizarea ariei unui patrulater”, Jurnalul de matematică al colegiului T. 34 (4): 315–6
26. Prasolov, Viktor, ,
27. Alsina, Claudi & Nelsen, Roger (2009), , , Asociația de matematică din America, p. 64, ISBN 978-0-88385-342-9 ,
28. Sastry, K.R.S. (2002). "" (PDF). Forum Geometricorum 2 : 167–173.
29. Posamentier, Alfred S. & Salkind, Charles T. (1970), . Probleme provocatoare în geometrie(ed. a II-a), Courier Dover, ss. 104–5, ISBN 978-0-486-69154-1
30. .
31. .
32. .

Vezi si

După numărul de laturi Corect triunghiuri Cadrilatere Vezi si

Articolul conține referințe scurte („Harvard”) la publicații care nu sunt enumerate sau descrise incorect în secțiunea bibliografică. Lista de link-uri nefuncționale: , , , , , , , , , , - Ei, ce, cazacul meu? (Maria Dmitrievna a numit-o pe Natasha cazac) - a spus ea, mângâindu-l cu mâna pe Natasha, care s-a apropiat de mâna ei fără teamă și veselă. - Știu că poțiunea este o fată, dar o ador. Ea a scos cercei de yakhon în formă de para din reticulul ei imens și, dându-i-i Natasha, care era radiant și îmbujorat de ziua de naștere, s-a întors imediat de la ea și s-a întors către Pierre. — Eh, eh! drăguț! vino aici, spuse ea cu o voce batjocoritor de liniștită și subțire. - Hai, draga mea... Și ea și-a suflecat mânecile amenințător și mai sus. Pierre se apropie, privind-o naiv prin ochelari. „Vino, vino, dragă!” I-am spus numai tatălui tău adevărul, când s-a întâmplat să fie, și atunci Dumnezeu îți poruncește. Ea făcu o pauză. Toată lumea tăcea, așteptând ce avea să vină și simțind că există doar o prefață. - Bine, nimic de spus! băiat bun!... Tatăl se întinde pe pat, și se distrează, pune sfertul pe un urs călare. Să-ți fie rușine, tată, să-ți fie rușine! Mai bine mergi la război. Se întoarse și îi întinse mâna contelui, care cu greu se putea abține să râdă. - Ei bine, la masă, am ceai, e timpul? spuse Maria Dmitrievna. Contele a mers înainte cu Maria Dmitrievna; apoi contesa, care era condusă de un colonel de husar, persoana potrivita, cu care Nicholas a trebuit să ajungă din urmă cu regimentul. Anna Mikhailovna este cu Shinshin. Berg îi întinse mâna Verei. Zâmbitoare Julie Karagina s-a dus cu Nikolai la masă. În spatele lor veneau alte cupluri, întinse pe hol, iar în spatele lor, toți singuri, copii, tutori și guvernante. Chelnerii s-au agitat, scaunele zdrăngăneau, muzica cânta în tarabele corului, iar oaspeții s-au instalat. Sunetele muzicii de acasă a contelui au fost înlocuite de sunetele de cuțite și furculițe, vocile oaspeților, pașii liniștiți ai chelnilor. La un capăt al mesei, contesa stătea în cap. În dreapta este Marya Dmitrievna, în stânga este Anna Mikhailovna și alți oaspeți. La celălalt capăt stătea un conte, în stânga un colonel de husar, în dreapta Shinshin și alți oaspeți bărbați. Pe o parte a mesei lungi, tineri mai în vârstă: Vera lângă Berg, Pierre lângă Boris; pe de altă parte, copiii, tutorele și guvernantele. Din spatele cristalului, sticlelor și vaselor cu fructe, contele s-a uitat la soția sa și la șapca ei înaltă cu panglici albastre și a turnat cu sârguință vin vecinilor săi, fără a uita de sine. Contesa, de asemenea, din cauza ananasului, fără a uita de îndatoririle ei de gazdă, a aruncat priviri semnificative către soțul ei, a cărui chelie și față, i se părea, se distingeau cu roșeață de părul gri. Se auzi o bâlbâială obișnuită la capătul doamnelor; se auzeau din ce în ce mai tare voci asupra masculului, în special asupra colonelului husar, care a mâncat și a băut atât de mult, roșind din ce în ce mai mult, încât contele l-a dat deja ca exemplu celorlalți oaspeți. Berg, cu un zâmbet blând, i-a vorbit Verei despre faptul că iubirea este un sentiment nu pământesc, ci ceresc. Boris l-a sunat pe noul său prieten Pierre oaspeții care erau la masă și a schimbat priviri cu Natasha, care stătea în fața lui. Pierre vorbea puțin, se uita la fețe noi și mânca mult. Pornind de la două supe, dintre care a ales a la tortue, [broasca țestoasă] și kulebyaki, și până la cocoși, nu i-a lipsit nici măcar un fel de mâncare și nici măcar un vin, pe care majordomul într-o sticlă învelită într-un șervețel i-a lipit în mod misterios. iese din spatele umărului vecinului său, spunând sau „Drey Madeira, sau ungur, sau vin de Rin. A înlocuit primul dintre cele patru pahare de cristal cu monograma contelui, care stătea în fața fiecărui aparat, și a băut cu plăcere, privind din ce în ce mai plăcut la oaspeți. Natasha, care stătea în fața lui, se uită la Boris, ca fetele de treisprezece ani se uită la băiatul cu care tocmai s-au sărutat pentru prima dată și de care sunt îndrăgostiți. Aceeași privire a ei se întorcea uneori către Pierre și, sub privirea acestei fete amuzante și pline de viață, voia să râdă el însuși, fără să știe de ce. Nikolai stătea departe de Sonya, lângă Julie Karagina și din nou, cu același zâmbet involuntar, îi spuse ceva. Sonya a zâmbit măreț, dar se pare că era chinuită de gelozie: a devenit palidă, apoi a înroșit și a ascultat cu toată puterea ce își spuneau Nikolai și Julie. Guvernanta se uită neliniștită în jur, parcă s-ar fi pregătit pentru o respingere, dacă cineva s-a gândit să jignească copiii. Profesorul german a încercat să memoreze categoriile de mâncăruri, deserturi și vinuri pentru a descrie totul în detaliu într-o scrisoare către familia sa din Germania și a fost foarte jignit de faptul că majordomul, cu o sticlă învelită într-un șervețel, a înconjurat l. Germanul s-a încruntat, a încercat să arate că nu vrea să primească acest vin, dar s-a jignit pentru că nimeni nu a vrut să înțeleagă că are nevoie de vin să nu-și potolească setea, nu din lăcomie, ci din curiozitate conștiincioasă. La capătul masculin al mesei conversația devenea din ce în ce mai animată. Colonelul a spus că manifestul de declarare a războiului a fost deja publicat la Petersburg și că copia, pe care o văzuse el însuși, fusese acum predată prin curier comandantului șef. - Și de ce ne este greu să ne luptăm cu Bonaparte? spuse Shinshin. - II a deja rabattu le caquet a l "Autriche. Je crains, que cette fois ce ne soit notre tour. [Deja a doborât aroganța din Austria. Mă tem că nu ne va veni rândul acum.] Colonelul era un german robust, înalt și plin de sânge, evident un militant și un patriot. A fost jignit de cuvintele lui Shinshin. „Și atunci, suntem un suveran gras”, a spus el, pronunțând e în loc de e și b în loc de b. "Atunci, că împăratul știe acest lucru. El a spus în manifestul său că nu poate privi cu indiferentă pericolele care amenință Rusia și că securitatea imperiului, demnitatea acestuia și sfințenia alianțelor", a spus el, din anumite motive, înclinându-se mai ales. asupra cuvântului „uniuni”, de parcă aceasta ar fi toată esența problemei. Și cu memoria sa infailibilă, oficială, a repetat cuvintele introductive ale manifestului... „și dorința, unicul și indispensabil scop al suveranului, este de a stabili pacea în Europa pe baze solide - au decis să trimită o parte din armată acum în străinătate și depune noi eforturi pentru a realiza „această intenție”. „Iată de ce, suntem un suveran demn”, a concluzionat el, bând în mod instructiv un pahar de vin și privind înapoi la contor pentru încurajare. - Connaissez vous le proverbe: [Știi proverbul:] „Yerema, Yerema, dacă ai sta acasă, ascuți-ți fusurile”, a spus Shinshin, tresărind și zâmbind. – Cela nous convient a merveille. [Acesta este apropo pentru noi.] De ce Suvorov - și a fost despicat, o farfurie, [pe cap,] și unde sunt Suvorov-urile noastre acum? Je vous demande un peu, [te întreb] - sărind constant de la rusă la limba franceza el a spus. „Trebuie să luptăm până a doua zi după picătura de sânge”, a spus colonelul, lovind în masă, „și să murim pentru împăratul nostru, și atunci totul va fi bine”. Și să se certe cât mai mult (mai ales și-a scos vocea pe cuvântul „posibil”), cât mai puțin, a terminat el, întorcându-se din nou către conte. - Deci îi judecăm pe vechii husari, asta-i tot. Și cum judeci, tinere și husar tânăr? adăugă el, întorcându-se către Nikolai, care, auzind că era vorba de război, și-a părăsit interlocutorul și s-a uitat cu toți ochii și l-a ascultat cu toate urechile pe colonel. „Sunt complet de acord cu tine”, a răspuns Nikolai, înroșindu-se peste tot, întorcând farfuria și rearanjând paharele cu o privire atât de hotărâtă și disperată, de parcă în momentul de față ar fi în mare pericol, „Sunt convins că rușii trebuie mor sau câștigă”, a spus el, simțind el, la fel de bine ca și alții, după ce cuvântul fusese deja spus, că era prea entuziast și pompos pentru această ocazie și, prin urmare, stingher. - C "est bien beau ce que vous venez de dire, [Minunat! ce ai spus este minunat]", spuse Julie, care stătea lângă el, oftând. Sonya tremura peste tot și se înroși până la urechi, după urechi și la gâtul şi umerii ei, în timp ce Nikolai vorbea.Pierre ascultă discursurile colonelului şi dădu din cap aprobator. — E frumos, spuse el. — Un adevărat husar, tinere, strigă colonelul, lovind din nou masa. - Despre ce vorbesti acolo? Vocea de bas a Mariei Dmitrievna se auzi deodată peste masă. Pentru ce te lovești de masă? se întoarse spre husar, „de cine te entuziasmezi? corect, crezi că francezii sunt în fața ta? — Spun adevărul, spuse husarul zâmbind. „Totul ține de război”, strigă contele peste masă. „La urma urmei, vine fiul meu, Marya Dmitrievna, vine fiul meu. - Și am patru fii în armată, dar nu mă întristez. Totul este voia lui Dumnezeu: vei muri întins pe aragaz și Dumnezeu va avea milă în luptă ”, a răsunat fără niciun efort vocea groasă a Mariei Dmitrievna, de la celălalt capăt al mesei. - Asta este adevărat. Și conversația sa concentrat din nou - doamnele la capătul mesei, bărbații la al lor. „Dar nu vei cere”, i-a spus frățiorul Natasha, „dar nu vei cere!” „Voi întreba”, a răspuns Natasha. Fața ei s-a aprins brusc, exprimând o determinare disperată și veselă. Se ridică pe jumătate, invitându-l pe Pierre, care stătea în fața ei, să asculte cu o privire și se întoarse către mama ei: - Mamă! vocea ei copilărească din piept răsuna peste tot pe masă. - Ce vrei? întrebă înspăimântată contesa, dar, văzând din chipul fiicei ei că este o farsă, flutură cu severitate mâna, făcând cu capul un gest amenințător și negativ. Conversația a încetat. - Mamă! ce tort va fi? - Vocea Natasha suna si mai hotarata, fara sa se rupa. Contesa a vrut să se încruntă, dar nu a putut. Marya Dmitrievna își scutură degetul gros. — Cazac, spuse ea amenințător. Majoritatea oaspeților s-au uitat la bătrâni, neștiind cum să facă această cascadorie. - Iată-mă aici! spuse contesa. - Mamă! care va fi tortul? Natasha strigă deja cu îndrăzneală și capricios, veselă, încrezătoare dinainte că trucul ei va fi bine primit. Sonya și grasa Petya se ascundeau de râs. „Așa că am întrebat”, le-a șoptit Natasha fratelui ei mai mic și lui Pierre, la care s-a uitat din nou. „Înghețată, dar nu vă vor da”, a spus Marya Dmitrievna. Natasha a văzut că nu avea de ce să se teamă și, prin urmare, nici nu i-a fost frică de Marya Dmitrievna. — Maria Dmitrievna? ce inghetata! Nu-mi place untul. - Morcov. - Nu ce? Marya Dmitrievna, care? aproape a țipat ea. - Vreau să știu! Maria Dmitrievna și contesa au râs și toți oaspeții au urmat. Toți râdeau nu de răspunsul Mariei Dmitrievna, ci de curajul și dexteritatea de neînțeles ale acestei fete, care a știut și a îndrăznit să o trateze în acest fel pe Marya Dmitrievna. Natasha a rămas în urmă doar când i s-a spus că va fi ananas. Sampanie era servita inainte de inghetata. Din nou a început să sune muzica, contele a sărutat-o ​​pe contesa, iar oaspeții, ridicându-se, au felicitat-o ​​pe contesă, au clintit pahare peste masă cu contele, copiii și unul pe altul. Din nou chelnerii au alergat, scaunele zdrăngăneau și în aceeași ordine, dar cu fețele mai roșii, oaspeții s-au întors în salon și în biroul contelui. Mesele din Boston au fost mutate deoparte, s-au făcut petreceri, iar oaspeții contelui au fost cazați în două sufragerie, o canapea și o bibliotecă. Contele, întinzându-și cărțile ca un evantai, cu greu a rezistat obiceiului unui pui de somn de după-amiază și a râs de toate. Tineretul, incitat de contesa, s-a adunat in jurul clavicordului si harpei. Julie a fost prima, la cererea tuturor, care a cântat o piesă cu variații la harpă și, împreună cu alte fete, a început să le roage pe Natasha și Nikolai, cunoscuți pentru muzicalitatea lor, să cânte ceva. Natasha, căreia i s-a adresat una mare, se pare că era foarte mândră de asta, dar în același timp era timidă. - Ce vom cânta? ea a intrebat. — Cheia, răspunse Nikolai. - Ei bine, hai să ne grăbim. Boris, vino aici, spuse Natasha. - Unde este Sonya? S-a uitat în jur și, văzând că prietena ei nu era în cameră, a alergat după ea. A alergat în camera Sonyei și nu și-a găsit prietena acolo, Natasha a fugit în creșă - iar Sonya nu era acolo. Natasha și-a dat seama că Sonya era pe un cufăr pe coridor. Cufărul de pe coridor era locul durerilor tinerei generații feminine din casa rostovilor. Într-adevăr, Sonya, în rochia ei roz aerisită, zdrobind-o, s-a întins cu fața în jos pe patul de pene al asistentei în dungi murdare, pe piept și, acoperindu-și fața cu degetele, a plâns amar, tremurând cu umerii goi. Chipul Natasha, plin de viață, toată ziua, s-a schimbat brusc: ochii i s-au oprit, apoi gâtul i s-a cutremurat, colțurile buzelor i s-au căzut. — Sonya! ce ești?... Ce, ce se întâmplă cu tine? Woo woo!… Iar Natasha, desfăcându-și gura mare și devenind complet urâtă, a răcnit ca un copil, neștiind motivul și doar pentru că Sonya plângea. Sonya a vrut să ridice capul, a vrut să răspundă, dar nu a putut și s-a ascuns și mai mult. Natasha plângea, stătea pe un pat albastru cu pene și își îmbrățișa prietena. Adunându-și puterile, Sonya s-a ridicat, a început să-și șteargă lacrimile și să povestească. - Nikolenka pleacă într-o săptămână, a... hârtia lui... a ieșit... el însuși mi-a spus... Da, n-aș plânge... (a arătat hârtia pe care o ținea în mână: a fost poezie scrisă de Nikolai) N-aș plânge, dar nu vei putea... nimeni nu poate înțelege... ce fel de suflet are. Și a început să plângă din nou pentru că sufletul lui era atât de bun. „Este bine pentru tine... Nu te invidiez... Te iubesc și pe Boris”, a spus ea, adunându-și puțin puterile, „e drăguț... nu există obstacole pentru tine. Și Nikolai este vărul meu... este necesar... mitropolitul însuși... și asta este imposibil. Și apoi, dacă mama mea ... (Sonya a considerat-o pe contesă și a numit-o pe mama ei), ea va spune că îi stric cariera lui Nikolai, nu am inimă, că sunt ingrată, dar dreptate ... Doamne ... ( și-a făcut cruce) Și eu o iubesc atât de mult și pe toți, doar Vera este una... Pentru ce? Ce i-am făcut? Îți sunt atât de recunoscător că aș fi bucuros să sacrific totul, dar nu am nimic... Sonya nu mai putea vorbi și și-a ascuns din nou capul în mâini și în patul de pene. Natasha a început să se calmeze, dar din chipul ei era clar că înțelegea importanța durerii prietenei ei. — Sonya! spuse ea deodată, de parcă ar fi ghicit adevăratul motiv al durerii vărului ei. „Bine, a vorbit Vera cu tine după cină?” Da? - Da, Nikolai însuși a scris aceste poezii, iar eu am scris altele; le-a găsit pe masa mea și a spus că i-ar arăta mamei și, de asemenea, a spus că sunt nerecunoscătoare, că mama nu i-ar permite niciodată să se căsătorească cu mine și el se va căsători cu Julie. Vezi cum e cu ea toată ziua... Natasha! Pentru ce?… Și din nou a plâns amar. Natasha a ridicat-o, a îmbrățișat-o și, zâmbind printre lacrimi, a început să o mângâie. „Sonya, nu ai încredere în ea, dragă, nu. Îți amintești cum am vorbit toți trei cu Nikolenka în camera canapelei? iti amintesti dupa cina? La urma urmei, am decis cum va fi. Nu-mi amintesc cum, dar amintesc cum totul a fost bine și totul este posibil. Aici fratele unchiului Shinshin este căsătorit văr iar noi suntem veri ai treilea. Și Boris a spus că este foarte posibil. Știi, i-am spus totul. Și este atât de deștept și atât de bun", a spus Natasha... "Tu, Sonya, nu plânge, draga mea, draga, Sonya. Și ea a sărutat-o ​​râzând. - Credința este rea, Dumnezeu să fie cu ea! Și totul va fi bine, iar ea nu îi va spune mamei; Nikolenka își va spune și nici măcar nu s-a gândit la Julie. Și ea a sărutat-o ​​pe cap. Sonya s-a ridicat, iar pisoiul s-a însuflețit, ochii îi scânteiau și părea gata să-și fluture coada, să sară pe labele moi și să se joace din nou cu mingea, așa cum i se cuvine. - Crezi? Dreapta? De către Dumnezeu? spuse ea, îndreptându-și repede rochia și părul. - Corect, Doamne! – răspunse Natasha, îndreptându-și prietena sub coasă o șuviță de păr aspru căzută. Și au râs amândoi. - Ei bine, hai să cântăm „Key”. - Să mergem la. - Și știi, acest Pierre gras, care stătea în fața mea, este atât de amuzant! spuse deodată Natasha, oprindu-se. - Mă distrez copios! Și Natasha a alergat pe coridor. Sonya, periând puful și ascunzând poeziile în sân, până la gât cu sânii proeminente, cu pași ușori, veseli, cu fața îmbujorată, alergă după Natasha pe coridor până la canapea. La cererea invitaților, tinerii au cântat cvartetul „Key”, care le-a plăcut foarte mult tuturor; apoi Nikolai a cântat din nou cântecul pe care îl învățase. Într-o noapte plăcută, la lumina lunii, Imaginează-ți că ești fericit Că există altcineva pe lume Cine se gândește și la tine! Că ea, cu o mână frumoasă, Mergând de-a lungul harpei de aur, Cu armonia sa pasională Chemând la sine, chemându-te! Încă o zi, două și va veni paradisul... Dar ah! prietenul tău nu va trăi! Și încă nu a terminat ultimele cuvinte când tinerii din sală s-au pregătit să danseze iar muzicienii din coruri zdrăngăneau din picioare și tușiră. Pierre stătea în sufragerie, unde Shinshin, ca și cu un vizitator din străinătate, a început o conversație politică cu el, care a fost plictisitoare pentru Pierre, căreia i s-au alăturat și alții. Când a început muzica, Natasha a intrat în sufragerie și, mergând direct la Pierre, râzând și roșind, a spus: „Mama mi-a spus să te rog să dansezi. „Mi-e teamă să încurc cifrele”, a spus Pierre, „dar dacă vrei să fii profesorul meu... Și și-a dat mâna groasă, coborând-o spre fata slabă. În timp ce cuplurile se instalau și muzicienii construiau, Pierre s-a așezat cu domnișoara lui. Natasha era perfect fericită; a dansat cu unul mare venit din străinătate. S-a așezat în fața tuturor și a vorbit cu el ca un mare. Avea un evantai în mână, pe care o domnișoară i-a dat să-l țină. Și, adoptând cea mai seculară ipostază (Dumnezeu știe unde și când a aflat asta), ea, vântându-se cu un evantai și zâmbind prin evantai, a vorbit cu domnul ei. - Ce este, ce este? Uite, uite, - spuse bătrâna contesă, trecând prin hol și arătând spre Natasha. Natasha se înroși și râse. - Păi, ce ești, mamă? Ei bine, ce cauți? Ce este surprinzător aici? În mijlocul celei de-a treia ecosaise, scaunele din salonul unde se jucau contele și Maria Dmitrievna au început să se miște, iar majoritatea oaspeților de cinste și bătrânii, întinzându-se după o lungă ședință și punând portofele și poșetele în buzunarele lor, au ieșit pe ușile holului. Maria Dmitrievna a mers în față cu contele, amândoi cu fețe vesele. Cu o politețe jucăușă, parcă într-o manieră de balet, contele întinse mâna rotunjită către Marya Dmitrievna. S-a îndreptat, iar chipul i s-a luminat de un zâmbet deosebit de viteaz și viclean și, de îndată ce ultima figură a ecossaise a fost dansată, a bătut din palme muzicienilor și a strigat la coruri, întorcându-se spre prima vioară: - Semyon! O cunoști pe Danila Kupor? Era dansul preferat al contelui, dansat de el în tinerețe. (Danilo Kupor era de fapt o figură englezească.) „Uită-te la tata”, a strigat Natasha în toată sala (uitând complet că dansa cu una mare), aplecându-și capul creț până la genunchi și izbucnind în hohote de râs sonor. Într-adevăr, totul în sală se uita cu un zâmbet de bucurie la bătrânul vesel, care, alături de demnita sa doamnă, Maria Dmitrievna, care era mai înaltă decât el, și-a rotunjit brațele, scuturându-le la timp, și-a îndreptat umerii, și-a răsucit. picioarele, bătând ușor din picioare și cu un zâmbet din ce în ce mai înflorit pe chipul rotund a pregătit publicul pentru ceea ce avea să urmeze. De îndată ce s-au auzit sunetele vesele, sfidătoare ale Danilei Kupor, asemănătoare unui zdrăngănitor vesel, toate ușile sălii au fost făcute brusc, pe de o parte, de bărbați, pe de altă parte, de fețele zâmbitoare feminine ale curților care veneau. afară să se uite la domnul vesel. - Tatăl este al nostru! Vultur! spuse dădaca cu voce tare de la o uşă. Contele dansa bine și știa asta, dar doamna lui nu știa cum și nu voia să danseze bine. Corpul ei uriaș stătea drept cu ea mâini puternice(i-a întins reticulul contesei); doar unul strict, dar Fata frumoasa ea dansa. Ceea ce s-a exprimat în toată figura rotundă a contelui, cu Maria Dmitrievna s-a exprimat doar într-o față din ce în ce mai zâmbitoare și un nas zvâcnit. Dar, pe de altă parte, dacă contele, din ce în ce mai împrăștiat, a cucerit publicul cu neașteptarea trucurilor dibace și a sărituri ușoare ale picioarelor ei moi, Marya Dmitrievna, cu cea mai mică râvnă în a-și mișca umerii sau a rotunji brațele pe rând și călcând, a făcut nu mai puțină impresie asupra meritului, care a fost apreciat de toată lumea la corpulența și veșnica ei severitate. Dansul devenea din ce în ce mai vioi. Omologuli nu au putut să atragă atenția asupra lor nici măcar un minut și nici nu au încercat să facă acest lucru. Totul era ocupat de conte și Maria Dmitrievna. Natasha a tras de mânecile și rochiile tuturor celor prezenți, care deja nu și-au luat ochii de la dansatori și le-a cerut să se uite la tata. În intervalele de dans, contele a tras aer în piept, a făcut cu mâna și a strigat muzicienilor să cânte mai repede. Din ce în ce mai repede, din ce în ce mai repede, din ce în ce mai mult, contele se desfășura, când în vârful picioarelor, când pe călcâie, repezindu-se în jurul Mariei Dmitrievna și, în cele din urmă, întorcându-și doamna la locul ei, făcu ultimul pas, ridicându-și piciorul moale în sus din în spate, aplecându-și capul transpirat cu o față zâmbitoare și fluturând rotund mana dreapta printre hohote de aplauze și râsete, în special Natasha. Ambii dansatori s-au oprit, respirând greu și ștergându-se cu batiste cambrice. „Așa dansau pe vremea noastră, ma chere”, a spus contele. - Da Danila Kupor! spuse Maria Dmitrievna, dându-și răsuflarea greu și continuu și suflecându-și mânecile. În timp ce cea de-a șasea engleză se dansa în sala de la Rostov pe sunetele muzicienilor obosiți, care erau în ton, iar chelnerii obosiți și bucătarii pregăteau cina, a șasea lovitură a avut loc cu contele Bezukhim. Medicii au anunțat că nu există nicio speranță de recuperare; pacientului i s-a făcut mărturisire surdă și împărtășire; s-au făcut pregătiri pentru ungere, iar casa era plină de tam-tam și neliniște de așteptare, obișnuită în astfel de momente. În afara casei, în spatele porților, se înghesuiau pompe funebre, ascunzându-se de trăsurile care se apropiau, așteptând o ordin bogat pentru înmormântarea contelui. Comandantul-șef al Moscovei, care trimitea constant adjutanți pentru a afla despre poziția contelui, în acea seară el însuși a venit să-și ia rămas bun de la faimosul nobil al Ecaterinei, contele Bezukhim. Sala magnifică de recepție era plină. Toată lumea s-a ridicat respectuos când comandantul șef, fiind singur cu pacientul de aproximativ o jumătate de oră, a plecat de acolo, răspunzând ușor la plecăciuni și încercând cât mai repede să treacă de ochii medicilor, clericilor și rudelor fixați pe l. Prințul Vasily, care în aceste zile se slăbise și mai palid, l-a desprins pe comandantul șef și i-a repetat în liniște ceva de mai multe ori. După ce l-a desprins pe comandantul șef, prințul Vasily s-a așezat singur în sală pe un scaun, aruncându-și picioarele sus peste picioare, sprijinindu-și cotul pe genunchi și închizând ochii cu mâna. După ce a stat așa ceva vreme, s-a ridicat și cu pași neobișnuit de grăbiți, privind în jur cu ochi speriați, a trecut printr-un coridor lung până în jumătatea din spate a casei, către prințesa mai mare. Cei care se aflau în camera slab luminată vorbeau în șoaptă neuniformă între ei și tăceau de fiecare dată, iar cu ochii plini de întrebări și așteptări s-au uitat înapoi la ușa care dădea în camerele muribundului și au scos un sunet slab când cineva a lăsat-o sau a intrat în ea. „Limita umană”, i-a spus bătrânul, duhovnic, doamnei care s-a așezat lângă el și l-a ascultat naiv, „limita este stabilită, dar nu o poți trece”. – Cred că nu e prea târziu pentru ungere? - adăugând un titlu duhovnicesc, a întrebat doamna, de parcă n-ar avea nicio părere în această chestiune.

Inapoi inainte

Atenţie! Previzualizarea slide-ului are doar scop informativ și este posibil să nu reprezinte întreaga amploare a prezentării. Dacă sunteți interesat acest lucru vă rugăm să descărcați versiunea completă.

Goluri.

Educational. Crearea condițiilor pentru asimilarea cu succes a conceptului de patrulater descris, proprietățile, caracteristicile acestuia și stăpânirea abilităților de a le aplica în practică.

În curs de dezvoltare. Dezvoltarea abilităților matematice, crearea condițiilor pentru capacitatea de a generaliza și de a aplica trenul direct și invers al gândirii.

Educational. Creșterea unui sentiment de frumusețe cu estetica desenelor, surprinderea cu neobișnuit

decizie, formarea organizației, responsabilitatea pentru rezultatele muncii lor.

1. Studiați definiția patrulaterului circumscris.

2. Demonstrați proprietatea laturilor patrulaterului circumscris.

3. Introduceți dualitatea proprietăților sumelor laturilor opuse și unghiurilor opuse ale patrulaterelor înscrise și circumscrise.

4. Să dea experienţă în aplicarea practică a teoremelor avute în vedere în rezolvarea problemelor.

5. Efectuați controlul primar al nivelului de asimilare a noului material.

Echipament:

• calculator, proiector;
• manual „Geometrie. Clasele 10-11” pentru învățământul general. instituţii: de bază şi de profil. niveluri automate. A.V. Pogorelov.

Software: Microsoft Word, Puterea Microsoft punct.

Folosirea unui computer pentru a pregăti un profesor pentru o lecție.

Folosind programul standard al sistemului de operare Windows creat pentru lecție:

1. Prezentare.
2. Mese.
3. Planuri.
4. Înmânează.

Planul lecției

Organizarea timpului. (2 minute.)

Verificarea temelor. (5 minute.)

Învățarea de materiale noi. (28 min.)

Muncă independentă. (7 min.)

Teme pentru acasă.(1 min.)

Rezumatul lecției. (2 minute.)

În timpul orelor

1. Moment organizatoric. Salutari. Mesaj despre subiectul și scopul lecției. Scrieți în caiet data și tema lecției.

2. Verificarea temelor.

3. Învățarea de material nou.

Lucrați conceptul de poligon circumscris.

Definiție. Poligonul se numește descrisîn jurul cercului dacă Toate partea lui îngrijorare vreun cerc.

Întrebare. Care dintre poligoane propuse sunt circumscrise și care nu și de ce?

<Презентация. Слайд №2>

Dovada proprietăților patrulaterului circumscris.

<Презентация. Слайд №3>

Teorema. În patrulaterul circumscris, sumele laturilor opuse sunt egale.

Elevii lucrează cu manualul, notează formularea teoremei într-un caiet.

1. Prezentați enunțul teoremei sub forma unei propoziții condiționate.

2. Care este starea teoremei?

3. Care este concluzia teoremei?

Răspuns. Dacă patrulater circumscris unui cerc, Acea sumele laturilor opuse sunt egale.

Se face dovada, elevii fac notițe într-un caiet.

<Презентация. Слайд №4>

Profesor. Notă dualitate situații pentru laturile și unghiurile patrulaterelor circumscrise și înscrise.

Consolidarea cunoștințelor dobândite.

Sarcini.

Laturile opuse ale patrulaterului circumscris au 8 m și 12 m. Puteți găsi perimetrul?

Sarcini conform desenelor gata făcute.<Презентация. Слайд №5>

Răspuns. 1. 10 m 2. 20 m 3. 21 m

Dovada caracteristicii patrulaterului circumscris.

Prezentați teorema inversă.

Răspuns. Dacă într-un patrulater sumele laturilor opuse sunt egale, atunci se poate înscrie în el un cerc. (Reveniți la diapozitivul 2, Fig. 7) <Презентация. Слайд №2>

Profesor. Rafinați formularea teoremei.

Teorema. Dacă sumele laturilor opuse convex patrulaterele sunt egale, atunci poate fi înscris în el un cerc.

Lucrați cu manualul. Pentru a se familiariza cu dovada semnului patrulaterului descris conform manualului.

Aplicarea cunoștințelor dobândite.

3. Sarcini conform desenelor gata făcute.

1. Este posibil să se înscrie un cerc într-un patrulater cu laturile opuse 9 m și 4 m, 10 m și 3 m?

2. Este posibil să se înscrie un cerc într-un trapez isoscel cu bazele 1 m și 9 m, înălțimea 3 m?

<Презентация. Слайд №6>

Lucrări scrise în caiete

.

Sarcină. Aflați raza unui cerc înscris într-un romb cu diagonalele 6 m și 8 m.

<Презентация. Слайд № 7>

4. Munca independentă.

1 opțiune

1. Este posibil să se înscrie un cerc

1) într-un dreptunghi cu laturile de 7 m și 10 m,

2. Laturile opuse ale unui patrulater circumscris unui cerc sunt 7 m și 10 m.

Aflați perimetrul patrulaterului.

3. Un trapez isoscel cu bazele de 4 m și 16 m este circumscris unui cerc.

1) raza cercului înscris,

Opțiunea 2

1. Este posibil să înscrieți un cerc:

1) într-un paralelogram cu laturile de 6 m și 13 m,

2) într-un pătrat?

2. Laturile opuse ale unui patrulater circumscris unui cerc au 9 m și 11 m. Aflați perimetrul patrulaterului.

3. Un trapez isoscel cu latura laterală de 5 m este circumscris unui cerc cu raza de 2 m.

1) baza trapezului,

2) raza cercului circumscris.

5. Tema pentru acasă. P.86, Nr. 28, 29, 30.

6. Rezultatul lecției. Se verifică munca independentă, se acordă note.

<Презентация. Слайд № 8>

„Cercul circumscris” am văzut că un cerc poate fi circumscris în jurul oricărui triunghi. Adică, pentru orice triunghi există un astfel de cerc încât toate cele trei vârfuri ale triunghiului „se așează” pe el. Ca aceasta:

Întrebare: Se poate spune același lucru despre un patrulater? Este adevărat că va exista întotdeauna un cerc pe care se vor „așeza” toate cele patru vârfuri ale patrulaterului?

Se dovedește că acest lucru NU ESTE ADEVĂRAT! NU ÎNTOTDEAUNA un patrulater poate fi înscris într-un cerc. Există o condiție foarte importantă:

În desenul nostru:

.

Uite, unghiurile și se află unul față de celălalt, ceea ce înseamnă că sunt opuse. Dar colțurile atunci? Par să fie și ele opuse? Este posibil să luăm colțuri și în loc de colțuri și?

Sigur ca poti! Principalul lucru este că patrulaterul are două unghiuri opuse, a căror sumă va fi. Cele două unghiuri rămase se vor aduna și ele însele. Nu crede? Să ne asigurăm. Uite:

Lasa. Îți amintești care este suma tuturor celor patru unghiuri ale oricărui patrulater? Cu siguranță, . Adică - întotdeauna! . Dar, → .

Magie drept!

Deci, amintiți-vă cu fermitate:

Dacă un patrulater este înscris într-un cerc, atunci suma oricăror două dintre unghiurile sale opuse este

si invers:

Dacă un patrulater are două unghiuri opuse a căror sumă este egală, atunci un astfel de patrulater este înscris.

Nu vom demonstra toate acestea aici (dacă sunteți interesat, priviți următoarele niveluri de teorie). Dar să vedem la ce duce acest fapt minunat, că suma unghiurilor opuse ale unui patrulater înscris este egală.

De exemplu, îmi vine în minte întrebarea, este posibil să descrii un cerc în jurul unui paralelogram? Să încercăm mai întâi „metoda poke”.

Cumva nu merge.

Acum aplicați cunoștințele:

să presupunem că am reușit cumva să potrivim un cerc pe un paralelogram. Atunci cu siguranță trebuie să fie:, adică.

Și acum să ne amintim proprietățile unui paralelogram:

Fiecare paralelogram are unghiuri opuse.

Am înțeles asta

Și cum rămâne cu colțurile? Ei bine, la fel desigur.

Înscris → →

Paralelogram → →

Uimitor, nu?

S-a dovedit că, dacă un paralelogram este înscris într-un cerc, atunci toate unghiurile sale sunt egale, adică este un dreptunghi!

Și în același timp - centrul cercului coincide cu punctul de intersecție al diagonalelor acestui dreptunghi. Acesta, ca să spunem așa, este atașat ca bonus.

Ei bine, asta înseamnă că am aflat că un paralelogram înscris într-un cerc - dreptunghi.

Acum să vorbim despre trapez. Ce se întâmplă dacă un trapez este înscris într-un cerc?Și se dovedește că va fi trapez isoscel . De ce?

Fie ca trapezul să fie înscris într-un cerc. Apoi din nou, dar din cauza paralelismului liniilor și.

Prin urmare, avem: → → un trapez isoscel.

Chiar mai ușor decât cu un dreptunghi, nu? Dar trebuie să vă amintiți cu fermitate - veniți la îndemână:

Să enumeram cele mai multe afirmațiile principale tangentă la un patrulater înscris într-un cerc:

1. Un patrulater este înscris într-un cerc dacă și numai dacă suma celor două unghiuri opuse este
2. Paralelogram înscris într-un cerc dreptunghi iar centrul cercului coincide cu punctul de intersecție al diagonalelor
3. Un trapez înscris într-un cerc este isoscel.

Patrulaterul înscris. Nivel mediu

Se știe că pentru orice triunghi există un cerc circumscris (am demonstrat acest lucru în subiectul „Cerc circumscris”). Ce se poate spune despre patrulater? Aici se dovedește că NU Orice patrulater poate fi înscris într-un cerc, dar există această teoremă:

Un patrulater este înscris într-un cerc dacă și numai dacă suma unghiurilor sale opuse este.

În desenul nostru -

Să încercăm să înțelegem de ce? Cu alte cuvinte, acum vom demonstra această teoremă. Dar înainte de a dovedi, trebuie să înțelegeți cum funcționează afirmația în sine. Ați observat cuvintele „atunci și numai atunci” în declarație? Astfel de cuvinte înseamnă că matematicienii dăunători au împins două afirmații într-una singură.

Descifrare:

1. „Atunci” înseamnă: Dacă un patrulater este înscris într-un cerc, atunci suma oricăror două dintre unghiurile sale opuse este egală.
2. „Numai atunci” înseamnă: Dacă un patrulater are două unghiuri opuse, a căror sumă este egală, atunci un astfel de patrulater poate fi înscris într-un cerc.

La fel ca Alice: „Gândesc ceea ce spun” și „Spun ceea ce gândesc”.

Acum să ne dăm seama de ce atât 1, cât și 2 sunt adevărate?

Primul 1.

Fie ca patrulaterul să fie înscris într-un cerc. Îi marchem centrul și desenăm razele și. Ce se va intampla? Vă amintiți că un unghi înscris este jumătate din unghiul central corespunzător? Dacă vă amintiți - aplicabil acum, și dacă nu este așa - uitați-vă la subiect "Cerc. Unghi înscris".

Inscris

Inscris

Dar uite: .

Obținem că dacă - este înscris, atunci

Ei bine, este clar și, de asemenea, se adună. (de asemenea, ar trebui luate în considerare).

Acum „invers”, adică 2.

Să se dovedească că suma oricăror două unghiuri opuse ale unui patrulater este egală. Să spunem lasă

Încă nu știm dacă putem descrie un cerc în jurul lui. Dar știm cu siguranță că suntem siguri că putem descrie un cerc în jurul unui triunghi. Deci hai sa o facem.

Dacă punctul nu s-a „așezat” pe cerc, atunci s-a dovedit inevitabil fie în exterior, fie în interior.

Să luăm în considerare ambele cazuri.

Lasă punctul să fie mai întâi afară. Apoi segmentul intersectează cercul la un moment dat. Conectați-vă și. Rezultatul este un patrulater înscris (!).

Știm deja despre el că suma unghiurilor lui opuse este egală, adică, dar după condiție avem.

Se pare că ar trebui să fie așa.

Dar acest lucru nu poate fi în niciun fel, deoarece - colțul exterior pentru și înseamnă .

Și înăuntru? Să facem un lucru asemănător. Lasă punctul înăuntru.

Apoi continuarea segmentului intersectează cercul într-un punct. Din nou - un patrulater înscris, și conform condiției trebuie îndeplinit, dar - un unghi extern pentru și înseamnă, adică din nou, nu poate fi așa.

Adică, un punct nu poate fi nici în afara, nici în interiorul cercului - ceea ce înseamnă că este pe cerc!

A demonstrat întreaga teoremă!

Acum să vedem ce consecințe bune dă această teoremă.

Corolarul 1

Un paralelogram înscris într-un cerc nu poate fi decât dreptunghi.

Să înțelegem de ce. Să fie înscris paralelogramul într-un cerc. Atunci ar trebui făcut.

Dar din proprietățile unui paralelogram, știm că.

Și la fel, desigur, pentru unghiuri și.

Deci, dreptunghiul s-a dovedit - toate colțurile sunt de-a lungul.

Dar, în plus, există un alt fapt plăcut suplimentar: centrul cercului circumscris dreptunghiului coincide cu punctul de intersecție al diagonalelor.

Să înțelegem de ce. Sper să vă amintiți foarte bine că unghiul bazat pe diametru este un unghi drept.

Diametru,

Diametru

și de aici centrul. Asta e tot.

Consecința 2

Un trapez înscris într-un cerc este isoscel.

Fie ca trapezul să fie înscris într-un cerc. Apoi.

Si deasemenea.

Am discutat totul? Nu chiar. De fapt, există o altă modalitate, „secretă”, de a recunoaște un patrulater înscris. Vom formula această metodă nu foarte strict (dar clar), dar o vom demonstra doar în ultimul nivel al teoriei.

Dacă într-un patrulater se poate observa o astfel de imagine ca aici în figură (aici unghiurile „care privesc” pe latura punctelor și sunt egale), atunci un astfel de patrulater este unul înscris.

Acesta este un desen foarte important - în probleme este adesea mai ușor de găsit unghiuri egale decât suma unghiurilor şi.

În ciuda lipsei totale de rigoare în formularea noastră, este corectă și, în plus, este întotdeauna acceptată de examinatorii USE. Ar trebui sa scrii asa:

„- inscriptionat” - și totul va fi bine!

Nu uitați acest semn important - amintiți-vă imaginea și poate că vă va atrage atenția la timp atunci când rezolvați problema.

Patrulaterul înscris. Scurtă descriere și formule de bază

Dacă un patrulater este înscris într-un cerc, atunci suma oricăror două dintre unghiurile sale opuse este

si invers:

Dacă un patrulater are două unghiuri opuse a căror sumă este egală, atunci un astfel de patrulater este înscris.

Un patrulater este înscris într-un cerc dacă și numai dacă suma celor două unghiuri opuse este egală.

Paralelogram înscris într-un cerc- neapărat un dreptunghi, iar centrul cercului coincide cu punctul de intersecție al diagonalelor.

Un trapez înscris într-un cerc este isoscel.