Associez les inégalités aux intervalles qui sont leurs solutions. Inégalités linéaires, exemples, solutions

Que devez-vous savoir sur les icônes d'inégalité ? Inégalités d'icônes Suite (> ), ou moins (< ) sont appelés stricte. Avec icônes plus ou égal (≥ ), inférieur ou égal (≤ ) sont appelés non strict. Icône inégal (≠ ) est autonome, mais vous devez également résoudre des exemples avec une telle icône tout le temps. Et nous allons.)

L'icône elle-même n'a pas beaucoup d'effet sur le processus de résolution. Mais à la fin de la solution, au moment de choisir la réponse finale, la signification de l'icône apparaît en pleine force ! Comme nous le verrons plus loin, dans les exemples. Il y a des blagues...

Les inégalités, comme les égalités, sont fidèle et infidèle. Tout est simple ici, sans trucages. disons 5 > 2 est la bonne inégalité. 5 < 2 est incorrect.

Une telle préparation fonctionne pour les inégalités toute sorte et simple à l'horreur.) Il suffit d'effectuer correctement deux (seulement deux !) actions élémentaires. Ces actions sont connues de tous. Mais, ce qui est typique, les montants de ces actions sont la principale erreur dans la résolution des inégalités, oui ... Par conséquent, ces actions doivent être répétées. Ces actions s'appellent ainsi :

Transformations identitaires des inégalités.

Les transformations d'identité des inégalités sont très similaires aux transformations d'identité des équations. En fait, c'est le principal problème. Les différences échappent à la tête et ... arrivent.) Par conséquent, je soulignerai ces différences en particulier. Ainsi, la première transformation identique des inégalités :

1. Le même nombre ou la même expression peut être ajouté (soustrait) aux deux parties de l'inégalité. N'importe quel. Le signe de l'inégalité ne changera pas.

En pratique, cette règle s'applique comme un transfert de termes du côté gauche de l'inégalité vers le côté droit (et vice versa) avec un changement de signe. Avec un changement de signe du terme, pas d'inégalité ! La règle du un contre un est la même que la règle des équations. Et voici les suivants transformations identiques dans les inégalités diffère significativement de celles dans les équations. Je les surligne donc en rouge :

2. Les deux parties de l'inégalité peuvent être multipliées (divisées) par le mêmepositifNuméro. Pour toutepositif Ne changera pas.

3. Les deux parties de l'inégalité peuvent être multipliées (divisées) par le mêmenégatif Numéro. Pour toutenégatifNuméro. Le signe d'inégalité de cettechangera à l'opposé.

Vous vous souvenez (j'espère...) qu'une équation peut être multipliée/divisée par n'importe quoi. Et pour tout nombre, et pour une expression avec x. Tant que ce n'est pas nul. Lui, l'équation, n'est ni chaud ni froid à cause de cela.) Cela ne change pas. Mais les inégalités sont plus sensibles à la multiplication/division.

Exemple illustratif sur le longue mémoire. On écrit une inégalité qui ne fait pas de doute :

5 > 2

Multipliez les deux côtés par +3, on a:

15 > 6

Y a-t-il des objections ? Il n'y a pas d'objections.) Et si nous multiplions les deux parties de l'inégalité originale par -3, on a:

15 > -6

Et c'est un mensonge éhonté.) Un mensonge complet ! Tromper les gens ! Mais dès que le signe de l'inégalité s'inverse, tout se met en place :

15 < -6

À propos des mensonges et de la tromperie - je ne fais pas que jurer.) "J'ai oublié de changer le signe de l'inégalité..."- c'est domicile erreur dans la résolution des inégalités. Cette règle insignifiante et simple a blessé tant de gens ! Qui ont oublié ...) Alors je le jure. Souvenez-vous peut-être...)

Les plus attentifs remarqueront que l'inégalité ne peut pas être multipliée par une expression avec x. Respect attentif !) Et pourquoi pas ? La réponse est simple. On ne connaît pas le signe de cette expression avec x. Elle peut être positive, négative... Par conséquent, on ne sait pas quel signe d'inégalité mettre après la multiplication. Le changer ou pas ? Inconnue. Bien entendu, cette limitation (l'interdiction de multiplier/diviser une inéquation par une expression avec x) peut être contournée. Si vous en avez vraiment besoin. Mais c'est un sujet pour d'autres leçons.

Ce sont toutes des transformations identiques d'inégalités. Permettez-moi de vous rappeler à nouveau qu'ils travaillent pour n'importe quel inégalités. Et maintenant, vous pouvez passer à des types spécifiques.

Inégalités linéaires. Solution, exemples.

Les inégalités linéaires sont appelées inégalités dans lesquelles x est au premier degré et il n'y a pas de division par x. Taper:

x+3 > 5x-5

Comment ces inégalités sont-elles résolues ? Ils sont très faciles à résoudre ! A savoir: avec l'aide, nous réduisons l'inégalité linéaire la plus confuse droit à la réponse. C'est toute la solution. Je vais souligner les principaux points de la solution. Pour éviter les erreurs stupides.)

On résout cette inégalité :

x+3 > 5x-5

On résout de la même façon qu'une équation linéaire. A la seule différence près :

Faites bien attention au signe de l'inégalité !

La première étape est la plus courante. Avec x - à gauche, sans x - à droite ... C'est la première transformation identique, simple et sans problème.) Seulement, n'oubliez pas de changer les signes des membres transférés.

Le signe de l'inégalité est conservé :

x-5x > -5-3

Nous vous en présentons des similaires.

Le signe de l'inégalité est conservé :

4x > -8

Il reste à appliquer la dernière transformation identique : diviser les deux parties par -4.

Diviser par négatif Numéro.

Le signe de l'inégalité sera inversé :

X < 2

C'est la réponse.

C'est ainsi que toutes les inégalités linéaires sont résolues.

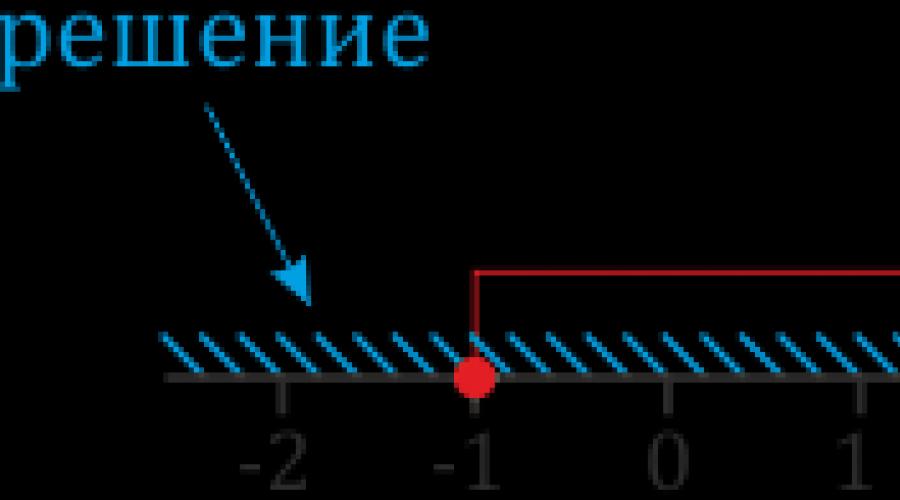
Attention! Le point 2 est dessiné en blanc, c'est-à-dire non peint. Vide à l'intérieur. Cela signifie qu'elle n'est pas incluse dans la réponse ! Je l'ai dessinée si saine exprès. Un tel point (vide, pas sain !)) en mathématiques s'appelle point poinçonné.

Les nombres restants sur l'axe peuvent être marqués, mais pas nécessaire. Les nombres étrangers qui ne sont pas liés à notre inégalité peuvent prêter à confusion, oui ... Vous devez juste vous rappeler que l'augmentation des nombres va dans le sens de la flèche, c'est-à-dire. nombres 3, 4, 5, etc. sommes À droite deux, et les nombres 1, 0, -1, etc. - À gauche.

Inégalité x < 2 - stricte. X est strictement inférieur à deux. En cas de doute, la vérification est simple. Nous substituons un nombre douteux dans l'inégalité et pensons : "Deux c'est moins que deux ? Bien sûr que non !" Exactement. Inégalité 2 < 2 mauvais. Un deux n'est pas bon pour une réponse.

Est-ce qu'un seul suffit ? Bien sûr. Moins... Et zéro c'est bien, et -17, et 0,34... Oui, tous les nombres inférieurs à deux sont bons ! Et même 1.9999.... Au moins un peu, mais moins !

Nous marquons donc tous ces nombres sur l'axe des nombres. Comment? Il y a des options ici. La première option est l'éclosion. Nous passons la souris sur l'image (ou touchons l'image sur la tablette) et voyons que la zone de tous les x qui correspondent à la condition x est ombrée < 2 . C'est tout.

Considérons la deuxième option dans le deuxième exemple :

X ≥ -0,5

Dessinez un axe, marquez le nombre -0,5. Comme ça:

Avez-vous remarqué la différence ?) Et bien oui, difficile de ne pas remarquer... Ce point est noir ! Repeint. Cela signifie que -0,5 inclus dans la réponse. Ici, au fait, vérifier et confondre quelqu'un. Nous remplaçons :

-0,5 ≥ -0,5

Comment? -0,5 n'est rien de plus que -0,5 ! Il y a plus d'icônes...

C'est bon. Dans une inégalité non stricte, tout ce qui correspond à l'icône convient. Et équivaut à en forme et Suite bien. Par conséquent, -0,5 est inclus dans la réponse.

Donc, nous avons marqué -0,5 sur l'axe, il reste à marquer tous les nombres supérieurs à -0,5. Cette fois, je marque la plage de valeurs x appropriées manille(du mot arc) plutôt que l'éclosion. Survolez l'image et voyez cet arc.

Il n'y a pas de différence particulière entre les hachures et les arcs. Faites comme le professeur dit. S'il n'y a pas d'enseignant, tirez les bras. Dans les tâches plus complexes, les hachures sont moins évidentes. Vous pouvez devenir confus.

C'est ainsi que les inégalités linéaires sont dessinées sur l'axe. On passe à la singularité suivante des inégalités.

Écris une réponse pour les inégalités.

C'était bien dans les équations.) Nous avons trouvé x et noté la réponse, par exemple: x \u003d 3. Dans les inégalités, il existe deux formes d'écriture des réponses. Un - sous la forme d'inégalité finale. Bon pour les cas simples. Par exemple:

X< 2.

Ceci est une réponse complète.

Parfois, il est nécessaire d'écrire la même chose, mais sous une forme différente, à travers des trous numériques. Ensuite, l'entrée commence à avoir l'air très scientifique):

x ∈ (-∞; 2)

Sous l'icône ∈ cacher le mot "fait parti".

L'entrée se lit comme ceci : x appartient à l'intervalle de moins l'infini à deux non compris. Assez logique. x peut être n'importe quel nombre de tous nombres possibles de moins l'infini à deux. Double X ne peut pas être, c'est ce que le mot nous dit "non compris".

Où est-ce dans la réponse que "non compris"? Ce fait est noté dans la réponse. tour parenthèse immédiatement après le deux. Si le deux était inclus, la parenthèse serait carré. C'est ici: ]. L'exemple suivant utilise une telle parenthèse.

Ecrivons la réponse : x ≥ -0,5 par intervalles :

x ∈ [-0,5 ; +∞)

Lit : x appartient à l'intervalle de moins 0,5, y compris, jusqu'à plus l'infini.

Infinity ne peut jamais s'allumer. Ce n'est pas un chiffre, c'est un symbole. Par conséquent, dans de telles entrées, l'infini coexiste toujours avec une parenthèse.

Cette forme d'enregistrement est pratique pour les réponses complexes composées de plusieurs lacunes. Mais - juste pour les réponses finales. Dans les résultats intermédiaires, où une autre solution est attendue, il est préférable d'utiliser la forme habituelle, sous la forme d'une inéquation simple. Nous en traiterons dans les rubriques correspondantes.

Tâches populaires avec inégalités.

Les inégalités linéaires elles-mêmes sont simples. Par conséquent, les tâches deviennent souvent plus difficiles. Alors, dire que c'était nécessaire. Ceci, si par habitude, n'est pas très agréable.) Mais c'est utile. Je vais montrer des exemples de telles tâches. Pas à vous de les apprendre, c'est superflu. Et pour ne pas avoir peur de rencontrer des exemples similaires. Une petite réflexion - et tout est simple!)

1. Trouvez deux solutions à l'inégalité 3x - 3< 0

Si ce n'est pas très clair quoi faire, rappelez-vous la règle principale des mathématiques:

Si vous ne savez pas quoi faire, faites ce que vous pouvez !

X < 1

Et alors? Rien de spécial. Que nous demande-t-on ? On nous demande de trouver deux nombres spécifiques qui sont la solution d'une inéquation. Ceux. correspond à la réponse. Deux n'importe quel Nombres. En fait, c'est embarrassant.) Un couple de 0 et 0,5 convient. Un couple -3 et -8. Oui, il y a une infinité de ces couples ! Quelle est la bonne réponse?!

Je réponds : tout ! Toute paire de nombres, dont chacun est inférieur à un, serait la bonne réponse.Écrivez ce que vous voulez. Allons plus loin.

2. Résolvez l'inégalité :

4x - 3 ≠ 0

Des emplois comme celui-ci sont rares. Mais, en tant qu'inégalités auxiliaires, lors de la recherche de l'ODZ, par exemple, ou lors de la recherche du domaine d'une fonction, elles se rencontrent tout le temps. Une telle inégalité linéaire peut être résolue comme une équation linéaire ordinaire. Uniquement partout, sauf pour le signe "=" ( équivaut à) mettre le signe " ≠ " (inégal). Vous arriverez donc à la réponse, avec un signe d'inégalité :

X ≠ 0,75

En plus exemples difficiles mieux vaut faire dans l'autre sens. Rendre l'inégalité égale. Comme ça:

4x - 3 = 0

Résolvez-le calmement comme enseigné et obtenez la réponse :

x = 0,75

L'essentiel, à la toute fin, lors de la rédaction de la réponse finale, est de ne pas oublier que l'on a trouvé x, ce qui donne égalité. Et nous avons besoin - inégalité. Par conséquent, nous n'avons tout simplement pas besoin de ce X.) Et nous devons l'écrire avec la bonne icône :

X ≠ 0,75

Cette approche entraîne moins d'erreurs. Ceux qui résolvent des équations sur la machine. Et pour ceux qui ne résolvent pas les équations, les inégalités, en fait, ne servent à rien...) Autre exemple de tâche populaire :

3. Trouvez la plus petite solution entière de l'inégalité :

3(x - 1) < 5x + 9

Tout d'abord, nous résolvons simplement l'inégalité. Nous ouvrons les parenthèses, transférons, donnons des similaires ... Nous obtenons:

X > - 6

N'est-ce pas arrivé!? Avez-vous suivi les panneaux? Et derrière les signes des membres, et derrière le signe de l'inégalité...

Imaginons à nouveau. Nous devons trouver un nombre spécifique qui correspond à la fois à la réponse et à la condition "plus petit entier". Si cela ne vous apparaît pas immédiatement, vous pouvez simplement prendre n'importe quel nombre et le comprendre. Deux est supérieur à moins six ? Bien sûr! Existe-t-il un nombre inférieur approprié ? Bien sûr. Par exemple, zéro est supérieur à -6. Et encore moins ? Il nous faut le plus petit possible ! Moins trois est plus que moins six ! Vous pouvez déjà attraper le modèle et arrêter de trier bêtement les chiffres, n'est-ce pas ?)

Nous prenons un nombre plus proche de -6. Par exemple, -5. Réponse exécutée, -5 > - 6. Peux-tu trouver un autre nombre inférieur à -5 mais supérieur à -6 ? Vous pouvez, par exemple, -5,5 ... Arrêtez! On nous a dit ensemble la solution! Ne roule pas -5.5 ! Et moins six ? Eee ! L'inégalité est stricte, moins 6 n'est pas moins que moins 6 !

La bonne réponse est donc -5.

Espérons qu'avec un choix de valeur de solution commune tout est clair. Un autre exemple:

4. Résolvez l'inégalité :

7 < 3x+1 < 13

Comment! Une telle expression s'appelle triple inégalité. Au sens strict, il s'agit d'une notation abrégée du système d'inégalités. Mais vous devez encore résoudre ces triples inégalités dans certaines tâches ... Il est résolu sans aucun système. Par les mêmes transformations identiques.

Il faut simplifier, ramener cette inégalité à un X pur. Mais... Quoi transférer où !? Voici le moment de se rappeler que le décalage gauche-droite est forme abrégée la première transformation identique.

MAIS formulaire complet ressemble à ceci: Vous pouvez ajouter/soustraire n'importe quel nombre ou expression aux deux parties de l'équation (inégalité).

Il y a trois parties ici. Nous allons donc appliquer des transformations identiques aux trois parties !

Alors, débarrassons-nous de celui qui se trouve au milieu de l'inégalité. Soustrayez un de toute la partie médiane. Pour que l'inégalité ne change pas, nous soustrayons un des deux parties restantes. Comme ça:

7 -1< 3x+1-1 < 13-1

6 < 3x < 12

Déjà mieux, non ?) Il reste à diviser les trois parties en trois :

2 < X < 4

C'est tout. C'est la réponse. X peut être n'importe quel nombre compris entre deux (non compris) et quatre (non compris). Cette réponse est également écrite à intervalles, ces entrées seront en inégalités carrées. Là, ils sont la chose la plus commune.

À la fin de la leçon, je répéterai la chose la plus importante. Le succès dans la résolution des inégalités linéaires dépend de la capacité à transformer et à simplifier les équations linéaires. Si en même temps suivre le signe de l'inégalité, il n'y aura pas de problèmes. Ce que je te souhaite. aucun problème.)

Si vous aimez ce site...

Au fait, j'ai quelques autres sites intéressants pour vous.)

Vous pouvez vous entraîner à résoudre des exemples et découvrir votre niveau. Test avec vérification instantanée. Apprendre - avec intérêt !)

vous pouvez vous familiariser avec les fonctions et les dérivés.

Par exemple, l'expression \(x>5\) est une inégalité.

Types d'inégalités :

Si \(a\) et \(b\) sont des nombres ou , alors l'inégalité est appelée numérique. En fait, ce n'est qu'une comparaison de deux chiffres. Ces inégalités se subdivisent en fidèle et infidèle.

Par exemple:
\(-5<2\) - верное числовое неравенство, ведь \(-5\) действительно меньше \(2\);

\(17+3\geq 115\) est une inégalité numérique invalide car \(17+3=20\) et \(20\) est inférieur à \(115\) (pas supérieur ou égal à).

Si \(a\) et \(b\) sont des expressions contenant une variable, alors on a inégalité à variable. Ces inégalités sont divisées en types en fonction du contenu:

\(2x+1\geq4(5-x)\)				Variable uniquement à la première puissance
\(3x^2-x+5>0\)				Il y a une variable dans la deuxième puissance (carré), mais pas de puissances supérieures (troisième, quatrième, etc.)
\(\log_(4)((x+1))<3\)
\(2^(x)\leq8^(5x-2)\)

... etc.

Quelle est la solution d'une inégalité ?

Si un nombre est substitué dans l'inégalité au lieu d'une variable, il se transformera en un nombre numérique.

Si la valeur donnée pour x rend l'inégalité d'origine vraie numérique, alors on l'appelle résoudre l'inégalité. Sinon, cette valeur n'est pas une solution. Et à résoudre l'inégalité- il faut trouver toutes ses solutions (ou montrer qu'elles n'existent pas).

Par exemple, si on est dans l'inégalité linéaire \(x+6>10\), on substitue le nombre \(7\) à la place de x, on obtient la bonne inégalité numérique : \(13>10\). Et si nous remplaçons \(2\), il y aura une inégalité numérique incorrecte \(8>10\). Autrement dit, \(7\) est une solution à l'inégalité d'origine, mais \(2\) ne l'est pas.

Cependant, l'inégalité \(x+6>10\) a d'autres solutions. En effet, nous obtiendrons les inégalités numériques correctes en substituant à la fois \(5\), et \(12\), et \(138\) ... Et comment pouvons-nous trouver tous solutions possibles? Pour ce faire, utilisez Pour notre cas, nous avons :

\(x+6>10\) \(|-6\)
\(x>4\)

Autrement dit, nous pouvons utiliser n'importe quel nombre supérieur à quatre. Maintenant, nous devons écrire la réponse. Les solutions aux inégalités, en règle générale, sont écrites numériquement, en les marquant en outre sur l'axe numérique avec des hachures. Pour notre cas nous avons :

Réponse: \(x\in(4;+\infty)\)

Quand le signe change-t-il dans une inégalité ?

Il y a un grand piège dans les inégalités, dans lequel les étudiants « aiment » vraiment tomber :

Lorsque l'on multiplie (ou divise) l'inégalité par un nombre négatif, elle est inversée ("supérieur à" par "inférieur", "supérieur ou égal à" par "inférieur ou égal à", etc.)

Pourquoi cela arrive-t-il? Pour comprendre cela, regardons les transformations de l'inégalité numérique \(3>1\). C'est correct, le triple c'est vraiment plus qu'un. Essayons d'abord de le multiplier par n'importe quel nombre positif, par exemple deux :

\(3>1\) \(|\cdot2\)
\(6>2\)

Comme vous pouvez le voir, après la multiplication, l'inégalité reste vraie. Et peu importe le nombre positif que nous multiplions, nous obtiendrons toujours la bonne inégalité. Et maintenant essayons de multiplier par un nombre négatif, par exemple, moins trois :

\(3>1\) \(|\cdot(-3)\)
\(-9>-3\)

Il s'est avéré qu'il s'agissait d'une inégalité incorrecte, car moins neuf est inférieur à moins trois ! Autrement dit, pour que l'inégalité devienne vraie (ce qui signifie que la transformation de la multiplication par un négatif était "légale"), vous devez inverser le signe de comparaison, comme ceci : \(−9<− 3\).
Avec la division, cela se passera de la même manière, vous pouvez le vérifier vous-même.

La règle écrite ci-dessus s'applique à tous les types d'inégalités, et pas seulement aux inégalités numériques.

Exemple: Résoudre l'inégalité \(2(x+1)-1<7+8x\)
La solution:

\(2x+2-1<7+8x\)	Déplaçons \(8x\) vers la gauche, et \(2\) et \(-1\) vers la droite, sans oublier de changer de signe
\(2x-8x<7-2+1\)
\(-6x<6\) \(|:(-6)\)	Diviser les deux côtés de l'inégalité par \(-6\), sans oublier de passer de "moins" à "plus grand"
	Marquons un intervalle numérique sur l'axe. Inégalité, donc la valeur \(-1\) est « poinçonnée » et nous ne la prenons pas en réponse
	Écrivons la réponse sous forme d'intervalle

Réponse: \(x\in(-1;\infty)\)

Inégalités et DHS

Les inégalités, ainsi que les équations, peuvent avoir des restrictions sur , c'est-à-dire sur les valeurs de x. En conséquence, les valeurs inacceptables selon l'ODZ doivent être exclues de l'intervalle de solution.

Exemple: Résoudre l'inégalité \(\sqrt(x+1)<3\)

La solution: Il est clair que pour que le côté gauche soit inférieur à \(3\), l'expression racine doit être inférieure à \(9\) (après tout, à partir de \(9\) juste \(3\)). On a:

\(x+1<9\) \(|-1\)
\(X<8\)

Tout? Toute valeur de x inférieure à \(8\) nous conviendra ? Pas! Car si nous prenons, par exemple, la valeur \(-5\) qui semble répondre à l'exigence, ce ne sera pas une solution à l'inégalité d'origine, car elle nous conduira à calculer la racine d'un nombre négatif.

\(\carré(-5+1)<3\)
\(\carré(-4)<3\)

Par conséquent, nous devons également prendre en compte les restrictions sur les valeurs de x - cela ne peut pas être tel qu'il y ait un nombre négatif sous la racine. Ainsi, nous avons la deuxième exigence pour x :

\(x+1\geq0\)
\(x\geq-1\)

Et pour que x soit une solution finale, il doit satisfaire les deux conditions à la fois : il doit être inférieur à \(8\) (pour être une solution) et supérieur à \(-1\) (pour être valide en principe). En traçant sur la droite numérique, nous avons la réponse finale :

Réponse: \(\gauche[-1;8\droite)\)

Dans l'article, nous considérerons solution des inégalités. Parlons franchement de comment construire une solution aux inégalités avec des exemples clairs !

Avant d'envisager la solution des inégalités avec des exemples, abordons les concepts de base.

Introduction aux inégalités

inégalité est appelée une expression dans laquelle les fonctions sont reliées par des signes de relation >, . Les inégalités peuvent être à la fois numériques et alphabétiques.
Les inégalités avec deux signes de relation sont appelées doubles, avec trois - triples, etc. Par exemple:
a(x) > b(x),
une(x) une(x) b(x),
a(x) b(x).
a(x) Les inégalités contenant le signe > ou ou ne sont pas strictes.
Solution d'inégalité est toute valeur de la variable pour laquelle cette inégalité est vraie.
"Résoudre l'inégalité" signifie que vous devez trouver l'ensemble de toutes ses solutions. Il existe différentes méthodes de résolution des inégalités. Pour solutions d'inégalité utiliser une droite numérique infinie. Par exemple, résoudre l'inégalité x > 3 est un intervalle de 3 à +, et le nombre 3 n'est pas inclus dans cet intervalle, donc le point sur la ligne est désigné par un cercle vide, car l'inégalité est stricte.
+
La réponse sera : x (3 ; +).
La valeur x=3 n'est pas incluse dans l'ensemble des solutions, donc la parenthèse est ronde. Le signe de l'infini est toujours entre parenthèses. Le signe signifie « appartenance ».
Considérez comment résoudre les inégalités en utilisant un autre exemple avec le signe :
x2
-+
La valeur x=2 est incluse dans l'ensemble des solutions, donc le crochet et le point sur la ligne sont désignés par un cercle plein.
La réponse sera : x.

L'algorithme complet décrit ci-dessus s'écrit comme suit :

3 x + 12 ≤ 0 ; 3x ≤ − 12 ; x ≤ − 4 .

Réponse: x ≤ − 4 ou (− ∞ , − 4 ] .

Exemple 2

Indiquez toutes les solutions disponibles de l'inégalité − 2 , 7 · z > 0 .

La solution

D'après la condition, nous voyons que le coefficient a en z est égal à - 2, 7 et b est explicitement absent ou égal à zéro. Vous ne pouvez pas utiliser la première étape de l'algorithme, mais passez immédiatement à la seconde.

Nous divisons les deux parties de l'équation par le nombre - 2, 7. Puisque le nombre est négatif, il est nécessaire de changer le signe de l'inégalité à l'opposé. Autrement dit, nous obtenons que (− 2 , 7 z) : (− 2 , 7)< 0: (− 2 , 7) , и дальше z < 0 .

Nous écrivons tout l'algorithme dans forme courte:

− 2 , 7 z > 0 ; z< 0 .

Réponse: z< 0 или (− ∞ , 0) .

Exemple 3

Résolvez l'inégalité - 5 · x - 15 22 ≤ 0 .

La solution

Selon la condition, on voit qu'il faut résoudre l'inégalité avec le coefficient a pour la variable x, qui est égal à - 5, avec le coefficient b, qui correspond à la fraction - 15 22 . Il faut résoudre l'inégalité en suivant l'algorithme, c'est-à-dire: transférer - 15 22 dans une autre partie de signe opposé, diviser les deux parties par - 5, changer le signe de l'inégalité:

5 x ≤ 15 22 ; - 5 x : - 5 ≥ 15 22 : - 5 x ≥ - 3 22

A la dernière transition pour le côté droit, la règle de division d'un nombre par différents signes 15 22 : - 5 = - 15 22 : 5 , après quoi on effectue la division fraction communeà un nombre naturel - 15 22 : 5 \u003d - 15 22 1 5 \u003d - 15 1 22 5 \u003d - 3 22.

Réponse: x ≥ - 3 22 et [ - 3 22 + ∞) .

Considérons le cas où a = 0. Expression linéaire de la forme a x + b< 0 является неравенством 0 · x + b < 0 , где на рассмотрение берется неравенство вида b < 0 , после чего выясняется, оно верное или нет.

Tout est basé sur la définition de la solution de l'inégalité. Pour toute valeur de x, on obtient une inégalité numérique de la forme b< 0 , потому что при подстановке любого t вместо переменной x , тогда получаем 0 · t + b < 0 , где b < 0 . В случае, если оно верно, то для его решения подходит любое значение. Когда b < 0 неверно, тогда линейное уравнение не имеет решений, потому как не имеется ни одного значения переменной, которое привело бы верному числовому равенству.

Nous considérons tous les jugements sous la forme d'un algorithme de résolution des inégalités linéaires 0 x + b< 0 (≤ , > , ≥) :

Définition 5

Inégalité numérique de la forme b< 0 (≤ , >, ≥) est vrai, alors l'inégalité d'origine a une solution pour toute valeur, et faux lorsque l'inégalité d'origine n'a pas de solution.

Exemple 4

Résolvez l'inégalité 0 · x + 7 > 0 .

La solution

Cette inégalité linéaire 0 · x + 7 > 0 peut prendre n'importe quelle valeur x . On obtient alors une inégalité de la forme 7 > 0 . La dernière inégalité est considérée comme vraie, donc n'importe quel nombre peut être sa solution.

Réponse: intervalle (− ∞ , + ∞) .

Exemple 5

Trouver une solution à l'inégalité 0 · x − 12 , 7 ≥ 0 .

La solution

En substituant la variable x à n'importe quel nombre, on obtient que l'inégalité prendra la forme − 12 , 7 ≥ 0 . C'est incorrect. Autrement dit, 0 · x − 12 , 7 ≥ 0 n'a pas de solution.

Réponse: il n'y a pas de solutions.

Considérons la solution des inégalités linéaires, où les deux coefficients sont égaux à zéro.

Exemple 6

Déterminer une inéquation insoluble à partir de 0 · x + 0 > 0 et 0 · x + 0 ≥ 0 .

La solution

En substituant n'importe quel nombre au lieu de x, nous obtenons deux inégalités de la forme 0 > 0 et 0 ≥ 0 . Le premier est incorrect. Cela signifie que 0 x + 0 > 0 n'a pas de solutions, et 0 x + 0 ≥ 0 a un nombre infini de solutions, c'est-à-dire n'importe quel nombre.

Réponse: l'inégalité 0 x + 0 > 0 n'a pas de solutions, et 0 x + 0 ≥ 0 a des solutions.

Cette méthode est envisagée dans le cours scolaire de mathématiques. La méthode des intervalles est capable de résoudre différentes sortes les inégalités sont également linéaires.

La méthode des intervalles est utilisée pour les inégalités linéaires lorsque la valeur du coefficient x n'est pas égale à 0 . Sinon, vous devrez calculer en utilisant une autre méthode.

Définition 6

La méthode d'espacement est la suivante :

• introduction de la fonction y = a x + b ;
• rechercher des zéros pour diviser le domaine de définition en intervalles ;
• détermination des signes pour le concept d'entre eux sur les intervalles.

Assemblons un algorithme pour résoudre les équations linéaires a x + b< 0 (≤ , >, ≥) pour a ≠ 0 en utilisant la méthode des intervalles :

• trouver les zéros de la fonction y = a · x + b pour résoudre une équation de la forme a · x + b = 0 . Si a ≠ 0, alors la solution sera la seule racine qui prendra la désignation x 0 ;
• construction d'une ligne de coordonnées avec l'image d'un point de coordonnée x 0, avec une inégalité stricte, le point est noté en pointillé, avec une inégalité non stricte, il est grisé ;
• détermination des signes de la fonction y = a x + b sur les intervalles, pour cela il faut trouver les valeurs de la fonction aux points de l'intervalle ;
• la solution de l'inégalité avec les signes > ou ≥ sur la ligne de coordonnées, des hachures sont ajoutées au-dessus de l'écart positif,< или ≤ над отрицательным промежутком.

Prenons plusieurs exemples de résolution d'une inégalité linéaire à l'aide de la méthode des intervalles.

Exemple 6

Résolvez l'inégalité − 3 · x + 12 > 0 .

La solution

Il découle de l'algorithme que vous devez d'abord trouver la racine de l'équation − 3 · x + 12 = 0 . Nous obtenons que − 3 · x = − 12 , x = 4 . Il est nécessaire de représenter la ligne de coordonnées, où nous marquons le point 4. Il sera piqué puisque l'inégalité est stricte. Considérez le dessin ci-dessous.

Il est nécessaire de déterminer les signes sur les intervalles. Pour le déterminer sur l'intervalle (− ∞ , 4) , il faut calculer la fonction y = − 3 · x + 12 pour x = 3 . De là, nous obtenons que − 3 3 + 12 = 3 > 0 . Le signe sur l'intervalle est positif.

Nous déterminons le signe à partir de l'intervalle (4, + ∞), puis nous substituons la valeur x \u003d 5. Nous avons − 3 5 + 12 = − 3< 0 . Знак на промежутке является отрицательным. Изобразим на числовой прямой, приведенной ниже.

Nous effectuons la solution de l'inégalité avec le signe > , et la hachure est effectuée sur l'écart positif. Considérez le dessin ci-dessous.

On peut voir sur le dessin que la solution recherchée a la forme (− ∞ , 4) ou x< 4 .

Réponse: (− ∞ , 4) ou x< 4 .

Pour comprendre comment représenter graphiquement, il faut considérer 4 inégalités linéaires comme exemple : 0, 5 x − 1< 0 , 0 , 5 · x − 1 ≤ 0 , 0 , 5 · x − 1 >0 et 0 , 5 x − 1 ≥ 0 . Leurs solutions seront x< 2 , x ≤ 2 , x >2 et x ≥ 2 . Pour ce faire, tracez un graphique fonction linéaire y = 0 , 5 x − 1 ci-dessous.

Il est clair que

Définition 7

• solution de l'inégalité 0 , 5 x − 1< 0 считается промежуток, где график функции y = 0 , 5 · x − 1 располагается ниже О х;
• la solution 0 , 5 x − 1 ≤ 0 est l'intervalle où la fonction y = 0 , 5 x − 1 est inférieure à 0 x ou coïncide ;
• la solution 0 , 5 x − 1 > 0 est considérée comme l'intervalle, où la fonction est située au-dessus de O x ;
• la solution 0 , 5 x − 1 ≥ 0 est l'intervalle où le graphe est supérieur à O x ou coïncide.

Le sens de la solution graphique des inégalités est de trouver les écarts, qui doivent être représentés sur le graphique. Dans ce cas, nous obtenons que le côté gauche a y \u003d a x + b, et le côté droit a y \u003d 0, et il coïncide avec A propos de x.

Définition 8

Le tracé de la fonction y = a x + b est effectué :

• en résolvant l'inégalité a x + b< 0 определяется промежуток, где график изображен ниже О х;
• tout en résolvant l'inégalité a x + b ≤ 0, l'intervalle est déterminé là où le graphique est affiché sous l'axe O x ou coïncide ;
• tout en résolvant l'inégalité a x + b > 0, l'intervalle est déterminé, où le graphique est affiché au-dessus de O x ;
• tout en résolvant l'inégalité a x + b ≥ 0, l'intervalle est déterminé là où le graphique est au-dessus de O x ou coïncide.

Exemple 7

Résolvez l'inégalité - 5 · x - 3 > 0 à l'aide du graphique.

La solution

Il faut construire un graphe d'une fonction linéaire - 5 · x - 3 > 0 . Cette droite est décroissante car le coefficient de x est négatif. Pour déterminer les coordonnées du point de son intersection avec O x - 5 · x - 3 > 0, on obtient la valeur - 3 5 . Représentons-le graphiquement.

La solution de l'inégalité avec le signe >, alors vous devez faire attention à l'intervalle au-dessus de O x. Nous mettons en évidence la partie nécessaire de l'avion en rouge et obtenons que

L'écart requis est la partie O x de la couleur rouge. Ainsi, le rayon ouvert - ∞ , - 3 5 sera la solution de l'inégalité. Si, par condition, ils avaient une inégalité non stricte, alors la valeur du point - 3 5 serait également une solution à l'inégalité. Et coïnciderait avec O x.

Réponse: - ∞ , - 3 5 ou x< - 3 5 .

La solution graphique est utilisée lorsque le côté gauche correspondra à la fonction y = 0 x + b , c'est-à-dire y = b . Ensuite, la ligne sera parallèle à O x ou coïncidera avec b \u003d 0. Ces cas montrent qu'une inégalité peut n'avoir aucune solution, ou que n'importe quel nombre peut être une solution.

Exemple 8

Déterminer à partir des inégalités 0 x + 7< = 0 , 0 · x + 0 ≥ 0 то, которое имеет хотя бы одно решение.

La solution

La représentation y = 0 x + 7 est y = 7 , alors un plan de coordonnées avec une droite parallèle à O x et au-dessus de O x sera donné. Donc 0 x + 7< = 0 решений не имеет, потому как нет промежутков.

Le graphique de la fonction y \u003d 0 x + 0 est considéré comme y \u003d 0, c'est-à-dire que la ligne coïncide avec O x. Ainsi, l'inégalité 0 · x + 0 ≥ 0 a plusieurs solutions.

Réponse: la deuxième inégalité admet une solution pour toute valeur de x .

Inégalités linéaires

La solution des inégalités se réduit à la solution équation linéaire, appelées inégalités linéaires.

Ces inégalités étaient prises en compte dans le cursus scolaire, car elles constituaient un cas particulier de résolution d'inégalités, ce qui entraînait l'ouverture de parenthèses et la réduction de termes similaires. Par exemple, considérons que 5 − 2 x > 0 , 7 (x − 1) + 3 ≤ 4 x − 2 + x , x - 3 5 - 2 x + 1 > 2 7 x .

Les inégalités données ci-dessus sont toujours réduites à la forme d'une équation linéaire. Après cela, les crochets sont ouverts et des termes similaires sont donnés, transférés de Différents composants, en changeant le signe à l'opposé.

En réduisant l'inégalité 5 − 2 x > 0 à une inégalité linéaire, nous la représentons de telle manière qu'elle ait la forme − 2 x + 5 > 0 , et pour réduire la seconde nous obtenons que 7 (x − 1) + 3 ≤ 4 X − 2 + X . Il est nécessaire d'ouvrir les parenthèses, d'amener des termes semblables, de déplacer tous les termes vers la gauche et d'amener des termes semblables. Il ressemble à ceci :

7 X - 7 + 3 ≤ 4 X - 2 + X 7 X - 4 ≤ ​​5 X - 2 7 X - 4 - 5 X + 2 ≤ 0 2 X - 2 ≤ 0

Cela apporte la solution à une inégalité linéaire.

Ces inégalités sont considérées comme linéaires, car elles ont le même principe de résolution, après quoi il est possible de les réduire à des inégalités élémentaires.

Pour résoudre ce type d'inégalité de ce type, il est nécessaire de la réduire à une inégalité linéaire. Cela devrait être fait comme ceci:

Définition 9

• parenthèses ouvertes ;
• collectez les variables à gauche et les nombres à droite ;
• apporter des termes similaires ;
• diviser les deux parties par le coefficient de x .

Exemple 9

Résolvez l'inégalité 5 · (x + 3) + x ≤ 6 · (x − 3) + 1 .

La solution

On élargit les parenthèses, puis on obtient une inégalité de la forme 5 · x + 15 + x ≤ 6 · x − 18 + 1 . Après réduction des termes similaires, nous avons que 6 · x + 15 ≤ 6 · x − 17 . Après avoir déplacé les termes de gauche à droite, on obtient que 6 x + 15 − 6 x + 17 ≤ 0 . Par conséquent, il a une inégalité de la forme 32 ≤ 0 à partir du résultat obtenu dans le calcul 0 · x + 32 ≤ 0 . On peut voir que l'inégalité est fausse, ce qui signifie que l'inégalité donnée par la condition n'a pas de solutions.

Réponse: aucune solution.

Il convient de noter qu'il existe de nombreuses inégalités d'un autre type, qui peuvent être réduites à une inégalité linéaire ou à une inégalité du type indiqué ci-dessus. Par exemple, 5 2 x − 1 ≥ 1 est équation exponentielle, qui se réduit à une solution linéaire 2 · x − 1 ≥ 0 . Ces cas seront considérés lors de la résolution d'inégalités de ce type.

Si vous remarquez une erreur dans le texte, veuillez le mettre en surbrillance et appuyer sur Ctrl+Entrée