Erreur relative d'un nombre approximatif. Erreur absolue et relative des calculs
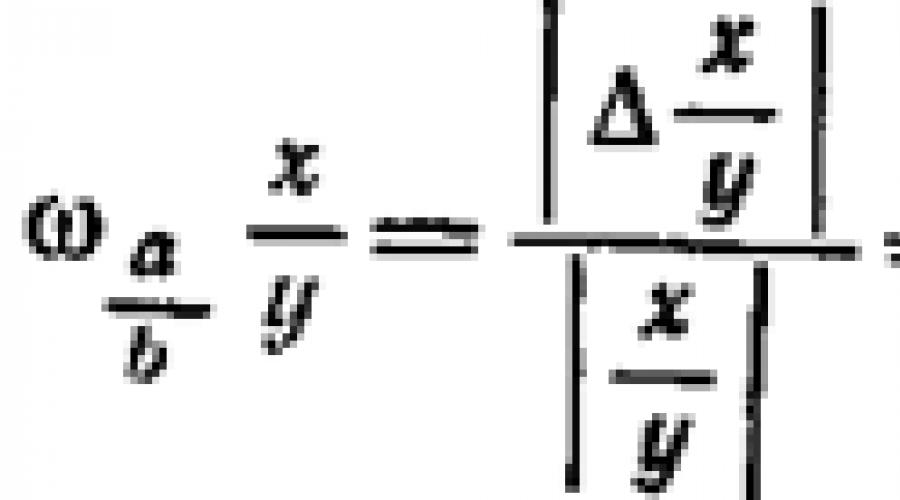
Lire aussi
Lors des calculs, il devient souvent nécessaire d'arrondir les nombres, c'est-à-dire en les remplaçant par des nombres avec moins chiffres significatifs.
Il existe trois façons d'arrondir les nombres :
Arrondir à k e chiffre significatif consiste à éliminer tous les chiffres commençant par (k+1) e.
L'arrondi supérieur diffère de l'arrondi inférieur en ce que le dernier chiffre stocké est augmenté de un.
L'arrondi avec la plus petite erreur diffère de l'arrondi avec un excès en ce que l'augmentation d'un des derniers chiffres mémorisés n'est effectuée que si le premier des chiffres ignorés est supérieur à 4.
Exception : si l'arrondi avec la plus petite erreur consiste à écarter un seul chiffre 5, alors le dernier chiffre mémorisé n'est pas modifié s'il est pair, et augmenté de 1 s'il est impair.
D'après les règles ci-dessus pour arrondir les nombres approximatifs, il s'ensuit que l'erreur causée par l'arrondi avec la plus petite erreur ne dépasse pas la moitié de l'unité du dernier chiffre stocké, et lors de l'arrondi avec un déficit ou un excès, l'erreur peut être supérieure à la moitié de la unité du dernier chiffre enregistré, mais pas plus d'une unité entière de cette décharge.
Regardons cela dans les exemples suivants.
1. L'erreur de montant. Laisser X un, à-- une certaine approximation de la valeur b. Laisser X et à-- erreurs absolues des approximations correspondantes X et à. Trouvons la limite d'erreur absolue h a+b les montants x+y, qui est une approximation de la somme a+b.
un = x + x,
b = y + y.
En additionnant ces deux égalités, on obtient
un + b = x + y + x + y.
Évidemment, l'erreur de la somme des approximations X et à est égal à la somme des erreurs des termes, c'est-à-dire
(x + y) = x + y
On sait que le module de la somme est inférieur ou égal à la somme des modules des termes. C'est pourquoi
(x + y) = x + y X + y
Cela implique que l'erreur absolue de la somme des approximations ne dépasse pas la somme des erreurs absolues des termes. Par conséquent, la somme des limites des erreurs absolues des termes peut être considérée comme la limite de l'erreur absolue de la somme.
Désignant la limite de l'erreur absolue de la quantité unà travers h un, et b à h b aura
h a+b = h un + h b
2. Erreur de différence. Soient x et y les erreurs dans les approximations x et y de a et b, respectivement.
un = x + x,
b = y + y.
Soustrayez la seconde de la première égalité, on obtient
a - b = (x - y) + (x - y)
Évidemment, l'erreur de la différence des approximations est égale à la différence entre les erreurs de la diminution et de la diminution, c'est-à-dire
(x - y) = x - y),
(x - y) = x + (-y)
Et puis, en raisonnant de la même manière que dans le cas de l'addition, on a
(x - y) = x + (-y) X + y
Il s'ensuit que l'erreur absolue de la différence ne dépasse pas la somme des erreurs absolues de la diminutrice et de la soustraite.
Pour la limite de l'erreur absolue de la différence, vous pouvez prendre la somme des limites des erreurs absolues de la réduction et de la soustraction. De cette façon.
h un B =h un + h b (9)
De la formule (9) il résulte que la limite de l'erreur absolue de la différence ne peut être inférieure à la limite de l'erreur absolue de chaque approximation. Cela implique la règle de soustraction des approximations, qui est parfois utilisée dans les calculs.
Lors de la soustraction de nombres qui sont des approximations de certaines quantités, le résultat doit être autant de chiffres après la virgule que l'approximation avec le plus petit nombre de chiffres après la virgule.
3. Erreur de produit. Considérez le produit de nombres X et à, qui sont des approximations des quantités un et b. Dénoter par X erreur d'approximation X, et à travers à-- erreur d'approximation à,
un = x + x,
b = y + y.
En multipliant ces deux égalités, on obtient
Erreur absolue de produit heu est égal à
Et donc
En divisant les deux côtés de l'inégalité résultante par heu, on a
Sachant que le module du produit est égal au produit des modules des facteurs, nous aurons
Ici, le côté gauche de l'inégalité est l'erreur relative du produit heu, -- erreur d'approximation relative X, et est l'erreur d'approximation relative à. Par conséquent, en écartant la petite valeur ici, nous obtenons l'inégalité
Ainsi, l'erreur relative du produit des approximations ne dépasse pas la somme des erreurs relatives des facteurs. Il s'ensuit que la somme des limites des erreurs relatives des facteurs est la limite de l'erreur relative du produit, c'est-à-dire
E un B =E un +E b (10)
De la formule (10), il s'ensuit que la limite de l'erreur relative du produit ne peut être inférieure à la limite de l'erreur relative du moins précis des facteurs. Par conséquent, ici, comme dans les étapes précédentes, cela n'a aucun sens de conserver un nombre excessif de chiffres significatifs dans les facteurs.
Il est parfois utile d'utiliser la règle suivante dans les calculs pour réduire la quantité de travail : lors de la multiplication d'approximations avec différents nombres de chiffres significatifs, le résultat doit conserver autant de chiffres significatifs que l'approximation avec le plus petit nombre de chiffres significatifs.
4. L'erreur du quotient. Si x est une approximation de a avec une erreur x et y est une approximation de b avec une erreur y, alors
Calculons d'abord l'erreur absolue du quotient :
puis l'erreur relative :

Tenant compte que y peu par rapport à y, la valeur absolue de la fraction peut être considérée comme égale à un. Alors
il résulte de la dernière formule que l'erreur relative du quotient ne dépasse pas la somme des erreurs relatives du dividende et du diviseur. Par conséquent, nous pouvons supposer que la limite de l'erreur relative du quotient est égale à la somme des limites des erreurs relatives du dividende et du diviseur, c'est-à-dire
5. Erreur de degré et de racine. 1) Laissez tu = un n, où n -- entier naturel, et soit un x. Puis si E un-- limite de l'erreur d'approximation relative X quantités un, alors
et donc
Ainsi, la limite de l'erreur relative du degré est égale au produit de la limite de l'erreur relative de la base par l'exposant, soit
E tu = nE un (11)
2) Laissez où n est un nombre naturel, et soit Oh.
Par la formule (11)
et donc
calcul de la franchise d'erreur
Ainsi, la limite de l'erreur relative de la racine nème degré en n fois inférieure à la limite de l'erreur relative du nombre radical.
6. Problème inverse de calculs approchés. Dans le problème direct, il faut trouver la valeur approchée de la fonction u=f(x, y, ..., n) en fonction des valeurs approchées données des arguments
et marge d'erreur h un, qui est exprimé en termes d'erreurs des arguments d'une fonction
h tu = (h X , h y , …, h z ) (12)
En pratique, il est souvent nécessaire de résoudre un problème inverse, dans lequel il faut savoir avec quelle précision les valeurs des arguments doivent être données x, y, …, z pour calculer les valeurs de fonction correspondantes u = f(x, y, …, z) avec une précision prédéterminée h u .
Ainsi, lors de la résolution du problème inverse, on cherche les limites d'erreur des arguments associés à la limite d'erreur donnée de la fonction h tu l'équation (12), et la solution du problème inverse se réduit à compiler et résoudre l'équation h tu = (h X , h y , …, h z ) relativement h X , h y , …, h z. Une telle équation a soit une infinité de solutions, soit aucune solution. Le problème est considéré comme résolu si au moins une solution d'une telle équation est trouvée.
Pour résoudre le problème inverse, qui est souvent indéterminé, il faut introduire des conditions supplémentaires sur les rapports des erreurs inconnues, par exemple, les considérer égaux et ainsi réduire le problème à une équation à une inconnue.
Lorsqu'il s'agit de calculs avec des fractions décimales infinies, il est nécessaire, par commodité, d'effectuer une approximation de ces nombres, c'est-à-dire de les arrondir. Des nombres approximatifs sont également obtenus à partir de diverses mesures.
Il peut être utile de savoir de combien la valeur approximative d'un nombre diffère de sa valeur exacte. Il est clair que plus cette différence est petite, mieux c'est, plus la mesure ou le calcul est effectué avec précision.
Pour déterminer la précision des mesures (calculs), un tel concept est introduit comme erreur d'approximation. Ils l'appellent différemment erreur absolue. L'erreur d'approximation est la différence modulo entre la valeur exacte d'un nombre et sa valeur approchée.
Si un est valeur exacte nombre, et b est sa valeur approximative, alors l'erreur d'approximation est déterminée par la formule |a – b|.
Supposons qu'à la suite de mesures, le nombre 1,5 ait été obtenu. Cependant, à la suite du calcul par la formule, la valeur exacte de ce nombre est de 1,552. Dans ce cas, l'erreur d'approximation sera égale à |1,552 – 1,5| = 0,052.
Dans le cas de fractions infinies, l'erreur d'approximation est déterminée par la même formule. Au lieu du nombre exact, la fraction infinie elle-même est écrite. Par exemple, |π – 3,14| = |3,14159... – 3,14| = 0,00159... . Ici, il s'avère que l'erreur d'approximation est exprimée par un nombre irrationnel.
Comme on le sait, l'approximation peut être effectuée à la fois en termes de carence et d'excès. Le même nombre π, à l'approche du déficit avec une précision de 0,01, est de 3,14, et à l'approche de l'excès avec une précision de 0,01, il est de 3,15. La raison de l'utilisation de son approximation par défaut dans les calculs est d'appliquer des règles d'arrondi. Selon ces règles, si le premier chiffre à écarter est cinq ou supérieur à cinq, alors une approximation excessive est effectuée. Si moins de cinq, alors par carence. Étant donné que le troisième chiffre après la virgule décimale du nombre π est 1, par conséquent, en s'approchant avec une précision de 0,01, il est effectué par défaut.
En effet, si on calcule les erreurs d'approximation jusqu'à 0,01 du nombre π en termes de déficit et d'excès, on obtient :
|3,14159... – 3,14| = 0,00159...
|3,14159... – 3,15| = 0,0084...
Depuis 0.00159...
En parlant de l'erreur d'approximation, ainsi que dans le cas de l'approximation elle-même (par excès ou défaut), indiquez sa précision. Ainsi dans l'exemple ci-dessus avec le nombre π, il faut dire qu'il est égal au nombre 3,14 avec une précision de 0,01. Après tout, le module de la différence entre le nombre lui-même et sa valeur approximative ne dépasse pas 0,01 (0,00159... ≤ 0,01).
De même, π est égal à 3,15 jusqu'à 0,01, car 0,0084... ≤ 0,01. Cependant, si nous parlons d'une plus grande précision, par exemple jusqu'à 0,005, alors nous pouvons dire que π est égal à 3,14 avec une précision de 0,005 (puisque 0,00159 ... ≤ 0,005). On ne peut pas dire cela par rapport à l'approximation de 3,15 (puisque 0,0084 ... > 0,005).
L'erreur de calcul absolue est trouvée par la formule :
Le signe modulo montre que nous ne nous soucions pas de savoir quelle valeur est la plus grande et laquelle est la plus petite. Important, jusqu'à quel point le résultat approximatif s'écarte de la valeur exacte dans un sens ou dans l'autre.
L'erreur de calcul relative est trouvée par la formule :
, ou, pareil : ![]()
L'erreur relative montre de quel pourcentage le résultat approximatif déviait de la valeur exacte. Il existe une version de la formule sans multiplier par 100%, mais en pratique je vois presque toujours la version ci-dessus avec des pourcentages.
Après un bref rappel, nous revenons à notre problème, dans lequel nous avons calculé la valeur approximative de la fonction ![]() à l'aide d'un différentiel.
à l'aide d'un différentiel.
Calculons la valeur exacte de la fonction à l'aide d'une microcalculatrice :
, à proprement parler, la valeur est encore approximative, mais nous la considérerons comme exacte. De telles tâches se produisent.
Calculer l'erreur absolue:
Calculons l'erreur relative :
, des millièmes de pour cent sont obtenus, de sorte que le différentiel n'a fourni qu'une grande approximation.
Réponse: ![]() , erreur de calcul absolue , erreur de calcul relative
, erreur de calcul absolue , erreur de calcul relative
L'exemple suivant pour solution indépendante:
Exemple 4
![]() au point . Calculer une valeur plus précise de la fonction en un point donné, évaluer les erreurs de calcul absolues et relatives.
au point . Calculer une valeur plus précise de la fonction en un point donné, évaluer les erreurs de calcul absolues et relatives.
Un exemple approximatif de travail de finition et une réponse à la fin de la leçon.
Beaucoup ont remarqué que dans tous les exemples considérés, des racines apparaissent. Ce n'est pas un hasard : dans la plupart des cas, dans le problème considéré, des fonctions avec racines sont bien proposées.
Mais pour les lecteurs souffrants, j'ai déniché petit exemple avec arc sinus :
Exemple 5
Calculer approximativement à l'aide du différentiel la valeur de la fonction ![]() à ce point
à ce point
Cet exemple court mais informatif est également destiné à une décision indépendante. Et je me suis un peu reposé pour envisager une tâche spéciale avec une vigueur renouvelée :
Exemple 6
Calculez approximativement en utilisant le différentiel, arrondissez le résultat à deux décimales.
La solution: Quoi de neuf dans la tâche ? Par condition, il est nécessaire d'arrondir le résultat à deux décimales. Mais là n'est pas la question, le problème de la ronde scolaire, je pense, n'est pas difficile pour vous. Le fait est que chez nous on donne la tangente avec l'argument exprimé en degrés. Que faire lorsqu'on vous demande de résoudre une fonction trigonométrique avec des degrés ? Par exemple , etc.
L'algorithme de solution est fondamentalement conservé, c'est-à-dire qu'il faut, comme dans les exemples précédents, appliquer la formule
Écrivez la fonction évidente
La valeur doit être représentée par . Une aide sérieuse sera tableau des valeurs des fonctions trigonométriques . Au fait, si vous ne l'avez pas imprimé, je vous recommande de le faire, car vous devrez y regarder tout au long de l'étude des mathématiques supérieures.
En analysant le tableau, on remarque une "bonne" valeur de la tangente, qui est proche de 47 degrés :
De cette façon: ![]()
Après analyse préliminaire les degrés doivent être convertis en radians. Oui, et seulement ainsi !
À cet exemple directement de table trigonométrique vous pouvez le découvrir. La formule pour convertir les degrés en radians est : ![]() (les formules se trouvent dans le même tableau).
(les formules se trouvent dans le même tableau).
Autre modèle :
De cette façon: ![]() (dans les calculs, nous utilisons la valeur ). Le résultat, tel que requis par la condition, est arrondi à deux décimales.
(dans les calculs, nous utilisons la valeur ). Le résultat, tel que requis par la condition, est arrondi à deux décimales.
Réponse:
Exemple 7
Calculez approximativement en utilisant le différentiel, arrondissez le résultat à trois décimales.
Ceci est un exemple à faire soi-même. Solution complète et la réponse à la fin de la leçon.
Comme vous pouvez le voir, rien de compliqué, nous traduisons les degrés en radians et respectons l'algorithme de solution habituel.
Calculs approximatifs utilisant le différentiel total d'une fonction de deux variables
Tout sera très, très similaire, donc si vous êtes venu sur cette page avec cette tâche particulière, alors je vous recommande d'abord de regarder au moins quelques exemples du paragraphe précédent.
Pour étudier un paragraphe, il faut pouvoir trouver dérivées partielles du second ordre , où sans eux. Dans la leçon ci-dessus, j'ai noté la fonction de deux variables avec la lettre . En ce qui concerne la tâche considérée, il est plus commode d'utiliser la notation équivalente .
Comme dans le cas d'une fonction d'une variable, la condition du problème peut être formulée de différentes manières, et je vais essayer de considérer toutes les formulations rencontrées.
Exemple 8
![]()
La solution: Peu importe comment la condition est écrite, dans la solution elle-même, pour désigner la fonction, je le répète, il vaut mieux ne pas utiliser la lettre "Z", mais .
Et voici la formule de travail :
Devant nous se trouve en fait la sœur aînée de la formule du paragraphe précédent. La variable vient de grossir. Que puis-je dire, moi-même l'algorithme de résolution sera fondamentalement le même!
Par condition, il faut trouver la valeur approchée de la fonction au point .
Représentons le nombre 3,04 par . Le bonhomme en pain d'épice demande à être mangé:
,
Représentons le nombre 3,95 par . Le tour est venu dans la seconde moitié de Kolobok:
,
Et ne regardez pas toutes sortes de trucs de renard, il y a un bonhomme en pain d'épice - vous devez le manger.
Calculons la valeur de la fonction au point :
La différentielle d'une fonction en un point se trouve par la formule :
De la formule, il s'ensuit que vous devez trouver dérivées partielles du premier ordre et calculer leurs valeurs au point .
Calculons les dérivées partielles du premier ordre au point :
![]()

Différentiel total au point :
Ainsi, d'après la formule, la valeur approchée de la fonction au point :
Calculons la valeur exacte de la fonction au point :
Cette valeur est tout à fait correcte.
Les erreurs sont calculées à l'aide de formules standard, qui ont déjà été abordées dans cet article.
Erreur absolue:
Erreur relative:![]()
Réponse : , erreur absolue : , erreur relative :
Exemple 9
Calculer la valeur approximative d'une fonction ![]() à un point utilisant un différentiel complet, évaluez l'erreur absolue et relative.
à un point utilisant un différentiel complet, évaluez l'erreur absolue et relative.
Ceci est un exemple à faire soi-même. Quiconque s'attarde plus en détail sur cet exemple fera attention au fait que les erreurs de calcul se sont avérées très, très perceptibles. Cela s'est produit pour la raison suivante : dans le problème proposé, les incréments des arguments sont suffisamment grands : .
Le modèle général est a - plus ces incréments de valeur absolue, plus la précision des calculs est faible. Ainsi, par exemple, pour un point similaire, les incréments seront petits : , et la précision des calculs approximatifs sera très élevée.
Cette particularité est également valable pour le cas d'une fonction à une variable (première partie de la leçon).
Exemple 10
![]()
La solution: Calculons approximativement cette expression en utilisant le différentiel total d'une fonction de deux variables :
La différence avec les exemples 8-9 est que nous devons d'abord composer une fonction à deux variables : ![]() . Je pense que la composition de la fonction est intuitivement claire pour tout le monde.
. Je pense que la composition de la fonction est intuitivement claire pour tout le monde.
La valeur 4,9973 est proche de "cinq", donc : , .
La valeur de 0,9919 est proche de "un", par conséquent, nous supposons : , .
Calculons la valeur de la fonction au point :
On trouve la différentielle en un point par la formule :
Pour ce faire, on calcule les dérivées partielles du premier ordre au point .
Les dérivés ici ne sont pas les plus simples, et vous devez faire attention :  ;
;![]()

![]() .
.
Différentiel total au point :
Ainsi, la valeur approximative de cette expression :
Calculons une valeur plus précise à l'aide d'une microcalculatrice : 2,998899527
Trouvons l'erreur de calcul relative :
Réponse: , ![]()
Juste une illustration de ce qui précède, dans le problème considéré, les incréments des arguments sont très petits et l'erreur s'est avérée incroyablement rare.
Exemple 11
En utilisant le différentiel total d'une fonction de deux variables, calculez approximativement la valeur de cette expression. Calculez la même expression à l'aide d'une microcalculatrice. Estimer en pourcentage l'erreur relative des calculs. ![]()
Ceci est un exemple à faire soi-même. Un échantillon approximatif de finition à la fin de la leçon.
Comme indiqué précédemment, l'invité le plus courant dans ce type de tâche est une sorte de racines. Mais de temps en temps, il y a d'autres fonctions. Et un dernier exemple simple pour se détendre :
Exemple 12
En utilisant le différentiel total d'une fonction de deux variables, calculez approximativement la valeur de la fonction si ![]()
La solution est plus proche du bas de la page. Encore une fois, faites attention à la formulation des tâches de la leçon, en divers exemples en pratique, les formulations peuvent être différentes, mais cela ne change pas fondamentalement l'essence et l'algorithme de la solution.
Pour être honnête, je me suis un peu fatigué, car le matériel était ennuyeux. Ce n'était pas pédagogique à dire au début de l'article, mais maintenant c'est déjà possible =) En effet, les problèmes de mathématiques computationnelles ne sont généralement pas très difficiles, pas très intéressants, le plus important, peut-être, n'est pas de faire un erreur dans les calculs ordinaires.
Que les touches de votre calculatrice ne soient pas effacées !
Solutions et réponses :
Exemple 2:
La solution: Nous utilisons la formule :
Dans ce cas: , ,

De cette façon: ![]()
Réponse:
Exemple 4 :
La solution: Nous utilisons la formule :
Dans ce cas: ![]() , ,
, ,

De cette façon:
Calculons une valeur plus précise de la fonction à l'aide d'une microcalculatrice :
Erreur absolue:
Erreur relative:
Réponse: ![]() , erreur de calcul absolue , erreur de calcul relative
, erreur de calcul absolue , erreur de calcul relative
Exemple 5 :
La solution: Nous utilisons la formule :
Dans ce cas: ![]() , ,
, ,

De cette façon:
Réponse: ![]()
Exemple 7 :
La solution: Nous utilisons la formule :
Dans ce cas: , , ![]()
Erreur absolue et relative du nombre.
En tant que caractéristiques de l'exactitude des quantités approchées de toute origine, les concepts d'erreurs absolues et relatives de ces quantités sont introduits.
Notons a l'approximation du nombre exact A.
Définir. La valeur est appelée l'erreur du nombre approximatifa.
Définition.
Erreur absolue  le nombre approximatif a est appelé la valeur
le nombre approximatif a est appelé la valeur  .
.
En pratique, le nombre exact A est généralement inconnu, mais on peut toujours indiquer les limites dans lesquelles l'erreur absolue évolue.
Définition.
Limiter l'erreur absolue  le nombre approximatif a est la plus petite des limites supérieures de la quantité
le nombre approximatif a est la plus petite des limites supérieures de la quantité  , que l'on peut trouver avec cette méthode d'obtention du nombre a.
, que l'on peut trouver avec cette méthode d'obtention du nombre a.
En pratique, comme  choisir l'une des bornes supérieures pour
choisir l'une des bornes supérieures pour  , assez proche des plus petits.
, assez proche des plus petits.
Parce que le  , alors
, alors  . Parfois, ils écrivent :
. Parfois, ils écrivent :  .
.
Erreur absolue est la différence entre le résultat de la mesure
et la valeur vraie (réelle) la valeur de mesure.
L'erreur absolue et l'erreur absolue limite ne suffisent pas à caractériser la précision d'une mesure ou d'un calcul. L'ampleur de l'erreur relative est qualitativement plus significative.
Définition.
Erreur relative  nombre approximatif a appelons la valeur :
nombre approximatif a appelons la valeur :

Définition.
Limitation de l'erreur relative  nombre approximatif a que nous appelons la valeur
nombre approximatif a que nous appelons la valeur

Car  .
.
Ainsi, l'erreur relative détermine en fait l'amplitude de l'erreur absolue par unité du nombre approximatif mesuré ou calculé a.
Exemple. En arrondissant les nombres exacts A à trois chiffres significatifs, déterminer
erreurs absolues D et relatives δ de l'approximation obtenue
Donné:
Trouver:
∆-erreur absolue
δ - erreur relative
La solution:
=|-13.327-(-13.3)|=0.027
 ,un
,un  0
0
 *100%=0.203%
*100%=0.203%
Réponse:=0,027 ; δ=0.203%
2. Notation décimale d'un nombre approximatif. Chiffre significatif. Signes vrais d'un nombre (définition des chiffres vrais et significatifs, exemples ; théorie sur la relation entre l'erreur relative et le nombre de signes corrects).
Signes fidèles Nombres.
Définition. Un chiffre significatif d'un nombre approximatif a est tout chiffre autre que zéro, et zéro s'il est compris entre des chiffres significatifs ou s'il est représentatif d'une décimale stockée.
Par exemple, dans le nombre 0.00507 =  nous avons 3 chiffres significatifs, et dans le nombre 0.005070=
nous avons 3 chiffres significatifs, et dans le nombre 0.005070=  chiffres significatifs, c'est-à-dire zéro à droite, en gardant la décimale, est significatif.
chiffres significatifs, c'est-à-dire zéro à droite, en gardant la décimale, est significatif.
Convenons désormais d'écrire des zéros à droite, si seulement ils sont significatifs. Ensuite, en d'autres termes,
tous les chiffres du nombre a sont significatifs, à l'exception des zéros à gauche.
Dans le système de numération décimale, tout nombre a peut être représenté comme une somme finie ou infinie (fraction décimale) :
où  ,
,
 - le premier chiffre significatif, m - un nombre entier, appelé la décimale la plus significative du nombre a.
- le premier chiffre significatif, m - un nombre entier, appelé la décimale la plus significative du nombre a.
Par exemple, 518,3 =, m=2.
En utilisant la notation, nous introduisons le concept de décimales correctes (en chiffres significatifs) approximativement
ème numéro.
Définition.
Ils disent que dans un nombre approximatif a de la forme n - les premiers chiffres significatifs  ,
,
où i= m, m-1,..., m-n+1 sont vrais si l'erreur absolue de ce nombre n'excède pas la moitié de l'unité du chiffre exprimé par le n-ième chiffre significatif :

Sinon, le dernier chiffre  dit douteux.
dit douteux.
Lors de l'écriture d'un nombre approximatif sans indiquer son erreur, il est nécessaire que tous les nombres enregistrés
étaient vraies. Cette exigence est satisfaite dans tous les tableaux mathématiques.
Le terme "n signes corrects" caractérise uniquement le degré de précision du nombre approximatif et ne doit pas être compris de telle manière que les n premiers chiffres significatifs du nombre approximatif a coïncident avec les chiffres correspondants du nombre exact A. Par exemple , pour les nombres A = 10, a = 9,997, tous les chiffres significatifs sont différents , mais le nombre a a 3 chiffres significatifs valides. En effet, ici m=0 et n=3 (trouver par sélection).
résultat de la mesure
L'erreur du résultat de la mesure vous permet de déterminer les chiffres du résultat qui sont fiables. Lors du calcul de la valeur d'erreur, en particulier à l'aide de calculatrices, la valeur d'erreur est obtenue avec un grand nombre de chiffres. Cela donne l'impression d'une grande précision de mesure, ce qui n'est pas vrai, puisque les données initiales pour le calcul sont le plus souvent les valeurs d'erreur normalisées du SI utilisé, qui sont indiquées avec seulement un ou deux chiffres significatifs. Par conséquent, la valeur finale de l'erreur calculée ne doit pas contenir plus de deux chiffres significatifs. La métrologie a les règles suivantes :
1. L'erreur du résultat de la mesure est indiquée par deux chiffres significatifs si le premier d'entre eux est 3 ou moins, et un - si le premier chiffre est 4 ou plus.
Les chiffres significatifs d'un nombre sont considérés comme étant tous les chiffres depuis le premier chiffre à gauche, non égal à zéro, jusqu'au dernier chiffre à droite, tandis que les zéros écrits comme un facteur de 10 n ne sont pas pris en compte.
2. Le résultat de la mesure est arrondi à la même décimale qui termine la valeur d'erreur absolue arrondie. (Par exemple, le résultat est 85,6342, l'erreur est 0,01. Le résultat est arrondi à 85,63. Le même résultat avec une erreur inférieure à 0,012 doit être arrondi à 85,634).
3. L'arrondi n'est effectué que dans la réponse finale et tous les calculs préliminaires sont effectués avec un ou deux signes supplémentaires.
4. L'arrondi doit être effectué immédiatement au nombre de chiffres significatifs souhaité, l'arrondi progressif conduit à des erreurs.
Lors de l'arrondi des valeurs numériques de l'erreur et du résultat de la mesure, les règles générales d'arrondi suivantes doivent être suivies.
Les chiffres supplémentaires dans les nombres entiers sont remplacés par des zéros, et dans fractions décimales sont jetés. (Par exemple, le nombre 165245 est arrondi à 165200 tout en conservant quatre chiffres significatifs, et le nombre 165,245 est arrondi à 165,2).
Si la décimale se termine par des zéros, ils ne sont ignorés que jusqu'au chiffre correspondant au chiffre de l'erreur. (Par exemple, le résultat de la mesure est de 235,200, l'erreur est de 0,05. Le résultat est arrondi à 235,20. Le même résultat avec une erreur de 0,015 doit être arrondi à 235,200).
Si le premier (en comptant de gauche à droite) des chiffres remplacés par zéro ou supprimés est inférieur à 5, les chiffres restants ne changez pas .
Si le premier de ces chiffres est 5 et n'est suivi d'aucun chiffre ou de zéros, alors si le dernier chiffre du nombre arrondi est pair ou zéro, il reste inchangé , si impair - augmente de un . (Par exemple, le nombre 1234,50 est arrondi à 1234 et le nombre 8765,50 est arrondi à 8766).
Si le premier des chiffres remplacés par des zéros ou supprimés est supérieur ou égal à 5, mais suivi d'un chiffre significatif, puis le dernier chiffre restant est augmenté d'un . (Par exemple, le nombre 6783,6, tout en conservant quatre chiffres significatifs, est arrondi à 6784, et le nombre 12,34520 est arrondi à 12,35).
Une attention particulière doit être portée à l'enregistrement du résultat de mesure sans préciser l'erreur, puisque les résultats de 2,4 10 3 V et 2400V ne sont pas identiques . La première entrée signifie que les nombres de milliers et de centaines de volts sont corrects et la vraie valeur peut être comprise entre 2,351 kV et 2,449 kV. L'entrée 2400 signifie que les unités de volts sont également correctes, donc la vraie valeur de tension peut être comprise entre 2399,51V et 2400,49V.
Par conséquent, enregistrer le résultat sans spécifier l'erreur hautement indésirable .
Enfin, les règles d'enregistrement du résultat de mesure peuvent être formulées comme suit.
1) Dans les calculs intermédiaires, les valeurs d'erreur enregistrent trois à quatre chiffres significatifs.
2) La valeur d'erreur finale et la valeur du résultat sont arrondies selon les règles ci-dessus.
3) Avec des mesures techniques simples, lorsque seule l'erreur principale du MI est prise en compte (les MI sont utilisés dans des conditions normales de fonctionnement), le résultat s'écrit :
(Par exemple, résultat de mesure de tension  B, erreur
B, erreur  B. Le résultat peut s'écrire :
B. Le résultat peut s'écrire :

4) Pour les mesures techniques simples dans des conditions de fonctionnement, lorsque les erreurs principales et supplémentaires sont prises en compte conformément aux données standard sur le SI et que l'erreur résultante est déterminée par la formule (1.35), le résultat s'écrit :

5) Dans les mesures statistiques, lorsque seule la grandeur de l'erreur aléatoire des données normalement distribuées est déterminée sous la forme d'un intervalle de confiance, le résultat est écrit conformément à (1.31) :

Si les bornes de l'intervalle de confiance ne sont pas symétriques, elles sont indiquées séparément.
Par exemple,

6) Dans les mesures statistiques, lorsque les limites des erreurs systématiques non exclues du résultat (NSP) et l'intervalle de confiance de l'erreur aléatoire des données normalement distribuées sont estimées, mais que le résultat est utilisé comme intermédiaire pour trouver d'autres valeurs (par exemple, avec des mesures statistiques indirectes) ou qu'il est censé être comparé à d'autres résultats d'une expérience de mesure similaire, le résultat s'écrit conformément à (1.39) :
si  , cela est indiqué en plus, comme au paragraphe 5.
, cela est indiqué en plus, comme au paragraphe 5.
Si les bornes du NSP ou les bornes de l'intervalle de confiance ne sont pas symétriques, alors elles sont indiquées séparément :
7) Si, pendant le mesurage, des estimations de l'erreur sont obtenues dans les conditions spécifiées au paragraphe 6, mais que le résultat est définitif et qu'il n'est pas prévu qu'il soit analysé davantage et comparé à d'autres résultats, il est écrit conformément à (1.41 ):

où  est déterminé par la formule (1.40),
est déterminé par la formule (1.40),
si  , ceci est indiqué en plus, comme au paragraphe 5.
, ceci est indiqué en plus, comme au paragraphe 5.
8) Lors de mesures statistiques, lorsque les bornes du NSP et l'intervalle de confiance d'erreur aléatoire sont estimés, mais lors du traitement des résultats, une loi de distribution autre que la normale est identifiée, des estimations de la valeur du résultat de mesure et de l'intervalle de confiance de erreur aléatoire sont trouvées selon les formules correspondantes, le résultat est présenté sous la forme similaire à la présentation du résultat en 6, mais des informations supplémentaires sont fournies sur la forme de la loi de distribution des données expérimentales.
9) Si, comme au paragraphe 8, les résultats des mesures statiques sont traités et que l'on sait à l'avance que la loi de distribution des données expérimentales diffère de la loi normale, mais qu'aucune mesure n'est prise pour identifier le type de loi réelle pour tout raison, alors le résultat peut être présenté sous une forme similaire au résultat de la représentation au paragraphe 6, mais l'intervalle de confiance de l'erreur aléatoire est déterminé conformément aux recommandations de GOST 11.001-73 comme  avec un niveau de confiance
avec un niveau de confiance  .
.
L'entrée de résultat pourrait ressembler à ceci :

 (à
(à  );
);
 ;
;
 ;
;
 .
.
Probabilité de confiance à laquelle le NSP total est déterminé -  , auquel cas il peut différer de
, auquel cas il peut différer de  .
.