Fonctions quadratiques, leurs propriétés et graphiques. Fonction quadratique et son graphique

Une fonction de la forme où est appelée fonction quadratique.

Graphique d'une fonction quadratique – parabole.

Considérons les cas :

I CASE, PARABOLE CLASSIQUE

C'est , ,

Pour construire, remplissez le tableau en substituant les valeurs x dans la formule :

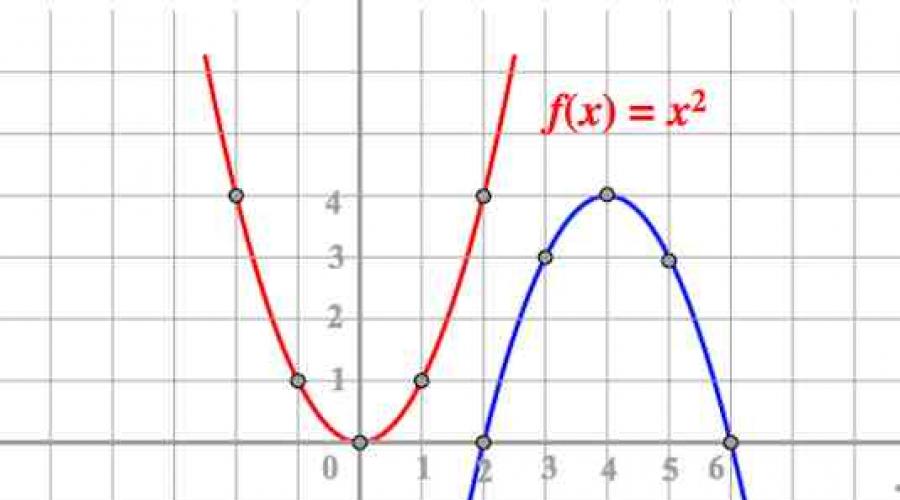
Marquez les points (0;0); (1;1); (-1;1), etc. sur le plan de coordonnées (plus on fait un pas petit avec les valeurs x (dans ce cas, l'étape 1), et plus on prend de valeurs x, plus la courbe sera lisse), on obtient une parabole :

Il est facile de voir que si l'on prend le cas , , , alors on obtient une parabole symétrique par rapport à l'axe (oh). Il est facile de le vérifier en remplissant un tableau similaire :

II CAS, « a » EST DIFFÉRENT DE L'UNITÉ

Que se passera-t-il si nous prenons , , ? Comment le comportement de la parabole va-t-il changer ? Avec title="(!LANG : Rendu par QuickLaTeX.com" height="20" width="55" style="vertical-align: -5px;"> парабола изменит форму, она “похудеет” по сравнению с параболой (не верите – заполните соответствующую таблицу – и убедитесь сами):!}

Sur la première image (voir ci-dessus) on voit clairement que les points du tableau de la parabole (1;1), (-1;1) ont été transformés en points (1;4), (1;-4), c'est-à-dire qu'avec les mêmes valeurs, l'ordonnée de chaque point est multipliée par 4. Cela arrivera à tous les points clés du tableau d'origine. Nous raisonnons de la même manière dans les cas des images 2 et 3.

Et quand la parabole « devient plus large » que la parabole :

Résumons :

1)Le signe du coefficient détermine la direction des branches. Avec title="(!LANG : Rendu par QuickLaTeX.com" height="14" width="47" style="vertical-align: 0px;"> ветви направлены вверх, при - вниз. !}

2) Valeur absolue Le coefficient (module) est responsable de la « dilatation » et de la « compression » de la parabole. Plus la parabole est grande, plus la parabole est étroite, plus |a| est petite, plus la parabole est large.

CAS III, "C" APPARAÎT

Introduisons maintenant dans le jeu (c'est-à-dire considérons le cas où), nous considérerons des paraboles de la forme . Il n'est pas difficile de deviner (vous pouvez toujours vous référer au tableau) que la parabole se déplacera vers le haut ou vers le bas le long de l'axe selon le signe :

CAS IV, « b » APPARAÎT

Quand la parabole va-t-elle « se détacher » de l'axe et finalement « marcher » le long de tout le plan de coordonnées ? Quand cessera-t-il d’être égal ?

Ici, pour construire une parabole, nous avons besoin formule de calcul du sommet : , .

Donc à ce stade (comme au point (0;0) nouveau système coordonnées), nous allons construire une parabole, ce que nous pouvons déjà faire. Si nous traitons du cas, alors à partir du sommet, nous plaçons un segment unitaire vers la droite, un vers le haut, - le point résultant est le nôtre (de même, un pas vers la gauche, un pas vers le haut est notre point) ; si nous avons affaire, par exemple, à partir du sommet, nous plaçons un segment unitaire vers la droite, deux vers le haut, etc.

Par exemple, le sommet d'une parabole :

Maintenant, la principale chose à comprendre est qu'à ce sommet, nous allons construire une parabole selon le modèle de parabole, car dans notre cas.

Lors de la construction d'une parabole après avoir trouvé les coordonnées du sommet trèsIl convient de considérer les points suivants :

1) parabole je passerai certainement par le point . En effet, en substituant x=0 dans la formule, nous obtenons que . C'est-à-dire que l'ordonnée du point d'intersection de la parabole avec l'axe (oy) est . Dans notre exemple (ci-dessus), la parabole coupe l'ordonnée au point , puisque .

2) axe de symétrie paraboles est une ligne droite, donc tous les points de la parabole seront symétriques par rapport à elle. Dans notre exemple, on prend immédiatement le point (0 ; -2) et on le construit symétriquement par rapport à l'axe de symétrie de la parabole, on obtient le point (4 ; -2) par lequel passera la parabole.

3) En égalant à , on retrouve les points d'intersection de la parabole avec l'axe (oh). Pour ce faire, nous résolvons l’équation. En fonction du discriminant, nous obtiendrons un (, ), deux ( title="Rendered by QuickLaTeX.com" height="14" width="54" style="vertical-align: 0px;">, ) или нИсколько () точек пересечения с осью (ох) !} . Dans l'exemple précédent, notre racine du discriminant n'est pas un entier ; lors de la construction, cela n'a pas beaucoup de sens pour nous de trouver les racines, mais on voit bien que nous aurons deux points d'intersection avec l'axe (oh) (depuis title="(!LANG : Rendu par QuickLaTeX.com" height="14" width="54" style="vertical-align: 0px;">), хотя, в общем, это видно и без дискриминанта.!}

Alors trouvons une solution

Algorithme de construction d'une parabole si elle est donnée sous la forme

1) déterminer la direction des branches (a>0 – vers le haut, a<0 – вниз)

2) on trouve les coordonnées du sommet de la parabole à l'aide de la formule , .

3) on trouve le point d'intersection de la parabole avec l'axe (oy) à l'aide du terme libre, on construit un point symétrique à ce point par rapport à l'axe de symétrie de la parabole (à noter qu'il arrive qu'il ne soit pas rentable de marquer ce point par exemple, car la valeur est grande... on saute ce point...)

4) Au point trouvé - le sommet de la parabole (comme au point (0;0) du nouveau système de coordonnées), nous construisons une parabole. Si title="(!LANG : Rendu par QuickLaTeX.com" height="20" width="55" style="vertical-align: -5px;">, то парабола становится у’же по сравнению с , если , то парабола расширяется по сравнению с !}

5) On retrouve les points d'intersection de la parabole avec l'axe (oy) (s'ils n'ont pas encore « fait surface ») en résolvant l'équation

Exemple 1

Exemple 2

Note 1. Si la parabole nous est initialement donnée sous la forme , où sont des nombres (par exemple ), alors il sera encore plus facile de la construire, car on nous a déjà donné les coordonnées du sommet . Pourquoi?

Prenons un trinôme quadratique et isolons le carré complet qu'il contient : Regardez, nous avons ça , . Vous et moi appelions auparavant le sommet d'une parabole, c'est-à-dire maintenant.

Par exemple, . On marque le sommet de la parabole sur le plan, on comprend que les branches sont dirigées vers le bas, la parabole est élargie (par rapport à ). C'est-à-dire que nous réalisons les points 1 ; 3 ; 4 ; 5 de l'algorithme de construction d'une parabole (voir ci-dessus).

Note 2. Si la parabole est donnée sous une forme similaire à celle-ci (c'est-à-dire présentée comme le produit de deux facteurs linéaires), alors nous voyons immédiatement les points d'intersection de la parabole avec l'axe (bœuf). Dans ce cas – (0;0) et (4;0). Pour le reste, nous agissons selon l'algorithme en ouvrant les parenthèses.

Comme le montre la pratique, les tâches sur les propriétés et les graphiques d'une fonction quadratique posent de sérieuses difficultés. C'est assez étrange, car ils étudient la fonction quadratique en 8e année, puis tout au long du premier quart de la 9e année, ils « tourmentent » les propriétés de la parabole et construisent ses graphiques pour divers paramètres.

Cela est dû au fait qu'en obligeant les élèves à construire des paraboles, ils ne consacrent pratiquement pas de temps à la « lecture » des graphiques, c'est-à-dire qu'ils ne s'entraînent pas à comprendre les informations reçues de l'image. Apparemment, on suppose qu'après avoir construit une douzaine ou deux graphiques, un étudiant intelligent découvrira et formulera lui-même la relation entre les coefficients de la formule et apparence arts graphiques. En pratique, cela ne fonctionne pas. Pour une telle généralisation, une expérience sérieuse en mini-recherche mathématique est requise, ce que la plupart des élèves de neuvième année ne possèdent bien sûr pas. En attendant, l'Inspection d'Etat propose de déterminer les signes des coefficients à l'aide du barème.

Nous n'exigerons pas l'impossible des écoliers et proposerons simplement l'un des algorithmes permettant de résoudre de tels problèmes.

Donc une fonction de la forme y = hache 2 + bx + c dit quadratique, son graphe est une parabole. Comme son nom l'indique, le terme principal est hache 2. C'est UN ne doit pas être égal à zéro, les coefficients restants ( b Et Avec) peut être égal à zéro.

Voyons comment les signes de ses coefficients affectent l'apparence d'une parabole.

La dépendance la plus simple pour le coefficient UN. La plupart des écoliers répondent avec assurance : « si UN> 0, alors les branches de la parabole sont dirigées vers le haut, et si UN < 0, - то вниз". Совершенно верно. Ниже приведен график квадратичной функции, у которой UN > 0.

y = 0,5x2 - 3x + 1

Dans ce cas UN = 0,5

Et maintenant pour UN < 0:

y = - 0,5x2 - 3x + 1

Dans ce cas UN = - 0,5

Impact du coefficient Avec C'est également assez facile à suivre. Imaginons que nous voulions trouver la valeur d'une fonction en un point X= 0. Remplacez zéro dans la formule :

oui = un 0 2 + b 0 + c = c. Il se trouve que y = c. C'est Avec est l'ordonnée du point d'intersection de la parabole avec l'axe des y. Généralement, ce point est facile à trouver sur le graphique. Et déterminez s’il se situe au-dessus de zéro ou en dessous. C'est Avec> 0 ou Avec < 0.

Avec > 0:

y = x 2 + 4x + 3

Avec < 0

y = x 2 + 4x - 3

En conséquence, si Avec= 0, alors la parabole passera nécessairement par l'origine :

y = x 2 + 4x

Plus difficile avec le paramètre b. Le point auquel nous le trouverons dépend non seulement de b mais aussi de UN. C'est le sommet de la parabole. Son abscisse (coordonnée de l'axe X) se trouve par la formule x dans = - b/(2a). Ainsi, b = - 2ax dans. Autrement dit, nous agissons de la manière suivante: sur le graphique on retrouve le sommet de la parabole, déterminer le signe de son abscisse, c'est-à-dire regarder à droite de zéro ( x dans> 0) ou vers la gauche ( x dans < 0) она лежит.

Cependant, ce n'est pas tout. Il faut aussi faire attention au signe du coefficient UN. Autrement dit, regardez où sont dirigées les branches de la parabole. Et seulement après cela, selon la formule b = - 2ax dans déterminer le signe b.

Regardons un exemple :

Les branches sont dirigées vers le haut, ce qui signifie UN> 0, la parabole coupe l'axe à en dessous de zéro, c'est-à-dire Avec < 0, вершина параболы лежит правее нуля. Следовательно, x dans> 0. Donc b = - 2ax dans = -++ = -. b < 0. Окончательно имеем: UN > 0, b < 0, Avec < 0.

Le maintien de votre vie privée est important pour nous. Pour cette raison, nous avons développé une politique de confidentialité qui décrit la manière dont nous utilisons et stockons vos informations. Veuillez consulter nos pratiques de confidentialité et faites-nous savoir si vous avez des questions.

Collecte et utilisation des informations personnelles

Les informations personnelles font référence aux données qui peuvent être utilisées pour identifier ou contacter une personne spécifique.

Il peut vous être demandé de fournir vos informations personnelles à tout moment lorsque vous nous contactez.

Vous trouverez ci-dessous quelques exemples des types d'informations personnelles que nous pouvons collecter et de la manière dont nous pouvons utiliser ces informations.

Quelles informations personnelles collectons-nous :

• Lorsque vous soumettez une candidature sur le site, nous pouvons collecter diverses informations, notamment votre nom, votre numéro de téléphone, votre adresse e-mail, etc.

Comment utilisons-nous vos informations personnelles:

• Les informations personnelles que nous collectons nous permettent de vous contacter avec des offres uniques, des promotions et d'autres événements et événements à venir.
• De temps en temps, nous pouvons utiliser vos informations personnelles pour envoyer des notifications et des communications importantes.
• Nous pouvons également utiliser les informations personnelles à des fins internes, telles que la réalisation d'audits, d'analyses de données et diverses recherches afin d'améliorer les services que nous fournissons et de vous fournir des recommandations concernant nos services.
• Si vous participez à un tirage au sort, un concours ou une promotion similaire, nous pouvons utiliser les informations que vous fournissez pour administrer ces programmes.

Divulgation d'informations à des tiers

Nous ne divulguons pas les informations reçues de votre part à des tiers.

Des exceptions:

• Si nécessaire, conformément à la loi, procédure judiciaire, dans le cadre de procédures judiciaires et/ou sur la base de demandes publiques ou de demandes d'agences gouvernementales de la Fédération de Russie - pour divulguer vos informations personnelles. Nous pouvons également divulguer des informations vous concernant si nous déterminons qu'une telle divulgation est nécessaire ou appropriée à des fins de sécurité, d'application de la loi ou à d'autres fins d'importance publique.
• En cas de réorganisation, de fusion ou de vente, nous pouvons transférer les informations personnelles que nous collectons au tiers successeur concerné.

Protection des informations personnelles

Nous prenons des précautions - notamment administratives, techniques et physiques - pour protéger vos informations personnelles contre la perte, le vol et l'utilisation abusive, ainsi que contre l'accès, la divulgation, l'altération et la destruction non autorisés.

Respecter votre vie privée au niveau de l'entreprise

Pour garantir la sécurité de vos informations personnelles, nous communiquons les normes de confidentialité et de sécurité à nos employés et appliquons strictement les pratiques de confidentialité.

Dans les cours de mathématiques à l'école, vous vous êtes déjà familiarisé avec les propriétés et le graphique les plus simples d'une fonction y = x 2. Développons nos connaissances sur fonction quadratique.

Exercice 1.

Représenter graphiquement la fonction y = x 2. Echelle : 1 = 2 cm Marquez un point sur l'axe Oy. F(0 ; 1/4). A l'aide d'un compas ou d'une bande de papier, mesurez la distance du point Fà un certain point M paraboles. Épinglez ensuite la bande au point M et faites-la pivoter autour de ce point jusqu'à ce qu'elle soit verticale. La fin de la bande tombera légèrement en dessous de l'axe des x (Fig. 1). Marquez sur la bande jusqu'où elle s'étend au-delà de l'axe des x. Prenez maintenant un autre point sur la parabole et répétez la mesure. Dans quelle mesure le bord de la bande est-il tombé en dessous de l’axe des x ?

Résultat: quel que soit le point de la parabole y = x 2 que vous prenez, la distance de ce point au point F(0; 1/4) sera supérieure à la distance du même point à l'axe des abscisses de toujours le même nombre - 1/4.

On peut le dire différemment : la distance de n'importe quel point de la parabole au point (0 ; 1/4) est égale à la distance du même point de la parabole à la droite y = -1/4. Ce merveilleux point F(0; 1/4) est appelé se concentrer paraboles y = x 2 et droite y = -1/4 – directrice cette parabole. Chaque parabole a une directrice et un foyer.

Propriétés intéressantes d'une parabole :

1. Tout point de la parabole est équidistant d'un certain point, appelé foyer de la parabole, et d'une ligne droite, appelée sa directrice.

2. Si vous faites pivoter une parabole autour de l'axe de symétrie (par exemple, la parabole y = x 2 autour de l'axe Oy), vous obtiendrez une surface très intéressante appelée paraboloïde de révolution.

La surface du liquide dans un récipient en rotation a la forme d’un paraboloïde de révolution. Vous pouvez voir cette surface si vous remuez vigoureusement avec une cuillère dans un verre de thé incomplet, puis retirez la cuillère.

3. Si vous jetez une pierre dans le vide à un certain angle par rapport à l'horizon, elle volera en parabole (Fig.2).

4. Si vous coupez la surface d'un cône avec un plan parallèle à l'une de ses génératrices, alors la section transversale donnera lieu à une parabole. (Fig.3).

5. Les parcs d'attractions proposent parfois un manège amusant appelé Paraboloïde des Merveilles. Il semble à tous ceux qui se trouvent à l’intérieur du paraboloïde en rotation qu’ils se tiennent au sol, tandis que le reste des gens s’accroche miraculeusement aux murs.

6. Dans les télescopes à réflexion, des miroirs paraboliques sont également utilisés : la lumière d'une étoile lointaine, arrivant dans un faisceau parallèle, tombant sur le miroir du télescope, est focalisée.

7. Les projecteurs ont généralement un miroir en forme de paraboloïde. Si vous placez une source de lumière au foyer d'un paraboloïde, les rayons réfléchis par le miroir parabolique forment un faisceau parallèle.

Représenter graphiquement une fonction quadratique

En cours de mathématiques, vous avez étudié comment obtenir des graphiques de fonctions de la forme à partir du graphique de la fonction y = x 2 :

1) y = hache 2– étirer le graphe y = x 2 le long de l'axe Oy en |a| fois (avec |a|< 0 – это сжатие в 1/|a| раз, riz. 4).

2) y = x 2 + n– déplacement du graphique de n unités le long de l'axe Oy, et si n > 0, alors le déplacement est vers le haut, et si n< 0, то вниз, (или же можно переносить ось абсцисс).

3) y = (x + m) 2– décalage du graphique de m unités le long de l’axe Ox : si m< 0, то вправо, а если m >0, puis je suis parti, (Fig.5).

4) y = -x 2– affichage symétrique par rapport à l'axe Ox du graphique y = x 2 .

Examinons de plus près le tracé de la fonction y = une(x – m) 2 + n.

Une fonction quadratique de la forme y = ax 2 + bx + c peut toujours se réduire à la forme

y = a(x – m) 2 + n, où m = -b/(2a), n = -(b 2 – 4ac)/(4a).

Prouvons-le.

Vraiment,

y = hache 2 + bx + c = a(x 2 + (b/a) x + c/a) =

A(x 2 + 2x · (b/a) + b 2 /(4a 2) – b 2 /(4a 2) + c/a) =

A((x + b/2a) 2 – (b 2 – 4ac)/(4a 2)) = a(x + b/2a) 2 – (b 2 – 4ac)/(4a).

Introduisons de nouvelles notations.

Laisser m = -b/(2a), UN n = -(b 2 – 4ac)/(4a),

alors nous obtenons y = a(x – m) 2 + n ou y – n = a(x – m) 2.

Faisons quelques substitutions supplémentaires : soit y – n = Y, x – m = X (*).

On obtient alors la fonction Y = aX 2 dont le graphique est une parabole.

Le sommet de la parabole est à l'origine. X = 0 ; Oui = 0.

En substituant les coordonnées du sommet dans (*), on obtient les coordonnées du sommet du graphe y = a(x – m) 2 + n : x = m, y = n.

Ainsi, afin de tracer une fonction quadratique représentée par

y = une(x – m) 2 + n

à travers les transformations, vous pouvez procéder comme suit :

un) tracer la fonction y = x 2 ;

b) par translation parallèle le long de l'axe Ox de m unités et le long de l'axe Oy de n unités - transférer le sommet de la parabole de l'origine au point de coordonnées (m ; n) (Fig.6).

Transformations d'enregistrement :

y = x 2 → y = (x – m) 2 → y = a(x – m) 2 → y = a(x – m) 2 + n.

Exemple.

À l'aide de transformations, construisez un graphique de la fonction y = 2(x – 3) 2 dans le système de coordonnées cartésiennes – 2.

Solution.

Chaîne de transformations :

y = x 2 (1) → y = (x – 3) 2 (2) → y = 2(x – 3) 2 (3) → y = 2(x – 3) 2 – 2 (4) .

Le tracé est montré dans riz. 7.

Vous pouvez vous entraîner à représenter graphiquement des fonctions quadratiques par vous-même. Par exemple, construisez un graphique de la fonction y = 2(x + 3) 2 + 2 dans un système de coordonnées à l'aide de transformations. Si vous avez des questions ou souhaitez obtenir des conseils d'un enseignant, vous avez la possibilité de procéder. cours gratuit de 25 minutes avec un tuteur en ligne après . Pour un travail ultérieur avec un professeur, vous pouvez choisir celui qui vous convient

Vous avez encore des questions ? Vous ne savez pas comment représenter graphiquement une fonction quadratique ?
Pour obtenir l'aide d'un tuteur -.
Le premier cours est gratuit !

blog.site, lors de la copie totale ou partielle du matériel, un lien vers la source originale est requis.