Pe baza unor semne suficiente se găsesc intervale de funcție crescătoare și descrescătoare.

Iată formularea semnelor:

• dacă derivata funcţiei y = f(x) pozitiv pentru oricine X din interval X, atunci funcția crește cu X;
• dacă derivata funcţiei y = f(x) negativ pentru oricine X din interval X, apoi funcția scade cu X.

Astfel, pentru a determina intervalele de creștere și scădere a unei funcții, este necesar:

• găsiți domeniul de definire al unei funcții;

• găsiți derivata unei funcții;

• la intervalele rezultate se adaugă puncte de limită la care funcția este definită și continuă.

Să ne uităm la un exemplu pentru a explica algoritmul.

Exemplu.

Aflați intervalele funcției crescătoare și descrescătoare.

Soluţie.

Primul pas este să găsiți definiția funcției. În exemplul nostru, expresia din numitor nu ar trebui să meargă la zero, prin urmare, .

Să trecem la funcția derivată:

Pentru a determina intervalele de creștere și scădere ale unei funcții pe baza unui criteriu suficient, rezolvăm inegalitățile Și pe domeniul definirii. Să folosim o generalizare a metodei intervalului. Singura rădăcină reală a numărătorului este x = 2, iar numitorul ajunge la zero la x = 0. Aceste puncte împart domeniul definiției în intervale în care derivata funcției își păstrează semnul. Să notăm aceste puncte pe linia numerică. În mod convențional notăm cu plusuri și minus intervalele la care derivata este pozitivă sau negativă. Săgețile de mai jos arată schematic creșterea sau scăderea funcției pe intervalul corespunzător.

Prin urmare, Și .

La punctul x = 2 funcția este definită și continuă, deci ar trebui adăugată atât la intervalele crescătoare, cât și la cele descrescătoare. La punctul x = 0 funcția nu este definită, așa că nu includem acest punct în intervalele necesare.

Prezentăm un grafic al funcției pentru a compara rezultatele obținute cu aceasta.

Răspuns: functia creste cu , scade pe interval (0; 2] .

- Puncte extreme ale unei funcții a unei variabile. Condiții suficiente pentru un extremum

Fie ca funcția f(x), definită și continuă în interval, să nu fie monotonă în ea. Există părți [ , ] ale intervalului în care cele mai mari și cele mai mici valori sunt atinse de funcția în punctul intern, adică. intre si.

Se spune că o funcție f(x) are un maxim (sau un minim) într-un punct dacă acest punct poate fi înconjurat de o astfel de vecinătate (x 0 - ,x 0 +) conținută în intervalul în care funcția este dată că inegalitatea este valabil pentru toate punctele sale.

f(x)< f(x 0)(или f(x)>f(x 0))

Cu alte cuvinte, punctul x 0 dă funcției f(x) un maxim (minim) dacă valoarea f(x 0) se dovedește a fi cea mai mare (mai mică) dintre valorile acceptate de funcție în unele cartier (cel puțin mic) din acest punct. Rețineți că însăși definiția maximului (minimului) presupune că funcția este specificată de ambele părți ale punctului x 0.

Dacă există o vecinătate în cadrul căreia (la x=x 0) inegalitatea strictă

f(x) f(x 0)

atunci ei spun că funcția are propriul maxim (minim) în punctul x 0, altfel are unul impropriu.

Dacă o funcție are maxime în punctele x 0 și x 1, atunci, aplicând a doua teoremă Weierstrass intervalului, vedem că funcția atinge cea mai mică valoare în acest interval la un punct x 2 între x 0 și x 1 și are o minim acolo. La fel, între două minime va fi cu siguranță un maxim. În cel mai simplu (și în practică cel mai important) caz, când o funcție are în general doar un număr finit de maxime și minime, ele pur și simplu alternează.

Rețineți că pentru a desemna un maxim sau un minim, există și un termen care le unește - extremum.

Conceptele de maxim (max f(x)) și minim (min f(x)) sunt proprietăți locale ale funcției și au loc la un anumit punct x 0. Conceptele de valori mai mari (sup f(x)) și cele mai mici (inf f(x)) se referă la un segment finit și sunt proprietăți globale ale unei funcții pe un segment.

Din figura 1 este clar că în punctele x 1 și x 3 există maxime locale, iar în punctele x 2 și x 4 există minime locale. Cu toate acestea, funcția își atinge valoarea minimă în punctul x=a, iar valoarea sa maximă în punctul x=b.

Să ne punem problema găsirii tuturor valorilor argumentului care dau funcției un extremum. La rezolvarea acesteia, derivatul va juca rolul principal.

Să presupunem mai întâi că funcția f(x) are o derivată finită în intervalul (a,b). Dacă în punctul x 0 funcția are un extremum, atunci, aplicând teorema lui Fermat la intervalul (x 0 - , x 0 +), despre care s-a discutat mai sus, concluzionăm că f (x) = 0 acesta constă conditie necesara extremum. Extremul ar trebui căutat numai în acele puncte în care derivata este egală cu zero.

Totuși, nu trebuie să credem că fiecare punct la care derivata este egală cu zero dă funcției un extremum: condiția necesară tocmai indicată nu este suficientă

Creșterea, descreșterea și extremele unei funcții

Găsirea intervalelor de creștere, scădere și extreme ale unei funcții este atât o sarcină independentă, cât și o parte esențială a altor sarcini, în special, studiu complet al funcției. Informațiile inițiale despre creșterea, scăderea și extremele funcției sunt date în capitol teoretic despre derivată, pe care îl recomand cu căldură pentru studiu preliminar (sau repetare)– și pentru motivul că următorul material se bazează pe foarte în esență derivată, fiind o continuare armonioasă a acestui articol. Deși, dacă timpul este scurt, atunci este posibilă și o practică pur formală a exemplelor din lecția de astăzi.

Și astăzi există un spirit de unanimitate rară în aer și pot simți direct că toți cei prezenți arde de dorință învață să explorezi o funcție folosind derivata ei. Prin urmare, terminologia rezonabilă, bună, eternă apare imediat pe ecranele monitorului dumneavoastră.

Pentru ce? Unul dintre motive este cel mai practic: astfel încât să fie clar ce ți se cere în general într-o anumită sarcină!

Monotonitatea funcției. Punctele extreme și extremele unei funcții

Să luăm în considerare o funcție. Pentru a spune simplu, presupunem că ea continuu pe întreaga linie numerică:

Pentru orice eventualitate, să scăpăm imediat de eventualele iluzii, mai ales pentru acei cititori care s-au familiarizat recent cu intervale de semn constant ale funcției. Acum noi NU SUNT INTERESAT, cum este situat graficul funcției în raport cu axa (deasupra, dedesubt, unde se intersectează axa). Pentru a fi convingător, ștergeți mental axele și lăsați un grafic. Pentru că acolo este interesul.

Funcţie crește pe un interval dacă pentru oricare două puncte ale acestui interval conectate prin relația , inegalitatea este adevărată. Acesta este, valoare mai mare argumentul corespunde unei valori mai mari a funcției, iar graficul acesteia merge „de jos în sus”. Funcția demonstrativă crește pe interval.

La fel, funcția scade pe un interval dacă pentru oricare două puncte dintr-un interval dat, astfel încât , inegalitatea este adevărată. Adică, o valoare mai mare a argumentului corespunde unei valori mai mici a funcției, iar graficul său merge „de sus în jos”. Funcția noastră scade pe intervale .

Dacă o funcție crește sau scade pe un interval, atunci se numește strict monoton la acest interval. Ce este monotonia? Luați-o la propriu – monotonie.

De asemenea, puteți defini nedescrescătoare funcția (condiție relaxată în prima definiție) și necrescătoare funcția (condiție atenuată în a 2-a definiție). Se numește o funcție nedescrescătoare sau necrescătoare pe un interval funcţie monotonă la acest interval (monotonitatea strictă este un caz special de monotonitate „pur și simplu”).

Teoria are în vedere și alte abordări pentru determinarea creșterii/scăderii unei funcții, inclusiv pe semiintervale, segmente, dar pentru a nu vă turna ulei-ulei-ulei pe cap, vom fi de acord să operam cu intervale deschise cu definiții categorice. - acest lucru este mai clar și pentru rezolvarea multor probleme practice destul de mult.

Prin urmare, în articolele mele formularea „monotonitatea unei funcții” va fi aproape întotdeauna ascunsă intervale monotonie strictă(funcție strict crescătoare sau strict descrescătoare).

Vecinătatea unui punct. Cuvinte după care elevii fug oriunde pot și se ascund îngroziți în colțuri. ...Deși după postare Limitele Cauchy Probabil că nu se mai ascund, ci doar tremură ușor =) Nu vă faceți griji, nu vor mai exista dovezi ale teoremelor acum analiză matematică– Aveam nevoie de împrejurimi pentru a formula definiții mai strict puncte extremum. Să ne amintim:

Vecinătatea unui punct numit intervalul care contine acest punct, în timp ce, pentru comoditate, intervalul este adesea considerat a fi simetric. De exemplu, un punct și vecinătatea sa standard:

De fapt, definițiile:

Punctul se numește punct maxim strict, Dacă există cartierul ei, pentru toți valori ale căror, cu excepția punctului în sine, inegalitatea . În a noastră exemplu concret acesta este ideea.

Punctul se numește punct minim strict, Dacă există cartierul ei, pentru toți valori ale căror, cu excepția punctului în sine, inegalitatea . În desen există punctul „a”.

Notă : cerința simetriei vecinătății nu este deloc necesară. În plus, este important însuşi faptul existenţei cartier (fie mic sau microscopic) care satisface conditiile specificate

Punctele sunt numite puncte strict extremum sau pur și simplu puncte extremum funcții. Adică este un termen generalizat pentru puncte maxime și puncte minime.

Cum înțelegem cuvântul „extrem”? Da, la fel de direct ca monotonia. Puncte extreme de roller coaster.

Ca și în cazul monotonității, postulate libere există și sunt chiar mai frecvente în teorie (în care, desigur, se încadrează cazurile stricte luate în considerare!):

Punctul se numește punct maxim, Dacă existăîmprejurimile sale sunt astfel încât pentru toți
Punctul se numește punct minim, Dacă existăîmprejurimile sale sunt astfel încât pentru toți valorile acestui cartier, inegalitatea este valabilă.

Rețineți că, conform ultimelor două definiții, orice punct al unei funcții constante (sau o „secțiune plată” a unei funcții) este considerat atât un punct maxim, cât și un punct minim! Funcția, apropo, este atât necreștere, cât și nedescrescătoare, adică monotonă. Cu toate acestea, vom lăsa aceste considerații în seama teoreticienilor, deoarece în practică aproape întotdeauna contemplăm „dealurile” și „golurile” tradiționale (vezi desenul) cu un „rege al dealului” sau „prințesa mlaștinii” unic. Ca varietate, apare bacsis, direcționat în sus sau în jos, de exemplu, minimul funcției în punct.

Oh, și vorbind despre regalitate:
– se numește sensul maxim funcții;
– se numește sensul minim funcții.

Denumirea comună – extreme funcții.

Vă rog să aveți grijă la cuvintele voastre!

Puncte extreme– acestea sunt valori „X”.
Extreme– semnificații „joc”.

! Notă : uneori termenii enumerați se referă la punctele „X-Y” care se află direct pe GRAFUL funcției ÎNSEȘI.

Câte extreme poate avea o funcție?

Niciuna, 1, 2, 3, ... etc. catre infinit. De exemplu, sinusul are infinit de minime și maxime.

IMPORTANT! Termenul „maxim de funcție” nu identice termenul „valoarea maximă a unei funcții”. Este ușor de observat că valoarea este maximă doar într-un cartier local, iar în stânga sus sunt „tovarăși mai cool”. La fel, „minimul unei funcții” nu este același lucru cu „valoarea minimă a unei funcții”, iar în desen vedem că valoarea este minimă doar într-o anumită zonă. În acest sens, se mai numesc puncte extremum punctele extreme locale, iar extrema - extreme locale. Se plimbă și se plimbă prin apropiere și global fraţi. Deci, orice parabolă are la vârf minim global sau maxim global. În plus, nu voi face distincția între tipurile de extreme, iar explicația este exprimată mai mult în scopuri educaționale generale - adjectivele suplimentare „local”/„global” nu ar trebui să vă ia prin surprindere.

Să rezumăm scurta noastră excursie în teorie cu un test: ce înseamnă sarcina „găsește intervalele de monotonitate și punctele extreme ale funcției”?

Formularea vă încurajează să găsiți:

– intervale de funcție crescătoare/descrescătoare (nedescrescătoare, necrescătoare apare mult mai rar);

– puncte maxime și/sau minime (dacă există). Ei bine, pentru a evita eșecul, este mai bine să găsiți ei înșiși minimele/maximurile ;-)

Cum să determine toate acestea? Folosind funcția derivată!

Cum să găsiți intervale de creștere, scădere,
punctele extreme și extremele funcției?

Multe reguli, de fapt, sunt deja cunoscute și înțelese din lecție despre semnificația unui derivat.

Derivată tangentă aduce vestea veselă că funcția crește pe tot parcursul domeniul definirii.

Cu cotangentă și derivatul său situatia este exact inversa.

Arcsinusul crește pe interval - derivata aici este pozitivă: .
Când funcția este definită, dar nu este diferențiabilă. Cu toate acestea, în punctul critic există o derivată de dreapta și o tangentă de dreapta, iar la cealaltă margine sunt omologii lor stângaci.

Cred că nu vă va fi prea dificil să efectuați un raționament similar pentru arccosinus și derivata sa.

Toate cazurile de mai sus, dintre care multe sunt derivate tabulare, vă reamintesc, urmăriți direct de la definiții derivate.

De ce să explorezi o funcție folosind derivata ei?

Pentru a înțelege mai bine cum arată graficul acestei funcții: unde merge „de jos în sus”, unde „de sus în jos”, unde ajunge la minime și maxime (dacă ajunge deloc). Nu toate funcțiile sunt atât de simple - în majoritatea cazurilor nu avem nicio idee despre graficul unei anumite funcții.

Este timpul să trecem la exemple mai semnificative și să luăm în considerare algoritm pentru găsirea intervalelor de monotonitate și a extremelor unei funcții:

Exemplul 1

Găsiți intervalele de creștere/descreștere și extremele funcției

Soluţie:

1) Primul pas este să găsești domeniul unei funcții, și, de asemenea, luați notă de punctele de întrerupere (dacă există). În acest caz, funcția este continuă pe întreaga linie numerică, iar această acțiune este într-o anumită măsură formală. Dar, într-un număr de cazuri, pasiuni serioase izbucnesc aici, așa că să tratăm paragraful fără dispreț.

2) Al doilea punct al algoritmului se datorează

o condiție necesară pentru un extremum:

Dacă există un extremum într-un punct, atunci fie valoarea nu există.

Confuz de final? Extremul funcției „modulu x”. .

Condiția este necesară, dar insuficient, iar inversul nu este întotdeauna adevărat. Deci, încă nu rezultă din egalitate că funcția să atingă un maxim sau un minim în punctul . Un exemplu clasic a fost deja evidențiat mai sus - aceasta este o parabolă cubică și punctul său critic.

Dar oricum ar fi, condiția necesară pentru un extremum dictează necesitatea de a găsi puncte suspecte. Pentru a face acest lucru, găsiți derivata și rezolvați ecuația:

La începutul primului articol despre graficele de funcțiiȚi-am spus cum să construiești rapid o parabolă folosind un exemplu : „...luăm derivata întâi și o echivalăm cu zero: ...Deci, soluția ecuației noastre: - în acest punct se află vârful parabolei...”. Acum, cred, toată lumea înțelege de ce vârful parabolei este situat exact în acest punct =) În general, ar trebui să începem cu un exemplu similar aici, dar este prea simplu (chiar și pentru un ceainic). În plus, există un analog la sfârșitul lecției despre derivata unei functii. Prin urmare, să creștem gradul:

Exemplul 2

Găsiți intervalele de monotonitate și extremele funcției

Acesta este un exemplu pentru decizie independentă. Soluție completăși un eșantion final aproximativ al sarcinii la sfârșitul lecției.

A sosit momentul mult așteptat al întâlnirii cu funcțiile fracționare-raționale:

Exemplul 3

Explorați o funcție folosind derivata întâi

Fiți atenți la cât de variabil poate fi reformulată una și aceeași sarcină.

Soluţie:

1) Funcția suferă discontinuități infinite în puncte.

2) Detectăm punctele critice. Să găsim prima derivată și să o echivalăm cu zero:

Să rezolvăm ecuația. O fracție este zero când numărătorul ei este zero:

Astfel, obținem trei puncte critice:

3) Trasăm TOATE punctele detectate pe linia numerică și metoda intervalului definim semnele DERIVATULUI:

Vă reamintesc că trebuie să luați un punct în interval și să calculați valoarea derivatei la acesta și determinați-i semnul. Este mai profitabil să nu numărăm, ci să „estimați” verbal. Să luăm, de exemplu, un punct aparținând intervalului și să efectuăm înlocuirea: .

Două „plus” și unul „minus” dau un „minus”, prin urmare, ceea ce înseamnă că derivata este negativă pe întreg intervalul.

Acțiunea, după cum înțelegeți, trebuie efectuată pentru fiecare dintre cele șase intervale. Apropo, rețineți că factorul numărător și numitorul sunt strict pozitive pentru orice punct din orice interval, ceea ce simplifică foarte mult sarcina.

Deci, derivata ne-a spus că FUNCȚIA ÎNSĂȘI crește cu si scade cu . Este convenabil să conectați intervale de același tip cu pictograma de alăturare.

În momentul în care funcția atinge maximul:
În momentul în care funcția atinge un minim:

Gândește-te de ce nu trebuie să recalculezi a doua valoare ;-)

Când trece printr-un punct, derivata nu își schimbă semnul, așa că funcția nu are NU EXTREM acolo - a scăzut și a rămas în scădere.

! Să repetăm punct important : punctele nu sunt considerate critice - conțin o funcție nedeterminat. În consecință, aici În principiu, nu pot exista extreme(chiar dacă derivata își schimbă semnul).

Răspuns: functia creste cu și scade cu În punctul în care se atinge maximul funcției: , iar la punctul – minimul: .

Cunoașterea intervalelor de monotonitate și a extremelor, cuplate cu stabilite asimptote dă deja o idee foarte bună despre aspect grafica functionala. O persoană de pregătire medie este capabilă să determine verbal că graficul unei funcții are două asimptote verticale și o asimptotă oblică. Iată eroul nostru:

Încercați încă o dată să corelați rezultatele studiului cu graficul acestei funcții.
Nu există extremum în punctul critic, dar există inflexia graficului(ceea ce, de regulă, se întâmplă în cazuri similare).

Exemplul 4

Găsiți extremele funcției

Exemplul 5

Găsiți intervalele de monotonitate, maximele și minimele funcției

… este aproape ca un fel de vacanță „X într-un cub” astăzi...
Soooo, cine din galerie s-a oferit să bea pentru asta? =)

Fiecare sarcină are propriile sale nuanțe de fond și subtilități tehnice, care sunt comentate la sfârșitul lecției.

Funcția este numită crescând pe interval
, dacă pentru orice puncte

inegalitatea este valabilă
(o valoare mai mare a argumentului corespunde unei valori mai mari a funcției).

La fel, funcția
numit descrescand pe interval
, dacă pentru orice puncte
din acest interval dacă condiția este îndeplinită
inegalitatea este valabilă
(o valoare a argumentului mai mare corespunde unei valori mai mici a funcției).

Creștere pe interval
și descrescătoare pe interval
sunt numite funcții monoton pe interval
.

Cunoașterea derivatei unei funcții diferențiabile permite găsirea intervalelor de monotonitate a acesteia.

Teoremă (condiție suficientă pentru o creștere a unei funcții).
funcții
pozitiv pe interval
, apoi funcția
crește monoton în acest interval.

Teoremă (condiție suficientă pentru ca o funcție să scadă). Dacă derivata este diferențiabilă pe interval
funcții
negativ pe interval
, apoi funcția
scade monoton în acest interval.

Sensul geometric dintre aceste teoreme este că pe intervale de funcții descrescătoare, tangentele la graficul funcției formează cu axa
unghiuri obtuze, iar la intervale crescătoare – acute (vezi Fig. 1).

Teoremă (o condiție necesară pentru monotonitatea unei funcții). Dacă funcţia
diferenţiabilă şi
(
) pe interval
, atunci nu scade (creste) pe acest interval.

Algoritm pentru găsirea intervalelor de monotonitate ale unei funcții
:

Exemplu. Găsiți intervalele de monotonitate ale unei funcții
.

Punct numit punctul maxim al funcției

astfel încât pentru toată lumea , îndeplinind condiția
, inegalitatea este valabilă
.

Funcție maximă este valoarea funcției în punctul maxim.

Figura 2 prezintă un exemplu de grafic al unei funcții care are maxime în puncte
.

Punct numit punctul minim al funcției
, dacă există un număr
astfel încât pentru toată lumea , îndeplinind condiția
, inegalitatea este valabilă
. Smochin. Funcția 2 are un minim la punct .

Există un nume comun pentru înalte și scăzute - extreme . În consecință, sunt numite punctele maxime și minime puncte extremum .

O funcție definită pe un segment poate avea un maxim și un minim doar în punctele situate în interiorul acestui segment. De asemenea, nu trebuie să confundăm maximul și minimul unei funcții cu cel mai mare și cea mai mică valoare pe un segment - acestea sunt concepte fundamental diferite.

În punctele extreme, derivata are proprietăți speciale.

Teoremă (condiție necesară pentru extremum). Lasă la punct funcţie
are un extremum. Atunci fie
nu există, sau
.

Acele puncte din domeniul definirii functiei la care
nu există sau în care
, sunt numite punctele critice ale funcției .

Astfel, punctele extreme se află printre punctele critice. În general, punctul critic nu trebuie să fie un punct extremum. Dacă derivata unei funcții într-un anumit punct este egală cu zero, aceasta nu înseamnă că funcția are un extremum în acest punct.

Exemplu. Sa luam in considerare
. Avem
, dar punct
nu este un punct extremum (vezi Figura 3).

Teoremă (prima condiție suficientă pentru un extremum). Lasă la punct funcţie
este continuă, iar derivata
la trecerea printr-un punct schimba semnul. Apoi – punct extrem: maxim dacă semnul se schimbă de la „+” la „–”, și minim dacă de la „–” la „+”.

Dacă, la trecerea printr-un punct derivata nu își schimbă semnul, atunci la punct nu exista extrema.

Teoremă (a doua condiție suficientă pentru extremum). Lasă la punct derivata unei functii de doua ori diferentiabile
egal cu zero (
), iar derivata sa a doua în acest punct este diferită de zero (
) și este continuă într-o vecinătate a punctului . Apoi – punctul extremum
; la
acesta este punctul minim, iar la
acesta este punctul maxim.

Algoritm pentru găsirea extremelor unei funcții folosind prima condiție suficientă pentru un extrem:

Găsiți derivata.

Găsiți punctele critice ale funcției.

Examinați semnul derivatei la stânga și la dreapta fiecărui punct critic și trageți o concluzie despre prezența extremei.

Găsiți valori extreme ale funcției.

Algoritm pentru găsirea extremelor unei funcții folosind a doua condiție suficientă pentru un extrem:

Exemplu. Găsiți extremele funcției
.

Funcții de creștere și scădere

funcţie y = f(X) se numește crescător pe intervalul [ A, b], dacă pentru orice pereche de puncte XȘi X", a ≤ x inegalitatea este valabilă f(X) ≤ f (X"), și strict în creștere - dacă inegalitatea f (X) f(X"). Funcțiile descrescătoare și strict descrescătoare sunt definite în mod similar. De exemplu, funcția la = X 2 (orez. , a) crește strict pe segmentul , și

(orez. , b) scade strict pe acest segment. Sunt desemnate funcții crescătoare f (X), și în scădere f (X)↓. Pentru o funcție diferențiabilă f (X) era în creștere pe segmentul [ A, b], este necesar și suficient ca derivata sa f"(X) a fost nenegativ la [ A, b].

Odată cu creșterea și scăderea unei funcții pe un segment, avem în vedere creșterea și scăderea unei funcții într-un punct. Funcţie la = f (X) se numește crescător la punct X 0 dacă există un interval (α, β) care conține punctul X 0, care pentru orice punct X din (α, β), x> X 0, inegalitatea este valabilă f (X 0) ≤ f (X), și pentru orice punct X din (α, β), x 0 , inegalitatea este valabilă f (X) ≤ f (X 0). Creșterea strictă a unei funcții în punct este definită în mod similar X 0 . Dacă f"(X 0) > 0, apoi funcția f(X) crește strict la punct X 0 . Dacă f (X) crește în fiecare punct al intervalului ( A, b), apoi crește în acest interval.

S. B. Stechkin.

Marea Enciclopedie Sovietică. - M.: Enciclopedia Sovietică. 1969-1978 .

Vedeți ce sunt „funcțiile de creștere și de descreștere” în alte dicționare:

Concepte de analiză matematică. Funcția f(x) se numește raportul dintre numerele diferitelor grupe de vârstă ale populației care crește pe segmentul STRUCTURA DE VÂRSTE A POPULAȚIEI. Depinde de rata natalității și mortalității, speranța de viață a oamenilor... Dicţionar enciclopedic mare

Concepte de analiză matematică. Se spune că o funcție f(x) este în creștere pe segment dacă pentru orice pereche de puncte x1 și x2, a≤x1 ... Dicţionar enciclopedic

Concepte de matematică. analiză. Se numește funcția f(x). crescând pe segmentul [a, b], dacă pentru orice pereche de puncte x1 și x2 și<или=х1 <х<или=b, выполняется неравенство f(x1)Științele naturii. Dicţionar enciclopedic

O ramură a matematicii care studiază derivatele și diferențialele funcțiilor și aplicațiile acestora în studiul funcțiilor. Proiectarea lui D. și. într-o disciplină matematică independentă este asociat cu numele lui I. Newton și G. Leibniz (a doua jumătate a 17 ... Marea Enciclopedie Sovietică

O ramură a matematicii în care sunt studiate conceptele de derivată și diferențială și modul în care acestea sunt aplicate la studiul funcțiilor. Dezvoltarea lui D. și. strâns legată de dezvoltarea calculului integral. Conținutul lor este, de asemenea, inseparabil. Împreună formează baza... ... Enciclopedie matematică

Acest termen are alte semnificații, vezi funcția. Solicitarea „Afișare” este redirecționată aici; vezi și alte sensuri... Wikipedia

Aristotel și peripateticii- Întrebarea lui Aristotel Viaţa lui Aristotel Aristotel sa născut în 384/383. î.Hr e. în Stagira, la graniţa cu Macedonia. Tatăl său, pe nume Nicomachus, era medic în slujba regelui macedonean Amyntas, tatăl lui Filip. Împreună cu familia sa, tânărul Aristotel... ... Filosofia occidentală de la origini până în zilele noastre

- (QCD), teoria câmpului cuantic a interacțiunii puternice dintre quarci și gluoni, construită în imaginea cuanticei. electrodinamică (QED) bazată pe simetria gauge „culoare”. Spre deosebire de QED, fermionii din QCD au proprietăți complementare. gradul cuantic de libertate număr,… … Enciclopedie fizică

I Inima Inima (latina cor, greaca cardia) este un organ fibromuscular gol care, functionand ca o pompa, asigura miscarea sangelui in sistemul circulator. Anatomie Inima este situată în mediastinul anterior (Mediastin) în pericard între... ... Enciclopedie medicală

Viața unei plante, ca orice alt organism viu, este un set complex de procese interconectate; Cel mai semnificativ dintre ele, după cum se știe, este schimbul de substanțe cu mediul. Mediul este sursa din care... ... Enciclopedie biologică

Extreme ale funcției

Definiția 2

Un punct $x_0$ se numește punct maxim al unei funcții $f(x)$ dacă există o vecinătate a acestui punct astfel încât pentru toți $x$ din această vecinătate inegalitatea $f(x)\le f(x_0) $ deține.

Definiția 3

Un punct $x_0$ este numit punct maxim al unei funcții $f(x)$ dacă există o vecinătate a acestui punct astfel încât pentru toți $x$ din această vecinătate inegalitatea $f(x)\ge f(x_0) $ deține.

Conceptul de extremum al unei funcții este strâns legat de conceptul de punct critic al unei funcții. Să introducem definiția lui.

Definiția 4

$x_0$ se numește punct critic al funcției $f(x)$ dacă:

1) $x_0$ - punct intern al domeniului de definire;

2) $f"\left(x_0\right)=0$ sau nu există.

Pentru conceptul de extremum, putem formula teoreme asupra condițiilor suficiente și necesare pentru existența acestuia.

Teorema 2

Condiție suficientă pentru un extremum

Fie punctul $x_0$ critic pentru funcția $y=f(x)$ și se află în intervalul $(a,b)$. Fie pe fiecare interval $\left(a,x_0\right)\ și\ (x_0,b)$ derivata $f"(x)$ există și menține un semn constant. Atunci:

1) Dacă pe intervalul $(a,x_0)$ derivata este $f"\left(x\right)>0$, iar pe intervalul $(x_0,b)$ derivata este $f"\left( x\dreapta)

2) Dacă pe intervalul $(a,x_0)$ derivata $f"\left(x\right)0$, atunci punctul $x_0$ este punctul minim pentru această funcție.

3) Dacă atât pe intervalul $(a,x_0)$ cât și pe intervalul $(x_0,b)$ derivata $f"\left(x\right) >0$ sau derivata $f"\left(x \dreapta)

Această teoremă este ilustrată în figura 1.

Figura 1. Condiție suficientă pentru existența extremei

Exemple de extreme (Fig. 2).

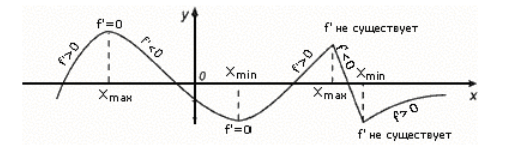
Figura 2. Exemple de puncte extreme

Regula pentru studierea unei funcții pentru extremum

2) Aflați derivata $f"(x)$;

7) Trageți concluzii despre prezența maximelor și minimelor pe fiecare interval, folosind teorema 2.

Funcții de creștere și scădere

Să introducem mai întâi definițiile funcțiilor crescătoare și descrescătoare.

Definiția 5

Se spune că o funcție $y=f(x)$ definită pe intervalul $X$ este în creștere dacă pentru orice puncte $x_1,x_2\in X$ la $x_1

Definiția 6

Se spune că o funcție $y=f(x)$ definită pe intervalul $X$ este descrescătoare dacă pentru orice puncte $x_1,x_2\in X$ pentru $x_1f(x_2)$.

Studierea unei funcții pentru creștere și scădere

Puteți studia funcțiile crescătoare și descrescătoare folosind derivata.

Pentru a examina o funcție pentru intervale de creștere și descreștere, trebuie să faceți următoarele:

1) Aflați domeniul de definiție al funcției $f(x)$;

2) Aflați derivata $f"(x)$;

3) Aflați punctele în care este valabilă egalitatea $f"\left(x\right)=0$;

4) Aflați punctele în care $f"(x)$ nu există;

5) Marcați pe linia de coordonate toate punctele găsite și domeniul de definire a acestei funcții;

6) Să se determine semnul derivatei $f"(x)$ pe fiecare interval rezultat;

7) Trageți o concluzie: la intervalele în care $f"\left(x\right)0$ funcția crește.

Exemple de probleme pentru studierea funcțiilor de creștere, scădere și prezența punctelor extreme

Exemplul 1

Examinați funcția de creștere și descreștere și prezența punctelor maxime și minime: $f(x)=(2x)^3-15x^2+36x+1$

Deoarece primele 6 puncte sunt aceleași, să le executăm mai întâi.

1) Domeniul definiției - toate numerele reale;

2) $f"\left(x\right)=6x^2-30x+36$;

3) $f"\left(x\right)=0$;

\ \ \

4) $f"(x)$ există în toate punctele domeniului de definiție;

5) Linia de coordonate:

Figura 3.

6) Determinați semnul derivatei $f"(x)$ pe fiecare interval:

\ \}