Multiplication et division de nombres rationnels. Multiplication
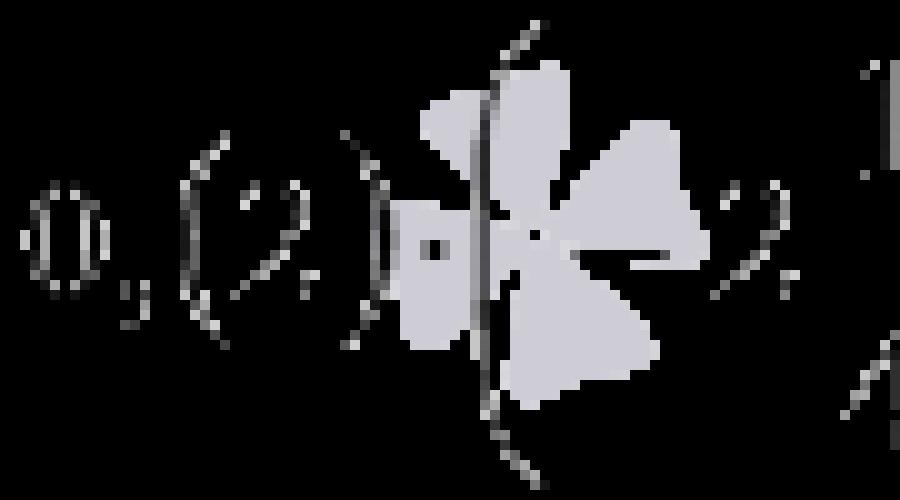
Lire aussi
Dans cet article, nous traiterons multiplier des nombres avec différents signes . Ici, nous formulerons d'abord la règle de multiplication des nombres positifs et négatifs, la justifierons, puis envisagerons l'application de cette règle lors de la résolution d'exemples.
Navigation dans les pages.
Règle pour multiplier des nombres avec des signes différents
La multiplication d'un nombre positif par un nombre négatif, ainsi que d'un nombre négatif par un nombre positif, s'effectue comme suit : la règle pour multiplier les nombres avec des signes différents: pour multiplier des nombres avec des signes différents, vous devez multiplier et mettre un signe moins devant le produit obtenu.
Écrivons cette règle sous forme de lettre. Pour tout nombre réel positif a et tout nombre réel négatif −b, l'égalité une·(−b)=−(|une|·|b|) , et aussi pour un nombre négatif −a et un nombre positif b l'égalité (−une)·b=−(|une|·|b|) .
La règle de multiplication des nombres avec des signes différents est tout à fait cohérente avec propriétés des opérations avec des nombres réels. En effet, sur cette base, il est facile de montrer que pour les nombres réels et positifs a et b une chaîne d'égalités de la forme une·(−b)+une·b=une·((−b)+b)=une·0=0, ce qui prouve que a·(−b) et a·b sont des nombres opposés, ce qui implique l'égalité a·(−b)=−(a·b) . Et de là découle la validité de la règle de multiplication en question.
Il convient de noter que la règle énoncée pour multiplier les nombres avec des signes différents est valable aussi bien pour les nombres réels que pour les nombres rationnels et pour les nombres entiers. Cela découle du fait que les opérations avec des nombres rationnels et entiers ont les mêmes propriétés que celles utilisées dans la preuve ci-dessus.
Il est clair que multiplier des nombres de signes différents selon la règle résultante revient à multiplier des nombres positifs.
Il ne reste plus qu'à considérer des exemples d'application de la règle de multiplication démontée lors de la multiplication de nombres avec des signes différents.
Exemples de multiplication de nombres avec différents signes
Examinons plusieurs solutions exemples de multiplication de nombres avec différents signes. Commençons par un cas simple pour nous concentrer sur les étapes de la règle plutôt que sur la complexité informatique.
Exemple.
Multipliez le nombre négatif −4 par le nombre positif 5.
Solution.
Selon la règle de multiplication des nombres avec des signes différents, nous devons d'abord multiplier les modules des facteurs d'origine. Le module de −4 est 4 et le module de 5 est 5, et multiplier les nombres naturels 4 et 5 donne 20. Enfin, il reste à mettre un signe moins devant le nombre obtenu, nous avons −20. Ceci termine la multiplication.
Brièvement, la solution peut s'écrire comme suit : (−4)·5=−(4·5)=−20.
Répondre:
(−4)·5=−20.
Lorsque vous multipliez des fractions avec des signes différents, vous devez être capable de multiplier des fractions ordinaires, de multiplier des décimales et leurs combinaisons avec des nombres naturels et fractionnaires.
Exemple.
Multipliez les nombres avec des signes différents 0, (2) et .
Solution.
En convertissant une fraction décimale périodique en une fraction commune, et également en convertissant un nombre fractionnaire en une fraction impropre, à partir du produit original  nous viendrons au produit fractions ordinaires avec différents signes de forme . Ce produit, selon la règle de multiplication des nombres de signes différents, est égal à . Il ne reste plus qu'à multiplier les fractions ordinaires entre parenthèses, on a
nous viendrons au produit fractions ordinaires avec différents signes de forme . Ce produit, selon la règle de multiplication des nombres de signes différents, est égal à . Il ne reste plus qu'à multiplier les fractions ordinaires entre parenthèses, on a  .
.
Maintenant, parlons de Multiplication et division.
Disons que nous devons multiplier +3 par -4. Comment faire?
Considérons un tel cas. Trois personnes sont endettées et chacune a une dette de 4 $. Quelle est la dette totale ? Pour le trouver, vous devez additionner les trois dettes : 4 dollars + 4 dollars + 4 dollars = 12 dollars. Nous avons décidé que l'addition de trois nombres 4 est notée 3x4. Puisque dans ce cas nous parlons de dette, il y a un signe « - » avant le 4. Nous savons que la dette totale est de 12 $, donc notre problème devient maintenant 3x(-4)=-12.
Nous obtiendrons le même résultat si, selon le problème, chacune des quatre personnes a une dette de 3 $. En d'autres termes, (+4)x(-3)=-12. Et comme l’ordre des facteurs n’a pas d’importance, on obtient (-4)x(+3)=-12 et (+4)x(-3)=-12.
Résumons les résultats. Lorsque vous multipliez un nombre positif et un nombre négatif, le résultat sera toujours un nombre négatif. La valeur numérique de la réponse sera la même que dans le cas de nombres positifs. Produit (+4)x(+3)=+12. La présence du signe « - » n'affecte que le signe, mais n'affecte pas la valeur numérique.
Comment multiplier deux nombres négatifs ?
Malheureusement, il est très difficile de réfléchir à ce sujet exemple approprié de la vie. Il est facile d’imaginer une dette de 3 ou 4 dollars, mais il est absolument impossible d’imaginer -4 ou -3 personnes s’endetter.
Peut-être que nous emprunterons une voie différente. En multiplication, lorsque le signe d'un des facteurs change, le signe du produit change. Si nous changeons les signes des deux facteurs, nous devons changer deux fois marque de travail, d'abord du positif au négatif, puis vice versa, du négatif au positif, c'est-à-dire que le produit aura un signe initial.
Il est donc assez logique, quoique un peu étrange, que (-3) x (-4) = +12.
Position du signe une fois multiplié, cela change comme ceci :
- nombre positif x nombre positif = nombre positif ;
- nombre négatif x nombre positif = nombre négatif ;
- nombre positif x nombre négatif = nombre négatif ;
- nombre négatif x nombre négatif = nombre positif.
Autrement dit, en multipliant deux nombres de mêmes signes, on obtient un nombre positif. En multipliant deux nombres de signes différents, on obtient un nombre négatif.
La même règle est vraie pour l'action opposée à la multiplication - pour.
Vous pouvez facilement le vérifier en exécutant opérations de multiplication inverse. Dans chacun des exemples ci-dessus, si vous multipliez le quotient par le diviseur, vous obtiendrez le dividende et vous assurerez qu'il a le même signe, par exemple (-3)x(-4)=(+12).
Puisque l’hiver approche, il est temps de réfléchir à quoi changer les fers de votre cheval de fer pour ne pas glisser sur la glace et se sentir en confiance sur les routes hivernales. Vous pouvez par exemple acheter des pneus Yokohama sur le site : mvo.ru ou quelques autres, l'essentiel est qu'ils soient de haute qualité, vous pouvez trouver plus d'informations et de prix sur le site Mvo.ru.
Cette leçon couvre la multiplication et la division. nombres rationnels.
Contenu de la leçonMultiplier des nombres rationnels
Les règles de multiplication des nombres entiers s'appliquent également aux nombres rationnels. En d’autres termes, pour multiplier des nombres rationnels, il faut être capable de
Aussi, vous devez connaître les lois fondamentales de la multiplication, telles que : la loi commutative de la multiplication, la loi associative de la multiplication, la loi distributive de la multiplication et la multiplication par zéro.
Exemple 1. Trouver la valeur d'une expression
C'est la multiplication de nombres rationnels de signes différents. Pour multiplier des nombres rationnels avec des signes différents, vous devez multiplier leurs modules et mettre un moins devant la réponse obtenue.
Pour bien voir qu'il s'agit de nombres qui ont des signes différents, nous mettons chaque nombre rationnel entre parenthèses avec ses signes.

Le module du nombre est égal à , et le module du nombre est égal à . Après avoir multiplié les modules résultants sous forme de fractions positives, nous avons reçu la réponse, mais avant la réponse nous avons mis un moins, comme la règle l'exigeait. Pour assurer ce moins avant la réponse, la multiplication des modules a été effectuée entre parenthèses, précédée d'un moins.
La solution courte ressemble à ceci :
![]()
Exemple 2. Trouver la valeur d'une expression 


Exemple 3. Trouver la valeur d'une expression 
C'est la multiplication de nombres rationnels négatifs. Pour multiplier des nombres rationnels négatifs, vous devez multiplier leurs modules et mettre un plus devant la réponse obtenue
Solution pour cet exemple peut s'écrire brièvement :

Exemple 4. Trouver la valeur d'une expression 
La solution pour cet exemple peut être écrite brièvement :

Exemple 5. Trouver la valeur d'une expression
C'est la multiplication de nombres rationnels de signes différents. Multiplions les modules de ces nombres et mettons un moins devant la réponse obtenue

La solution courte semblera beaucoup plus simple :
Exemple 6. Trouver la valeur d'une expression
Convertissons le nombre fractionnaire en une fraction impropre. Réécrivons le reste tel quel
Nous avons obtenu la multiplication de nombres rationnels de signes différents. Multiplions les modules de ces nombres et mettons un moins devant la réponse obtenue. L'entrée avec les modules peut être ignorée pour ne pas encombrer l'expression
La solution pour cet exemple peut être écrite brièvement
Exemple 7. Trouver la valeur d'une expression
C'est la multiplication de nombres rationnels de signes différents. Multiplions les modules de ces nombres et mettons un moins devant la réponse obtenue

Au début, la réponse s'est avérée être une fraction impropre, mais nous avons mis en évidence toute la partie qu'elle contient. Notez que la partie entière a été séparée du module fraction. Le nombre mixte résultant était placé entre parenthèses précédées d’un signe moins. Ceci est fait pour garantir que les exigences de la règle sont remplies. Et la règle exigeait que la réponse reçue soit précédée d'un moins.
La solution pour cet exemple peut être écrite brièvement :
Exemple 8. Trouver la valeur d'une expression 
Tout d'abord, multiplions et multiplions le nombre obtenu par le nombre restant 5. Nous sauterons l'entrée avec les modules afin de ne pas encombrer l'expression.
Répondre: valeur d'expression  est égal à −2.
est égal à −2.
Exemple 9. Trouvez le sens de l’expression : 
Convertissons les nombres fractionnaires en fractions impropres :

Nous avons obtenu la multiplication de nombres rationnels négatifs. Multiplions les modules de ces nombres et mettons un plus devant la réponse obtenue. L'entrée avec les modules peut être ignorée pour ne pas encombrer l'expression
Exemple 10. Trouver la valeur d'une expression
L'expression se compose de plusieurs facteurs. Selon la loi associative de multiplication, si une expression est composée de plusieurs facteurs, alors le produit ne dépendra pas de l'ordre des actions. Cela nous permet d'évaluer une expression donnée dans n'importe quel ordre.
Ne réinventons pas la roue, mais calculons cette expression de gauche à droite dans l'ordre des facteurs. Sautons l'entrée avec les modules pour ne pas encombrer l'expression
Troisième action :
Quatrième action :
Répondre: la valeur de l'expression est
Exemple 11. Trouver la valeur d'une expression
Rappelons la loi de la multiplication par zéro. Cette loi stipule qu'un produit est égal à zéro si au moins un des facteurs est égal à zéro.
Dans notre exemple, l'un des facteurs est égal à zéro, donc sans perdre de temps nous répondons que la valeur de l'expression est égale à zéro :

Exemple 12. Trouver la valeur d'une expression 
Le produit est égal à zéro si au moins un des facteurs est égal à zéro.
Dans notre exemple, l'un des facteurs est égal à zéro, donc sans perdre de temps nous répondons que la valeur de l'expression  est égal à zéro :
est égal à zéro :

Exemple 13. Trouver la valeur d'une expression 
Vous pouvez utiliser l'ordre des actions et calculer d'abord l'expression entre parenthèses et multiplier la réponse obtenue par une fraction.
Vous pouvez également utiliser la loi distributive de multiplication : multipliez chaque terme de la somme par une fraction et additionnez les résultats obtenus. Nous utiliserons cette méthode.

Selon l'ordre des opérations, si une expression contient une addition et une multiplication, alors la multiplication doit être effectuée en premier. Par conséquent, dans la nouvelle expression résultante, mettons entre parenthèses les paramètres qui doivent être multipliés. De cette façon, nous pouvons voir clairement quelles actions effectuer plus tôt et lesquelles plus tard :
Troisième action :
![]()
Répondre: valeur d'expression  équivaut à
équivaut à
La solution pour cet exemple peut être écrite beaucoup plus courte. Il ressemblera à ceci:
Il est clair que cet exemple pourrait être résolu même dans notre esprit. Par conséquent, vous devez développer la capacité d’analyser une expression avant de la résoudre. Il est probable que cela puisse être résolu mentalement et économiser beaucoup de temps et de nerfs. Et dans les tests et examens, comme vous le savez, le temps est très précieux.
Exemple 14. Trouver la valeur de l'expression −4,2 × 3,2
C'est la multiplication de nombres rationnels de signes différents. Multiplions les modules de ces nombres et mettons un moins devant la réponse obtenue

Remarquez comment les modules des nombres rationnels ont été multipliés. Dans ce cas, pour multiplier les modules des nombres rationnels, il fallait .
Exemple 15. Trouver la valeur de l'expression −0,15 × 4
C'est la multiplication de nombres rationnels de signes différents. Multiplions les modules de ces nombres et mettons un moins devant la réponse obtenue

Remarquez comment les modules des nombres rationnels ont été multipliés. Dans ce cas, pour multiplier les modules des nombres rationnels, il fallait pouvoir le faire.
Exemple 16. Trouver la valeur de l'expression −4,2 × (−7,5)
C'est la multiplication de nombres rationnels négatifs. Multiplions les modules de ces nombres et mettons un plus devant la réponse obtenue
Division de nombres rationnels
Les règles de division des nombres entiers s'appliquent également aux nombres rationnels. En d’autres termes, pour pouvoir diviser des nombres rationnels, il faut être capable de
Sinon, les mêmes méthodes de division des fractions ordinaires et décimales sont utilisées. Pour diviser une fraction commune par une autre fraction, vous devez multiplier la première fraction par l’inverse de la deuxième fraction.
Et diviser décimal vers une autre fraction décimale, vous devez déplacer la virgule décimale du dividende et du diviseur vers la droite d'autant de chiffres qu'il y a après la virgule décimale du diviseur, puis effectuer la division comme avec un nombre ordinaire.
Exemple 1. Trouvez le sens de l’expression :
C'est la division de nombres rationnels de signes différents. Pour calculer une telle expression, vous devez multiplier la première fraction par l'inverse de la seconde.
Alors, multiplions la première fraction par l'inverse de la seconde.
Nous avons obtenu la multiplication de nombres rationnels de signes différents. Et nous savons déjà comment calculer de telles expressions. Pour ce faire, vous devez multiplier les modules de ces nombres rationnels et mettre un moins devant la réponse obtenue.
Complétons cet exemple jusqu'à la fin. L'entrée avec les modules peut être ignorée pour ne pas encombrer l'expression
La valeur de l'expression est donc
La solution détaillée est la suivante :
Une solution courte ressemblerait à ceci :
Exemple 2. Trouver la valeur d'une expression
C'est la division de nombres rationnels de signes différents. Pour calculer cette expression, vous devez multiplier la première fraction par l’inverse de la seconde.
L'inverse de la deuxième fraction est la fraction . Multiplions la première fraction par celle-ci :

Une solution courte ressemblerait à ceci :
Exemple 3. Trouver la valeur d'une expression
C'est la division des nombres rationnels négatifs. Pour calculer cette expression, vous devez à nouveau multiplier la première fraction par l'inverse de la seconde.
L'inverse de la deuxième fraction est la fraction . Multiplions la première fraction par celle-ci :

Nous avons obtenu la multiplication de nombres rationnels négatifs. Nous savons déjà comment une telle expression est calculée. Vous devez multiplier les modules des nombres rationnels et mettre un plus devant la réponse obtenue.
Terminons cet exemple jusqu'au bout. Vous pouvez sauter l'entrée avec les modules pour ne pas encombrer l'expression :
Exemple 4. Trouver la valeur d'une expression
Pour calculer cette expression, vous devez multiplier le premier nombre −3 par la fraction inverse de .
L'inverse d'une fraction est la fraction . Multipliez le premier nombre −3 par celui-ci
Exemple 6. Trouver la valeur d'une expression
Pour calculer cette expression, vous devez multiplier la première fraction par l’inverse de 4.
L'inverse du nombre 4 est une fraction. Multipliez la première fraction par elle
Exemple 5. Trouver la valeur d'une expression
Pour calculer cette expression, vous devez multiplier la première fraction par l'inverse de −3
L'inverse de −3 est une fraction. Multiplions la première fraction par celle-ci :
Exemple 6. Trouver la valeur de l'expression −14,4 : 1,8
C'est la division de nombres rationnels de signes différents. Pour calculer cette expression, vous devez diviser le module du dividende par le module du diviseur et mettre un moins avant la réponse obtenue

Remarquez comment le module du dividende a été divisé par le module du diviseur. Dans ce cas, pour le faire correctement, il fallait pouvoir.
Si vous ne voulez pas vous embêter avec les décimales (et cela arrive souvent), alors convertissez ces nombres fractionnaires en fractions impropres, puis effectuez la division elle-même.
Calculons l'expression précédente −14,4 : 1,8 de cette façon. Convertissons les nombres décimaux en nombres fractionnaires :
![]()
Convertissons maintenant les nombres fractionnaires résultants en fractions impropres :

![]()
Vous pouvez désormais effectuer une division directement, c'est-à-dire diviser une fraction par une fraction. Pour ce faire, vous devez multiplier la première fraction par la fraction inverse de la seconde :

Exemple 7. Trouver la valeur d'une expression 
Convertissons la fraction décimale −2,06 en une fraction impropre et multiplions cette fraction par l'inverse de la deuxième fraction :

Fractions à plusieurs étages
Vous pouvez souvent rencontrer une expression dans laquelle la division des fractions s'écrit à l'aide d'une ligne de fraction. Par exemple, l’expression pourrait s’écrire ainsi :
Quelle est la différence entre les expressions et ? Il n'y a vraiment aucune différence. Ces deux expressions ont la même signification et un signe égal peut être placé entre elles :

Dans le premier cas, le signe de division est un deux-points et l'expression est écrite sur une seule ligne. Dans le second cas, la division des fractions s'écrit à l'aide d'une ligne de fraction. Le résultat est une fraction que les gens s’accordent à appeler à plusieurs étages.
Lorsque vous rencontrez de telles expressions à plusieurs étages, vous devez appliquer les mêmes règles pour diviser les fractions ordinaires. La première fraction doit être multipliée par l'inverse de la seconde.
Il est extrêmement gênant d'utiliser de telles fractions dans une solution, vous pouvez donc les écrire sous une forme compréhensible en utilisant des deux-points plutôt qu'une barre oblique comme signe de division.
Par exemple, écrivons une fraction à plusieurs étages sous une forme compréhensible. Pour ce faire, vous devez d'abord déterminer où se trouve la première fraction et où se trouve la seconde, car il n'est pas toujours possible de le faire correctement. Les fractions à plusieurs étages comportent plusieurs lignes de fraction qui peuvent prêter à confusion. La ligne de fraction principale, qui sépare la première fraction de la seconde, est généralement plus longue que les autres.
Après avoir déterminé la ligne fractionnaire principale, vous pouvez facilement comprendre où se trouve la première fraction et où se trouve la seconde :

Exemple 2.
On retrouve la droite de fraction principale (c'est la plus longue) et on voit que l'entier −3 est divisé par une fraction commune

Et si nous prenions par erreur la deuxième ligne fractionnaire comme principale (celle qui est la plus courte), alors il s'avérerait que nous divisons la fraction par l'entier 5. Dans ce cas, même si cette expression est calculée correctement, le le problème ne sera pas résolu correctement, car le dividende dans ce Dans ce cas, le nombre est −3 et le diviseur est la fraction .
Exemple 3.Écrivons la fraction à plusieurs niveaux sous une forme claire
On retrouve la ligne de fraction principale (c'est la plus longue) et on voit que la fraction est divisée par l'entier 2

Et si nous prenions par erreur la première ligne fractionnaire comme première (celle qui est la plus courte), alors il s'avérerait que nous divisons l'entier −5 par la fraction. Dans ce cas, même si cette expression est calculée correctement, le problème sera mal résolu, puisque le dividende dans ce cas est la fraction et que le diviseur est l'entier 2.
Malgré le fait que les fractions à plusieurs niveaux ne soient pas pratiques à utiliser, nous les rencontrerons très souvent, en particulier lors de l'étude des mathématiques supérieures.
Naturellement, il faut plus de temps et d’espace pour traduire une fraction à plusieurs étages sous une forme compréhensible. Vous pouvez donc utiliser davantage méthode rapide. Cette méthode est pratique et le résultat vous permet d'obtenir une expression toute faite dans laquelle la première fraction a déjà été multipliée par la fraction réciproque de la seconde.
Cette méthode est mise en œuvre de la manière suivante :
Si la fraction est de quatre étages, par exemple, alors le numéro situé au premier étage est élevé au dernier étage. Et le personnage situé au deuxième étage est élevé au troisième étage. Les nombres résultants doivent être reliés par des signes de multiplication (×)

Du coup, en contournant la notation intermédiaire, on obtient une nouvelle expression dans laquelle la première fraction a déjà été multipliée par la fraction réciproque de la seconde. La commodité et c'est tout !
Pour éviter les erreurs lors de l'utilisation cette méthode, vous pouvez vous laisser guider par la règle suivante :
Du premier au quatrième. Du deuxième au troisième.
La règle fait référence aux sols. Le personnage du premier étage doit être élevé au quatrième étage. Et le personnage du deuxième étage doit être élevé au troisième étage.
Essayons de calculer une fraction à plusieurs étages en utilisant la règle ci-dessus.
Ainsi, on élève le numéro situé au premier étage au quatrième étage, et on élève le numéro situé au deuxième étage au troisième étage.

Du coup, en contournant la notation intermédiaire, on obtient une nouvelle expression dans laquelle la première fraction a déjà été multipliée par la fraction réciproque de la seconde. Ensuite, vous pouvez utiliser vos connaissances existantes :

Essayons de calculer une fraction à plusieurs étages en utilisant un nouveau schéma.
Il n'y a que les premier, deuxième et quatrième étages. Il n'y a pas de troisième étage. Mais on ne s'écarte pas du schéma de base : on élève le chiffre du premier étage au quatrième étage. Et comme il n'y a pas de troisième étage, on laisse le numéro situé au deuxième étage tel quel

En conséquence, en contournant la notation intermédiaire, nous avons reçu une nouvelle expression dans laquelle le premier nombre −3 a déjà été multiplié par la fraction réciproque du second. Ensuite, vous pouvez utiliser vos connaissances existantes :

Essayons de calculer la fraction à plusieurs étages en utilisant le nouveau schéma.
Il n'y a que les deuxième, troisième et quatrième étages. Il n'y a pas de premier étage. Puisqu'il n'y a pas de premier étage, il n'y a rien pour monter au quatrième étage, mais on peut élever le chiffre du deuxième étage au troisième :

En conséquence, en contournant la notation intermédiaire, nous avons reçu une nouvelle expression dans laquelle la première fraction a déjà été multipliée par l'inverse du diviseur. Ensuite, vous pouvez utiliser vos connaissances existantes :

Utiliser des variables
Si l'expression est complexe et qu'il vous semble qu'elle vous confondra dans le processus de résolution du problème, alors une partie de l'expression peut être placée dans une variable et ensuite travailler avec cette variable.
Les mathématiciens font souvent cela. Une tâche difficile décomposez-les en sous-tâches plus faciles et résolvez-les. Ensuite, les sous-tâches résolues sont regroupées en un seul tout. Ce processus créatif et c'est quelque chose que l'on apprend au fil des années grâce à un entraînement intensif.
L'utilisation de variables est justifiée lorsque l'on travaille avec des fractions à plusieurs niveaux. Par exemple:
Trouver la valeur d'une expression
Ainsi, au numérateur et au dénominateur il y a une expression fractionnaire dont il y a des expressions fractionnaires. En d’autres termes, nous sommes à nouveau confrontés à une fraction à plusieurs étages, que nous n’aimons pas trop.
L'expression au numérateur peut être saisie dans une variable avec n'importe quel nom, par exemple :
Mais en mathématiques un tel cas Il est d'usage que les variables soient nommées en lettres majuscules latines. Ne brisons pas cette tradition et désignons la première expression par une lettre majuscule A
![]()
Et l'expression au dénominateur peut être désignée par la lettre majuscule B
![]()
Notre expression originale prend maintenant la forme . Autrement dit, nous avons effectué un remplacement expression numériqueà une lettre, après avoir préalablement saisi le numérateur et le dénominateur dans les variables A et B.
Nous pouvons maintenant calculer séparément les valeurs de la variable A et la valeur de la variable B. Nous allons insérer les valeurs finies dans l'expression.
Trouvons la valeur de la variable UN
Trouvons la valeur de la variable B
Remplaçons maintenant leurs valeurs dans l'expression principale au lieu des variables A et B :

Nous avons obtenu une fraction à plusieurs étages dans laquelle nous pouvons utiliser le schéma « du premier au quatrième, du deuxième au troisième », c'est-à-dire élever le numéro situé au premier étage jusqu'au quatrième étage et augmenter le numéro situé du deuxième étage au troisième étage. D'autres calculs ne seront pas difficiles :

Ainsi, la valeur de l’expression est −1.
Bien entendu, nous avons considéré exemple le plus simple, mais notre objectif était d'apprendre comment utiliser les variables pour nous faciliter la tâche et minimiser les erreurs.
Notez également que la solution de cet exemple peut être écrite sans utiliser de variables. Cela ressemblera à

Cette solution est plus rapide et plus courte, et dans ce cas, il est plus logique de l'écrire de cette façon, mais si l'expression s'avère complexe, composée de plusieurs paramètres, parenthèses, racines et puissances, alors il est conseillé de la calculer en plusieurs étapes, en entrant une partie de ses expressions dans des variables.
Avez-vous aimé la leçon?
Rejoignez notre nouveau groupe VKontakte et commencez à recevoir des notifications sur les nouvelles leçons
Éducatif:
- Favoriser l'activité ;
Type de cours
Équipement:
- Projecteur et ordinateur.
Plan de cours
1.Moment organisationnel
2. Actualisation des connaissances
3. Dictée mathématique
4.Exécution du test
5. Solution des exercices
6. Résumé de la leçon
7. Devoirs.
Pendant les cours
1. Moment organisationnel
Aujourd'hui, nous continuerons à travailler sur la multiplication et la division des nombres positifs et négatifs. La tâche de chacun de vous est de comprendre comment il a maîtrisé ce sujet et, si nécessaire, d'affiner ce qui n'est pas encore complètement résolu. De plus, vous apprendrez beaucoup de choses intéressantes sur le premier mois du printemps – mars. (Diapositive 1)
2. Actualisation des connaissances.
3x=27 ; -5x=-45 ; x:(2,5)=5.
3. Dictée mathématique(diapositive 6.7)
Option 1
Option 2
4. Exécution des tests ( diapositive 8)
Répondre : Martius
5.Solution des exercices
(Diapositives 10 à 19)
4 mars -
2) y×(-2,5)=-15
6 mars
3) -50, 4:x=-4, 2
4) -0,25:5×(-260)
13 mars
5) -29,12: (-2,08)
14 mars
6) (-6-3,6×2,5) ×(-1)
7) -81,6:48×(-10)
le 17 mars
8) 7,15×(-4) : (-1,3)
22 Mars
9) -12,5×50 : (-25)
10) 100+(-2,1:0,03)
30 mars
6. Résumé de la leçon
7. Devoirs :
Afficher le contenu du document
"Multiplier et diviser des nombres avec des signes différents"
Sujet de la leçon : « Multiplication et division de nombres avec des signes différents. »
Objectifs de la leçon: répétition du matériel étudié sur le thème « Multiplication et division de nombres avec différents signes », pratique des compétences d'utilisation des opérations de multiplication et de division d'un nombre positif par un nombre négatif et vice versa, ainsi qu'un nombre négatif par un nombre négatif.
Objectifs de la leçon:
Éducatif:
Consolidation des règles sur ce sujet ;
Formation de compétences et d'aptitudes pour travailler avec des opérations de multiplication et de division de nombres avec différents signes.
Éducatif:
Développement de l'intérêt cognitif ;
Développement de la pensée logique, de la mémoire, de l'attention ;
Éducatif:
Favoriser l'activité ;
Inculquer aux étudiants les compétences du travail indépendant ;
Favoriser l'amour de la nature, susciter un intérêt pour les signes folkloriques.
Type de cours. Leçon-répétition et généralisation.
Équipement:
Projecteur et ordinateur.
Plan de cours
1.Moment organisationnel
2. Actualisation des connaissances
3. Dictée mathématique
4.Exécution du test
5. Solution des exercices
6. Résumé de la leçon
7. Devoirs.
Pendant les cours
1. Moment organisationnel
Bonjour gars! Qu'avons-nous fait dans les leçons précédentes ? (Multiplication et division de nombres rationnels.)
Aujourd'hui, nous continuerons à travailler sur la multiplication et la division des nombres positifs et négatifs. La tâche de chacun de vous est de comprendre comment il a maîtrisé ce sujet et, si nécessaire, d'affiner ce qui n'est pas encore complètement résolu. De plus, vous apprendrez beaucoup de choses intéressantes sur le premier mois du printemps – mars. (Diapositive 1)
2. Actualisation des connaissances.
Revoyez les règles de multiplication et de division des nombres positifs et négatifs.
Rappelez-vous la règle mnémotechnique. (Diapositive 2)
Effectuer une multiplication : (diapositive 3)
5x3 ; 9×(-4); -10×(-8); 36×(-0,1); -20×0,5 ; -13×(-0,2).
2. Effectuer la division : (diapositive 4)
48:(-8); -24: (-2); -200:4; -4,9:7; -8,4: (-7); 15:(- 0,3).
3. Résolvez l'équation : (diapositive 5)
3x=27 ; -5x=-45 ; x:(2,5)=5.
3. Dictée mathématique(diapositive 6.7)
Option 1
Option 2
Les étudiants échangent leurs cahiers, terminent le test et donnent une note.
4. Exécution des tests ( diapositive 8)
Il était une fois en Russie, les années étaient comptées à partir du 1er mars, depuis le début du printemps agricole, depuis la première chute printanière. Mars a été le « starter » de l’année. Le nom du mois « Mars » vient des Romains. Ils ont donné ce mois-ci le nom d'un de leurs dieux, un test vous aidera à découvrir de quel genre de dieu il s'agit.
Répondre : Martius
Les Romains nommaient un mois de l'année Martius en l'honneur du dieu de la guerre, Mars. En Rus', ce nom a été simplifié en ne prenant que les quatre premières lettres (diapositive 9).
On dit : « Mars est infidèle, parfois il pleure, parfois il rit. » Il existe de nombreux signes folkloriques associés au mois de mars. Certaines de ses journées ont leur propre nom. Compilons maintenant tous ensemble un livre du mois folklorique pour mars.
5.Solution des exercices
Les élèves du tableau résolvent des exemples dont les réponses sont les jours du mois. Un exemple apparaît au tableau, puis le jour du mois avec le nom et signe folklorique.
(Diapositives 10 à 19)
4 mars - Arkhip. À Arkhip, les femmes étaient censées passer toute la journée dans la cuisine. Plus elle prépare de nourriture, plus la maison sera riche.
2) y×(-2,5)=-15
6 mars- Timofey-printemps. S'il y a de la neige le jour de Timofey, alors la récolte est pour le printemps.
3) -50, 4:x=-4, 2
4) -0,25:5×(-260)
13 mars- Vasily le goutteur : des gouttes tombent des toits. Les oiseaux nichent et les oiseaux migrateurs volent depuis des endroits chauds.
5) -29,12: (-2,08)
14 mars- Evdokia (Avdotya le Lierre) - la neige s'aplatit avec l'infusion. Le deuxième rendez-vous du printemps (le premier sur Meeting). Comme Evdokia, l'été aussi. Evdokia est rouge - et le printemps est rouge ; neige sur Evdokia - pour la récolte.
6) (-6-3,6×2,5) ×(-1)
7) -81,6:48×(-10)
le 17 mars- Gerasim la tour a amené les tours. Les freux atterrissent sur des terres arables et s'ils volent directement vers leurs nids, il y aura un printemps amical.
8) 7,15×(-4) : (-1,3)
22 Mars- Pies - le jour est égal à la nuit. L'hiver se termine, le printemps commence, les alouettes arrivent. Selon une ancienne coutume, les alouettes et les échassiers sont cuits à partir de la pâte.
9) -12,5×50 : (-25)
10) 100+(-2,1:0,03)
30 mars- Alexey est chaleureux. L'eau vient des montagnes et les poissons du camp (de la cabane d'hiver). Quelle que soit la nature des cours d'eau ce jour-là (grands ou petits), la plaine inondable (inondation) l'est également.
6. Résumé de la leçon
Les gars, avez-vous aimé la leçon d'aujourd'hui ? Qu'avez-vous appris de nouveau aujourd'hui ? Qu'avons-nous répété ? Je vous suggère de préparer votre propre livre mensuel pour avril. Vous devez retrouver les signes d'avril et créer des exemples avec des réponses correspondant au jour du mois.
7. Devoirs : p. 218 n° 1174, 1179(1) (Diapositive 20)