Points décroissants sur le graphique dérivé. Lecture du graphique dérivé

Résoudre les problèmes de la partie B de l'examen d'État unifié en mathématiques

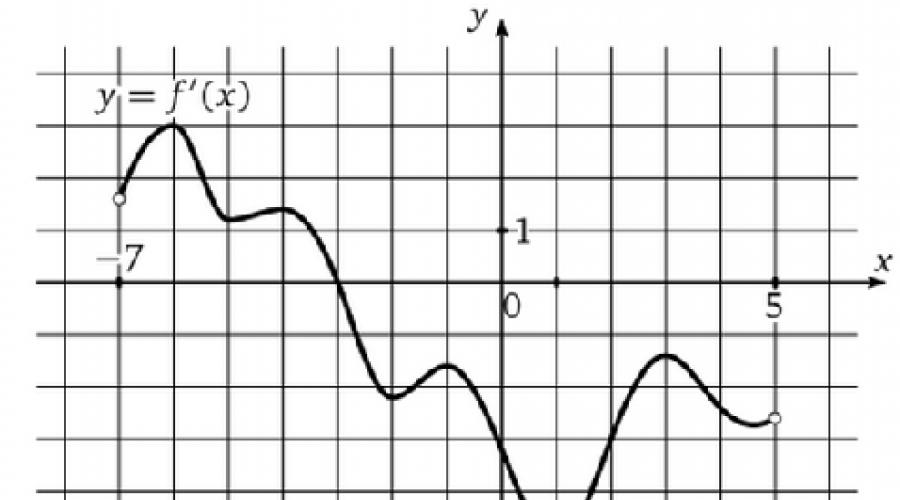
Solution. Les points maximum correspondent aux points où le signe de la dérivée passe du plus au moins. La figure montre un graphique de la dérivée de la fonction f(x) définie sur l'intervalle (−10 ; 8). Trouver le nombre de points maximum de la fonction f(x) sur l'intervalle [−9;6].

Solution. Les points maximum correspondent aux points où le signe de la dérivée passe du plus au moins. Sur le segment [−9;6] la fonction a deux points maximum x = − 4 et x = 4. Réponse : 2. La figure montre un graphique de la dérivée de la fonction f(x) définie sur l'intervalle (−10 ; 8). Trouver le nombre de points maximum de la fonction f(x) sur l'intervalle [−9;6].

Solution. La figure montre un graphique de la fonction y=f(x), définie sur l'intervalle (−1 ; 12). Déterminez le nombre de points entiers auxquels la dérivée de la fonction est négative. La dérivée d'une fonction est négative sur les intervalles sur lesquels la fonction décroît.

Solution. La figure montre un graphique de la fonction y=f(x), définie sur l'intervalle (−1 ; 12). Déterminez le nombre de points entiers auxquels la dérivée de la fonction est négative. La dérivée de la fonction est négative sur les intervalles sur lesquels la fonction diminue, c'est-à-dire sur les intervalles (0,5 ; 3), (6 ; 10) et (11 ; 12). Ils contiennent des points entiers 1, 2, 7, 8 et 9. Il y a 5 points au total. Réponse : 5.

La figure montre un graphique de la dérivée de la fonction f(x), définie sur l'intervalle (−10 ; 4). Trouver les intervalles de diminution de la fonction f(x). Dans votre réponse, indiquez la longueur du plus grand d’entre eux. Solution. Les intervalles où la fonction f(x) diminue correspondent aux intervalles où la dérivée de la fonction est négative.

La figure montre un graphique de la dérivée de la fonction f(x), définie sur l'intervalle (−10 ; 4). Trouver les intervalles de diminution de la fonction f(x). Dans votre réponse, indiquez la longueur du plus grand d’entre eux. Solution. Les intervalles décroissants de la fonction f(x) correspondent aux intervalles sur lesquels la dérivée de la fonction est négative, soit l'intervalle (−9 ; −6) de longueur 3 et l'intervalle (−2 ; 3) de longueur 5. La longueur du plus grand d’entre eux est 5. Réponse : 5.

La figure montre un graphique de la dérivée de la fonction f(x) définie sur l'intervalle (−7 ; 14). Trouver le nombre de points maximum de la fonction f(x) sur l'intervalle [−6; 9]. Solution. Les points maximum correspondent aux points où le signe de la dérivée passe du positif au négatif.

La figure montre un graphique de la dérivée de la fonction f(x) définie sur l'intervalle (−7 ; 14). Trouver le nombre de points maximum de la fonction f(x) sur l'intervalle [−6; 9]. Solution. Les points maximum correspondent aux points où le signe de la dérivée passe du positif au négatif. Sur le segment [−6 ; 9] la fonction a un point maximum x = 7. Réponse : 1.

La figure montre un graphique de la dérivée de la fonction f(x), définie sur l'intervalle (−8 ; 6). Trouver les intervalles d'augmentation de la fonction f(x). Dans votre réponse, indiquez la longueur du plus grand d’entre eux. Solution. Les intervalles d'augmentation de la fonction f(x) correspondent aux intervalles sur lesquels la dérivée de la fonction est positive.

La figure montre un graphique de la dérivée de la fonction f(x), définie sur l'intervalle (−8 ; 6). Trouver les intervalles d'augmentation de la fonction f(x). Dans votre réponse, indiquez la longueur du plus grand d’entre eux. Solution. Les intervalles d'augmentation de la fonction f(x) correspondent aux intervalles sur lesquels la dérivée de la fonction est positive, soit les intervalles (−7 ; −5), (2 ; 5). Le plus grand d'entre eux est l'intervalle (2 ; 5), dont la longueur est de 3.

La figure montre un graphique de la dérivée de la fonction f(x) définie sur l'intervalle (−7 ; 10). Trouver le nombre de points minimum de la fonction f(x) sur l'intervalle [−3; 8]. Solution. Les points minimaux correspondent aux points où le signe de la dérivée passe du moins au plus.

La figure montre un graphique de la dérivée de la fonction f(x) définie sur l'intervalle (−7 ; 10). Trouver le nombre de points minimum de la fonction f(x) sur l'intervalle [−3; 8]. Solution. Les points minimaux correspondent aux points où le signe de la dérivée passe du moins au plus. Sur le segment [−3; 8] la fonction a un point minimum x = 2. Réponse : 1.

La figure montre un graphique de la dérivée de la fonction f(x) définie sur l'intervalle (−16 ; 4). Trouver le nombre de points extremum de la fonction f(x) sur l'intervalle [−14; 2]. Solution. Les points extremum correspondent aux points où le signe de la dérivée change - les zéros de la dérivée indiqués sur le graphique. La dérivée disparaît aux points −13, −11, −9, −7. Sur le segment [−14 ; 2] la fonction comporte 4 points extremum. Réponse : 4.

La figure montre un graphique de la fonction y=f(x) définie sur l'intervalle (−2 ; 12). Trouver la somme des points extremum de la fonction f(x). Solution. La fonction donnée a des maxima aux points 1, 4, 9, 11 et des minima aux points 2, 7, 10. Par conséquent, la somme des points extrêmes est 1 + 4 + 9 + 11 + 2 + 7 + 10 = 44. Réponse : 44.

La figure montre un graphique de la fonction y=f(x) et une tangente à celle-ci au point d'abscisse x 0. Trouver la valeur de la dérivée de la fonction f(x) au point x 0 .

La figure montre un graphique de la fonction y=f(x) et une tangente à celle-ci au point d'abscisse x 0. Trouver la valeur de la dérivée de la fonction f(x) au point x 0 . Solution. La valeur de la dérivée au point de tangence est égale à la pente de la tangente, qui à son tour égal à la tangente l'angle d'inclinaison de cette tangente à l'axe des abscisses. Construisons un triangle avec des sommets aux points A (2; −2), B (2; 0), C (−6; 0). L'angle d'inclinaison de la tangente à l'axe des abscisses sera égal à l'angle, adjacent à l'angle ACB

La figure montre un graphique de la fonction y = f(x) et une tangente à ce graphique au point d'abscisse égale à 3. Trouver la valeur de la dérivée de cette fonction au point x = 3. Pour résoudre, on utilise le signification géométrique de la dérivée : la valeur de la dérivée de la fonction en ce point est égale à la pente de la tangente au graphique de cette fonction tracé en ce point. L'angle tangentiel est égal à la tangente de l'angle entre la tangente et la direction positive de l'axe des x (tg α). Angle α = β, sous forme d'angles transversaux avec des lignes parallèles y=0, y=1 et une sécante-tangente. Pour le triangle ABC

La figure montre le graphique de la fonction y=f(x) et la tangente à celle-ci au point d'abscisse x 0. Trouver la valeur de la dérivée de la fonction f(x) au point x 0 .

La figure montre le graphique de la fonction y=f(x) et la tangente à celle-ci au point d'abscisse x 0. Trouver la valeur de la dérivée de la fonction f(x) au point x 0 . D'après les propriétés de la tangente y=f ′ (x 0)⋅x+b, b=const La figure montre que la tangente à la fonction f(x) au point x 0 passe par les points (-3;2 ), (5,4) . On peut donc créer un système d'équations

Sources http://reshuege.ru/

(Fig. 1)

Figure 1. Graphique dérivé

Propriétés du graphique dérivé

1. À intervalles croissants, la dérivée est positive. Si la dérivée à un certain point d'un certain intervalle a valeur positive, alors le graphique de la fonction augmente sur cet intervalle.
2. A intervalles décroissants, la dérivée est négative (avec un signe moins). Si la dérivée à un certain point d'un certain intervalle a Sens négatif, alors le graphique de la fonction diminue sur cet intervalle.
3. La dérivée au point x est égale à la pente de la tangente tracée au graphique de la fonction au même point.
4. Aux points maximum et minimum de la fonction, la dérivée est égale à zéro. La tangente au graphique de la fonction en ce point est parallèle à l'axe OX.

Exemple 1

A l'aide du graphique (Fig. 2) de la dérivée, déterminez à quel point du segment [-3 ; 5] la fonction est maximale.

Figure 2. Graphique dérivé

Solution : Sur ce segment, la dérivée est négative, ce qui signifie que la fonction décroît de gauche à droite et que la plus grande valeur est du côté gauche au point -3.

Exemple 2

A l'aide du graphique (Fig. 3) de la dérivée, déterminez le nombre de points maximum sur le segment [-11 ; 3].

Figure 3. Graphique dérivé

Solution : Les points maximum correspondent aux points où le signe de la dérivée passe du positif au négatif. Sur cet intervalle, la fonction change de signe du plus au moins deux fois - au point -10 et au point -1. Cela signifie que le nombre maximum de points est de deux.

Exemple 3

A l'aide du graphique (Fig. 3) de la dérivée, déterminez le nombre de points minimum dans le segment [-11 ; -1].

Solution : Les points minimaux correspondent aux points où le signe de la dérivée passe du négatif au positif. Sur ce segment, un tel point n'est que de -7. Cela signifie que le nombre minimum de points sur un segment donné est de un.

Exemple 4

A l'aide du graphique (Fig. 3) de la dérivée, déterminez le nombre de points extremum.

Solution : Les points extrêmes sont à la fois les points minimum et maximum. Trouvons le nombre de points auxquels la dérivée change de signe.

La droite y=3x+2 est tangente au graphique de la fonction y=-12x^2+bx-10. Trouvez b, étant donné que l'abscisse du point tangent est inférieure à zéro.

Solution

Soit x_0 l'abscisse du point du graphe de la fonction y=-12x^2+bx-10 par lequel passe la tangente à ce graphe.

La valeur de la dérivée au point x_0 est égale à la pente de la tangente, soit y"(x_0)=-24x_0+b=3. Par contre, le point de tangence appartient simultanément au graphe du fonction et la tangente, c'est-à-dire -12x_0^2+bx_0-10= 3x_0+2 Nous obtenons un système d'équations. \begin(cases) -24x_0+b=3,\\-12x_0^2+bx_0-10=3x_0+2. \end(cas)

En résolvant ce système, nous obtenons x_0^2=1, ce qui signifie soit x_0=-1, soit x_0=1. D'après la condition d'abscisse, les points tangents sont inférieurs à zéro, donc x_0=-1, alors b=3+24x_0=-21.

Répondre

Condition

La figure montre un graphique de la fonction y=f(x) (qui est une ligne brisée composée de trois segments droits). À l’aide de la figure, calculez F(9)-F(5), où F(x) est l’une des primitives de la fonction f(x).

Solution

D'après la formule de Newton-Leibniz, la différence F(9)-F(5), où F(x) est l'une des primitives de la fonction f(x), est égale à l'aire du trapèze curviligne limité par le graphique de la fonction y=f(x), droites y=0 , x=9 et x=5. À partir du graphique, nous déterminons que le trapèze courbe indiqué est un trapèze de bases égales à 4 et 3 et de hauteur 3.

Sa superficie est égale \frac(4+3)(2)\cdot 3=10.5.

Répondre

Source : « Mathématiques. Préparation à l'examen d'État unifié 2017. Niveau de profil" Éd. F. F. Lysenko, S. Yu. Kulabukhova.

Condition

La figure montre un graphique de y=f"(x) - la dérivée de la fonction f(x), définie sur l'intervalle (-4 ; 10). Trouvez les intervalles de la fonction décroissante f(x). Dans votre réponse, indiquer la longueur du plus grand d'entre eux.

Solution

Comme on le sait, la fonction f(x) décroît sur les intervalles en chaque point dont la dérivée f"(x) est inférieure à zéro. Considérant qu'il est nécessaire de trouver la longueur du plus grand d'entre eux, trois de ces intervalles sont se distingue naturellement de la figure : (-4 ; -2) ; (0 ; 3) ;

La longueur du plus grand d'entre eux - (5 ; 9) est de 4.

Répondre

Source : « Mathématiques. Préparation à l'examen d'État unifié 2017. Niveau profil." Éd. F. F. Lysenko, S. Yu. Kulabukhova.

Condition

La figure montre un graphique de y=f"(x) - la dérivée de la fonction f(x), définie sur l'intervalle (-8 ; 7). Trouvez le nombre de points maximum de la fonction f(x) appartenant à l'intervalle [-6; -2].

Solution

Le graphique montre que la dérivée f"(x) de la fonction f(x) change de signe de plus à moins (à ces points il y aura un maximum) en exactement un point (entre -5 et -4) de l'intervalle [ -6; -2 ] Il y a donc exactement un point maximum dans l'intervalle [-6; -2].

Répondre

Source : « Mathématiques. Préparation à l'examen d'État unifié 2017. Niveau profil." Éd. F. F. Lysenko, S. Yu. Kulabukhova.

Condition

La figure montre un graphique de la fonction y=f(x), définie sur l'intervalle (-2 ; 8). Déterminer le nombre de points auxquels la dérivée de la fonction f(x) est égale à 0.

Solution

L'égalité de la dérivée en un point à zéro signifie que la tangente au graphique de la fonction tracée en ce point est parallèle à l'axe Ox. Par conséquent, nous trouvons des points où la tangente au graphique de la fonction est parallèle à l'axe Ox. Sur ce graphique, ces points sont des points extremum (points maximum ou minimum). Comme vous pouvez le constater, il y a 5 points extrêmes.

Répondre

Source : « Mathématiques. Préparation à l'examen d'État unifié 2017. Niveau profil." Éd. F. F. Lysenko, S. Yu. Kulabukhova.

Condition

La droite y=-3x+4 est parallèle à la tangente au graphique de la fonction y=-x^2+5x-7. Trouvez l'abscisse du point tangent.

Solution

Le coefficient angulaire de la droite du graphique de la fonction y=-x^2+5x-7 en un point arbitraire x_0 est égal à y"(x_0). Mais y"=-2x+5, ce qui signifie y" (x_0)=-2x_0+5. Angulaire le coefficient de la ligne y=-3x+4 spécifié dans la condition est égal à -3. pistes. On trouve donc une valeur de x_0 telle que =-2x_0 +5=-3.

On obtient : x_0 = 4.

Répondre

Source : « Mathématiques. Préparation à l'examen d'État unifié 2017. Niveau profil." Éd. F. F. Lysenko, S. Yu. Kulabukhova.

Condition

La figure montre un graphique de la fonction y=f(x) et les points -6, -1, 1, 4 sont marqués en abscisse. En lequel de ces points la dérivée est-elle la plus petite ? Veuillez indiquer ce point dans votre réponse.

Le problème B9 donne le graphique d’une fonction ou d’une dérivée à partir de laquelle vous devez déterminer l’une des quantités suivantes :

1. La valeur de la dérivée à un moment donné x 0,
2. Points maximum ou minimum (points extremum),
3. Intervalles de fonctions croissantes et décroissantes (intervalles de monotonie).

Les fonctions et dérivées présentées dans ce problème sont toujours continues, ce qui rend la solution beaucoup plus facile. Malgré le fait que la tâche appartient à la section analyse mathematique, c'est tout à fait à la portée des étudiants, même les plus faibles, puisqu'aucune connaissance théorique approfondie n'est requise ici.

Pour trouver la valeur de la dérivée, des points extrêmes et des intervalles de monotonie, il existe des algorithmes simples et universels - ils seront tous discutés ci-dessous.

Lisez attentivement les conditions du problème B9 pour éviter de commettre des erreurs stupides : parfois vous tombez sur des textes assez longs, mais conditions importantes, qui influencent le cours de la décision, il y en a peu.

Calcul de la valeur dérivée. Méthode en deux points

Si le problème est donné un graphique d'une fonction f(x), tangente à ce graphique en un certain point x 0, et qu'il est nécessaire de trouver la valeur de la dérivée à ce point, l'algorithme suivant est appliqué :

1. Trouvez deux points « adéquats » sur le graphique tangent : leurs coordonnées doivent être entières. Notons ces points comme A (x 1 ; y 1) et B (x 2 ; y 2). Notez correctement les coordonnées - c'est un point clé de la solution, et toute erreur ici entraînera une réponse incorrecte.
2. Connaissant les coordonnées, il est facile de calculer l'incrément de l'argument Δx = x 2 − x 1 et l'incrément de la fonction Δy = y 2 − y 1 .
3. Enfin, on retrouve la valeur de la dérivée D = Δy/Δx. En d'autres termes, vous devez diviser l'incrément de la fonction par l'incrément de l'argument - et ce sera la réponse.

Notons encore une fois : les points A et B doivent être recherchés précisément sur la tangente, et non sur le graphe de la fonction f(x), comme cela arrive souvent. La ligne tangente contiendra nécessairement au moins deux de ces points - sinon le problème ne sera pas formulé correctement.

Considérez les points A (−3 ; 2) et B (−1 ; 6) et trouvez les incréments :
Δx = x 2 − x 1 = −1 − (−3) = 2 ; Δy = y 2 − y 1 = 6 − 2 = 4.

Trouvons la valeur de la dérivée : D = Δy/Δx = 4/2 = 2.

Tâche. La figure montre un graphique de la fonction y = f(x) et une tangente à celle-ci au point d'abscisse x 0. Trouver la valeur de la dérivée de la fonction f(x) au point x 0 .

Considérez les points A (0 ; 3) et B (3 ; 0), trouvez les incréments :
Δx = x 2 − x 1 = 3 − 0 = 3 ; Δy = y 2 − y 1 = 0 − 3 = −3.

On trouve maintenant la valeur de la dérivée : D = Δy/Δx = −3/3 = −1.

Tâche. La figure montre un graphique de la fonction y = f(x) et une tangente à celle-ci au point d'abscisse x 0. Trouver la valeur de la dérivée de la fonction f(x) au point x 0 .

Considérez les points A (0 ; 2) et B (5 ; 2) et trouvez les incréments :
Δx = x 2 − x 1 = 5 − 0 = 5 ; Δy = y 2 − y 1 = 2 − 2 = 0.

Reste à trouver la valeur de la dérivée : D = Δy/Δx = 0/5 = 0.

A partir du dernier exemple, on peut formuler une règle : si la tangente est parallèle à l'axe OX, la dérivée de la fonction au point de tangence est nulle. Dans ce cas, vous n’avez même pas besoin de compter quoi que ce soit : il suffit de regarder le graphique.

Calcul des points maximum et minimum

Parfois, au lieu d'un graphique d'une fonction, le problème B9 donne un graphique de la dérivée et nécessite de trouver le point maximum ou minimum de la fonction. Dans cette situation, la méthode en deux points est inutile, mais il existe un autre algorithme encore plus simple. Tout d'abord, définissons la terminologie :

1. Le point x 0 est appelé le point maximum de la fonction f(x) si dans un certain voisinage de ce point l'inégalité suivante est vraie : f(x 0) ≥ f(x).
2. Le point x 0 est appelé le point minimum de la fonction f(x) si dans un certain voisinage de ce point l'inégalité suivante est vraie : f(x 0) ≤ f(x).

Afin de trouver les points maximum et minimum à partir du graphique dérivé, suivez simplement ces étapes :

1. Redessinez le graphique dérivé en supprimant toutes les informations inutiles. Comme le montre la pratique, les données inutiles ne font qu'interférer avec la décision. Par conséquent, nous marquons les zéros de la dérivée sur l'axe des coordonnées - et c'est tout.
2. Découvrez les signes de la dérivée sur les intervalles entre zéros. Si pour un point x 0 on sait que f'(x 0) ≠ 0, alors seules deux options sont possibles : f'(x 0) ≥ 0 ou f'(x 0) ≤ 0. Le signe de la dérivée est facile à déterminer à partir du dessin original : si le graphe dérivé se situe au-dessus de l'axe OX, alors f'(x) ≥ 0. Et vice versa, si le graphe dérivé se situe en dessous de l'axe OX, alors f'(x) ≤ 0.
3. Nous vérifions à nouveau les zéros et les signes de la dérivée. Là où le signe passe de moins à plus, c'est le point minimum. A l’inverse, si le signe de la dérivée passe du plus au moins, c’est le point maximum. Le comptage se fait toujours de gauche à droite.

Ce schéma ne fonctionne que pour les fonctions continues – il n’y en a pas d’autres dans le problème B9.

Tâche. La figure montre un graphique de la dérivée de la fonction f(x) définie sur l'intervalle [−5; 5]. Trouvez le point minimum de la fonction f(x) sur ce segment.

Débarrassons-nous des informations inutiles et ne laissons que les limites [−5; 5] et les zéros de la dérivée x = −3 et x = 2,5. On note également les signes :

Évidemment, au point x = −3, le signe de la dérivée passe de moins à plus. C'est le point minimum.

Tâche. La figure montre un graphique de la dérivée de la fonction f(x) définie sur l'intervalle [−3; 7]. Trouvez le point maximum de la fonction f(x) sur ce segment.

Redessinons le graphique en ne laissant que les limites [−3; 7] et les zéros de la dérivée x = −1,7 et x = 5. Notons les signes de la dérivée sur le graphique résultant. Nous avons:

Évidemment, au point x = 5, le signe de la dérivée passe du plus au moins - c'est le point maximum.

Tâche. La figure montre un graphique de la dérivée de la fonction f(x), définie sur l'intervalle [−6; 4]. Trouver le nombre de points maximum de la fonction f(x) appartenant au segment [−4; 3].

Des conditions du problème il résulte qu'il suffit de considérer uniquement la partie du graphe limitée par le segment [−4 ; 3]. Par conséquent, nous construisons un nouveau graphe sur lequel nous marquons uniquement les frontières [−4 ; 3] et les zéros de la dérivée à l'intérieur. A savoir, les points x = −3,5 et x = 2. On obtient :

Sur ce graphique il n'y a qu'un seul point maximum x = 2. C'est à ce point que le signe de la dérivée passe du plus au moins.

Une petite note sur les points avec des coordonnées non entières. Par exemple, dans le dernier problème, le point x = −3,5 a été considéré, mais avec le même succès nous pouvons prendre x = −3,4. Si le problème est correctement rédigé, de tels changements ne devraient pas affecter la réponse, puisque les points « sans domicile fixe » ne participent pas directement à la résolution du problème. Bien entendu, cette astuce ne fonctionnera pas avec des points entiers.

Trouver des intervalles de fonctions croissantes et décroissantes

Dans un tel problème, comme les points maximum et minimum, il est proposé d'utiliser le graphe dérivé pour trouver les zones dans lesquelles la fonction elle-même augmente ou diminue. Tout d’abord, définissons ce que sont l’augmentation et la diminution :

1. Une fonction f(x) est dite croissante sur un segment si pour deux points quelconques x 1 et x 2 de ce segment l'énoncé suivant est vrai : x 1 ≤ x 2 ⇒ f(x 1) ≤ f(x 2) . En d’autres termes, plus la valeur de l’argument est grande, plus la valeur de la fonction est grande.
2. Une fonction f(x) est appelée décroissante sur un segment si pour deux points quelconques x 1 et x 2 de ce segment l'énoncé suivant est vrai : x 1 ≤ x 2 ⇒ f(x 1) ≥ f(x 2). Ceux. valeur plus élevée L’argument correspond à la plus petite valeur de la fonction.

Formulons des conditions suffisantes pour augmenter et diminuer :

1. Pour fonction continue f(x) augmente sur le segment , il suffit que sa dérivée à l'intérieur du segment soit positive, c'est à dire f'(x) ≥ 0.
2. Pour qu'une fonction continue f(x) décroisse sur le segment , il suffit que sa dérivée à l'intérieur du segment soit négative, c'est-à-dire f'(x) ≤ 0.

Acceptons ces déclarations sans preuves. Ainsi, nous obtenons un schéma pour trouver des intervalles d'augmentation et de diminution, qui est à bien des égards similaire à l'algorithme de calcul des points extremum :

1. Supprimez toutes les informations inutiles. Dans le graphique original de la dérivée, nous nous intéressons principalement aux zéros de la fonction, nous ne les laisserons donc que.
2. Marquez les signes de la dérivée aux intervalles entre les zéros. Où f’(x) ≥ 0, la fonction augmente, et où f’(x) ≤ 0, elle diminue. Si le problème impose des restrictions sur la variable x, nous les marquons en plus sur un nouveau graphique.
3. Maintenant que l'on connaît le comportement de la fonction et les contraintes, il reste à calculer la quantité requise dans le problème.

Tâche. La figure montre un graphique de la dérivée de la fonction f(x) définie sur l'intervalle [−3; 7.5]. Trouver les intervalles de diminution de la fonction f(x). Dans votre réponse, indiquez la somme des entiers compris dans ces intervalles.

Comme d'habitude, redessinons le graphique et marquons les limites [−3 ; 7,5], ainsi que les zéros de la dérivée x = −1,5 et x = 5,3. Puis on note les signes de la dérivée. Nous avons:

Puisque la dérivée est négative sur l'intervalle (− 1,5), c'est l'intervalle de fonction décroissante. Il reste à additionner tous les entiers qui se trouvent à l'intérieur de cet intervalle :
−1 + 0 + 1 + 2 + 3 + 4 + 5 = 14.

Tâche. La figure montre un graphique de la dérivée de la fonction f(x), définie sur l'intervalle [−10 ; 4]. Trouver les intervalles d'augmentation de la fonction f(x). Dans votre réponse, indiquez la longueur du plus grand d’entre eux.

Débarrassons-nous des informations inutiles. Laissons seulement les frontières [−10 ; 4] et les zéros de la dérivée, qui étaient cette fois quatre : x = −8, x = −6, x = −3 et x = 2. Marquons les signes de la dérivée et obtenons l'image suivante :

Nous nous intéressons aux intervalles de fonction croissante, c'est-à-dire tel que f'(x) ≥ 0. Il existe deux de ces intervalles sur le graphique : (−8 ; −6) et (−3 ; 2). Calculons leurs longueurs :
l 1 = − 6 − (−8) = 2 ;
l 2 = 2 − (−3) = 5.

Puisque nous devons trouver la longueur du plus grand des intervalles, nous notons la valeur l 2 = 5 comme réponse.