Géométrie descriptive.
Lire aussi
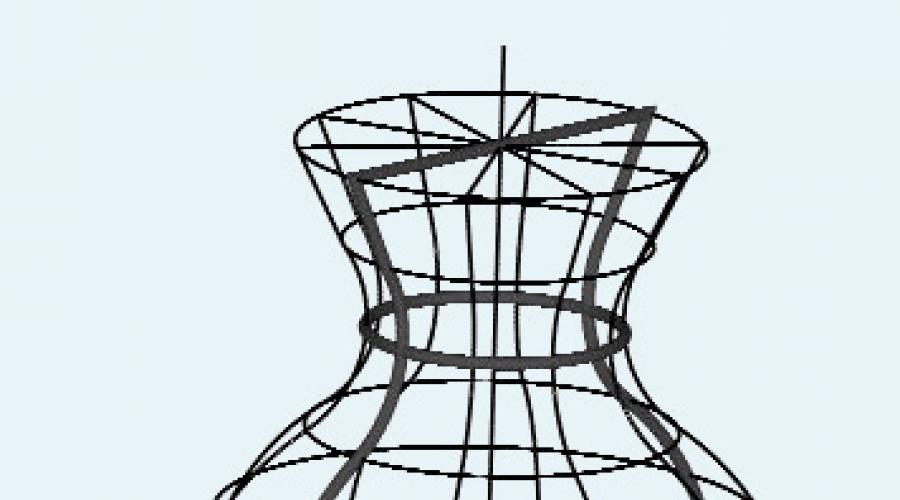
Surfaces de révolution - surfaces formées par la rotation d'une génératrice arbitraire autour d'un axe fixe (Fig. 51, a). La surface directrice de révolution est un cercle de rayon constant (cylindre) ou variable (cône, sphère). Normal - perpendiculaire à l'axe de section de rotation de toute surface de révolution, est un cercle centré sur son axe.

Riz. 51. Surface de révolution : a - lignes principales sur la surface de révolution ; b - représentation de la surface de révolution sous forme de réseau
Les guides sont aussi appelés surfaces parallèles de révolution. Les plans des parallèles sont perpendiculaires à l'axe de la surface. Le plus grand des parallèles s'appelle l'équateur de la surface, le plus petit s'appelle la gorge. Les plans passant par l'axe de la surface de révolution sont appelés méridiens et les lignes le long desquelles ils coupent la surface sont appelées méridiens. La surface de révolution peut être représentée par des parallèles ou des méridiens de la surface, ainsi qu'un réseau constitué de parallèles et de méridiens (Fig. 51, b).
Une surface de révolution est dite fermée si la section méridienne de la surface est une ligne courbe fermée qui coupe l'axe de la surface en deux points.
Lorsqu'une courbe algébrique plane ou spatiale d'ordre n tourne autour de l'axe, il se forme, dans le cas général, une surface algébrique de révolution d'ordre 2. Si une courbe de second ordre tourne autour de son axe, alors elle forme une surface de second ordre.
Selon le type de génératrice, il existe :
Surfaces toriques – surfaces formées par la rotation d'un cercle ou d'un arc de cercle :




Riz. 52. Surfaces toriques : a - sphère ; b est un tore ouvert (anneau); c est un tore fermé ; d - globoïde
- Sphère formé en faisant tourner un cercle autour d'un axe passant par son centre (Fig. 52, a).
- Thor se forme en faisant tourner un cercle autour d'un axe situé dans le plan de ce cercle et ne passant pas par son centre (un tore est une surface du quatrième ordre). Distinguer tore ouvert, formé par la rotation d'un cercle autour d'un axe qui ne coupe pas la génératrice (Fig. 52, b) et tore fermé, formé par la rotation d'un cercle autour d'un axe qui coupe le cercle générateur ou le touche (Fig. 52, c).
- Globoïde est formé en faisant tourner un cercle de rayon suffisamment grand autour d'un axe qui ne coupe pas la génératrice (Fig. 52, d).
Ellipsoïde la rotation est formée en faisant tourner une ellipse autour de son axe. Si l'axe de rotation est pris grand axe ellipse, l'ellipsoïde de révolution est appelé allongé (Fig. 53. a), s'il est petit - comprimé ou sphéroïde (Fig. 53, b). Le globe, par exemple, a une forme proche d'un sphéroïde


Riz. 53. Surfaces de révolution : a - ellipsoïde allongé ; b - sphéroïde
Paraboloïde de révolution formé par la rotation d'une parabole autour de son axe (Fig. 54). Les paraboloïdes de révolution sont utilisés comme surface réfléchissante dans les projecteurs et les phares de voiture pour produire un faisceau lumineux parallèle.

Riz. 54. Paraboloïde de révolution
Hyperboloïde de révolution formé par la rotation d'une hyperbole. Distinguer hyperboloïde à une nappe(Fig. 55, a), formé par la rotation d'une hyperbole autour de son axe imaginaire, et hyperboloïde à deux nappes(Fig. 55, b), formé par la rotation d'une hyperbole autour de son axe réel.
- (grec, de l'hyperbole, hyperbole et eidos similarité). Surface courbe non fermée du 2ème ordre, résultant de la rotation d'une hyperbole. Dictionnaire des mots étrangers inclus dans la langue russe. Chudinov A.N., 1910. HYPERBOLOÏDE grec, de l'hyperbole, ... ... Dictionnaire des mots étrangers de la langue russe
hyperboloïde- a, M. hyperboloïde m. tapis. Surface ouverte formée en faisant tourner une hyperbole autour de l'un de ses axes. BAS 2. Ingénieur hyperboloïde Garin. Lex. Jan. 1803 : hyperboloïde ; SAN 1847 : hyperbolique/d : BAS 1954 : hyperbolique/id... Dictionnaire historique des gallicismes de la langue russe
HYPERBOLOÏDE, hyperboloïde, mâle. (tapis.). La surface formée par la rotation d'une hyperbole (en 1 valeur). Dictionnaire explicatif d'Ouchakov. DN Ouchakov. 1935 1940 ... Dictionnaire explicatif d'Ouchakov
Exist., nombre de synonymes : 2 conoïde (4) surface (32) Dictionnaire de synonymes ASIS. V.N. Trichine. 2013 ... Dictionnaire des synonymes
Hyperboloïde- Hyperboloïde à une feuille. HYPERBOLOÏDE (de l'hyperbole et de la vue grecque eidos), une surface obtenue en faisant tourner une hyperbole autour de l'un des axes de symétrie. Dans un cas, un hyperboloïde à deux nappes est formé, dans l'autre, un à une nappe ... ... Dictionnaire encyclopédique illustré
hyperboloïde- statuts hiperboloidas T sritis fizika atitikmenys: engl. vok hyperboloïde. Hyperboloïde, m rus. hyperboloïde, m pranc. hyperboloïde, m … Fizikos terminų žodynas
- (mat.) Sous ce nom, on connaît deux types de surfaces de second ordre. 1) Un sexe G. Cette surface, liée aux axes de symétrie, a l'équation x2 / a2 + y2 / b2 z2 / c2 \u003d 1. Un un sexe G. est une surface réglée et deux systèmes reposent dessus ... ... Dictionnaire encyclopédique F. Brockhaus et I.A. Efron
M. Une surface ouverte formée par la rotation d'une hyperbole [hyperbole II] autour d'un de ses axes (en géométrie). Dictionnaire explicatif d'Ephraïm. T.F. Efremova. 2000... Moderne dictionnaire Langue russe Efremova
Hyperboloïdes, hyperboloïdes, hyperboloïdes, hyperboloïdes, hyperboloïdes, hyperboloïdes, hyperboloïdes, hyperboloïdes, hyperboloïdes, hyperboloïdes, hyperboloïdes, hyperboloïdes (Source : "Paradigme accentué complet selon A. A. Zaliznyak") ... Formes de mots
Surface centrale non fermée du second ordre. Il existe deux types de G. : un G. à une feuille et un G à deux feuilles. Dans le système de coordonnées approprié (voir figure), l'équation d'un G. à une feuille a la forme : et une forme à deux feuilles : les nombres a, b et c (et segments tels ... ... Encyclopédie mathématique
Livres
- , Alexeï Tolstoï. Le livre comprend des romans de science-fiction d'A. N. Tolstoï, créés dans les années 20 du siècle dernier ...
- Ingénieur hyperboloïde Garin. Aelita, Alexeï Tolstoï. Le roman "L'hyperboloïde de l'ingénieur Garin" et l'histoire "Aelita" ont marqué le début de la littérature de science-fiction soviétique. Ils diffèrent en ce que des thèmes fantastiques sont donnés en combinaison avec…
Chapitre VI. Les surfaces courbes et les corps de révolution les plus simples.
§ 75*. Surfaces de révolution
1. Laissez entrer dans l'avion R courbe L et une ligne droite je. La surface obtenue en faisant tourner la courbe L autour d'une droite je, est appelé surface de révolution.
Laissez la courbe L se situer dans le plan oh(Fig. 216) et a l'équation
y=f(X), X [un; b]. (1)
On retrouve l'équation de la surface, qui s'obtient en faisant tourner la courbe L autour de l'axe Oh(Fig. 217).

Évidemment, le point M de coordonnées (x; y; z), où X [un; b], appartient à la surface de révolution recherchée si et seulement si
√y 2 +z 2 =|F(X)|.
En effet, les points ( X; y; z) et ( X; F(X); 0) reposent sur le même cercle centré au point ( X; 0; 0).
Ainsi, l'équation de la surface obtenue en faisant tourner la courbe (1) autour de l'axe Oh, a la forme
y 2 +z 2 = (F(X)) 2 , X [un; b]. (2)
Notez que l'équation (2) est obtenue à partir de l'équation (1) comme suit :
les deux membres de l'équation (1) sont au carré et y 2 est remplacé par y 2 +z 2 ,
En particulier, si la courbe L est donnée par l'équation
y 2 = F( X), (3)
puis l'équation de la surface obtenue en faisant tourner cette courbe autour de l'axe Oh, a la forme
y 2 +z 2 = F( X) (4)
c'est-à-dire juste y 2 est remplacé par y 2 +z 2 .
2. La surface obtenue en faisant tourner une ellipse autour de l'un de ses axes s'appelle ellipsoïde de révolution.
Laissez dans l'avion oh l'ellipse est donnée par l'équation
 (5)
(5)
Composons l'équation de la surface obtenue en la faisant tourner autour de l'axe Oh. L'équation de l'ellipse (5) se réduit à la forme (3), donc, pour obtenir l'équation de l'ellipsoïde de rotation, il suffit dans l'équation (5) y 2 remplacer par y 2 +z 2. Après le remplacement, on obtient
![]() (6)
(6)
Cette équation s'écrit généralement comme suit :
![]()
À un > b l'équation (6) définit un ellipsoïde de révolution étendu le long de l'axe Oh(Fig. 218), avec un< b l'équation (6) définit un ellipsoïde de révolution comprimé selon l'axe Oh(Fig. 219), et quand un = b il définit la portée.

Tache 1. Ellipse avec demi-axes b= 6 et un= 4 et centré à l'origine tourne autour de son petit axe, coïncidant avec l'axe Oh. Écrivez une équation pour la surface décrite par l'ellipse lors de sa rotation.
Écrivons une équation pour cette ellipse :
![]()
En remplaçant dans cette équation y 2 sur le y 2 +z 2 , on obtient l'équation recherchée de l'ellipsoïde de révolution :
3. La surface obtenue en faisant tourner une hyperbole autour de l'un de ses axes s'appelle hyperboloïde de révolution. Lorsqu'une hyperbole est tournée autour de son axe réel, un hyperboloïde de révolution à deux nappes est obtenu (Fig. 220), et lorsqu'une hyperbole est tournée autour de son axe imaginaire, un hyperboloïde de révolution à une nappe est obtenu (Fig. 221) .

Laissez dans l'avion oh l'hyperbole est donnée par l'équation
Composons l'équation de la surface obtenue en faisant tourner l'hyperbole autour de son axe réel Oh. L'équation hyperbolique (7) se réduit à la forme (3) ; donc, pour obtenir l'équation de la surface d'un hyperboloïde à deux nappes de rotation, il suffit dans l'équation d'hyperbole (7) y 2 remplacer par y 2 +z 2. Après le remplacement, on obtient
![]() (8)
(8)
Lorsque l'hyperbole (7) tourne autour de son axe imaginaire, dans l'équation (7) X 2 remplacer par X 2 +z 2 ; après remplacement nous obtenons
![]() (9)
(9)
Tâche 2. Hyperbole avec demi-axes un= 3 et b= 4 tourne autour de son axe imaginaire, qui est le même que l'axe UO. Le centre de l'hyperbole coïncide avec l'origine. Ecrire une équation de la surface obtenue en faisant tourner cette hyperbole.
Écrivons l'équation de l'hyperbole :
![]()
Pour obtenir l'équation de l'hyperboloïde de révolution, dans l'équation de l'hyperbole X 2 sera remplacé par X 2 +z 2. Après le remplacement, on obtient
4. La surface obtenue en faisant tourner une parabole autour de son axe de symétrie est appelée paraboloïde de révolution(Fig. 222).

Laissez dans l'avion oh la parabole est donnée par l'équation
X 2 = 2RU. (10)
Pour obtenir l'équation de la surface de révolution, il faut dans l'équation (10) X 2 sera remplacé par X 2 +z 2 ; après remplacement nous obtenons
X 2 +z 2 = 2py.
On note une propriété remarquable de cette surface. Si la surface interne du paraboloïde de révolution est rendue miroir et qu'une source lumineuse est placée dans son foyer (le foyer du paraboloïde de révolution est le foyer de la parabole tournée), alors tous les rayons lumineux réfléchis par la surface du paraboloïde, ira parallèlement à l'axe du paraboloïde.
Cette propriété est largement utilisée dans la fabrication de dispositifs réfléchissants (projecteurs, phares de voitures, projecteurs de films et autres dispositifs).
Tâche 3.Écrire une équation pour la surface obtenue en faisant tourner une parabole y 2 = 2X autour de l'axe Oh.
Formuler l'équation d'un paraboloïde de révolution obtenu en faisant tourner une parabole autour d'un axe Oh, nécessaire dans l'équation y 2 = 2X remplacer y 2 sur y 2 +z 2, après le remplacement, nous obtenons
y 2 +z 2 = 2X.
5. Si vous faites pivoter une ligne droite parallèle à n'importe quel axe de coordonnées autour de cet axe, vous obtenez surface cylindrique circulaire.
Laissez une ligne droite se trouver dans le plan yOz et ayant l'équation y = un. Il est facile de voir que la surface de révolution de cette droite autour de l'axe onces a l'équation
X 2 +y 2 = un 2
Cette surface cylindrique est représentée sur la Fig. 223.

Tâche 4.Écrire une équation pour une surface cylindrique obtenue en faisant tourner une droite à= 3 couché dans l'avion oh autour de l'axe Oh.
Dans l'équation y 2 = 3 2 remplacer y 2 sur y 2 + z 2 , on obtient alors
y 2 + z 2 = 9.
6. Laissez une ligne droite se trouvant dans le plan yOz et passant par l'origine :
y=kz, k =/= 0.
Évidemment, l'équation de la surface de révolution de cette droite autour de l'axe onces a la forme
X 2 + y 2 = k 2 z 2 .
L'équation résultante est l'équation de la surface de révolution désirée, qui s'appelle surface conique circulaire(Fig. 224).

Tâche 5. Ecrire l'équation de la surface de révolution d'une droite 2 X = 3à, z=0 autour de l'axe Oh.
De l'équation 3 à = 2X, en utilisant la formule (2), on trouve 9( y 2 + z 2) = 4X 2. C'est l'équation requise.
Parmi les surfaces courbes - réglées et non linéaires - il existe des surfaces de révolution largement utilisées dans la pratique. Surface de révolution ils appellent la surface obtenue à partir de la rotation de toute génératrice autour d'une droite fixe - axes de surface 1).
La surface de révolution peut être spécifiée par la génératrice et la position de l'axe. Sur la fig. 330 montre une telle surface. Ici la génératrice est la courbe ABC, l'axe est la droite OO 1 située dans le même plan avec ABC. Chaque point de la génératrice décrit un cercle. Ainsi, un plan perpendiculaire à l'axe d'une surface de révolution coupe cette surface selon un cercle. De tels cercles
1) Lors de la formation de la surface de révolution, l'axe est immobile.
ça s'appelle parallèles. Le plus grand des parallèles est appelé équateur, le plus petit - gorge surfaces 1).
Le plan passant par l'axe de la surface de révolution est appelé plan méridien. La ligne d'intersection de la surface de révolution par le plan méridien est appelée méridien superficiel.
Peut être appelé sommet de la surface de révolution le point d'intersection du méridien de cette surface avec son axe, si l'intersection ne forme pas un angle droit.
Si l'axe de la surface de révolution est parallèle au carré. π 2, puis la méridienne située dans un plan parallèle au carré. π 2 est appelé premier méridien. Dans cette position, la méridienne principale est projetée sur le carré. ts 2 sans distorsion. Si l'axe de la surface de révolution est perpendiculaire au carré. π 1 alors la projection horizontale de la surface a un contour en forme de cercle. La plus appropriée du point de vue des images est la perpendicularité de l'axe de la surface de révolution au carré. π 1 ou à π 2, ou à π 3.
Certaines surfaces de révolution sont des cas particuliers des surfaces considérées au § 50. Ce sont : 1) un cylindre de révolution, 2) un cône de révolution, 3) un hyperboloïde à une nappe de révolution, 4) un ellipsoïde de révolution, 5 ) un paraboloïde de révolution, 6) un hyperboloïde à deux nappes de révolution.
Pour cylindre et cône de révolution les méridiens sont des lignes droites - dans le premier cas, parallèles à l'axe et équidistantes de celui-ci, dans le second cas, croisant l'axe au même point au même angle avec l'axe. Le cylindre et le cône de révolution étant des surfaces qui s'étendent à l'infini dans la direction de leurs génératrices, ils sont généralement limités dans les images par quelques lignes, par exemple, des traces de ces surfaces sur les plans de projection ou l'une des parallèles. Connu par stéréométrie cylindre circulaire droit et droit cône circulaire délimité par une surface de révolution et des plans perpendiculaires à son axe. Les méridiens d'un tel cylindre sont des rectangles et les cônes sont des triangles.
Pour hyperboloïde de révolution la méridienne est une hyperbole, et si l'axe réel de l'hyperbole sert d'axe de rotation, alors un hyperboloïde de révolution à deux nappes est formé ; si nous faisons tourner l'hyperbole autour de son axe imaginaire, alors simple cavité.
Hyperboloïde de révolution à une feuille peut également être formé par la rotation d'une droite dans le cas si la génératrice et l'axe de rotation sont des lignes obliques.
Sur la fig. 331 montre un hyperboloïde de révolution à une nappe formé par la rotation de la droite AB autour de l'axe spécifié et délimité par deux parallèles ; le cercle tiré du centre 0 1 est le col de la surface.
Sur un hyperboloïde de révolution à une feuille, des générateurs rectilignes peuvent être appliqués dans deux directions, par exemple, comme le montre la Fig. 331, et avec une pente en verso, au même angle avec l'axe.
En plus des lignes droites (paires), cette surface peut également contenir des hyperboles, des paraboles, des ellipses et des cercles.
1) Plus précisément, l'équateur est appelé celui des parallèles, qui est plus grand que les parallèles qui lui sont adjacents de part et d'autre de celui-ci, considéré jusqu'à la première gorge ; gorge - le plus petit des parallèles voisins au premier équateur. Ainsi, la surface de révolution peut avoir plusieurs équateurs et gorges.
Sur la fig. 331 à droite montre la construction d'une projection frontale d'un hyperboloïde à une nappe de révolution selon son axe et sa génératrice. Tout d'abord, le rayon de la gorge de la surface est trouvé. Pour cela, une perpendiculaire O "1 1" est tracée à la projection horizontale de la génératrice. Cela définit la projection horizontale de la perpendiculaire commune à l'axe et à la génératrice. La valeur propre du segment, exprimée par les projections O" 1 1" et O" 1 1", est égale au rayon du col de la surface. De plus, en tournant les points avec des projections 2",2";3",3";A",A" sont affichés dans le plan α, parallèle au carré. π 2 que

permet de tracer une ligne d'esquisse de la projection frontale de l'hyperboloïde. Sa projection horizontale sera de trois cercles concentriques.
Pour le paraboloïde du méridien de révolution est une parabole, dont l'axe sert d'axe de surface.
Pour l'ellipsoïde de méridien de révolution est une ellipse. Une surface peut être formée en faisant tourner une ellipse autour de son grand axe ( ellipsoïde de révolution "prolate"- riz. 332, à gauche) ou autour de son petit axe ( ellipsoïde de révolution "comprimé"- riz, 332, à droite). Ellipsoïde de révolution - surface bornée ; il peut être montré dans son intégralité. Une sphère peut également être entièrement représentée. Pour une sphère, l'équateur et les méridiens sont des cercles égaux.
Faisons encore une fois attention au fait que des surfaces de révolution telles qu'un cylindre, un cône et un hyperboloïde à une feuille sont réglées, c'est-à-dire qu'elles peuvent être
former en faisant tourner une ligne droite 1). Mais un ellipsoïde, un paraboloïde et un hyperboloïde à deux nappes se forment lors de la rotation non pas d'une droite, mais d'une ellipse, d'une parabole et d'une hyperbole, et l'axe de rotation est choisi de manière à ce que la courbe génératrice soit située symétriquement par rapport à cette axe. La même chose peut être dite à propos d'un hyperboloïde de révolution à une feuille s'il est formé à la suite de la rotation de l'hyperbole autour de son axe imaginaire.
Puisque l'axe de rotation est choisi pour coïncider avec l'axe de symétrie de l'ellipse, de la parabole, de l'hyperbole, alors l'ellipse et l'hyperbole forment chacune deux surfaces, puisqu'elles ont deux axes de symétrie, et la parabole - une surface, puisqu'elle a un axe de symétrie, Par conséquent, chacune des surfaces formées n'est obtenue qu'en tournant dans un sens. Pendant ce temps, une sphère, qui peut être considérée comme un ellipsoïde avec des axes majeurs et mineurs égaux de la génératrice de l'ellipse, qui dans ce cas se transforme en cercle, peut être formée par rotation de plus d'un

façon : la génératrice du cercle est symétrique par rapport à chacun de ses diamètres.
Lorsqu'un cercle (ou son arc) tourne autour d'un axe qui se trouve dans le plan de ce cercle, mais ne passe pas par son centre, une surface est obtenue avec le nom torus 2). C'est aussi le nom d'un corps délimité par un tore - une surface.
Il y a (fig. 333) :
1) un tore ouvert, sinon un anneau circulaire,
2) fermé,
3) auto-sécante.
Sur la fig. 333 ils sont représentés dans la position la plus simple : l'axe du tore est perpendiculaire au plan de projection, en l'occurrence au carré. pi 1 .
La génératrice pour un tore ouvert et fermé est un cercle, pour un tore auto-sécant, un arc de cercle. Les sphères peuvent être inscrites dans des tores ouverts et fermés. Un tore peut être vu comme une surface enveloppant des sphères identiques dont les centres sont sur un cercle.
Le tore a deux systèmes de sections circulaires : dans des plans perpendiculaires à son axe et dans des plans passant par l'axe du tore 3).
1) Le modèle de disposition des générateurs rectilignes d'un hyperboloïde de révolution à une nappe est appliqué dans la conception connue sous le nom de "tour Choukhov". V. G. Shukhov (1853 - 1939) - l'un des ingénieurs russes les plus remarquables. La "tour Shukhov" est utilisée dans la construction de mâts radio, de châteaux d'eau, etc.
2) Fr. déchiré (du tore (lat.) - renflement, nœud) - un rebord annulaire sur une colonne.
3) Il existe un troisième système de sections circulaires d'un tore ouvert, qui n'est pas considéré dans le livre.
La surface, appelée tore, est très courante en génie mécanique et en architecture. Sur la fig. 334 à gauche est une pièce dont la surface de révolution contient un tore autosécant et un tore ouvert, et à droite sur la même figure est représentée schématiquement

la surface de transition d'une voûte cylindrique à une autre, ayant la forme d'un tore fermé d'axe OO 1
Parmi les surfaces de révolution, nous mentionnons également caténoïde une). Cette surface se forme lors d'une rotation complète caténaire 2) autour d'un axe horizontal situé avec lui dans le même plan.
La position d'un point sur la surface de révolution est déterminée par le cercle passant par ce point sur la surface de révolution.
Mais cela n'exclut pas la possibilité d'utiliser des génératrices rectilignes dans le cas de surfaces réglées de révolution, comme le montre la Fig. 314 pour cylindres et cônes généraux.
Sur la fig. 330 montre l'utilisation d'une parallèle pour construire la projection d'un point appartenant à une surface de révolution donnée. Si la projection M est donnée, alors nous dessinons la projection frontale F "F" 1 du parallèle, puis avec le rayon R \u003d O "1 F" nous dessinons un cercle - la projection horizontale du parallèle - et dessus on retrouve la projection M". Si la projection M" était donnée, il faudrait alors tracer un cercle de rayon R \u003d O" 1 F ", trouver F" au point F "et dessiner F" F "1 - la projection frontale du parallèle sur laquelle doit se trouver la projection M". La figure 332 montre la construction des projections du point K, qui appartient à l'ellipsoïde de révolution, et sur la fig. 335 - point M, appartenant à la surface de l'anneau circulaire.
Sur la fig. 335 à droite montre comment trouver les projections de points sur la sphère. Selon la projection donnée A" du point A, la projection frontale A" a été construite ; sur la projection donnée B" on trouve la projection horizontale B" du point B, qui satisfait à la condition supplémentaire que le point B soit invisible en regardant le carré. π 2 .
Le point C est placé sur l'équateur : sa projection C" est sur le contour de la projection horizontale de la sphère, c'est-à-dire sur la projection horizontale de l'équateur. Les points K et M se situent sur le méridien principal ; ils appartiennent aux parallèles sur lequel se trouvent les points A et B. Le point D est également situé sur le méridien principal, et il est invisible si vous regardez le carré π 1.
Considérons un exemple de construction de projections de points appartenant à une surface de révolution. Qu'il soit demandé d'amener le point A, en le faisant tourner autour d'un axe donné MN, à une surface de révolution donnée (Fig. 336, a). Puisque dans ce cas l'axe de la surface de rotation et l'axe de rotation du point A sont perpendiculaires au plan des projections π 1, alors le cercle de rotation du point A est projeté sur π 1 sans distorsion, ainsi que la parallèle de la surface de révolution, qui s'obtient en croisant cette surface avec le plan de rotation du point A Le centre de rotation du point A est également situé dans ce plan - le point O (le point d'intersection de l'axe de rotation MN avec le plan de rotation α). Le reste ressort clairement du dessin. En position A 2 sur la surface, le point sera invisible sur le carré. π 2 .
2) Catena (lat.) - une chaîne.
2) Caténaire - une courbe dont la forme est prise par une chaîne suspendue à ses deux points, ou en général par un fil lourd inextensible suspendu par ses extrémités.

Supposons que la question du choix de l'axe de rotation se pose pour que de plus le point A puisse se trouver sur une surface de rotation donnée, On p. 100 une question similaire a été envisagée, mais là il fallait choisir un axe pour qu'en tournant autour de lui on puisse introduire un point dans le plan, puis on a trouvé qu'il y a une zone dans laquelle il est impossible de prendre des axes , car en tournant autour de tels axes, le point n'entrera pas en contact avec le plan. Cette zone était déterminée par un cylindre parabolique, et la parabole est apparue en considérant la position relative du point tourné et la ligne droite sur laquelle ce point aurait dû être en contact avec le plan.
Maintenant, évidemment, la question sera résolue en considérant la position relative du point A et du cercle (parallèle) sur la surface du corps de révolution,
De la fig. 336, et il s'ensuit que la projection O" du centre de rotation doit être située de telle sorte que R A ne soit pas inférieure à la distance du point O" au point le plus proche sur la projection d'un cercle de rayon r, mais si l'on prend le point O "à égales distances de A" et de la projection de cette circonférence
sti (par exemple, dans O "1 ou O" 2; voir Fig. 336.6), alors il est déjà possible d'y définir l'axe de rotation; le cercle de rotation du point A touchera le cercle de rayon r, m, e, le point A touchera la surface de révolution.
Où sont tous les points du dessin qui sont également distants du point A " et du cercle de rayon r? Ils sont situés sur l'hyperbole (riz, 336,6), pour laquelle le point A " sert d'un des foyers, le point O "1, dans lequel le segment A "1" est divisé en deux, - l'un des sommets. Si nous divisons le segment A "Z" en deux, nous obtiendrons le deuxième sommet de l'hyperbole (point O "3); le deuxième foyer sera situé au point C", c'est-à-dire au centre du cercle obtenu en croisant la surface du corps de révolution avec le plan α (Fig. 336, a).
Il résulte de ce qui précède que les points situés sur les deux branches de l'hyperbole ou entre elles peuvent être choisis chacun comme une projection horizontale de l'axe de rotation.
Il peut y avoir un cas où le point est à l'intérieur de la surface de révolution. Par conséquent, en traçant un plan de révolution passant par un point, nous obtenons une projection A "à l'intérieur de la projection d'un cercle de rayon r, le long duquel le plan de révolution du point A coupe la surface de révolution (riz, 336, c). Et cette fois il est évident que R A ne doit pas être inférieure à la distance du point O" (m, e, projection de l'axe) au point le plus proche de la projection d'un cercle de rayon r. Les positions limites des projections des axes seront maintenant situées comme des points d'une ellipse avec des foyers aux points A "et C", avec un grand axe sur la droite 1"Z", avec des sommets aux points O" 3 et O " 3. A l'intérieur de cette ellipse il ne faut pas prendre de projections des axes ; de tels axes ne permettront pas d'introduire le point A dans la surface de révolution,
Ainsi, la question de savoir comment choisir un axe de rotation pour que, en faisant tourner un point autour de lui, introduise ce point dans un plan ou dans une surface de rotation dont l'axe est parallèle à l'axe de rotation, nous conduit à une ellipse (Fig. 336, c), -parabole (Fig. 244 ), hyperbole (Fig. 336.6) comme lieux géométriques des centres de rotation.
Au moment de décider diverses tâches certaines surfaces sont utilisées comme lieux géométriques des points ou des lignes remplissant certaines conditions. Par exemple, étant donné m². α et le point K hors de ce plan ; déterminer comment ils seront situés dans le carré. α points séparés du point K par une distance r donnée (la distance r est supérieure à la distance du point K à la zone α). Dans ce cas, la solution est associée à l'utilisation d'une sphère comme lieu de points espacés du point K à une distance r. Le plan α coupera cette sphère selon un cercle, ce qui donnera la solution du problème.
S'il était nécessaire de construire en m². α sont des points qui sont à une distance r non pas d'un point, mais d'une ligne AB qui ne se trouve pas dans le carré. α, alors le lieu de tels points dans l'espace serait la surface d'un cylindre de révolution d'axe AB et de rayon r, et ceux recherchés en pl. on obtiendrait des points α sur la ligne d'intersection de ce cylindre pl. un.
Plus tard dans la Fig. 368 à droite et 401 vous pouvez voir des exemples d'utilisation de surfaces coniques de révolution comme lieu de droites passant par un point donné.
Si le problème soulève la question des points équidistants du plan donné α et du point M, alors comme lieu de ces points dans l'espace, on devrait utiliser un paraboloïde de révolution avec le foyer de la parabole au point M.
L'utilisation de certaines surfaces comme lieux géométriques n'est bien entendu pas limitée aux exemples donnés.
Questions au § 51
- Qu'est-ce qu'une surface de révolution ?
- Quelle est la surface de révolution ?
- Qu'appelle-t-on les parallèles et les méridiens sur les surfaces de révolution, l'équateur, la gorge, le méridien principal ?
- Lequel des axes de l'hyperbole sert d'axe de rotation pour la formation : a) d'un hyperboloïde de révolution à une nappe, b) d'un hyperboloïde à deux nappes ?
- Est-il possible de former un hyperboloïde de révolution à une nappe à l'aide d'une droite ?
- Quelles surfaces de révolution (sauf pour un hyperboloïde à une nappe) sont réglées ?
- Comment se forme une surface appelée tore ?
- Dans quel cas le terme « anneau circulaire » est-il utilisé pour un tore ?
- Combien de systèmes de sections circulaires possède un tore ?
- Comment déterminer la position d'un point sur une surface de révolution ?
1) Nous invitons le lecteur à dessiner un dessin et à compléter la solution de cette tâche et des suivantes.
autour de l'axe qui le coupe (autour de l'axe réel).
ré  Pour passer de l'équation de droite (43) à l'équation de la surface de révolution, on remplace X sur le
Pour passer de l'équation de droite (43) à l'équation de la surface de révolution, on remplace X sur le  , on obtient l'équation d'un hyperboloïde à deux nappes de révolution
, on obtient l'équation d'un hyperboloïde à deux nappes de révolution
 .
.
Par compression de cette surface, on obtient une surface donnée par l'équation
 .
(44)
.
(44)
Une surface qui a une équation de la forme (44) dans un système de coordonnées cartésien est appelée hyperboloïde à deux nappes. Les deux branches de l'hyperbole correspondent ici à deux parties non connectées ("cavités") de la surface, tandis que lors de la construction d'un hyperboloïde de révolution à une nappe, chaque branche de l'hyperbole décrit toute la surface (Fig. 60).
 Le cône asymptotique d'un hyperboloïde à deux nappes est défini de la même manière que pour un hyperboloïde à une nappe (Fig. 61).
Le cône asymptotique d'un hyperboloïde à deux nappes est défini de la même manière que pour un hyperboloïde à une nappe (Fig. 61).
Considérons maintenant les intersections de l'hyperboloïde à deux nappes (44) avec des plans parallèles aux plans de coordonnées.
Avion z = hà | h| < c coupe la surface (44) selon des ellipses imaginaires, pour | h| > c par réel. Si un un = b, alors ces ellipses sont des cercles, et l'hyperboloïde est un hyperboloïde de révolution. Quand | h| = c on a
 ,
,
c'est-à-dire une paire de lignes conjuguées avec un point réel (0 ; 0 ; Avec) (ou (0 ; 0 ; – Avec) respectivement).
Avions X= α et y= β coupe l'hyperboloïde (44) le long des hyperboles
 et
et  .
.
8. paraboloïde elliptique
Quand la parabole tourne X 2 = 2pz autour de son axe de symétrie, on obtient une surface d'équation
X 2 + y 2 = 2pz,
n  appelé paraboloïde de révolution. Compression au plan à= 0 prend le paraboloïde de révolution dans une surface d'équation
appelé paraboloïde de révolution. Compression au plan à= 0 prend le paraboloïde de révolution dans une surface d'équation
 .
(45)
.
(45)
Une surface qui a une telle équation dans un système de coordonnées rectangulaires cartésien est appelée paraboloïde elliptique.
L'apparence d'un paraboloïde elliptique ressort clairement de la façon dont il a été construit. Tout est situé d'un côté de l'avion z= 0, dans le demi-espace z > 0 (fig. 62). Coupes par avions z = h, h> 0 ont l'équation :


et sont des ellipses.
Coupes d'un paraboloïde elliptique (45) par plans à= 0 et X= 0 sont des paraboles
X 2 = 2un 2 z, y = 0; (46)
y 2 = 2b 2 z, X = 0. (47)
Ces paraboles sont appelées paraboles principales paraboloïde elliptique, tandis que la parabole (46) est classiquement appelée immobile, et parabole (47) – portable.
On peut donner la construction très visuelle suivante d'un paraboloïde elliptique en faisant glisser une parabole le long de l'autre (le système de coordonnées est supposé être rectangulaire).
Prenons la section du paraboloïde (45) par le plan X= α, on obtient dans ce plan contenant le repère O 0 e 2 e 3 , où O 0 = (α, 0, 0), une courbe dont l'équation sera
 ,
X
= α
,
X
= α
y 2 = 2b 2 (z – γ), X= α, (48)
où  .
.
Passons à l'avion X= α du système de coordonnées Oe 2 e 3 au système de coordonnées O′ e 2 e 3 , où O′ = (α, 0, γ) est le point d'intersection du plan X= α à parabole fixe X 2 = 2un 2 z, y = 0.
Déplacer l'origine du système O 0 e 2 e 3 au point O′, a effectué la transformation de coordonnées suivante :
y = y′, z = z′ + γ.
Suite à cette transformation, l'équation (48) prend la forme :
y 2 = 2 pz′, X = α.
La courbe (48) est la même parabole "mobile", mais transférée parallèlement à elle-même dans le plan X= α. Ce transfert peut se faire de la manière suivante. Le sommet de la parabole mobile glisse le long de la parabole fixe à partir du point O exactement O′, tandis que la parabole elle-même se déplace comme un corps rigide, restant tout le temps dans un plan parallèle au plan yOz.
Ce résultat peut être formulé sous la forme de l'assertion suivante.
Un paraboloïde elliptique est une surface décrite lorsqu'une parabole (« mobile ») (47) se déplace le long d'une autre, fixe (46), de sorte que le sommet de la parabole mobile glisse le long de la parabole fixe, et le plan et l'axe de la parabole mobile les paraboles restent parallèles à elles-mêmes tout le temps, et on suppose que les deux paraboles (mobile et fixe) font face à la concavité dans la même direction (à savoir, dans côté positif axes onces).
Notez que le paraboloïde elliptique n'a pas de générateurs rectilignes. En effet, une droite parallèle au plan xOy, ne peut couper la section du paraboloïde que par un plan z = h, et cette section, comme déjà noté, est une ellipse. Cela signifie que la droite a au plus deux points communs avec le paraboloïde.
Si la droite n'est pas parallèle au plan xOy, alors sa demi-droite appartient au demi-espace z < 0, где нет ни одной точки параболоида. Таким образом, нет прямой, которая всеми своими точками лежала бы на эллиптическом параболоиде.
9. paraboloïde hyperbolique
Par analogie avec l'équation (45), on peut écrire l'équation
 .
(49)
.
(49)
Une surface qui a une équation de la forme (49) dans un certain système de coordonnées est appelée paraboloïde hyperbolique.
 Nous étudions l'apparence d'un paraboloïde hyperbolique à l'aide de sections (Fig. 63). Section d'avion z
= h est une hyperbole, qui dans ce plan a pour équation :
Nous étudions l'apparence d'un paraboloïde hyperbolique à l'aide de sections (Fig. 63). Section d'avion z
= h est une hyperbole, qui dans ce plan a pour équation :
 ou
ou  .
.
Pour les grandes valeurs h demi-axes d'hyperbole  et
et  grand et diminue avec la diminution h. Dans ce cas, l'axe de l'hyperbole qui la coupe est parallèle au vecteur e
1 .
grand et diminue avec la diminution h. Dans ce cas, l'axe de l'hyperbole qui la coupe est parallèle au vecteur e
1 .
À h= 0 l'hyperbole dégénère en une paire de droites sécantes
 =>
=>

 ,
,
 .
.
Si un h < 0, то ось гиперболы, которая ее пересекает, параллельна вектору e 2. Les demi-arbres grandissent avec l'augmentation | h|. Le rapport des demi-axes pour toutes les hyperboles de même signe h même. Par conséquent, si nous dessinons toutes les sections d'un paraboloïde hyperbolique sur le même plan, alors nous obtenons une famille de toutes les hyperboles ayant comme asymptotes une paire de lignes sécantes avec les équations
 ,
,
 .
.
Sections d'un paraboloïde hyperbolique avec plans à= 0 et X= 0 sont deux "paraboles principales":
X 2 = 2un 2 z, y = 0 (50)
est une parabole fixe, et
y 2 = –2b 2 z, X = 0 (51)
- parabole mobile.
Ces paraboles sont tournées par concavité dans des sens opposés : fixe - "vers le haut" (c'est-à-dire dans le sens positif de l'axe onces), et le mobile - "vers le bas" (c'est-à-dire dans le sens négatif de l'axe onces). Section dans le plan X= α a dans le système de coordonnées O 0 e 2 e 3 , où O 0 = (α, 0, 0), équation
 ,
X
= α
,
X
= α
y 2 = –2b 2 (z – z 0), X= α, (52)
où  .
.
Après avoir déplacé l'origine au point O′ = (α, 0, z 0), l'équation (51) prendra la forme :
y 2 = -2 b 2 z′, X = α,
où y = y′, z = z′ + z 0 . La dernière équation montre que la courbe (52) est la même parabole mobile (51), seulement décalée parallèlement à elle-même lorsque son sommet glisse le long de la parabole fixe à partir du point O dans O′.
Cela implique l'assertion suivante. Le paraboloïde hyperbolique donné (dans un repère rectangulaire) par l'équation (49) est la surface décrite par la parabole y 2
= –2b 2 z,
X= 0 lorsqu'il se déplace le long de la parabole fixe (50) de sorte que le sommet de la parabole mobile glisse le long de la parabole fixe, et le plan et l'axe de la parabole mobile restent parallèles à eux-mêmes tout le temps, tandis que les deux paraboles à concavité se font toujours face dans des directions opposées: la parabole fixe - avec concavité "vers le haut", c'est-à-dire dans le sens positif de l'axe O  z, et mobile - "vers le bas".
z, et mobile - "vers le bas".
Il ressort de cette construction que le paraboloïde hyperbolique a la forme d'une selle.
Un paraboloïde hyperbolique, comme un hyperboloïde à une nappe, possède deux familles de génératrices rectilignes (Fig. 64). À travers chaque point d'un paraboloïde hyperbolique, il y a deux lignes droites qui se trouvent sur ce plan avec tous les points.
Trouvons les équations des générateurs rectilignes. Réécrivons l'équation (49) sous la forme
 .
.
Considérons une droite définie comme l'intersection de deux plans
 (53)
(53)

Évidemment, tout point qui satisfait les équations (53) satisfait également l'équation (49), qui est le produit des équations (53)

 .
.
Cela signifie que chaque point de la droite (53) appartient au paraboloïde hyperbolique (49).
La ligne droite est considérée de la même manière.


La droite (54) repose également en tous ses points sur le paraboloïde hyperbolique.