Lorsque la dérivée d'une fonction est positive sur le graphique. A quel point la valeur de la dérivée est-elle la plus grande ?

Dans le problème B9, un graphique d'une fonction ou d'une dérivée est donné, à partir duquel il est nécessaire de déterminer l'une des quantités suivantes :

1. La valeur de la dérivée à un certain point x 0,
2. Points hauts ou bas (points extrêmes),
3. Intervalles de fonctions croissantes et décroissantes (intervalles de monotonie).

Les fonctions et dérivées présentées dans ce problème sont toujours continues, ce qui simplifie grandement la solution. Malgré le fait que la tâche appartient à la section analyse mathematique, c'est tout à fait à la portée des étudiants, même les plus faibles, puisqu'aucune connaissance théorique approfondie n'est requise ici.

Pour trouver la valeur de la dérivée, des points extrêmes et des intervalles de monotonie, il existe des algorithmes simples et universels - tous seront discutés ci-dessous.

Lisez attentivement la condition du problème B9 pour ne pas faire de bêtises : des textes parfois assez volumineux se présentent, mais conditions importantes, qui affectent le cours de la solution, il y en a peu.

Calcul de la valeur de la dérivée. Méthode à deux points

Si l'on donne au problème un graphe de la fonction f(x), tangente à ce graphe en un point x 0 , et qu'il faut trouver la valeur de la dérivée en ce point, l'algorithme suivant est appliqué :

1. Trouver deux points "adéquats" sur le graphe tangent : leurs coordonnées doivent être entières. Notons ces points A (x 1 ; y 1) et B (x 2 ; y 2). Notez correctement les coordonnées - c'est le point clé de la solution, et toute erreur ici conduit à la mauvaise réponse.
2. Connaissant les coordonnées, il est facile de calculer l'incrément de l'argument Δx = x 2 − x 1 et l'incrément de la fonction Δy = y 2 − y 1 .
3. Enfin, on trouve la valeur de la dérivée D = Δy/Δx. En d'autres termes, vous devez diviser l'incrément de la fonction par l'incrément de l'argument - et ce sera la réponse.

Encore une fois, on note : les points A et B doivent être recherchés précisément sur la tangente, et non sur le graphe de la fonction f(x), comme c'est souvent le cas. La tangente contiendra nécessairement au moins deux de ces points, sinon le problème est mal formulé.

Considérez les points A (−3 ; 2) et B (−1 ; 6) et trouvez les incréments :
Δx \u003d x 2 - x 1 \u003d -1 - (-3) \u003d 2; Δy \u003d y 2 - y 1 \u003d 6 - 2 \u003d 4.

Trouvons la valeur de la dérivée : D = Δy/Δx = 4/2 = 2.

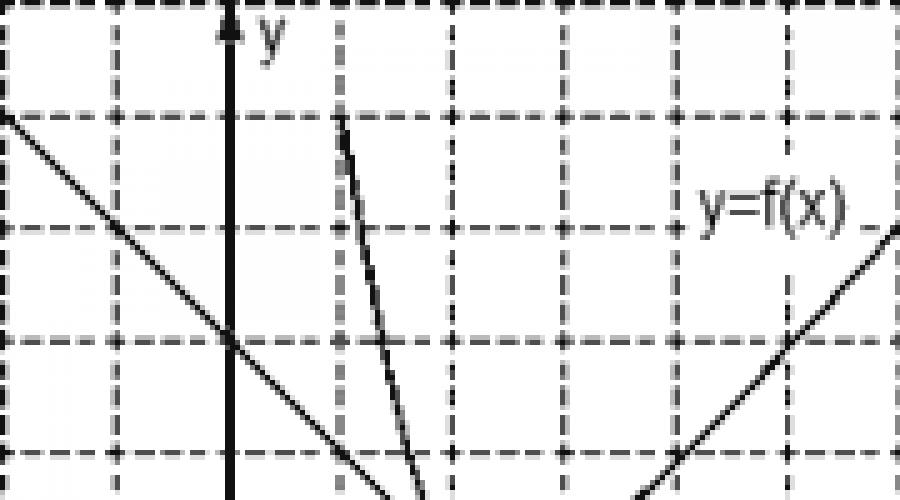
Une tâche. La figure montre le graphique de la fonction y \u003d f (x) et sa tangente au point d'abscisse x 0. Trouver la valeur de la dérivée de la fonction f(x) au point x 0 .

Considérez les points A (0 ; 3) et B (3 ; 0), trouvez les incréments :
Δx \u003d x 2 - x 1 \u003d 3 - 0 \u003d 3; Δy \u003d y 2 - y 1 \u003d 0 - 3 \u003d -3.

On trouve maintenant la valeur de la dérivée : D = Δy/Δx = −3/3 = −1.

Une tâche. La figure montre le graphique de la fonction y \u003d f (x) et sa tangente au point d'abscisse x 0. Trouver la valeur de la dérivée de la fonction f(x) au point x 0 .

Considérez les points A (0 ; 2) et B (5 ; 2) et trouvez les incréments :
Δx \u003d x 2 - x 1 \u003d 5 - 0 \u003d 5; Δy = y 2 - y 1 = 2 - 2 = 0.

Il reste à trouver la valeur de la dérivée : D = Δy/Δx = 0/5 = 0.

A partir du dernier exemple, on peut formuler la règle : si la tangente est parallèle à l'axe OX, la dérivée de la fonction au point de contact est égale à zéro. Dans ce cas, vous n'avez même pas besoin de calculer quoi que ce soit - regardez simplement le graphique.

Calcul des points hauts et bas

Parfois, au lieu d'un graphique d'une fonction dans le problème B9, un graphique dérivé est donné et il est nécessaire de trouver le point maximum ou minimum de la fonction. Dans ce scénario, la méthode à deux points est inutile, mais il existe un autre algorithme encore plus simple. Définissons d'abord la terminologie :

1. Le point x 0 est appelé le point maximum de la fonction f(x) si l'inégalité suivante est vraie dans un certain voisinage de ce point : f(x 0) ≥ f(x).
2. Le point x 0 est appelé le point minimum de la fonction f(x) si l'inégalité suivante est vraie dans un certain voisinage de ce point : f(x 0) ≤ f(x).

Afin de trouver les points maximum et minimum sur le graphique de la dérivée, il suffit d'effectuer les étapes suivantes :

1. Redessinez le graphique de la dérivée en supprimant toutes les informations inutiles. Comme le montre la pratique, les données supplémentaires ne font qu'interférer avec la solution. Par conséquent, nous marquons les zéros de la dérivée sur l'axe des coordonnées - et c'est tout.
2. Découvrez les signes de la dérivée sur les intervalles entre les zéros. Si pour un point x 0 on sait que f'(x 0) ≠ 0, alors seulement deux options sont possibles : f'(x 0) ≥ 0 ou f'(x 0) ≤ 0. Le signe de la dérivée est facile à déterminer à partir du dessin d'origine : si le graphe dérivé se situe au-dessus de l'axe OX, alors f'(x) ≥ 0. Inversement, si le graphe dérivé se situe en dessous de l'axe OX, alors f'(x) ≤ 0.
3. Nous vérifions à nouveau les zéros et les signes de la dérivée. Là où le signe passe du moins au plus, il y a un point minimum. Inversement, si le signe de la dérivée passe de plus à moins, c'est le point maximum. Le comptage se fait toujours de gauche à droite.

Ce schéma ne fonctionne que pour les fonctions continues - il n'y en a pas d'autres dans le problème B9.

Une tâche. La figure montre un graphique de la dérivée de la fonction f(x) définie sur le segment [−5 ; 5]. Trouver le point minimum de la fonction f(x) sur ce segment.

Débarrassons-nous des informations inutiles - nous ne laisserons que les frontières [−5 ; 5] et les zéros de la dérivée x = −3 et x = 2,5. Notez également les signes :

Évidemment, au point x = −3, le signe de la dérivée passe de moins à plus. C'est le point minimum.

Une tâche. La figure montre un graphique de la dérivée de la fonction f(x) définie sur le segment [−3 ; sept]. Trouver le point maximum de la fonction f(x) sur ce segment.

Redessinons le graphe en ne laissant que les bornes [−3; 7] et les zéros de la dérivée x = −1,7 et x = 5. Notez les signes de la dérivée sur le graphique résultant. Nous avons:

Évidemment, au point x = 5, le signe de la dérivée passe de plus à moins - c'est le point maximum.

Une tâche. La figure montre un graphique de la dérivée de la fonction f(x) définie sur l'intervalle [−6 ; quatre]. Trouver le nombre de points maximum de la fonction f(x) appartenant à l'intervalle [−4 ; 3].

Il résulte des conditions du problème qu'il suffit de ne considérer que la partie du graphe délimitée par le segment [−4 ; 3]. On construit donc un nouveau graphe, sur lequel on ne marque que les bornes [−4 ; 3] et les zéros de la dérivée à l'intérieur. A savoir, les points x = −3.5 et x = 2. On obtient :

Sur ce graphique, il n'y a qu'un seul point maximum x = 2. C'est en lui que le signe de la dérivée passe du plus au moins.

Une petite note sur les points avec des coordonnées non entières. Par exemple, dans le dernier problème, le point x = −3,5 a été considéré, mais avec le même succès on peut prendre x = −3,4. Si le problème est correctement formulé, de tels changements ne devraient pas affecter la réponse, car les points "sans lieu de résidence fixe" ne sont pas directement impliqués dans la résolution du problème. Bien sûr, avec des points entiers, une telle astuce ne fonctionnera pas.

Trouver les intervalles d'augmentation et de diminution d'une fonction

Dans un tel problème, comme les points de maximum et de minimum, il est proposé de trouver des zones dans lesquelles la fonction elle-même augmente ou diminue à partir du graphique de la dérivée. Tout d'abord, définissons ce que sont l'ascendant et le descendant :

1. Une fonction f(x) est dite croissante sur un segment si pour deux points quelconques x 1 et x 2 de ce segment l'énoncé est vrai : x 1 ≤ x 2 ⇒ f(x 1) ≤ f(x 2). En d'autres termes, plus la valeur de l'argument est grande, plus la valeur de la fonction est grande.
2. Une fonction f(x) est dite décroissante sur un segment si pour deux points quelconques x 1 et x 2 de ce segment l'énoncé est vrai : x 1 ≤ x 2 ⇒ f(x 1) ≥ f(x 2). Ceux. plus grande valeur l'argument correspond à la plus petite valeur de la fonction.

Nous formulons des conditions suffisantes pour augmenter et diminuer :

1. À fonction continue f(x) augmente sur le segment , il suffit que sa dérivée à l'intérieur du segment soit positive, c'est-à-dire f'(x) ≥ 0.
2. Pour qu'une fonction continue f(x) décroisse sur le segment , il suffit que sa dérivée à l'intérieur du segment soit négative, c'est-à-dire f'(x) ≤ 0.

Nous acceptons ces affirmations sans preuve. Ainsi, nous obtenons un schéma pour trouver des intervalles d'augmentation et de diminution, qui est à bien des égards similaire à l'algorithme de calcul des points extrêmes :

1. Supprimez toutes les informations redondantes. Sur le graphique original de la dérivée, nous nous intéressons principalement aux zéros de la fonction, nous ne laissons donc que ceux-ci.
2. Marquez les signes de la dérivée aux intervalles entre les zéros. Où f'(x) ≥ 0, la fonction augmente, et où f'(x) ≤ 0, elle diminue. Si le problème a des restrictions sur la variable x, nous les marquons en plus sur le nouveau graphique.
3. Maintenant que nous connaissons le comportement de la fonction et de la contrainte, il reste à calculer la valeur requise dans le problème.

Une tâche. La figure montre un graphique de la dérivée de la fonction f(x) définie sur le segment [−3 ; 7.5]. Trouver les intervalles de la fonction décroissante f(x). Dans votre réponse, écrivez la somme des nombres entiers compris dans ces intervalles.

Comme d'habitude, on redessine le graphe et on marque les bornes [−3 ; 7.5], ainsi que les zéros de la dérivée x = −1.5 et x = 5.3. Ensuite, nous marquons les signes de la dérivée. Nous avons:

Comme la dérivée est négative sur l'intervalle (− 1,5), c'est l'intervalle de fonction décroissante. Il reste à additionner tous les entiers qui sont à l'intérieur de cet intervalle :
−1 + 0 + 1 + 2 + 3 + 4 + 5 = 14.

Une tâche. La figure montre un graphique de la dérivée de la fonction f(x) définie sur le segment [−10 ; quatre]. Trouver les intervalles de la fonction croissante f(x). Dans votre réponse, écrivez la longueur du plus grand d'entre eux.

Débarrassons-nous des informations redondantes. On ne laisse que les bornes [−10 ; 4] et les zéros de la dérivée, qui cette fois se sont avérés être quatre : x = −8, x = −6, x = −3 et x = 2. Notez les signes de la dérivée et obtenez l'image suivante :

On s'intéresse aux intervalles de fonction croissante, c'est-à-dire où f'(x) ≥ 0. Il existe deux de ces intervalles sur le graphique : (−8 ; −6) et (−3 ; 2). Calculons leurs longueurs :
l 1 = − 6 − (−8) = 2 ;
l 2 = 2 − (−3) = 5.

Puisqu'il est nécessaire de trouver la longueur du plus grand des intervalles, nous écrivons la valeur l 2 = 5 en réponse.

Etude d'une fonction à l'aide d'une dérivée. Dans cet article, nous allons analyser quelques-unes des tâches associées à l'étude du graphe d'une fonction. Dans de telles tâches, un graphique de la fonction y = f (x) est donné et des questions sont soulevées concernant la détermination du nombre de points auxquels la dérivée de la fonction est positive (ou négative), ainsi que d'autres. Ils sont classés comme des tâches pour l'application de la dérivée à l'étude des fonctions.

La solution de tels problèmes, et en général des problèmes liés à l'étude, n'est possible qu'avec une compréhension complète des propriétés de la dérivée pour l'étude des graphes de fonctions et de la dérivée. Par conséquent, je vous recommande fortement d'étudier la théorie pertinente. Vous pouvez étudier et aussi regarder (mais il contient un résumé).

Nous envisagerons également des tâches où le graphe de la dérivée est donné dans de futurs articles, ne le manquez pas ! Donc les tâches sont :

La figure montre un graphique de la fonction y \u003d f (x), définie sur l'intervalle (−6; 8). Définir:

1. Le nombre de points entiers auxquels la dérivée de la fonction est négative ;

2. Le nombre de points où la tangente au graphique de la fonction est parallèle à la droite y = 2 ;

1. La dérivée de la fonction est négative sur les intervalles sur lesquels la fonction décroît, c'est-à-dire sur les intervalles (−6 ; -3), (0 ; 4,2), (6,9 ; 8). Ils contiennent des points entiers -5, -4, 1, 2, 3, 4 et 7. Nous avons obtenu 7 points.

2. Directe y= 2 axes parallèlesohy= 2 uniquement aux points extrêmes (aux points où le graphique change son comportement d'augmentation à diminution ou vice versa). Il existe quatre points de ce type : –3 ; 0 ; 4.2 ; 6.9

Décider vous-même:

Déterminez le nombre de points entiers où la dérivée de la fonction est positive.

La figure montre un graphique de la fonction y \u003d f (x), définie sur l'intervalle (−5; 5). Définir:

2. Le nombre de points entiers auxquels la tangente au graphique de la fonction est parallèle à la droite y \u003d 3;

3. Le nombre de points où la dérivée est nulle ;

1. D'après les propriétés de la dérivée d'une fonction, on sait qu'elle est positive sur les intervalles sur lesquels la fonction croît, c'est-à-dire sur les intervalles (1.4 ; 2.5) et (4.4 ; 5). Ils contiennent un seul point entier x = 2.

2. Directe y= 3 axes parallèlesoh. La tangente sera parallèle à la droitey= 3 uniquement aux points extrêmes (aux points où le graphique change son comportement d'augmentation à diminution ou vice versa).

Ces points sont au nombre de quatre : –4,3 ; 1.4 ; 2,5 ; 4.4

3. La dérivée est égale à zéro en quatre points (aux points extrêmes), nous les avons déjà indiqués.

Décider vous-même:

Déterminez le nombre de points entiers où la dérivée de la fonction f(x) est négative.

La figure montre un graphique de la fonction y \u003d f (x), définie sur l'intervalle (−2; 12). Trouver:

1. Le nombre de points entiers auxquels la dérivée de la fonction est positive ;

2. Le nombre de points entiers auxquels la dérivée de la fonction est négative ;

3. Le nombre de points entiers auxquels la tangente au graphique de la fonction est parallèle à la droite y \u003d 2;

4. Le nombre de points où la dérivée est égale à zéro.

1. D'après les propriétés de la dérivée d'une fonction, on sait qu'elle est positive sur les intervalles sur lesquels la fonction croît, c'est-à-dire sur les intervalles (–2 ; 1), (2 ; 4), (7 ; 9 ) et (10 ; 11). Ils contiennent des points entiers : -1, 0, 3, 8. Il y en a quatre au total.

2. La dérivée de la fonction est négative sur les intervalles sur lesquels la fonction décroît, c'est-à-dire sur les intervalles (1 ; 2), (4 ; 7), (9 ; 10), (11 ; 12). Ils contiennent les points entiers 5 et 6. Nous avons obtenu 2 points.

3. Directe y= 2 axes parallèlesoh. La tangente sera parallèle à la droitey= 2 uniquement aux points extrêmes (aux points où le graphique change son comportement d'augmentation à diminution ou vice versa). Ces points sont au nombre de sept : 1 ; 2 ; quatre ; sept; 9; Dix; Onze.

4. La dérivée est égale à zéro en sept points (aux points extrêmes), nous les avons déjà indiqués.

Montrer la relation du signe de la dérivée avec la nature de la monotonie de la fonction.

Veuillez être extrêmement prudent dans ce qui suit. Regardez, le planning de QUOI vous est donné ! Fonction ou sa dérivée

Étant donné un graphique de la dérivée, alors nous ne nous intéressons qu'aux signes de fonction et aux zéros. Aucun "monticule" et "creux" ne nous intéressent en principe !

Tache 1.

La figure montre un graphique d'une fonction définie sur un intervalle. Déterminez le nombre de points entiers où la dérivée de la fonction est négative.

La solution:

Dans la figure, les zones de fonction décroissante sont mises en évidence en couleur :

4 valeurs entières entrent dans ces zones de fonction décroissante.

Tâche 2.

La figure montre un graphique d'une fonction définie sur un intervalle. Trouvez le nombre de points où la tangente au graphique de la fonction est parallèle ou coïncide avec la droite.

La solution:

Puisque la tangente à la fonction graphique est parallèle (ou coïncide) avec une droite (ou, ce qui revient au même, ) ayant pente, égal à zéro, alors la tangente a une pente .

Cela signifie à son tour que la tangente est parallèle à l'axe, puisque la pente est la tangente de l'angle d'inclinaison de la tangente à l'axe.

On retrouve donc des points extrêmes sur le graphe (points maximum et minimum), - c'est en eux que les fonctions tangentes au graphe seront parallèles à l'axe.

Il y a 4 points de ce type.

Tâche 3.

La figure montre un graphique de la dérivée d'une fonction définie sur l'intervalle . Trouvez le nombre de points où la tangente au graphique de la fonction est parallèle ou coïncide avec la droite.

La solution:

Puisque la tangente au graphique de la fonction est parallèle (ou coïncide) avec une ligne droite, qui a une pente, alors la tangente a une pente.

Cela signifie à son tour qu'aux points de contact.

Par conséquent, nous regardons combien de points sur le graphique ont une ordonnée égale à .

Comme vous pouvez le voir, il y a quatre points de ce type.

Tâche 4.

La figure montre un graphique d'une fonction définie sur un intervalle. Trouver le nombre de points où la dérivée de la fonction est 0.

La solution:

La dérivée est nulle aux points extrêmes. Nous en avons 4 :

Tâche 5.

La figure montre un graphique de fonction et onze points sur l'axe des x :. En combien de ces points la dérivée de la fonction est-elle négative ?

La solution:

Sur des intervalles de fonction décroissante, sa dérivée prend des valeurs négatives. Et la fonction diminue aux points. Il y a 4 points de ce type.

Tâche 6.

La figure montre un graphique d'une fonction définie sur un intervalle. Trouver la somme des points extrêmes de la fonction .

La solution:

points extrêmes sont les points maximum (-3, -1, 1) et les points minimum (-2, 0, 3).

La somme des points extrêmes : -3-1+1-2+0+3=-2.

Tâche 7.

La figure montre un graphique de la dérivée d'une fonction définie sur l'intervalle . Trouver les intervalles de la fonction croissante. Dans votre réponse, indiquez la somme des points entiers compris dans ces intervalles.

La solution:

La figure met en évidence les intervalles sur lesquels la dérivée de la fonction est non négative.

Il n'y a pas de points entiers sur le petit intervalle d'augmentation, sur l'intervalle d'augmentation il y a quatre valeurs entières : , , et .

Leur somme :

Tâche 8.

La figure montre un graphique de la dérivée d'une fonction définie sur l'intervalle . Trouver les intervalles de la fonction croissante. Dans votre réponse, écrivez la longueur du plus grand d'entre eux.

La solution:

Sur la figure, tous les intervalles sur lesquels la dérivée est positive sont mis en évidence, ce qui signifie que la fonction elle-même croît sur ces intervalles.

La longueur du plus grand d'entre eux est de 6.

Tâche 9.

La figure montre un graphique de la dérivée d'une fonction définie sur l'intervalle . À quel point du segment valeur la plus élevée.

La solution:

Nous regardons comment le graphe se comporte sur le segment, à savoir, nous nous intéressons à signe dérivé uniquement .

Le signe de la dérivée sur est moins, puisque le graphique sur ce segment est en dessous de l'axe.

Dérivée première Si la dérivée d'une fonction est positive (négative) dans un intervalle, alors la fonction dans cet intervalle est monotone croissante (décroissante monotone). Si la fonction dérivée est positive (négative) dans un intervalle, alors la fonction dans cet intervalle est monotone croissante (décroissante monotone). Plus loin

Définition Une courbe est dite convexe en un point si au voisinage de ce point elle est située sous sa tangente en un point Une courbe est dite convexe en un point si en un voisinage de ce point elle est située sous sa tangente en un point point , elle est située au-dessus de sa tangente en un point Une courbe est dite concave en un point si, au voisinage de ce point, elle est située au-dessus de sa tangente en un point Suivant

Signe de concavité et de convexité Si la dérivée seconde d'une fonction dans un intervalle donné est positive, alors la courbe est concave dans cet intervalle, et si elle est négative, elle est convexe dans cet intervalle. Si la dérivée seconde d'une fonction dans un intervalle donné est positive, alors la courbe est concave dans cet intervalle, et si elle est négative, elle est convexe dans cet intervalle. Définition

Planifier l'étude de la fonction et la construction de son graphe 1. Trouver le domaine de la fonction et déterminer les points de rupture, le cas échéant 1. Trouver le domaine de la fonction et déterminer les points de rupture, le cas échéant 2. Rechercher si la fonction est paire ou impair ; vérifier sa périodicité 2. Déterminer si la fonction est paire ou impaire ; vérifier sa périodicité 3. Déterminer les points d'intersection du graphe de fonction avec les axes de coordonnées 3. Déterminer les points d'intersection du graphe de fonction avec les axes de coordonnées 4. Trouver les points critiques du 1er type 4. Trouver les points critiques du 1er 5. Déterminer les intervalles de monotonie et les extrema de la fonction 5. Déterminer les intervalles de monotonie et les extrema de la fonction 6. Déterminer les intervalles de convexité et de concavité et trouver les points d'inflexion 6. Déterminer les intervalles de convexité et de concavité et trouver les points d'inflexion 7 À l'aide des résultats de l'étude, reliez les points obtenus d'une courbe lisse 7. À l'aide des résultats de l'étude, reliez les points obtenus d'une courbe lisse Quitter

(Fig. 1)

Figure 1. Graphique de la dérivée

Propriétés du tracé dérivé

1. A intervalles croissants, la dérivée est positive. Si la dérivée à un certain point d'un certain intervalle a valeur positive, alors le graphe de la fonction sur cet intervalle augmente.
2. Sur des intervalles décroissants, la dérivée est négative (avec un signe moins). Si la dérivée à un certain point d'un certain intervalle a Sens négatif, alors le graphe de la fonction décroît sur cet intervalle.
3. La dérivée au point x est coefficient angulaire tangente tracée au graphe de la fonction au même point.
4. Aux points maximum-minimum de la fonction, la dérivée est égale à zéro. La tangente au graphique de la fonction en ce point est parallèle à l'axe OX.

Exemple 1

D'après le graphique (Fig. 2) de la dérivée, déterminer en quel point du segment [-3 ; 5] la fonction est maximale.

Figure 2. Graphique de la dérivée

Solution : Sur ce segment, la dérivée est négative, ce qui signifie que la fonction décroît de gauche à droite, et la plus grande valeur se trouve du côté gauche au point -3.

Exemple 2

D'après le graphique (Fig. 3) de la dérivée, déterminer le nombre de points maximum sur le segment [-11 ; 3].

Figure 3. Graphique de la dérivée

Solution : Les points maximum correspondent aux points où le signe de la dérivée passe du positif au négatif. Sur cet intervalle, la fonction change deux fois de signe du plus au moins - au point -10 et au point -1. Le nombre maximum de points est donc de deux.

Exemple 3

Selon le graphique (Fig. 3) de la dérivée, déterminer le nombre de points minimum dans le segment [-11 ; -une].

Solution : Les points minimaux correspondent aux points où le signe de la dérivée passe du négatif au positif. Sur ce segment, seul -7 est un tel point. Cela signifie que le nombre de points minimum sur un segment donné est de un.

Exemple 4

Selon le graphique (Fig. 3) de la dérivée, déterminez le nombre de points extrêmes.

Solution : L'extremum est le point du minimum et du maximum. Trouver le nombre de points auxquels la dérivée change de signe.