Eine Kugel wird um ein regelmäßiges viereckiges Prisma herum beschrieben. Rechtes Prisma (viereckig regelmäßig)

Das Thema „Verschiedene Probleme zu Polyedern, Zylinder, Kegel und Kugel“ ist eines der schwierigsten im Geometriekurs der 11. Klasse. Bevor sie geometrische Probleme lösen, studieren sie normalerweise die relevanten Abschnitte der Theorie, auf die sie sich bei der Lösung von Problemen beziehen. Im Lehrbuch von S. Atanasyan und anderen zu diesem Thema (S. 138) findet man nur Definitionen eines um eine Kugel beschriebenen Polyeders, eines in eine Kugel eingeschriebenen Polyeders, einer in ein Polyeder eingeschriebenen Kugel und einer um a beschriebenen Kugel Polyeder. In den methodischen Empfehlungen zu diesem Lehrbuch (siehe das Buch „Studying Geometry in Grades 10–11“ von S.M. Sahakyan und V.F. Butuzov, S. 159) wird angegeben, welche Körperkombinationen bei der Lösung der Probleme Nr. 629–646 berücksichtigt werden, und es wird darauf hingewiesen darauf, dass „bei der Lösung eines bestimmten Problems zunächst sichergestellt werden muss, dass die Studierenden die relativen Positionen der in der Bedingung angegebenen Körper gut verstehen.“ Im Folgenden finden Sie die Lösung für die Probleme Nr. 638(a) und Nr. 640.

In Anbetracht all dessen und der Tatsache, dass die Kombination eines Balls mit anderen Körpern die schwierigsten Probleme für Studierende sind, ist es notwendig, die relevanten theoretischen Grundlagen zu systematisieren und sie den Studierenden zu vermitteln.

Definitionen.

1. Eine Kugel heißt in ein Polyeder eingeschrieben und ein um eine Kugel herum beschriebenes Polyeder, wenn die Oberfläche der Kugel alle Flächen des Polyeders berührt.

2. Eine um ein Polyeder umschriebene Kugel und ein in eine Kugel eingeschriebenes Polyeder heißen, wenn die Oberfläche der Kugel durch alle Eckpunkte des Polyeders verläuft.

3. Eine Kugel soll in einen Zylinder, Kegelstumpf (Kegel) eingeschrieben sein, und ein Zylinder, Kegelstumpf (Kegel), soll um die Kugel herum eingeschrieben sein, wenn die Oberfläche der Kugel die Basen (Basis) und alles berührt die Erzeugenden des Zylinders, Kegelstumpfes (Kegel).

(Aus dieser Definition folgt, dass der Großkreis einer Kugel in jeden axialen Abschnitt dieser Körper eingeschrieben werden kann.)

4. Eine Kugel heißt umschrieben von einem Zylinder, einem Kegelstumpf (Kegel), wenn die Kreise der Grundflächen (Grundkreis und Scheitelpunkt) zur Oberfläche der Kugel gehören.

(Aus dieser Definition folgt, dass um jeden axialen Abschnitt dieser Körper der Kreis eines größeren Kreises der Kugel beschrieben werden kann).

Allgemeine Hinweise zur Lage der Kugelmitte.

1. Der Mittelpunkt einer in ein Polyeder eingeschriebenen Kugel liegt im Schnittpunkt der Winkelhalbierenden aller Diederwinkel des Polyeders. Es befindet sich nur innerhalb des Polyeders.

2. Der Mittelpunkt einer von einem Polyeder umschriebenen Kugel liegt im Schnittpunkt von Ebenen, die senkrecht zu allen Kanten des Polyeders stehen und durch deren Mittelpunkte verlaufen. Es kann sich innerhalb, auf der Oberfläche oder außerhalb des Polyeders befinden.

Kombination aus einer Kugel und einem Prisma.

1. Eine Kugel, die in ein gerades Prisma eingeschrieben ist.

Satz 1. Eine Kugel kann genau dann in ein gerades Prisma eingeschrieben werden, wenn an der Basis des Prismas ein Kreis eingeschrieben werden kann und die Höhe des Prismas gleich dem Durchmesser dieses Kreises ist.

Folgerung 1. Der Mittelpunkt einer in ein gerades Prisma eingeschriebenen Kugel liegt in der Mitte der Höhe des Prismas, die durch den Mittelpunkt des in die Basis eingeschriebenen Kreises verläuft.

Folgerung 2. Insbesondere eine Kugel kann in gerade Linien eingeschrieben werden: dreieckig, regelmäßig, viereckig (bei denen die Summen der gegenüberliegenden Seiten der Grundfläche einander gleich sind) unter der Bedingung H = 2r, wobei H die Höhe der ist Prisma, r ist der Radius des in die Basis eingeschriebenen Kreises.

2. Eine von einem Prisma umschriebene Kugel.

Satz 2. Eine Kugel kann um ein Prisma genau dann beschrieben werden, wenn das Prisma gerade ist und ein Kreis um seine Basis beschrieben werden kann.

Folgerung 1. Der Mittelpunkt einer um ein gerades Prisma umschriebenen Kugel liegt in der Mitte der Höhe des Prismas, die durch den Mittelpunkt eines um die Basis umschriebenen Kreises gezogen wird.

Folgerung 2. Insbesondere kann eine Kugel beschrieben werden: in der Nähe eines geraden dreieckigen Prismas, in der Nähe eines regelmäßigen Prismas, in der Nähe eines rechteckigen Parallelepipeds, in der Nähe eines geraden viereckigen Prismas, bei dem die Summe der entgegengesetzten Winkel der Grundfläche 180 Grad beträgt.

Aus dem Lehrbuch von L.S. Atanasyan können die Aufgaben Nr. 632, 633, 634, 637(a), 639(a,b) für die Kombination einer Kugel und eines Prismas vorgeschlagen werden.

Kombination einer Kugel mit einer Pyramide.

1. Eine Kugel, die in der Nähe einer Pyramide beschrieben wird.

Satz 3. Eine Kugel kann genau dann um eine Pyramide herum beschrieben werden, wenn um ihre Basis ein Kreis beschrieben werden kann.

Folgerung 1. Der Mittelpunkt einer um eine Pyramide umschriebenen Kugel liegt im Schnittpunkt einer geraden Linie senkrecht zur Basis der Pyramide, die durch den Mittelpunkt eines um diese Basis umschriebenen Kreises und einer Ebene senkrecht zu einer durch die Mitte gezogenen Seitenkante verläuft diese Kante.

Folgerung 2. Sind die Seitenkanten der Pyramide einander gleich (oder gleich zur Grundebene geneigt), so lässt sich um eine solche Pyramide eine Kugel beschreiben, deren Mittelpunkt in diesem Fall im Schnittpunkt von liegt die Höhe der Pyramide (bzw. ihrer Verlängerung), wobei die Symmetrieachse der Seitenkante in der Ebene Seitenkante und Höhe liegt.

Folgerung 3. Insbesondere eine Kugel kann beschrieben werden: in der Nähe einer dreieckigen Pyramide, in der Nähe einer regelmäßigen Pyramide, in der Nähe einer viereckigen Pyramide, bei der die Summe der entgegengesetzten Winkel 180 Grad beträgt.

2. Eine in eine Pyramide eingeschriebene Kugel.

Satz 4. Wenn die Seitenflächen der Pyramide gleichmäßig zur Grundfläche geneigt sind, kann in eine solche Pyramide eine Kugel eingeschrieben werden.

Folgerung 1. Der Mittelpunkt einer Kugel, die in eine Pyramide eingeschrieben ist, deren Seitenflächen gleichmäßig zur Grundfläche geneigt sind, liegt im Schnittpunkt der Höhe der Pyramide mit der Winkelhalbierenden eines beliebigen Diederwinkels an der Grundfläche der Pyramide, der Seite Davon ist die Höhe der Seitenfläche, die von der Spitze der Pyramide ausgeht.

Folgerung 2. Sie können eine Kugel in eine regelmäßige Pyramide einbauen.

Aus dem Lehrbuch von L.S. Atanasyan können die Aufgaben Nr. 635, 637(b), 638, 639(c), 640, 641 für die Kombination einer Kugel mit einer Pyramide vorgeschlagen werden.

Kombination einer Kugel mit einem Pyramidenstumpf.

1. Eine Kugel, die um einen regelmäßigen Pyramidenstumpf herum umschrieben ist.

Satz 5. Eine Kugel kann um jeden regelmäßigen Pyramidenstumpf herum beschrieben werden. (Diese Bedingung ist ausreichend, aber nicht notwendig)

2. Eine Kugel, die in einen regelmäßigen Pyramidenstumpf eingraviert ist.

Satz 6. Eine Kugel kann genau dann in einen regelmäßigen Pyramidenstumpf eingeschrieben werden, wenn das Apothem der Pyramide gleich der Summe der Apotheme der Grundflächen ist.

Für die Kombination einer Kugel mit einem Pyramidenstumpf gibt es im Lehrbuch von L.S. Atanasyan (Nr. 636) nur ein Problem.

Kombination aus Kugel und rundem Körper.

Satz 7. Eine Kugel kann um einen Zylinder, einen Kegelstumpf (gerader Kreis) oder einen Kegel herum beschrieben werden.

Satz 8. Eine Kugel kann genau dann in einen (geraden Kreis-)Zylinder eingeschrieben werden, wenn der Zylinder gleichseitig ist.

Satz 9. Sie können eine Kugel in jeden Kegel (geraden Kreis) einbauen.

Satz 10. Eine Kugel kann genau dann in einen Kegelstumpf (geraden Kreis) eingeschrieben werden, wenn ihr Generator gleich der Summe der Radien der Grundflächen ist.

Aus dem Lehrbuch von L.S. Atanasyan lassen sich die Aufgaben Nr. 642, 643, 644, 645, 646 für die Kombination einer Kugel mit runden Körpern vorschlagen.

Um den Stoff zu diesem Thema erfolgreicher zu studieren, ist es notwendig, mündliche Aufgaben in den Unterricht einzubeziehen:

1. Die Kante des Würfels ist gleich a. Finden Sie die Radien der Kugeln: in den Würfel eingeschrieben und umschrieben. (r = a/2, R = a3).

2. Ist es möglich, eine Kugel (Ball) um Folgendes zu beschreiben: a) einen Würfel; b) rechteckiges Parallelepiped; c) ein geneigtes Parallelepiped mit einem Rechteck an seiner Basis; d) gerades Parallelepiped; e) ein geneigtes Parallelepiped? (a) ja; b) ja; c) nein; d) nein; d) nein)

3. Stimmt es, dass eine Kugel um jede dreieckige Pyramide herum beschrieben werden kann? (Ja)

4. Ist es möglich, eine Kugel um eine viereckige Pyramide herum zu beschreiben? (Nein, nicht in der Nähe einer viereckigen Pyramide)

5. Welche Eigenschaften muss eine Pyramide haben, um eine sie umgebende Kugel zu beschreiben? (An seiner Basis sollte sich ein Polygon befinden, um das herum ein Kreis beschrieben werden kann)

6. Eine Pyramide ist in eine Kugel eingeschrieben, deren Seitenkante senkrecht zur Basis steht. Wie finde ich den Mittelpunkt einer Kugel? (Der Mittelpunkt der Kugel ist der Schnittpunkt zweier geometrischer Orte von Punkten im Raum. Der erste ist eine Senkrechte, die zur Ebene der Basis der Pyramide durch den Mittelpunkt eines um sie herum beschriebenen Kreises gezogen wird. Der zweite ist eine Ebene senkrecht zu einer bestimmten Seitenkante und durch deren Mitte gezogen)

7. Unter welchen Bedingungen kann man eine Kugel um ein Prisma herum beschreiben, an dessen Basis sich ein Trapez befindet? (Erstens muss das Prisma gerade sein, und zweitens muss das Trapez gleichschenklig sein, damit ein Kreis darum beschrieben werden kann)

8. Welche Bedingungen muss ein Prisma erfüllen, damit eine Kugel um es herum beschrieben werden kann? (Das Prisma muss gerade sein und seine Basis muss ein Polygon sein, um das ein Kreis beschrieben werden kann)

9. Eine Kugel wird um ein dreieckiges Prisma herum beschrieben, dessen Mittelpunkt außerhalb des Prismas liegt. Welches Dreieck ist die Basis des Prismas? (Stumpfes Dreieck)

10. Ist es möglich, eine Kugel um ein geneigtes Prisma herum zu beschreiben? (Nein, geht nicht)

11. Unter welcher Bedingung liegt der Mittelpunkt einer um ein rechtwinkliges dreieckiges Prisma umschriebenen Kugel auf einer der Seitenflächen des Prismas? (Die Basis ist ein rechtwinkliges Dreieck)

12. Die Basis der Pyramide ist ein gleichschenkliges Trapez. Die orthogonale Projektion der Spitze der Pyramide auf die Ebene der Basis ist ein Punkt, der außerhalb des Trapezes liegt. Kann man um ein solches Trapez eine Kugel beschreiben? (Ja, das können Sie. Die Tatsache, dass die orthogonale Projektion der Spitze der Pyramide außerhalb ihrer Basis liegt, spielt keine Rolle. Es ist wichtig, dass an der Basis der Pyramide ein gleichschenkliges Trapez liegt – ein Polygon, um das sich ein Kreis bilden kann beschrieben)

13. Eine Kugel wird in der Nähe einer regelmäßigen Pyramide beschrieben. Wie liegt sein Mittelpunkt relativ zu den Elementen der Pyramide? (Der Mittelpunkt der Kugel liegt auf einer Senkrechten, die durch ihren Mittelpunkt zur Ebene der Grundfläche gezogen wird.)

14. Unter welchen Bedingungen liegt der Mittelpunkt einer um ein rechtwinkliges dreieckiges Prisma beschriebenen Kugel: a) innerhalb des Prismas; b) außerhalb des Prismas? (An der Basis des Prismas: a) ein spitzes Dreieck; b) stumpfes Dreieck)

15. Eine Kugel wird um ein rechteckiges Parallelepiped herum beschrieben, dessen Kanten 1 dm, 2 dm und 2 dm betragen. Berechnen Sie den Radius der Kugel. (1,5 dm)

16. In welchen Kegelstumpf passt eine Kugel? (In einem Kegelstumpf, in dessen axialen Abschnitt ein Kreis eingeschrieben werden kann. Der axiale Abschnitt des Kegels ist ein gleichschenkliges Trapez, die Summe seiner Grundflächen muss gleich der Summe seiner Seitenflächen sein. Mit anderen Worten, die Summe der Radien der Kegelbasen muss gleich dem Generator sein)

17. Eine Kugel ist in einen Kegelstumpf eingeschrieben. In welchem ​​Winkel ist die Erzeugende des Kegels vom Mittelpunkt der Kugel aus sichtbar? (90 Grad)

18. Welche Eigenschaften muss ein gerades Prisma haben, damit eine Kugel darin eingeschrieben werden kann? (Erstens muss sich an der Basis eines geraden Prismas ein Polygon befinden, in das ein Kreis eingeschrieben werden kann, und zweitens muss die Höhe des Prismas gleich dem Durchmesser des in die Basis eingeschriebenen Kreises sein.)

19. Nennen Sie ein Beispiel für eine Pyramide, die nicht in eine Kugel passt? (Zum Beispiel eine viereckige Pyramide mit einem Rechteck oder Parallelogramm an der Basis)

20. An der Basis eines geraden Prismas befindet sich eine Raute. Ist es möglich, eine Kugel in dieses Prisma einzubauen? (Nein, das ist unmöglich, da es im Allgemeinen unmöglich ist, einen Kreis um eine Raute zu beschreiben)

21. Unter welcher Bedingung kann eine Kugel in ein rechtwinkliges dreieckiges Prisma eingeschrieben werden? (Wenn die Höhe des Prismas das Doppelte des Radius des in die Basis eingeschriebenen Kreises beträgt)

22. Unter welcher Bedingung kann eine Kugel in einen regelmäßigen viereckigen Pyramidenstumpf eingeschrieben werden? (Wenn der Querschnitt einer bestimmten Pyramide eine Ebene ist, die durch die Mitte der dazu senkrechten Seite der Basis verläuft, handelt es sich um ein gleichschenkliges Trapez, in das ein Kreis eingeschrieben werden kann.)

23. Eine Kugel ist in einen dreieckigen Pyramidenstumpf eingeschrieben. Welcher Punkt der Pyramide ist der Mittelpunkt der Kugel? (Der Mittelpunkt der in diese Pyramide eingeschriebenen Kugel liegt am Schnittpunkt von drei Winkelhalbierenden, die durch die Seitenflächen der Pyramide mit der Basis gebildet werden.)

24. Ist es möglich, eine Kugel um einen Zylinder (rechts kreisförmig) zu beschreiben? (Ja, du kannst)

25. Ist es möglich, eine Kugel um einen Kegel, einen Kegelstumpf (geraden Kreis) herum zu beschreiben? (Ja, das können Sie, in beiden Fällen)

26. Kann eine Kugel in jeden Zylinder eingeschrieben werden? Welche Eigenschaften muss ein Zylinder haben, damit eine Kugel hineinpasst? (Nein, nicht immer: Der axiale Querschnitt des Zylinders muss quadratisch sein)

27. Kann eine Kugel in jeden Kegel eingeschrieben werden? Wie lässt sich die Position des Mittelpunkts einer Kugel bestimmen, die in einen Kegel eingeschrieben ist? (Ja, absolut. Der Mittelpunkt der beschrifteten Kugel liegt im Schnittpunkt der Höhe des Kegels und der Winkelhalbierenden des Neigungswinkels der Erzeugenden zur Ebene der Basis.)

Der Autor ist der Ansicht, dass es ratsam ist, von den drei Planungslektionen zum Thema „Verschiedene Probleme bei Polyedern, Zylinder, Kegel und Kugel“ zwei Lektionen der Lösung von Problemen bei der Kombination einer Kugel mit anderen Körpern zu widmen. Es wird nicht empfohlen, die oben genannten Theoreme zu beweisen, da die Unterrichtszeit nicht ausreicht. Sie können Schüler, die über ausreichende Fähigkeiten dafür verfügen, einladen, diese nachzuweisen, indem sie (nach Ermessen des Lehrers) den Verlauf oder Plan des Nachweises angeben.

Um eine Kugel herum wird ein regelmäßiges viereckiges Prisma beschrieben, dessen Volumen 65 dm 3 beträgt. Berechnen Sie das Verhältnis der Gesamtoberfläche des Prismas zum Volumen der Kugel
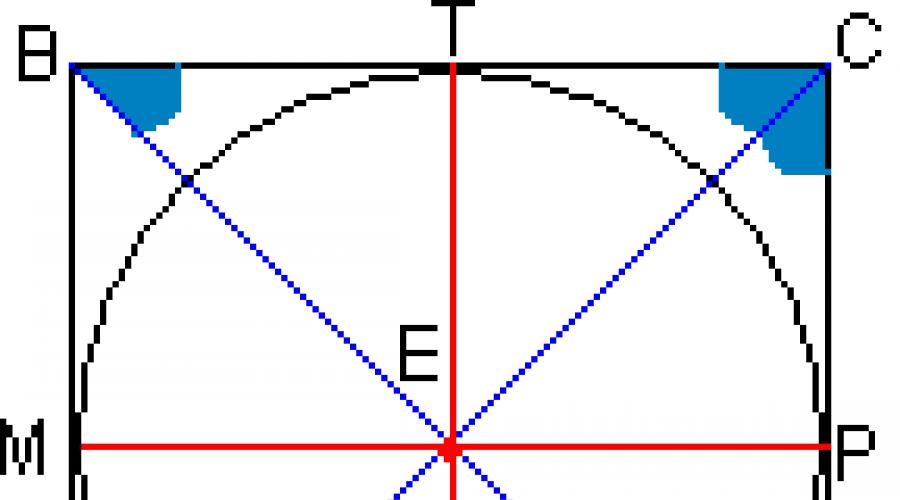
Ein Prisma heißt regelmäßig, wenn seine Grundflächen regelmäßige Vielecke sind und seine Seitenkanten senkrecht zur Grundfläche stehen. Ein regelmäßiges Viereck ist ein Quadrat. Der Schnittpunkt der Diagonalen eines Quadrats ist sein Mittelpunkt sowie der Mittelpunkt des darin eingeschriebenen Kreises. Lassen Sie uns diese Tatsache beweisen. obwohl dieser Beweis wahrscheinlich nicht verlangt wird und weggelassen werden kann
Als besondere Art von Parallelogramm, Rechteck und Raute hat das Quadrat seine eigenen Eigenschaften: Die Diagonalen sind gleich und werden durch den Schnittpunkt halbiert, und sie sind Winkelhalbierende der Ecken des Quadrats. Durch Punkt E zeichnen wir eine Gerade TK parallel zu AB. AB ist senkrecht zu BC, was bedeutet, dass TC auch senkrecht zu BC ist (wenn eine von zwei parallelen Linien senkrecht zu einer dritten Linie steht, dann steht die zweite parallele Linie senkrecht zu dieser (dritten) Linie). Auf die gleiche Weise werden wir die direkte MR durchführen. Die rechtwinkligen Dreiecke BET und AEK haben die gleiche Hypotenuse und den gleichen spitzen Winkel (BE=AE – die Hälfte der Diagonalen, ∠ EBT=∠ EAK – die Hälfte des rechten Winkels), was ET=EK bedeutet. Auf die gleiche Weise beweisen wir, dass EM=EP. Und aus der Gleichheit der Dreiecke CEP und CET (gleiches Vorzeichen) sehen wir, dass ET = EP, d.h. ET=EP=EK=EM oder einfach sagen, dass der Punkt M von den Seiten des Quadrats gleich weit entfernt ist, und dies ist eine notwendige Bedingung, um ihn als Mittelpunkt eines in dieses Quadrat eingeschriebenen Kreises zu erkennen.
Betrachten Sie das Rechteck AVTC (dieses Viereck ist ein Rechteck, da alle Winkel darin konstruktionsbedingt rechte Winkel sind). In einem Rechteck sind die gegenüberliegenden Seiten gleich – AB = CT (es ist zu beachten, dass CT der Durchmesser der Grundfläche ist) – das bedeutet, dass die Seite der Grundfläche gleich dem Durchmesser des eingeschriebenen Kreises ist.
Zeichnen wir Ebenen parallel (zwei Geraden senkrecht zur gleichen Ebene sind parallel) AA 1, CC 1 und BB 1 bzw. DD 1 (parallele Geraden definieren nur eine Ebene). Die Ebenen AA 1 C 1 C und BB 1 D 1 D stehen senkrecht zur Basis ABCD, weil durch gerade Linien (Seitenrippen) senkrecht dazu verlaufen.
Vom Punkt H (Schnittpunkt der Diagonalen) in der Ebene AA 1 C 1 C senkrecht zur Basis ABCD. Dann machen wir dasselbe in der Ebene BB 1 D 1 D. Aus dem Satz: Wenn wir von einem Punkt, der zu einer von zwei senkrechten Ebenen gehört, eine Senkrechte zur anderen Ebene zeichnen, dann liegt diese Senkrechte vollständig in der ersten Ebene, wir Finden Sie heraus, dass diese Senkrechte in der Ebene AA 1 C 1 C und in der Ebene BB 1 D 1 D liegen muss. Dies ist nur möglich, wenn diese Senkrechte mit der Schnittlinie dieser Ebenen übereinstimmt – NICHT. Diese. Das Segment ist KEINE Gerade, auf der der Mittelpunkt des eingeschriebenen Kreises liegt (da es NICHT den gleichen Abstand von den Ebenen der Seitenflächen hat, und dies wiederum folgt aus dem gleichen Abstand der Punkte E und H von den Eckpunkten der entsprechenden Basen (nach dem, was bewiesen wurde: Der Schnittpunkt der Diagonalen ist von den Seiten des Quadrats gleich weit entfernt), und aus der Tatsache, dass NOT senkrecht zu den Basen steht, können wir schließen, dass NOT der Durchmesser der Kugel ist. Satz . Eine Kugel kann genau dann in ein regelmäßiges Prisma eingeschrieben werden, wenn ihre Höhe gleich dem Durchmesser des in die Basis eingeschriebenen Kreises ist. Nun, sie ist bereits in unsere Prismenkugel eingeschrieben, was bedeutet, dass ihre Höhe gleich dem Durchmesser von ist der in die Basis eingeschriebene Kreis. Wenn wir die Seite der Basis als bezeichnen A, und die Höhe des Prismas ist h, dann schließen wir mit diesem Satz A=h und dann wird das Volumen des Prismas wie folgt ermittelt:

Als nächstes ermitteln wir unter Ausnutzung der Tatsache, dass die Höhe gleich dem Durchmesser der eingeschriebenen Kugel und der Seite der Basis des Prismas ist, den Radius der Kugel und dann ihr Volumen:

Es muss gesagt werden, dass die Seitenkanten gleich der Höhe sind (Segmente paralleler Linien, die zwischen parallelen Ebenen eingeschlossen sind, sind gleich), und da die Höhe gleich der Seite der Basis ist, sind im Allgemeinen alle Kanten des Prismas gleich zueinander, und alle Flächen sind im Wesentlichen Quadrate mit der Fläche A 2. Tatsächlich wird eine solche Figur als Würfel bezeichnet – ein Sonderfall eines Parallelepipeds. Es bleibt noch, die Gesamtoberfläche des Würfels zu ermitteln und sie mit dem Volumen der Kugel in Beziehung zu setzen:

2. Basisseite

Aufgaben

1. Finden Sie die Oberfläche eines geraden Prismas, an dessen Basis eine Raute mit Diagonalen von 3 und 4 und einer Seitenkante von 5 liegt.

Antwort: 62.

2. An der Basis eines geraden Prismas liegt eine Raute mit den Diagonalen 6 und 8. Ihre Oberfläche beträgt 248. Finden Sie die Seitenkante dieses Prismas.

Antwort: 10.

3. Finden Sie die Seitenkante eines regelmäßigen viereckigen Prismas, wenn die Seiten seiner Grundfläche 3 und die Oberfläche 66 beträgt.

Antwort: 4.

4. Ein regelmäßiges viereckiges Prisma wird um einen Zylinder herum beschrieben, dessen Basisradius und -höhe gleich 2 sind. Ermitteln Sie die Mantelfläche des Prismas.

Antwort: 32.

5. Ein regelmäßiges viereckiges Prisma wird um einen Zylinder herum beschrieben, dessen Basisradius 2 beträgt. Die Mantelfläche des Prismas beträgt 48. Ermitteln Sie die Höhe des Zylinders.

Rechtes Prisma (sechseckig regelmäßig)

Ein Prisma, bei dem die Seitenkanten senkrecht zu den Grundflächen stehen und die Grundflächen gleiche Quadrate sind.

1. Seitenflächen – gleiche Rechtecke

2. Basisseite

Aufgaben

1. Ermitteln Sie das Volumen eines regelmäßigen sechseckigen Prismas, dessen Grundseiten gleich 1 und dessen Seitenkanten gleich sind.

Antwort: 4.5.

2. Finden Sie die Mantelfläche eines regelmäßigen sechseckigen Prismas, dessen Grundseiten 3 und dessen Höhe 6 beträgt.

Antwort: 108.

3. Ermitteln Sie das Volumen eines regelmäßigen sechseckigen Prismas, dessen Kanten alle gleich √3 sind.

Antwort: 13.5

4. Finden Sie das Volumen des Polyeders, dessen Eckpunkte die Punkte A, B, C, D, A1, B1, C1, D1 eines regelmäßigen sechseckigen Prismas ABCDEFA1B1C1D1E1F1 sind, dessen Grundfläche 6 und dessen Seitenkante 2 beträgt.

Gerades Prisma (beliebig N-Kohle)

Ein Prisma, dessen Seitenkanten senkrecht zu den Grundflächen stehen und dessen Grundflächen gleiche n-Ecke sind.

1. Wenn die Basis ein regelmäßiges Vieleck ist, dann sind die Seitenflächen gleiche Rechtecke.

2. Basisseite .

Pyramide

Eine Pyramide ist ein Polyeder, das aus einem n-Eck A1A2...AnA1 und n Dreiecken (A1A2P, A1A3P usw.) besteht.

1. Der Abschnitt parallel zur Basis der Pyramide ist ein der Basis ähnliches Polygon. Die Querschnittsflächen und Grundflächen werden als Quadrate ihrer Abstände zur Spitze der Pyramide in Beziehung gesetzt.

2. Eine Pyramide heißt regelmäßig, wenn ihre Grundfläche ein regelmäßiges Vieleck ist und ihre Spitze in die Mitte der Grundfläche projiziert wird.

3. Alle Seitenkanten einer regelmäßigen Pyramide sind gleich und die Seitenflächen sind gleichschenklige Dreiecke.

4. Die Höhe der Seitenfläche einer regelmäßigen Pyramide wird Apothem genannt.

5. Die Fläche der Seitenfläche einer regelmäßigen Pyramide entspricht der Hälfte des Produkts aus dem Umfang der Basis und dem Apothem.

Aufgaben

1. Wie oft vergrößert sich das Volumen eines regelmäßigen Tetraeders, wenn alle seine Kanten verdoppelt werden?

Antwort: 8.

2. Die Seiten der Basis einer regelmäßigen sechseckigen Pyramide sind gleich 10, die Seitenkanten sind gleich 13. Ermitteln Sie die Fläche der Seitenfläche der Pyramide.

Antwort: 360.

5. Ermitteln Sie das Volumen der in der Abbildung gezeigten Pyramide. Seine Basis ist ein Polygon, dessen angrenzende Seiten senkrecht stehen und eine der Seitenkanten senkrecht zur Ebene der Basis steht und gleich 3 ist.

Antwort: 27.

6. Ermitteln Sie das Volumen einer regelmäßigen dreieckigen Pyramide, deren Grundseiten gleich 1 und deren Höhe gleich ist.

Antwort: 0,25.

7. Die Seitenkanten einer dreieckigen Pyramide stehen senkrecht zueinander, jede von ihnen ist gleich 3. Bestimmen Sie das Volumen der Pyramide.

Antwort: 4.5.

8. Die Diagonale der Basis einer regelmäßigen viereckigen Pyramide beträgt 8. Die Seitenkante beträgt 5. Ermitteln Sie das Volumen der Pyramide.

Antwort: 32.

9. In einer regelmäßigen viereckigen Pyramide beträgt die Höhe 12 und das Volumen 200. Finden Sie die Seitenkante der Pyramide.

Antwort: 13.

10. Die Seiten der Basis einer regelmäßigen viereckigen Pyramide sind gleich 6, die Seitenkanten sind gleich 5. Ermitteln Sie die Oberfläche der Pyramide.

Antwort: 84.

11. Das Volumen einer regelmäßigen sechseckigen Pyramide beträgt 6. Die Seite der Grundfläche beträgt 1. Finden Sie die Seitenkante.

12. Wie oft vergrößert sich die Oberfläche eines regelmäßigen Tetraeders, wenn alle seine Kanten verdoppelt werden?

Antwort: 4.

13. Das Volumen einer regelmäßigen viereckigen Pyramide beträgt 12. Finden Sie das Volumen der Pyramide, das von ihr durch eine Ebene abgeschnitten wird, die durch die Diagonale der Grundfläche und die Mitte der gegenüberliegenden Seitenkante verläuft.

Antwort: 3.

14. Wie oft verringert sich das Volumen des Oktaeders, wenn alle seine Kanten halbiert werden?

Antwort: 8.

15. Das Volumen einer dreieckigen Pyramide beträgt 15. Die Ebene geht durch die Seite der Basis dieser Pyramide und schneidet die gegenüberliegende Seitenkante an einem Punkt, der sie im Verhältnis 1:2 teilt, gezählt von der Spitze der Pyramide. Finden Sie das größte Volumen der Pyramiden, in das die Ebene die ursprüngliche Pyramide teilt.

Antwort: 10.

16. Ermitteln Sie die Höhe einer regelmäßigen dreieckigen Pyramide, deren Grundseiten gleich 2 und deren Volumen gleich ist.

Antwort: 3.

17. In einer regelmäßigen viereckigen Pyramide beträgt die Höhe 6, die Seitenkante 10. Bestimmen Sie ihr Volumen.

Antwort: 256.

18. Von einer dreieckigen Pyramide, deren Volumen 12 beträgt, wird eine dreieckige Pyramide durch eine Ebene abgeschnitten, die durch die Spitze der Pyramide und die Mittellinie der Basis verläuft. Finden Sie das Volumen der abgeschnittenen dreieckigen Pyramide.

Antwort: 3.

Zylinder

Ein Zylinder ist ein Körper, der durch eine Zylinderfläche und zwei Kreise mit Begrenzungen begrenzt wird.

H

R

Körpervolumen	Seitenfläche	Grundfläche	Gesamtfläche

1. Generatoren eines Zylinders – zwischen den Basen eingeschlossene Generatrixsegmente.

2. Die Höhe des Zylinders ist die Länge der Erzeugenden.

3. Der axiale Abschnitt ist ein Rechteck, dessen zwei Seiten Erzeugende sind und die anderen beiden die Durchmesser der Grundflächen des Zylinders sind.

4. Kreisförmiger Abschnitt – ein Abschnitt, dessen Schnittebene senkrecht zur Zylinderachse verläuft.

5. Entwicklung der Seitenfläche des Zylinders – ein Rechteck, das zwei Kanten des Schnitts der Seitenfläche des Zylinders entlang der Mantellinie darstellt.

6. Die Fläche der Mantelfläche des Zylinders ist die Fläche seiner Entwicklung.

7. Die Gesamtoberfläche eines Zylinders nennt man die Summe der Flächen der Mantelfläche und der beiden Grundflächen.

8. Man kann immer eine Kugel um einen Zylinder herum beschreiben. Sein Mittelpunkt liegt in der Mitte der Höhe. , wobei R der Radius der Kugel, r der Radius der Basis des Zylinders und H die Höhe des Zylinders ist.

9. Sie können eine Kugel in einen Zylinder passen, wenn der Durchmesser der Basis des Zylinders gleich seiner Höhe ist. .

Aufgaben

1. Ein Teil wird in ein zylindrisches Gefäß mit 6 Litern Wasser abgesenkt. Gleichzeitig stieg der Flüssigkeitsspiegel im Gefäß um das 1,5-fache. Wie groß ist das Volumen des Teils?

Antwort: 3.

2. Ermitteln Sie das Volumen eines Zylinders, dessen Grundfläche 1 ist, dessen Erzeugende 6 ist und der in einem Winkel von 30° zur Ebene der Grundfläche geneigt ist.

Antwort: 3.

3. Zylinder und Kegel haben eine gemeinsame Grundfläche und Höhe. Ermitteln Sie das Volumen des Zylinders, wenn das Volumen des Kegels 50 beträgt.

Antwort: 150.

4. Wasser, das sich in einem zylindrischen Gefäß auf einer Höhe von 12 cm befand, wurde in ein zylindrisches Gefäß mit doppelt so großem Durchmesser gegossen. Auf welcher Höhe wird der Wasserstand im zweiten Gefäß liegen?

5. Die axiale Querschnittsfläche des Zylinders ist gleich. Finden Sie die Mantelfläche des Zylinders.

Antwort: 2.

6. Ein regelmäßiges viereckiges Prisma wird um einen Zylinder herum beschrieben, dessen Basisradius und -höhe gleich 2 sind. Ermitteln Sie die Mantelfläche des Prismas.

Antwort: 32.

7. Der Umfang der Basis des Zylinders beträgt 3. Die Mantelfläche beträgt 6. Ermitteln Sie die Höhe des Zylinders.

8. Ein zylindrischer Becher ist doppelt so hoch wie der zweite, aber der zweite ist anderthalbmal breiter. Finden Sie das Verhältnis des Volumens des zweiten Bechers zum Volumen des ersten.

Antwort: 1.125.

9. In einem zylindrischen Gefäß erreicht der Flüssigkeitsspiegel 18 cm. Wie hoch wird der Flüssigkeitsspiegel sein, wenn er in ein zweites Gefäß gegossen wird, dessen Durchmesser dreimal größer ist als der des ersten?

Antwort: 2.

Kegel

Ein Kegel ist ein Körper, der von einer Kegelfläche und einem Kreis begrenzt wird.

Kegelachse

R

Scheitel

Bildung

Seitenfläche

R

Körpervolumen	Seitenfläche	Grundfläche	Gesamtfläche

1. Die Fläche der Mantelfläche des Kegels ist die Fläche seiner Entwicklung.

2. Zusammenhang zwischen dem Pfeilungswinkel und dem Scheitelwinkel des Axialschnitts .

1. Ein Zylinder und ein Kegel haben eine gemeinsame Grundfläche und Höhe. Ermitteln Sie das Volumen des Zylinders, wenn das Volumen des Kegels 50 beträgt.

Antwort: 150.

2. Ermitteln Sie das Volumen eines Kegels mit einer Grundfläche von 2, einer Erzeugenden von 6 und einer Neigung zur Grundebene in einem Winkel von 30°.

Antwort: 2.

3. Das Volumen des Kegels beträgt 12. Parallel zur Basis des Kegels wird ein Abschnitt gezeichnet, der die Höhe in zwei Hälften teilt. Finden Sie das Volumen des abgeschnittenen Kegels.

Antwort: 1.5.

4. Wie oft ist das Volumen eines Kegels, der von einer regelmäßigen viereckigen Pyramide umschrieben wird, größer als das Volumen eines Kegels, der in diese Pyramide eingeschrieben ist?

Antwort: 2.

5. Die Höhe des Kegels beträgt 6, die Erzeugende beträgt 10. Ermitteln Sie sein Volumen dividiert durch .

Antwort: 128.

6. Zylinder und Kegel haben eine gemeinsame Grundfläche und Höhe. Ermitteln Sie das Volumen des Kegels, wenn das Volumen des Zylinders 48 beträgt.

Antwort: 16.

7. Der Durchmesser der Kegelbasis beträgt 6, und der Winkel an der Spitze des axialen Abschnitts beträgt 90°. Berechnen Sie das Volumen des Kegels dividiert durch.

8. Ein Kegel wird um eine regelmäßige viereckige Pyramide mit einer Grundseite von 4 und einer Höhe von 6 beschrieben. Ermitteln Sie sein Volumen dividiert durch .

9. Einen Kegel erhält man, indem man ein gleichschenkliges rechtwinkliges Dreieck um ein Bein gleich 6 dreht. Ermitteln Sie sein Volumen dividiert durch .

Kugel und Kugel

Eine Kugel ist eine Fläche, die aus allen Punkten im Raum besteht, die sich in einem bestimmten Abstand von einem bestimmten Punkt befinden. Eine Kugel ist ein Körper, der von einer Kugel begrenzt wird.

1. Ein Schnitt einer Kugel durch eine Ebene ist ein Kreis, wenn der Abstand vom Mittelpunkt der Kugel zur Ebene kleiner ist als der Radius der Kugel.

2. Der Schnitt einer Kugel durch eine Ebene ist ein Kreis.

3. Eine Tangentenebene an eine Kugel ist eine Ebene, die mit der Kugel nur einen gemeinsamen Punkt hat.

4. Der Radius der Kugel, gezeichnet zum Berührungspunkt der Kugel und der Ebene, steht senkrecht zur Tangentenebene.

5. Wenn der Radius einer Kugel senkrecht zu der Ebene steht, die durch ihr auf der Kugel liegendes Ende verläuft, dann ist diese Ebene tangential zur Kugel.

6. Ein Polyeder heißt umschrieben um eine Kugel, wenn die Kugel alle ihre Flächen berührt.

7. Tangentensegmente an eine Kugel, die von einem Punkt aus gezogen werden, sind gleich und bilden gleiche Winkel mit einer geraden Linie, die durch diesen Punkt und den Mittelpunkt der Kugel verläuft.

8. Eine Kugel ist in eine zylindrische Oberfläche eingeschrieben, wenn sie alle ihre Generatoren berührt.

9. Eine Kugel ist in eine konische Oberfläche eingeschrieben, wenn sie alle ihre Generatoren berührt.

Aufgaben

1. Die Radien zweier Kugeln betragen 6 und 8. Finden Sie den Radius einer Kugel, deren Oberfläche gleich der Summe ihrer Oberflächen ist.

Antwort: 10.

2. Die Fläche des Großkreises der Kugel beträgt 1. Finden Sie die Oberfläche der Kugel.

3. Wie oft vergrößert sich die Oberfläche des Balls, wenn sein Radius verdoppelt wird?

4. Die Radien von drei Kugeln betragen 3, 4 und 5. Finden Sie den Radius einer Kugel, deren Volumen gleich der Summe ihrer Volumina ist.

Antwort: 6.

5. Ein rechteckiges Parallelepiped wird um eine Kugel mit dem Radius 2 beschrieben. Finden Sie seine Oberfläche.

Antwort: 96.

6. Ein Würfel ist in eine Kugel mit dem Radius eingeschrieben. Finden Sie die Oberfläche des Würfels.

Antwort: 24.

7. Ein rechteckiges Parallelepiped wird um eine Kugel mit dem Radius 2 beschrieben. Bestimmen Sie sein Volumen.

8. Das Volumen eines rechteckigen Parallelepipeds, das eine Kugel umschreibt, beträgt 216. Finden Sie den Radius der Kugel.

Antwort: 3.

9. Die Oberfläche eines rechteckigen Parallelepipeds, das eine Kugel umschreibt, beträgt 96. Finden Sie den Radius der Kugel.

Antwort: 2.

10. Um die Kugel herum wird ein Zylinder beschrieben, dessen Mantelfläche 9 beträgt. Finden Sie die Oberfläche der Kugel.

Antwort: 9.

11. Wie oft ist die Oberfläche einer um einen Würfel umschriebenen Kugel größer als die Oberfläche einer Kugel, die in denselben Würfel eingeschrieben ist?

Antwort: 3.

12. Ein Würfel ist in eine Kugel mit dem Radius eingeschrieben. Finden Sie das Volumen des Würfels.

Antwort: 8.

Zusammengesetzte Polyeder

Aufgaben

1. Die Abbildung zeigt ein Polyeder; alle Diederwinkel des Polyeders sind rechte Winkel. Ermitteln Sie den Abstand zwischen den Eckpunkten A und C2.

Antwort: 3.

2. Ermitteln Sie den Winkel CAD2 des in der Abbildung gezeigten Polyeders. Alle Diederwinkel eines Polyeders sind rechte Winkel. Geben Sie Ihre Antwort in Grad an.

Antwort: 60.

3. Ermitteln Sie die Oberfläche des in der Abbildung gezeigten Polyeders (alle Diederwinkel sind rechte Winkel).

Antwort: 18.

4. Ermitteln Sie die Oberfläche des in der Abbildung gezeigten Polyeders (alle Diederwinkel sind rechte Winkel).

Antwort: 132

5. Finden Sie die Oberfläche des in der Abbildung gezeigten räumlichen Kreuzes, das aus Einheitswürfeln besteht.

Antwort: 30

6. Ermitteln Sie das Volumen des in der Abbildung gezeigten Polyeders (alle Diederwinkel sind richtig).

Antwort:8

7. Ermitteln Sie das Volumen des in der Abbildung gezeigten Polyeders (alle Diederwinkel sind richtig).

Antwort: 78

8. Die Abbildung zeigt ein Polyeder; alle Diederwinkel des Polyeders sind rechte Winkel. Finden Sie den Tangens des Winkels ABB3.

Antwort: 2

10. Die Abbildung zeigt ein Polyeder; alle Diederwinkel des Polyeders sind rechte Winkel. Finden Sie den Tangens des Winkels C3D3B3.

Antwort: 3

11. Durch die Mittellinie der Basis des dreieckigen Prismas wird eine Ebene parallel zur Seitenkante gezogen. Finden Sie die Seitenfläche des Prismas, wenn die Seitenfläche des beschnittenen dreieckigen Prismas 37 beträgt.

Antwort: 74.

12. Die Abbildung zeigt ein Polyeder; alle Diederwinkel des Polyeders sind rechte Winkel. Ermitteln Sie das Quadrat des Abstands zwischen den Eckpunkten B2 und D3.

Antwort: 11.

Eine Kugel kann genau dann um eine Pyramide herum beschrieben werden, wenn um ihre Basis ein Kreis beschrieben werden kann.

Um den Mittelpunkt O dieser Kugel zu konstruieren, benötigen Sie:

1. Finden Sie den Mittelpunkt O des um die Basis umschriebenen Kreises.

2. Zeichnen Sie durch Punkt O eine gerade Linie senkrecht zur Basisebene.

3. Zeichnen Sie eine Ebene durch die Mitte einer beliebigen Seitenkante der Pyramide senkrecht zu dieser Kante.

4. Finden Sie den Punkt O des Schnittpunkts der konstruierten Geraden und der Ebene.

Sonderfall: Die Seitenkanten der Pyramide sind gleich. Dann:

der Ball kann beschrieben werden;

der Mittelpunkt O der Kugel liegt auf der Höhe der Pyramide;

Wo ist der Radius der umschriebenen Kugel? - seitliche Rippe; H ist die Höhe der Pyramide.

5.2. Kugel und Prisma

Eine Kugel kann um ein Prisma genau dann beschrieben werden, wenn das Prisma gerade ist und ein Kreis um seine Basis beschrieben werden kann.

Der Mittelpunkt der Kugel ist die Mitte des Segments, das die Mittelpunkte der in der Nähe der Basen beschriebenen Kreise verbindet.

Wo ist der Radius der umschriebenen Kugel? - Radius des in der Nähe der Basis beschriebenen Kreises; H ist die Höhe des Prismas.

5.3. Kugel und Zylinder

Eine Kugel kann immer um einen Zylinder herum beschrieben werden. Der Mittelpunkt der Kugel ist das Symmetriezentrum des axialen Abschnitts des Zylinders.

5.4. Kugel und Kegel

Eine Kugel kann immer um einen Kegel herum beschrieben werden. Die Mitte des Balls; dient als Mittelpunkt eines Kreises, der den axialen Abschnitt des Kegels umschreibt.

Um Präsentationsvorschauen zu nutzen, erstellen Sie ein Google-Konto und melden Sie sich an: https://accounts.google.com

Folienunterschriften:

Beschriebene Kugeln um Polyeder.

Definition. Ein Polyeder heißt in eine Kugel eingeschrieben (und eine um ein Polyeder beschriebene Kugel) sein, wenn alle Eckpunkte des Polyeders zu dieser Kugel gehören. Folge. Der Mittelpunkt der umschriebenen Kugel ist ein Punkt, der von allen Eckpunkten des Polyeders den gleichen Abstand hat. O O O . . .

Satz 1. Die Menge der Punkte mit gleichem Abstand zu zwei gegebenen Punkten ist eine Ebene senkrecht zu einem Segment mit Enden an gegebenen Punkten, die durch dessen Mitte (die Ebene der Mittelsenkrechten zu diesem Segment) verläuft. AB ┴ α AO=OB α A B O

Satz 2. Die Menge der Punkte mit gleichem Abstand zu n gegebenen Punkten, die auf demselben Kreis liegen, ist eine gerade Linie senkrecht zur Ebene dieser Punkte, die durch den Mittelpunkt des sie umgebenden Kreises verläuft. C E A B D O a . . . . . . C E A B D . . . . .

Ein in eine Kugel eingeschriebenes Prisma. OA=OB=…=OX=R sf. O 1. Ö. O sf a 1 a .A 1 .B 1 .C 1 .D 1 E 1 . X 1. .A .B .C .D E. X. a a 1 . Ö. O 1

Folgen. 1)Eine Kugel kann um ein gerades dreieckiges Prisma herum beschrieben werden, weil Man kann immer einen Kreis um ein Dreieck beschreiben. 2) Eine Kugel kann um jedes reguläre Prisma beschrieben werden, weil Ein regelmäßiges Prisma ist gerade und ein Kreis kann immer um ein regelmäßiges Polyeder beschrieben werden. Ö. Ö. .

Aufgabe Nr. 1. Die Kugel wird von einem Prisma umschrieben, an dessen Basis ein rechtwinkliges Dreieck mit den Schenkeln 6 und 8 liegt. Die Seitenkante des Prismas beträgt 24. Finden Sie den Radius der Kugel. Gegeben: ∆ ABC – rechteckig; AC=6, BC=8, AA 1 =24. Finden Sie: Rw = ? Lösung: 1)OO 1 ┴AB 1 ; OO 1 =AA 1 =24. 2) ABC: AB=10. 3) O w OB: R w = O w B=√OO w 2 + OB 2 = = √144+25=13 Antwort: 13. O 1 O. . . R w O sh C 1 B 1 A 1 A C B

Aufgabe Nr. 3. Die Abmessungen eines Quaders betragen 2,3 und 5. Ermitteln Sie den Radius der umschriebenen Kugel. Gegeben:AB=a=2; BC=b=3; CC 1 =c=5. Finden Sie: Rw = ? Lösung: 1) AC 2 =a 2 +b 2 +c 2. 2) A 1 C 2 =25+9+4=38 (Eigenschaft der Diagonalen eines rechteckigen Parallelepipeds) 3) A 1 C=√38; R w = O w C = √38 /2 Antwort: √38 /2 D 1 C 1 B 1 A 1 A B C D 5 2 3 . . . Oh sh

Aufgabe Nr. 3. Die Seite der Basis eines regelmäßigen dreieckigen Prismas ist gleich a und die Seitenkante ist gleich 2 a. Finden Sie den Radius der umschriebenen Kugel. Gegeben: AB=BC=AC=a, AA 1 ┴ABC ; AA 1= 2a. Finden Sie: Rw = ? Lösung: 1)AB=AO √3; AO=a/√3. 2)R w =√ a 2 + a 2 /3=2a/ √ 3 Antwort: 2a/ √ 3 C 1 B A 1 C B 1 A O w R w. O O 1

Folgen. 1) Man kann immer eine Kugel um eine dreieckige Pyramide beschreiben, da man immer einen Kreis um ein Dreieck beschreiben kann. 2) Man kann immer eine Kugel um eine regelmäßige Pyramide herum beschreiben. 3) Wenn die Seitenkanten der Pyramide gleich sind (gleich zur Grundfläche geneigt), dann kann um eine solche Pyramide immer eine Kugel beschrieben werden. *In den letzten beiden Fällen liegt der Mittelpunkt der Kugel auf der Geraden, die die Höhe der Pyramide enthält. Ö. Ö.

Probleme (beschriebene Kugel in der Nähe der Pyramide). Um die Pyramide PABC wird eine Kugel beschrieben, deren Basis ein regelmäßiges Dreieck ABC mit der Seite 4√3 ist. Die Seitenkante PA steht senkrecht zur Ebene der Pyramidenbasis und ist gleich 6. Finden Sie den Radius der Kugel. Gegeben: AB=BC=AC=4 √3 ; PA ┴(ABC); PA=6. Finden Sie: Rw = ? Lösung: 1) OO SF ┴(ABC); O – Mittelpunkt eines um ∆ABC umschriebenen Kreises; K O SF ┴ PA; KP=AK (KO SF Eine der Mittelsenkrechten zur Seitenkante PA); O SF ist das Zentrum der umschriebenen Kugel. 2) OO SF ┴(ABC); OO SF gehört zu (AKO); PA ┴(ABC); AK gehört zu (AKO); bedeutet KA|| OO SF; . O SF. O K. P. A. B. C

Probleme (beschriebene Kugel in der Nähe der Pyramide). 3) KO c f ┴AP; KO c f gehört zu (AOK); AO┴AP; AO gehört zu (AOK) ; bedeutet KO c f || AO; 4) Aus (2) und (3): AOO c f K-Rechteck, AK=PA/2=3; 5) AO=AB/ √3 =4; 6) ∆ AO O c f: AO c f = R w =5 Antwort: 5

Probleme (beschriebene Kugel in der Nähe der Pyramide). Bei einer regelmäßigen viereckigen Pyramide ist die Seitenkante in einem Winkel von 45° zur Grundfläche geneigt. Die Höhe der Pyramide beträgt h. Finden Sie den Radius der umschriebenen Kugel. Gegeben: PABCD – regelmäßige Pyramide; (AP^(ABC))=45 ˚; PO=h. Finden Sie: Rw = ? Lösung: 1) AO=OP=h; AP=h √ 2; 2) ∆PAP ​​​​1 – rechteckig; PP 1 – Kugeldurchmesser; PP 1 = 2 R w; AP 2 = PP 1 *OP; (h √ 2) 2 =2 R w *h; R w = 2h 2 /2h=h. Antwort: h. C. B A. .D .P .P 1 . Ö

Aufgaben (beschriebene Kugel in der Nähe der Pyramide). Auf sich allein. Der Radius einer von einem regelmäßigen Tetraeder umschriebenen Kugel ist gleich R. Finden Sie die Gesamtoberfläche des Tetraeders.

Probleme (beschriebene Kugel in der Nähe der Pyramide). Auf sich allein. Gegeben: DABC – regelmäßiges Tetraeder; R ist der Radius der Kugel. Fund: S Vollsalmler. =? Lösung: 1) Da das Tetraeder regelmäßig ist, gehört der Mittelpunkt der umschriebenen Kugel zu der Geraden, die die Höhe der Pyramide enthält; 2) S Vollsalmler. = a 2 √ 3/4*4= a 2 √ 3; 3) Die Punkte D, A, D 1 gehören zum selben Kreis – dem Schnitt der Kugel durch die Ebene DAD 1, was bedeutet, dass der Winkel DAD 1 ein eingeschriebener Winkel basierend auf dem Durchmesser DD 1 ist; Winkel DAD 1 =90 ˚; 4) AO – Höhe ∆ ADD 1, gezeichnet vom Scheitelpunkt des rechten Winkels. AD 2 = DO*DD 1 ; 5) AO=a/ √ 3; DO= √ a 2 -a 2 /3=a √ 2 / √ 3; a 2 = a √ 2 / √ 3*2R; a= √ 2 / √ 3*2R; a 2 = 8R 2 /3; .D 1 .D .O .B .C A. a a

Probleme (beschriebene Kugel in der Nähe der Pyramide). Auf sich allein. 6) S voll tet. = 8R 2 √ 3/3 Antwort: 8R 2 √ 3/3