Смежные грани параллелепипеда параллельны. Прямоугольный параллелепипед — Гипермаркет знаний

На этом уроке все желающие смогут изучить тему «Прямоугольный параллелепипед». В начале урока мы повторим, что такое произвольный и прямой параллелепипеды, вспомним свойства их противоположных граней и диагоналей параллелепипеда. Затем рассмотрим, что такое прямоугольный параллелепипед, и обсудим его основные свойства.

Тема: Перпендикулярность прямых и плоскостей

Урок: Прямоугольный параллелепипед

Поверхность, составленная из двух равных параллелограммов АВСD и А 1 В 1 С 1 D 1 и четырех параллелограммов АВВ 1 А 1 , ВСС 1 В 1 , СDD 1 С 1 , DАА 1 D 1 , называется параллелепипедом (рис. 1).

Рис. 1 Параллелепипед

То есть: имеем два равных параллелограмма АВСD и А 1 В 1 С 1 D 1 (основания), они лежат в параллельных плоскостях так, что боковые ребра АА 1 , ВВ 1 , DD 1 , СС 1 параллельны. Таким образом, составленная из параллелограммов поверхность называется параллелепипедом .

Таким образом, поверхность параллелепипеда - это сумма всех параллелограммов, из которых составлен параллелепипед.

1. Противоположные грани параллелепипеда параллельны и равны.

(фигуры равны, то есть их можно совместить наложением)

Например:

АВСD = А 1 В 1 С 1 D 1 (равные параллелограммы по определению),

АА 1 В 1 В = DD 1 С 1 С (так как АА 1 В 1 В и DD 1 С 1 С - противоположные грани параллелепипеда),

АА 1 D 1 D = ВВ 1 С 1 С (так как АА 1 D 1 D и ВВ 1 С 1 С - противоположные грани параллелепипеда).

2. Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.

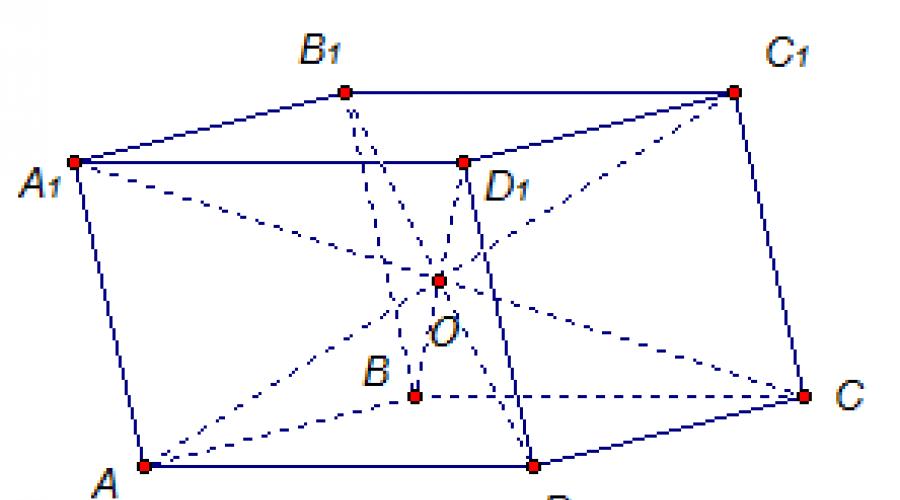
Диагонали параллелепипеда АС 1 , В 1 D, А 1 С, D 1 В пересекаются в одной точке О, и каждая диагональ делится этой точкой пополам (рис. 2).

Рис. 2 Диагонали параллелепипеда пересекаются и деляться точкой пересечения пополам.

3. Имеются три четверки равных и параллельных ребер параллелепипеда : 1 - АВ, А 1 В 1 , D 1 C 1 , DC, 2 - AD, A 1 D 1 , B 1 C 1 , BC, 3 - АА 1 , ВВ 1 , СС 1 , DD 1 .

Определение. Параллелепипед называется прямым, если его боковые ребра перпендикулярны основаниям.

Пусть боковое ребро АА 1 перпендикулярно основанию (рис. 3). Это означает, что прямая АА 1 перпендикулярна прямым АD и АВ, которые лежат в плоскости основания. А, значит, в боковых гранях лежат прямоугольники. А в основаниях лежат произвольные параллелограммы. Обозначим, ∠BAD = φ, угол φ может быть любым.

Рис. 3 Прямой параллелепипед

Итак, прямой параллелепипед - это параллелепипед, в котором боковые ребра перпендикулярны основаниям параллелепипеда.

Определение. Параллелепипед называется прямоугольным, если его боковые ребра перпендикулярны к основанию. Основания являются прямоугольниками.

Параллелепипед АВСDА 1 В 1 С 1 D 1 - прямоугольный (рис. 4), если:

1. АА 1 ⊥ АВСD (боковое ребро перпендикулярно плоскости основания, то есть параллелепипед прямой).

2. ∠ВАD = 90°, т. е. в основании лежит прямоугольник.

Рис. 4 Прямоугольный параллелепипед

Прямоугольный параллелепипед обладает всеми свойствами произвольного параллелепипеда. Но есть дополнительные свойства, которые выводятся из определения прямоугольного параллелепипеда.

Итак, прямоугольный параллелепипед - это параллелепипед, у которого боковые ребра перпендикулярны основанию. Основание прямоугольного параллелепипеда - прямоугольник .

1. В прямоугольном параллелепипеде все шесть граней прямоугольники.

АВСD и А 1 В 1 С 1 D 1 - прямоугольники по определению.

2. Боковые ребра перпендикулярны основанию . Значит, все боковые грани прямоугольного параллелепипеда - прямоугольники.

3. Все двугранные углы прямоугольного параллелепипеда прямые.

Рассмотрим, например, двугранный угол прямоугольного параллелепипеда с ребром АВ, т. е. двугранный угол между плоскостями АВВ 1 и АВС.

АВ - ребро, точка А 1 лежит в одной плоскости - в плоскости АВВ 1 , а точка D в другой - в плоскости А 1 В 1 С 1 D 1 . Тогда рассматриваемый двугранный угол можно еще обозначить следующим образом: ∠А 1 АВD.

Возьмем точку А на ребре АВ. АА 1 - перпендикуляр к ребру АВ в плоскости АВВ- 1 , AD перпендикуляр к ребру АВ в плоскости АВС. Значит, ∠А 1 АD - линейный угол данного двугранного угла. ∠А 1 АD = 90°, значит, двугранный угол при ребре АВ равен 90°.

∠(АВВ 1 , АВС) = ∠(АВ) = ∠А 1 АВD= ∠А 1 АD = 90°.

Аналогично доказывается, что любые двугранные углы прямоугольного параллелепипеда прямые.

Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.

Примечание. Длины трех ребер, исходящих из одной вершины прямоугольного параллелепипеда, являются измерениями прямоугольного параллелепипеда. Их иногда называют длина, ширина, высота.

Дано: АВСDА 1 В 1 С 1 D 1 - прямоугольный параллелепипед (рис. 5).

Доказать: .

Рис. 5 Прямоугольный параллелепипед

Доказательство:

Прямая СС 1 перпендикулярна плоскости АВС, а значит, и прямой АС. Значит, треугольник СС 1 А - прямоугольный. По теореме Пифагора:

Рассмотрим прямоугольный треугольник АВС. По теореме Пифагора:

Но ВС и AD - противоположные стороны прямоугольника. Значит, ВС = AD. Тогда:

Так как , а , то. Поскольку СС 1 = АА 1 , то что и требовалось доказать.

Диагонали прямоугольного параллелепипеда равны.

Обозначим измерения параллелепипеда АВС как a, b, c (см. рис. 6), тогда АС 1 = СА 1 = В 1 D = DВ 1 =

Параллелепипед – это геометрическая фигура, все 6 граней которой представляют собой параллелограммы.

В зависимости от вида этих параллелограммов различают следующие виды параллелепипеда:

• прямой;
• наклонный;
• прямоугольный.

Прямым параллелепипедом называют четырехугольную призму, ребра которой составляют с плоскостью основания угол 90 °.

Прямоугольным параллелепипедом называют четырехугольную призму, все грани которой являются прямоугольниками. Куб есть разновидность четырехугольной призмы, у которой все грани и ребра равны между собой.

Особенности фигуры предопределяют ее свойства. К ним относят 4 следующих утверждений:

Запомнить все приведенные свойства просто, они легки для понимания и выводятся логически исходя из вида и особенностей геометрического тела. Однако, незамысловатые утверждения могут быть невероятно полезны при решении типовых заданий ЕГЭ и позволят сэкономить время необходимое для прохождения теста.

Формулы параллелепипеда

Для поиска ответов на поставленную задачу недостаточно знать только свойства фигуры. Также могут понадобиться и некоторые формулы для нахождения площади и объема геометрического тела.

Площадь оснований находится также как и соответствующий показатель параллелограмма или прямоугольника. Выбирать основание параллелограмма можно самостоятельно. Как правило, при решении задач проще работать с призмой, в основании которой лежит прямоугольник.

Формула нахождения боковой поверхности параллелепипеда, также может понадобиться в тестовых заданиях.

Примеры решения типовых заданий ЕГЭ

Задание 1.

Дано : прямоугольный параллелепипед с измерениями 3, 4 и 12 см.
Необходимо найти длину одной из главных диагоналей фигуры.
Решение : Любое решение геометрической задачи должно начинаться с построения правильного и четкого чертежа, на котором будет обозначено «дано» и искомая величина. На рисунке ниже приведен пример правильного оформления условий задания.

Рассмотрев сделанный рисунок и вспомнив все свойства геометрического тела, приходим к единственно верному способу решения. Применив 4 свойство параллелепипеда, получим следующее выражение:

После несложных вычислений получим выражение b2=169, следовательно, b=13. Ответ задания найден, на его поиск и чертеж необходимо потратить не более 5 минут.

Различается несколько типов параллелепипедов:

· Прямоугольный параллелепипед - это параллелепипед, у которого все грани - прямоугольники ;

· Прямой параллелепипед - это параллелепипед, у которого 4 боковые грани - параллелограммы;

· Наклонный параллелепипед - это параллелепипед, боковые грани которого не перпендикулярны основаниям.

Основные элементы

Две грани параллелепипеда, не имеющие общего ребра, называются противоположными, а имеющие общее ребро - смежными. Две вершины параллелепипеда, не принадлежащие одной грани, называются противоположными. Отрезок, соединяющий противоположные вершины, называется диагональю параллелепипеда. Длины трёх рёбер прямоугольного параллелепипеда, имеющих общую вершину, называют его измерениями.

Свойства

· Параллелепипед симметричен относительно середины его диагонали.

· Любой отрезок с концами, принадлежащими поверхности параллелепипеда и проходящий через середину его диагонали, делится ею пополам; в частности, все диагонали параллелепипеда пересекаются в одной точке и делятся ею пополам.

· Противолежащие грани параллелепипеда параллельны и равны.

· Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений

Основные формулы

Прямой параллелепипед

· Площадь боковой поверхности S б =Р о *h, где Р о - периметр основания, h - высота

· Площадь полной поверхности S п =S б +2S о, где S о - площадь основания

· Объём V=S о *h

Прямоугольный параллелепипед

· Площадь боковой поверхности S б =2c(a+b), где a, b - стороны основания, c - боковое ребро прямоугольного параллелепипеда

· Площадь полной поверхности S п =2(ab+bc+ac)

· Объём V=abc, где a, b, c - измерения прямоугольного параллелепипеда.

· Площадь боковой поверхности S=6*h 2 , где h – высота ребра куба

34. Тетраэдр - правильный многогранник, имеет 4 грани, которые являются правильными треугольниками. Вершин у тетраэдра 4 , к каждой вершине сходится 3 ребра, а всего ребер 6 . Также тетраэдр является пирамидой.

Треугольники, из которых состоит тетраэдр, называются гранями (АОС, ОСВ, ACB, AOB) , их стороны --- ребрами (AO, OC, OB) , а вершины ---вершинами (A, B, C, O) тетраэдра. Два ребра тетраэдра, не имеющие общих вершин, называются противоположными ... Иногда выделяют одну одну из граней тетраэдра и называют ее основанием , а три другие --- боковыми гранями .

Тетраэдр называется правильным , если все его грани - равносторонние треугольники. При этом правильный тетраэдр и правильная треугольная пирамида – это не одно и то же.

У правильного тетраэдра все двугранные углы при рёбрах и все трёхгранные углы при вершинах равны.

35. Правильная призма

Призмой называется многогранник, у которого две грани (основания) лежат в параллельных плоскостях, а все ребра вне этих граней параллельны между собой. Грани, отличные от оснований, называются боковыми гранями, а их ребра называются боковыми ребрами. Все боковые ребра равны между собой как параллельные отрезки, ограниченные двумя параллельными плоскостями. Все боковые грани призмы являются параллелограммами. Соответствующие стороны оснований призмы равны и параллельны. Прямой называется призма, у которой боковое ребро перпендикулярно плоскости основания, другие призмы называются наклонными. В основании правильной призмы лежит правильный многоугольник. У такой призмы все грани – равные прямоугольники.

Поверхность призмы состоит из двух оснований и боковой поверхности. Высотой призмы называется отрезок, являющийся общим перпендикуляром плоскостей, в которых лежат основания призмы. Высота призмы есть расстояние H между плоскостями оснований.

Площадью боковой поверхности S б призмы называется сумма площадей ее боковых граней. Площадью полной поверхности S п призмы называется сумма площадей всех ее граней. S п = S б + 2S ,где S – площадь основания призмы, S б – площадь боковой поверхности.

36. Многогранник, у которого одна грань, называемая основанием , – многоугольник,
а другие грани – треугольники с общей вершиной, называется пирамидой .

Грани, отличные от основания, называются боковыми.
Общая вершина боковых граней называется вершиной пирамиды.
Ребра, соединяющие вершину пирамиды с вершинами основания, называются боковыми.
Высотой пирамиды называется перпендикуляр, проведенный из вершины пирамиды на ее основание.

Пирамида называется правильной, если ее основание – правильный многоугольник, а высота проходит через центр основания.

Апофемой боковой грани правильной пирамиды называется высота этой грани, проведенная из вершины пирамиды.

Плоскость, параллельная основанию пирамиды, отсекает ее на подобную пирамиду и усеченную пирамиду.

Свойства правильных пирамид

• Боковые ребра правильной пирамиды - равны.
• Боковые грани правильной пирамиды - равные друг другу равнобедренные треугольники.

Если все боковые ребра равны, то

·высота проектируется в центр описанной окружности;

·боковые ребра образуют с плоскостью основания равные углы.

Если боковые грани наклонены к плоскости основания под одним углом, то

·высота проектируется в центр вписанной окружности;

·высоты боковых граней равны;

·площадь боковой поверхности равна половине произведения периметра основания на высоту боковой грани

37. Функцию y=f(x), где x принадлежит множеству натуральных чисел, называют функцией натурального аргумента или числовой последовательностью. Обозначают ее y=f(n), или (y n)

Последовательности можно задавать различными способами, словесно, так задается последовательность простых чисел:

2, 3, 5, 7, 11 и т.д

Считают, что последовательность задана аналитически, если указана формула ее n-го члена:

1, 4, 9, 16, …, n 2 , …

2) y n = C. Такую последовательность называют постоянной или стационарной. Например:

2, 2, 2, 2, …, 2, …

3) y n =2 n . Например,

2, 2 2 , 2 3 , 2 4 , …, 2 n , …

Последовательность называют ограниченной сверху, если все ее члены не больше некоторого числа. Иными словами, последовательность можно назвать ограниченной, если есть такое число М, что выполняется неравенство y n меньше или равно M. Число М называют верхней границей последовательности. Например последовательность: -1, -4, -9, -16, …, - n 2 ; ограничена сверху.

Аналогично, последовательность можно назвать ограниченной снизу, если все ее члены больше некоторого числа. Если последовательность ограничена и сверху и снизу она называется ограниченной.

Последовательность называют возрастающей, если каждый ее последующий член больше предыдущего.

Последовательность называют убывающей, если каждый ее последующий член меньше предыдущего. Возрастающие и убывающие последовательности определяют одним термином – монотонные последовательности.

Рассмотрим две последовательности:

1) y n: 1, 3, 5, 7, 9, …, 2n-1, …

2) x n: 1, ½, 1/3, 1/ 4, …, 1/n, …

Если мы изобразим члены этой последовательности на числовой прямой, то заметим что, во втором случае члены последовательности сгущаются вокруг одной точки, а в первом случае такого нет. В подобных случаях говорят, что последовательность y n расходится, а последовательность x n сходится.

Число b называют пределом последовательности y n , если в любой заранее выбранной окрестности точки b, содержатся все члены последовательности, начиная с некоторого номера.

В данном случае мы можем написать:

Если частное прогрессии по модулю меньше единицы, то предел этой последовательности, при х, стремящимся к бесконечности равен нулю.

Если последовательность сходится, то только к одному пределу

Если последовательность сходится, то она ограничена.

Теорема Вейерштрасса: Если последовательность монотонно сходится, то она ограничена.

Предел стационарной последовательности равен любому члену последовательности.

Свойства:

1) Предел суммы равен сумме пределов

2) Предел произведения равен произведению пределов

3) Предел частного равен частному пределов

4) Постоянный множитель можно вынести за знак предела

Вопрос 38
сумма бесконечной геометрической прогрессии

Геометрическая прогрессия - последовательность чисел b 1 , b 2 , b 3 ,.. (членов прогрессии), в которой каждое последующее число, начиная со второго, получается из предыдущего умножением его на определённое число q (знаменатель прогрессии), где b 1 ≠0 , q≠0.

Сумма бесконечной геометрической прогрессии – это предельное число, к которому сходится последовательность прогрессии.

Говоря иначе, какой бы длинной не была геометрическая прогрессия, сумма ее членов не больше какого-то определенного числа и практически равна этому числу. Оно и называется суммой геометрической прогрессии.

Не любая геометрическая прогрессия имеет такую предельную сумму. Она может быть только у такой прогрессии, знаменатель которой – дробное число меньше 1.

Или (равносильно) многогранник, у которого шесть граней и каждая из них - параллелограмм .

Типы параллелепипеда

Различается несколько типов параллелепипедов:

• Прямоугольный параллелепипед - это параллелепипед, у которого все грани - прямоугольники .
• Прямой параллелепипед - это параллелепипед, у которого 4 боковые грани прямоугольники.
• Наклонный параллелепипед - это параллелепипед, боковые грани которого не перпендикулярны основаниям.

Основные элементы

Две грани параллелепипеда, не имеющие общего ребра, называются противоположными, а имеющие общее ребро - смежными. Две вершины параллелепипеда, не принадлежащие одной грани, называются противоположными. Отрезок , соединяющий противоположные вершины, называется диагональю параллелепипеда. Длины трёх рёбер прямоугольного параллелепипеда, имеющих общую вершину, называют его измерениями.

Свойства

• Параллелепипед симметричен относительно середины его диагонали.
• Любой отрезок с концами, принадлежащими поверхности параллелепипеда и проходящий через середину его диагонали, делится ею пополам; в частности, все диагонали параллелепипеда пересекаются в одной точке и делятся ею пополам.
• Противолежащие грани параллелепипеда параллельны и равны.
• Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений.

Основные формулы

Прямой параллелепипед

Площадь боковой поверхности S б =Р о *h, где Р о - периметр основания, h - высота

Площадь полной поверхности S п =S б +2S о, где S о - площадь основания

Объём V=S о *h

Прямоугольный параллелепипед

Площадь боковой поверхности S б =2c(a+b), где a, b - стороны основания, c - боковое ребро прямоугольного параллелепипеда

Площадь полной поверхности S п =2(ab+bc+ac)

Объём V=abc, где a, b, c - измерения прямоугольного параллелепипеда.

Куб

Площадь поверхности : $S=6a^2$
Объём : $V=a^3$, где $a$ - ребро куба.

Произвольный параллелепипед

Объём и соотношения в наклонном параллелепипеде часто определяются с помощью векторной алгебры. Объём параллелепипеда равен абсолютной величине смешанного произведения трёх векторов, определяемых тремя сторонами параллелепипеда, исходящими из одной вершины. Соотношение между длинами сторон параллелепипеда и углами между ними даёт утверждение, что определитель Грама указанных трёх векторов равен квадрату их смешанного произведения :215 .

В математическом анализе

В математическом анализе под n-мерным прямоугольным параллелепипедом $B$ понимают множество точек $x\; =\; (x\_1,\backslash ldots,x\_n)$ вида $B\; =\; \backslash \{x|a\_1\backslash leqslant\; x\_1\backslash leqslant\; b\_1,\backslash ldots,a\_n\backslash leqslant\; x\_n\backslash leqslant\; b\_n\backslash \}$

Напишите отзыв о статье "Параллелепипед"

Примечания

Ссылки

Правильные Правильные невыпуклые Выпуклые Формулы , теоремы , теории Прочее

Отрывок, характеризующий Параллелепипед

– On dit que les rivaux se sont reconcilies grace a l"angine… [Говорят, что соперники примирились благодаря этой болезни.]
Слово angine повторялось с большим удовольствием.
– Le vieux comte est touchant a ce qu"on dit. Il a pleure comme un enfant quand le medecin lui a dit que le cas etait dangereux. [Старый граф очень трогателен, говорят. Он заплакал, как дитя, когда доктор сказал, что случай опасный.]
– Oh, ce serait une perte terrible. C"est une femme ravissante. [О, это была бы большая потеря. Такая прелестная женщина.]
– Vous parlez de la pauvre comtesse, – сказала, подходя, Анна Павловна. – J"ai envoye savoir de ses nouvelles. On m"a dit qu"elle allait un peu mieux. Oh, sans doute, c"est la plus charmante femme du monde, – сказала Анна Павловна с улыбкой над своей восторженностью. – Nous appartenons a des camps differents, mais cela ne m"empeche pas de l"estimer, comme elle le merite. Elle est bien malheureuse, [Вы говорите про бедную графиню… Я посылала узнавать о ее здоровье. Мне сказали, что ей немного лучше. О, без сомнения, это прелестнейшая женщина в мире. Мы принадлежим к различным лагерям, но это не мешает мне уважать ее по ее заслугам. Она так несчастна.] – прибавила Анна Павловна.
Полагая, что этими словами Анна Павловна слегка приподнимала завесу тайны над болезнью графини, один неосторожный молодой человек позволил себе выразить удивление в том, что не призваны известные врачи, а лечит графиню шарлатан, который может дать опасные средства.
– Vos informations peuvent etre meilleures que les miennes, – вдруг ядовито напустилась Анна Павловна на неопытного молодого человека. – Mais je sais de bonne source que ce medecin est un homme tres savant et tres habile. C"est le medecin intime de la Reine d"Espagne. [Ваши известия могут быть вернее моих… но я из хороших источников знаю, что этот доктор очень ученый и искусный человек. Это лейб медик королевы испанской.] – И таким образом уничтожив молодого человека, Анна Павловна обратилась к Билибину, который в другом кружке, подобрав кожу и, видимо, сбираясь распустить ее, чтобы сказать un mot, говорил об австрийцах.
– Je trouve que c"est charmant! [Я нахожу, что это прелестно!] – говорил он про дипломатическую бумагу, при которой отосланы были в Вену австрийские знамена, взятые Витгенштейном, le heros de Petropol [героем Петрополя] (как его называли в Петербурге).
– Как, как это? – обратилась к нему Анна Павловна, возбуждая молчание для услышания mot, которое она уже знала.
И Билибин повторил следующие подлинные слова дипломатической депеши, им составленной:
– L"Empereur renvoie les drapeaux Autrichiens, – сказал Билибин, – drapeaux amis et egares qu"il a trouve hors de la route, [Император отсылает австрийские знамена, дружеские и заблудшиеся знамена, которые он нашел вне настоящей дороги.] – докончил Билибин, распуская кожу.
– Charmant, charmant, [Прелестно, прелестно,] – сказал князь Василий.
– C"est la route de Varsovie peut etre, [Это варшавская дорога, может быть.] – громко и неожиданно сказал князь Ипполит. Все оглянулись на него, не понимая того, что он хотел сказать этим. Князь Ипполит тоже с веселым удивлением оглядывался вокруг себя. Он так же, как и другие, не понимал того, что значили сказанные им слова. Он во время своей дипломатической карьеры не раз замечал, что таким образом сказанные вдруг слова оказывались очень остроумны, и он на всякий случай сказал эти слова, первые пришедшие ему на язык. «Может, выйдет очень хорошо, – думал он, – а ежели не выйдет, они там сумеют это устроить». Действительно, в то время как воцарилось неловкое молчание, вошло то недостаточно патриотическое лицо, которого ждала для обращения Анна Павловна, и она, улыбаясь и погрозив пальцем Ипполиту, пригласила князя Василия к столу, и, поднося ему две свечи и рукопись, попросила его начать. Все замолкло.