Sept points sont marqués sur le graphique dérivé. A quel point la valeur de la dérivée est-elle la plus grande ? Trouver les intervalles d'augmentation et de diminution d'une fonction
Lire aussi
Chers amis! Le groupe de tâches liées à la dérivée comprend des tâches - dans la condition, le graphe de la fonction est donné, plusieurs points sur ce graphe et la question est :
À quel point la valeur de la dérivée est-elle la plus grande (la plus petite) ?
Répétons brièvement :
La dérivée au point est égale à la pente de la tangente passant parce point sur le graphique.
Àle coefficient global de la tangente, quant à lui, est égal à la tangente de la pente de cette tangente.
*Il s'agit de l'angle entre la tangente et l'axe des x.


1. Sur des intervalles de fonction croissante, la dérivée a une valeur positive.
2. Sur les intervalles de sa diminution, la dérivée a une valeur négative.

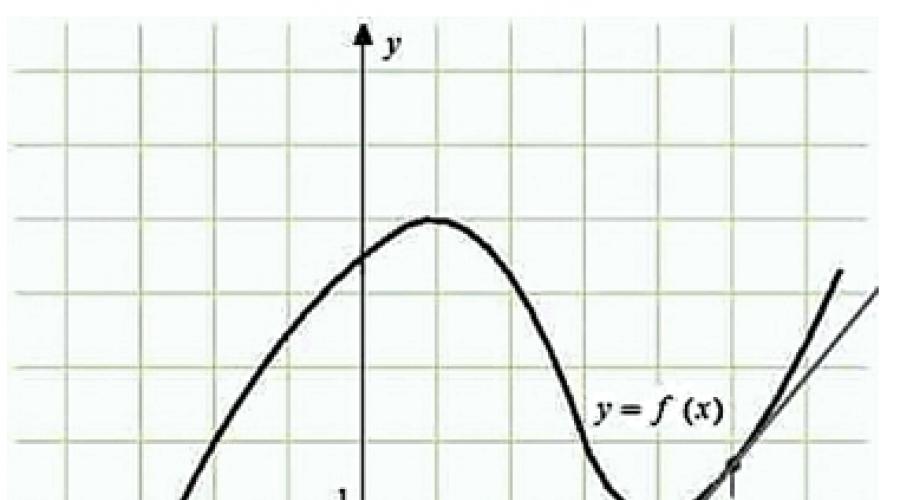
Considérez le croquis suivant :

Aux points 1,2,4, la dérivée de la fonction a une valeur négative, puisque ces points appartiennent aux intervalles décroissants.
Aux points 3,5,6, la dérivée de la fonction a une valeur positive, puisque ces points appartiennent aux intervalles d'augmentation.
Comme vous pouvez le voir, tout est clair avec la valeur de la dérivée, c'est-à-dire qu'il n'est pas difficile de déterminer son signe (positif ou négatif) à un certain point du graphique.
De plus, si nous construisons mentalement des tangentes en ces points, nous verrons que les droites passant par les points 3, 5 et 6 forment des angles avec l'axe oX compris entre 0 et 90°, et les droites passant par les points 1, 2 et 4 forment avec l'axe oX, des angles allant de 90 o à 180 o.
* La relation est claire : les tangentes passant par des points appartenant à des intervalles de fonctions croissantes forment des angles aigus avec l'axe oX, les tangentes passant par des points appartenant à des intervalles de fonctions décroissantes forment des angles obtus avec l'axe oX.
Maintenant la question importante !
Comment évolue la valeur de la dérivée ? Après tout, la tangente en différents points du graphique d'une fonction continue forme des angles différents, selon le point du graphique par lequel elle passe.
* Ou, en termes simples, la tangente est située, pour ainsi dire, "plus horizontalement" ou "plus verticalement". Voir:
Les lignes droites forment des angles avec l'axe oX allant de 0 à 90 o

Les lignes droites forment des angles avec l'axe oX allant de 90 o à 180 o

Donc s'il y a des questions :
- Auquel des points donnés sur le graphique la valeur de la dérivée a-t-elle la plus petite valeur ?
- Auquel des points donnés du graphique la valeur de la dérivée a-t-elle la plus grande valeur ?
alors pour la réponse il faut comprendre comment la valeur de la tangente de l'angle de la tangente change dans la plage de 0 à 180 o.
*Comme déjà mentionné, la valeur de la dérivée de la fonction en un point est égale à la tangente de la pente de la tangente à l'axe des abscisses.
La valeur de la tangente change comme suit :
Lorsque la pente de la droite passe de 0 o à 90 o, la valeur de la tangente, et donc de la dérivée, passe de 0 à +∞, respectivement ;
Lorsque la pente de la droite passe de 90 o à 180 o, la valeur de la tangente, et donc de la dérivée, change en conséquence –∞ en 0.
Cela peut être clairement vu sur le graphique de la fonction tangente :

En termes simples :
Lorsque l'angle d'inclinaison de la tangente est de 0 o à 90 o
Plus il est proche de 0 o, plus la valeur de la dérivée sera proche de zéro (du côté positif).
Plus l'angle est proche de 90°, plus la valeur de la dérivée augmentera vers +∞.
Lorsque l'angle d'inclinaison de la tangente est de 90 o à 180 o
Plus il est proche de 90 o, plus la valeur de la dérivée va décroître vers –∞.
Plus l'angle est proche de 180°, plus la valeur de la dérivée sera proche de zéro (du côté négatif).
317543. La figure montre un graphique de la fonction y = F(X) et points marqués–2, –1, 1, 2. Auquel de ces points la valeur de la dérivée est-elle la plus grande ? Veuillez indiquer ce point dans votre réponse.

Nous avons quatre points : deux d'entre eux appartiennent aux intervalles sur lesquels la fonction diminue (ce sont les points –1 et 1) et deux aux intervalles sur lesquels la fonction augmente (ce sont les points –2 et 2).
Nous pouvons immédiatement conclure qu'aux points -1 et 1 la dérivée a une valeur négative, aux points -2 et 2 elle a une valeur positive. Par conséquent, dans ce cas, il est nécessaire d'analyser les points -2 et 2 et de déterminer lequel d'entre eux aura la plus grande valeur. Construisons des tangentes passant par les points indiqués :

La valeur de la tangente de l'angle entre la droite a et l'axe des abscisses sera supérieure à la valeur de la tangente de l'angle entre la droite b et cet axe. Cela signifie que la valeur de la dérivée au point -2 sera la plus grande.
Répondons à la question suivante : en quel point -2, -1, 1 ou 2 la valeur de la dérivée est-elle la plus grande négative ? Veuillez indiquer ce point dans votre réponse.
La dérivée aura une valeur négative aux points appartenant aux intervalles décroissants, donc considérons les points -2 et 1. Construisons les tangentes qui les traversent :

On voit que l'angle obtus entre la droite b et l'axe oX est "plus proche" de 180 sur , donc sa tangente sera supérieure à la tangente de l'angle formé par la droite a et l'axe des abscisses.
Ainsi, au point x = 1, la valeur de la dérivée sera la plus grande négative.
317544. La figure montre un graphique de la fonction y = F(X) et points marqués–2, –1, 1, 4. Auquel de ces points la valeur de la dérivée est-elle la plus petite ? Veuillez indiquer ce point dans votre réponse.

Nous avons quatre points : deux d'entre eux appartiennent aux intervalles sur lesquels la fonction décroît (ce sont les points –1 et 4) et deux aux intervalles sur lesquels la fonction croît (ce sont les points –2 et 1).
Nous pouvons immédiatement conclure qu'aux points -1 et 4 la dérivée a une valeur négative, aux points -2 et 1 elle a une valeur positive. Par conséquent, dans ce cas, il est nécessaire d'analyser les points -1 et 4 et de déterminer lequel d'entre eux aura la plus petite valeur. Construisons des tangentes passant par les points indiqués :

La valeur de la tangente de l'angle entre la droite a et l'axe des abscisses sera supérieure à la valeur de la tangente de l'angle entre la droite b et cet axe. Cela signifie que la valeur de la dérivée au point x = 4 sera la plus petite.
Réponse : 4
J'espère que je ne vous "surcharge" pas avec la quantité d'écriture. En fait, tout est très simple, il suffit de comprendre les propriétés de la dérivée, sa signification géométrique et comment la valeur de la tangente de l'angle passe de 0 à 180°.
1. Tout d'abord, déterminez les signes de la dérivée en ces points (+ ou -) et sélectionnez les points nécessaires (selon la question posée).
2. Construisez des tangentes en ces points.
3. À l'aide du tracé tangésoïde, marquez schématiquement les coins et affichezAlexandre.
P.S: Je vous serais reconnaissant de parler du site dans les réseaux sociaux.
Bonjour! Frappons l'UTILISATION qui approche avec une formation systématique de haute qualité et de la persévérance dans le broyage du granit de la science !!! ÀÀ la fin de la publication, il y a une tâche compétitive, soyez le premier ! Dans l'un des articles de cette section, nous sommes avec vous, dans lequel le graphique de la fonction a été donné, et diverses questions ont été soulevées concernant les extrema, les intervalles d'augmentation (diminution) et autres.
Dans cet article, nous examinerons les tâches incluses dans l'USE en mathématiques, dans lesquelles le graphique de la dérivée d'une fonction est donné, et les questions suivantes sont posées :
1. À quel point d'un segment donné la fonction prend-elle la plus grande (ou la plus petite) valeur.
2. Trouver le nombre de points maximum (ou minimum) de la fonction qui appartiennent à un segment donné.
3. Trouver le nombre de points extrêmes de la fonction qui appartiennent à un segment donné.
4. Trouvez le point extrême de la fonction qui appartient au segment donné.
5. Trouvez les intervalles d'augmentation (ou de diminution) de la fonction et dans la réponse indiquez la somme des points entiers inclus dans ces intervalles.
6. Trouvez les intervalles d'augmentation (ou de diminution) de la fonction. Dans votre réponse, indiquez la longueur du plus grand de ces intervalles.
7. Trouvez le nombre de points où la tangente au graphique de la fonction est parallèle à la droite y = kx + b ou coïncide avec elle.
8. Trouvez l'abscisse du point auquel la tangente au graphique de la fonction est parallèle à l'axe des abscisses ou coïncide avec lui.
Il peut y avoir d'autres questions, mais elles ne vous poseront aucune difficulté si vous comprenez et (des liens sont fournis vers des articles qui fournissent les informations nécessaires à la résolution, je vous recommande de répéter).
Informations de base (brièvement):
1. La dérivée sur les intervalles croissants a un signe positif.
Si la dérivée à un certain point d'un certain intervalle a une valeur positive, alors le graphique de la fonction sur cet intervalle augmente.
2. Sur les intervalles de décroissant, la dérivée a un signe négatif.
Si la dérivée à un certain point d'un certain intervalle a une valeur négative, alors le graphique de la fonction sur cet intervalle diminue.
3. La dérivée au point x est égale à la pente de la tangente tracée au graphique de la fonction au même point.
4. Aux points d'extremum (maximum-minimum) de la fonction, la dérivée est égale à zéro. La tangente au graphique de la fonction en ce point est parallèle à l'axe des x.
Cela doit être clairement compris et rappelé !!!
Le graphique de la dérivée "confond" beaucoup de gens. Certains le prennent par inadvertance pour le graphe de la fonction elle-même. Par conséquent, dans de tels bâtiments, où vous voyez qu'un graphe est donné, concentrez immédiatement votre attention dans la condition sur ce qui est donné : un graphe d'une fonction ou un graphe d'une dérivée d'une fonction ?
S'il s'agit d'un graphique de la dérivée d'une fonction, traitez-le comme un "reflet" de la fonction elle-même, ce qui vous donne simplement des informations sur cette fonction.
Considérez la tâche :
La figure montre un graphique y=F'(X)- fonction dérivée F(X), défini sur l'intervalle (–2;21).

Nous répondrons aux questions suivantes :
1. En quel point du segment se trouve la fonction F(X) prend la plus grande valeur.
Sur un segment donné, la dérivée de la fonction est négative, ce qui signifie que la fonction décroît sur ce segment (elle décroît de la borne gauche de l'intervalle vers la droite). Ainsi, la valeur maximale de la fonction est atteinte sur la limite gauche du segment, c'est-à-dire au point 7.
Réponse : 7
2. En quel point du segment se trouve la fonction F(X)
À partir de ce graphique de la dérivée, nous pouvons dire ce qui suit. Sur un segment donné, la dérivée de la fonction est positive, ce qui signifie que la fonction croît sur ce segment (elle croît du bord gauche de l'intervalle vers celui de droite). Ainsi, la plus petite valeur de la fonction est atteinte sur le bord gauche du segment, c'est-à-dire au point x = 3.
Réponse : 3
3. Trouver le nombre de points maximum de la fonction F(X)
Les points maximum correspondent aux points où le signe de la dérivée passe du positif au négatif. Considérez où le signe change de cette façon.
Sur le segment (3;6) la dérivée est positive, sur le segment (6;16) elle est négative.
Sur le segment (16;18) la dérivée est positive, sur le segment (18;20) elle est négative.
Ainsi, sur un segment donné, la fonction a deux points maximum x = 6 et x = 18.
Réponse : 2
4. Trouver le nombre de points minimum de la fonction F(X) appartenant au segment.
Les points minimaux correspondent aux points où le signe de la dérivée passe du négatif au positif. On a une dérivée négative sur l'intervalle (0 ; 3), et positive sur l'intervalle (3 ; 4).
Ainsi, sur le segment, la fonction n'a qu'un seul point minimum x = 3.
*Soyez prudent lorsque vous écrivez la réponse - le nombre de points est enregistré, pas la valeur x, une telle erreur peut être commise par inattention.
Réponse 1
5. Trouver le nombre de points extrêmes de la fonction F(X) appartenant au segment.
Veuillez noter que vous devez trouver montant points extrêmes (il s'agit à la fois des points maximum et minimum).
Les points extrêmes correspondent aux points où le signe de la dérivée change (de positif à négatif ou inversement). Sur le graphique donné dans la condition, ce sont les zéros de la fonction. La dérivée s'annule aux points 3, 6, 16, 18.
Ainsi, la fonction a 4 points extrêmes sur le segment.
Réponse : 4
6. Trouver les intervalles de la fonction croissante F(X)
Intervalles d'augmentation de cette fonction F(X) correspondent aux intervalles sur lesquels sa dérivée est positive, soit les intervalles (3;6) et (16;18). Veuillez noter que les limites de l'intervalle n'y sont pas incluses (parenthèses - les limites ne sont pas incluses dans l'intervalle, les crochets sont inclus). Ces intervalles contiennent des points entiers 4, 5, 17. Leur somme est : 4 + 5 + 17 = 26
Réponse : 26
7. Trouver les intervalles de la fonction décroissante F(X)à un intervalle donné. Dans votre réponse, indiquez la somme des points entiers inclus dans ces intervalles.
Fonction Intervalles décroissants F(X) correspondent à des intervalles sur lesquels la dérivée de la fonction est négative. Dans ce problème, ce sont les intervalles (–2;3), (6;16), (18;21).
Ces intervalles contiennent les points entiers suivants : -1, 0, 1, 2, 7, 8, 9, 10, 11, 12, 13, 14, 15, 19, 20. Leur somme est :
(–1) + 0 + 1 + 2 + 7 + 8 + 9 + 10 +
11 + 12 + 13 + 14 + 15 + 19 + 20 = 140
Réponse : 140
*Faites attention à la condition : si les limites sont incluses dans l'intervalle ou non. Si les frontières sont incluses, alors ces frontières doivent également être prises en compte dans les intervalles considérés dans le processus de résolution.
8. Trouver les intervalles de la fonction croissante F(X)
Intervalles d'augmentation de fonction F(X) correspondent aux intervalles sur lesquels la dérivée de la fonction est positive. Nous les avons déjà indiquées : (3;6) et (16;18). Le plus grand d'entre eux est l'intervalle (3;6), sa longueur est de 3.
Réponse : 3
9. Trouver les intervalles de la fonction décroissante F(X). Dans votre réponse, écrivez la longueur du plus grand d'entre eux.
Fonction Intervalles décroissants F(X) correspondent à des intervalles sur lesquels la dérivée de la fonction est négative. Nous les avons déjà indiqués, ce sont les intervalles (–2 ; 3), (6 ; 16), (18 ; 21), leurs longueurs sont respectivement égales à 5, 10, 3.
La longueur du plus grand est 10.
Réponse : 10
10. Trouvez le nombre de points où la tangente au graphique de la fonction F(X) parallèle à la ligne y \u003d 2x + 3 ou coïncide avec elle.
La valeur de la dérivée au point de contact est égale à la pente de la tangente. Puisque la tangente est parallèle à la ligne y \u003d 2x + 3 ou coïncide avec elle, alors leurs pentes sont égales à 2. Par conséquent, il est nécessaire de trouver le nombre de points auxquels y (x 0) \u003d 2. Géométriquement , cela correspond au nombre de points d'intersection du graphe dérivé avec la droite y = 2. Il y a 4 points de ce type sur cet intervalle.
Réponse : 4
11. Trouver le point extrême de la fonction F(X) appartenant au segment.
Un point extremum d'une fonction est un point auquel sa dérivée est égale à zéro, et au voisinage de ce point, la dérivée change de signe (de positif à négatif ou inversement). Sur le segment, le graphique de la dérivée croise l'axe des abscisses, la dérivée change de signe de négatif à positif. Par conséquent, le point x = 3 est un point extrême.
Réponse : 3
12. Trouvez les abscisses des points où les tangentes au graphique y \u003d f (x) sont parallèles à l'axe des abscisses ou coïncident avec lui. Dans votre réponse, indiquez le plus grand d'entre eux.
La tangente au graphique y \u003d f (x) peut être parallèle à l'axe des x ou coïncider avec lui, uniquement aux points où la dérivée est nulle (il peut s'agir de points extrêmes ou de points stationnaires, au voisinage desquels la dérivée ne change pas de signe). Ce graphique montre que la dérivée est nulle aux points 3, 6, 16,18. Le plus grand a 18 ans.
L'argument peut être structuré comme ceci :
La valeur de la dérivée au point de contact est égale à la pente de la tangente. Puisque la tangente est parallèle ou confondue avec l'axe des abscisses, sa pente est 0 (en effet, la tangente d'un angle de zéro degré est nulle). Par conséquent, nous recherchons un point où la pente est égale à zéro, ce qui signifie que la dérivée est égale à zéro. La dérivée est égale à zéro au point où son graphique croise l'axe des x, et ce sont les points 3, 6, 16,18.
Réponse : 18
La figure montre un graphique y=F'(X)- fonction dérivée F(X) défini sur l'intervalle (–8;4). En quel point du segment [–7;–3] est la fonction F(X) prend la plus petite valeur.

La figure montre un graphique y=F'(X)- fonction dérivée F(X), défini sur l'intervalle (–7;14). Trouver le nombre de points maximum d'une fonction F(X) appartenant au segment [–6;9].

La figure montre un graphique y=F'(X)- fonction dérivée F(X) défini sur l'intervalle (–18;6). Trouver le nombre de points minimum d'une fonction F(X) appartenant au segment [–13;1].

La figure montre un graphique y=F'(X)- fonction dérivée F(X), défini sur l'intervalle (–11 ; –11). Trouver le nombre de points extrêmes d'une fonction F(X), appartenant au segment [–10 ; -Dix].

La figure montre un graphique y=F'(X)- fonction dérivée F(X) défini sur l'intervalle (–7;4). Trouver les intervalles de la fonction croissante F(X). Dans votre réponse, indiquez la somme des points entiers inclus dans ces intervalles.

La figure montre un graphique y=F'(X)- fonction dérivée F(X), défini sur l'intervalle (–5 ; 7). Trouver les intervalles de la fonction décroissante F(X). Dans votre réponse, indiquez la somme des points entiers inclus dans ces intervalles.

La figure montre un graphique y=F'(X)- fonction dérivée F(X) défini sur l'intervalle (–11;3). Trouver les intervalles de la fonction croissante F(X). Dans votre réponse, écrivez la longueur du plus grand d'entre eux.

F La figure montre un graphique
La condition du problème est la même (que nous avons considérée). Trouver la somme de trois nombres :
1. La somme des carrés des extrema de la fonction f (x).
2. La différence des carrés de la somme des points maximaux et de la somme des points minimaux de la fonction f (x).
3. Le nombre de tangentes à f (x) parallèles à la droite y \u003d -3x + 5.
Le premier à donner la bonne réponse recevra un prix d'encouragement - 150 roubles. Écrivez vos réponses dans les commentaires. S'il s'agit de votre premier commentaire sur le blog, alors il n'apparaîtra pas tout de suite, un peu plus tard (rassurez-vous, le temps de rédaction d'un commentaire est enregistré).
Bonne chance à toi!
Cordialement, Alexandre Krutitsikh.
P.S: Je vous serais reconnaissant de parler du site dans les réseaux sociaux.
La dérivée d'une fonction est l'un des sujets les plus difficiles du programme scolaire. Tous les diplômés ne répondront pas à la question de savoir ce qu'est un dérivé.
Cet article explique simplement et clairement ce qu'est un dérivé et pourquoi il est nécessaire.. Nous ne chercherons pas maintenant à la rigueur mathématique de la présentation. Le plus important est de comprendre le sens.
Rappelons la définition :
La dérivée est le taux de variation de la fonction.
La figure montre des graphiques de trois fonctions. Selon vous, lequel pousse le plus vite ?

La réponse est évidente - la troisième. Il a le taux de variation le plus élevé, c'est-à-dire la plus grande dérivée.
Voici un autre exemple.
Kostya, Grisha et Matvey ont obtenu des emplois en même temps. Voyons comment leurs revenus ont changé au cours de l'année :

Vous pouvez tout voir sur le graphique tout de suite, n'est-ce pas ? Les revenus de Kostya ont plus que doublé en six mois. Et les revenus de Grisha ont également augmenté, mais juste un peu. Et le revenu de Matthew est tombé à zéro. Les conditions de départ sont les mêmes, mais le taux de variation de la fonction, c'est-à-dire dérivé, - différent. Quant à Matvey, la dérivée de son revenu est généralement négative.
Intuitivement, nous pouvons facilement estimer le taux de variation d'une fonction. Mais comment fait-on ?
Ce que nous examinons vraiment, c'est à quel point le graphique de la fonction monte (ou descend). En d'autres termes, à quelle vitesse y change avec x. De toute évidence, la même fonction à différents points peut avoir une valeur différente de la dérivée - c'est-à-dire qu'elle peut changer plus rapidement ou plus lentement.
La dérivée d'une fonction est notée .
Montrons comment trouver en utilisant le graphique.

Un graphique d'une fonction est tracé. Prenez-y un point avec une abscisse. Tracez une tangente au graphique de la fonction en ce point. Nous voulons évaluer à quel point le graphique de la fonction monte. Une valeur pratique pour cela est tangente de la pente de la tangente.
La dérivée d'une fonction en un point est égale à la tangente de la pente de la tangente tracée au graphique de la fonction en ce point.
Veuillez noter - comme angle d'inclinaison de la tangente, nous prenons l'angle entre la tangente et la direction positive de l'axe.
Parfois, les élèves demandent quelle est la tangente au graphique d'une fonction. C'est une droite qui a d'ailleurs le seul point commun avec le graphique de cette section, comme le montre notre figure. Cela ressemble à une tangente à un cercle.
Allons trouver . Rappelons que la tangente d'un angle aigu dans un triangle rectangle est égale au rapport de la jambe opposée à la jambe adjacente. Du triangle :
Nous avons trouvé la dérivée en utilisant le graphique sans même connaître la formule de la fonction. De telles tâches se retrouvent souvent dans l'examen de mathématiques sous le numéro.
Il existe une autre corrélation importante. Rappelons que la droite est donnée par l'équation
La quantité dans cette équation est appelée pente d'une droite. Elle est égale à la tangente de l'angle d'inclinaison de la droite à l'axe.
.
On comprend ça
Rappelons cette formule. Il exprime la signification géométrique de la dérivée.
La dérivée d'une fonction en un point est égale à la pente de la tangente tracée au graphique de la fonction en ce point.
Autrement dit, la dérivée est égale à la tangente de la pente de la tangente.
Nous avons déjà dit qu'une même fonction peut avoir différentes dérivées en différents points. Voyons comment la dérivée est liée au comportement de la fonction.
Traçons un graphique d'une fonction. Laissez cette fonction augmenter dans certains domaines et diminuer dans d'autres, et à des rythmes différents. Et laissez cette fonction avoir des points maximum et minimum.

À un moment donné, la fonction est croissante. La tangente au graphique, dessinée au point, forme un angle aigu avec la direction positive de l'axe. La dérivée est donc positive au point.
Au point, notre fonction est décroissante. La tangente en ce point forme un angle obtus avec la direction positive de l'axe. Puisque la tangente d'un angle obtus est négative, la dérivée au point est négative.
Voici ce qui se passe :
Si une fonction est croissante, sa dérivée est positive.
S'il diminue, sa dérivée est négative.
Et que se passera-t-il aux points maximum et minimum ? On voit qu'en (point maximum) et (point minimum) la tangente est horizontale. Par conséquent, la tangente de la pente de la tangente en ces points est nulle et la dérivée est également nulle.
Le point est le point maximum. À ce stade, l'augmentation de la fonction est remplacée par une diminution. Par conséquent, le signe de la dérivée change au point de "plus" à "moins".
Au point - le point minimum - la dérivée est également égale à zéro, mais son signe passe de "moins" à "plus".
Conclusion : à l'aide de la dérivée, vous pouvez découvrir tout ce qui nous intéresse sur le comportement de la fonction.
Si la dérivée est positive, alors la fonction est croissante.
Si la dérivée est négative, alors la fonction est décroissante.
Au point maximum, la dérivée est nulle et change de signe de plus à moins.
Au point minimum, la dérivée est également nulle et change de signe de moins à plus.
Nous écrivons ces résultats sous forme de tableau :
| augmente | point maximum | diminue | note minimale | augmente | |
| + | 0 | - | 0 | + |
Apportons deux petites précisions. Vous en aurez besoin pour résoudre des problèmes d'examen. Un autre - en première année, avec une étude plus sérieuse des fonctions et des dérivés.
Un cas est possible lorsque la dérivée d'une fonction à un certain point est égale à zéro, mais la fonction n'a ni maximum ni minimum à ce point. Ce soi-disant :

En un point, la tangente au graphe est horizontale et la dérivée est nulle. Cependant, avant le point, la fonction a augmenté - et après le point, elle continue d'augmenter. Le signe de la dérivée ne change pas - il est resté positif tel qu'il était.
Il arrive aussi qu'au point de maximum ou de minimum, la dérivée n'existe pas. Sur le graphique, cela correspond à une cassure nette, lorsqu'il est impossible de tracer une tangente en un point donné.

Mais comment trouver la dérivée si la fonction n'est pas donnée par un graphe, mais par une formule ? Dans ce cas, il s'applique
Dans le problème B9, un graphique d'une fonction ou d'une dérivée est donné, à partir duquel il est nécessaire de déterminer l'une des quantités suivantes :
- La valeur de la dérivée à un certain point x 0,
- Points hauts ou bas (points extrêmes),
- Intervalles de fonctions croissantes et décroissantes (intervalles de monotonie).
Les fonctions et dérivées présentées dans ce problème sont toujours continues, ce qui simplifie grandement la solution. Bien que la tâche appartienne à la section de l'analyse mathématique, elle est tout à fait à la portée des étudiants, même les plus faibles, car aucune connaissance théorique approfondie n'est requise ici.
Pour trouver la valeur de la dérivée, des points extrêmes et des intervalles de monotonie, il existe des algorithmes simples et universels - tous seront discutés ci-dessous.
Lisez attentivement la condition du problème B9 pour ne pas commettre d'erreurs stupides : des textes parfois assez volumineux se présentent, mais il y a peu de conditions importantes qui influent sur le cours de la solution.
Calcul de la valeur de la dérivée. Méthode à deux points
Si l'on donne au problème un graphe de la fonction f(x), tangente à ce graphe en un point x 0 , et qu'il faut trouver la valeur de la dérivée en ce point, l'algorithme suivant est appliqué :
- Trouver deux points "adéquats" sur le graphe tangent : leurs coordonnées doivent être entières. Notons ces points A (x 1 ; y 1) et B (x 2 ; y 2). Notez correctement les coordonnées - c'est le point clé de la solution, et toute erreur ici conduit à la mauvaise réponse.
- Connaissant les coordonnées, il est facile de calculer l'incrément de l'argument Δx = x 2 − x 1 et l'incrément de la fonction Δy = y 2 − y 1 .
- Enfin, on trouve la valeur de la dérivée D = Δy/Δx. En d'autres termes, vous devez diviser l'incrément de la fonction par l'incrément de l'argument - et ce sera la réponse.
Encore une fois, on note : les points A et B doivent être recherchés précisément sur la tangente, et non sur le graphe de la fonction f(x), comme c'est souvent le cas. La tangente contiendra nécessairement au moins deux de ces points, sinon le problème est mal formulé.
Considérez les points A (−3 ; 2) et B (−1 ; 6) et trouvez les incréments :
Δx \u003d x 2 - x 1 \u003d -1 - (-3) \u003d 2; Δy \u003d y 2 - y 1 \u003d 6 - 2 \u003d 4.
Trouvons la valeur de la dérivée : D = Δy/Δx = 4/2 = 2.
Une tâche. La figure montre le graphique de la fonction y \u003d f (x) et sa tangente au point d'abscisse x 0. Trouver la valeur de la dérivée de la fonction f(x) au point x 0 .
Considérez les points A (0 ; 3) et B (3 ; 0), trouvez les incréments :
Δx \u003d x 2 - x 1 \u003d 3 - 0 \u003d 3; Δy \u003d y 2 - y 1 \u003d 0 - 3 \u003d -3.
On trouve maintenant la valeur de la dérivée : D = Δy/Δx = −3/3 = −1.
Une tâche. La figure montre le graphique de la fonction y \u003d f (x) et sa tangente au point d'abscisse x 0. Trouver la valeur de la dérivée de la fonction f(x) au point x 0 .
Considérez les points A (0 ; 2) et B (5 ; 2) et trouvez les incréments :
Δx \u003d x 2 - x 1 \u003d 5 - 0 \u003d 5; Δy = y 2 - y 1 = 2 - 2 = 0.
Il reste à trouver la valeur de la dérivée : D = Δy/Δx = 0/5 = 0.
A partir du dernier exemple, on peut formuler la règle : si la tangente est parallèle à l'axe OX, la dérivée de la fonction au point de contact est égale à zéro. Dans ce cas, vous n'avez même pas besoin de calculer quoi que ce soit - regardez simplement le graphique.
Calcul des points hauts et bas
Parfois, au lieu d'un graphique d'une fonction dans le problème B9, un graphique dérivé est donné et il est nécessaire de trouver le point maximum ou minimum de la fonction. Dans ce scénario, la méthode à deux points est inutile, mais il existe un autre algorithme encore plus simple. Définissons d'abord la terminologie :
- Le point x 0 est appelé le point maximum de la fonction f(x) si l'inégalité suivante est vraie dans un certain voisinage de ce point : f(x 0) ≥ f(x).
- Le point x 0 est appelé le point minimum de la fonction f(x) si l'inégalité suivante est vraie dans un certain voisinage de ce point : f(x 0) ≤ f(x).
Afin de trouver les points maximum et minimum sur le graphique de la dérivée, il suffit d'effectuer les étapes suivantes :
- Redessinez le graphique de la dérivée en supprimant toutes les informations inutiles. Comme le montre la pratique, les données supplémentaires ne font qu'interférer avec la solution. Par conséquent, nous marquons les zéros de la dérivée sur l'axe des coordonnées - et c'est tout.
- Découvrez les signes de la dérivée sur les intervalles entre les zéros. Si pour un point x 0 on sait que f'(x 0) ≠ 0, alors seulement deux options sont possibles : f'(x 0) ≥ 0 ou f'(x 0) ≤ 0. Le signe de la dérivée est facile à déterminer à partir du dessin d'origine : si le graphe dérivé se situe au-dessus de l'axe OX, alors f'(x) ≥ 0. Inversement, si le graphe dérivé se situe en dessous de l'axe OX, alors f'(x) ≤ 0.
- Nous vérifions à nouveau les zéros et les signes de la dérivée. Là où le signe passe du moins au plus, il y a un point minimum. Inversement, si le signe de la dérivée passe de plus à moins, c'est le point maximum. Le comptage se fait toujours de gauche à droite.
Ce schéma ne fonctionne que pour les fonctions continues - il n'y en a pas d'autres dans le problème B9.
Une tâche. La figure montre un graphique de la dérivée de la fonction f(x) définie sur l'intervalle [−5 ; 5]. Trouver le point minimum de la fonction f(x) sur ce segment.
Débarrassons-nous des informations inutiles - nous ne laisserons que les frontières [−5 ; 5] et les zéros de la dérivée x = −3 et x = 2,5. Notez également les signes :
Évidemment, au point x = −3, le signe de la dérivée passe de moins à plus. C'est le point minimum.
Une tâche. La figure montre un graphique de la dérivée de la fonction f(x) définie sur le segment [−3 ; sept]. Trouver le point maximum de la fonction f(x) sur ce segment.
Redessinons le graphe en ne laissant que les bornes [−3; 7] et les zéros de la dérivée x = −1,7 et x = 5. Notez les signes de la dérivée sur le graphique résultant. Nous avons:
![]()
Évidemment, au point x = 5, le signe de la dérivée passe de plus à moins - c'est le point maximum.
Une tâche. La figure montre un graphique de la dérivée de la fonction f(x) définie sur l'intervalle [−6 ; quatre]. Trouver le nombre de points maximum de la fonction f(x) appartenant à l'intervalle [−4 ; 3].
Il résulte des conditions du problème qu'il suffit de ne considérer que la partie du graphe délimitée par le segment [−4 ; 3]. On construit donc un nouveau graphe, sur lequel on ne marque que les bornes [−4 ; 3] et les zéros de la dérivée à l'intérieur. A savoir, les points x = −3.5 et x = 2. On obtient :
![]()
Sur ce graphique, il n'y a qu'un seul point maximum x = 2. C'est en lui que le signe de la dérivée passe du plus au moins.
Une petite note sur les points avec des coordonnées non entières. Par exemple, dans le dernier problème, le point x = −3,5 a été considéré, mais avec le même succès on peut prendre x = −3,4. Si le problème est correctement formulé, de tels changements ne devraient pas affecter la réponse, car les points "sans lieu de résidence fixe" ne sont pas directement impliqués dans la résolution du problème. Bien sûr, avec des points entiers, une telle astuce ne fonctionnera pas.
Trouver les intervalles d'augmentation et de diminution d'une fonction
Dans un tel problème, comme les points de maximum et de minimum, il est proposé de trouver des zones dans lesquelles la fonction elle-même augmente ou diminue à partir du graphique de la dérivée. Tout d'abord, définissons ce que sont l'ascendant et le descendant :
- Une fonction f(x) est dite croissante sur un segment si pour deux points quelconques x 1 et x 2 de ce segment l'énoncé est vrai : x 1 ≤ x 2 ⇒ f(x 1) ≤ f(x 2). En d'autres termes, plus la valeur de l'argument est grande, plus la valeur de la fonction est grande.
- Une fonction f(x) est dite décroissante sur un segment si pour deux points quelconques x 1 et x 2 de ce segment l'énoncé est vrai : x 1 ≤ x 2 ⇒ f(x 1) ≥ f(x 2). Ceux. une plus grande valeur de l'argument correspond à une plus petite valeur de la fonction.
Nous formulons des conditions suffisantes pour augmenter et diminuer :
- Pour qu'une fonction continue f(x) croît sur le segment , il suffit que sa dérivée à l'intérieur du segment soit positive, c'est-à-dire f'(x) ≥ 0.
- Pour qu'une fonction continue f(x) décroisse sur le segment , il suffit que sa dérivée à l'intérieur du segment soit négative, c'est-à-dire f'(x) ≤ 0.
Nous acceptons ces affirmations sans preuve. Ainsi, nous obtenons un schéma pour trouver des intervalles d'augmentation et de diminution, qui est à bien des égards similaire à l'algorithme de calcul des points extrêmes :
- Supprimez toutes les informations redondantes. Sur le graphique original de la dérivée, nous nous intéressons principalement aux zéros de la fonction, nous ne laissons donc que ceux-ci.
- Marquez les signes de la dérivée aux intervalles entre les zéros. Où f'(x) ≥ 0, la fonction augmente, et où f'(x) ≤ 0, elle diminue. Si le problème a des restrictions sur la variable x, nous les marquons en plus sur le nouveau graphique.
- Maintenant que nous connaissons le comportement de la fonction et de la contrainte, il reste à calculer la valeur requise dans le problème.
Une tâche. La figure montre un graphique de la dérivée de la fonction f(x) définie sur le segment [−3 ; 7.5]. Trouver les intervalles de la fonction décroissante f(x). Dans votre réponse, écrivez la somme des nombres entiers compris dans ces intervalles.
Comme d'habitude, on redessine le graphe et on marque les bornes [−3 ; 7.5], ainsi que les zéros de la dérivée x = −1.5 et x = 5.3. Ensuite, nous marquons les signes de la dérivée. Nous avons:
![]()
Comme la dérivée est négative sur l'intervalle (− 1,5), c'est l'intervalle de fonction décroissante. Il reste à additionner tous les entiers qui sont à l'intérieur de cet intervalle :
−1 + 0 + 1 + 2 + 3 + 4 + 5 = 14.
Une tâche. La figure montre un graphique de la dérivée de la fonction f(x) définie sur le segment [−10 ; quatre]. Trouver les intervalles de la fonction croissante f(x). Dans votre réponse, écrivez la longueur du plus grand d'entre eux.
Débarrassons-nous des informations redondantes. On ne laisse que les bornes [−10 ; 4] et les zéros de la dérivée, qui cette fois se sont avérés être quatre : x = −8, x = −6, x = −3 et x = 2. Notez les signes de la dérivée et obtenez l'image suivante :
On s'intéresse aux intervalles de fonction croissante, c'est-à-dire où f'(x) ≥ 0. Il existe deux de ces intervalles sur le graphique : (−8 ; −6) et (−3 ; 2). Calculons leurs longueurs :
l 1 = − 6 − (−8) = 2 ;
l 2 = 2 − (−3) = 5.
Puisqu'il est nécessaire de trouver la longueur du plus grand des intervalles, nous écrivons la valeur l 2 = 5 en réponse.






