Transformations géométriques. mouvements
Lire aussi
Gymnase Maloyazovsky Bashkir
Résumé de la géométrie
« Transformations de formes »
Réalisé par : élève de la classe 10 B
Khaliullin A.N.
Vérifié par: Israfilova R.Kh.
Maloyaz 2003
I. Transformation.
II. Types de transformation
1. Homothétie
2. Ressemblance
3. Mouvement
III. Types de mouvement
1. Symétrie autour d'un point
2. Symétrie par rapport à une droite
3. Symétrie par rapport au plan
4. Tournez
5. Transfert parallèle dans l'espace
I. Transformation - déplacer chaque point d'une figure donnée d'une manière ou d'une autre et obtenir une nouvelle figure.
II. Types de transformation dans l'espace : similarité, homothétie, mouvement.
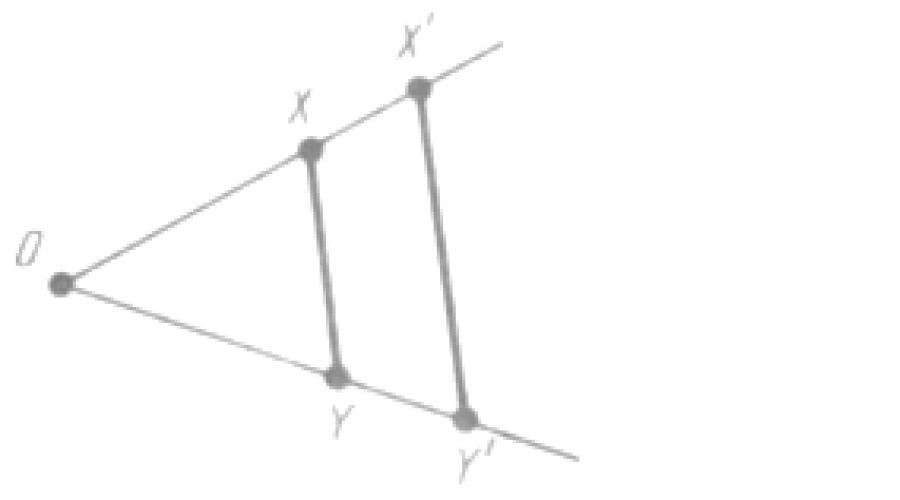
Similitude Une transformation d'une figure F est dite transformation de similarité si, au cours de cette transformation, les distances entre points changent du même nombre de fois, c'est-à-dire pour tous les points X et Y de la figure F et les points X', Y' de la figure F' auxquels il passe, X'Y' = k * XY.
Propriétés de similarité : 1. La similarité transforme les droites en droites, les demi-droites en demi-droites, les segments en segments.
2. La similarité préserve les angles entre les demi-droites
3. La similarité traduit les plans en plans.
Deux figures sont dites similaires si elles sont traduites l'une dans l'autre par une transformation de similarité.
Homothétie
L'homothétie est la transformation la plus simple autour du centre O avec le coefficient d'homothétie k. C'est une transformation qui translate un point quelconque X' du rayon OX tel que OX' = k*OX.
Propriété d'une homothétie : 1. En transformant une homothétie, elle transforme tout plan qui ne passe pas par le centre de l'homothétie en un plan parallèle (ou en lui-même si k=1).
Preuve. En effet, soit O le centre de l'homothétie et soit a un plan quelconque ne passant pas par le point O. Soit une droite quelconque AB dans le plan a. La transformation d'homothétie transforme le point A en point A' sur le rayon OA, et le point B en point B' sur le rayon OB, où OA'/OA = k, OB'/OB = k, où k est le coefficient d'homothétie. Ceci implique la similarité des triangles AOB et A'OB'. De la similitude des triangles découle l'égalité des angles correspondants OAB et OA'B', et donc le parallélisme des droites AB et A'B'. Prenons maintenant une autre droite AC dans le plan a. Par homothétie, il passe sur la parallèle A'C'. Sous l'homothétie considérée, le plan a passe dans le plan a' passant par les droites A'B', A'C'. Puisque A'B'||AB et A'C'||AC, alors par le théorème sur deux lignes d'intersection d'un plan, respectivement, parallèles aux lignes d'intersection d'un autre plan, les plans a et a' sont parallèles, ce qui était à prouver.
Trafic
Mouvement - la transformation d'une figure en une autre si elle préserve la distance entre les points, c'est-à-dire traduit deux points quelconques X et Y d'une figure en points X , Y d'une autre figure de sorte que XY = X Y
Propriétés du mouvement : 1. Les points situés sur une ligne droite, lors du déplacement, passent en points situés sur une ligne droite, et leur ordre est conservé position relative. Cela signifie que si A, B, C, se trouvant sur la ligne, allez aux points A 1 ,B 1 ,C 1 . Ensuite, ces points se trouvent également sur la ligne ; si le point B est compris entre les points A et C, alors le point B 1 est compris entre les points A 1 et C 1.
Preuve. Soit le point B de la droite AC entre les points A et C. Montrons que les points A 1 ,B 1 ,C 1 se trouvent sur la même droite.
Si les points A 1 ,B 1 ,C 1 ne sont pas sur une droite, alors ce sont les sommets d'un triangle. Donc A 1 C 1< A 1 B 1 + B 1 C 1 . По определению движения отсюда следует, что AC Nous sommes arrivés à une contradiction. Par conséquent, le point B 1 se trouve sur la ligne A 1 C 1 . La première assertion du théorème est démontrée. Montrons maintenant que le point B 1 est compris entre A 1 et C 1 . Supposons que le point A 1 se situe entre les points B 1 et C 1 . Alors A 1 B 1 + A 1 C 1 = B 1 C 1 , et donc AB+AC=BC. Mais cela contredit l'inégalité AB+BC=AC. Ainsi le point A 1 ne peut pas être compris entre les points B 1 et C 1 . De même, nous prouvons que le point C 1 ne peut pas être compris entre les points A 1 et B 1 . Comme l'un des trois points A 1 ,B 1 ,C 1 est compris entre les deux autres, ce point ne peut être que B 1 . Le théorème est démontré complètement. 2. Lors du déplacement, les lignes droites se transforment en lignes droites, les demi-lignes en demi-lignes, les segments en segments 3. Lors du déplacement, les angles entre les demi-lignes sont conservés. Preuve. Soient AB et AC deux demi-droites issues du point A et non situées sur cette droite. En se déplaçant, ces demi-droites passent dans des demi-droites A 1 B 1 et A 1 C 1 . Puisque le mouvement préserve la distance, les triangles ABC et A 1 B 1 C 1 sont égaux selon le troisième critère d'égalité des triangles. L'égalité des triangles implique l'égalité des angles BAC et B 1 A 1 C 1 , ce qui restait à démontrer. C2. Les triangles A2BC2 et A1B1C1 sont égaux dans le troisième critère. De l'égalité des triangles découle l'égalité des angles A2BC2 et A1B1C1. Donc, les angles ABC et A1B1C1 sont égaux, ce qui restait à prouver. 3. SIMILARITE DES FIGURES Deux figures sont dites similaires si elles sont converties l'une dans l'autre par une transformation de similarité. Pour indiquer la similarité des chiffres, une icône spéciale est utilisée : ∞. L'entrée F∞F" se lit... Médianes des triangles ; 4. , où BH et B1H1 sont des hauteurs de triangles. §5. Travail expérimental Le but du travail expérimental: identifier les caractéristiques méthodologiques de l'étude du thème "Triangles similaires" au lycée. Idée: afin d'identifier les particularités méthodologiques, il est nécessaire de mener plusieurs leçons selon la méthodologie développée, à la fin de la formation, effectuer un travail de contrôle, dans l'analyse duquel on peut juger sur ... Les différences entre les sujets des groupes contrôle et expérimental ont servi de base à la réalisation d'un travail pédagogique ciblé pour développer les idées des enfants du groupe expérimental sur la forme des objets. 2.2 L'utilisation de tâches de puzzle dans le développement d'idées sur la forme des objets chez les enfants du groupe expérimental Les idées des enfants sur la forme des objets sont d'une grande importance quand ... Transformation en forme de F
en forme de F
appelée la transformation de similarité ,
si, sous cette transformation, les distances entre points changent du même nombre de fois (Fig. 1). Cela signifie que si des points arbitraires X, Y
Formes F
lors de la transformation de la similarité, ils vont aux points X", Y"
chiffres F",
puis X"Y" =
k-XY ,
où le nombre k
-- le même pour tous les points X, Y .
Nombre k
appelé coefficient de similarité .
Pour k = l
la transformation de similarité est évidemment un mouvement. Soient F une figure donnée et O un point fixe (Fig. 2). Traçons un rayon OX passant par un point quelconque X de la figure F et traçons sur lui le segment OX" égal à k? OX, où k est un nombre positif. homothétie par rapport au centre O. Le nombre k est appelé le coefficient d'homothétie, les chiffres F et F" sont dits homothétiques. Théorème 1. L'homothétie est une transformation de similarité Preuve. Soient O le centre d'homothétie, k le coefficient d'homothétie, X et Y deux points arbitraires de la figure (Fig. 3) Fig.3 Par homothétie, les points X et Y vont aux points X" et Y" sur les rayons OX et OY, respectivement, et OX" = k?OX, OY" = k?OY. Ceci implique les égalités vectorielles OX" = kOX, OY" = kOY. En soustrayant ces égalités terme à terme, on obtient : OY "-OX" = k (OY- OX). Depuis OY "- OX" \u003d X "Y", OY -OX \u003d XY, puis X "Y" \u003d kXY. Par conséquent, /X"Y"/=k /XY/, c'est-à-dire X"Y" = kXY. L'homothétie est donc une transformation de similarité. Le théorème a été prouvé. La transformation de similarité est largement utilisée dans la pratique lors de la réalisation de dessins de pièces de machine, de structures, de plans de terrain, etc. Ces images sont des transformations similaires d'images imaginaires en taille réelle. Le facteur de similarité s'appelle l'échelle. Par exemple, si un morceau de terrain est représenté à l'échelle 1:100, cela signifie qu'un centimètre sur le plan correspond à 1 m au sol. Une tâche. La figure 4 montre un plan du domaine à l'échelle 1:1000. Déterminez les dimensions du domaine (longueur et largeur). La solution. La longueur et la largeur du domaine sur le plan sont de 4 cm et 2,7 cm. Le plan étant réalisé à l'échelle 1:1000, les dimensions du domaine sont de 2,7 x 1000 cm = 27 m, 4 x 100 cm = 40 m, respectivement. De même que pour le mouvement, on prouve que sous la transformation de similarité, trois points A, B, C, situés sur la même ligne, passent en trois points A 1 , B 1 , C 1 , également situés sur la même ligne. De plus, si le point B se situe entre les points A et C, alors le point B 1 se situe entre les points A 1 et C 1. Il s'ensuit que la transformation de similarité transforme les lignes en lignes, les demi-lignes en demi-lignes, les segments en segments. Montrons que la transformation de similarité préserve les angles entre les demi-droites. En effet, transformons l'angle ABC par la transformation de similarité avec le coefficient k en l'angle A 1 B 1 C 1 (Fig. 5). On soumet l'angle ABC à une transformation d'homothétie par rapport à son sommet B avec le coefficient d'homothétie k. Dans ce cas, les points A et C iront aux points A 2 et C 2. Les triangles A 2 BC 2 et A 1 B 1 C 1 sont égaux dans le troisième critère. De l'égalité des triangles découle l'égalité des angles A 2 BC 2 et A 1 B 1 C 1. Par conséquent, les angles ABC et A 1 B 1 C 1 sont égaux, ce qui devait être prouvé. Les transformations des figures sont étudiées dans le cours de géométrie sur le plan et dans l'espace. Si chaque point d'une figure donnée sur un plan ou dans l'espace est déplacé d'une certaine manière, alors nous obtiendrons une nouvelle figure. On dit que ce chiffre est obtenu par une transformation à partir de celui donné. Voici quelques exemples de transformations de forme. 1. Symétrie autour d'un point (symétrie centrale). La symétrie par rapport à un point est définie comme suit. Soit O un point fixe et X un point quelconque. Un point est dit symétrique au point X par rapport au point O si les points se trouvent sur la même ligne et que le point symétrique au point O est lui-même le point O. Dans la figure 203, les points X et sont symétriques entre eux par rapport au point O . Soient F une figure donnée et O un point fixe du plan. La transformation d'une figure F en une figure dans laquelle chacun de ses points X va vers un point symétrique de X par rapport à un point donné O est appelée une transformation de symétrie autour du point O. La figure 204 montre une symétrique autour du centre O. La figure 205 montre deux cubes symétriques par rapport au point O. Si la transformation de symétrie autour du point O se traduit figure en elle-même, alors la figure est dite à symétrie centrale, et le point O est son centre de symétrie. Par exemple, un parallélogramme est une figure à symétrie centrale. Le centre de sa symétrie est le point d'intersection des diagonales (Fig. 206, a). Un cercle avec un centre O est aussi une figure à symétrie centrale avec un centre de symétrie O (Fig. 206, b) Toutes les figures énumérées sont plates. Dans l'espace, ainsi que sur le plan, il existe de nombreux exemples de figures à symétrie centrale. Par exemple, la figure 207 montre les figures suivantes : un cube, une sphère, un parallélépipède. 2. Symétrie par rapport à une droite (symétrie axiale). Soit I une droite fixe (Fig. 208). Un point est dit symétrique d'un point X par rapport à la droite I si la droite est perpendiculaire à la droite I et où O est le point d'intersection des droites et I. Si le point X est sur la droite I, alors le point qui lui est symétrique est le point X lui-même. Le point symétrique au point est le point X. Sur la figure 208, et les points sont symétriques par rapport à la ligne I. La transformation de la figure F en où chaque point X se dirige vers un point symétrique par rapport à la droite I est appelée transformation de symétrie par rapport à la droite I. Dans ce cas, les figures sont dites symétriques par rapport à ligne I. La figure 208, b montre des cercles symétriques autour de la ligne I. La figure 209 montre deux sphères symétriques par rapport à la ligne I. Si une transformation de symétrie par rapport à la ligne I transforme la figure F en elle-même, alors la figure est dite symétrique par rapport à la ligne 19, et la ligne I est appelée axe de symétrie de la figure. Par exemple, les lignes droites passant par le point d'intersection des diagonales d'un rectangle parallèle à ses côtés sont les axes de symétrie du rectangle (Fig. 210, a). Les lignes droites sur lesquelles reposent les diagonales du losange sont ses axes de symétrie (Fig. 210, b). Le cercle est symétrique par rapport à toute ligne droite passant par son centre (Fig. 210, c). Tous ces chiffres sont plats. Dans l'espace, ainsi que sur le plan, il existe de nombreux exemples de figures qui ont des axes de symétrie. La figure 211 montre de telles figures : c'est un parallélépipède rectangle, un cône, une pyramide quadrangulaire régulière. 3. Symétrie par rapport au plan. Soit a un plan fixe quelconque. Du point X, une perpendiculaire est abaissée au plan a (O est le point d'intersection de celui-ci avec le plan a) et sur sa continuation au-delà du point O poser un segment égal au point X et sont dits symétriques par rapport au plan a (Fig. 212). La transformation de la figure F en en laquelle chaque point X de la figure F va vers un point symétrique de X par rapport au plan a est appelée transformation de symétrie par rapport au plan. Dans ce cas, les figures sont dites symétriques de respect pour l'avion La figure 213 montre deux sphères symétriques par rapport au plan a. Si une transformation de symétrie par rapport à un plan transforme une figure en elle-même, alors la figure est dite symétrique par rapport au plan ; le plan a est appelé plan de symétrie. La figure 214 montre deux plans de symétrie de la sphère. Notez que la sphère a un nombre infini de tels plans de symétrie. Le cube possède également des plans de symétrie. La figure 215 en montre deux. 4. Homothétie. Soient F une figure donnée et O un point fixe (fig. 216). Traçons un rayon passant par un point arbitraire X de la figure F et traçons dessus un segment et égal à où est un nombre positif. La transformation d'une figure, dans laquelle chacun de ses points X va vers un point construit de la manière spécifiée, s'appelle une homothétie par rapport à Une transformation géométrique d'un plan est une application univoque de ce plan sur lui-même. Les transformations géométriques les plus importantes sont les mouvements, c'est-à-dire transformations préservant la distance. En d'autres termes, si est le mouvement du plan, alors pour deux points quelconques de ce plan la distance entre les points et est égale à . Les mouvements sont associés à la notion d'égalité (congruence) des figures : deux figures et plans a sont dits égaux s'il y a un mouvement de ce plan qui transfère la première figure à la seconde. En fait, cette définition a été utilisée par Euclide (voir Géométrie), qui a appelé deux figures égales si l'une d'elles peut être superposée à l'autre de sorte qu'elles coïncident avec tous leurs points ; en imposant ici il faut comprendre le réarrangement de la figure comme un tout solide (sans changer les distances), c'est-à-dire Circulation. Des exemples de mouvements plans sont la symétrie axiale et centrale, la translation parallèle, la rotation. A titre d'exemple, nous rappelons la définition de la traduction parallèle. Soit un vecteur plan . Une transformation géométrique qui transfère chaque point à un point tel que (Fig. 1) est appelée transfert parallèle à un vecteur. La translation parallèle est un mouvement : si les pointes et vont vers et , c'est-à-dire , , puis , et donc . Lors de la résolution de problèmes géométriques à l'aide de mouvements, la propriété de conservation de l'intersection est souvent utilisée: pour tout mouvement, l'intersection des figures se transforme en intersection de leurs images, c'est-à-dire si sont des figures arbitraires, alors la figure passe à la suite d'un mouvement dans la figure . (Une propriété similaire vaut pour l'union.) Problème 1. Un cercle dont le centre appartient à la bissectrice de l'angle coupe ses côtés aux points et (Fig. 2). Prouve-le . La solution. Désignons par un des côtés de l'angle, et par - le cercle dont la limite est le cercle en question. Avec une symétrie autour de la bissectrice de l'angle, le rayon passe dans le rayon, qui forme le second côté de l'angle, et le cercle passe sur lui-même : , . Selon la propriété de conservation de l'intersection, la figure passe dans , c'est-à-dire dans . En d'autres termes, le segment passe dans le segment , et donc . Tâche 2. À travers un point donné à l'intérieur d'un angle (plus petit que celui élargi), tracez une ligne droite dont le segment, enfermé entre les côtés de l'angle, est divisé en deux en ce point. La solution. Désignons par la symétrie par rapport au point , et par et - les lignes sur lesquelles se trouvent les côtés de l'angle (Fig. 3). En raison de la symétrie, la ligne passe dans une ligne parallèle à celle-ci, qui coupe le deuxième côté de l'angle au point. Puisque , alors le point , qui est symétrique, appartient à la droite, qui est symétrique, c'est-à-dire . Ainsi, les points et sont symétriques par rapport à , et donc le segment est divisé en deux au point, c'est-à-dire ligne droite - souhaitée. Il est facile de comprendre pourquoi la symétrie axiale a été utilisée dans le problème 1 et la symétrie centrale dans le problème 2. Puisque la bissectrice d'un angle est son axe de symétrie, alors une tentative d'application de la symétrie axiale dans le problème 1 est tout à fait naturelle (ainsi que l'utilisation de la symétrie centrale dans le problème 2, puisque le segment doit être divisé en deux en un point, c'est-à-dire que les points souhaités doivent être symétriques par rapport au point). Et dans d'autres cas, l'analyse des conditions du problème vous permet de trouver un mouvement dont l'application donne une solution. Problème 3. Sur les côtés et d'un triangle, des carrés et sont construits à l'extérieur de celui-ci. Montrer que le segment est perpendiculaire à la médiane du triangle et deux fois plus long que cette médiane. La solution. Essayons d'appliquer une rotation de 90°, c'est-à-dire assurez-vous que lors d'une rotation de 90° autour d'un point (dans le sens des aiguilles d'une montre), le segment entrera dans un segment parallèle et double de longueur. Avec cette rotation, le vecteur entre dans (Fig. 4) et le vecteur dans . Par conséquent, le vecteur Le lien entre les mouvements et l'orientation est très significatif. Sur la fig. 5 montre un polygone , sur le contour duquel un sens de contournement positif (sens anti-horaire) est spécifié. La translation parallèle donne un polygone avec la même direction de traversée, c'est-à-dire la translation parallèle préserve le sens de la traversée, ou, comme on dit, préserve l'orientation. La rotation (en particulier la symétrie centrale, qui est une rotation de 180°) préserve également l'orientation (Fig. 6). Au contraire, la symétrie axiale inverse le sens de la dérivation (Fig. 7), c'est-à-dire change d'orientation. Un autre exemple de mouvement qui change d'orientation est la symétrie glissante, c'est-à-dire composition de symétrie par rapport à une droite et une translation parallèle dont le vecteur est parallèle (Fig. 8). Mécanicien et géomètre français du XIXe siècle. M. Shall a formulé le théorème suivant : tout mouvement conservant l'orientation d'un plan est soit une translation parallèle, soit une rotation ; tout mouvement de changement d'orientation d'un plan est une symétrie axiale ou glissante. Problème 4. Démontrer que la composition de deux symétries axiales avec des axes qui se coupent est une rotation. La solution. Soient et des symétries axiales dont les axes (droites et ) se coupent au point . Puisque les deux mouvements changent d'orientation, leur composition (d'abord effectuée , puis ) est un mouvement préservant l'orientation. D'après le théorème de Chall, il y a soit translation parallèle, soit rotation. Mais comme le point est immobile lors de chaque mouvement, le point reste en place lors de leur composition. Il y a donc une rotation autour du point . Comment trouver l'angle de rotation, il ressort de la Fig. 9 : si est l'angle entre les droites et , alors (puisque le point est traduit par mouvement en lui-même, et par mouvement en un point symétrique par rapport à ) le mouvement qui se traduit par est une rotation (autour du point ) d'un angle . Le deuxième groupe le plus important de transformations de plans géométriques sont les transformations de similarité. La plus simple d'entre elles est l'homothétie. Rappelons qu'une homothétie avec un centre et un coefficient est une transformation géométrique qui amène un point pris arbitrairement en un point tel que (Fig. 10). L'homothétie prend chaque ligne dans une ligne parallèle à elle et ramène chaque cercle dans un cercle. L'homothétie préserve les angles, et augmente toutes les longueurs d'un facteur : si les points vont vers , alors Puisque dans l'homothétie toutes les longueurs changent du même nombre de fois, le rapport des longueurs ne change pas. Diverses façons d'estimer les distances sont basées sur cela; par exemple, connaissant la longueur de la main et la longueur du pouce et estimant combien de fois le pouce de la main tendue rentre dans l'image visible de l'objet, on peut trouver le rapport de la hauteur d'un objet vertical à la distance (sur la Fig. 11, nous avons Tâche 5. Construire un carré inscrit dans un secteur donné (deux sommets du carré se trouvent sur le même rayon, le troisième sur l'autre, le quatrième sur l'arc du secteur). La solution. Soient et (Fig. 12) deux carrés inscrits dans l'angle . Avec une homothétie de centre qui amène le point à , (le coefficient de cette homothétie est ), le segment rentre dans le segment , et donc le carré rentre dans un carré (puisque les angles, ainsi que le rapport des segments, sont conservés). Il s'ensuit que les sommets et se trouvent sur le même rayon issu du point . Maintenant, il est clair qu'en construisant un carré inscrit dans l'angle , et en traçant un rayon , nous pouvons trouver le sommet du carré désiré (c'est-à-dire le point d'intersection du rayon avec l'arc du secteur), puis compléter le carré requis (Fig. 13). Une transformation plane est appelée similarité avec un coefficient si pour tout point du plan la distance entre les points et est égale à . Toute similitude (ainsi que l'homothétie - un cas particulier de similitude) préserve les angles, ainsi que le rapport des longueurs, c'est-à-dire conserve la forme des personnages. Cependant, contrairement à l'homothétie, la similitude peut amener une droite à une droite qui ne lui est pas parallèle. Sur la fig. 14 montre deux plans et , d'un même terrain, réalisés à des échelles différentes et couchés différemment sur le plan. Ces plans sont des figures semblables mais non homothétiques ; par exemple, une droite et sa droite correspondante ne sont pas parallèles. Pour obtenir un plan à partir d'un plan, vous pouvez procéder comme suit : faites d'abord pivoter le plan afin que ses côtés deviennent parallèles aux côtés du plan, puis appliquez l'homothétie. En d'autres termes, un plan comme , s'obtient en utilisant la composition du mouvement (tour) et l'homothétie. Cette circonstance est générale, c'est-à-dire toute similitude est représentée comme une composition , où est le mouvement, et est l'homothétie. Il en ressort clairement que lors de la résolution de problèmes par la méthode de similarité, on peut se limiter à considérer une homothétie (accompagnée d'un certain mouvement). Cela a certaines commodités: rappelez-vous avec quelle attention intense les côtés correspondants de triangles similaires situés différemment sont trouvés lors de l'écriture de l'égalité des rapports des côtés (et avec quelle facilité ces rapports sont écrits pour les triangles homothétiques). Problème 6. Les côtés d'un triangle sont liés par la relation . Démontrer que l'angle est le double de l'angle . La solution. Soit un point de la droite tel que , et se situe entre et (Fig. 15). Alors le triangle est isocèle, donc ;
En outre, . Avec une symétrie autour de la bissectrice de l'angle, les points et iront à tels points et , que , d'où il suit que sous l'homothétie de centre et de coefficient les points vont à . D'où et donc, c'est-à-dire . Puisque est l'angle extérieur du triangle, alors il est égal à la somme des angles et, c'est-à-dire égal au double de l'angle. En conclusion de l'histoire sur les transformations de similarité, nous notons qu'elles constituent un groupe de transformations et donc (voir Géométrie) selon le programme d'Erlangen définissent "leur" géométrie. Les invariants de ce groupe (c'est-à-dire les propriétés conservées sous toutes les transformations de similarité et étudiées dans la géométrie des similarités) sont l'angle, le rapport des longueurs de deux segments, le parallélisme de deux droites, etc. Bien que la longueur du segment ne soit plus conservée, mais du fait de la conservation du rapport des longueurs dans la géométrie des similitudes, on peut parler d'un triangle isocèle (c'est-à-dire d'un triangle dans lequel le rapport des longueurs des côtés est égal à 1). Le théorème selon lequel dans un triangle isocèle les angles à la base sont égaux est également conservé dans la géométrie des similitudes. Le théorème de Pythagore est également conservé (sous la forme Cependant, il ne faut pas penser que la géométrie des similitudes ne diffère en rien de la géométrie euclidienne, si ce n'est par la forme de présentation. Il y a des faits qui distinguent ces deux géométries. Par exemple, on s'accorde à dire qu'une droite peut glisser sur elle-même si pour deux points quelconques de cette droite il y a une transformation (appartenant au groupe définissant la géométrie considérée) qui ramène la droite à elle-même et le point à . Dans la géométrie d'Euclide (c'est-à-dire dans la géométrie définie par le groupe de mouvements du plan), il n'y a que deux types de lignes connectées (c'est-à-dire constituées d'une seule pièce) qui peuvent glisser sur elles-mêmes : les lignes droites et les cercles. Et dans la géométrie des similitudes il y a des lignes, autres que droites et cercles, qui peuvent glisser sur elles-mêmes ; ce sont des spirales logarithmiques, définies en coordonnées polaires par l'équation (Fig. 16). Nous obtiendrons un autre fait inhabituel de la géométrie des similitudes en considérant la transformation , où est la rotation autour du point par l'angle , et est l'homothétie avec le centre et le coefficient . Soit une séquence de points passant les uns dans les autres lors de la transformation , c'est-à-dire pour tout entier (Fig. 17). Ces points se trouvent sur la même spirale logarithmique, et pour tout entier l'angle a la même valeur. En reliant constamment ces points, nous obtenons une ligne brisée infinie Notez que la transformation de similarité considérée (appelée étirement rotationnel) est étroitement liée aux nombres complexes. Un nombre complexe peut être représenté comme un segment orienté allant de l'origine à un point. Avec une telle représentation géométrique, les nombres complexes sont ajoutés sous forme de vecteurs (Fig. 18). Et pour obtenir une interprétation géométrique de la multiplication des nombres complexes, il convient de faire tourner l'extension considérée ci-dessus. À savoir, laissez - un certain nombre complexe, - son module (c'est-à-dire la longueur du segment représentant) et - son argument (c'est-à-dire l'angle d'inclinaison du segment dirigé représentant par rapport à la partie positive de l'axe des x). Le nombre est obtenu à partir du nombre 1 si, d'une part, le vecteur représentant le nombre 1 est étiré d'un facteur et, d'autre part, s'il est tourné d'un angle (Fig. 19), c'est-à-dire que le vecteur est obtenu à partir du vecteur 1 par la métamorphose Problème 7. Des triangles similaires les uns aux autres sont construits sur les côtés d'un triangle. Démontrer que le point d'intersection des médianes est le même que le point d'intersection des médianes . La solution. Dénoter par Puisque (puisque l'argument nombre est non nul), il s'ensuit de là que . En passant à la notation vectorielle et en divisant par 3, on obtient et cela signifie que les points d'intersection des médianes et coïncident (voir Vecteur). Parlons brièvement d'autres transformations qui jouent un rôle important dans la géométrie moderne. Une transformation du plan euclidien est dite affine si elle ramène chaque ligne à une ligne et des lignes parallèles entre elles - à nouveau à parallèles (Fig. 22). Si un système de coordonnées est introduit sur le plan, alors la transformation affine est donnée par des relations linéaires, c'est-à-dire le point auquel le point passe est déterminé par les formules où (et vice versa : une certaine transformation affine est donnée par de telles formules). De plus, s'il y a trois points du plan qui ne se trouvent pas sur la même droite, et s'il y a trois autres points qui ne se trouvent pas non plus sur la même droite, alors il existe, et de plus une seule, une transformation affine qui prend les points, respectivement, à . Notez que les longueurs et les angles peuvent changer sous des transformations affines. Non enregistré (contrairement aux transformations de similarité) et le rapport des longueurs des segments. Cependant, le rapport des longueurs de deux segments parallèles est conservé sous toute transformation affine. En particulier, le milieu d'un segment repasse sous une transformation affine au milieu d'un segment, un parallélogramme passe dans un parallélogramme, une médiane d'un triangle dans une médiane, etc. Sous une transformation affine, un cercle passe dans une ellipse , et d'après les propriétés des transformations affines notées ci-dessus, il s'ensuit facilement que les points médians du parallèle entre les cordes de l'ellipse se situent sur un segment passant par le centre de l'ellipse (Fig. 23). Toutes les transformations affines du plan, prises ensemble, forment un groupe de transformations, et donc (voir Géométrie) elles définissent une certaine géométrie. C'est ce qu'on appelle la géométrie affine. Les invariants de ce groupe (c'est-à-dire les propriétés des figures étudiées en géométrie affine) sont la disposition rectiligne des points, le parallélisme, le rapport des longueurs des segments parallèles et d'autres propriétés obtenues à partir de ceux-ci (par exemple, la présence de un centre de symétrie dans une figure). Sans parler plus en détail de cette géométrie, nous montrerons par des exemples comment les propriétés des transformations affines notées ci-dessus peuvent être appliquées à la résolution de problèmes. Problème 8. Démontrer que dans un trapèze arbitraire les milieux des bases, le point d'intersection des diagonales et le point d'intersection des extensions des côtés latéraux se trouvent sur la même droite. La solution. Pour un trapèze isocèle, c'est évident (puisqu'un trapèze isocèle est symétrique à une droite relative passant par les milieux des bases). Soit maintenant un trapèze arbitraire et soit un trapèze isocèle avec les mêmes longueurs de base (Fig. 24). Considérons une transformation affine qui mappe les points sur , respectivement. Avec cette transformation, les droites iront à (puisque , et le parallélisme des droites est conservé). De plus, puisque , alors le point ira à (puisque le rapport des segments parallèles est conservé). En d'autres termes, le trapèze entrera dans un trapèze. Par conséquent, la disposition rectiligne des points sera conservée, c'est-à-dire les points d'un trapèze se trouvent également sur la même ligne. Problème 9. Une ellipse est inscrite dans un triangle et trois segments sont dessinés, chacun reliant le sommet et le point de contact de l'ellipse avec le côté opposé. Montrer que ces trois segments se coupent en un point. La solution. Soit une transformation affine qui transforme un cercle en l'ellipse considérée, et soit un triangle qui se transforme en . Puisque la propriété considérée, comme il est facile de le prouver, est vraie pour le cercle inscrit (côté gauche de la figure 25), elle est également vraie pour l'ellipse inscrite (côté droit de la figure). L'article "Géométrie projective" décrit comment l'achèvement d'un plan avec des points impropres ("infiniment distants") le transforme en un plan projectif. Les transformations géométriques du plan projectif qui préservent la disposition rectiligne des points sont appelées transformations projectives. Les transformations projectives sont données en coordonnées par des formules linéaires fractionnaires : Plus en détail : si est le plan euclidien dans lequel le système de coordonnées est spécifié, et est le plan projectif obtenu en ajoutant des éléments impropres, alors toute transformation projective du plan s'écrit dans les coordonnées considérées par les formules (1) à condition que le point et le point dans lequel il passe, ne sont pas impropres. Les transformations projectives forment un groupe de transformations du plan projectif. Selon le programme Erlangen, ce groupe définit une certaine géométrie - c'est la géométrie projective. Les invariants des transformations projectives (c'est-à-dire les propriétés des figures étudiées en géométrie projective) sont la disposition rectiligne des points, le rapport anharmonique de quatre points situés sur une droite, etc. Si - quatre points du plan projectif, dont trois ne se trouvent pas sur la même ligne, et - quatre autres points de ce plan, dont trois non plus se trouvent sur la même ligne, alors il existe, et de plus, un seul, projectif transformation qui se traduit, se situe évidemment sur la même droite (sur la ligne médiane de la bande entre les droites et ). En appliquant la transformation inverse, nous concluons que dans la Fig. 26 à gauche, les points sont sur la même droite (puisque la disposition rectiligne des points est conservée sous la transformation projective). Toutes les transformations envisagées ci-dessus ont conservé la disposition rectiligne des points (sur le plan euclidien ou sur le plan projectif). En d'autres termes, le système de toutes les lignes droites du plan est à nouveau traduit dans le même système de lignes. Il existe une classe intéressante de transformations qui a une propriété similaire par rapport à un autre système de lignes. À savoir : considérez un système de plan (euclidien) composé de toutes les lignes droites et de tous les cercles. Les transformations qui traduisent ce système de lignes dans le même système sont appelées transformations circulaires. En d'autres termes, une ligne droite passe sous une transformation circulaire soit à nouveau en une ligne droite, soit dans un certain cercle (et il en est de même pour un cercle). Un peu plus tard, nous clarifierons une convention concernant le plan euclidien qui est nécessaire lors de l'examen des transformations circulaires, mais nous considérons d'abord un exemple important d'une transformation circulaire - la soi-disant inversion. Et un rayon. Sur cette base, nous avons convenu de considérer qu'il y a un point impropre sur le plan de ces lignes qui se coupent au même angle. Si, en particulier, le cercle est orthogonal au cercle d'inversion, c'est-à-dire le coupe à angle droit (de tels cercles ont été discutés à la fin de l'article de Lobachevsky sur la géométrie), puis ce cercle rentre en lui-même lors de l'inversion (seules ses parties situées à l'intérieur et à l'extérieur du cercle d'inversion changent de place). L'inversion est la plus importante des transformations circulaires : on peut prouver que toute transformation circulaire du plan est soit une inversion, soit une similitude, soit une composition d'une inversion et d'une similitude. Prises ensemble, les transformations circulaires constituent un groupe de transformations qui définit une sorte de géométrie ("circulaire") sur un plan circulaire. Nous avons parlé des transformations géométriques les plus importantes du plan. On peut également considérer les transformations géométriques de l'espace tridimensionnel, du plan (ou de l'espace) Lobachevsky et d'autres objets géométriques. Notez, en particulier, que si est le mouvement de l'espace tridimensionnel (car et , et transforment une ligne droite en une ligne droite). Il s'avère que toute transformation projective du plan peut être représentée sous cette forme. La connaissance des transformations géométriques et la capacité de les appliquer est un élément important de la culture mathématique. 1. L'essence de la méthode des transformations, sa place dans le cours scolaire de géométrie. 2. Types de transformation : a) les mouvements et leurs propriétés ; égalité des chiffres; b) transformation de similarité ; chiffres similaires. 3. Applications de la méthode des transformations. (1) Pour différents auteurs de manuels pour lycées de géométrie, les transformations occupent des positions différentes en termes de volume et de niveau de rigueur. Dans le manuel édité par A. N. Kolmogorov, les transformations servent de base pour prouver de nombreux théorèmes (un axiome spécial de mobilité est consacré à leur justification). Le manuel de A. P. Kiselev ne dit rien du tout sur les transformations. Dans Géométrie 7-11 A. V. Pogorelov, le sujet de la transformation des figures est abordé en huitième année. Le sujet n'est pas grand. Le concept de « transformation » est dérivé à un niveau visuel-intuitif : « Si chaque point d'une figure donnée est déplacé d'une manière ou d'une autre, nous obtiendrons une nouvelle figure. On dit que ce chiffre est obtenu par une transformation à partir de celui donné. La définition descriptive est accompagnée d'un dessin. La définition du mouvement est donnée et ses propriétés sont considérées. De plus, des types spécifiques de transformations sont clairement définis. Dans ce didacticiel, la symétrie autour d'un point, la symétrie autour d'une ligne, l'homothétie et la similarité sont définies comme des transformations avec les propriétés correspondantes ; la translation parallèle est définie comme une transformation sous forme de coordonnées ; et tourner est défini comme une sorte de mouvement. Parallèlement à la définition des transformations, une méthode de construction de figures sous transformations est également donnée. Dans le guide d'étude géométrie 7-9 (auteurs: L. S. Atanasyan et autres), le matériel sur les transformations est présenté par le sujet «Mouvement» en 9e année. C'est le dernier sujet de ce tutoriel. Ici, les concepts de « cartographier un plan sur lui-même », de « mouvement » sont introduits et les principaux types de mouvements sont examinés. De plus, l'importante question de la relation entre les concepts superpositions et mouvements, leur équivalence est prouvée. L'objectif principal du sujet est d'initier les étudiants à la notion de mouvement sur un plan, avec des types de mouvement spécifiques : symétrie centrale et axiale, translation parallèle, rotation. Le concept de mappage d'un plan sur lui-même n'est considéré que comme une base pour introduire le concept de mouvement. La cartographie d'un plan sur lui-même à un niveau visuel-intuitif est considérée avec l'implication des concepts de symétrie axiale et centrale déjà connus des étudiants. Étant donné que le programme d'études d'une école d'enseignement général en mathématiques ne prévoit pas encore une étude détaillée des diverses propriétés de ces transformations, la question de l'utilisation des transformations devrait être retirée en cours optionnels ou envisagée dans la salle de classe d'un cercle mathématique. Comme mentionné ci-dessus, dans le cours de géométrie d'une école d'enseignement général, ils n'entrent pas dans les détails de la définition mathématique du concept de "transformation". Mais un professeur de mathématiques doit comprendre qu'en géométrie une transformation (dans le cas d'un plan) est comprise comme "une application du plan entier sur lui-même, dans laquelle chaque point X mappé à un seul point X 1 , et chaque point Oui 1 correspond à un seul point Oui». Pour les élèves, on parle de transformation de formes. Une figure, contrairement à un plan, est finie, donc le concept de transformation de figures est plus accessible. On peut dire aux élèves que la transformation d'un plan est une fonction, qui plus est, une formation, mais en géométrie on parle de correspondance de points, pas de nombres. (2) Parmi les transformations étudiées à l'école, il en existe deux types : le mouvement et la transformation par similarité. Tous les types de transformations ne sont pas étudiés à l'école. « La transformation d'une figure en une autre s'appelle un mouvement si elle conserve la distance entre les points, c'est-à-dire traduit deux points quelconques X et Oui une forme par point X 1 et Oui 1 autre figure pour que XY = X 1 Oui une ". Si l'exécution séquentielle de deux ou plusieurs transformations est considérée, alors le résultat d'une telle exécution séquentielle de transformations en géométrie est appelé composition métamorphoses. Dans ce tutoriel, une seule propriété de composition est donnée : deux mouvements exécutés successivement redonnent du mouvement. La transformation inverse de celle donnée est également considérée. Il est prouvé qu'une transformation inverse d'un mouvement est un mouvement. La propriété est implicitement présente : la composition de la transformation de son inverse est la transformation identique. Les élèves doivent comprendre qu'après avoir prouvé les propriétés du mouvement, il est possible d'opérer non seulement avec des points, mais aussi de soumettre des segments, des droites, des rayons, des angles, etc. à des transformations. Et vous pouvez être absolument sûr que les figures qui ont subi la transformation du mouvement porteront le même nom : les segments iront en segments, les angles en angles, etc. ; de plus, les segments iront en segments égaux, les angles en angles égaux, etc. Dans le manuel de A. V. Pogorelov, il est prouvé que la symétrie par rapport à un point est un mouvement (en utilisant le premier critère d'égalité des triangles); la symétrie par rapport à une droite est un mouvement (prouvé par la méthode des coordonnées). Dans le second cas, l'axe de symétrie est choisi comme axe des ordonnées. La prochaine étape dans l'apprentissage des mouvements consiste à les utiliser pour déterminer égalité Les figures. L'égalité des figures dans les différents cours de géométrie scolaire est introduite de différentes manières. Parfois, une définition générale des "chiffres égaux" n'est pas donnée du tout, parfois elle est introduite immédiatement. Dans le manuel A.V. Pogorelov introduit d'abord le concept d'égalité de figures spécifiques (segments, angles, triangles), puis une définition générale de l'égalité des figures est donnée en utilisant le concept de mouvement: " Deux figures sont dites égales si elles sont transférées de l'une à l'autre par le mouvement. Un fait important est prouvé : l'égalité des triangles, définie par leur combinaison par le mouvement, et l'égalité, telle que nous l'avons entendue jusqu'ici, expriment la même chose. En d'autres termes, on peut prouver l'équivalence des deux définitions. La preuve se compose de deux parties : 1) à partir de l'hypothèse que 2 triangles abc et UN 1 À 1 DE 1 sont combinés par mouvement, l'égalité de leurs angles et côtés respectifs est prouvée ; 2) on suppose que les côtés et les angles correspondants de ces triangles sont égaux, et on prouve qu'ils peuvent être combinés par un mouvement. La première partie de la preuve repose sur la définition du mouvement et sa propriété que les angles sont conservés en mouvement. La solution à la deuxième partie du problème dépend de l'emplacement des triangles. Considérons une des variantes de la preuve, différente de celle donnée dans le manuel d'A.V. Pogorelov. Triangle MAIS 2 À 1 DE 2 dérivé de triangle abc translation parallèle dans la direction donnée par le rayon AA 2 pour la distance AA 2. Triangle UN 1 À 1 DE 1 obtenu à partir de triangle MAIS 2 À 1 DE 2 en tournant de l'angle α dans le sens des aiguilles d'une montre (voir Fig. 1). Le but principal de l'étude de ce sujet est d'initier les élèves à des exemples de transformations géométriques. Lorsque vous travaillez sur un sujet, l'attention principale doit être accordée au développement des compétences de construction d'images des figures les plus simples (points, segments, triangles) avec des mouvements spécifiques. Dans ce cas, la propriété de mouvement est utilisée à un niveau visuel-intuitif, les théorèmes correspondants peuvent être considérés sans preuve. Au cours de la résolution de problèmes, les élèves doivent se familiariser avec des exemples de figures qui ont une symétrie. Le concept général d'égalité des chiffres ne peut être considéré que dans un plan d'introduction (par exemple, sous forme de cours magistral) sans reproduction ultérieure des preuves par les étudiants. Dans le guide d'étude géométrie 7-9 L.S. Atanasyan et d'autres, le sujet du "Mouvement" commence par l'introduction du concept de cartographie d'un plan sur lui-même, dont la définition est donnée de manière descriptive. L'étude du sujet commence par une répétition du concept de point symétrique par rapport à un point donné (symétrie centrale) et à une ligne donnée (symétrie axiale). Plus tôt, en 8e année, les élèves considéraient la symétrie centrale et axiale comme une propriété des formes géométriques. Maintenant, ces concepts généralement familiers sont présentés comme des exemples de mappage d'un plan sur lui-même. Pendant la répétition, les élèves doivent être amenés au concept de maintien de la distance entre les points. Les tâches suivantes peuvent servir cet objectif. 1. Construire des points MAIS 1 , À 1 , symétrique aux points MAIS et À relativement droit je(voir Fig. 2a – 2c). 2. Existe-t-il un point du plan pour lequel il n'existe aucun point symétrique par rapport à la droite donnée ? 3. Prouver que dans chacun des cas 2a – 2b MAIS 1 À 1 = UN B. 5. Existe-t-il un tel point du plan pour lequel il n'existe aucun point symétrique par rapport à ce point ? 6. Démontrer que dans chacun des cas considérés au problème 4 MAIS 1 À 1 = UN B. Nous pouvons maintenant introduire le concept de mappage d'un plan sur lui-même et l'illustrer avec des exemples de symétrie centrale et axiale. Il est important de souligner que lorsqu'un plan est mappé sur lui-même, deux conditions sont remplies : 1) Chaque point du plan est associé à un point du plan ; 2) Chaque point du plan est affecté à un point du plan. Après cela, vous pouvez envisager des tâches pour consolider ce concept. Maintenant, sur la base des tâches 3 et 6 discutées ci-dessus, nous introduisons le concept de mouvement : "Le mouvement d'un avion est une cartographie d'un avion sur lui-même qui préserve la distance." Après cela, le théorème de cartographie des segments et son corollaire sont considérés. Les étudiants doivent se concentrer sur le fait que la preuve se compose de 2 parties : 1) on prouve que chaque point R ce segment MN cartographié à un certain point R 1 coupe M 1 N 1 ; 2) on prouve qu'en chaque point R 1 coupe M 1 N 1 un point passe R ce segment MN. L'élément "Superposition et mouvement" est facultatif, mais dans une classe bien préparée, il peut être envisagé. Ce matériel peut être présenté sous forme de conférence. Le concept d'imposition, sur la base duquel l'égalité des figures a été déterminée, est l'un des concepts de base (non définis) de ce cours de géométrie. Les superpositions sont de telles applications du plan sur lui-même, qui ont les propriétés exprimées dans les axiomes 7-13 (Atanasyan L.S. et al. Geo. 7-9). Le mouvement est un concept défini : c'est une application d'un plan sur lui-même qui préserve la distance. Il découle directement de la définition du mouvement et des axiomes d'imposition que tout recouvrir est mouvement. L'assertion inverse est aussi démontrée : tout Circulation est recouvrir. Ainsi, le concept d'imposition coïncide avec le concept de mouvement. Les étudiants n'ont pas à être tenus de prouver les faits énoncés au paragraphe 115. Le matériel sur la translation et la rotation parallèles de deux autres types de mouvements peut également être présenté sous la forme d'un cours magistral. Il est utile d'attirer l'attention des élèves sur le fait que lors d'une translation parallèle, une ligne est projetée sur une ligne parallèle à elle ou sur elle-même. De là découle une méthode simple pour construire des images de lignes et de segments avec translation parallèle. Prouvant que la traduction parallèle et la rotation sont des mouvements, les élèves forts peuvent déchiffrer le manuel de leur propre chef dans la classe, suivi d'une discussion générale. Les élèves faibles ne devraient pas être tenus de reproduire des preuves. À la fin du chapitre, des problèmes géométriques sont donnés, pour la solution desquels il est recommandé d'utiliser des mouvements. Certains de ces problèmes sont donnés avec des solutions. (2b) La transformation de similarité joue un rôle important en géométrie. C'est compréhensible. Notre espace réel a un groupe de similarité. Tous les objets géométriques de l'espace, s'ils sont formés de segments de ligne, peuvent être divisés en 2 ensembles: figures similaires et dissemblables. Dans l'ensemble des figures similaires, il peut y en avoir des égales. Le concept de similitude des figures chez un enfant apparaît beaucoup plus tôt que le concept de leur taille. Cela est dû aux particularités de la perception visuelle : Deux figures de tailles différentes, mais de forme identique, elles ne diffèrent pas. La forme des figures ne change pas lorsque la distance à partir de laquelle la figure est visible change. Les principaux signes de l'invariabilité de la forme d'une figure sont égalité coins et proportionnalité les segments correspondants. Dans le manuel A.V. La géométrie de Pogorelov 7 – 11 de la définition de la transformation de similarité est introduite de la même manière que la définition du mouvement : La transformation d'une figure F en une figure F 1 est dite transformation de similarité si, au cours de cette transformation, la distance entre points augmente (ou diminue) du même nombre de fois. Cela signifie que si des points arbitraires MAIS et À Les figures F sous cette transformation aller aux points UN 1 et À 1 chiffres F 1 , alors MAIS 1 À 1 = kAB. Numéro k est appelé coefficient de similarité. Après introduction de ce concept, il est prouvé que homothétie est une transformation de similarité. Ce fait est prouvé par la méthode vectorielle. De même, comme pour le mouvement, on prouve que sous la transformation de similarité trois points MAIS, À, DE, allongé sur une ligne droite, aller à trois points MAIS 1 , À 1 , DE 1 se trouvant sur la même ligne droite, et l'ordre de leur arrangement mutuel est préservé. Il s'ensuit que la transformation de similarité transforme les lignes en lignes, les rayons en rayons, les segments en segments. En utilisant l'homothétie, on prouve que la transformation de similarité préserve les angles entre les demi-droites. Les élèves doivent savoir que toutes les transformations de similarité ne sont pas une homothétie. A l'aide du concept de transformation de similarité, une définition des figures similaires est donnée. Dans le manuel A.V. Pogorelov donne d'abord une définition des figures semblables : « Deux figures sont dites semblables si elles se traduisent l'une dans l'autre par une transformation de similarité. Le symbole spécial ~ () est utilisé pour désigner ces chiffres. F ~ F 1). Ensuite, la similitude des triangles est considérée. ∆ enregistré abc~∆MAIS 1 À 1 DE 1, on suppose que les sommets appariés par la transformation de similarité se trouvent aux endroits correspondants, c'est-à-dire MAIS va dans MAIS 1 etc D'après les propriétés de la transformation de similarité, il s'ensuit que pour les triangles similaires, les angles correspondants sont égaux et les côtés correspondants sont proportionnels. La preuve des signes de similarité est effectuée à l'aide du concept d'homothétie. Les signes de similitude des triangles rectangles sont considérés séparément. Le thème "Polygones" traite de la question de la similarité des polygones convexes réguliers. Le thème "Aires de figures" traite de l'aire de figures similaires : "les aires de figures similaires sont liées comme les carrés de leurs dimensions linéaires respectives". Le concept de transformation de figures dans l'espace est introduit de la même manière que sur un avion. Cependant, il existe certaines fonctionnalités. Lorsque l'on considère la transformation de la symétrie dans l'espace, en plus de la symétrie par rapport à un point et à une ligne, la symétrie par rapport à un plan est ajoutée. Une nouvelle propriété du mouvement dans l'espace est que le mouvement traduit les plans en plans. Une nouvelle propriété de la translation parallèle dans l'espace est la propriété suivante : lors de la translation parallèle dans l'espace, chaque plan passe soit sur lui-même, soit dans un plan qui lui est parallèle. Lors de l'examen du sujet "Similarités des figures spatiales", les déclarations suivantes sont ajoutées : "la transformation de similarité transforme les plans en plans" et "la transformation d'homothétie dans l'espace transforme tout plan qui ne passe pas par le centre d'homothétie en un plan parallèle (ou en lui-même lorsque k=1). Lorsque l'on considère les transformations dans l'espace, on peut se limiter à leurs représentations visuelles intuitives et ne pas se concentrer sur la dérivation des faits utilisés. Et l'accent devrait être mis sur l'utilisation des transformations pour prouver des théorèmes et résoudre des problèmes. Dans le manuel L.S. Atanasyan et d'autres en 8e année au chapitre VII, le sujet «Triangles similaires» est examiné, qui commence par l'introduction du concept de segments proportionnels. On explique aux élèves que, dans la vie de tous les jours, ils doivent composer avec des objets de même forme, mais de tailles différentes. De tels objets sont les prototypes de telles formes géométriques. L'accent est mis sur les triangles similaires. La similitude des triangles est introduite non pas à l'aide d'une transformation de similitude, mais par l'égalité des angles et la proportionnalité des côtés similaires. Les signes de similitude des triangles sont très simplement prouvés, sur la base du théorème: "Si l'angle d'un triangle est égal à l'angle d'un autre triangle, alors les aires de ces triangles sont liées comme le produit des côtés contenant des angles égaux." Après avoir prouvé les signes de similarité, l'application de la similarité pour prouver des théorèmes et résoudre des problèmes est montrée. En tant qu'applications pratiques de la similarité des triangles, des méthodes pour modifier la hauteur d'un objet et la distance à un point inaccessible sont décrites. Une idée est donnée sur l'application de la méthode de similarité dans la résolution de problèmes de construction. Sous une forme très brève, il est décrit comment vous pouvez déterminer la similitude de chiffres arbitraires. symboles utilisés : ∆ abc~∆MAIS 1 À 1 DE 1 (triangle abc semblable à un triangle MAIS 1 À 1 DE une). Le concept de figures centrales est donné : « chaque point M Les figures F point cartographié M 1 plan pour que les points M et M 1 se situer sur un rayon ayant pour origine un point fixe O, en outre OM 1 = kOM(Voir figure 3). À la suite d'une telle comparaison, un chiffre F 1 est obtenu, similaire au chiffre F. Dans ce cas, les chiffres F et F 1 sont dits centrés. (3) La méthode de transformation est utilisée lors de l'examen de divers problèmes théoriques du cours de géométrie : Application du mouvement dans la détermination de l'égalité des figures : application de la transformation de similarité dans l'étude des triangles similaires (dans le manuel d'A.V. Pogorelov) ; la traduction parallèle et les vecteurs sont étroitement liés. La méthode de transformation est largement utilisée pour résoudre divers problèmes géométriques. Cependant, les élèves ne sont pas initiés à l'utilisation de cette méthode pour résoudre des problèmes dans les cours de mathématiques à l'école. Cette question est soumise à des activités facultatives ou parascolaires. La méthode des transformations est utilisée pour résoudre des problèmes de preuve, de construction, pour résoudre les problèmes dits géométriques pour trouver le maximum et le minimum. Dans ce cas, tous les types de transformations sont utilisés.






TRANSFORMATION DE SIMILITUDE

PROPRIÉTÉS DE TRANSFORMATION DE SIMILARITÉ

75. Exemples de transformations de chiffres.











![]() va à , c'est-à-dire à . Mais depuis, alors. Ainsi, lorsqu'il est tourné de 90°, le vecteur passe dans , c'est-à-dire dans un vecteur égal à . Il en résulte que et .
va à , c'est-à-dire à . Mais depuis, alors. Ainsi, lorsqu'il est tourné de 90°, le vecteur passe dans , c'est-à-dire dans un vecteur égal à . Il en résulte que et .





![]() . Il s'ensuit que l'homothétie préserve la forme (mais non la taille) des figures ; si, par exemple, , alors la figure , dans laquelle la figure va quand homothétie avec le centre et le coefficient , est une copie agrandie de la figure (Fig. 10), et si - une copie réduite.
. Il s'ensuit que l'homothétie préserve la forme (mais non la taille) des figures ; si, par exemple, , alors la figure , dans laquelle la figure va quand homothétie avec le centre et le coefficient , est une copie agrandie de la figure (Fig. 10), et si - une copie réduite.
![]() , d'où, en mesurant, vous pouvez trouver, et donc la hauteur du tuyau, qui est environ trois fois plus grande).
, d'où, en mesurant, vous pouvez trouver, et donc la hauteur du tuyau, qui est environ trois fois plus grande).



![]() ; En outre . L'égalité peut être réécrite comme
; En outre . L'égalité peut être réécrite comme
![]() , où et sont les rapports des longueurs des jambes à la longueur de l'hypoténuse), etc.
, où et sont les rapports des longueurs des jambes à la longueur de l'hypoténuse), etc.
![]() , qui se traduit par une transformation en lui-même, chaque sommet étant traduit en un sommet voisin .
, qui se traduit par une transformation en lui-même, chaque sommet étant traduit en un sommet voisin .
![]() , où est une homothétie centrée à l'origine et coefficient , et est une rotation autour de l'origine d'un angle . Alors, . Si maintenant est un autre nombre complexe, alors lors de l'application de la transformation (c'est-à-dire lorsque le vecteur représentant est étiré d'un facteur et tourné d'un angle), le nombre entre dans (Fig. 19). Cela peut être dit d'une autre manière: les triangles de la Fig. 19 sont similaires. Cela donne une interprétation géométrique de la multiplication des nombres complexes. Il ressort clairement de ce qui a été dit que lorsque tous les nombres complexes sont multipliés par le même nombre complexe, tout le plan des nombres complexes est soumis à un étirement rotationnel. En particulier, pour trois nombres complexes quelconques, nous avons
, où est une homothétie centrée à l'origine et coefficient , et est une rotation autour de l'origine d'un angle . Alors, . Si maintenant est un autre nombre complexe, alors lors de l'application de la transformation (c'est-à-dire lorsque le vecteur représentant est étiré d'un facteur et tourné d'un angle), le nombre entre dans (Fig. 19). Cela peut être dit d'une autre manière: les triangles de la Fig. 19 sont similaires. Cela donne une interprétation géométrique de la multiplication des nombres complexes. Il ressort clairement de ce qui a été dit que lorsque tous les nombres complexes sont multipliés par le même nombre complexe, tout le plan des nombres complexes est soumis à un étirement rotationnel. En particulier, pour trois nombres complexes quelconques, nous avons ![]() , où est un nombre complexe dont le module est égal au rapport des longueurs des vecteurs et , et l'argument est égal à l'angle entre ces vecteurs (Fig. 20).
, où est un nombre complexe dont le module est égal au rapport des longueurs des vecteurs et , et l'argument est égal à l'angle entre ces vecteurs (Fig. 20).


![]() nombres complexes représentés par des vecteurs , , , , , . Alors
nombres complexes représentés par des vecteurs , , , , , . Alors ![]() ,
, ![]() ,
, ![]() , où est un nombre complexe dont le module est égal au rapport des côtés des triangles semblables considérés, et l'argument est (Fig. 21). En additionnant ces égalités, on obtient (après simplifications évidentes) :
, où est un nombre complexe dont le module est égal au rapport des côtés des triangles semblables considérés, et l'argument est (Fig. 21). En additionnant ces égalités, on obtient (après simplifications évidentes) :
![]() ,
,



 (1)
(1) 4. Points d'accrochage MAIS 1 et À 1 , symétrique aux points MAIS et À par rapport au point O, si a) pointe O se trouve sur la ligne UN B; b) pointe O ne repose pas sur une ligne droite UN B.
4. Points d'accrochage MAIS 1 et À 1 , symétrique aux points MAIS et À par rapport au point O, si a) pointe O se trouve sur la ligne UN B; b) pointe O ne repose pas sur une ligne droite UN B.