Gimnaziul Maloyazovsky Bashkir

Geometrie Rezumat

„Transformări de formă”

Completat de: elev clasa a 10-a B

Khaliullin A.N.

Verificat de: Israfilova R.Kh.

Maloyaz 2003

I. Transformare.

II. Tipuri de transformări

1. Omotetie

2. Asemănarea

3. Mișcarea

III. Tipuri de mișcare

1. Simetrie despre un punct

2. Simetrie față de o dreaptă

3. Simetria fata de plan

4. Întoarce-te

5. Transferul paralel în spațiu

I. Transformare - deplasarea fiecărui punct al unei figuri date într-un fel și obținerea unei noi figuri.

II. Tipuri de transformare în spațiu: asemănarea, homotezia, mișcarea.

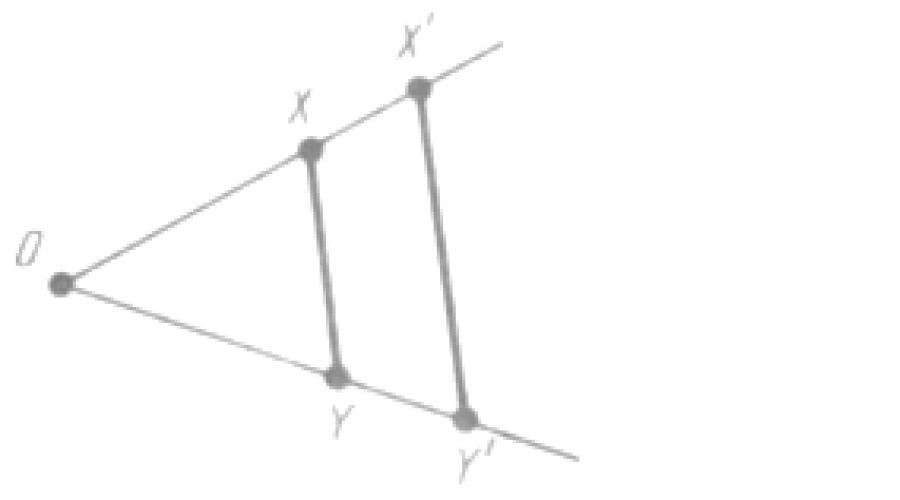
Similaritate O transformare a unei figuri F se numește transformare de asemănare dacă, în timpul acestei transformări, distanțele dintre puncte se modifică de același număr de ori, adică. pentru orice puncte X și Y ale figurii F și punctele X', Y' ale figurii F' la care trece, X'Y' = k * XY.

Proprietăți de similaritate: 1. Similaritatea transformă linii drepte în linii drepte, semilinii în semilinii, segmentele în segmente.

2. Similitudinea păstrează unghiurile dintre jumătățile de linii

3. Asemănarea traduce planurile în planuri.

Două figuri sunt numite similare dacă sunt transpuse una în alta printr-o transformare de asemănare.

Omotezia

Omotezia este cea mai simplă transformare în jurul centrului O cu coeficientul de homoteție k. Aceasta este o transformare care traduce un punct arbitrar X' al razei OX astfel încât OX' = k*OX.

Proprietatea unei homotetii: 1. Prin transformarea unei homotetii, transforma orice plan care nu trece prin centrul homotetiei intr-un plan paralel (sau in sine daca k=1).

Dovada. Într-adevăr, fie O centrul homoteziei și fie a orice plan care nu trece prin punctul O. Luați orice dreaptă AB în planul a. Transformarea omoteziei transformă punctul A în punctul A' pe raza OA și punctul B în punctul B' pe raza OB, unde OA'/OA = k, OB'/OB = k, unde k este coeficientul de homotezie. Aceasta implică asemănarea triunghiurilor AOB și A'OB'. Din asemănarea triunghiurilor rezultă egalitatea unghiurilor corespunzătoare OAB și OA'B', și de aici paralelismul dreptelor AB și A'B'. Să luăm acum o altă linie AC în planul a. Sub omotezie, trece pe linia paralelă A'C'. Sub homotezia considerată, planul a trece în planul a' trecând prin liniile A'B', A'C'. Deoarece A'B'||AB și A'C'||AC, atunci după teorema pe două drepte care se intersectează ale unui plan, respectiv, paralele cu liniile care se intersectează ale altui plan, planurile a și a' sunt paralele, ceea ce a fost necesar a fi dovedit.

Circulaţie

Mișcare - transformarea unei figuri în alta dacă păstrează distanța dintre puncte, adică. traduce oricare două puncte X și Y ale unei figuri în puncte X , Y ale altei figuri astfel încât XY = X Y

Proprietățile mișcării: 1. Punctele aflate pe linie dreaptă, la mișcare, trec în puncte situate pe linie dreaptă, iar ordinea lor este păstrată poziție relativă. Aceasta înseamnă că dacă A, B, C, întins pe linie, mergi la punctele A 1 ,B 1 ,C 1 . Atunci aceste puncte se află și ele pe linie; dacă punctul B se află între punctele A și C, atunci punctul B 1 se află între punctele A 1 și C 1.

Dovada. Fie punctul B al dreptei AC se află între punctele A și C. Să demonstrăm că punctele A 1 ,B 1 ,C 1 se află pe aceeași dreaptă.

Dacă punctele A 1 ,B 1 ,C 1 nu se află pe o dreaptă, atunci ele sunt vârfurile unui triunghi. Prin urmare A 1 C 1< A 1 B 1 + B 1 C 1 . По определению движения отсюда следует, что AC

Am ajuns la o contradicție. Prin urmare, punctul B 1 se află pe dreapta A 1 C 1 . Se demonstrează prima afirmație a teoremei.

Să arătăm acum că punctul B 1 se află între A 1 și C 1 . Să presupunem că punctul A 1 se află între punctele B 1 și C 1 . Atunci A 1 B 1 + A 1 C 1 = B 1 C 1 , și deci AB+AC=BC. Dar aceasta contrazice inegalitatea AB+BC=AC. Astfel, punctul A 1 nu poate fi situat între punctele B 1 și C 1 .

În mod similar, demonstrăm că punctul C 1 nu poate fi situat între punctele A 1 și B 1 .

Deoarece unul dintre cele trei puncte A 1 ,B 1 ,C 1 se află între celelalte două, acest punct poate fi doar B 1 . Teorema este demonstrată complet.

2. La mișcare, liniile drepte se transformă în linii drepte, semilinii în semilinii, segmentele în segmente

3. La deplasare, unghiurile dintre semilinii sunt păstrate.

Dovada. Fie AB și AC două semidrepte care emană din punctul A și nu se află pe această dreaptă. Când se deplasează, aceste semi-linii trec în niște semi-linii A 1 B 1 și A 1 C 1 . Deoarece mișcarea păstrează distanța, triunghiurile ABC și A 1 B 1 C 1 sunt egale conform celui de-al treilea criteriu de egalitate a triunghiurilor. Egalitatea triunghiurilor implică egalitatea unghiurilor BAC și B 1 A 1 C 1 , ceea ce urma să fie demonstrat.

C2. Triunghiurile A2BC2 și A1B1C1 sunt egale la al treilea criteriu. Din egalitatea triunghiurilor rezultă egalitatea unghiurilor A2BC2 și A1B1C1. Prin urmare, unghiurile ABC și A1B1C1 sunt egale, ceea ce trebuia demonstrat. 3. SIMILITATEA FIGURILOR Două figuri se numesc similare dacă sunt transformate una în alta printr-o transformare de asemănare. Pentru a indica asemănarea figurilor, se folosește o pictogramă specială: ∞. Intrarea F∞F" spune...

Medianele triunghiurilor; 4. , unde BH și B1H1 sunt înălțimi ale triunghiurilor. §5. Lucrare experimentală Scopul lucrării experimentale: identificarea trăsăturilor metodologice ale studiului temei „Triunghiuri similare” în liceu. Idee: pentru a identifica caracteristicile metodologice, este necesar să se desfășoare mai multe lecții conform metodologiei dezvoltate, la sfârșitul instruirii, să efectueze un test, în a cărui analiză se poate judeca despre ...

Diferențele dintre subiecții grupului de control și experimental au servit drept bază pentru desfășurarea lucrărilor pedagogice vizate pentru a dezvolta ideile copiilor din grupul experimental despre forma obiectelor. 2.2 Utilizarea sarcinilor puzzle în dezvoltarea ideilor despre forma obiectelor la copiii din grupul experimental Ideile copiilor despre forma obiectelor sunt de mare importanță atunci când...

TRANSFORMAREA ASEMĂNĂRII

Transformarea formei F într-o formă de F numită transformarea asemănării , dacă, în cadrul acestei transformări, distanţele dintre puncte se modifică de acelaşi număr de ori (Fig. 1). Aceasta înseamnă că dacă punctele arbitrare X, Y forme F la transformarea asemănării, ei merg la punctele X", Y" cifrele F", apoi X"Y" = k-XY , unde numărul k -- același pentru toate punctele X, Y . Numărul k numit coeficient de similitudine . Pentru k = l transformarea asemănării este evident o mișcare.

Fie F o figură dată și O un punct fix (Fig. 2). Să trasăm o rază OX printr-un punct arbitrar X al figurii F și să trasăm pe ea segmentul OX" egal cu k? OX, unde k este un număr pozitiv. homotezia față de centrul O. Numărul k se numește coeficient de homotezie, figurile F și F" se numesc omotetice.

Teorema 1. Omotetia este o transformare de similaritate

Dovada. Fie O centrul de homotezie, k coeficientul de homotezie, X și Y două puncte arbitrare ale figurii (Fig. 3)

Fig.3

Sub omotezie, punctele X și Y merg la punctele X" și Y" de pe razele OX și, respectiv, OY, și OX" = k?OX, OY" = k?OY. Aceasta implică egalitățile vectoriale OX" = kOX, OY" = kOY.

Scăzând aceste egalități termen cu termen, obținem: OY "-OX" = k (OY- OX).

Deoarece OY "- OX" \u003d X "Y", OY -OX \u003d XY, apoi X "Y" \u003d kXY. Prin urmare, /X"Y"/=k /XY/, adică. X"Y" = kXY. Prin urmare, homotezia este o transformare de similaritate. Teorema a fost demonstrată.

Transformarea similarității este utilizată pe scară largă în practică atunci când se realizează desene ale pieselor de mașini, structuri, planuri de teren etc. Aceste imagini sunt transformări similare ale imaginilor imaginare la dimensiune completă. Factorul de asemănare se numește scară. De exemplu, dacă o bucată de teren este reprezentată la scara 1:100, atunci aceasta înseamnă că un centimetru pe plan corespunde cu 1 m pe sol.

Sarcină. Figura 4 prezintă un plan al moșiei la scară 1:1000. Determinați dimensiunile proprietății (lungime și lățime).

Soluţie. Lungimea și lățimea moșiei pe plan sunt de 4 cm și 2,7 cm.Deoarece planul este realizat la scară 1:1000, dimensiunile moșiei sunt 2,7 x 1000 cm = 27 m, 4 x 100 cm = 40 m, respectiv.

PROPRIETĂȚI DE TRANSFORMARE DE SIMILITATE

La fel ca și pentru mișcare, se demonstrează că la transformarea de asemănare trei puncte A, B, C, situate pe aceeași linie, trec în trei puncte A 1 , B 1 , C 1 , situate de asemenea pe aceeași linie. În plus, dacă punctul B se află între punctele A și C, atunci punctul B 1 se află între punctele A 1 și C 1. Rezultă că transformarea asemănării transformă linii în linii, semi-linii în semi-linii, segmentele în segmente.

Să demonstrăm că transformarea de asemănare păstrează unghiurile dintre semidrepte.

Într-adevăr, să fie transformat unghiul ABC prin transformarea de similitudine cu coeficientul k în unghiul A 1 B 1 C 1 (Fig. 5). Supunem unghiul ABC unei transformări de homotezie în raport cu vârful său B cu coeficientul de homotezie k. În acest caz, punctele A și C vor merge la punctele A 2 și C 2. Triunghiurile A 2 BC 2 și A 1 B 1 C 1 sunt egale la al treilea criteriu. Din egalitatea triunghiurilor rezultă egalitatea unghiurilor A 2 BC 2 și A 1 B 1 C 1. Prin urmare, unghiurile ABC și A 1 B 1 C 1 sunt egale, ceea ce trebuia demonstrat.

75. Exemple de transformări ale figurilor.

Transformările figurilor sunt studiate în cursul geometriei în plan și în spațiu. Dacă fiecare punct al unei figuri date pe un plan sau în spațiu este deplasat într-un fel, atunci vom obține o nouă figură. Se spune că această cifră este obținută printr-o transformare din cea dată. Iată câteva exemple de transformări de formă.

1. Simetrie în jurul unui punct (simetrie centrală). Simetria față de un punct este definită după cum urmează. Fie O un punct fix și X un punct arbitrar. Un punct se numește simetric față de punctul X față de punctul O dacă punctele se află pe aceeași dreaptă, iar punctul simetric față de punctul O este punctul O. În Figura 203, punctele X și sunt simetrice între ele în raport cu punctul O .

Fie F o figură dată și O un punct fix al planului. Transformarea unei figuri F într-o figură în care fiecare dintre punctele sale X merge într-un punct simetric față de X față de un punct dat O se numește o transformare de simetrie față de punctul O. Figura 204 arată o simetrică față de centrul O.

Figura 205 prezintă două cuburi simetrice față de punctul O.

Dacă transformarea de simetrie în jurul punctului O se translată

figura în sine, atunci figura se numește simetrică centrală, iar punctul O este centrul său de simetrie. De exemplu, un paralelogram este o figură simetrică central. Centrul simetriei sale este punctul de intersecție al diagonalelor (Fig. 206, a). Un cerc cu un centru O este, de asemenea, o figură simetrică central cu un centru de simetrie O (Fig. 206, b) Toate figurile enumerate sunt plate.

În spațiu, precum și în plan, există multe exemple de figuri simetrice central. De exemplu, Figura 207 prezintă următoarele figuri: un cub, o sferă, un paralelipiped.

2. Simetrie față de o dreaptă (simetrie axială). Fie I o linie dreaptă fixă ​​(Fig. 208). Un punct se numește simetric față de un punct X față de dreapta I dacă linia este perpendiculară pe dreapta I și unde O este punctul de intersecție al dreptelor și I. Dacă punctul X se află pe dreapta I, atunci punctul simetric cu acesta este însuși punctul X. Punctul simetric față de punctul este punctul X. În figura 208, iar punctele sunt simetrice față de dreapta I.

Transformarea figurii F în care fiecare punct X merge într-un punct simetric față de dreapta I se numește transformare de simetrie față de dreapta I. În acest caz, figurile sunt numite simetrice față de

linia I. Figura 208, b prezintă cercuri simetrice față de dreapta I.

Figura 209 prezintă două sfere simetrice față de linia I.

Dacă o transformare de simetrie față de dreapta I transformă figura F în sine, atunci figura se numește simetrică față de dreapta 19, iar dreapta I se numește axa de simetrie a figurii.

De exemplu, liniile drepte care trec prin punctul de intersecție al diagonalelor unui dreptunghi paralel cu laturile sale sunt axele de simetrie ale dreptunghiului (Fig. 210, a). Dreaptele pe care se află diagonalele rombului sunt axele sale de simetrie (Fig. 210, b). Cercul este simetric față de orice dreaptă care trece prin centrul său (Fig. 210, c). Toate aceste cifre sunt plate.

În spațiu, precum și în plan, există multe exemple de figuri care au axe de simetrie. Figura 211 prezintă astfel de figuri: acesta este un paralelipiped dreptunghiular, un con, o piramidă patruunghiulară obișnuită.

3. Simetria fata de plan. Fie a un plan fix arbitrar. Din punctul X, o perpendiculară se coboară pe planul a (O este punctul de intersecție al acesteia cu planul a) și pe continuarea ei dincolo de punctul O

așează un segment egal cu Punctul X și se numesc simetrice față de planul a (Fig. 212).

Transformarea figurii F în care fiecare punct X al figurii F merge într-un punct simetric față de X față de planul a se numește transformare de simetrie față de plan.În acest caz, figurile se numesc simetrice cu fata de avion

Figura 213 prezintă două sfere simetrice față de planul a.

Dacă o transformare de simetrie față de un plan transformă o figură în sine, atunci se spune că figura este simetrică față de plan; planul a se numește plan de simetrie.

Figura 214 prezintă două planuri de simetrie ale sferei. Rețineți că sfera are un număr infinit de astfel de planuri de simetrie. Cubul are și planuri de simetrie. Figura 215 prezintă două dintre ele.

4. Omotezia. Fie F o figură dată și O un punct fix (Fig. 216). Să desenăm o rază printr-un punct arbitrar X al figurii F și să trasăm pe ea un segment și egal cu unde este un număr pozitiv. Transformarea unei figuri, în care fiecare dintre punctele sale X merge la un punct construit în modul specificat, se numește omotezie în raport cu

O transformare geometrică a unui plan este o mapare unu-la-unu a acestui plan pe sine. Cele mai importante transformări geometrice sunt mișcările, adică. transformări care păstrează distanța. Cu alte cuvinte, dacă este mișcarea planului, atunci pentru oricare două puncte ale acestui plan distanța dintre puncte și este egală cu .

Mișcările sunt asociate cu conceptul de egalitate (congruență) a figurilor: două figuri și planuri a se numesc egale dacă există o mișcare a acestui plan care transferă prima figură pe a doua. De fapt, această definiție a fost folosită de Euclid (vezi Geometrie), care a numit două figuri egale dacă una dintre ele poate fi suprapusă peste cealaltă astfel încât să coincidă cu toate punctele lor; prin impunerea aici ar trebui să se înțeleagă rearanjarea figurii ca un întreg solid (fără a modifica distanțele), adică. circulaţie.

Exemple de mișcări plane sunt simetria axială și centrală, translația paralelă, rotația. Ca exemplu, ne amintim definiția traducerii paralele. Să fie un vector plan. O transformare geometrică care transferă fiecare punct într-un astfel de punct care (Fig. 1) se numește transfer paralel la un vector. Translația paralelă este o mișcare: dacă punctele și merg la și , i.e. , , atunci , și prin urmare .

La rezolvarea problemelor geometrice cu ajutorul mișcărilor, se folosește adesea proprietatea de conservare a intersecției: pentru orice mișcare, intersecția figurilor se transformă în intersecția imaginilor lor, adică. dacă sunt figuri arbitrare, atunci figura trece ca urmare a mișcării în figură. (O proprietate similară este valabilă pentru unire.)

Problema 1. Un cerc al cărui centru aparține bisectoarei unghiului își intersectează laturile în puncte și (Fig. 2). Demonstrează că.

Soluţie. Se notează cu una dintre laturile unghiului și prin - cercul, a cărui limită este cercul în cauză. Cu simetrie față de bisectoarea unghiului, raza trece în rază, care formează a doua latură a unghiului, iar cercul trece în sine: , . Conform proprietății de conservare a intersecției, figura trece în , adică în . Cu alte cuvinte, segmentul trece în segmentul , și, prin urmare, .

Sarcina 2. Printr-un punct dat în interiorul unui unghi (mai mic decât cel extins), trageți o linie dreaptă, al cărei segment, închis între laturile unghiului, este împărțit în jumătate în acest punct.

Soluţie. Notați prin simetria față de punctul , și prin și - liniile pe care se află laturile unghiului (Fig. 3). Ca rezultat al simetriei, linia trece într-o linie paralelă cu ea, care intersectează a doua latură a unghiului în punct. Deoarece , atunci punctul , care este simetric, aparține dreptei, care este simetrică, adică. . Astfel, punctele și sunt simetrice față de , și, prin urmare, segmentul este împărțit la jumătate în punctul, adică. linie dreaptă – dorită.

Este ușor de înțeles de ce a fost folosită simetria axială în problema 1 și simetria centrală în problema 2. Deoarece bisectoarea unui unghi este axa sa de simetrie, atunci o încercare de a aplica simetria axială în problema 1 este complet naturală (precum și utilizarea simetriei centrale în problema 2, deoarece segmentul trebuie împărțit în jumătate într-un punct, adică punctele dorite trebuie să fie simetrice în raport cu punctul). Și în alte cazuri, analiza condițiilor problemei vă permite să găsiți o mișcare, a cărei aplicare oferă o soluție.

Problema 3. Pe laturile și ale unui triunghi se construiesc pătrate și în afara acestuia. Demonstrați că segmentul este perpendicular pe mediana triunghiului și de două ori mai lung decât această mediană.

Soluţie. Să încercăm să aplicăm o rotație de 90°, adică să ne asigurăm că atunci când se rotește cu 90° în jurul unui punct (în sensul acelor de ceasornic), segmentul va intra într-un segment care este paralel și are o lungime de două ori mai mare. Cu această rotație, vectorul intră în (Fig. 4), iar vectorul în . Prin urmare, vectorul merge la , adică la . Dar de atunci . Deci, atunci când este rotit cu 90°, vectorul intră în , i.e. într-un vector egal cu . Din aceasta rezultă că și .

Legătura dintre mișcări și orientare este foarte semnificativă. Pe fig. 5 prezintă un poligon , pe conturul căruia este specificată o direcție pozitivă de bypass (în sens invers acelor de ceasornic). Translația paralelă are ca rezultat un poligon cu aceeași direcție de traversare, adică. translația paralelă păstrează direcția traversării sau, după cum se spune, păstrează orientarea. Rotația (în special simetria centrală, care este o rotație de 180°) păstrează și orientarea (Fig. 6). Dimpotrivă, simetria axială inversează direcția bypass-ului (Fig. 7), adică. schimbă orientarea. Un alt exemplu de mișcare care își schimbă orientarea este simetria de alunecare, adică. compoziția de simetrie în raport cu o linie dreaptă și o translație paralelă, al căror vector este paralel (Fig. 8).

Mecanic și geometru francez al secolului al XIX-lea. M. Va formula următoarea teoremă: orice mișcare de păstrare a orientării a unui plan este fie o translație paralelă, fie o rotație; orice mișcare de schimbare a orientării a unui plan este fie simetrie axială, fie alunecare.

Problema 4. Demonstrați că alcătuirea a două simetrii axiale cu axe care se intersectează este o rotație.

Soluţie. Fie și simetrii axiale ale căror axe (linii și ) se intersectează în punctul . Deoarece ambele mișcări își schimbă orientarea, compoziția lor (mai întâi efectuată, apoi) este o mișcare care păstrează orientarea. Conform teoremei lui Chall, există fie o translație paralelă, fie o rotație. Dar, deoarece punctul este staționar în timpul fiecărei mișcări, punctul rămâne pe loc în timpul compoziției lor. Prin urmare, există o rotație în jurul punctului . Cum să găsiți unghiul de rotație, este clar din Fig. 9: dacă este unghiul dintre linii și , atunci (deoarece punctul este translatat prin mișcare în sine și prin mișcare într-un punct simetric față de ) mișcarea care se traduce în este o rotație (în jurul punctului ) cu o unghi .

Următorul cel mai important grup de transformări plane geometrice sunt transformările de similaritate. Cea mai simplă dintre acestea este homotezia. Reamintim că o homotezie cu un centru și un coeficient este o transformare geometrică care duce un punct luat în mod arbitrar într-un punct astfel încât (Fig. 10). Omotezia ia fiecare linie într-o linie paralelă cu ea și ia fiecare cerc înapoi într-un cerc. Omotetia păstrează unghiurile și mărește toate lungimile cu un factor: dacă punctele merg la , atunci . De aici rezultă că homotezia păstrează forma (dar nu mărimea) figurilor; dacă, de exemplu, , atunci figura , în care figura intră atunci când homotezia cu centru și coeficient , este o copie mărită a figurii (Fig. 10), iar dacă - o copie redusă.

Deoarece în homotezie toate lungimile se modifică de același număr de ori, raportul lungimii nu se modifică. Pe aceasta se bazează diverse moduri de estimare a distanțelor; de exemplu, cunoscând lungimea mâinii și lungimea degetului mare și estimând de câte ori degetul mare al mâinii întinse se potrivește în imaginea vizibilă a obiectului, putem găsi raportul dintre înălțimea unui obiect vertical și distanța la aceasta (în Fig. 11 avem , de unde, prin măsurare, puteți găsi, și deci înălțimea țevii, care este de aproximativ trei ori mai mare).

Sarcina 5. Construiți un pătrat înscris într-un sector dat (două vârfuri ale pătratului se află pe aceeași rază, al treilea pe celălalt, al patrulea pe arcul sectorului).

Soluţie. Fie și (Fig. 12) două pătrate înscrise în unghiul . Cu o homotezie cu un centru care ia punctul la , (coeficientul acestei homoteții este ), segmentul intră în segmentul , și, prin urmare, pătratul intră într-un pătrat (deoarece unghiurile, precum și raportul segmentelor, sunt conservate). De aici rezultă că vârfurile și se află pe aceeași rază care emană din punctul . Acum este clar că prin construirea unui pătrat înscris în unghiul , și desenând o rază , putem găsi vârful pătratului dorit (adică punctul de intersecție al razei cu arcul sectorului) și apoi completăm pătratul necesar (Fig. 13).

O transformare plană se numește similaritate cu un coeficient dacă pentru orice puncte ale planului distanța dintre puncte și este egală cu . Orice asemănare (precum și homotezia - un caz special de similitudine) păstrează unghiurile, precum și raportul lungimilor, adică. păstrează forma figurilor. Cu toate acestea, spre deosebire de homotezie, asemănarea poate duce o linie la o linie care nu este paralelă cu ea.

Pe fig. 14 prezintă două planuri și , ale aceleiași bucăți de teren, realizate la scări diferite și situate diferit pe plan. Aceste planuri sunt figuri asemănătoare, dar nu omotetice; de exemplu, o linie și linia ei corespunzătoare nu sunt paralele. Pentru a obține un plan dintr-un plan, puteți face acest lucru: mai întâi rotiți planul astfel încât părțile sale să devină paralele cu laturile planului, apoi aplicați omotezia. Cu alte cuvinte, un plan ca , se obține din utilizarea compoziției mișcării (turnii) și homoteziei.

Această împrejurare este generală, adică orice asemănare este reprezentată ca o compoziție, unde este mișcare și este homotezie. Din aceasta rezultă clar că atunci când rezolvăm probleme prin metoda similarității, se poate limita la a considera o homotezie (însoțită de o anumită mișcare). Acest lucru are anumite avantaje: amintiți-vă cu ce atenție intensă se găsesc laturile corespunzătoare ale triunghiurilor similare situate diferit atunci când scrieți egalitatea raporturilor laturilor (și cu ce ușurință sunt scrise aceste rapoarte pentru triunghiuri homotetice).

Problema 6. Laturile unui triunghi sunt legate prin relația . Demonstrați că unghiul este de două ori unghiul .

Soluţie. Fie un astfel de punct al dreptei care , și se află între și (Fig. 15). Atunci triunghiul este isoscel și, prin urmare ; In afara de asta, . Cu simetrie față de bisectoarea unghiului, punctele și vor merge la astfel de puncte și , că , ; In afara de asta . Egalitatea poate fi rescrisă ca

de unde rezultă că sub omotetia cu centru şi coeficient punctele merg la . Prin urmare și prin urmare, i.e. . Deoarece este unghiul exterior al triunghiului, atunci este egal cu suma unghiurilor și, i.e. egal cu dublul unghiului.

În concluzia poveștii despre transformările de similaritate, observăm că acestea constituie un grup de transformări și de aceea (vezi Geometrie) conform programului Erlangen definesc geometria „lor”. Invarianții acestui grup (adică acele proprietăți care se păstrează sub toate transformările de similaritate și sunt studiate în geometria asemănărilor) sunt unghiul, raportul lungimilor a două segmente, paralelismul a două drepte etc. Deși lungimea segmentului nu se mai păstrează, ci datorită păstrării raportului lungimii în geometria asemănărilor, se poate vorbi de un triunghi isoscel (adică un triunghi în care raportul lungimilor laturilor). este egal cu 1). În geometria asemănărilor se păstrează și teorema conform căreia într-un triunghi isoscel unghiurile de la bază sunt egale. Se păstrează și teorema lui Pitagora (sub forma , unde și sunt rapoartele dintre lungimile catetelor și lungimea ipotenuzei), etc.

Cu toate acestea, nu trebuie să credem că geometria asemănărilor nu diferă de geometria euclidiană în niciun fel, cu excepția formei de prezentare. Există fapte care disting aceste două geometrii. De exemplu, să fim de acord să spunem că o linie poate aluneca pe ea însăși dacă pentru oricare două puncte ale acestei linii există o transformare (aparținând grupului care definește geometria luată în considerare) care ia linia la sine și punctul în . În geometria lui Euclid (adică în geometria definită de grupul de mișcări plane) există doar două tipuri de linii conectate (adică, formate dintr-o singură bucată) care pot aluneca pe ele însele: linii drepte și cercuri. Și în geometria asemănărilor există linii, altele decât drepte și cercuri, care pot aluneca peste ele însele; acestea sunt spirale logaritmice, definite în coordonate polare prin ecuație (Fig. 16).

Vom obține un alt fapt neobișnuit al geometriei asemănărilor luând în considerare transformarea, unde este rotația în jurul punctului prin unghi și este omotetia cu centrul și coeficientul. Fie o succesiune de puncte care trec unele în altele în timpul transformării, adică. pentru orice număr întreg (Fig. 17). Aceste puncte se află pe aceeași spirală logaritmică, iar pentru orice număr întreg unghiul are aceeași valoare. Conectând în mod constant aceste puncte, obținem o linie întreruptă infinită , care se traduce printr-o transformare în sine, fiecare vârf fiind tradus într-un vârf învecinat .

Rețineți că transformarea de similaritate considerată (se numește întindere rotațională) este strâns legată de numerele complexe. Un număr complex poate fi reprezentat ca un segment direcționat care merge de la origine la un punct. Cu o astfel de reprezentare geometrică, numerele complexe sunt adăugate ca vectori (Fig. 18). Și pentru a obține o interpretare geometrică a înmulțirii numerelor complexe, este convenabil să rotiți extensia considerată mai sus. Și anume, fie - un număr complex, - modulul său (adică lungimea segmentului reprezentativ) și - argument (adică, unghiul de înclinare al segmentului direcționat reprezentativ față de partea pozitivă a axei x). Numărul se obține din numărul 1 dacă, în primul rând, vectorul care reprezintă numărul 1 este întins cu un factor și, în al doilea rând, dacă este rotit cu un unghi (Fig. 19), adică vectorul este obținut din vectorul 1 prin transformare , unde este o homotezie centrată la origine și coeficient și este o rotație în jurul originii printr-un unghi. Asa de, . Dacă acum este un alt număr complex, atunci când se aplică transformarea (adică atunci când vectorul reprezentativ este întins cu un factor și rotit cu un unghi), numărul intră în (Fig. 19). Se poate spune în alt fel: triunghiurile din Fig. 19 sunt similare. Aceasta oferă o interpretare geometrică a înmulțirii numerelor complexe. Din ceea ce s-a spus, este clar că atunci când toate numerele complexe sunt înmulțite cu același număr complex, întregul plan al numerelor complexe este supus unei întinderi rotaționale. În special, pentru oricare trei numere complexe avem , unde este un număr complex al cărui modul este egal cu raportul dintre lungimile vectorilor și , iar argumentul este egal cu unghiul dintre acești vectori (Fig. 20).

Problema 7. Triunghiuri asemănătoare între ele sunt construite pe laturile unui triunghi. Demonstrați că punctul de intersecție al medianelor este același cu punctul de intersecție al medianelor.

Soluţie. Notează prin numere complexe reprezentate prin vectori , , , , , . Apoi , , , unde este un număr complex al cărui modul este egal cu raportul laturilor triunghiurilor similare considerate, iar argumentul este (Fig. 21). Adăugând aceste egalități, obținem (după simplificări evidente):

Deoarece (deoarece argumentul numărului este diferit de zero), de aici rezultă că . Trecând la notația vectorială și împărțind la 3, obținem

iar aceasta înseamnă că punctele de intersecție ale medianelor și coincid (vezi Vector).

Să vorbim pe scurt despre alte transformări care joacă un rol important în geometria modernă. O transformare a planului euclidian se numește afină dacă duce fiecare linie înapoi la o linie, iar liniile paralele între ele - din nou la paralel (Fig. 22). Dacă pe plan este introdus un sistem de coordonate, atunci transformarea afină este dată de relații liniare, adică. punctul la care trece punctul este determinat de formule

,

unde (și invers: o oarecare transformare afină este dată de astfel de formule). În plus, dacă există trei puncte ale planului care nu se află pe aceeași linie dreaptă și alte trei puncte care, de asemenea, nu se află pe aceeași linie dreaptă, atunci există, și numai una, o transformare afină care ia punctele respectiv la . Rețineți că lungimile și unghiurile se pot schimba în cazul transformărilor afine. Nesalvat (spre deosebire de transformările de similaritate) și raportul dintre lungimile segmentelor. Cu toate acestea, raportul dintre lungimile a două segmente paralele este păstrat sub orice transformare afină. În special, punctul de mijloc al unui segment trece din nou sub o transformare afină în punctul de mijloc al unui segment, un paralelogram trece într-un paralelogram, mediana unui triunghi într-o mediană etc. Sub o transformare afină, un cerc trece într-o elipsă , și rezultă cu ușurință din proprietățile transformărilor afine notate mai sus că punctele medii de paralelă dintre coardele elipsei se află pe un segment care trece prin centrul elipsei (Fig. 23).

Toate transformările afine ale planului, luate împreună, formează un grup de transformări și, prin urmare (vezi Geometrie), ele definesc o anumită geometrie. Se numește geometrie afină. Invarianții acestui grup (adică acele proprietăți ale figurilor care sunt studiate în geometria afină) sunt aranjarea rectilinie a punctelor, paralelismul, raportul dintre lungimile segmentelor paralele și alte proprietăți obținute din acestea (de exemplu, prezența a unui centru de simetrie dintr-o figură). Fără a vorbi mai în detaliu despre această geometrie, vom arăta prin exemple modul în care proprietățile transformărilor afine notate mai sus pot fi aplicate în rezolvarea problemelor.

Problema 8. Demonstrați că într-un trapez arbitrar punctele medii ale bazelor, punctul de intersecție al diagonalelor și punctul de intersecție al prelungirilor laturilor laterale se află pe aceeași dreaptă.

Soluţie. Pentru un trapez isoscel, acest lucru este evident (deoarece un trapez isoscel este simetric față de o dreaptă relativă care trece prin punctele medii ale bazelor). Să fie acum un trapez arbitrar și să fie un trapez isoscel cu aceleași lungimi de bază (Fig. 24). Să considerăm o transformare afină care mapează punctele la , respectiv. Cu această transformare, liniile vor merge la (din moment ce , iar paralelismul liniilor este păstrat). Mai mult, din moment ce , atunci punctul va merge la (deoarece raportul segmentelor paralele este păstrat). Cu alte cuvinte, trapezul va intra într-un trapez. În consecință, se va păstra dispunerea rectilinie a punctelor, adică. punctele dintr-un trapez se află și ele pe aceeași dreaptă.

Problema 9. O elipsă este înscrisă într-un triunghi și se desenează trei segmente, fiecare dintre ele leagă vârful și punctul de contact al elipsei cu latura opusă. Demonstrați că aceste trei segmente se intersectează într-un punct.

Soluţie. Fie o transformare afină care transformă un cerc în elipsa luată în considerare și fie un triunghi care se transformă în . Deoarece proprietatea luată în considerare, așa cum este ușor de demonstrat, este adevărată pentru cercul înscris (partea stângă a Fig. 25), este adevărată și pentru elipsa înscrisă (partea dreaptă a figurii).

Articolul „Geometrie proiectivă” descrie modul în care finalizarea unui plan cu puncte improprii („infinit depărtate”) îl transformă într-un plan proiectiv. Transformările geometrice ale planului proiectiv care păstrează aranjamentul rectilinie a punctelor se numesc transformări proiective. Transformările proiective sunt date în coordonate prin formule liniar-fracționale:

(1)

Mai detaliat: dacă este planul euclidian în care este specificat sistemul de coordonate și este planul proiectiv obținut prin adăugarea de elemente improprii, atunci orice transformare proiectivă a planului se scrie în coordonatele luate în considerare prin formulele (1) cu condiția ca punctul și punctul în care trece, nu sunt improprii.

Transformările proiective formează un grup de transformări ale planului proiectiv. Conform programului Erlangen, acest grup definește o anumită geometrie - aceasta este geometria proiectivă. Invarianții transformărilor proiective (adică acele proprietăți ale figurilor care sunt studiate în geometria proiectivă) sunt aranjamentul rectiliniu al punctelor, raportul anarmonic a patru puncte situate pe o singură dreaptă etc.

Dacă - patru puncte ale planului proiectiv, dintre care trei nu se află pe aceeași linie și - alte patru puncte ale acestui plan, dintre care nici trei nu se află pe aceeași linie, atunci există și, în plus, doar unul proiectiv transformare care se traduce, evident, se află pe aceeași linie dreaptă (pe linia mediană a benzii dintre liniile drepte și ). Aplicând transformarea inversă, concluzionăm că în Fig. 26 din stânga, punctele se află pe aceeași linie dreaptă (deoarece aranjarea rectilinie a punctelor se păstrează sub transformarea proiectivă).

Toate transformările considerate mai sus au păstrat dispunerea rectilinie a punctelor (pe euclidian sau pe plan proiectiv). Cu alte cuvinte, sistemul tuturor liniilor drepte de pe plan este tradus din nou în același sistem de linii. Există o clasă interesantă de transformări care au o proprietate similară cu un alt sistem de linii. Și anume: să considerăm un sistem plan (euclidian) format din toate liniile drepte și toate cercurile. Transformările care traduc acest sistem de linii înapoi în același sistem se numesc transformări circulare. Cu alte cuvinte, o linie dreaptă trece sub o transformare circulară fie din nou într-o linie dreaptă, fie într-un anumit cerc (și același lucru este valabil și pentru un cerc). Puțin mai târziu vom clarifica o convenție referitoare la planul euclidian care este necesară atunci când luăm în considerare transformările circulare, dar mai întâi vom lua în considerare un exemplu important de transformare circulară - așa-numita inversare.

Și o rază. Pe această bază, am convenit să considerăm că există un punct impropriu pe planul acestor drepte care se intersectează la același unghi. Dacă, în special, cercul este ortogonal cu cercul de inversare, i.e. îl intersectează în unghi drept (astfel de cercuri au fost discutate la sfârșitul articolului lui Lobachevsky despre geometrie), apoi acest cerc intră în sine în timpul inversării (doar părțile sale situate în interiorul și în afara cercului de inversare își schimbă locurile). Inversarea este cea mai importantă dintre transformările circulare: se poate dovedi că orice transformare circulară a planului este fie o inversare, fie o asemănare, fie o compoziție a unei inversări și a unei asemănări. Luate împreună, transformările circulare constituie un grup de transformări care definesc un fel de geometrie („circulară”) pe un plan circular.

Am vorbit despre cele mai importante transformări geometrice ale planului. Se pot lua în considerare și transformările geometrice ale spațiului tridimensional, planul (sau spațiul) Lobaciovski și alte obiecte geometrice. Rețineți, în special, că if este mișcarea spațiului tridimensional (deoarece și , și transformă o linie dreaptă înapoi într-o linie dreaptă). Rezultă că orice transformare proiectivă a planului poate fi reprezentată în această formă.

Cunoașterea transformărilor geometrice și abilitatea de a le aplica este un element important al culturii matematice.

1. Esența metodei transformărilor, locul ei în cursul școlar de geometrie.

2. Tipuri de transformări:

a) mișcările și proprietățile acestora; egalitatea cifrelor;

b) transformarea asemănării; cifre similare.

3. Aplicaţii ale metodei transformărilor.

(1) Pentru diferiți autori de manuale pentru școlile secundare de geometrie, transformările ocupă poziții diferite ca volum și nivel de rigoare. În manualul editat de A. N. Kolmogorov, transformările servesc drept bază pentru demonstrarea multor teoreme (o axiomă specială a mobilității este dedicată justificării lor). Manualul lui A. P. Kiselev nu spune absolut nimic despre transformări.

În Geometrie 7-11 A. V. Pogorelov, tema transformării figurilor este luată în considerare în clasa a VIII-a. Subiectul nu este mare. Conceptul de „transformare” este derivat la un nivel vizual-intuitiv: „Dacă fiecare punct al unei figuri date este deplasat într-un fel, atunci vom obține o nouă figură. Se spune că această cifră este obținută printr-o transformare din cea dată.

Definiția descriptivă este însoțită de un desen. Este dată definiția mișcării și sunt luate în considerare proprietățile acesteia. Mai mult, tipurile specifice de transformări sunt clar definite. În acest tutorial, simetria față de un punct, simetria față de o dreaptă, homotezia și asemănarea sunt definite ca transformări cu proprietățile corespunzătoare; translația paralelă este definită ca o transformare în formă de coordonate; iar întoarcerea este definită ca un fel de mișcare. Concomitent cu definirea transformărilor, este dată și o metodă de construire a figurilor sub transformări.

În ghidul de studiu geometria 7-9 (autori: L. S. Atanasyan și alții), materialul despre transformări este prezentat prin tema „Mișcarea” în clasa a 9-a. Acesta este ultimul subiect din acest tutorial. Aici sunt introduse conceptele de „cartografia unui plan pe sine”, „mișcare” și sunt luate în considerare principalele tipuri de mișcări. În plus, întrebarea importantă a relației dintre concepte suprapuneriȘi miscarile, se dovedește echivalența lor.

Scopul principal al temei este introducerea elevilor în conceptul de mișcare pe plan, cu tipuri specifice de mișcare: simetrie centrală și axială, translație paralelă, rotație. Conceptul de cartografiere a unui plan pe sine este considerat doar ca bază pentru introducerea conceptului de mișcare. Maparea unui plan pe el însuși la nivel vizual-intuitiv este luată în considerare cu implicarea conceptelor de simetrie axială și centrală deja cunoscute elevilor.

Întrucât curriculum-ul unei școli de învățământ general de matematică nu prevede încă un studiu detaliat al diferitelor proprietăți ale acestor transformări, chestiunea utilizării transformărilor ar trebui luată ca clase opționale sau luată în considerare în sala de clasă a unui cerc matematic. După cum sa menționat mai sus, în cursul de geometrie al unei școli de învățământ general, aceștia nu intră în detaliile definiției matematice a conceptului de „transformare”. Dar un profesor de matematică ar trebui să înțeleagă că în geometrie o transformare (în cazul unui plan) este înțeleasă ca „o mapare a întregului plan pe sine, în care fiecare punct X mapat la un singur punct X 1 și fiecare punct Y 1 corespunde unui singur punct Y».

Pentru elevi, vorbim despre transformarea formelor. O figură, spre deosebire de un avion, este finită, deci conceptul de transformare a figurilor este mai accesibil. Elevilor li se poate spune că transformarea unui plan este o funcție, în plus, o formațiune, dar în geometrie vorbim despre corespondența punctelor, nu a numerelor.

(2) Printre transformările studiate la școală, se numără două tipuri de ele: mișcarea și transformarea asemănării. Nu toate tipurile de transformări sunt studiate la școală.

„Transformarea unei figuri în alta se numește mișcare dacă păstrează distanța dintre puncte, adică. traduce oricare două puncte XȘi Y o formă pe punct X 1 și Y 1 altă cifră astfel încât X Y = X 1 Y 1".

Dacă se ia în considerare execuția secvențială a două sau mai multe transformări, atunci rezultatul unei astfel de execuții secvențiale a transformărilor în geometrie se numește compoziţie transformări.

În acest tutorial, este dată o singură proprietate a compoziției: două mișcări efectuate succesiv dau din nou mișcare.

Se ia în considerare și transformarea inversă celei date. Se dovedește că o transformare inversă unei mișcări este o mișcare.

Proprietatea este implicit prezentă: compoziția transformării inversului său este transformarea identică.

Elevii ar trebui să înțeleagă că, după demonstrarea proprietăților mișcării, este posibil să se opereze nu numai cu puncte, ci și pe segmente, linii drepte, raze, unghiuri etc. la transformări. Și poți fi absolut sigur că figurile care au fost supuse transformării mișcării vor intra în același nume: segmentele vor intra în segmente, unghiurile în unghiuri etc.; mai mult, segmentele vor merge în segmente egale, unghiurile în unghiuri egale etc.

În manualul lui A. V. Pogorelov, se demonstrează că simetria față de un punct este o mișcare (folosind primul criteriu pentru egalitatea triunghiurilor); simetria față de o dreaptă este mișcare (demonstrată prin metoda coordonatelor). În al doilea caz, axa de simetrie este aleasă ca axa y.

Următorul pas în învățarea mișcărilor este folosirea lor pentru a determina egalitate cifre.

Egalitatea figurilor în diferite cursuri de geometrie școlară este introdusă în moduri diferite. Uneori o definiție generală a „cifrelor egale” nu este deloc dată, uneori este introdusă imediat. În manualul A.V. Pogorelov introduce mai întâi conceptul de egalitate a unor figuri specifice (segmente, unghiuri, triunghiuri), apoi este dată o definiție generală a egalității figurilor folosind conceptul de mișcare: Se spune că două figuri sunt egale dacă sunt transferate de la una la alta prin mișcare.

Se dovedește un fapt important: egalitatea triunghiurilor, definită prin combinarea lor prin mișcare, și egalitatea, așa cum am înțeles-o până acum, exprimă același lucru. Cu alte cuvinte, se poate demonstra echivalența celor două definiții. Demonstrarea constă din două părți: 1) din ipoteza că 2 triunghiuri ABCȘi A 1 ÎN 1 CU 1 sunt combinate prin mișcare, se dovedește egalitatea unghiurilor și laturilor lor respective; 2) se presupune că laturile și unghiurile corespunzătoare acestor triunghiuri sunt egale și se demonstrează că ele pot fi combinate printr-o mișcare.

Prima parte a demonstrației se bazează pe definiția mișcării și pe proprietatea acesteia că unghiurile sunt păstrate în mișcare. Soluția la a doua parte a problemei depinde de locația triunghiurilor. Luați în considerare una dintre variantele dovezii, diferită de cea dată în manual de A.V. Pogorelov. Triunghi A 2 ÎN 1 CU 2 derivat din triunghi ABC translație paralelă în direcția dată de rază AA 2 pentru distanta AA 2. Triunghi A 1 ÎN 1 CU 1 obtinut din triunghi A 2 ÎN 1 CU 2 prin rotirea prin unghiul α în sensul acelor de ceasornic (vezi Fig. 1).

Scopul principal al studierii acestui subiect este de a prezenta elevilor exemple de transformări geometrice.

Când lucrați la un subiect, atenția principală trebuie acordată dezvoltării abilităților de a construi imagini ale celor mai simple figuri (puncte, segmente, triunghiuri) cu mișcări specifice. În acest caz, proprietatea mișcării este utilizată la nivel vizual-intuitiv, teoremele corespunzătoare pot fi considerate fără dovezi. În cursul rezolvării problemelor, elevii ar trebui să se familiarizeze cu exemple de figuri care au simetrie.

Conceptul general de egalitate a cifrelor poate fi luat în considerare numai într-un plan introductiv (de exemplu, într-o formă de prelegere) fără reproducerea ulterioară a dovezilor de către studenți.

În ghidul de studiu geometria 7-9 L.S. Atanasyan și alții, subiectul „Mișcării” începe cu introducerea conceptului de cartografiere a unui plan pe sine, a cărui definiție este dată descriptiv.

Studiul temei începe cu o repetare a conceptului de punct care este simetric față de un punct dat (simetrie centrală) și o dreaptă dată (simetrie axială).

Mai devreme, în clasa a VIII-a, elevii considerau simetria centrală și axială ca o proprietate a formelor geometrice. Acum, aceste concepte, în general, familiare sunt introduse ca exemple de mapare a unui avion pe el însuși. În timpul repetiției, elevii ar trebui să fie conduși la conceptul de menținere a distanței dintre puncte. Următoarele sarcini pot servi acestui scop.

1. Construiți puncte A 1 , ÎN 1, simetric față de puncte AȘi ÎN relativ drept l(vezi Fig. 2a – 2c).

2. Există un punct pe plan pentru care nu există un punct simetric față de dreapta dată?

3. Demonstrați că în fiecare dintre cazurile 2a – 2b A 1 ÎN 1 = AB.

4. Puncte de suspendare A 1 și ÎN 1, simetric față de puncte AȘi ÎN relativ la punct DESPRE, dacă a) punctul DESPRE se află pe linie AB; b) punctul DESPRE nu se află pe o linie dreaptă AB.

5. Există un astfel de punct în plan pentru care nu există un punct simetric în raport cu acest punct?

6. Demonstrați că în fiecare dintre cazurile luate în considerare la problema 4 A 1 ÎN 1 = AB.

Acum putem introduce conceptul de mapare a unui plan pe el însuși și îl putem ilustra cu exemple de simetrie centrală și axială. Este important de subliniat că atunci când un avion este mapat pe el însuși, sunt îndeplinite două condiții:

1) Fiecare punct din plan este asociat cu un punct al planului;

2) Fiecare punct al planului este atribuit unui punct al planului.

După aceea, puteți lua în considerare sarcini pentru a consolida acest concept.

Acum, pe baza sarcinilor 3 și 6 discutate mai sus, introducem conceptul de mișcare:

„Mișcarea unui avion este o mapare a unui avion pe sine care păstrează distanța.”

După aceea, se iau în considerare teorema de cartografiere a segmentelor și corolarul acesteia. Elevii ar trebui să se concentreze pe faptul că dovada constă din 2 părți:

1) se demonstrează că fiecare punct R acest segment MN cartografiat la un moment dat R 1 tăietură M 1 N 1 ;

2) se demonstrează că în fiecare punct R 1 tăietură M 1 N 1 trece un punct R acest segment MN.

Elementul „Suprapunere și mișcare” este opțional, dar într-o clasă bine pregătită, poate fi luat în considerare. Acest material poate fi prezentat sub formă de prelegeri. Conceptul de impunere, pe baza căruia s-a determinat egalitatea figurilor, este unul dintre conceptele de bază (nedefinite) din acest curs de geometrie. Suprapunerile sunt astfel de mapări ale planului pe el însuși, care au proprietățile exprimate în axiomele 7-13 (Atanasyan L.S. și colab. Geo. 7-9).

Mișcarea este un concept definit: este o mapare a unui plan pe sine care păstrează distanța.

Rezultă direct din definiția mișcării și axiomele de impunere că oricare acoperire este circulaţie. Se dovedește și afirmația inversă: orice circulaţie este acoperire.

Astfel, conceptul de impunere coincide cu conceptul de mișcare.

Elevilor nu trebuie să li se solicite să dovedească faptele menționate la paragraful 115.

Materialul despre translația și rotația paralelă a încă două tipuri de mișcări poate fi prezentat și sub forma unei prelegeri. Este util să atragem atenția elevilor asupra faptului că în timpul translației paralele, o linie este mapată pe o linie paralelă cu ea sau pe ea însăși. De aici rezultă o metodă simplă de construire a imaginilor liniilor și segmentelor cu translație paralelă.

Demonstrând că translația și rotația paralelă sunt mișcări, elevii puternici se pot desluși din manual în clasă, urmate de o discuție generală. Elevilor slabi nu ar trebui să li se ceară să reproducă dovezi.

La sfarsitul capitolului sunt date probleme geometrice, pentru rezolvarea carora se recomanda folosirea miscarilor.

Unele dintre aceste probleme sunt date cu soluții.

(2b) Transformarea similarității joacă un rol important în geometrie. Acest lucru este de înțeles. Spațiul nostru real are un grup de similitudini. Toate obiectele geometrice ale spațiului, dacă sunt formate din segmente de linie, pot fi împărțite în 2 seturi: figuri similare și diferite. În setul de cifre similare pot exista unele egale. Conceptul de similitudine a figurilor la un copil apare mult mai devreme decât conceptul de dimensiunea lor. Acest lucru se datorează particularităților percepției vizuale: două figuri de dimensiuni diferite, dar identice ca formă, nu diferă.

Forma figurilor nu se schimbă atunci când se schimbă distanța de la care figura este vizibilă. Principalele semne ale invariabilității formei unei figuri sunt egalitate colţuri şi proporționalitatea segmentele corespunzătoare.

În manualul A.V. Geometria Pogorelov 7 – 11 din definiția transformării similarității este introdusă în mod similar cu definiția mișcării:

Transformarea unei figuri F într-o figură F 1 se numește transformare de similaritate dacă, în timpul acestei transformări, distanța dintre puncte crește (sau scade) de același număr de ori.

Aceasta înseamnă că dacă punctele arbitrare AȘi ÎN cifre F sub această transformare mergi la puncte A 1 și ÎN 1 cifre F 1, atunci A 1 ÎN 1 = kAB. Număr k se numește coeficient de similitudine.

După introducerea acestui concept, se demonstrează că homotezie este o transformare de asemănare. Acest fapt este dovedit prin metoda vectorială. În mod similar, în ceea ce privește mișcarea, se demonstrează că sub transformarea asemănării trei puncte A, ÎN, CU, întins pe o linie dreaptă, mergeți la trei puncte A 1 , ÎN 1 , CU 1 situată pe aceeași linie dreaptă și se păstrează ordinea aranjamentului lor reciproc. Rezultă că transformarea asemănării transformă liniile în linii, razele în raze, segmentele în segmente.

Folosind omotezie, se demonstrează că transformarea de similitudine păstrează unghiurile dintre semi-drepte.

Elevii ar trebui să fie conștienți de faptul că nu orice transformare de similitudine este o homotezie.

Cu ajutorul conceptului de transformare a asemănării, este dată o definiție a figurilor similare. În manualul A.V. Pogorelov dă mai întâi o definiție a figurilor similare: „Două figuri sunt numite similare dacă sunt traduse una în alta printr-o transformare de similitudine”.

Simbolul special ~ () este folosit pentru a desemna astfel de cifre. F ~ F 1).

Apoi se ia în considerare asemănarea triunghiurilor.

∆ înregistrat ABC~∆A 1 ÎN 1 CU 1, se presupune că vârfurile potrivite prin transformarea de similaritate sunt în locurile corespunzătoare, i.e. A intră în A 1 etc.

Din proprietățile transformării de similaritate rezultă că pentru triunghiuri similare unghiurile corespunzătoare sunt egale, iar laturile corespunzătoare sunt proporționale.

Dovada semnelor de similitudine se realizează folosind conceptul de homotezie. Semnele de similitudine ale triunghiurilor dreptunghiulare sunt considerate separat.

Subiectul „Poligoane” tratează problema asemănării poligoanelor convexe regulate.

Subiectul „Areele figurilor” tratează zona figurilor similare: „ariile figurilor similare sunt legate ca pătratele dimensiunilor lor liniare respective”.

Conceptul de transformare a figurilor în spațiu este introdus în același mod ca și pe un avion. Cu toate acestea, există câteva caracteristici.

Când se consideră transformarea simetriei în spațiu, pe lângă simetria față de un punct și o dreaptă, se adaugă simetria față de un plan. O nouă proprietate a mișcării în spațiu este că mișcarea traduce planurile în planuri. O nouă proprietate pentru translația paralelă în spațiu este următoarea proprietate: în timpul translației paralele în spațiu, fiecare plan trece fie în sine, fie într-un plan paralel cu el.

Când se analizează subiectul „Asemănări ale figurilor spațiale”, se adaugă următoarele afirmații: „transformarea asemănării transformă planurile în planuri” și „transformarea omoteției în spațiu transformă orice plan care nu trece prin centrul homoteției într-un plan paralel (sau în el însuși). când k=1).

Când luăm în considerare transformările în spațiu, te poți limita la reprezentările lor vizuale intuitive și nu te concentrezi pe derivarea faptelor folosite. Iar accentul principal ar trebui să fie pus pe utilizarea transformărilor în demonstrarea teoremelor și în rezolvarea problemelor.

În manualul L.S. Atanasyan și alții din clasa a VIII-a în capitolul VII, este luat în considerare subiectul „Triunghiuri similare”, care începe cu introducerea conceptului de segmente proporționale. Elevilor li se explică că în viața de zi cu zi au de-a face cu obiecte de aceeași formă, dar de dimensiuni diferite. Astfel de obiecte sunt prototipurile unor astfel de forme geometrice. Accentul este pus pe triunghiuri similare. Asemănarea triunghiurilor este introdusă nu cu ajutorul unei transformări de similaritate, ci prin egalitatea unghiurilor și proporționalitatea laturilor similare. Semnele asemănării triunghiurilor sunt dovedite foarte simplu, pe baza teoremei: „Dacă unghiul unui triunghi este egal cu unghiul altui triunghi, atunci ariile acestor triunghiuri sunt legate ca produsul laturilor care conțin unghiuri egale. "

După demonstrarea semnelor de asemănare, se arată aplicarea asemănării la demonstrarea teoremelor și la rezolvarea problemelor. Ca aplicații practice ale asemănării triunghiurilor, sunt descrise metode de modificare a înălțimii unui obiect și a distanței până la un punct inaccesibil. Se dă o idee despre aplicarea metodei similarității în rezolvarea problemelor de construcție.

Într-o formă foarte scurtă, este descris cum puteți determina similitudinea cifrelor arbitrare. simboluri folosite: ∆ ABC~∆A 1 ÎN 1 CU 1 (triunghi ABC asemănător cu un triunghi A 1 ÎN 1 CU 1). Este dat conceptul de figuri asemănătoare centralei: „fiecare punct M cifre F punct cartografiat M 1 plan astfel încât punctele MȘi M 1 se află pe o rază cu originea într-un punct fix DESPRE, în plus OM 1 = kOM(Vezi fig. 3). Ca urmare a unei astfel de comparații, se obține o cifră F 1, similară figurii F. În acest caz, formele FȘi F 1 se numesc ca centru.

(3) Metoda transformării este utilizată atunci când se analizează diverse aspecte teoretice ale cursului de geometrie: Aplicarea mișcării în determinarea egalității figurilor: aplicarea transformării de similaritate în studiul triunghiurilor similare (în manualul lui A.V. Pogorelov); translația paralelă și vectorii sunt strâns legate.

Metoda transformării este utilizată pe scară largă în rezolvarea diferitelor probleme geometrice. Cu toate acestea, elevii nu sunt introduși în utilizarea acestei metode în rezolvarea problemelor din lecțiile de matematică din școală. Această întrebare este depusă la activități opționale sau extrașcolare.

Metoda transformărilor este utilizată în rezolvarea problemelor pentru demonstrație, pentru construcție, pentru rezolvarea așa-ziselor probleme geometrice pentru găsirea maximului și minimului. În acest caz, se folosesc toate tipurile de transformări.