В какой четверти косинус отрицательный. Основные свойства тригонометрических функций: четность, нечетность, периодичность

Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.

Сбор и использование персональной информации

Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.

От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.

Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.

Какую персональную информацию мы собираем:

• Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.

Как мы используем вашу персональную информацию:

• Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
• Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
• Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
• Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам

Мы не раскрываем полученную от Вас информацию третьим лицам.

Исключения:

• В случае если необходимо - в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ - раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
• В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.

Защита персональной информации

Мы предпринимаем меры предосторожности - включая административные, технические и физические - для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.

Соблюдение вашей конфиденциальности на уровне компании

Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.

В этой статье будут рассмотрены три основных свойства тригонометрических функций: синуса, косинуса, тангенса и котангенса.

Первое свойство - знак функции в зависимости от того, какой четверти единичной окружности приналдежит угол α . Второе свойство - периодичность. Согласно этому свойству, тигонометрическая функция не меняет значения при изменении угла на целое число оборотов. Третье свойсто определяет, как меняются значения функций sin, cos, tg, ctg при противоположных углах α и - α .

Yandex.RTB R-A-339285-1

Часто в математическом тексте или в контексте задачи можно встретить фразу: "угол первой, второй, третьей или четвертой координатной четверти". Что это такое?

Обратимся к единичной окружности. Она разделена на четыре четверти. Отметим на окружности начальную точку A 0 (1 , 0) и, поворачивая ее вокруг точки O на угол α , попадем в точку A 1 (x , y) . В зависимости от того, в какой четверти будет лежать точка A 1 (x , y) , угол α будет называться углом первой, второй, третьей и четвертой четвети соответственно.

Для наглядности приведем иллюстрацию.

Угол α = 30 ° лежит в первой четверти. Угол - 210 ° является углом второй четверти. Угол 585 ° - угол третьей четверти. Угол - 45 ° - это угол четвертой четверти.

При этом углы ± 90 ° , ± 180 ° , ± 270 ° , ± 360 ° не принадлежат ни одной четверти, так как лежат на координатных осях.

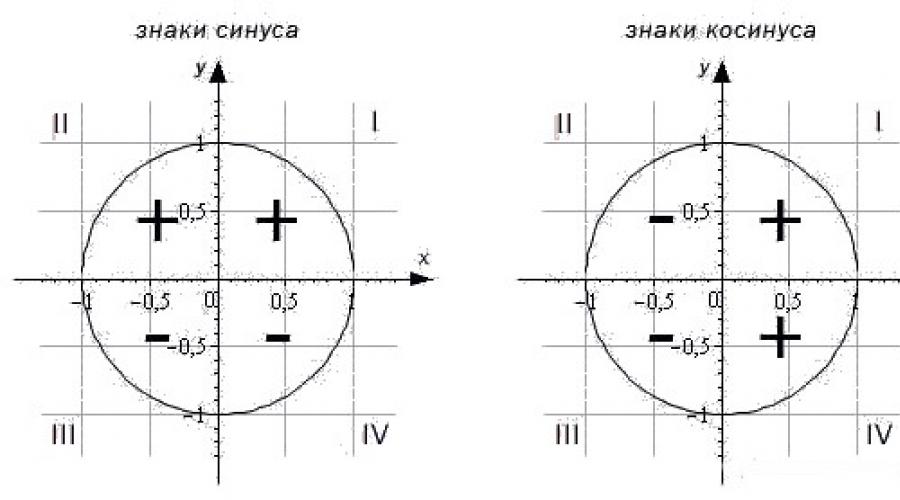
Теперь рассмотрим знаки, которые принимают синус, косинус, тангенс и котангенс в зависимости от того, в какой четверти лежит угол.

Чтобы определить знаки синуса по четвертям, вспомним опредение. Синус - это ордината точки A 1 (x , y) . Из рисунка видно, что в первой и второй четвертях она положительна, а в третьей и четверной - отрицательна.

Косинус - это абсцисса точки A 1 (x , y) . В соответсии с этим, определяем знаки косинуса на окружности. Косинус положителен в первой и четвертой четвертях, а отрицателен во второй и третьей четверти.

Для определения знаков тангенса и котангенса по четвертям также вспоминаем определения этих тригонометрических функций. Тангенс - отношение ординаты точки к абсциссе. Значит, по правилу деления чисел с разными знаками, когда ордината и абсцисса имеют одинаковые знаки, знак тангенса на окружности будет положительным, а когда ордината и абсцисса имеют разные знаки - отрицательным. Аналогично определяются знаки котангенса по четвертям.

Важно помнить!

1. Синус угла α имеет знак плюс в 1 и 2 четвертях, знак минус - в 3 и 4 четвертях.
2. Косинус угла α имеет знак плюс в 1 и 4 четвертях, знак минус - в 2 и 3 четвертях.
3. Тангенс угла α имеет знак плюс в 1 и 3 четвертях, знак минус - в 2 и 4 четвертях.
4. Котангенс угла α имеет знак плюс в 1 и 3 четвертях, знак минус - в 2 и 4 четвертях.

Свойство периодичности

Свойство периодичности - одно из самых очевидных свойств тригонометрических функций.

Свойство периодичности

При изменении угла на целое число полных оборотов значения синуса, косинуса, тангенса и котангенса данного угла остаются неизменными.

Действительно, при изменении угла на целое число оборотов мы всегда будем попадать из начальной точки A на единичной окружности в точку A 1 с одними и теми же координатами. Соответственно, не будут меняться и значения синуса, косинуса, тангенса и котангенса.

Математически данное свойство записывается так:

sin α + 2 π · z = sin α cos α + 2 π · z = cos α t g α + 2 π · z = t g α c t g α + 2 π · z = c t g α

Какое применение на практике находит это свойство? Свойство периодичности, как и формулы приведения, часто используется для вычисления значений синусов, косинусов, тангенсов и котангенсов больших углов.

Приведем примеры.

sin 13 π 5 = sin 3 π 5 + 2 π = sin 3 π 5

t g (- 689 °) = t g (31 ° + 360 ° · (- 2)) = t g 31 ° t g (- 689 °) = t g (- 329 ° + 360 ° · (- 1)) = t g (- 329 °)

Вновь обратимся к единичной окружности.

Точка A 1 (x , y) - результат поворота начальной точки A 0 (1 , 0) вокруг центра окружности на угол α . Точка A 2 (x , - y) - результат поворота начальной точки на угол - α .

Точки A 1 и A 2 симметричны относительно оси абсцисс. В случае, когда α = 0 ° , ± 180 ° , ± 360 ° точки A 1 и A 2 совпадают. Пусть одна точка имеет координаты (x , y) , а вторая - (x , - y) . Вспомним определения синуса, косинуса, тангенса, котангенса и запишем:

sin α = y , cos α = x , t g α = y x , c t g α = x y sin - α = - y , cos - α = x , t g - α = - y x , c t g - α = x - y

Отсюда следует свойство синусов, косинусов, тангенсов и котангенсов противоположных углов.

Свойство синусов, косинусов, тангенсов и котангенсов противоположных углов

sin - α = - sin α cos - α = cos α t g - α = - t g α c t g - α = - c t g α

Согласно этому свойству, справедливы равенства

sin - 48 ° = - sin 48 ° , c t g π 9 = - c t g - π 9 , cos 18 ° = cos - 18 °

Рассмотренное свойство часто используется при решении практических задач в случаях, когда нужно избавиться от отрицательных знаков углов в агрументах тригонометрических функций.

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Если вы уже знакомы с тригонометрическим кругом , и хотите лишь освежить в памяти отдельные элементы, или вы совсем нетерпеливы, – то вот он, :

Мы же здесь будем все подробно разбирать шаг за шагом.

Тригонометрический круг – не роскошь, а необходимость

Тригонометрия у многих ассоциируется с непроходимой чащей. Вдруг наваливается столько значений тригонометрических функций, столько формул… А оно ведь, как, – незаладилось вначале, и… пошло-поехало… сплошное непонимание…

Очень важно не махать рукой на значения тригонометрических функций , – мол, всегда можно посмотреть в шпору с таблицей значений.

Если вы постоянно смотрите в таблицу со значениями тригонометрических формул, давайте избавляться от этой привычки!

Нас выручит ! Вы несколько раз поработаете с ним, и далее он у вас сам будет всплывать в голове. Чем он лучше таблицы? Да в таблице-то вы найдете ограниченное число значений, а на круге – ВСЕ!

К примеру, скажите, глядя в стандартную таблицу значений тригонометрических формул , чему равен синус, скажем, 300 градусов, или -45.

Никак?.. можно, конечно, подключить формулы приведения … А глядя на тригонометрический круг, легко можно ответить на такие вопросы. И вы скоро будете знать как!

А при решении тригонометрических уравнений и неравенств без тригонометрического круга – вообще никуда.

Знакомство с тригонометрическим кругом

Давайте по порядку.

Сначала выпишем вот такой ряд чисел:

А теперь такой:

И, наконец, такой:

Конечно, понятно, что, на самом-то деле, на первом месте стоит , на втором месте стоит , а на последнем – . То есть нас будет больше интересовать цепочка .

Но как красиво она получилась! В случае чего – восстановим эту «лесенку-чудесенку».

И зачем оно нам?

Эта цепочка – и есть основные значения синуса и косинуса в первой четверти.

Начертим в прямоугольной системе координат круг единичного радиуса (то есть радиус-то по длине берем любой, а его длину объявляем единичной).

От луча «0-Старт» откладываем в направлении стрелки (см. рис.) углы .

Получаем соответствующие точки на круге. Так вот если спроецировать точки на каждую из осей, то мы выйдем как раз на значения из указанной выше цепочки.

Это почему же, спросите вы?

Не будем разбирать все. Рассмотрим принцип , который позволит справиться и с другими, аналогичными ситуациями.

Треугольник АОВ – прямоугольный, в нем . А мы знаем, что против угла в лежит катет вдвое меньший гипотенузы (гипотенуза у нас = радиусу круга, то есть 1).

Значит, АВ= (а следовательно, и ОМ=). А по теореме Пифагора

Надеюсь, уже что-то становится понятно?

Так вот точка В и будет соответствовать значению , а точка М – значению

Аналогично с остальными значениями первой четверти.

Как вы понимаете, привычная нам ось (ox) будет осью косинусов , а ось (oy) – осью синусов . позже.

Слева от нуля по оси косинусов (ниже нуля по оси синусов) будут, конечно, отрицательные значения.

Итак, вот он, ВСЕМОГУЩИЙ , без которого никуда в тригонометрии.

А вот как пользоваться тригонометрическим кругом, мы поговорим в .

Позволяют установить ряд характерных результатов – свойств синуса, косинуса, тангенса и котангенса . В этой статье мы рассмотрим три основных свойства. Первое из них указывает знаки синуса, косинуса, тангенса и котангенса угла α в зависимости от того, углом какой координатной четверти является α . Дальше мы рассмотрим свойство периодичности, устанавливающее неизменность значений синуса, косинуса, тангенса и котангенса угла α при изменении этого угла на целое число оборотов. Третье свойство выражает зависимость между значениями синуса, косинуса, тангенса и котангенса противоположных углов α и −α .

Если же Вас интересуют свойства функций синуса, косинуса, тангенса и котангенса, то их можно изучить в соответствующем разделе статьи .

Навигация по странице.

Знаки синуса, косинуса, тангенса и котангенса по четвертям

Ниже в этом пункте будет встречаться фраза «угол I , II , III и IV координатной четверти». Объясним, что же это за углы.

Возьмем единичную окружность , отметим на ней начальную точку А(1, 0) , и повернем ее вокруг точки O на угол α , при этом будем считать, что мы попадем в точку A 1 (x, y) .

Говорят, что угол α является углом I , II , III , IV координатной четверти , если точка А 1 лежит в I , II , III , IV четверти соответственно; если же угол α таков, что точка A 1 лежит на любой из координатных прямых Ox или Oy , то этот угол не принадлежит ни одной из четырех четвертей.

Для наглядности приведем графическую иллюстрацию. На чертежах ниже изображены углы поворота 30 , −210 , 585 и −45 градусов, которые являются углами I , II , III и IV координатных четвертей соответственно.

Углы 0, ±90, ±180, ±270, ±360, … градусов не принадлежат ни одной из координатных четвертей.

Теперь разберемся, какие знаки имеют значения синуса, косинуса, тангенса и котангенса угла поворота α в зависимости от того, углом какой четверти является α .

Для синуса и косинуса это сделать просто.

По определению синус угла α - это ордината точки А 1 . Очевидно, что в I и II координатных четвертях она положительна, а в III и IV четвертях – отрицательна. Таким образом, синус угла α имеет знак плюс в I и II четвертях, а знак минус – в III и VI четвертях.

В свою очередь косинус угла α - это абсцисса точки A 1 . В I и IV четвертях она положительна, а во II и III четвертях – отрицательна. Следовательно, значения косинуса угла α в I и IV четвертях положительны, а во II и III четвертях – отрицательны.

Чтобы определить знаки по четвертям тангенса и котангенса нужно вспомнить их определения: тангенс – это отношение ординаты точки A 1 к абсциссе, а котангенс – отношение абсциссы точки A 1 к ординате. Тогда из правил деления чисел с одинаковыми и разными знаками следует, что тангенс и котангенс имеют знак плюс, когда знаки абсциссы и ординаты точки A 1 одинаковые, и имеют знак минус – когда знаки абсциссы и ординаты точки A 1 различны. Следовательно, тангенс и котангенс угла имеют знак + в I и III координатных четвертях, и знак минус – во II и IV четвертях.

Действительно, например, в первой четверти и абсцисса x , и ордината y точки A 1 положительны, тогда и частное x/y , и частное y/x – положительно, следовательно, тангенс и котангенс имеют знаки + . А во второй четверти абсцисса x – отрицательна, а ордината y – положительна, поэтому и x/y , и y/x – отрицательны, откуда тангенс и котангенс имеют знак минус.

Переходим к следующему свойству синуса, косинуса, тангенса и котангенса.

Свойство периодичности

Сейчас мы разберем, пожалуй, самое очевидное свойство синуса, косинуса, тангенса и котангенса угла. Оно состоит в следующем: при изменении угла на целое число полных оборотов значения синуса, косинуса, тангенса и котангенса этого угла не изменяются.

Это и понятно: при изменении угла на целое число оборотов мы из начальной точки А всегда будем попадать в точку А 1 на единичной окружности, следовательно, значения синуса, косинуса, тангенса и котангенса остаются неизменными, так как неизменны координаты точки A 1 .

С помощью формул рассматриваемое свойство синуса, косинуса, тангенса и котангенса можно записать так: sin(α+2·π·z)=sinα , cos(α+2·π·z)=cosα , tg(α+2·π·z)=tgα , ctg(α+2·π·z)=ctgα , где α - угол поворота в радианах, z – любое , абсолютная величина которого указывает количество полных оборотов, на которые изменяется угол α , а знак числа z указывает направление поворота.

Если же угол поворота α задан в градусах, то указанные формулы перепишутся в виде sin(α+360°·z)=sinα , cos(α+360°·z)=cosα , tg(α+360°·z)=tgα , ctg(α+360°·z)=ctgα .

Приведем примеры использования этого свойства. Например, , так как , а . Вот еще пример: или .

Это свойство вместе с формулами приведения очень часто используется при вычислении значений синуса, косинуса, тангенса и котангенса «больших» углов.

Рассмотренное свойство синуса, косинуса, тангенса и котангенса иногда называют свойством периодичности.

Свойства синусов, косинусов, тангенсов и котангенсов противоположных углов

Пусть А 1 – точка, полученная в результате поворота начальной точки А(1, 0) вокруг точки O на угол α , а точка А 2 – это результат поворота точки А на угол −α , противоположный углу α .

Свойство синусов, косинусов, тангенсов и котангенсов противоположных углов базируется на достаточно очевидном факте: упомянутые выше точки А 1 и А 2 либо совпадают (при ), либо располагаются симметрично относительно оси Ox . То есть, если точка A 1 имеет координаты (x, y) , то точка А 2 будет иметь координаты (x, −y) . Отсюда по определениям синуса, косинуса, тангенса и котангенса записываем равенства и .
Сопоставляя их, приходим к соотношениям между синусами, косинусами, тангенсами и котангенсами противоположных углов α и −α вида .
Это и есть рассматриваемое свойство в виде формул.

Приведем примеры использования этого свойства. Например, справедливы равенства и .

Остается лишь заметить, что свойство синусов, косинусов, тангенсов и котангенсов противоположных углов, как и предыдущее свойство, часто используется при вычислении значений синуса, косинуса, тангенса и котангенса, и позволяет полностью уйти от отрицательных углов.

Список литературы.

• Алгебра: Учеб. для 9 кл. сред. шк./Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под ред. С. А. Теляковского.- М.: Просвещение, 1990.- 272 с.: ил.- ISBN 5-09-002727-7
• Алгебра и начала анализа: Учеб. для 10-11 кл. общеобразоват. учреждений / А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др.; Под ред. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.- 384 с.: ил.- ISBN 5-09-013651-3.
• Башмаков М. И. Алгебра и начала анализа: Учеб. для 10-11 кл. сред. шк. - 3-е изд. - М.: Просвещение, 1993. - 351 с.: ил. - ISBN 5-09-004617-4.
• Гусев В. А., Мордкович А. Г. Математика (пособие для поступающих в техникумы): Учеб. пособие.- М.; Высш. шк., 1984.-351 с., ил.

Разнообразны. Некоторые из них - о том, в каких четвертях косинус положительный и отрицательный, в каких четвертях синус положительный и отрицательный. Все оказывается просто, если знаешь, как вычислить значение данных функций в разных углах и знаком с принципом построения функций на графике.

Какие значения косинуса

Если рассматривать то мы имеем следующее соотношение сторон, которое его определяет: косинусом угла а является отношение прилегающего катета ВС к гипотенузе АВ (рис. 1): cos a = ВС/АВ.

С помощью этого же треугольника можно найти синус угла, тангенс и котангенс. Синусом будет соотношение противоположного к углу катета АС к гипотенузе АВ. Тангенс угла находится, если синус искомого угла разделить на косинус того же угла; подставив соответственные формулы нахождения синуса и косинуса, получим, что tg a = АС/ВС. Котангенс, как обратная к тангенсу функция, будет находиться так: ctg a = ВС/АС.

То есть, при одинаковых значениях угла обнаружилось, что в прямоугольном треугольнике соотношение сторон всегда одинаковое. Казалось бы, стало ясно, откуда эти значения, но почему получаются отрицательные числа?

Для этого нужно рассматривать треугольник в декартовой системе координат, где присутствуют как положительные, так и отрицательные значения.

Наглядно про четверти, где какая

Что такое декартовые координаты? Если говорить о двумерном пространстве, мы имеем две направленные прямые, которые пересекаются в точке О - это ось абсцисс (Ох) и ось ординат (Оу). От точки О в направлении прямой располагаются положительные числа, а в обратную сторону - отрицательные. От этого, в конечном итоге, напрямую зависит, в каких четвертях косинус положительный, а в каких, соответственно, отрицательный.

Первая четверть

Если разместить прямоугольный треугольник в первой четверти (от 0 о до 90 о), где ось х и у имеют положительные значения (отрезки АО и ВО лежат на осях там, где значения имеют знак "+"), то что синус, что косинус тоже будут иметь положительные значения, и им присвоено значение со знаком «плюс». Но что происходит, если переместить треугольник во вторую четверть (от 90 о до 180 о)?

Вторая четверть

Видим, что по оси у катет АО получил отрицательное значение. Косинус угла a теперь имеет в соотношении эту сторону с минусом, потому и итоговое его значение становится отрицательным. Выходит, что то, в какой четверти косинус положительный, зависит от размещения треугольника в системе декартовых координат. И в этом случае косинус угла получает отрицательное значение. А вот для синуса ничего не изменилось, ведь для определения его знака нужна сторона ОВ, которая осталась в данном случае со знаком плюс. Подведем итог по первым двум четвертям.

Чтобы выяснить, в каких четвертях косинус положительный, а в каких отрицательный (а также синус и другие тригонометрические функции), необходимо смотреть на то, какой знак присвоен тому или иному катету. Для косинуса угла a важен катет АО, для синуса - ОВ.

Первая четверть пока что стала единственной, отвечающей на вопрос: «В каких четвертях синус и косинус положительный одновременно?». Посмотрим далее, будут ли еще совпадения по знаку этих двух функций.

Во второй четверти катет АО стал иметь отрицательное значение, а значит и косинус стал отрицательным. Для синуса сохранено положительное значение.

Третья четверть

Теперь оба катета АО и ОВ стали отрицательными. Вспомним соотношения для косинуса и синуса:

Cos a = АО/АВ;

Sin a = ВО/АВ.

АВ всегда имеет положительный знак в данной системе координат, так как не направлена ни в одну из двух определённых осями сторон. А вот катеты стали отрицательными, а значит и результат для обоих функций тоже отрицательный, ведь если производить операции умножения или деления с числами, среди которых одно и только одно имеет знак «минус», то результат тоже будет с этим знаком.

Итог на данном этапе:

1) В какой четверти косинус положительный? В первой из трех.

2) В какой четверти синус положительный? В первой и второй из трёх.

Четвёртая четверть (от 270 о до 360 о)

Здесь катет АО вновь приобретает знак «плюс», а значит и косинус тоже.

Для синуса дела всё еще «отрицательны», ведь катет ОВ остался ниже начальной точки О.

Выводы

Для того чтобы понимать, в каких четвертях косинус положительный, отрицательный и т.д., нужно запомнить соотношение для вычисления косинуса: прилегающий к углу катет, деленный на гипотенузу. Некоторые учителя предлагают запомнить так: к(осинус) = (к) углу. Если запомнить этот «чит», то автоматически понимаешь, что синус - это отношение противоположного к углу катета к гипотенузе.

Запомнить, в каких четвертях косинус положительный, а в каких отрицательный, довольно сложно. Тригонометрических функций много, и все они имеют свои значения. Но все же, как итог: положительные значения для синуса - 1, 2 четверти (от 0 о до 180 о); для косинуса 1, 4 четверти (от 0 о до 90 о и от 270 о до 360 о). В остальных четвертях функции имеют значения с минусом.

Возможно, кому-то будет легче запомнить, где какой знак, по изображению функции.

Для синуса видно, что от нуля до 180 о гребень находится над линией значений sin(x), значит и функция здесь положительна. Для косинуса так же: в какой четверти косинус положительный (фото 7), а в какой отрицательный видно по перемещению линии над и под осью cos(x). Как итог, мы можем запомнить два способа определения знака функций синус, косинус:

1. По мнимому кругу с радиусом равным единице (хотя, на самом деле, не важно, какой радиус у круга, но в учебниках чаще всего приводят именно такой пример; это облегчает восприятие, но в то же время, если не оговориться, что это не суть важно, дети могут запутаться).

2. По изображению зависимости функции по (х) от самого аргумента х, как на последнем рисунке.

С помощью первого способа можно ПОНЯТЬ, от чего именно зависит знак, и мы подробно разъяснили это выше. Рисунок 7, построенный по этим данным, как нельзя лучше визуализирует полученную функцию и ее знакопринадлежность.